Deciphering Selectivity Mechanism of BRD9 and TAF1(2) toward Inhibitors Based on Multiple Short Molecular Dynamics Simulations and MM-GBSA Calculations
Abstract
1. Introduction
2. Results and Discussion
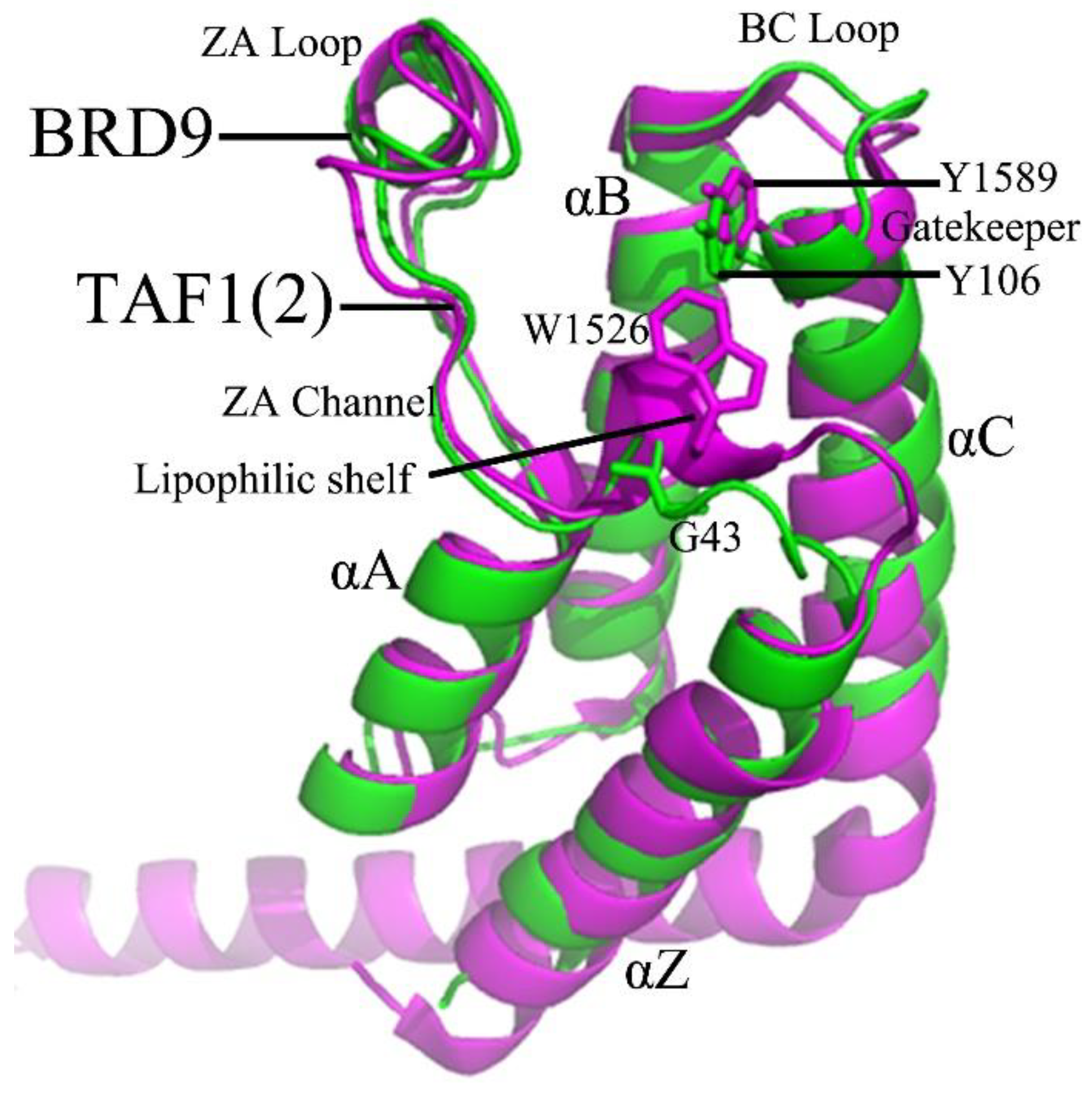
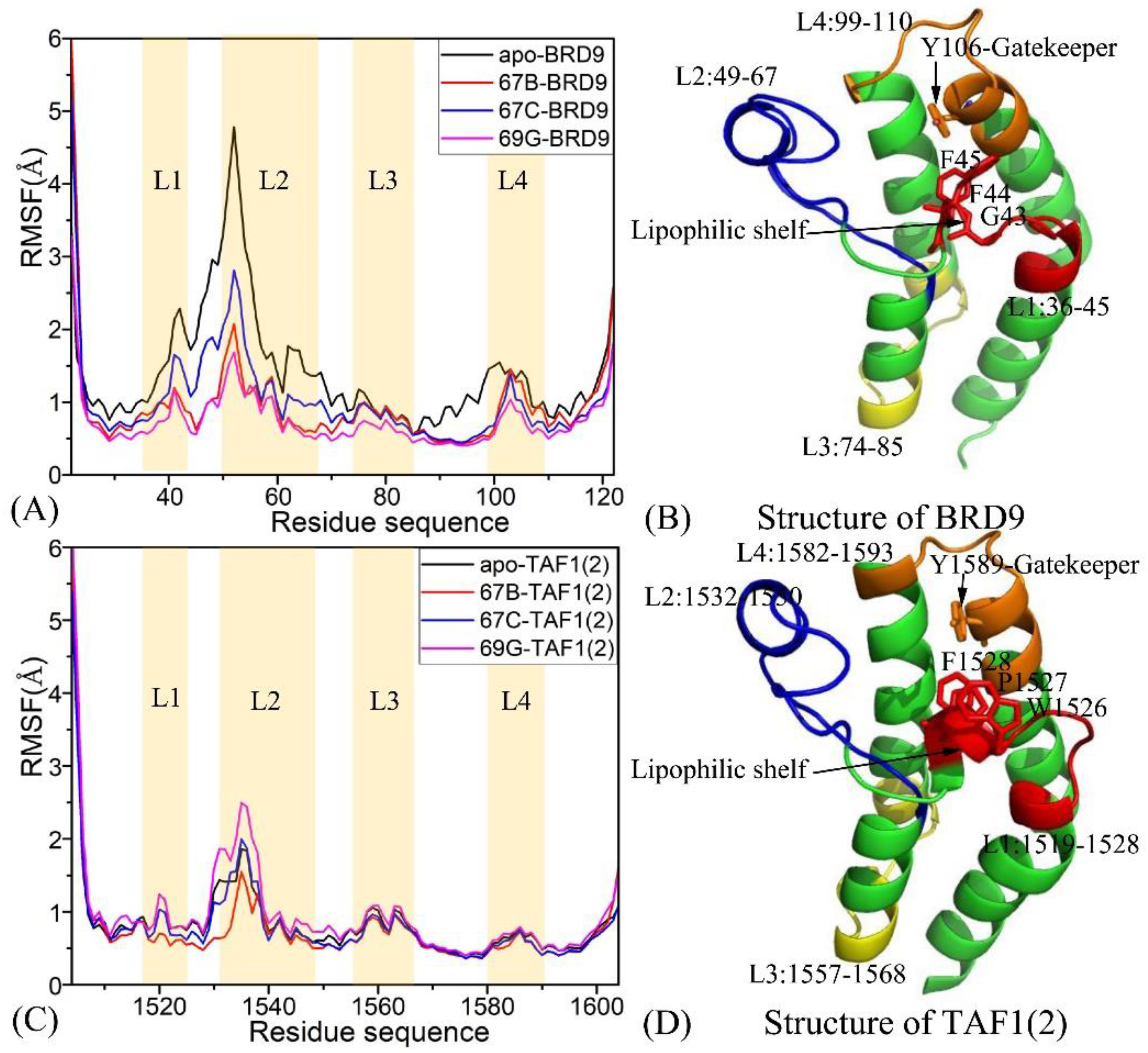
2.1. Structural Flexibilities and Fluctuations of BRD9 and TAF1(2)
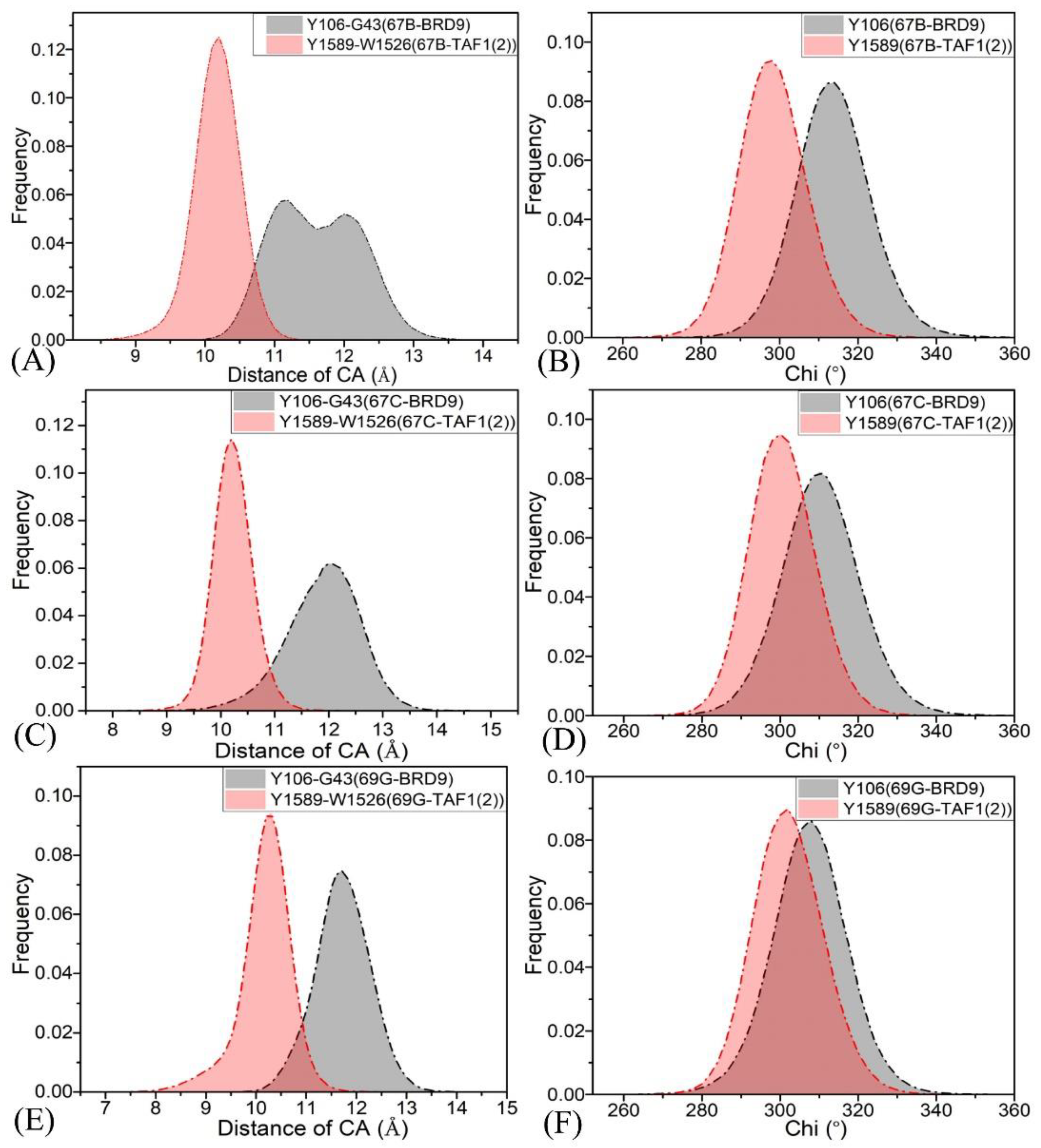
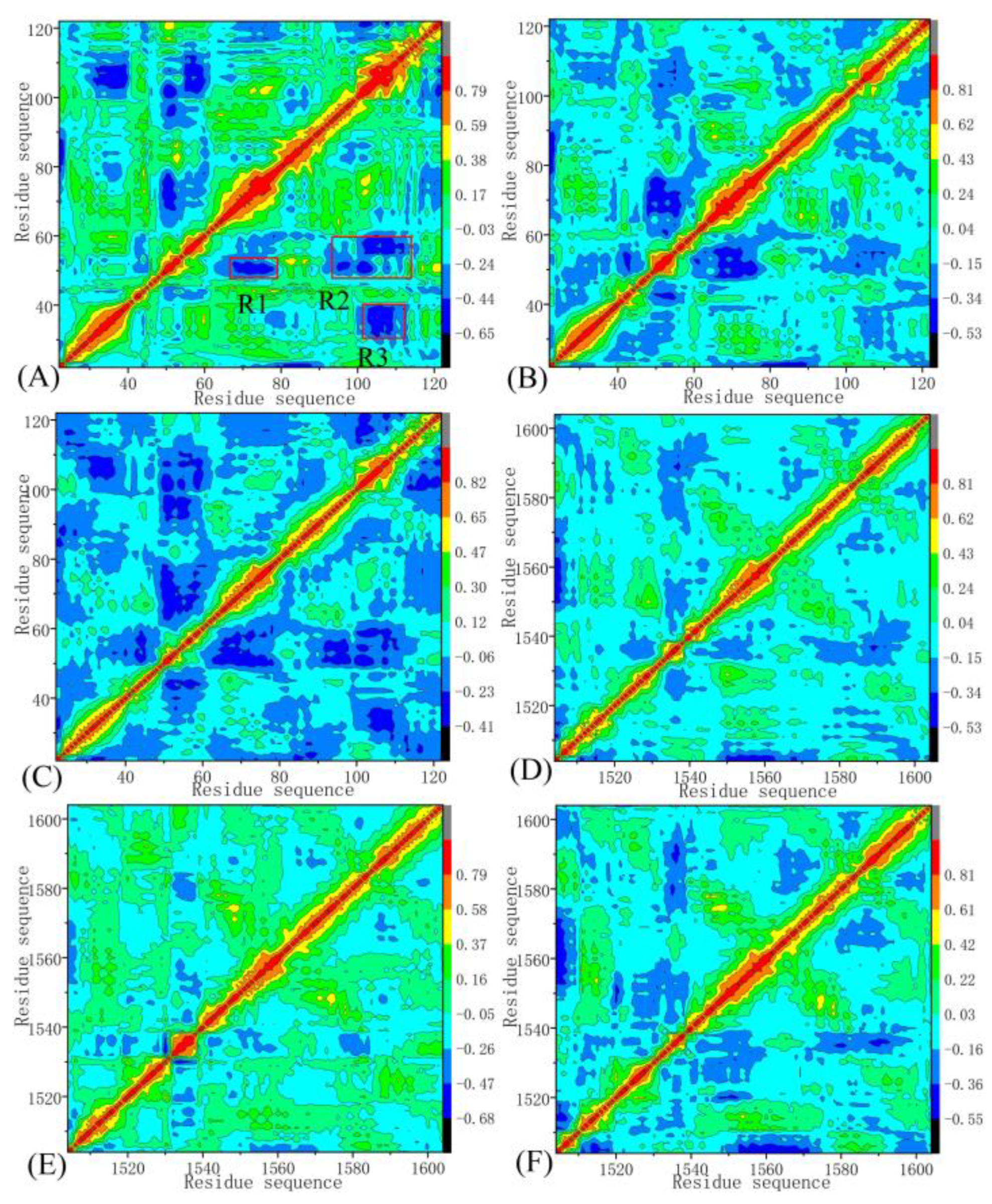
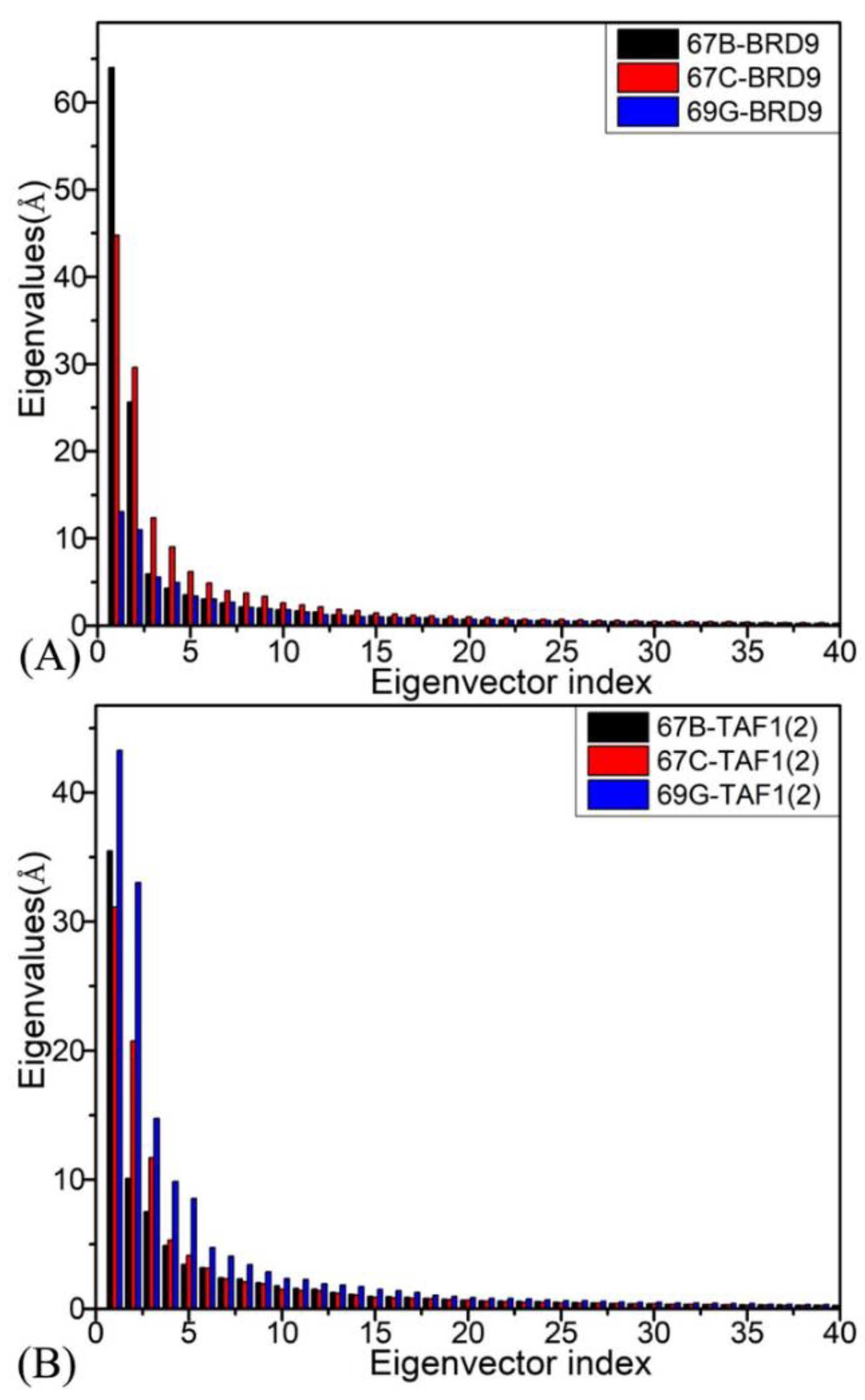
2.2. Internal Dynamics of BRD9 and TAF1(2)
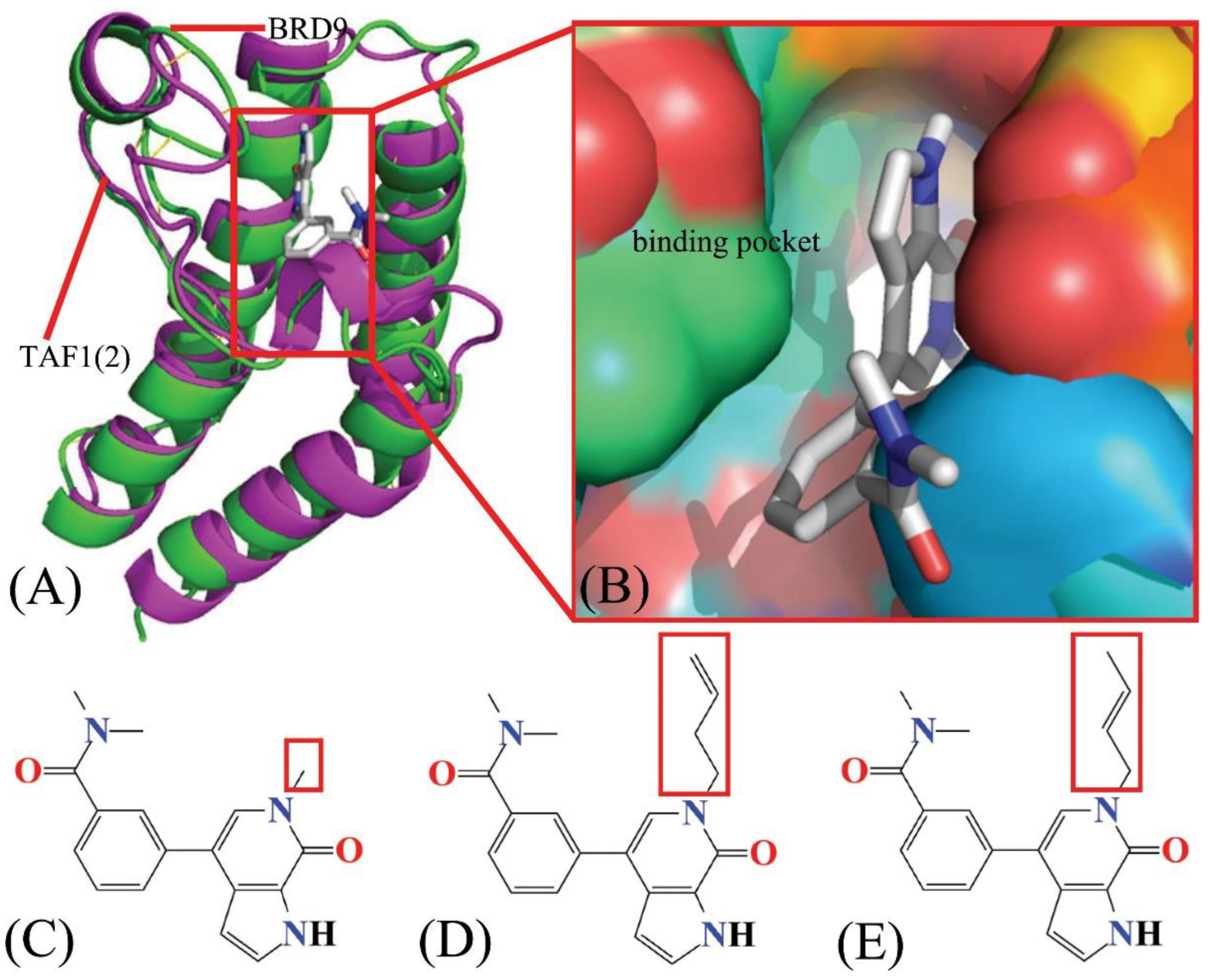
2.3. Binding Ability of Inhibitors to BRD9 and TAF1(2)
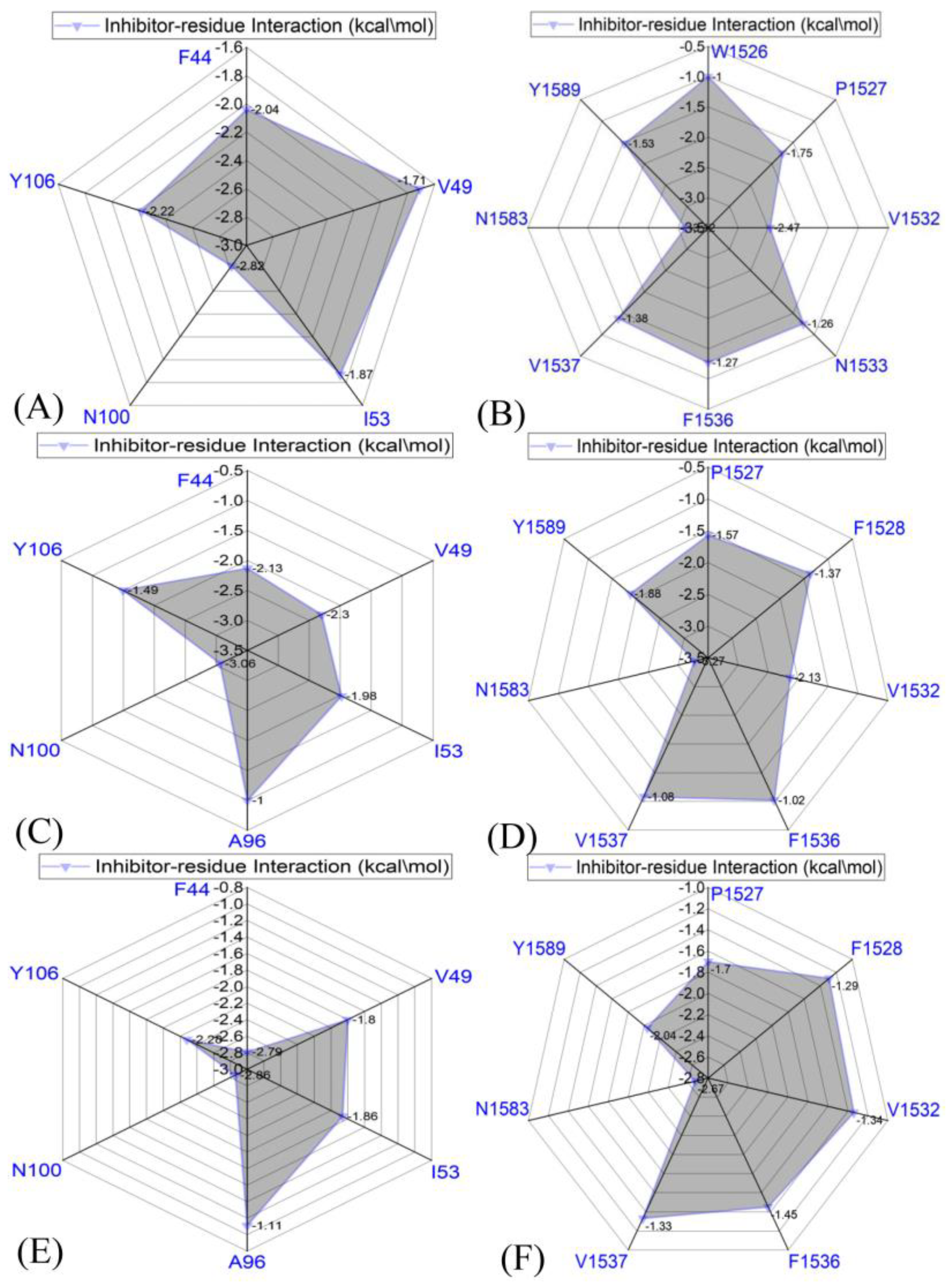
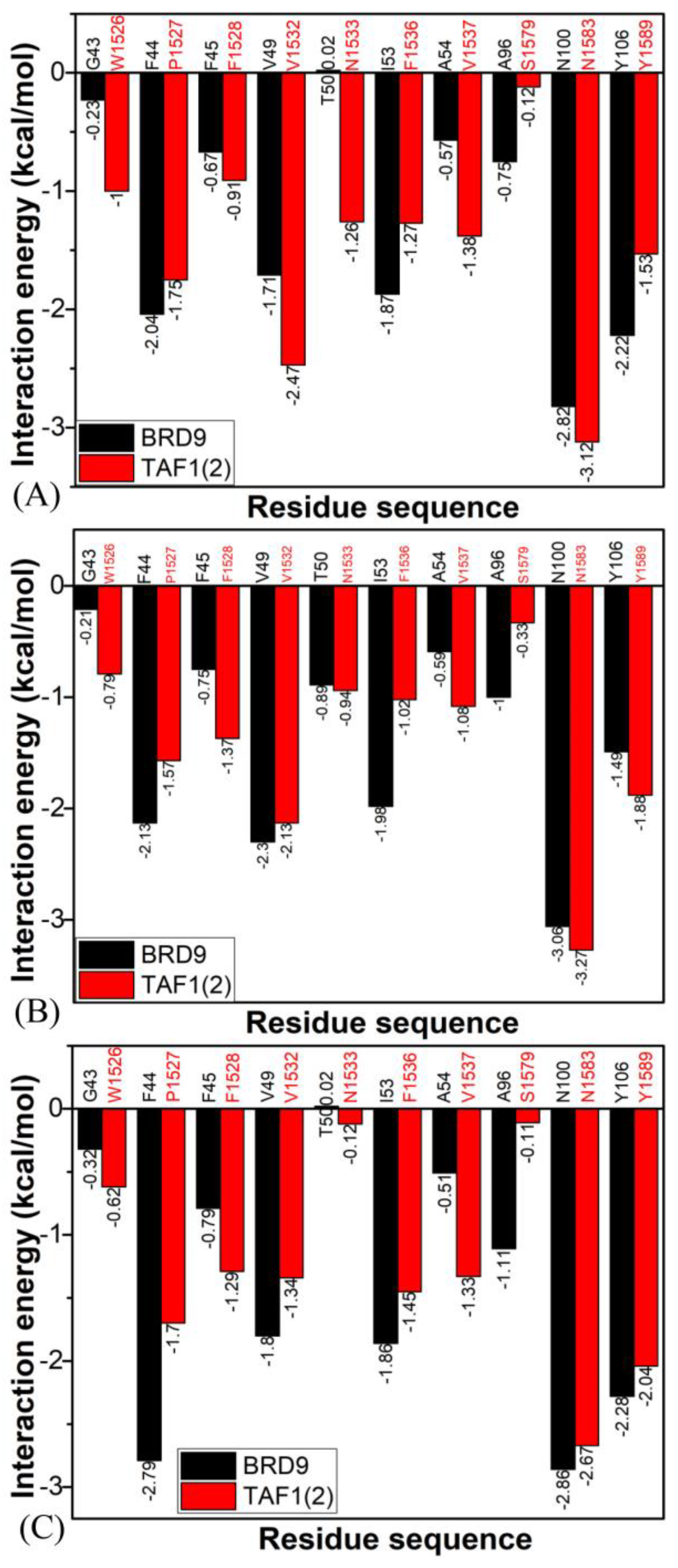
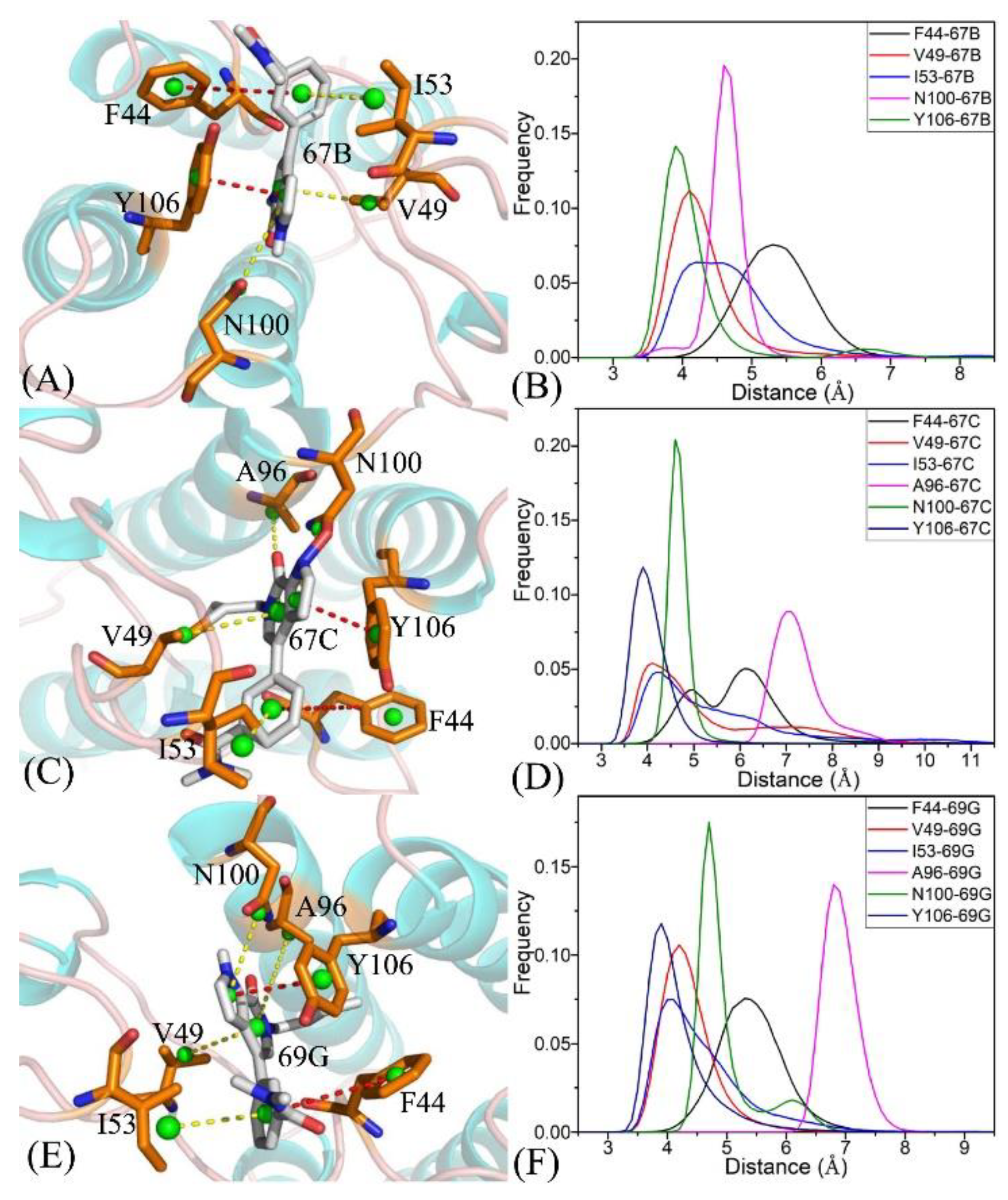
2.4. Binding Selectivity Probed by Ligand–Residue Interactions
2.4.1. Bound BRD9 against the 67B-Bound TAF1(2)
2.4.2. 67C-Bound BRD9 Versus the 67C-Bound TAF1(2)
2.4.3. The 69G-Bound BRD9 over the 69G-Bound TAF1(2)
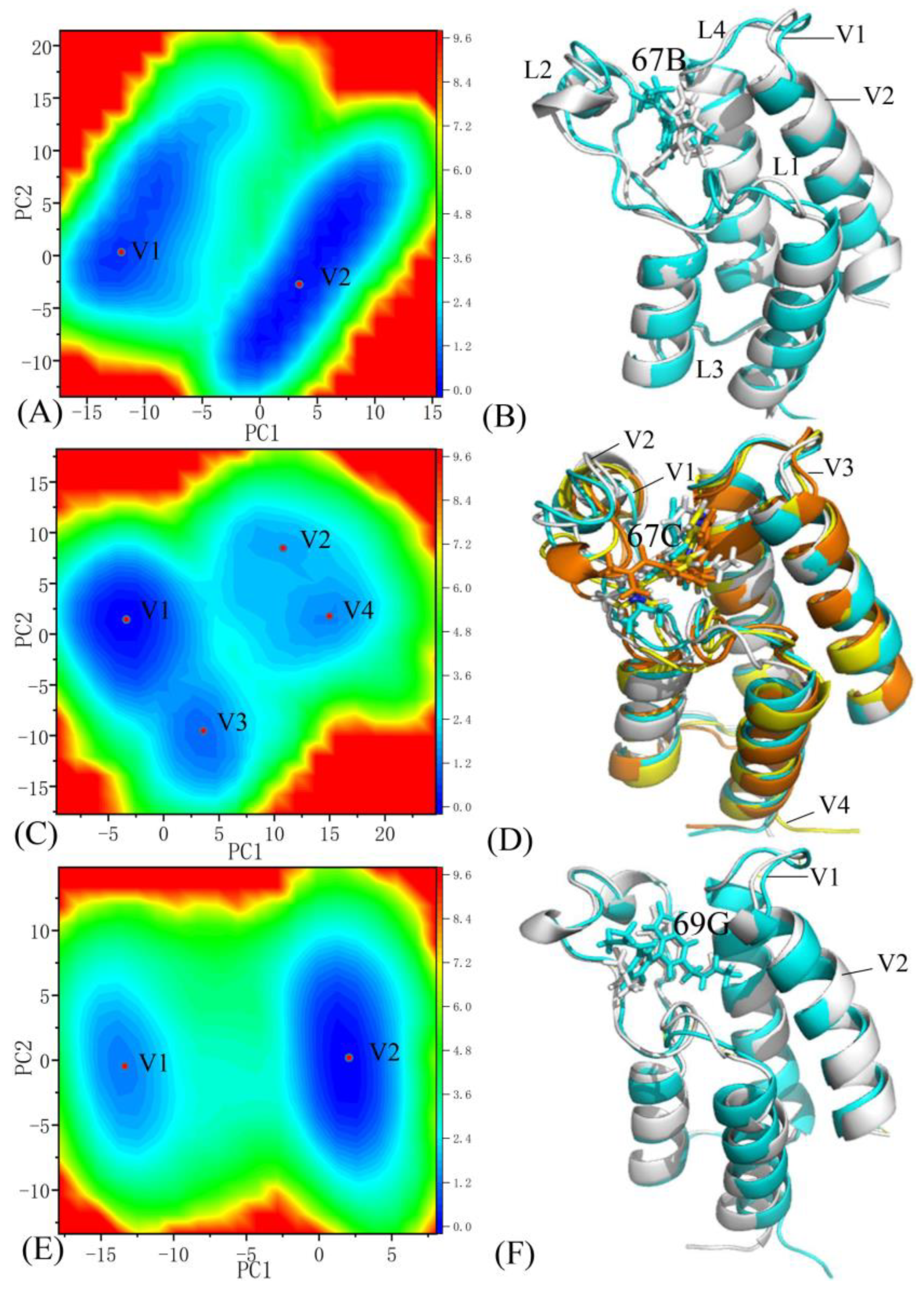
2.5. Alterations in the Free Energy Landscapes of BRD9 and TAF1(2) Caused by Inhibitor Bindings
2.5.1. The 67B-Associated BRD9 against the 67B-Bound TAF1(2)
2.5.2. The 67C-Associated BRD9 versus the 67C-Bound TAF1(2)
2.5.3. The 69G-Bound BRD9 over the 69G-Associated TAF1(2)
3. Materials and Methods
3.1. Modeling Simulated Systems
3.2. Multiple Short Molecular Dynamics (MSMD) Simulations
3.3. MM-GBSA Free Energy Computations and Decomposition
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Wojcicki, A.; Kasowski, M.M.; Sakamoto, K.M.; Lacayo, N. Metabolomics in acute myeloid leukemia. Mol. Genet. Metab. 2020, 130, 230–238. [Google Scholar] [CrossRef] [PubMed]
- Egan, G.; Chopra, Y.; Mourad, S.; Chiang, K.; Hitzler, J. Treatment of acute myeloid leukemia in children: A practical perspective. Pediatr. Blood Cancer 2021, 68, e28979. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Liu, L.; Zhang, R.; Wan, Y.; Gong, X.; Zhang, L.; Yang, W.; Chen, X.; Zou, Y.; Chen, Y.; et al. Development and validation of a prognostic scoring model to risk stratify childhood acute myeloid leukaemia. Br. J. Haematol. 2022, 198, 1041–1050. [Google Scholar] [CrossRef] [PubMed]
- Kharenko, O.A.; Patel, R.G.; Brown, S.D.; Calosing, C.; White, A.; Lakshminarasimhan, D.; Suto, R.K.; Duffy, B.C.; Kitchen, D.B.; McLure, K.G.; et al. Design and Characterization of Novel Covalent Bromodomain and Ex-tra-Terminal Domain (BET) Inhibitors Targeting a Methionine. J. Med. Chem. 2018, 61, 8202–8211. [Google Scholar] [CrossRef]
- Yadav, M.; Abdalla, M.; Madhavi, M.; Chopra, I.; Bhrdwaj, A.; Soni, L.; Shaheen, U.; Prajapati, L.; Sharma, M.; Sikarwar, M.S.; et al. Structure-Based Virtual Screening, Molecular Docking, Molecular Dynamics Simulation and Pharmacokinetic modelling of Cyclooxygenase-2 (COX-2) inhibitor for the clinical treatment of Colorectal Cancer. Mol. Simulat. 2022, 48, 1081–1101. [Google Scholar] [CrossRef]
- Yalçin-Özkat, G. Computational studies with flavonoids and terpenoids as BRPF1 inhibitors: In silico biological activity prediction, molecular docking, molecular dynamics simulations, MM/PBSA calculations. SAR. QSAR. Environ. Res. 2022, 33, 533–550. [Google Scholar] [CrossRef]
- Xu, L.; Mu, X.; Liu, M.; Wang, Z.; Shen, C.; Mu, Q.; Feng, B.; Xu, Y.; Hou, T.; Gao, L.; et al. Novel thieno[2,3-b]quinoline-procaine hybrid molecules: A new class of allosteric SHP-1 activators evolved from PTP1B inhibitors. Chin. Chem. Lett. 2022, 108063. [Google Scholar] [CrossRef]
- Li, X.; Wu, Y.; Tian, G.; Jiang, Y.; Liu, Z.; Meng, X.; Bao, X.; Feng, L.; Sun, H.; Deng, H.; et al. Chemical Proteomic Pro-filing of Bromodomains Enables the Wide-Spectrum Evaluation of Bromodomain Inhibitors in Living Cells. J. Am. Chem. Soc. 2019, 141, 11497–11505. [Google Scholar] [CrossRef] [PubMed]
- Prieto-Martínez, F.D.; Medina-Franco, J.L. Chapter Five-Current advances on the development of BET in-hibitors: Insights from computational methods. In Advances in Protein Chemistry and Structural Biology; Karabencheva-Christova, T., Christov, C., Eds.; Academic Press: Cambridge, MA, USA, 2020; Volume 122, pp. 127–180. [Google Scholar]
- Luo, D.; Tong, J.; Xiao, X.; Bian, S.; Zhang, X.; Wang, J.; Xu, H. Theoretically exploring selective-binding mechanisms of BRD4 through integrative computational approaches. SAR QSAR Environ. Res. 2021, 32, 985–1011. [Google Scholar] [CrossRef]
- Wang, S.; Shen, D.; Zhao, L.; Yuan, X.; Cheng, J.; Yu, B.; Zheng, Y.; Liu, H. Discovery of [1,2,4]triazolo[1,5-a]pyrimidine derivatives as new bromodomain-containing protein 4 (BRD4) inhibitors. Chin. Chem. Lett. 2020, 31, 418–422. [Google Scholar] [CrossRef]
- Hohmann, A.F.; Martin, L.J.; Minder, J.L.; Roe, J.-S.; Shi, J.; Steurer, S.; Bader, G.; McConnell, D.; Pearson, M.; Gerstberger, T.; et al. Sensitivity and engineered resistance of myeloid leukemia cells to BRD9 inhibition. Nat. Chem. Biol. 2016, 12, 672–679. [Google Scholar] [CrossRef] [PubMed]
- Del Gaudio, N.; Di Costanzo, A.; Liu, N.Q.; Conte, L.; Migliaccio, A.; Vermeulen, M.; Martens, J.H.A.; Stunnenberg, H.G.; Nebbioso, A.; Altucci, L. BRD9 binds cell type-specific chromatin regions regulating leukemic cell survival via STAT5 inhibition. Cell Death Dis. 2019, 10, 338. [Google Scholar] [CrossRef] [PubMed]
- Weisberg, E.; Chowdhury, B.; Meng, C.; Case, A.E.; Ni, W.; Garg, S.; Sattler, M.; Azab, A.K.; Sun, J.; Muz, B.; et al. BRD9 degraders as chemosensitizers in acute leukemia and multiple myeloma. Blood Cancer J. 2022, 12, 110. [Google Scholar] [CrossRef]
- Karim, M.R.; Shutz, Z.; Yang, L.; Chen, J.; Lopchuk, J.; Schönbrunn, E. Ligand-induced global conformational changes in TBP-associated factor 1 (TAF1) tandem bromodomains—A novel strategy for targeting the TAF1. Acta Crystallogr. Sect. A Found. Adv. 2021, 77, a40. [Google Scholar] [CrossRef]
- Xu, Y.; Man, N.; Karl, D.; Martinez, C.; Liu, F.; Sun, J.; Martinez, C.J.; Martin, G.M.; Beckedorff, F.; Lai, F.; et al. TAF1 plays a critical role in AML1-ETO driven leukemogenesis. Nat. Commun. 2019, 10, 4925. [Google Scholar] [CrossRef]
- Gudmundsson, S.; Wilbe, M.; Filipek-Górniok, B.; Molin, A.-M.; Ekvall, S.; Johansson, J.; Allalou, A.; Gylje, H.; Kalscheuer, V.M.; Ledin, J.; et al. TAF1, associated with intellectual disability in humans, is essential for em-bryogenesis and regulates neurodevelopmental processes in zebrafish. Sci. Rep. 2019, 9, 10730. [Google Scholar] [CrossRef] [PubMed]
- Remillard, D.; Buckley, D.L.; Seo, H.-S.; Ferguson, F.M.; Dhe-Paganon, S.; Bradner, J.E.; Gray, N.S. Dual Inhibition of TAF1 and BET Bromodomains from the BI-2536 Kinase Inhibitor Scaffold. ACS Med. Chem. Lett. 2019, 10, 1443–1449. [Google Scholar] [CrossRef]
- McKeown, M.R.; Shaw, D.L.; Fu, H.; Liu, S.; Xu, X.; Marineau, J.J.; Huang, Y.; Zhang, X.; Buckley, D.L.; Kadam, A.; et al. Biased Multicomponent Reactions to Develop Novel Bromodomain Inhibitors. J. Med. Chem. 2014, 57, 9019–9027. [Google Scholar] [CrossRef] [PubMed]
- Sdelci, S.; Lardeau, C.-H.; Tallant, C.; Klepsch, F.; Klaiber, B.; Bennett, J.; Rathert, P.; Schuster, M.; Penz, T.; Fedorov, O.; et al. Mapping the chemical chromatin reactivation landscape identifies BRD4-TAF1 cross-talk. Nat. Chem. Biol. 2016, 12, 504–510. [Google Scholar] [CrossRef]
- Dhalluin, C.; Carlson, J.E.; Zeng, L.; He, C.; Aggarwal, A.K.; Zhou, M.-M. Structure and ligand of a histone acetyltransferase bromodomain. Nature 1999, 399, 491–496. [Google Scholar] [CrossRef]
- Crawford, T.D.; Tsui, V.; Flynn, E.M.; Wang, S.; Taylor, A.M.; Côté, A.; Audia, J.E.; Beresini, M.H.; Burdick, D.J.; Cummings, R.; et al. Diving into the Water: Inducible Binding Conformations for BRD4, TAF1(2), BRD9, and CECR2 Bromodomains. J. Med. Chem. 2016, 59, 5391–5402. [Google Scholar] [CrossRef]
- Jeanmougin, F.; Wurtz, J.-M.; Le Douarin, B.; Chambon, P.; Losson, R. The bromodomain revisited. Trends Biochem. Sci. 1997, 22, 151–153. [Google Scholar] [CrossRef] [PubMed]
- Mazurek, A.H.; Szeleszczuk, L.; Gubica, T. Application of Molecular Dynamics Simulations in the Analysis of Cyclodextrin Complexes. Int. J. Mol. Sci. 2021, 22, 9422. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Yang, F.; Wang, P.; Zheng, G.; Chen, Y.; Yao, X.; Zhu, F. What Contributes to Serotonin–Norepinephrine Reuptake Inhibitors’ Dual-Targeting Mechanism? The Key Role of Transmembrane Domain 6 in Human Serotonin and Norepinephrine Transporters Revealed by Molecular Dynamics Simulation. ACS Chem. Neurosci. 2018, 9, 1128–1140. [Google Scholar] [CrossRef]
- Hou, T.; Yu, R. Molecular Dynamics and Free Energy Studies on the Wild-type and Double Mutant HIV-1 Protease Complexed with Amprenavir and Two Amprenavir-Related Inhibitors: Mechanism for Binding and Drug Resistance. J. Med. Chem. 2007, 50, 1177–1188. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.-J.; Pang, X.-Q.; Zhang, X.; Han, K.-L. Molecular dynamics simulation reveals preorganization of the chloroplast FtsY towards complex formation induced by GTP binding. J. Struct. Biol. 2011, 173, 57–66. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Sun, H.; Zhao, J.; Wang, Q. Theoretical insight into molecular mechanisms of inhibitor bindings to bromodomain-containing protein 4 using molecular dynamics simulations and calculations of binding free energies. Chem. Phys. Lett. 2019, 736, 136785. [Google Scholar] [CrossRef]
- Sun, Z.; Gong, Z.; Xia, F.; He, X. Ion dynamics and selectivity of Nav channels from molecular dynamics simulation. Chem. Phys. 2021, 548, 111245. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Yin, B.; Pang, L.; Wang, W.; Zhu, W. Molecular Mechanism of Binding Selectivity of Inhibitors toward BACE1 and BACE2 Revealed by Multiple Short Molecular Dynamics Simulations and Free-Energy Predictions. ACS Chem. Neurosci. 2019, 10, 4303–4318. [Google Scholar] [CrossRef]
- Grant, B.J.; Gorfe, A.A.; McCammon, J.A. Ras Conformational Switching: Simulating Nucleotide-Dependent Conformational Transitions with Accelerated Molecular Dynamics. PLoS Comput. Biol. 2009, 5, e1000325. [Google Scholar] [CrossRef]
- Duan, L.; Guo, X.; Cong, Y.; Feng, G.; Li, Y.; Zhang, J.Z.H. Accelerated Molecular Dynamics Simulation for Helical Proteins Folding in Explicit Water. Front. Chem. 2019, 7, 540. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Yin, B.; Wang, W.; Sun, H. Effects of Disulfide Bonds on Binding of Inhibitors to β-Amyloid Cleaving Enzyme 1 Decoded by Multiple Replica Accelerated Molecular Dynamics Simulations. ACS Chem. Neurosci. 2020, 11, 1811–1826. [Google Scholar] [CrossRef]
- Miao, Y.; Feher, V.A.; McCammon, J.A. Gaussian Accelerated Molecular Dynamics: Unconstrained Enhanced Sampling and Free Energy Calculation. J. Chem. Theory Comput. 2015, 11, 3584–3595. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Miao, Y. Mechanistic Insights into Specific G Protein Interactions with Adenosine Receptors. J. Phys. Chem. B 2019, 123, 6462–6473. [Google Scholar] [CrossRef]
- Wang, J.; Miao, Y. Peptide Gaussian accelerated molecular dynamics (Pep-GaMD): Enhanced sampling and free energy and kinetics calculations of peptide binding. J. Chem. Phys. 2020, 153, 154109. [Google Scholar] [CrossRef]
- An, X.; Bai, Q.; Bing, Z.; Liu, H.; Zhang, Q.; Liu, H.; Yao, X. Revealing the Positive Binding Cooperativity Mechanism between the Orthosteric and the Allosteric Antagonists of CCR2 by Metadynamics and Gaussian Accelerated Molecular Dynamics Simulations. ACS Chem. Neurosci. 2020, 11, 628–637. [Google Scholar] [CrossRef]
- Wang, J.; Arantes, P.R.; Bhattarai, A.; Hsu, R.V.; Pawnikar, S.; Huang, Y.-M.M.; Palermo, G.; Miao, Y. Gaussian accelerated molecular dynamics: Principles and applications. WIREs Comput. Mol. Sci. 2021, 11, e1521. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, W.; Sun, H.; Pang, L.; Bao, H. Binding mechanism of inhibitors to p38α MAP kinase deciphered by using multiple replica Gaussian accelerated molecular dynamics and calculations of binding free energies. Comput. Biol. Med. 2021, 134, 104485. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, S.; Wang, W.; Sun, H.; Zhang, Q.; Liu, X. Binding of Inhibitors to BACE1 Affected by pH-Dependent Protonation: An Exploration from Multiple Replica Gaussian Accelerated Molecular Dynamics and MM-GBSA Calculations. ACS Chemi. Neurosci. 2021, 12, 2591–2607. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, L.; Wang, W.; Sun, H.; Pang, L.; Bao, H. Conformational transformation of switch domains in GDP/K-Ras induced by G13 mutants: An investigation through Gaussian accelerated molecular dynamics simulations and principal component analysis. Comput. Biol. Med. 2021, 135, 104639. [Google Scholar] [CrossRef] [PubMed]
- Ha, Y.; Jang, M.; Lee, S.; Lee, J.-Y.; Lee, W.C.; Bae, S.; Kang, J.; Han, M.; Kim, Y. Identification of inhibitor binding hotspots in Acinetobacter baumannii β-ketoacyl acyl carrier protein synthase III using molecular dynamics simulation. J. Mol. Graph. Model. 2020, 100, 107669. [Google Scholar] [CrossRef]
- Mou, L.; Ma, Z.; Meng, X.; Li, W.; Liang, S.; Chen, X. Exploration of the selective binding mechanism of GSK3β via molecular modeling and molecular dynamics simulation studies. Med. Chem. Res. 2020, 29, 690–698. [Google Scholar] [CrossRef]
- Sun, Z.; Huai, Z.; He, Q.; Liu, Z. A General Picture of Cucurbit[8]uril Host–Guest Binding. J. Chem. Inf. Model. 2021, 61, 6107–6134. [Google Scholar] [CrossRef]
- Yan, F.; Liu, X.; Zhang, S.; Su, J.; Zhang, Q.; Chen, J. Molecular Dynamics Exploration of Selectivity of Dual Inhibitors 5M7, 65X, and 65Z toward Fatty Acid Binding Proteins 4 and 5. Int. J. Mol. Sci. 2018, 19, 2496. [Google Scholar] [CrossRef]
- Wu, S.; Wang, L.; Zhang, L.; Xu, X.; Zhao, J. Molecular dynamics insights into binding selectivity of inhibitors toward BRD4 and CBP. Chem. Phys. Lett. 2021, 769, 138435. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Zhao, J.; Yu, Y.; Kang, N.; Yang, Z. Theoretical exploration of the binding selectivity of inhib-itors to BRD7 and BRD9 with multiple short molecular dynamics simulations. RSC Adv. 2022, 12, 16663–16676. [Google Scholar] [CrossRef]
- Akher, F.B.; Farrokhzadeh, A.; Ravenscroft, N.; Kuttel, M.M. Deciphering the Mechanism of Binding Selectivity of Chlorofluoroacetamide-Based Covalent Inhibitors toward L858R/T790M Resistance Mutation. J. Chem. Inf. Model. 2022, 62, 997–1013. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wu, S.; Wang, L.; Yang, Z.; Zhao, J.; Zhang, L. Binding selectivity of inhibitors toward the first over the second bromodomain of BRD4: Theoretical insights from free energy calculations and multiple short molecular dynamics simulations. RSC Adv. 2020, 11, 745–759. [Google Scholar] [CrossRef]
- Zhu, M.; Song, L.T.; Liu, R.R.; Zhai, H.L.; Meng, Y.J.; Ren, C.L. Selective inhibition mechanism of nitroxoline to the BET family: Insight from molecular simulations. Life Sci. 2021, 270, 119141. [Google Scholar] [CrossRef]
- Shi, S.; Sui, K.; Liu, W.; Lei, Y.; Zhang, S.; Zhang, Q. Revealing binding selectivity of ligands toward murine double minute 2 and murine double minute X based on molecular dynamics simulations and binding free energy calculations. J. Biomol. Struct. Dyn. 2019, 38, 5081–5094. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, H.; Yu, L.; Sun, H.; Chen, Y.; Cai, Y.; Li, H.; Jin, J. Computational investigation of the selectivity mechanisms of PI3Kδ inhibition with marketed idelalisib: Combined molecular dynamics simulation and free energy calculation. Struct. Chem. 2020, 32, 699–707. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.F.; Zhang, L.L.; Sun, H.B.; Zhao, J. Molecular mechanism of inhibitor bindings to bromo-domain-containing protein 9 explored based on molecular dynamics simulations and calculations of binding free energies. SAR QSAR Environ. Res. 2020, 31, 149–170. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Liu, X.; Zhang, S.; Sun, J.; Zhang, Q.; Chen, J. Selective Mechanism of Inhibitors to Two Bromodomains of BRD4 Revealed by Multiple Replica Molecular Dynamics Simulations and Free Energy Analyses. Chin. J. Chem. Phys. 2023, 1–15. [Google Scholar] [CrossRef]
- Su, J.; Liu, X.; Zhang, S.; Yan, F.; Zhang, Q.; Chen, J. Insight into selective mechanism of class of I-BRD9 inhibitors toward BRD9 based on molecular dynamics simulations. Chem. Biol. Drug Des. 2018, 93, 163–176. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Liu, X.; Zhang, S.; Yan, F.; Zhang, Q.; Chen, J. A theoretical insight into selectivity of inhibitors toward two domains of bromodomain-containing protein 4 using molecular dynamics simulations. Chem. Biol. Drug Des. 2017, 91, 828–840. [Google Scholar] [CrossRef] [PubMed]
- Song, L.T.; Tu, J.; Liu, R.R.; Zhu, M.; Meng, Y.J.; Zhai, H.L. Molecular mechanism study of several inhibitors binding to BRD9 bromodomain based on molecular simulations. J. Biomol. Struct. Dyn. 2018, 37, 2970–2979. [Google Scholar] [CrossRef]
- Magno, A.; Steiner, S.; Caflisch, A. Mechanism and Kinetics of Acetyl-Lysine Binding to Bromodomains. J. Chem. Theory Comput. 2013, 9, 4225–4232. [Google Scholar] [CrossRef]
- Wang, L.; Lu, D.; Wang, Y.; Xu, X.; Zhong, P.; Yang, Z. Binding selectivity-dependent molecular mechanism of inhibitors towards CDK2 and CDK6 investigated by multiple short molecular dynamics and free energy landscapes. J. Enzym. Inhib. Med. Ch. 2023, 38, 84–99. [Google Scholar] [CrossRef]
- Chen, J.; Liu, X.; Zhang, S.; Chen, J.; Sun, H.; Zhang, L.; Zhang, Q. Molecular mechanism with regard to the binding selectivity of inhibitors toward FABP5 and FABP7 explored by multiple short molecular dynamics simulations and free energy analyses. Phys. Chem. Chem. Phys. 2019, 22, 2262–2275. [Google Scholar] [CrossRef]
- Li, M.; Liu, X.; Zhang, S.; Liang, S.; Zhang, Q.; Chen, J. Deciphering the binding mechanism of inhibitors of the SARS-CoV-2 main protease through multiple replica accelerated molecular dynamics simulations and free energy landscapes. Phys. Chem. Chem. Phys. 2022, 24, 22129–22143. [Google Scholar] [CrossRef]
- Amadei, A.; Linssen, A.B.M.; Berendsen, H.J.C. Essential dynamics of proteins. Proteins Struct. Funct. Bioinform. 1993, 17, 412–425. [Google Scholar] [CrossRef] [PubMed]
- Ichiye, T.; Karplus, M. Collective motions in proteins: A covariance analysis of atomic fluctuations in molecular dynamics and normal mode simulations. Proteins Struct. Funct. Bioinform. 1991, 11, 205–217. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, Q.; Wang, W.; Hu, Q.; Bao, H. Q61 mutant-mediated dynamics changes of the GTP-KRAS complex probed by Gaussian accelerated molecular dynamics and free energy landscapes. RSC Adv. 2022, 12, 1742–1757. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, S.; Zeng, Q.; Wang, W.; Zhang, Q.; Liu, X. Free Energy Profiles Relating with Conformational Transition of the Switch Domains Induced by G12 Mutations in GTP-Bound KRAS. Front. Mol. Biosci. 2022, 9, 912518. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Su, H.; Chen, J.; Hu, G. Deciphering Conformational Changes of the GDP-Bound NRAS Induced by Mutations G13D, Q61R, and C118S through Gaussian Accelerated Molecular Dynamic Simulations. Molecules 2022, 27, 5596. [Google Scholar] [CrossRef] [PubMed]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2012, 3, 198–210. [Google Scholar] [CrossRef]
- Case, D.A.; Cheatham, T.E., III; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef]
- Tian, C.; Kasavajhala, K.; Belfon, K.A.A.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; et al. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2019, 16, 528–552. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Izaguirre, J.A.; Catarello, D.P.; Wozniak, J.M.; Skeel, R.D. Langevin stabilization of molecular dynamics. J. Chem. Phys. 2001, 114, 2090–2098. [Google Scholar] [CrossRef]
- Roe, D.R.; Cheatham, T.E., III. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Yang, Z.; Zhao, J.; Sun, H.; Wu, S. Revealing binding selectivity of inhibitors toward bromodomain-containing proteins 2 and 4 using multiple short molecular dynamics simulations and free energy analyses. SAR QSAR Environ. Res. 2020, 31, 373–398. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Yang, Z.; Xu, S.; Li, H. Binding Selectivity of Inhibitors toward Bromodomains BAZ2A and BAZ2B Uncovered by Multiple Short Molecular Dynamics Simulations and MM-GBSA Calculations. ACS Omega 2021, 6, 12036–12049. [Google Scholar] [CrossRef]
- Chen, J.; Wang, X.; Zhu, T.; Zhang, Q.; Zhang, J.Z.H. A Comparative Insight into Amprenavir Resistance of Mutations V32I, G48V, I50V, I54V, and I84V in HIV-1 Protease Based on Thermodynamic Integration and MM-PBSA Methods. J. Chem. Inf. Model. 2015, 55, 1903–1913. [Google Scholar] [CrossRef] [PubMed]
- Leonis, G.; Steinbrecher, T.; Papadopoulos, M.G. A Contribution to the Drug Resistance Mechanism of Darunavir, Amprenavir, Indinavir, and Saquinavir Complexes with HIV-1 Protease Due to Flap Mutation I50V: A Systematic MM–PBSA and Thermodynamic Integration Study. J. Chem. Inf. Model. 2013, 53, 2141–2153. [Google Scholar] [CrossRef]
- Tzoupis, H.; Leonis, G.; Mavromoustakos, T.; Papadopoulos, M.G. A Comparative Molecular Dynamics, MM–PBSA and Thermodynamic Integration Study of Saquinavir Complexes with Wild-Type HIV-1 PR and L10I, G48V, L63P, A71V, G73S, V82A and I84V Single Mutants. J. Chem. Theory Comput. 2013, 9, 1754–1764. [Google Scholar] [CrossRef]
- Chen, J.; Wang, X.; Pang, L.; Zhang, J.Z.H.; Zhu, T. Effect of mutations on binding of ligands to guanine riboswitch probed by free energy perturbation and molecular dynamics simulations. Nucleic Acids Res. 2019, 47, 6618–6631. [Google Scholar] [CrossRef] [PubMed]
- Aldeghi, M.; Heifetz, A.; Bodkin, M.J.; Knapp, S.; Biggin, P.C. Predictions of Ligand Selectivity from Absolute Binding Free Energy Calculations. J. Am. Chem. Soc. 2017, 139, 946–957. [Google Scholar] [CrossRef] [PubMed]
- Aldeghi, M.; Heifetz, A.; Bodkin, M.J.; Knapp, S.; Biggin, P.C. Accurate calculation of the absolute free energy of binding for drug molecules. Chem. Sci. 2015, 7, 207–218. [Google Scholar] [CrossRef] [PubMed]
- Shirts, M.R.; Pitera, J.W.; Swope, W.C.; Pande, V.S. Extremely precise free energy calculations of amino acid side chain analogs: Comparison of common molecular mechanics force fields for proteins. J. Chem. Phys. 2003, 119, 5740–5761. [Google Scholar] [CrossRef]
- Bao, H.; Wang, W.; Sun, H.; Chen, J. Binding modes of GDP, GTP and GNP to NRAS deciphered by using Gaussian accelerated molecular dynamics simulations. SAR QSAR Environ. Res. 2023, 34, 65–89. [Google Scholar] [CrossRef]
- Chen, J. Drug resistance mechanisms of three mutations V32I, I47V and V82I in HIV-1 protease toward inhibitors probed by molecular dynamics simulations and binding free energy predictions. RSC Adv. 2016, 6, 58573–58585. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, S.; Wang, W.; Pang, L.; Zhang, Q.; Liu, X. Mutation-Induced Impacts on the Switch Transformations of the GDP- and GTP-Bound K-Ras: Insights from Multiple Replica Gaussian Accelerated Molecular Dynamics and Free Energy Analysis. J. Chem. Inf. Model. 2021, 61, 1954–1969. [Google Scholar] [CrossRef] [PubMed]
- Rizzuti, B.; Grande, F. Virtual screening in drug discovery: A precious tool for a still-demanding challenge. In Protein Homeostasis Diseases; Academic Press: Cambridge, MA, USA, 2020; pp. 309–327. [Google Scholar] [CrossRef]
- Wang, E.; Fu, W.; Jiang, D.; Sun, H.; Wang, J.; Zhang, X.; Weng, G.; Liu, H.; Tao, P.; Hou, T. VAD-MM/GBSA: A Variable Atomic Dielectric MM/GBSA Model for Improved Accuracy in Protein–Ligand Binding Free Energy Calculations. J. Chem. Inf. Model. 2021, 61, 2844–2856. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, Y.; Fong, P.; Mao, S.; Wang, Q. The application of the MM/GBSA method in the binding pose prediction of FGFR inhibitors. Phys. Chem. Chem. Phys. 2020, 22, 9656–9663. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.; Liu, H.; Wang, J.; Weng, G.; Sun, H.; Wang, Z.; Kang, Y.; Hou, T. Development and Evaluation of MM/GBSA Based on a Variable Dielectric GB Model for Predicting Protein–Ligand Binding Affinities. J. Chem. Inf. Model. 2020, 60, 5353–5365. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zeng, Q.; Wang, W.; Sun, H.; Hu, G. Decoding the Identification Mechanism of an SAM-III Riboswitch on Ligands through Multiple Independent Gaussian-Accelerated Molecular Dynamics Simulations. J. Chem. Inf. Model. 2022, 62, 6118–6132. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Wu, J.; Shen, Y.; Cheng, H.; Xiang, Y. Exploration of the selective binding mechanism of protein kinase Aurora A selectivity via a comprehensive molecular modeling study. PeerJ 2019, 7, e7832. [Google Scholar] [CrossRef]
- Xie, T.; Yu, J.; Fu, W.; Wang, Z.; Xu, L.; Chang, S.; Wang, E.; Zhu, F.; Zeng, S.; Kang, Y.; et al. Insight into the selective binding mechanism of DNMT1 and DNMT3A inhibitors: A molecular simulation study. Phys. Chem. Chem. Phys. 2019, 21, 12931–12947. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zheng, L.; Cong, Y.; Gong, Z.; Yin, Z.; Zhang, J.Z.H.; Liu, Z.; Sun, Z. Comprehensive evaluation of end-point free energy techniques in carboxylated-pillar[6]arene host–guest binding: II. regression and dielectric constant. J. Comput. Aid. Mol. Des. 2022, 36, 879–894. [Google Scholar] [CrossRef]
- Sun, H.; Li, Y.; Shen, M.; Tian, S.; Xu, L.; Pan, P.; Guan, Y.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 5. Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring. Phys. Chem. Chem. Phys. 2014, 16, 22035–22045. [Google Scholar] [CrossRef]
- Sun, H.; Li, Y.; Tian, S.; Xu, L.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set. Phys. Chem. Chem. Phys. 2014, 16, 16719–16729. [Google Scholar] [CrossRef]
- Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins: Struct. Funct. Bioinform. 2004, 55, 383–394. [Google Scholar] [CrossRef] [PubMed]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into Protein–Protein Binding by Binding Free Energy Calculation and Free Energy Decomposition for the Ras–Raf and Ras–RalGDS Complexes. J. Mol. Biol. 2003, 330, 891–913. [Google Scholar] [CrossRef]


| Components a | 67B−BRD9 | 67B−TAF1(2) | 67C−BRD9 | 67C−TAF1(2) | 69G−BRD9 | 69G−TAF1(2) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | b Sem | Mean | b Sem | Mean | b Sem | Mean | b Sem | Mean | b Sem | Mean | b Sem | |
| −27.41 | 0.42 | −34.82 | 0.36 | −20.00 | 0.39 | −31.69 | 0.45 | −14.95 | 0.18 | −16.73 | 0.43 | |
| −33.53 | 0.27 | −35.93 | 0.25 | −35.95 | 0.40 | −38.99 | 0.31 | −38.83 | 0.24 | −36.04 | 0.24 | |
| 36.73 | 0.38 | 43.24 | 0.36 | 29.66 | 0.37 | 41.68 | 0.43 | 26.45 | 0.12 | 27.63 | 0.38 | |
| −2.92 | 0.02 | −3.29 | 0.02 | −3.33 | 0.04 | −3.67 | 0.02 | −3.44 | 0.01 | −3.29 | 0.02 | |
| c | 9.32 | 0.40 | 8.42 | 0.36 | 9.66 | 0.38 | 9.99 | 0.44 | 11.5 | 0.15 | 10.9 | 0.41 |
| d | −36.45 | 0.14 | −39.22 | 0.13 | −39.28 | 0.22 | −42.66 | 0.17 | −42.27 | 0.13 | −39.33 | 0.13 |
| e | −27.13 | 0.23 | −30.80 | 0.23 | −29.62 | 0.35 | −32.67 | 0.31 | −30.77 | 0.19 | −28.43 | 0.21 |
| − | 16.08 | 0.77 | 17.02 | 0.64 | 20.59 | 0.69 | 18.65 | 0.60 | 18.19 | 0.73 | 17.62 | 0.71 |
| −11.05 | −13.78 | −9.03 | −14.02 | −12.58 | −10.81 | |||||||
| IC50 (nM) | 230 | 59 | 1400 | 46 | 160 | 410 | ||||||
| f | −9.08 | −9.89 | −8.01 | −10.0 | −9.29 | −8.73 | ||||||
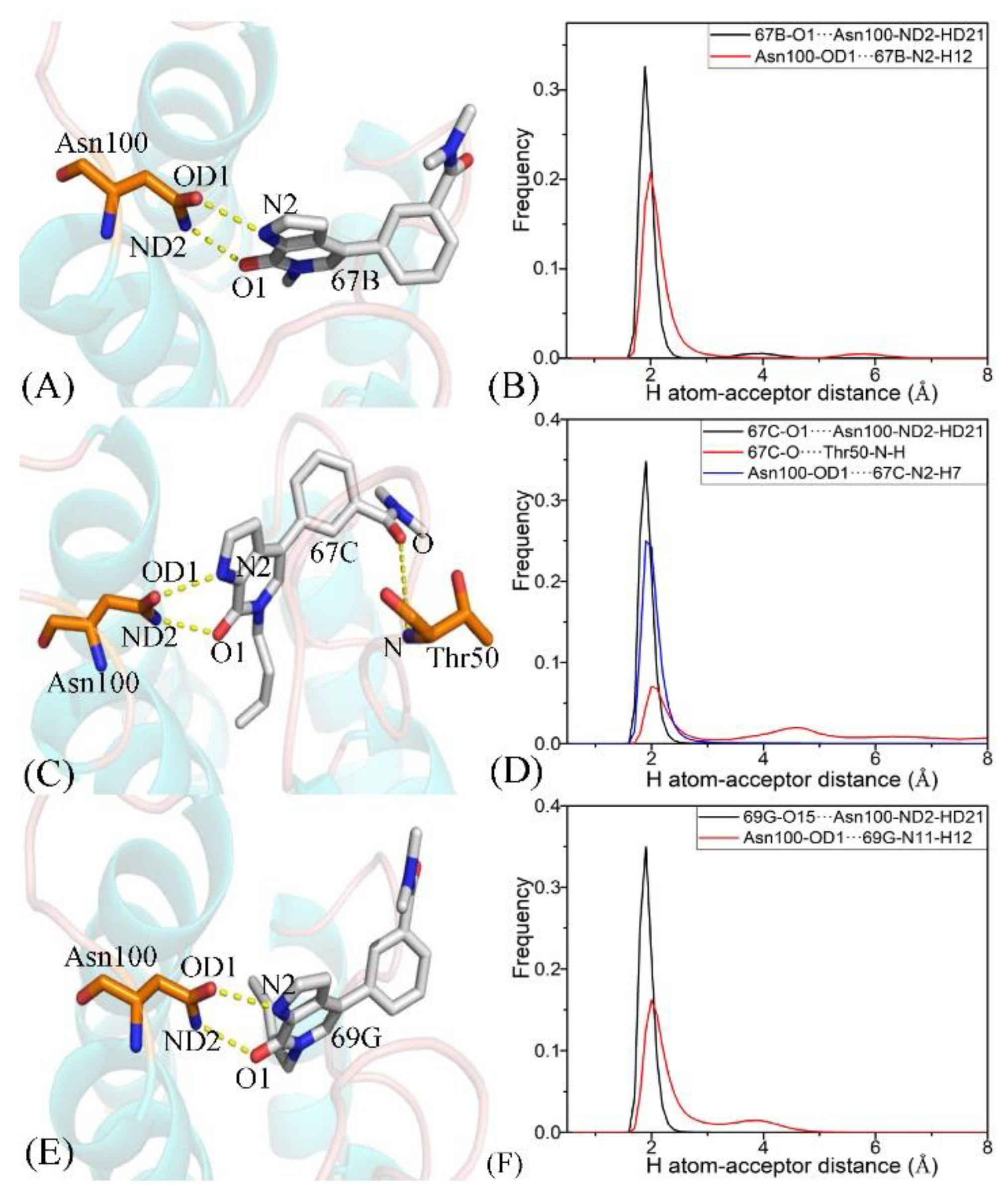
| Complexes | Hydrogen Bonds | Distance/(Å) a | Angle/(°) a | Occupancy/(%) b |
|---|---|---|---|---|
| 67B–BRD9 | 67B-O1···Asn100-ND2-HD21 c | 2.85 | 159.98 | 94.64 |
| Asn100-OD1···67B-N2-H12 | 2.95 | 151.93 | 91.54 | |
| 67B–TAF1(2) | 67B-O1···Asn1583-ND2-HD21 | 2.87 | 163.93 | 99.72 |
| 67B-O···Asn1533-N-H | 3.05 | 160.73 | 82.41 | |
| Asn1583-OD1···67B-N2-H12 | 2.91 | 163.09 | 99.42 | |
| 67C–BRD9 | 67C-O1···Asn100-ND2-HD21 | 2.85 | 162.56 | 98.72 |
| 67C-O···Thr50-N-H | 3.00 | 150.92 | 29.81 | |
| Asn100-OD1···67C-N2-H7 | 2.93 | 157.22 | 94.89 | |
| 67C–TAF1(2) | 67C-O1···Asn1583-ND2-HD21 | 2.85 | 164.30 | 93.97 |
| 67C-O···Asn1533-N-H | 3.04 | 162.59 | 63.61 | |
| Asn1583-OD1···67C-N2-H4 | 2.95 | 163.10 | 88.87 | |
| 69G–BRD9 | 69G-O15···Asn100-ND2-HD21 | 2.84 | 160.96 | 99.94 |
| Asn100-OD1···69G-N11-H12 | 3.01 | 155.82 | 78.93 | |
| 69G–TAF1(2) | 69G-O15···Asn1583-ND2-HD21 | 2.89 | 161.39 | 96.94 |
| Asn1583-OD1···69G-N11-H12 | 2.92 | 159.63 | 71.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Wang, Y.; Yu, Y.; Liu, D.; Zhao, J.; Zhang, L. Deciphering Selectivity Mechanism of BRD9 and TAF1(2) toward Inhibitors Based on Multiple Short Molecular Dynamics Simulations and MM-GBSA Calculations. Molecules 2023, 28, 2583. https://doi.org/10.3390/molecules28062583
Wang L, Wang Y, Yu Y, Liu D, Zhao J, Zhang L. Deciphering Selectivity Mechanism of BRD9 and TAF1(2) toward Inhibitors Based on Multiple Short Molecular Dynamics Simulations and MM-GBSA Calculations. Molecules. 2023; 28(6):2583. https://doi.org/10.3390/molecules28062583
Chicago/Turabian StyleWang, Lifei, Yan Wang, Yingxia Yu, Dong Liu, Juan Zhao, and Lulu Zhang. 2023. "Deciphering Selectivity Mechanism of BRD9 and TAF1(2) toward Inhibitors Based on Multiple Short Molecular Dynamics Simulations and MM-GBSA Calculations" Molecules 28, no. 6: 2583. https://doi.org/10.3390/molecules28062583
APA StyleWang, L., Wang, Y., Yu, Y., Liu, D., Zhao, J., & Zhang, L. (2023). Deciphering Selectivity Mechanism of BRD9 and TAF1(2) toward Inhibitors Based on Multiple Short Molecular Dynamics Simulations and MM-GBSA Calculations. Molecules, 28(6), 2583. https://doi.org/10.3390/molecules28062583






