Development of AMBER Parameters for Molecular Simulations of Selected Boron-Based Covalent Ligands
Abstract
1. Introduction
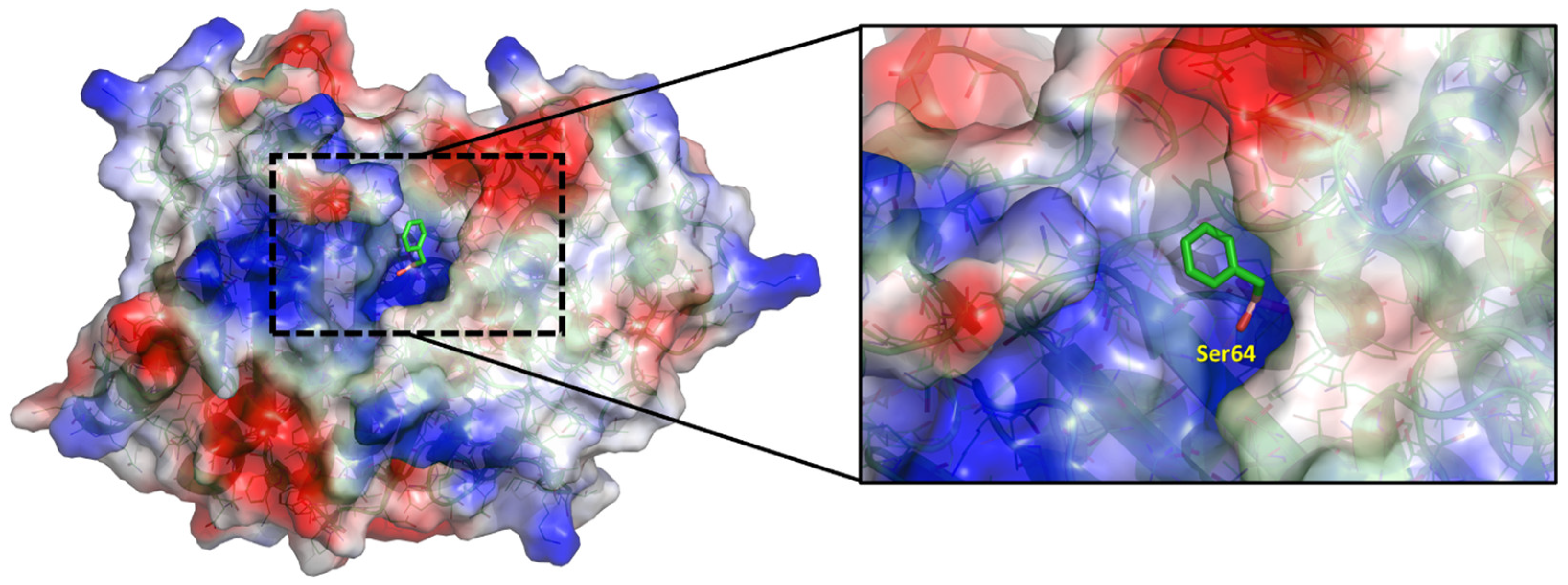
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Dembitsky, V.M.; Smoum, R.; Al-Quntar, A.A.; Ali, H.A.; Pergament, I.; Srebnik, M. Natural Occurrence of Boron-Containing Compounds in Plants, Algae and Microorganisms. Plant Sci. 2002, 163, 931–942. [Google Scholar] [CrossRef]
- Gorustovich, A.A.; Steimetz, T.; Nielsen, F.H.; Guglielmotti, M.B. A Histomorphometric Study of Alveolar Bone Modelling and Remodelling in Mice Fed a Boron-Deficient Diet. Arch. Oral Biol. 2008, 53, 677–682. [Google Scholar] [CrossRef] [PubMed]
- Kohno, J.; Kawahata, T.; Otake, T.; Morimoto, M.; Mori, H.; Ueba, N.; Nishio, M.; Kinumaki, A.; Komatsubara, S.; Kawashima, K. Boromycin, an Anti-HIV Antibiotic. Biosci. Biotechnol. Biochem. 1996, 60, 1036–1037. [Google Scholar] [CrossRef]
- Moreira, W.; Aziz, D.B.; Dick, T. Boromycin Kills Mycobacterial Persisters without Detectable Resistance. Front. Microbiol. 2016, 7, 199. [Google Scholar] [CrossRef] [PubMed]
- Elewski, B.E.; Aly, R.; Baldwin, S.L.; González Soto, R.F.; Rich, P.; Weisfeld, M.; Wiltz, H.; Zane, L.T.; Pollak, R. Efficacy and Safety of Tavaborole Topical Solution, 5%, a Novel Boron-Based Antifungal Agent, for the Treatment of Toenail Onychomycosis: Results from 2 Randomized Phase-III Studies. J. Am. Acad. Dermatol. 2015, 73, 62–69. [Google Scholar] [CrossRef]
- Curran, M.P.; McKeage, K. Bortezomib. Drugs 2009, 69, 859–888. [Google Scholar] [CrossRef]
- Lamotte-Brasseur, J.; Knox, J.; Kelly, J.A.; Charlier, P.; Fonzé, E.; Dideberg, O.; Frère, J.-M. The Structures and Catalytic Mechanisms of Active-Site Serine β-Lactamases. Biotechnol. Genet. Eng. Rev. 1994, 12, 189–230. [Google Scholar] [CrossRef]
- Sgrignani, J.; de Luca, F.; Torosyan, H.; Docquier, J.-D.; Duan, D.; Novati, B.; Prati, F.; Colombo, G.; Grazioso, G. Structure-Based Approach for Identification of Novel Phenylboronic Acids as Serine-β-Lactamase Inhibitors. J. Comput. Aided Mol. Des. 2016, 30, 851–861. [Google Scholar] [CrossRef]
- Sgrignani, J.; Novati, B.; Colombo, G.; Grazioso, G. Covalent Docking of Selected Boron-Based Serine Beta-Lactamase Inhibitors. J. Comput. Aided Mol. Des. 2015, 29, 441–450. [Google Scholar] [CrossRef]
- Bassini, E.; Gazzotti, S.; Sannio, F.; lo Presti, L.; Sgrignani, J.; Docquier, J.-D.; Grazioso, G.; Silvani, A. Isonitrile-Based Multicomponent Synthesis of β-Amino Boronic Acids as β-Lactamase Inhibitors. Antibiotics 2020, 9, 249. [Google Scholar] [CrossRef]
- Tooke, C.L.; Hinchliffe, P.; Bragginton, E.C.; Colenso, C.K.; Hirvonen, V.H.A.; Takebayashi, Y.; Spencer, J. β-Lactamases and β-Lactamase Inhibitors in the 21st Century. J. Mol. Biol. 2019, 431, 3472–3500. [Google Scholar] [CrossRef]
- Tafi, A.; Agamennone, M.; Tortorella, P.; Alcaro, S.; Gallina, C.; Botta, M. AMBER Force Field Implementation of the Boronate Function to Simulate the Inhibition of β-Lactamases by Alkyl and Aryl Boronic Acids. Eur. J. Med. Chem. 2005, 40, 1134–1142. [Google Scholar] [CrossRef]
- Fassi, E.M.A.; Manenti, M.; Citarella, A.; Dei Cas, M.; Casati, S.; Micale, N.; Schirmeister, T.; Roda, G.; Silvani, A.; Grazioso, G. Computational Design, Synthesis and Biophysical Evaluation of β-Amido Boronic Acids as Potent SARS-CoV-2 Mpro Inhibi-Tors. Molecules 2023, 28, 2356. [Google Scholar] [CrossRef]
- Farhang, M.; Akbarzadeh, A.R.; Rabbani, M.; Ghadiri, A.M. A Retrospective-Prospective Review of Suzuki–Miyaura Reaction: From Cross-Coupling Reaction to Pharmaceutical Industry Applications. Polyhedron 2022, 227, 116124. [Google Scholar] [CrossRef]
- Naghii, M.R.; Samman, S. The Effect of Boron Supplementation on Its Urinary Excretion and Selected Cardiovascular Risk Factors in Healthy Male Subjects. Biol. Trace Elem. Res. 1997, 56, 273–286. [Google Scholar] [CrossRef]
- Charzewski, Ł.; Krzyśko, K.A.; Lesyng, B. Exploring Covalent Docking Mechanisms of Boron-Based Inhibitors to Class A, C and D β-Lactamases Using Time-Dependent Hybrid QM/MM Simulations. Front. Mol. Biosci. 2021, 8, 633181. [Google Scholar] [CrossRef]
- Lu, C.; Wu, C.; Ghoreishi, D.; Chen, W.; Wang, L.; Damm, W.; Ross, G.A.; Dahlgren, M.K.; Russell, E.; von Bargen, C.D.; et al. OPLS4: Improving Force Field Accuracy on Challenging Regimes of Chemical Space. J. Chem. Theory Comput. 2021, 17, 4291–4300. [Google Scholar] [CrossRef]
- Kurt, B.; Temel, H. Development of AMBER Parameters for Molecular Dynamics Simulations of Boron Compounds Containing Aromatic Structure. Chem. Phys. Lett. 2021, 775, 138656. [Google Scholar] [CrossRef]
- James, J.J.; Whiting, A. Force Field Parameters for the Boronate Function and Their Carbonyl Complexes and Application to Modelling Boronate Esters. J. Chem. Soc. Perkin Trans. 1996, 2, 1861–1867. [Google Scholar] [CrossRef]
- Eidam, O.; Romagnoli, C.; Dalmasso, G.; Barelier, S.; Caselli, E.; Bonnet, R.; Shoichet, B.K.; Prati, F. Fragment-Guided Design of Subnanomolar β-Lactamase Inhibitors Active in Vivo. Proc. Natl. Acad. Sci. USA 2012, 109, 17448–17453. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Xia, Z.; Kovela, S.; Robinson, W.L.; Johnson, M.E.; Kneller, D.W.; Wang, Y.; Aoki, M.; Takamatsu, Y.; Weber, I.T.; et al. Potent HIV-1 Protease Inhibitors Containing Carboxylic and Boronic Acids: Effect on Enzyme Inhibition and Antiviral Activity and Protein-Ligand X-ray Structural Studies. ChemMedChem 2019, 14, 1863–1872. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhong, Q.; Zhang, Q.; Zheng, S.; Miele, L.; Wang, G. Boronic Prodrug of Endoxifen as an Effective Hormone Therapy for Breast Cancer. Breast Cancer Res. Treat. 2015, 152, 283–291. [Google Scholar] [CrossRef] [PubMed]
- Betz, R.M.; Walker, R.C. Paramfit: Automated Optimization of Force Field Parameters for Molecular Dynamics Simulations. J. Comput. Chem. 2015, 36, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Powers, R.A.; Shoichet, B.K. Structure-Based Approach for Binding Site Identification on AmpC β-Lactamase. J. Med. Chem. 2002, 45, 3222–3234. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Ogata, K.; Nakamura, S. Improvement of Parameters of the AMBER Potential Force Field for Phospholipids for Description of Thermal Phase Transitions. J. Phys. Chem. B 2015, 119, 9726–9739. [Google Scholar] [CrossRef]
- Kamenik, A.S.; Handle, P.H.; Hofer, F.; Kahler, U.; Kraml, J.; Liedl, K.R. Polarizable and Non-Polarizable Force Fields: Protein Folding, Unfolding, and Misfolding. J. Chem. Phys. 2020, 153, 185102. [Google Scholar] [CrossRef]
- Case, D.A.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Ghoreishi, D.; Gilson, M.K.; et al. AMBER; University of California: San Francisco, CA, USA, 2018. [Google Scholar]
- Jones, G.; Willett, P.; Glen, R.C.; Leach, A.R.; Taylor, R. Development and Validation of a Genetic Algorithm for Flexible Docking. J. Mol. Biol. 1997, 267, 727–748. [Google Scholar] [CrossRef]
- Amendola, V.; Bergamaschi, G.; Boiocchi, M.; Legnani, L.; Lo Presti, E.; Miljkovic, A.; Monzani, E.; Pancotti, F. Chloride-binding in organic-water mixtures: The powerful synergy of C–H donor groups within a bowl-shaped cavity. Chem. Commun. 2016, 52, 10910–10913. [Google Scholar] [CrossRef]
- Legnani, L.; Porta, A.; Caramella, P.; Toma, L.; Zanoni, G.; Vidari, G. Computational mechanistic study of the Julia-Kocieński reaction. J. Org. Chem. 2015, 80, 3092–3100. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian16 (Revision A.03); Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. Ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from Ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Legnani, L.; Trusso Sfrazzetto, G.; Pappalardo, A.; Puglisi, R.; Chiacchio, M.A. Supramolecular Recognition of Phosphocholine by Enzyme-Like Cavitand Receptor. Chem. Commun. 2020, 56, 539–542. [Google Scholar] [CrossRef]
- Merino, P.; Chiacchio, M.A.; Legnani, L.; Delso, I.; Tejero, T. Introducing Topology to Assess Synchronicity of Organic Reactions. Dual Reactivity of Oximes with Alkenes as a Case Study. Org. Chem. Front. 2017, 4, 1541–1554. [Google Scholar] [CrossRef]
- Mennucci, B.; Tomasi, J.; Cammi, R.; Cheeseman, J.R.; Frisch, M.J.; Devlin, F.J.; Gabriel, S.; Stephens, P.J. Polarizable Continuum Model (PCM) Calculations of Solvent Effects on Optical Rotations of Chiral Molecules. J. Phys. Chem. A 2002, 106, 6102–6113. [Google Scholar] [CrossRef]

| Dihedral | Divider | Vn (kcal/mol) | γ | n |
|---|---|---|---|---|
| oh-b-ca-ca | 1 | 15.7206 | 170.366 | −1.001 |
| b-c2-ca-ca | 1 | 0.7000 | 180.000 | 2.000 |
| b-o-c3-c3 | 1 | 3.4800 | 106.880 | 1.500 |
| b-o-c3-h1 | 1 | 4.1053 | 256.511 | 2.000 |
| o-b-o-ho | 1 | 0.8361 | 0.000 | 3.000 |
| o-b-c2-ha | 1 | 2.5070 | 172.978 | 0.129 |
| o-b-c2-ca | 1 | 15.7206 | 170.366 | −1.000 |
| o-b-o-c3 | 1 | 0.8347 | 0.000 | 3.000 |
| ho-o-b-c2 | 1 | 2.0509 | 112.044 | 5.000 |
| c2-b-o-c3 | 1 | 2.3740 | 114.599 | −0.197 |
| cx-2c-oh-b | 1 | 3.4800 | 106.881 | 1.500 |
| ho-oh-b-o | 1 | 0.8361 | 0.000 | 3.000 |
| ho-oh-b-c2 | 1 | 2.0509 | 112.044 | 5.000 |
| ho-oh-b-ca | 1 | 2.0509 | 112.044 | 5.000 |
| oh-b-o-ho | 1 | 0.8361 | 0.000 | 3.000 |
| oh-b-oh-ho | 1 | 0.8361 | 0.000 | 3.000 |
| oh-b-c2-ha | 1 | 2.5070 | 172.978 | 0.129 |
| oh-b-c3-h1 | 1 | 2.5070 | 172.978 | 0.129 |
| oh-b-c2-ca | 1 | 15.7206 | 170.366 | −1.000 |
| oh-b-c3-ca | 1 | 15.7205 | 170.366 | 0.000 |
| h1-2c-oh-b | 1 | 4.1053 | 256.511 | 2.000 |
| 2c-oh-b-o | 1 | 2.3743 | 114.599 | −0.197 |
| 2c-oh-b-c2 | 1 | 2.3743 | 114.599 | −0.197 |
| h1-2c-oh-b | 1 | 4.1053 | 256.511 | 2.000 |
| oh-b-c3-n3 | 1 | −2.2276 | 0.000 | 2.156 |
| 2c-oh-b-oh | 1 | −44.4201 | 0.000 | 1.251 |
| 2c-oh-b-c3 | 1 | −12.2011 | 0.000 | 2.000 |
| ho-oh-b-c3 | 1 | 8.0608 | 0.000 | −0.101 |
| oh-b-c3-h1 | 1 | 0.5691 | 0.000 | 2.385 |
| oh-b-ca-ca | 1 | 15.7206 | 170.366 | −1.001 |
| 2c-oh-b-ca | 1 | 2.3743 | 114.599 | −0.197 |
| b-ha-c2-ha | Improper | 1.1000 | 180.000 | 2.000 |
| Bond | Kr (kcal (mol·Å2) −1 | req (Å) |
|---|---|---|
| b-o * | 450.00 | 1.510 |
| oh-b * | 450.00 | 1.510 |
| b-c2 | 340.00 | 1.630 |
| b-ca | 340.00 | 1.630 |
| b-c3 | 326.80 | 1.510 |
| Angle | Kθ (kcal/(mol·radian2) | θeq (°) |
| ca-c2-ha | 47.90 | 123.30 |
| b-o-ho * | 35.00 | 109.50 |
| ho-oh-b * | 35.00 | 109.50 |
| b-c2-ha ** | 50.00 | 109.50 |
| b-c3-h1 ** | 50.00 | 109.50 |
| b-c3-hc ** | 50.00 | 109.50 |
| b-c3-c3 ** | 50.00 | 109.50 |
| b-c3-n3 ** | 50.00 | 109.31 |
| b-c2-ca ** | 127.38 | 120.97 |
| b-ca-ca ** | 127.38 | 120.97 |
| b-o-c3 * | 90.00 | 109.50 |
| o-b-o * | 90.00 | 109.50 |
| oh-b-o * | 90.00 | 109.50 |
| oh-b-oh * | 90.00 | 109.50 |
| oh-b-c2 * | 60.00 | 109.50 |
| oh-b-ca * | 60.00 | 109.50 |
| oh-b-c3 * | 60.00 | 109.50 |
| o-b-c2 * | 60.00 | 109.50 |
| 2c-oh-b * | 60.00 | 109.50 |
| b-c3-ca ** | 127.38 | 111.90 |
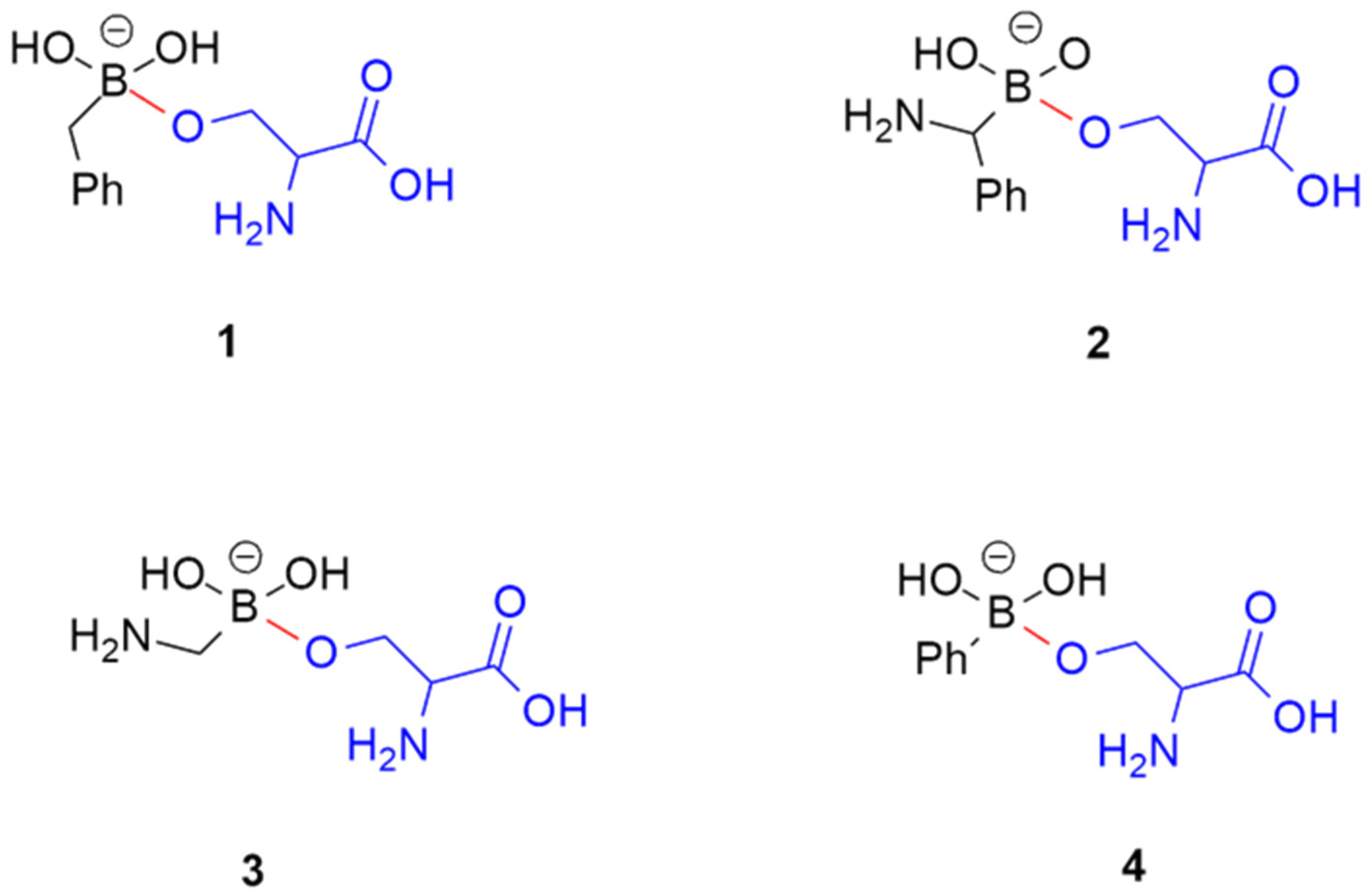
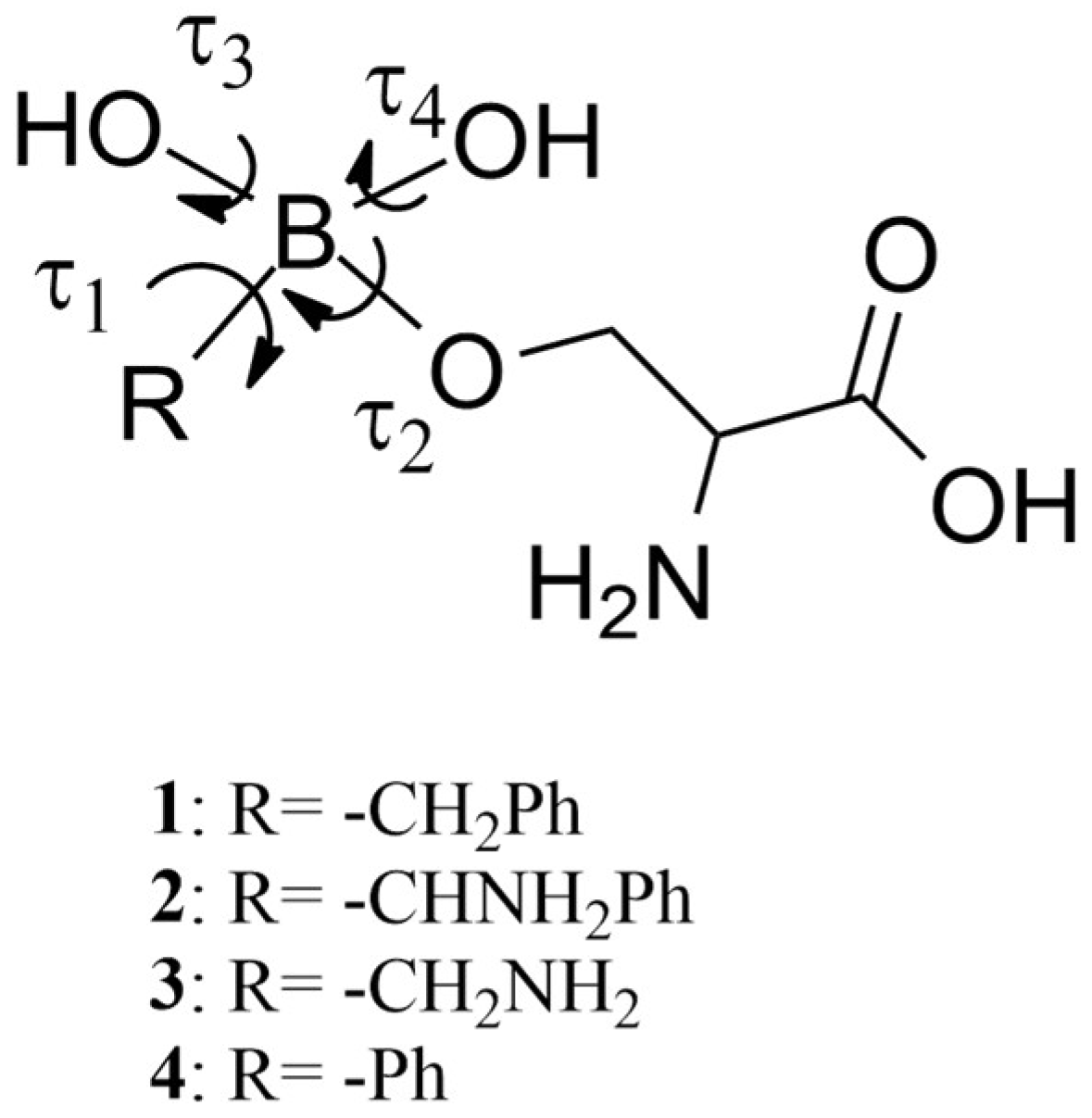
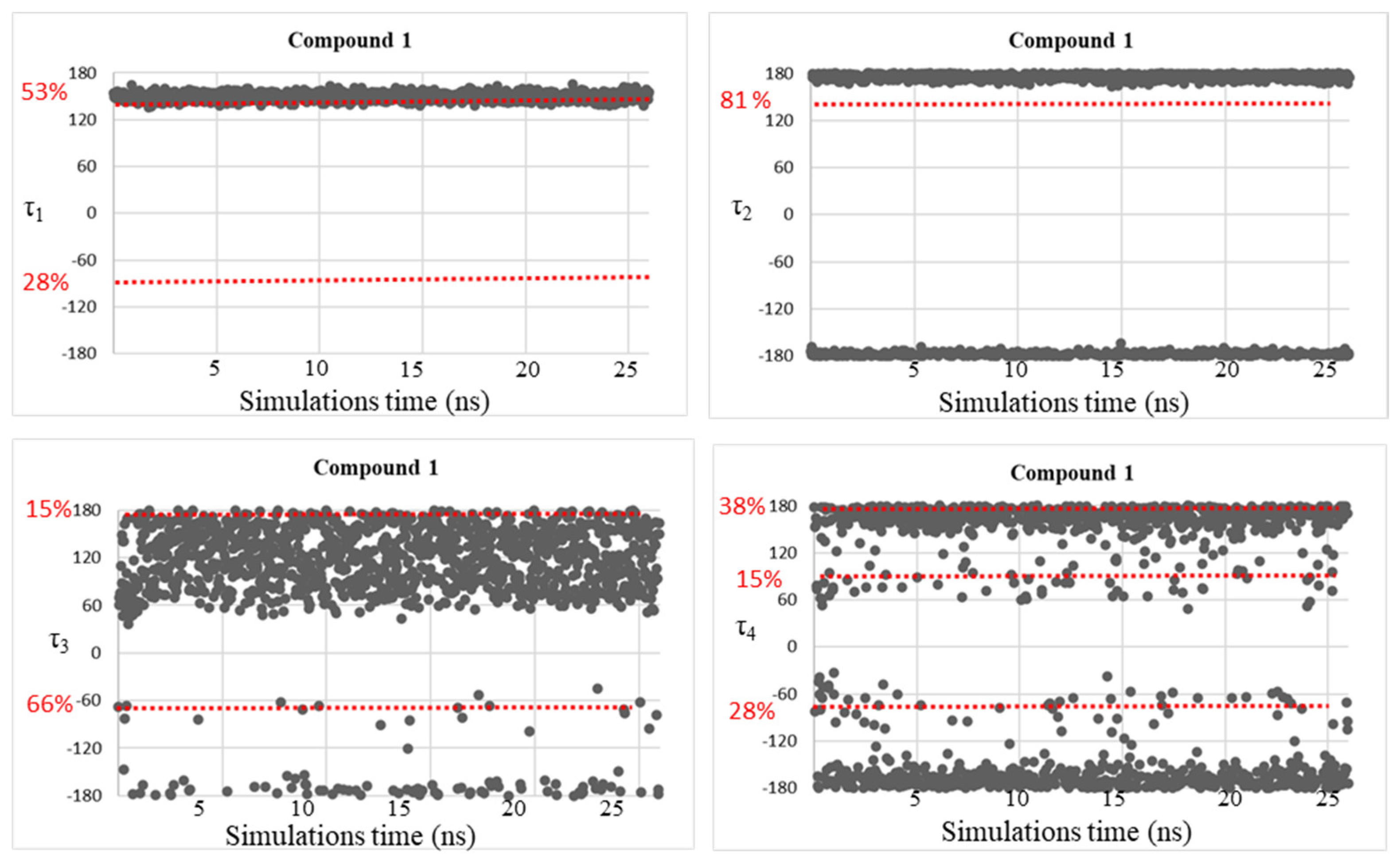
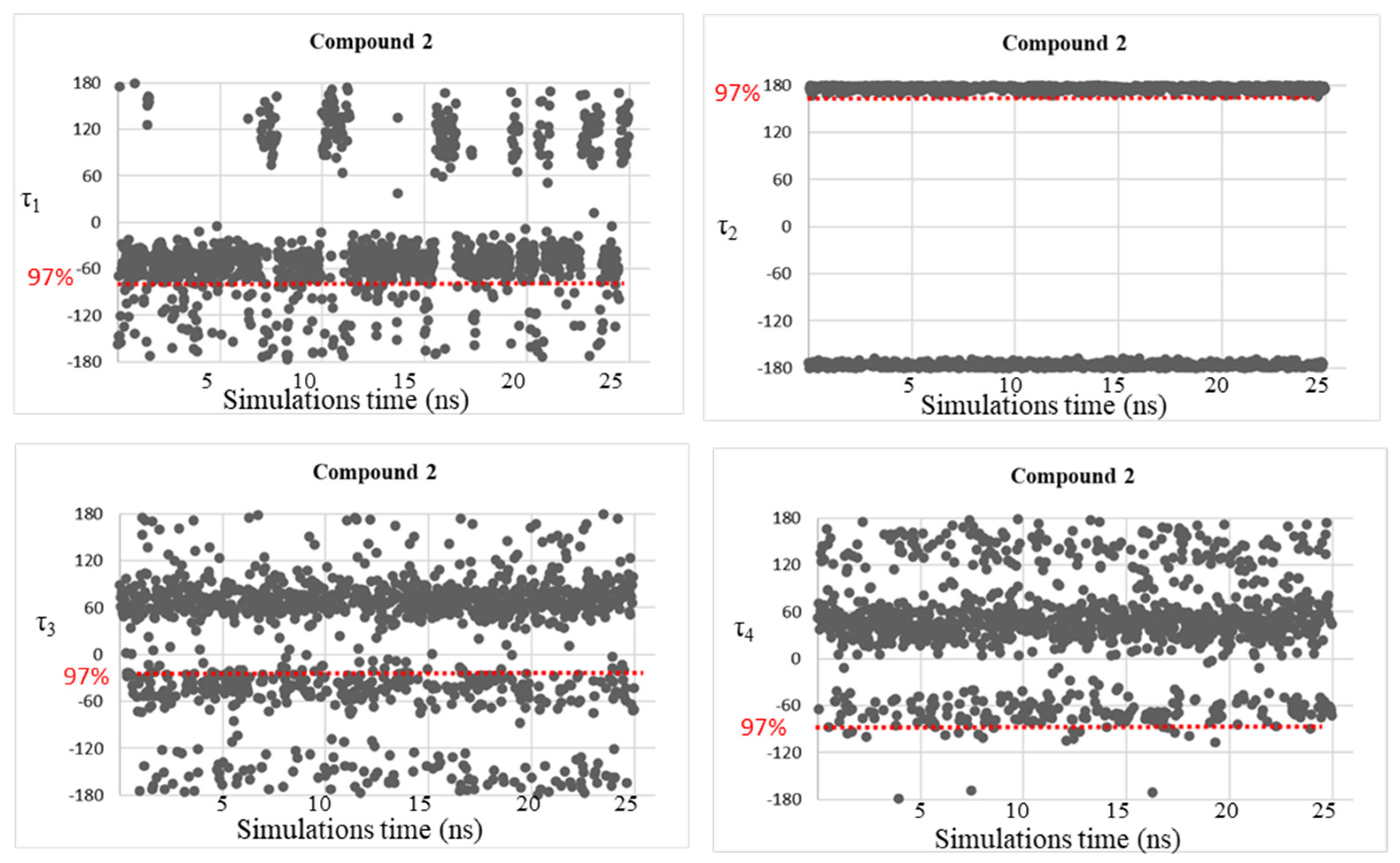
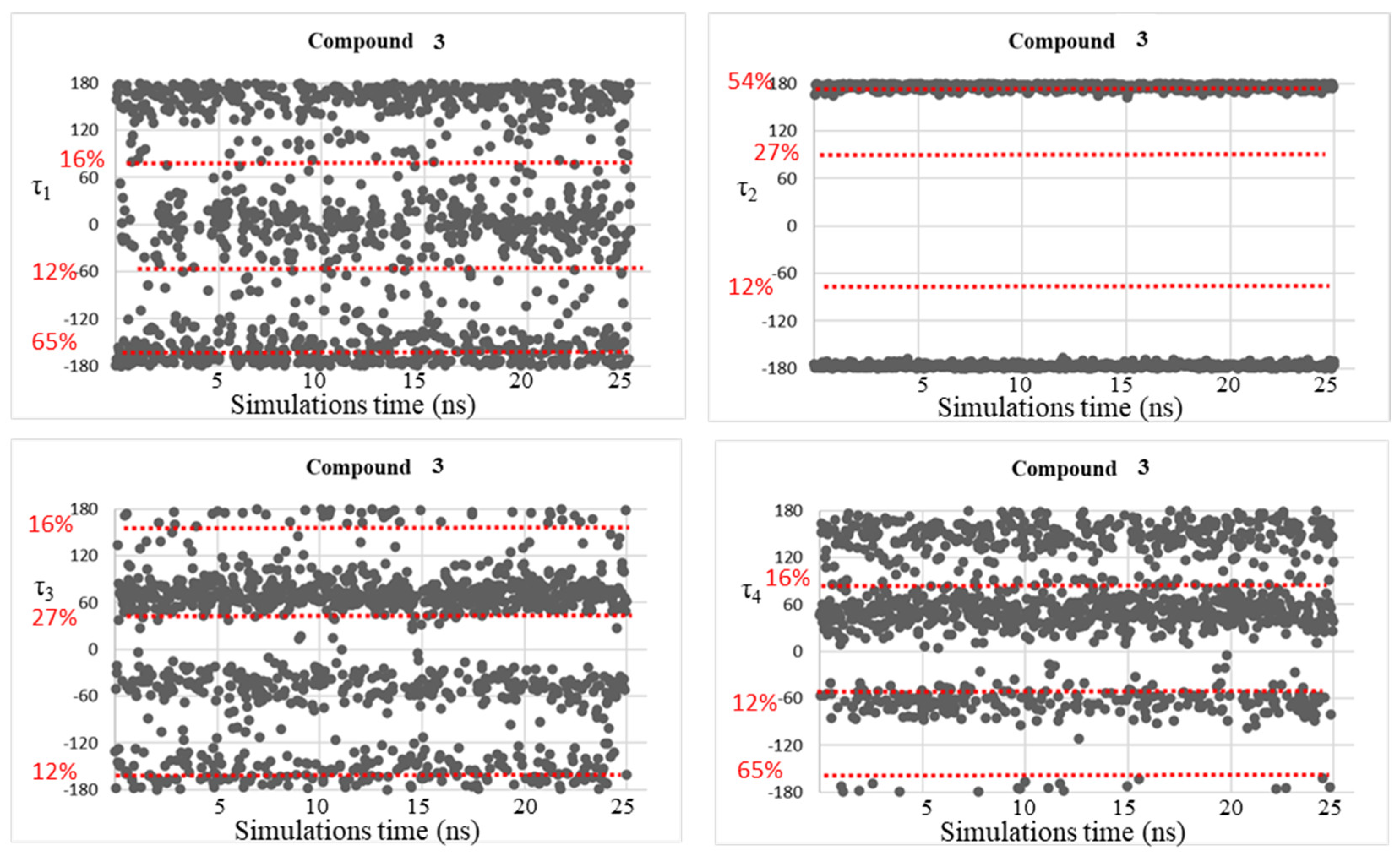
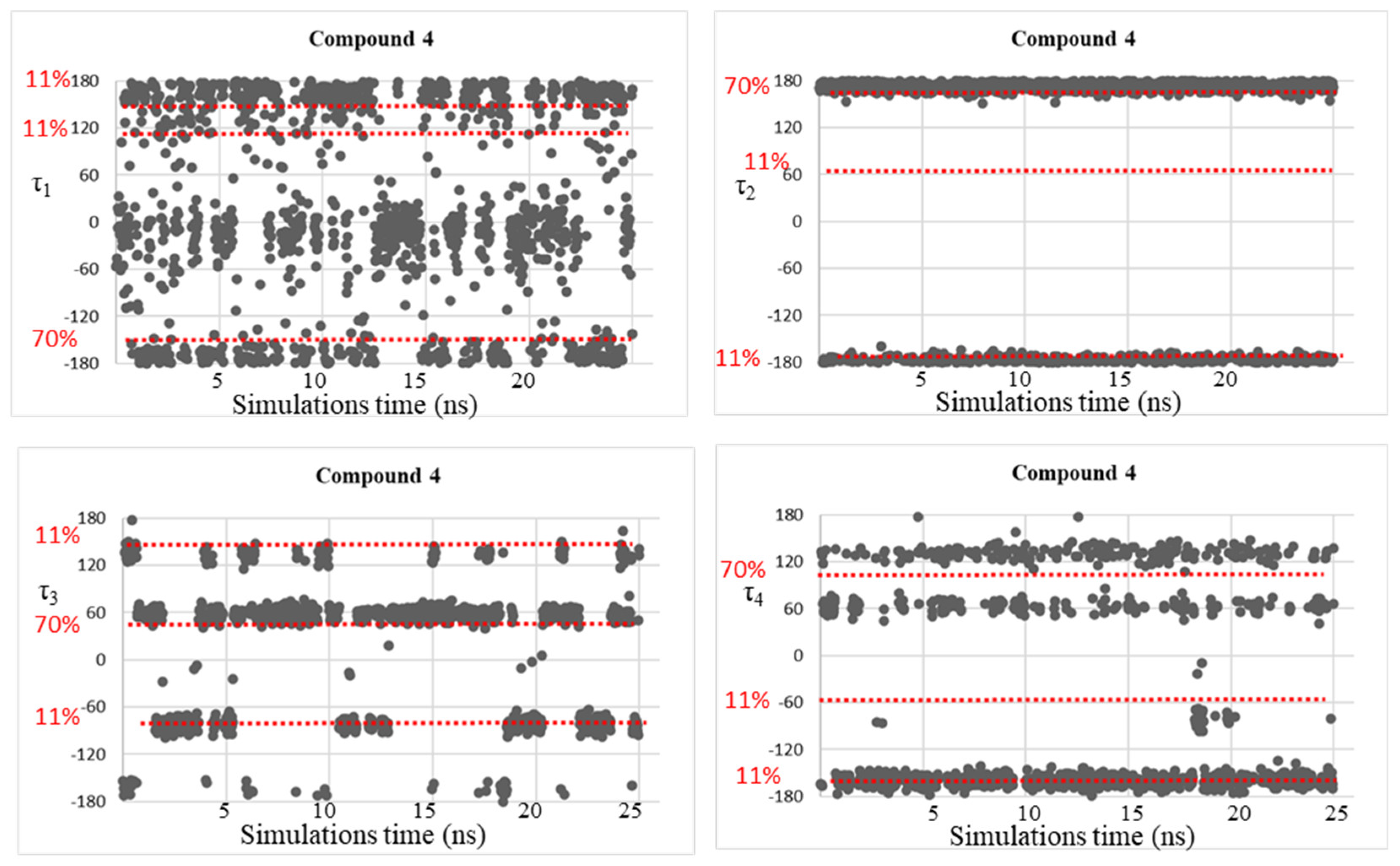
| Compound | τ1 (°) | τ2 (°) | τ3 (°) | τ4 (°) |
|---|---|---|---|---|
| 1 | 150 | −177, 175 | −169, −65, 54, 179 | −164, 152 |
| 2 | −154, −69, 88, 143 | −176, 176 | −36, 49 | −49, 58, 154 |
| 3 | −155, −28, 87 | −176, 176 | −138, −44, 49 | −169, −58, 52, 151 |
| 4 | −150, 153 | −175, 175 | −137, 59 | −165, 56, 133 |
| ΔE (kcal/mol) | % | τ1 (°) | τ2 (°) | τ3 (°) | τ4 (°) | |
|---|---|---|---|---|---|---|
| 1A | 0.00 | 37.9 | 171 | 142 | −68 | 176 |
| 1B | 0.18 | 28.0 | −71 | 154 | −42 | −85 |
| 1C | 0.54 | 15.1 | 174 | 141 | 177 | 72 |
| 1D | 0.91 | 8.1 | −65 | 173 | −142 | −63 |
| 1E | 1.25 | 4.6 | −66 | −70 | −62 | −178 |
| 1F | 1.34 | 4.0 | 177 | 158 | −43 | −80 |
| 1G | 2.28 | 0.8 | 68 | −166 | −146 | −79 |
| 1H | 2.32 | 0.8 | 171 | −76 | 170 | −51 |
| 1I | 2.39 | 0.7 | −64 | −70 | −65 | −178 |
| 2A | 0.00 | 96.5 | −76 | 155 | −38 | −102 |
| 2B | 2.16 | 2.5 | −156 | −146 | −91 | −147 |
| 2C | 2.97 | 0.6 | −69 | −71 | −54 | −162 |
| 2D | 3.54 | 0.2 | 75 | −78 | −136 | −167 |
| 2E | 4.10 | 0.1 | −71 | −73 | −56 | −162 |
| 3A | 0.00 | 53.7 | −174 | 173 | 30 | −135 |
| 3B | 0.73 | 15.6 | 64 | 38 | 170 | 111 |
| 3C | 0.90 | 11.7 | −59 | −68 | −168 | −48 |
| 3D | 0.91 | 11.6 | −169 | 74 | 26 | −161 |
| 3E | 1.33 | 5.7 | 75 | −144 | −97 | −151 |
| 3F | 2.18 | 1.4 | 174 | −170 | −72 | −142 |
| 3G | 2.93 | 0.4 | 173 | −77 | −149 | −160 |
| 4A | 0.00 | 69.9 | −139 | 177 | 50 | 95 |
| 4B | 1.12 | 10.6 | 159 | −171 | −74 | −143 |
| 4C | 1.12 | 10.5 | 37 | 68 | 170 | −57 |
| 4D | 1.21 | 9.0 | 103 | −70 | −153 | 178 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiacchio, M.A.; Legnani, L.; Fassi, E.M.A.; Roda, G.; Grazioso, G. Development of AMBER Parameters for Molecular Simulations of Selected Boron-Based Covalent Ligands. Molecules 2023, 28, 2866. https://doi.org/10.3390/molecules28062866
Chiacchio MA, Legnani L, Fassi EMA, Roda G, Grazioso G. Development of AMBER Parameters for Molecular Simulations of Selected Boron-Based Covalent Ligands. Molecules. 2023; 28(6):2866. https://doi.org/10.3390/molecules28062866
Chicago/Turabian StyleChiacchio, Maria Assunta, Laura Legnani, Enrico Mario Alessandro Fassi, Gabriella Roda, and Giovanni Grazioso. 2023. "Development of AMBER Parameters for Molecular Simulations of Selected Boron-Based Covalent Ligands" Molecules 28, no. 6: 2866. https://doi.org/10.3390/molecules28062866
APA StyleChiacchio, M. A., Legnani, L., Fassi, E. M. A., Roda, G., & Grazioso, G. (2023). Development of AMBER Parameters for Molecular Simulations of Selected Boron-Based Covalent Ligands. Molecules, 28(6), 2866. https://doi.org/10.3390/molecules28062866