Scattering of e± by C2H6 Molecule over a Wide Range of Energy: A Theoretical Investigation
Abstract
1. Introduction
2. Outline of the Theory
2.1. Interaction Potential
2.2. Partial Wave Analysis
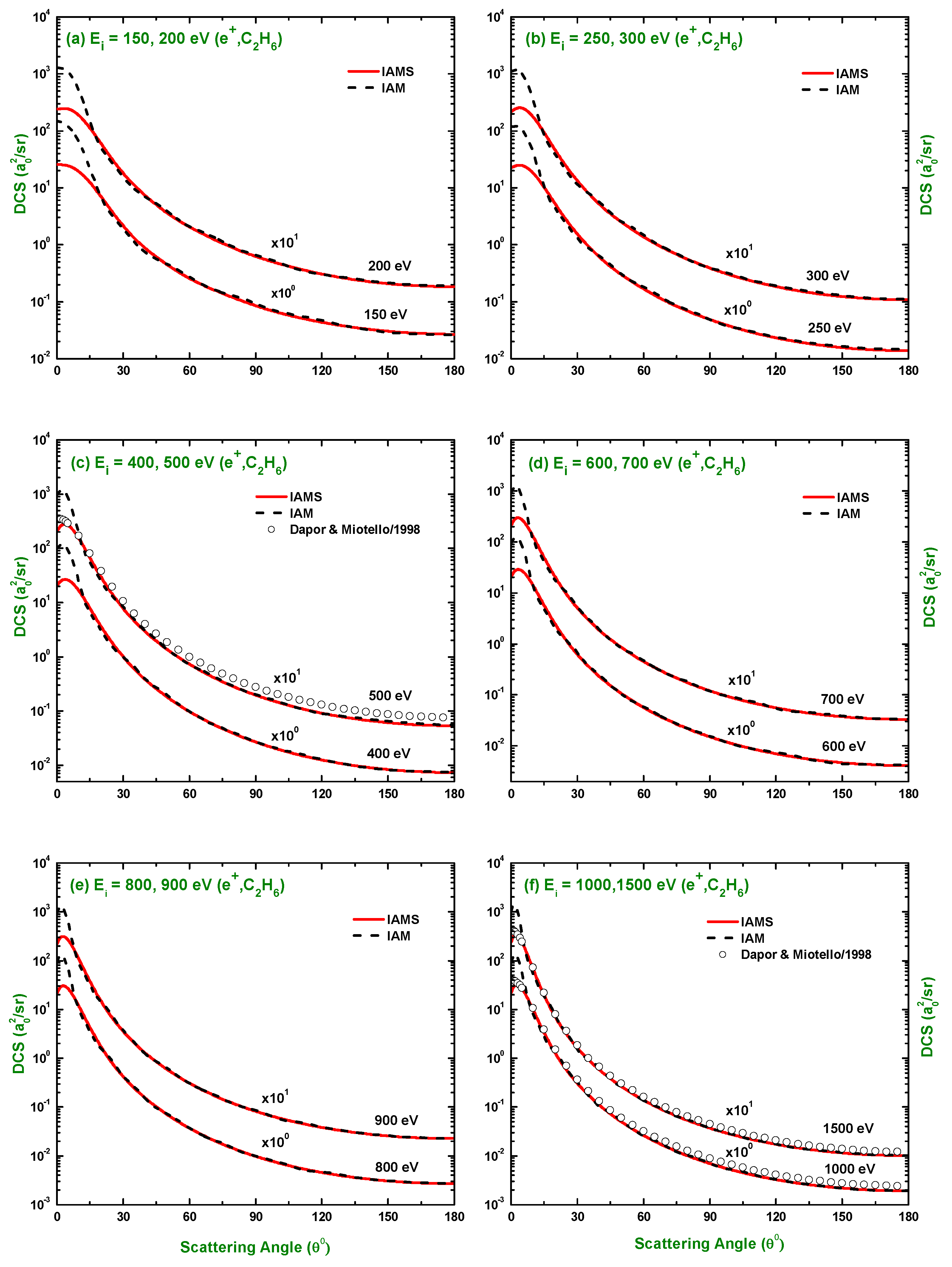
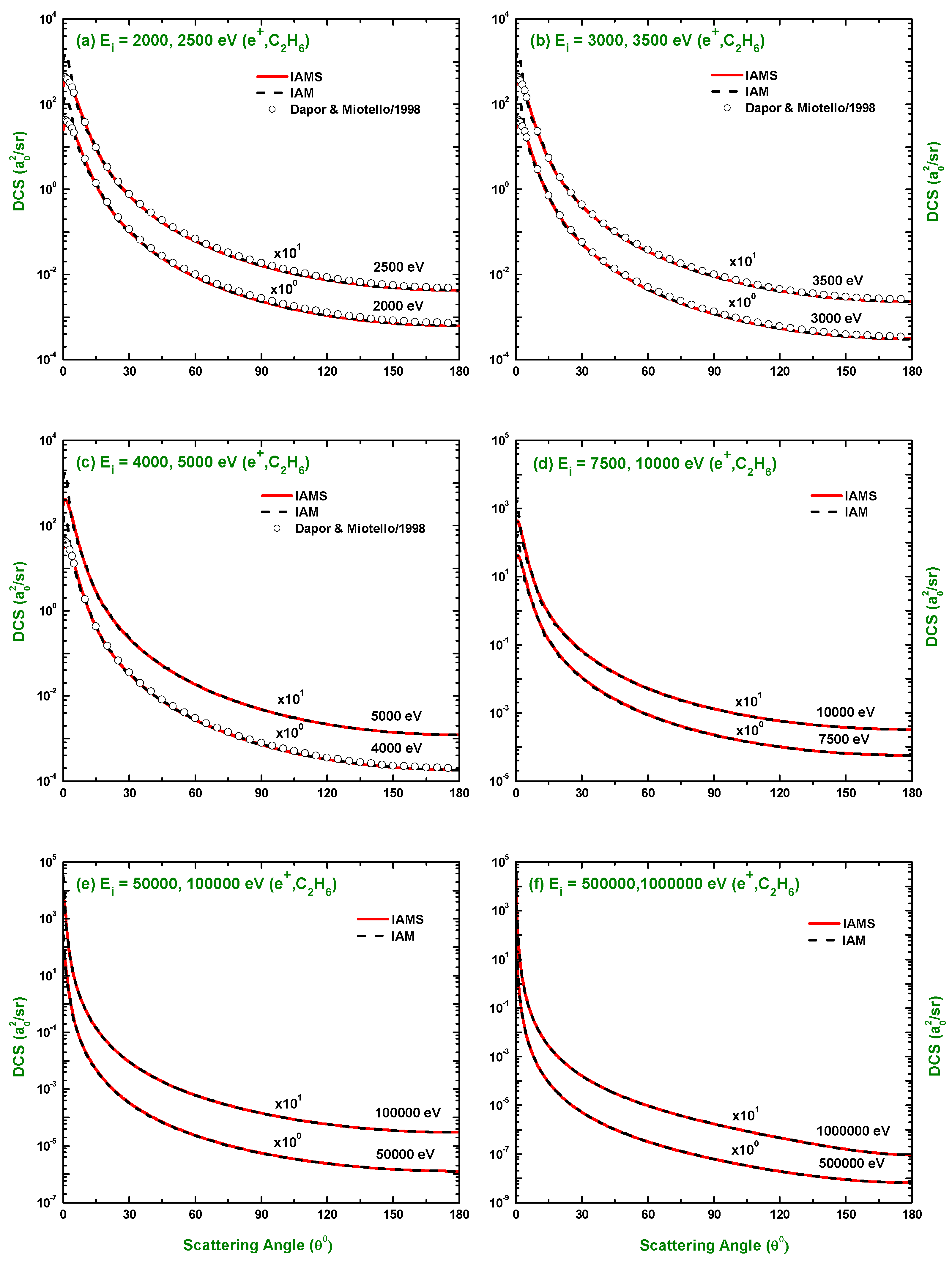
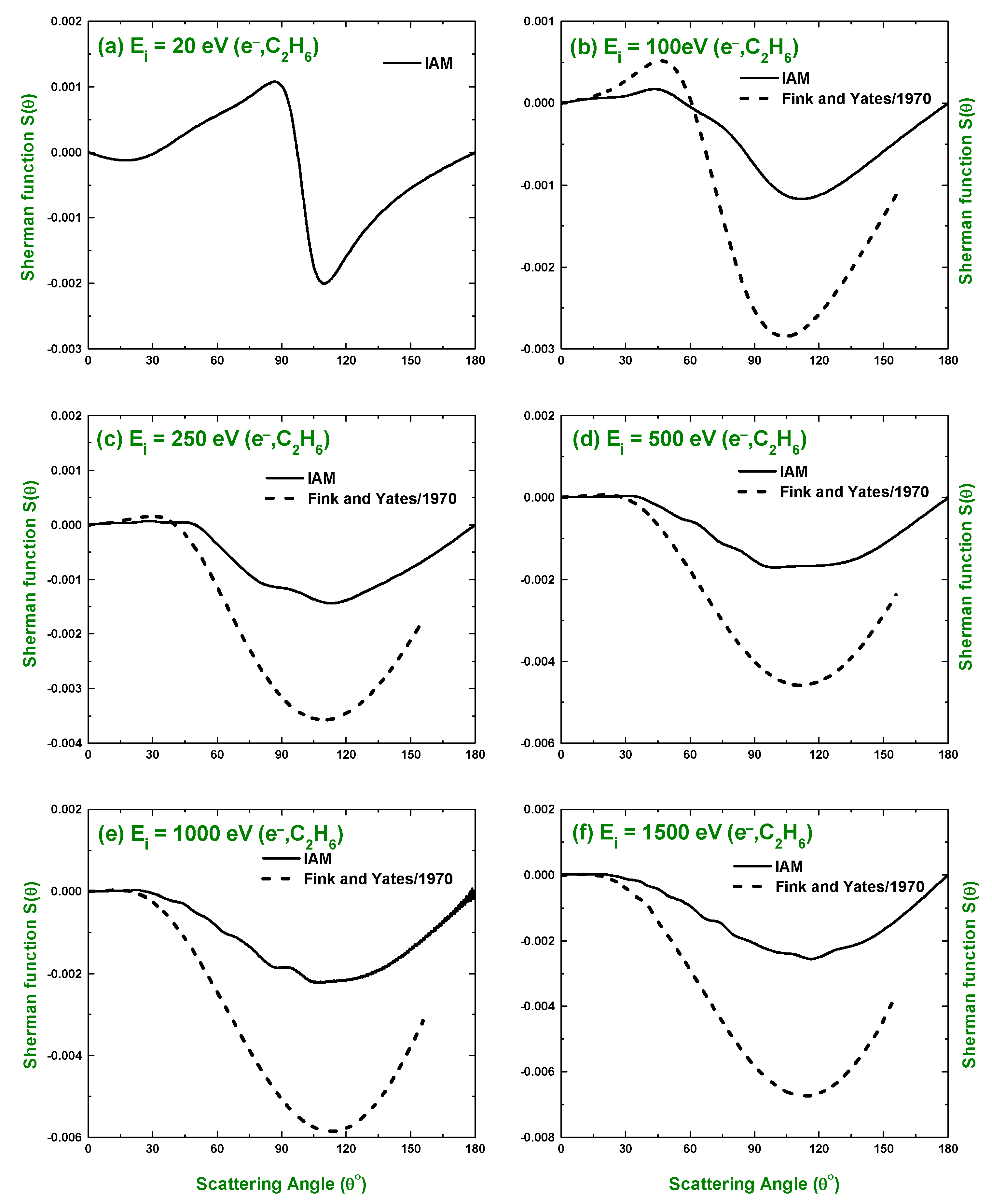
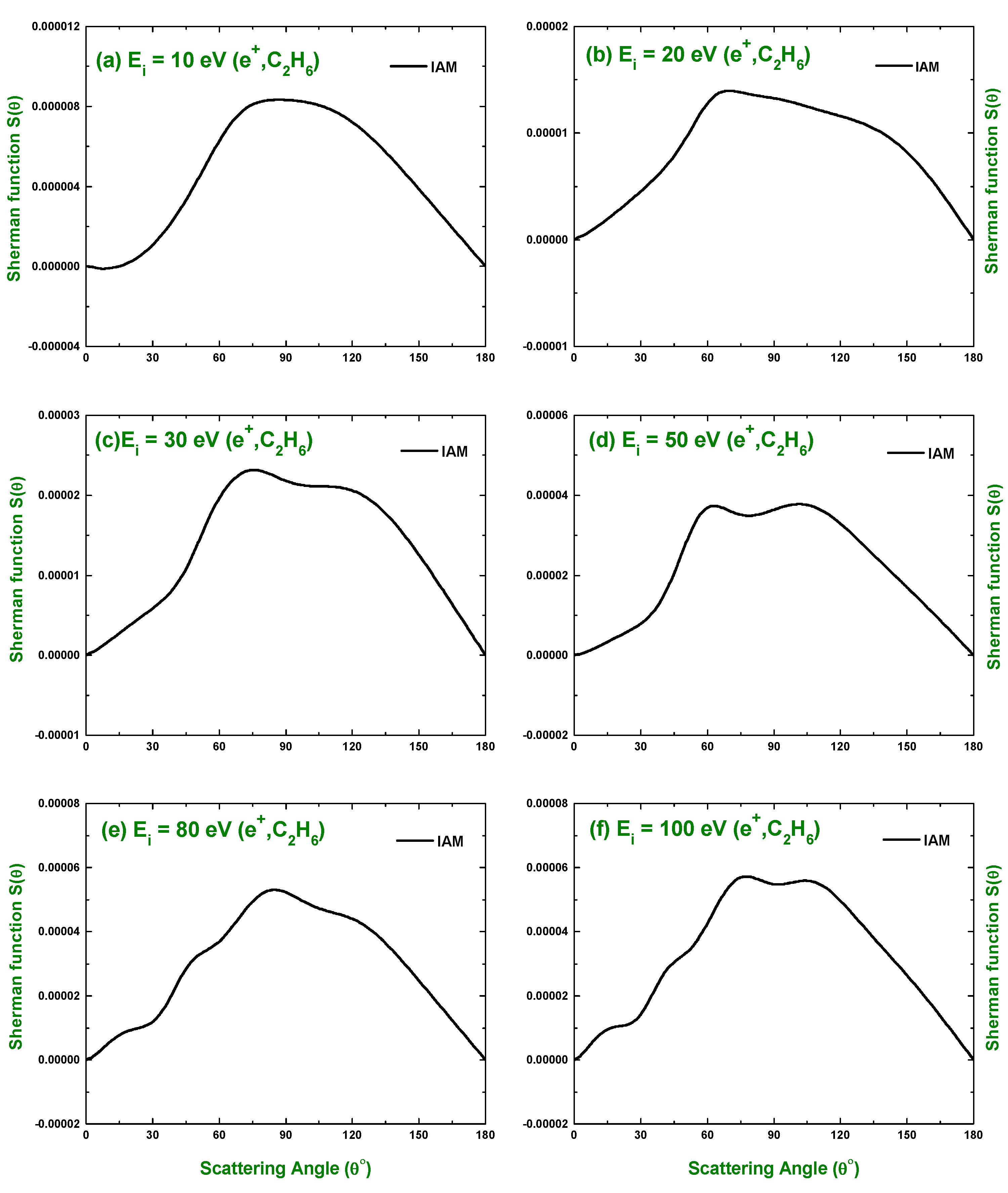
3. Results and Discussion
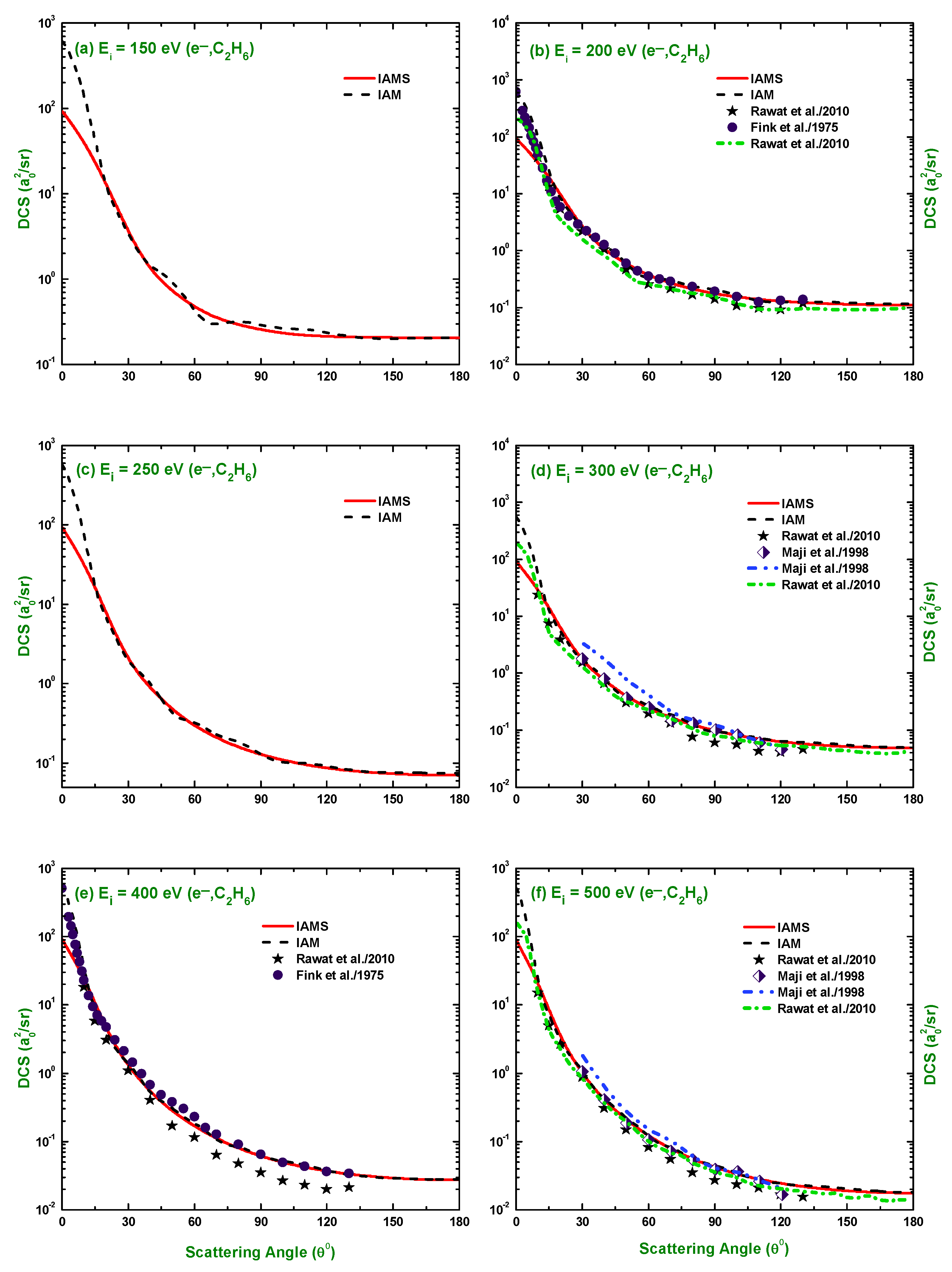
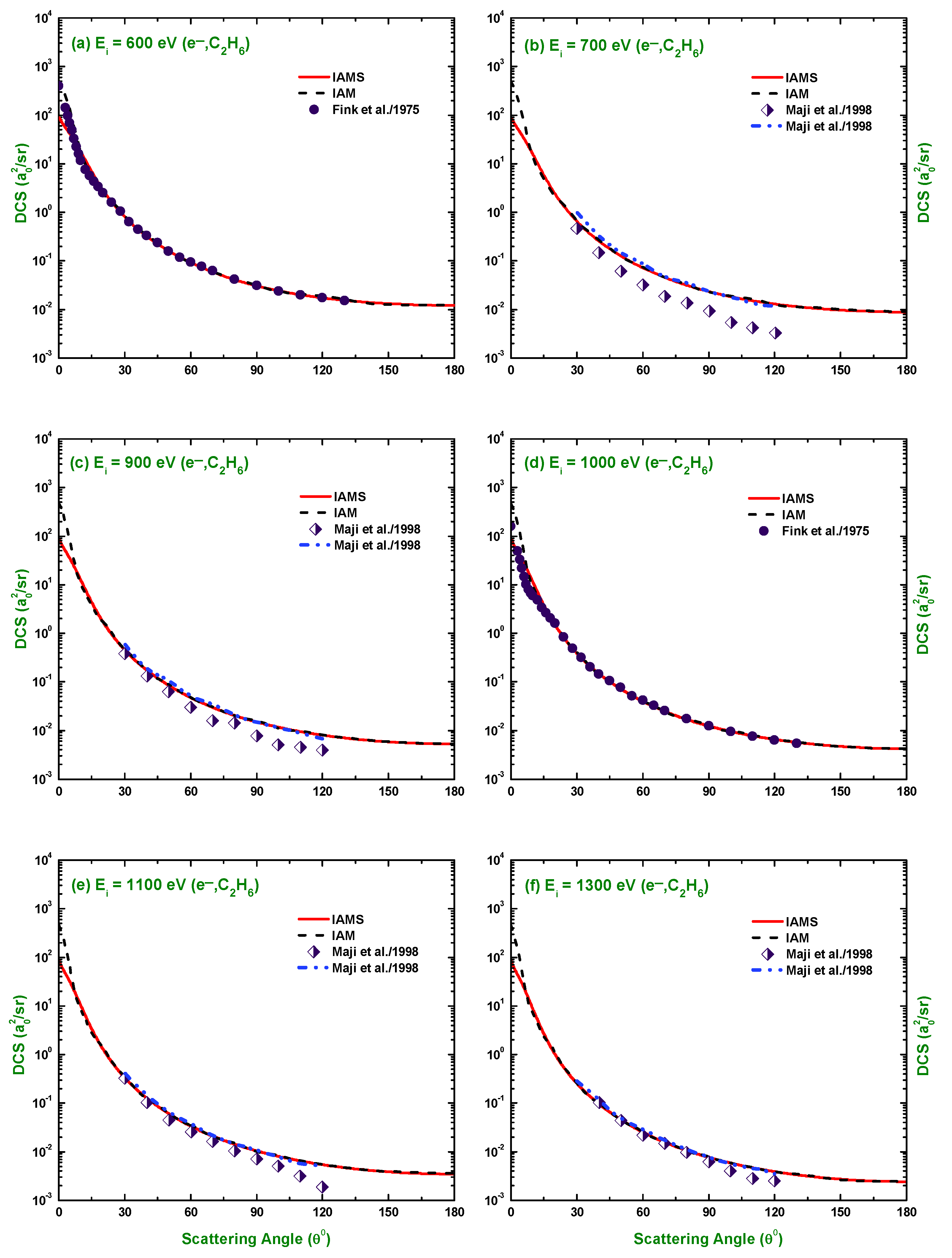
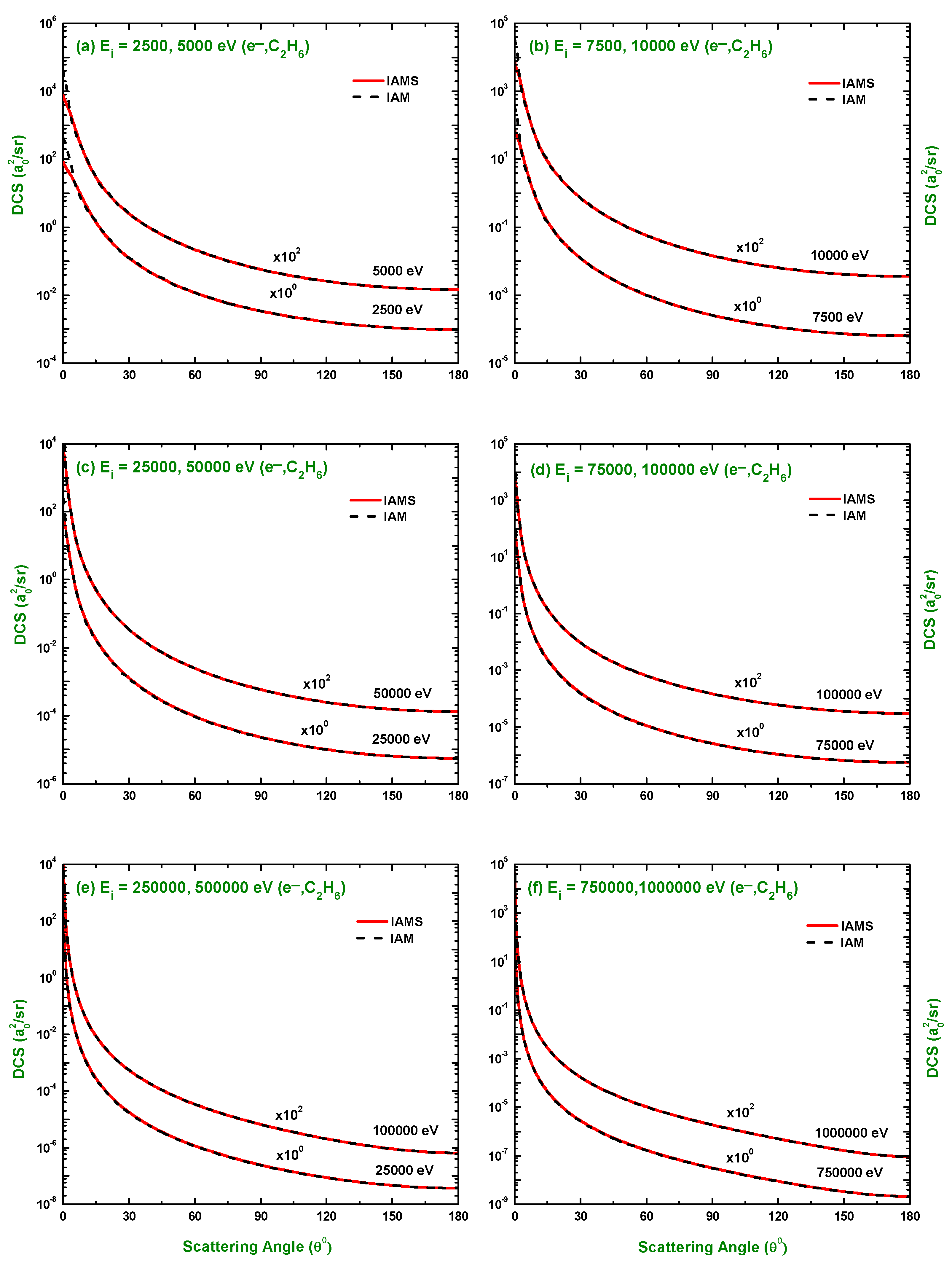
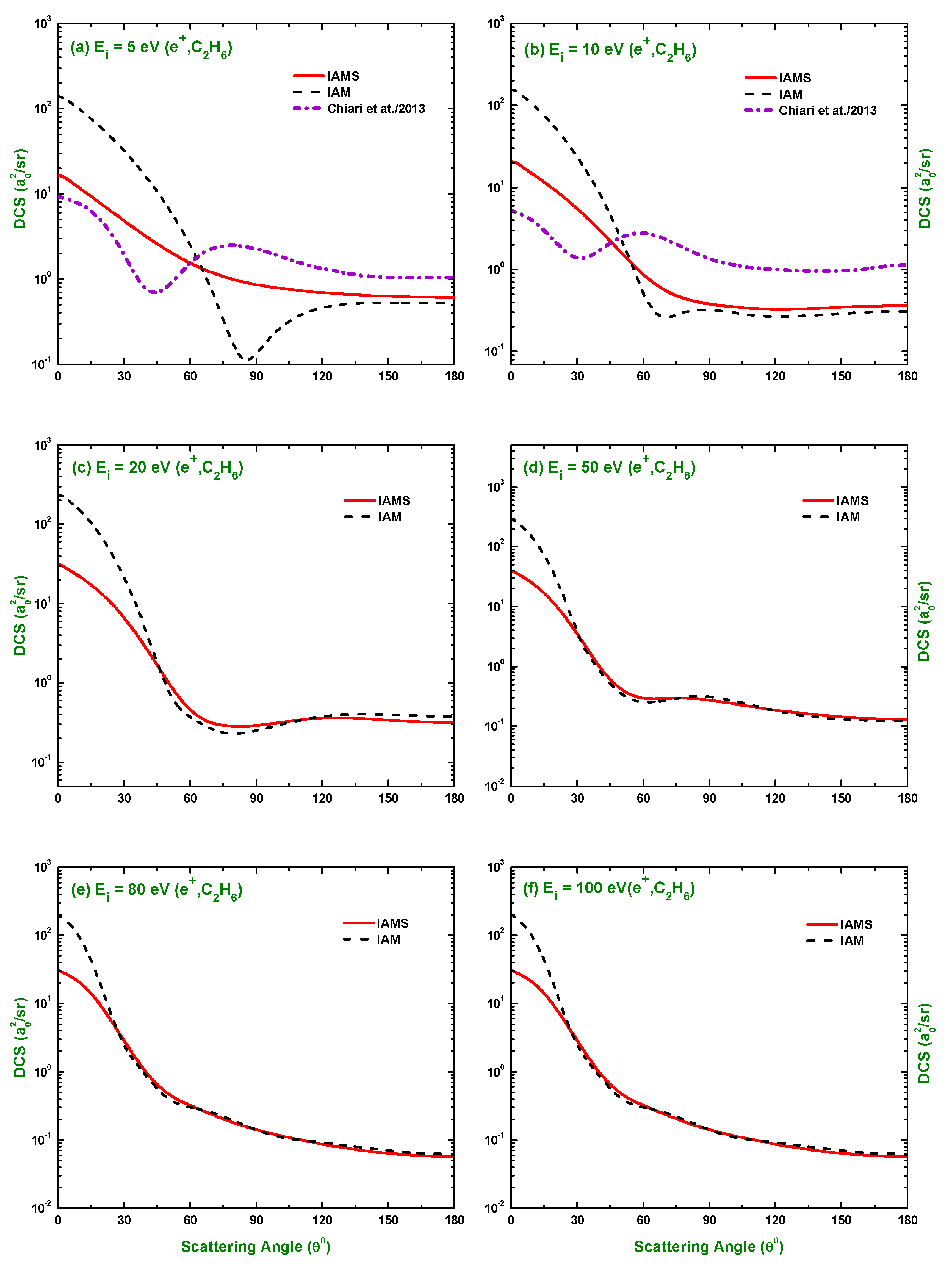
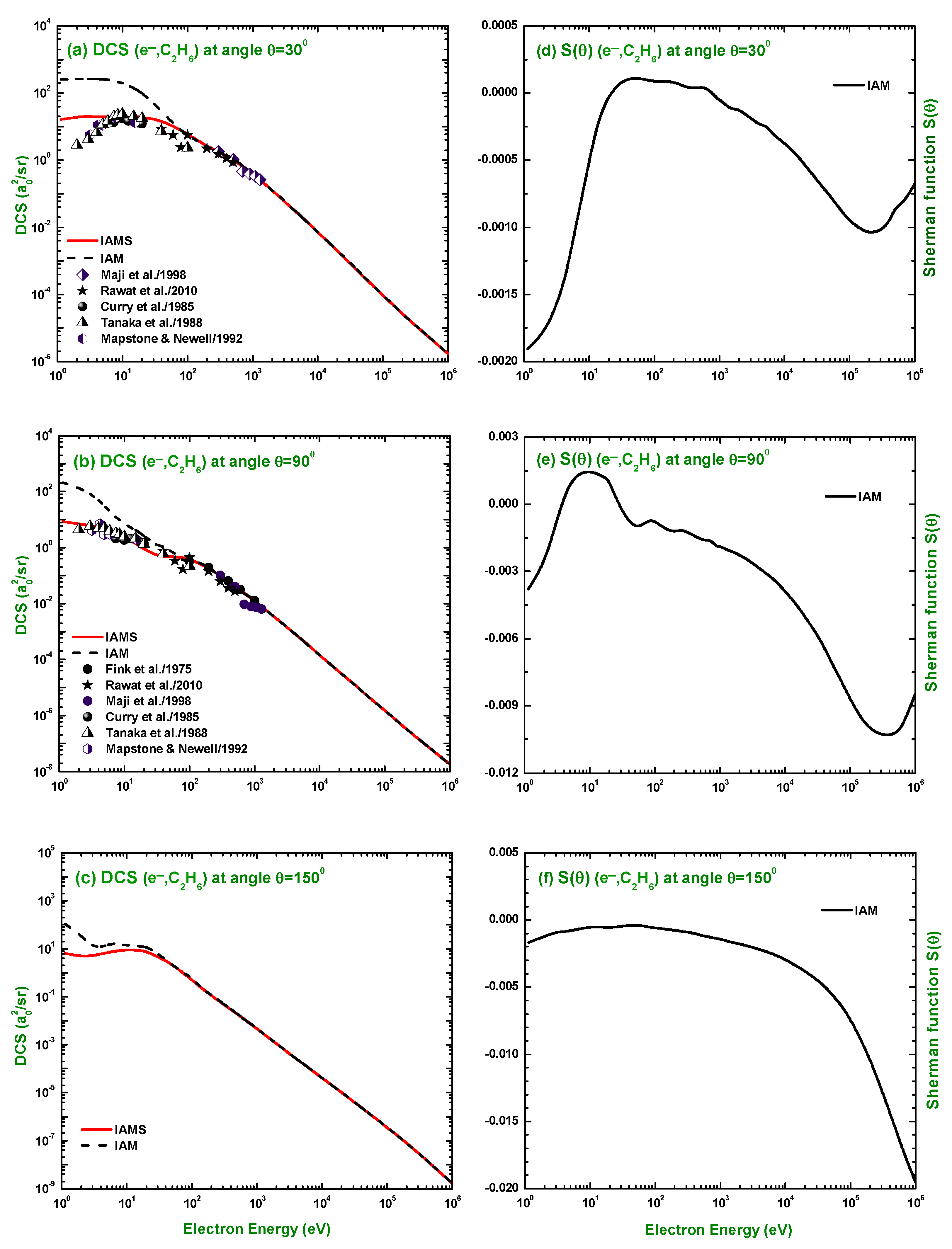
3.1. Differential Cross-Section and Sherman Function
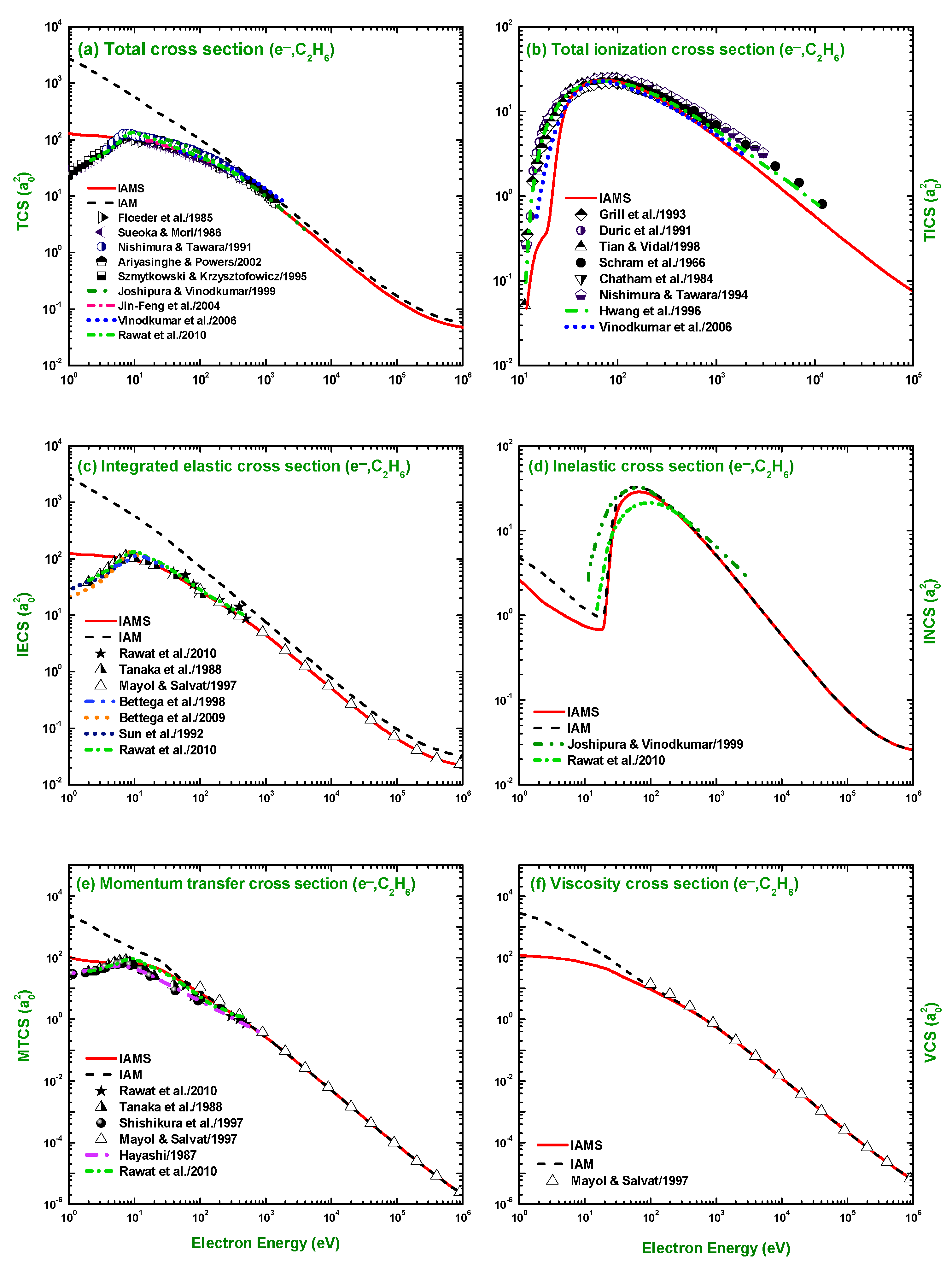
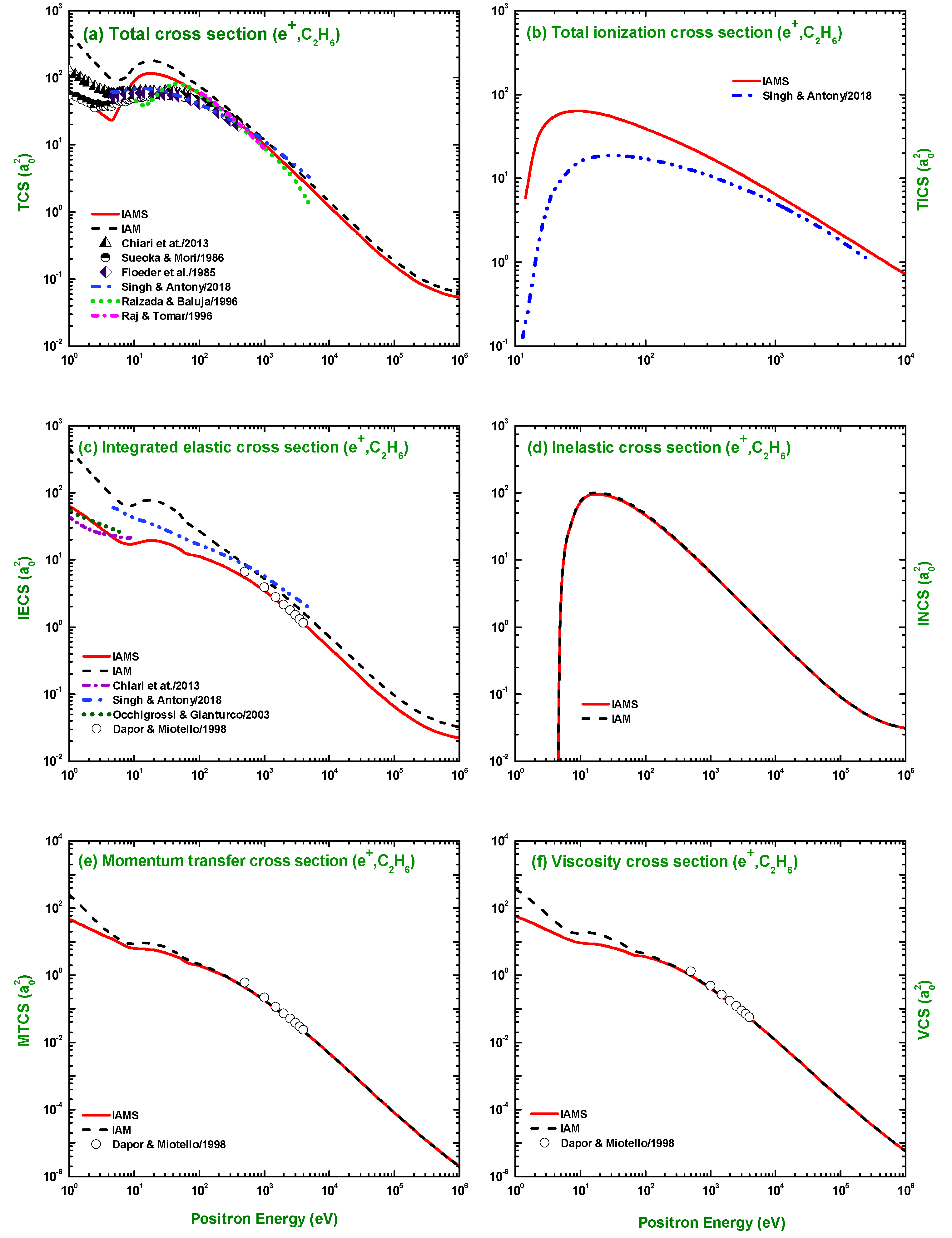
3.2. TCS, TICS, IECS, INCS, MTCS, and VCS
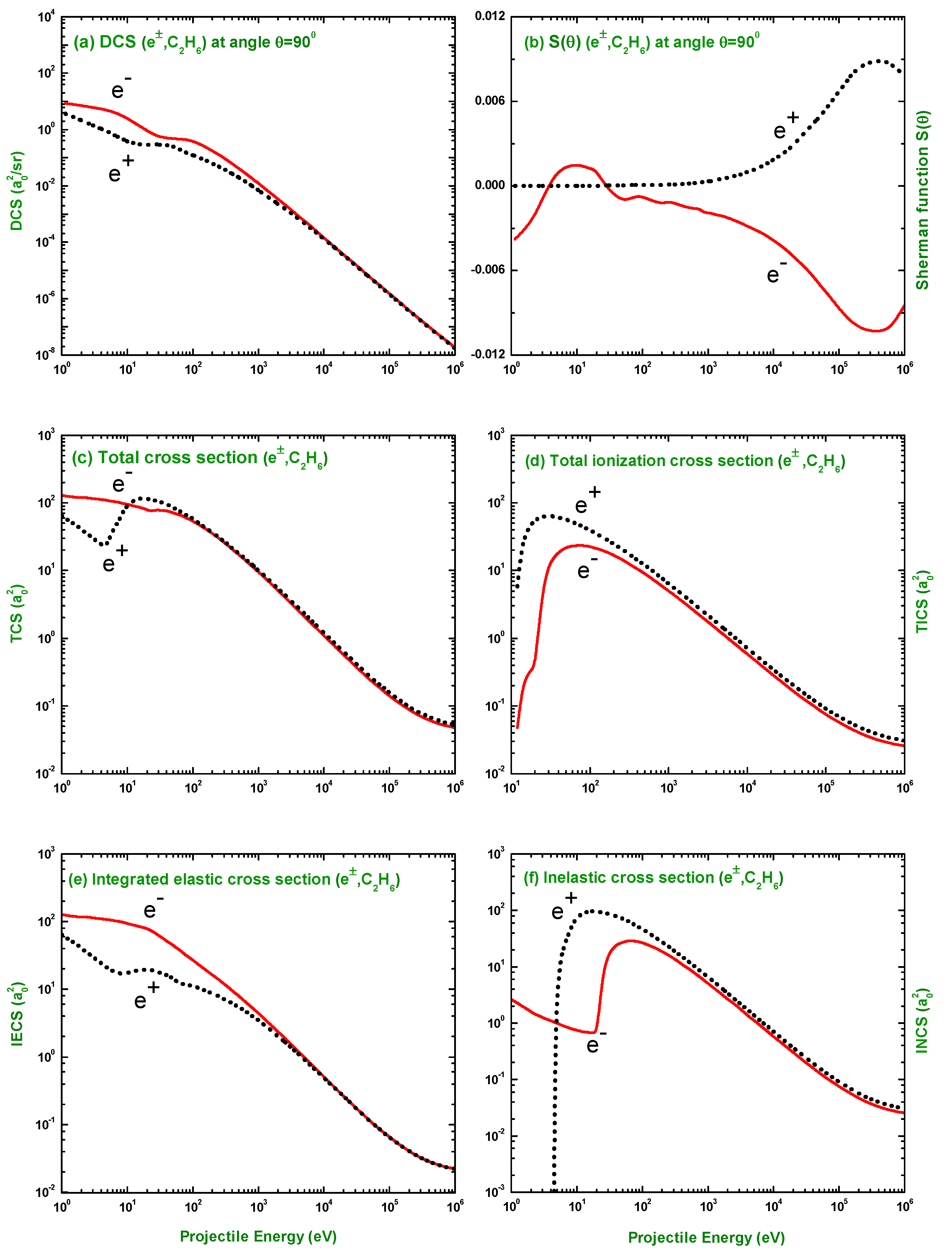
3.3. Comparison of DCS and for Electron and Positron Scattering
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Khandker, M.H.; Arony, N.T.; Haque, A.; Maaza, M.; Billah, M.M.; Uddin, M.A. Scattering of e± from N2 in the energy range 1 eV–10 keV. Mol. Phys. 2020, 118, e1699183. [Google Scholar] [CrossRef]
- Khandker, M.H.; Khatun, M.M.; Billah, M.M.; Haque, M.; Watabe, H.; Haque, A.F.; Uddin, M.A. Scattering of e± from CF3I Molecule. Atoms 2022, 10, 85. [Google Scholar] [CrossRef]
- Billah, M.M.; Khatun, M.M.; Haque, M.M.; Ali, M.Y.; Khandker, M.H.; Haque, A.K.F.; Watabe, H.; Uddin, M.A. A Theoretical Study of Scattering of Electrons and Positrons by CO2 Molecule. Atoms 2022, 10, 31. [Google Scholar] [CrossRef]
- Singh, S.; Dutta, S.; Naghma, R.; Antony, B. Positron scattering from simple molecules. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 135202. [Google Scholar] [CrossRef]
- Lane, N.F. The theory of electron-molecule collisions. Rev. Mod. Phys. 1980, 52, 29–119. [Google Scholar] [CrossRef]
- Phaneuf, R.A. Critical assessment of atomic collision cross-section data for fusion plasma applications. Phys. Scr. 1993, T47, 124–127. [Google Scholar] [CrossRef]
- Kohl, D.; Bartell, L.S. Electron Densities from Gas-Phase Electron Diffraction Intensities. I. Preliminary Considerations. J. Chem. Phys. 1969, 51, 2891–2895. [Google Scholar] [CrossRef]
- Dirac, P.A.M.; Fowler, R.H. The quantum theory of the electron. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1928, 117, 610–624. [Google Scholar] [CrossRef]
- Anderson, C.D. The Positive Electron. Phys. Rev. 1933, 43, 491–494. [Google Scholar] [CrossRef]
- Blackett, P.M.S.; Occhialini, G.P.S.; Rutherford, E. Some photographs of the tracks of penetrating radiation. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1933, 139, 699–726. [Google Scholar] [CrossRef]
- Ghosh, A.; Sil, N.; Mandal, P. Positron-atom and positron-molecule collisions. Phys. Rep. 1982, 87, 313–406. [Google Scholar] [CrossRef]
- Crannell, C.J.; Joyce, G.; Ramaty, R.; Werntz, C. Formation of the 0.511 MeV line in solar flares. Astrophys. J. 1976, 210, 582–592. [Google Scholar] [CrossRef]
- Broadfoot, A.; Belton, M.; Takacs, P.; Sandel, B.; Shemansky, D.; Holberg, J.; Ajello, J.; Atreya, S.; Donahue, T.; Moos, H.; et al. Extreme ultraviolet observations from Voyager 1 encounter with Jupiter. Science 1979, 204, 979–982. [Google Scholar] [CrossRef]
- Tawara, H.; Itikawa, Y.; Nishimura, H.; Yoshino, M. Cross Sections and Related Data for Electron Collisions with Hydrogen Molecules and Molecular Ions. J. Phys. Chem. Ref. Data 1990, 19, 617–636. [Google Scholar] [CrossRef]
- Duncan, C.W.; Walker, I.C. Collision cross-sections for low-energy electrons in some simple hydrocarbons. J. Chem. Soc. Faraday Trans. 2 1974, 70, 577–585. [Google Scholar] [CrossRef]
- Fink, M.; Jost, K.; Herrmann, D. Differential cross-sections for elastic electron scattering. III. The C2H2, C2H4, and C2H6 results. J. Chem. Phys. 1975, 63, 1985–1987. [Google Scholar] [CrossRef]
- Christophorou, L.G.; McCorkle, D.L. Experimental evidence for the existence of a Ramsauer–Townsend minimum in liquid CH4 and Ar (Kr and Xe) and in gaseous C2H6 and C3H8. Can. J. Chem. 1977, 55, 1876–1884. [Google Scholar] [CrossRef]
- McCorkle, D.; Christophorou, L.; Maxey, D.; Carter, J. Ramsauer-Townsend minima in the electron-scattering cross-sections of polyatomic gases: Methane, ethane, propane, butane, and neopentane. J. Phys. B At. Mol. Phys. 1978, 11, 3067. [Google Scholar] [CrossRef]
- Floeder, K.; Fromme, D.; Raith, W.; Schwab, A.; Sinapius, G. Total cross-section measurements for positron and electron scattering on hydrocarbons between 5 and 400 eV. J. Phys. B At. Mol. Phys. 1985, 18, 3347. [Google Scholar] [CrossRef]
- Curry, P.; Newell, W.; Smith, A. Elastic and inelastic scattering of electrons by methane and ethane. J. Phys. B At. Mol. Phys. 1985, 18, 2303. [Google Scholar] [CrossRef]
- Sueoka, O.; Mori, S. Total cross-sections for low and intermediate energy positrons and electrons colliding with CH4, C2H4 and C2H6 molecules. J. Phys. B At. Mol. Phys. 1986, 19, 4035. [Google Scholar] [CrossRef]
- Tanaka, H.; Boesten, L.; Matsunaga, D.; Kudo, T. Differential elastic electron scattering cross-sections for ethane in the energy range from 2 to 100 eV. J. Phys. B At. Mol. Phys. 1988, 21, 1255. [Google Scholar] [CrossRef]
- Rawat, P.; Homem, M.; Sugohara, R.; Sanches, I.; Iga, I.; de Souza, G.; dos Santos, A.; Lucchese, R.; Machado, L.; Brescansin, L.; et al. Cross sections for electron scattering by ethane in the low-and intermediate-energy ranges. J. Phys. B At. Mol. Phys. 2010, 43, 225202. [Google Scholar] [CrossRef]
- Mapstone, B.; Newell, W. Elastic differential electron scattering from CH4, C2H4 and C2H6. J. Phys. B At. Mol. Phys. 1992, 25, 491. [Google Scholar] [CrossRef]
- Nishimura, H.; Tawara, H. Some aspects of total scattering cross-sections of electrons for simple hydrocarbon molecules. J. Phys. B At. Mol. Phys. 1991, 24, L363. [Google Scholar] [CrossRef]
- Szmytkowski, C.; Krzysztofowicz, A. Electron scattering from isoelectronic, Ne= 18, CH3X molecules (X= F, OH, NH2 and CH3). J. Phys. B At. Mol. Phys. 1995, 28, 4291. [Google Scholar] [CrossRef]
- Maji, S.; Basavaraju, G.; Bharathi, S.; Bhushan, K.; Khare, S. Elastic scattering of electrons by polyatomic molecules in the energy range 300-1300 eV: CO, H and. J. Phys. B At. Mol. Phys. 1998, 31, 4975. [Google Scholar] [CrossRef]
- Chiari, L.; Zecca, A.; Trainotti, E.; Bettega, M.; Sanchez, S.d.; Varella, M.d.N.; Lima, M.; Brunger, M. Cross sections for positron scattering from ethane. Phys. Rev. A 2013, 87, 032707. [Google Scholar] [CrossRef]
- Ariyasinghe, W.; Powers, D. Total electron scattering cross-sections of CH4, C2H2, C2H4, and C2H6 in the energy range 200–1400 eV. Phys. Rev. A 2002, 66, 052716. [Google Scholar] [CrossRef]
- Fink, M.; Yates, A.C. Theoretical electron scattering amplitudes and spin polarizations: Selected targets, electron energies 100 to 1500 eV. At. Data Nucl. Data Tables 1969, 1, 385–456. [Google Scholar] [CrossRef]
- Winstead, C.; Hipes, P.; Lima, M.; McKoy, V. Studies of electron collisions with polyatomic molecules using distributed-memory parallel computers. J. Chem. Phys. 1991, 94, 5455–5461. [Google Scholar] [CrossRef]
- Sun, W.; McCurdy, C.; Lengsfield, B., III. Ab initio study of low-energy electron-ethane scattering. J. Chem. Phys. 1992, 97, 5480–5488. [Google Scholar] [CrossRef]
- Bettega, M.; Oliveira, A.; Natalense, A.; Lima, M.; Ferreira, L. Static-exchange cross-sections for electron-collisions with BH, CH, Si H, and Ge H. Eur. Phys. J. At. Mol. Opt. Plasma Phys. 1998, 1, 291–296. [Google Scholar]
- Dapor, M.; Miotello, A. Differential, total, and transport cross-sections for elastic scattering of low energy positrons by neutral atoms (Z= 1–92, E= 500–4000 eV). At. Data Nucl. Data Tables 1998, 69, 1–100. [Google Scholar] [CrossRef]
- Grill, V.; Walder, G.; Scheier, P.; Kurdel, M.; Märk, T. Absolute partial and total electron impact ionization cross-sections for C2H6 from threshold up to 950 eV. Int. J. Mass Spectrom. Ion Process. 1993, 129, 31–42. [Google Scholar] [CrossRef]
- Durić, N.; Čadež, I.; Kurepa, M. Electron impact total ionization cross-sections for methane, ethane and propane. Int. J. Mass Spectrom. Ion Process. 1991, 108, R1–R10. [Google Scholar] [CrossRef]
- Tian, C.; Vidal, C. Electron impact dissociative ionization of ethane: Cross sections, appearance potentials, and dissociation pathways. J. Chem. Phys. 1998, 109, 1704–1712. [Google Scholar] [CrossRef]
- Schram, B.; Van der Wiel, M.; De Heer, F.; Moustafa, H. Absolute gross ionization cross-sections for electrons (0.6–12 keV) in hydrocarbons. J. Chem. Phys. 1966, 44, 49–54. [Google Scholar] [CrossRef]
- Nishimura, H.; Tawara, H. Total electron impact ionization cross-sections for simple hydrocarbon molecules. J. Phys. B At. Mol. Phys. 1994, 27, 2063. [Google Scholar] [CrossRef]
- Shishikura, Y.; Asano, K.; Nakamura, Y. Low-energy electron collision cross-sections of ethane by electron swarm study. J. Phys. Appl. Phys. 1997, 30, 1610. [Google Scholar] [CrossRef]
- Bettega, M.H.; da Costa, R.; Lima, M.A. Low-energy electron collisions with ethane. Braz. J. Phys. 2009, 39, 69–73. [Google Scholar] [CrossRef]
- Joshipura, K.; Vinodkumar, M. Various total cross-sections for electron impact on, and. Eur. Phys. J. D-At. Mol. Opt. Plasma Phys. 1999, 5, 229–235. [Google Scholar]
- Jin-Feng, S.; Chao-Ling, D.; De-Heng, S.; Yu-Fang, L. Additivity rule for electron scattering on hydrocarbon molecules—Considering two different shielding effects. Chin. Phys. 2004, 13, 1418. [Google Scholar] [CrossRef]
- Vinodkumar, M.; Joshipura, K.; Limbachiya, C.; Antony, B. Electron impact total and ionization cross-sections for some hydrocarbon molecules and radicals. Eur. Phys. J. D-At. Mol. Opt. Plasma Phys. 2006, 37, 67–74. [Google Scholar] [CrossRef]
- Hwang, W.; Kim, Y.K.; Rudd, M.E. New model for electron-impact ionization cross-sections of molecules. J. Chem. Phys. 1996, 104, 2956–2966. [Google Scholar] [CrossRef]
- Hayashi, M. Electron collision cross-sections for molecules determined from beam and swarm data. In Swarm Studies and Inelastic Electron-Molecule Collisions; Springer: New York, NY, USA, 1987; pp. 167–187. [Google Scholar]
- Raizada, R.; Baluja, K. Positron scattering from hydrocarbons. Pramana 1996, 46, 431–449. [Google Scholar] [CrossRef]
- Raj, D.; Tomar, S. Scattering of positrons by hydrocarbons at intermediate energies. Indian J. Phys. 1996, 70, 375–383. [Google Scholar]
- Singh, S.; Antony, B. Positron induced scattering cross-sections for hydrocarbons relevant to plasma. Phys. Plasmas 2018, 25, 053503. [Google Scholar] [CrossRef]
- Occhigrossi, A.; Gianturco, F. Low-energy positron dynamics in small hydrocarbon gases. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 1383. [Google Scholar] [CrossRef]
- Billah, M.M.; Khandker, M.H.; Shorifuddoza, M.; Sayed, M.; Watabe, H.; Haque, A.; Uddin, M.A. Theoretical investigations of e±–CO scattering. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 095203. [Google Scholar] [CrossRef]
- Hassan, R.; Nure Alam Abdullah, M.; Shorifuddoza, M.; Khandker, M.H.; Patoary, M.A.R.; Haque, M.; Das, P.K.; Maaza, M.; Masum Billah, M.; Haque, A.; et al. Scattering of e± off silver atom over the energy range 1 eV–1 MeV. Eur. Phys. J. D 2021, 75, 1–23. [Google Scholar] [CrossRef]
- Akter, N.; Nure Alam Abdullah, M.; Shorifuddoza, M.; Patoary, M.A.R.; Masum Billah, M.; Khandker, M.H.; Maaza, M.; Watabe, H.; Haque, A.; Alfaz Uddin, M. Theoretical study of e±-NH3 scattering. Mol. Phys. 2022, 120, e2097135. [Google Scholar] [CrossRef]
- Salvat, F. Optical-model potential for electron and positron elastic scattering by atoms. Phys. Rev. A 2003, 68, 012708. [Google Scholar] [CrossRef]
- Salvat, F.; Jablonski, A.; Powell, C.J. ELSEPA—Dirac partial wave calculation of elastic scattering of electrons and positrons by atoms, positive ions and molecules. Comput. Phys. Commun. 2005, 165, 157–190. [Google Scholar] [CrossRef]
- Desclaux, J. A multiconfiguration relativistic DIRAC-FOCK program. Comput. Phys. Commun. 1975, 9, 31–45. [Google Scholar] [CrossRef]
- Furness, J.B.; McCarthy, I.E. Semiphenomenological optical model for electron scattering on atoms. J. Phys. B 1973, 6, 2280–2291. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Jain, A. Low-energy positron-argon collisions by using parameter-free positron correlation polarization potentials. Phys. Rev. A 1990, 41, 2437–2444. [Google Scholar] [CrossRef]
- Walker, D. Relativistic effects in low energy electron scattering from atoms. Adv. Phys. 1971, 20, 257–323. [Google Scholar] [CrossRef]
- Khare, S.P. Introduction to the Theory of Collisions of Electrons with Atoms and Molecules; Springer Science & Business Media: New York, NY, USA, 2002. [Google Scholar]
- Mott, N.F.; Massey, H.S.W. The Theory of Atomic Collisions; The International Series of Monographs on Physics; Clarendon Press: Oxford, UK, 1965; Volume 35. [Google Scholar]
- Blanco, F.; Garcıa, G. Screening corrections for calculation of electron scattering from polyatomic molecules. Phys. Lett. A 2003, 317, 458–462. [Google Scholar] [CrossRef]
- Blanco, F.; Ellis-Gibbings, L.; García, G. Screening corrections for the interference contributions to the electron and positron scattering cross-sections from polyatomic molecules. Chem. Phys. Lett. 2016, 645, 71–75. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2004; Volume 85. [Google Scholar]
- Joshipura, K.N.; Vinodkumar, M.; Patel, U.M. Electron impact total cross-sections of CHx, NHx and OH radicals vis-à-vis their parent molecules. J. Phys. B At. Mol. Phys. 2001, 34, 509–519. [Google Scholar] [CrossRef]
- Johnson, R. NIST 101. Computational Chemistry Comparison and Benchmark Database. 1999. Available online: https://cccbdb.nist.gov/ (accessed on 5 January 2023).
- McEachran, R.; Stauffer, A.; Piwinski, M.; Pravica, L.; Williams, J.; Cvejanovic, D.; Samarin, S. Investigation of the behavior of the Sherman function for elastic electron scattering from Kr and Xe. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 215208. [Google Scholar] [CrossRef]
- Chatham, H.; Hils, D.; Robertson, R.; Gallagher, A. Total and partial electron collisional ionization cross-sections for CH4, C2H6, SiH4, and Si2H6. J. Chem. Phys. 1984, 81, 1770–1777. [Google Scholar] [CrossRef]
- Mayol, R.; Salvat, F. Total and transport cross-sections for elastic scattering of electrons by atoms. At. Data Nucl. Data Tables 1997, 65, 55–154. [Google Scholar] [CrossRef]
- Shyn, T.; Sharp, W. Angular distributions of electrons elastically scattered from H2. Phys. Rev. A 1981, 24, 1734. [Google Scholar] [CrossRef]


| (Å) | IP (eV) | |
|---|---|---|
| 4.226 | 11.52 | 10 |
| Atom | x | y | z |
|---|---|---|---|
| C | 0.0000 | 0.0000 | 0.7622 |
| C | 0.0000 | 0.0000 | −0.7622 |
| H | 0.0000 | 1.0189 | 1.1572 |
| H | −0.8824 | −0.5094 | 1.1572 |
| H | 0.8824 | −0.5094 | 1.1572 |
| H | 0.0000 | −1.0189 | −1.1572 |
| H | −0.8824 | 0.5094 | −1.1572 |
| H | 0.8824 | 0.5094 | −1.1572 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sathee, N.M.B.; Khatun, M.M.; Rani, A.; Billah, M.M.; Abdullah, M.N.A.; Khandker, M.H.; Watabe, H.; Haque, A.K.F.; Uddin, M.A. Scattering of e± by C2H6 Molecule over a Wide Range of Energy: A Theoretical Investigation. Molecules 2023, 28, 1255. https://doi.org/10.3390/molecules28031255
Sathee NMB, Khatun MM, Rani A, Billah MM, Abdullah MNA, Khandker MH, Watabe H, Haque AKF, Uddin MA. Scattering of e± by C2H6 Molecule over a Wide Range of Energy: A Theoretical Investigation. Molecules. 2023; 28(3):1255. https://doi.org/10.3390/molecules28031255
Chicago/Turabian StyleSathee, N. M. B., M. Mousumi Khatun, Anita Rani, M. Masum Billah, M. Nure Alam Abdullah, Mahmudul H. Khandker, Hiroshi Watabe, A. K. Fazlul Haque, and M. Alfaz Uddin. 2023. "Scattering of e± by C2H6 Molecule over a Wide Range of Energy: A Theoretical Investigation" Molecules 28, no. 3: 1255. https://doi.org/10.3390/molecules28031255
APA StyleSathee, N. M. B., Khatun, M. M., Rani, A., Billah, M. M., Abdullah, M. N. A., Khandker, M. H., Watabe, H., Haque, A. K. F., & Uddin, M. A. (2023). Scattering of e± by C2H6 Molecule over a Wide Range of Energy: A Theoretical Investigation. Molecules, 28(3), 1255. https://doi.org/10.3390/molecules28031255








