Next Article in Journal
Comprehensive Identification of Ginsenosides in the Roots and Rhizomes of Panax ginseng Based on Their Molecular Features-Oriented Precursor Ions Selection and Targeted MS/MS Analysis
Next Article in Special Issue
Evolution of the Electronic Structure of the trans-[Re6S8bipy4Cl2] Octahedral Rhenium Cluster during Reduction
Previous Article in Journal
Biological Assessment of Stevioside and Sucralose as Sucrose Substitutes for Diabetics on STZ-Induced Diabetes in Rats
Previous Article in Special Issue
Chirality and Relativistic Effects in Os3(CO)12
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 3
10.3390/molecules28030942
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

σ-Aromatic MAl6S6 (M = Ni, Pd, Pt) Stars Containing Planar Hexacoordinate Transition Metals

by
Li-Xia Bai
and
Jin-Chang Guo
*
Nanocluster Laboratory, Institute of Molecular Science, Shanxi University, Taiyuan 030006, China
*
Author to whom correspondence should be addressed.
Molecules 2023, 28(3), 942; https://doi.org/10.3390/molecules28030942
Submission received: 23 December 2022 / Revised: 12 January 2023 / Accepted: 14 January 2023 / Published: 17 January 2023
(This article belongs to the Special Issue DFT Quantum Chemical Calculation of Metal Clusters)
Browse Figures
Versions Notes

Abstract

:
Hypercoordinate transition-metal species are mainly dominated by the 18-valence-electron (18ve) counting. Herein, we report ternary MAl6S6 (M = Ni, Pd, Pt) clusters with the planar hexacoordinate metal (phM) centers, which feature 16ve counting instead of the classic 18ve rule. These global-minimum clusters are established via unbiased global searches, followed by PBE0 and single-point CCSD(T) calculations. The phM MAl6 units are stabilized by six peripheral bridging S atoms in these star-like species. Chemical bonding analyses reveal that there are 10 delocalized electrons around the phM center, which can render the aromaticity according to the (4n + 2) Hückel rule. It is worth noting that adding an (or two) electron(s) to its π-type lowest unoccupied molecular orbital (LUMO) will make the system unstable.

1. Introduction

The design, synthesis, and characterization of new two-dimensional (2D) materials have attracted wide attention in recent years, for unexpected properties and wide applications [1,2,3,4,5]. As its units or fragments, the corresponding planar clusters have gradually become one of the focuses in cluster science. Planar hypercoordinate carbon species have been explored for half a century due to their exotic structures, unusual chemical bonding, as well as potential applications since Hoffmann et al. put forward the strategies for stabilizing planar tetracoordinate carbon (ptC) structures in 1970 [6,7,8,9,10,11,12,13]. A variety of ptC, planar pentacoordinate carbon (ppC), planar hexacoordinate carbon (phC) species were predicted theoretically or characterized experimentally [14,15,16,17,18,19,20,21,22,23,24,25]. The atypical planar hypercoordination is not limited to carbon, which can be extended to other main group elements and transition metals. Due to the electron-deficiency nature of boron, Bn− clusters in the size range of n = 3–40 have been confirmed to assume planar or quasi-planar structures, in which some species can possess even higher coordination numbers [26,27]. Planar hepta- and octacoordinate boron (p7B, p8B) centers can be stabilized in the beautiful molecular wheels B8− and B9−, which were experimentally observed by Zhai in 2003 [28]. The wheel-like ppB B6H5+, ppBe BeCu5, p8Be BeB82−, p7Sc ScCu7, ppAl Cu5Al2+, ppGa Cu5Ga2+, and star-like ppB BBe5Au5, phGa GaBe6Au6 were identified as the global minima [29,30,31,32,33,34,35]. Using size-selected anion photoelectron spectroscopy combined with ab initio calculations, a series of transition-metal-centered monocyclic boron wheel clusters M©Bn (n = 8–10) were reported by Wang and Boldyrev [36]. Among them, D8h-Co©B8−, D9h-Ru©B9−, D10h-Ta©B10− are the most representative molecular wheels, containing the planar octacoordinate cobalt, planar nonacoordinate ruthenium, and planar decacoordinate tantalum, respectively [37,38]. More importantly, an effective principle was proposed for designing the stable M©Bnk−, that is x =12-n-k, where x is the required valence of the transition-metal M atom. Obviously, Co©B8− and Ru©B9− follow the formula exactly. For D10h-Ta©B10−, the corresponding electron counting formula needs to upgrade to x =16-n-k. It should be noted that these beautiful molecular wheels possess σ and π double aromaticity. In 2015, a series of planar wheel-type D6h M©B6H6−/0/+ (M = Mn, Fe, and Co) clusters were theoretically designed by Hou [39]. The H-bridged BenHn rings can be used to stabilize the ppC, phB, and p7Au [40,41,42]. However, it is a failure to stabilize the transition metal atom with a BenHn ring. Recently, the ppB BAl5S5+, ppC CAl5O5+, and CB5S5+ molecular stars were predicted in theory [43,44,45]. Very recently, the MB7O7+ (M = Ni, Pd, Pt) stars were reported as the global minima by Wu, which contain the p7M centers and possess the σ aromaticity alone [46]. To better broaden the research field of the planar hypercoordinate transition metals species, it is highly desirable to design the phM clusters, which is the theme of our present study. To host a planar hypercoordinate transition metal center, the M atom and surrounding ligands ring must match both geometrically and electronically. One interesting question arises regarding how to design molecular stars containing the planar hexacoordinate Ni/Pd/Pt centers.
Our design idea is shown in Scheme 1. Geometrically, the star-like B6O6 ring is too small to hold a Ni atom. It is imperative to increase the geometrical size of the ligand ring. Our preliminary calculations show that D6h NiAl6O6 is only a transition state structure. Can we stabilize the Ni/Pd/Pt atoms using a larger Al6S6 ring? The answer is positive. Geometrically, the Al6S6 ring is suitable to hold the Ni/Pd/Pt transition metal center. As we all know, 18-valence-electron (18ve) counting is popular for transition metal species. It is easy to think of MAl6S62− (M = Ni, Pd, Pt) systems first. However, MAl6S62− (M = Ni, Pd, Pt) are the third-order saddle points on the corresponding energy surfaces, at the PBE0/def2-TZVP level. Removing one electron from MAl6S62−, the MAl6S6− (M = Ni, Pd, Pt) are formed. Unfortunately, MAl6S6− (M = Ni, Pd, Pt) are still unstable, which are only the second-order saddle points. Thus, both 18ve and 17ve counting are invalid. Frequency analyses indicate that neutral MAl6S6 (M = Ni, Pd, Pt) are the true minima at the PBE0/def2-TZVP level. Thus, 16ve counting seems to be an appropriate electronic rule to design the phM species.
The present paper reports ternary S-bridged MAl6S6 (M = Ni, Pd, Pt) molecular stars, which contain the planar hexacoordinate transition metal centers. Interestingly, MAl6S6 (M = Ni, Pd, Pt) possesses 10σ aromaticity alone, whose transition metal centers follow the 16ve counting instead of the typical 18ve rule. The MAl6S6 (M = Ni, Pd, Pt) species reported in this paper will provide new candidates for further exploration of 2D materials.

2. Computational Details

The potential energy surfaces of MAl6S6 (M = Ni, Pd, Pt) were explored by the Coalescence Kick (CK) algorithm [47,48], at the PBE0/Lanl2DZ level of theory [49]. Both singlet and triplet surfaces were considered. More than 8000 stationary points (4000 singlets and 4000 triplets) were probed for each of the MAl6S6 (M = Ni, Pd, Pt) clusters. Subsequent structural optimizations were carried out for the low-lying isomers using the PBE0 method with the def2-TZVP basis set [50]. Frequency calculations were performed at the same level to ensure that all the structures are true minima on the potential energy surface. The energies were refined by the single point CCSD(T)/def2-TZVP calculations at the PBE1PBE/def2-TZVP geometries [51]. The final relative energies were determined by the CCSD(T)/def2-TZVP energy plus the PBE0/def2-TZVP zero-point energy corrections. Born–Oppenheimer molecular dynamic (BOMD) simulations were performed at the PBE0/def2-SVP level [52].
To obtain Wiberg bond indices (WBIs) and natural atomic charges, natural bond orbital (NBO) analyses were conducted at the PBE0/def2-TZVP level using NBO6.0 [53]. The atomic composition of canonical molecular orbitals (CMOs), adaptive natural density partitioning (AdNDP), and electron localization function (ELF) analyses were accomplished using the Multiwfn program [54,55,56]. Nucleus-independent chemical shifts (NICSs) and iso-chemical shielding surfaces in the z direction (ICSSzz) were calculated to assess aromaticity [57,58]. All electronic structure calculations were carried out using the Gaussian 16 package [59]. Molecular structures, CMO pictures, AdNDP, and ELF results were visualized using CYLview [60] and GaussView, respectively.

3. Results and Discussion

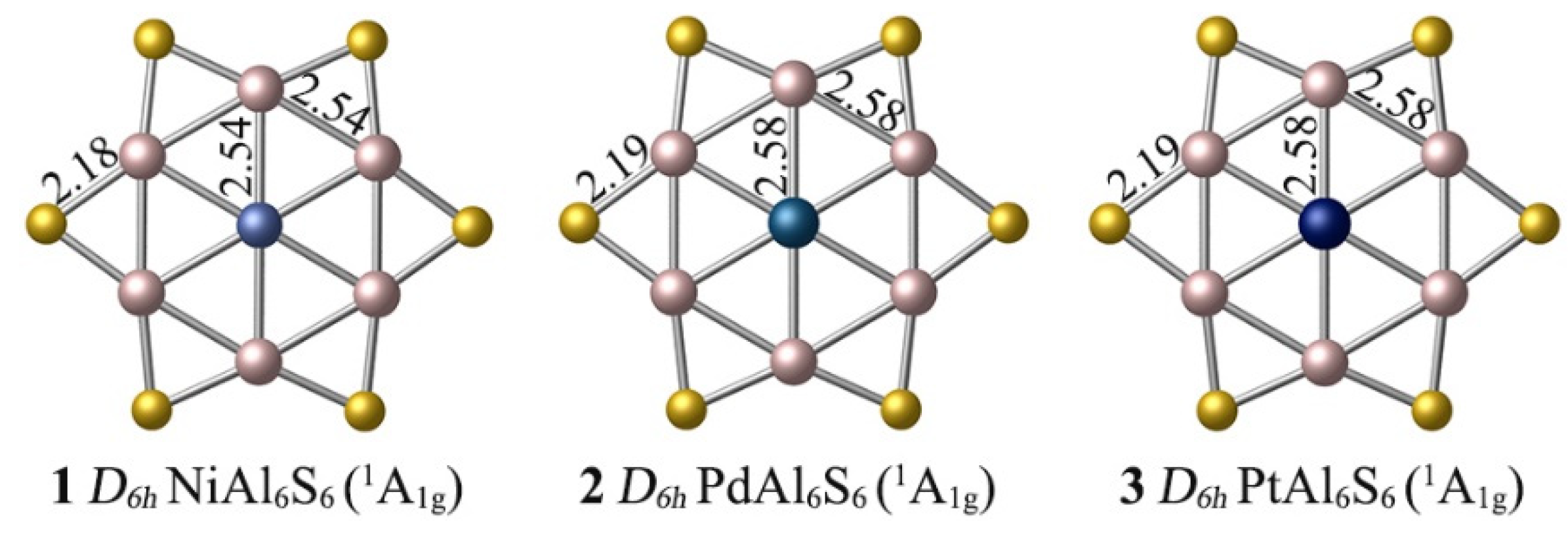
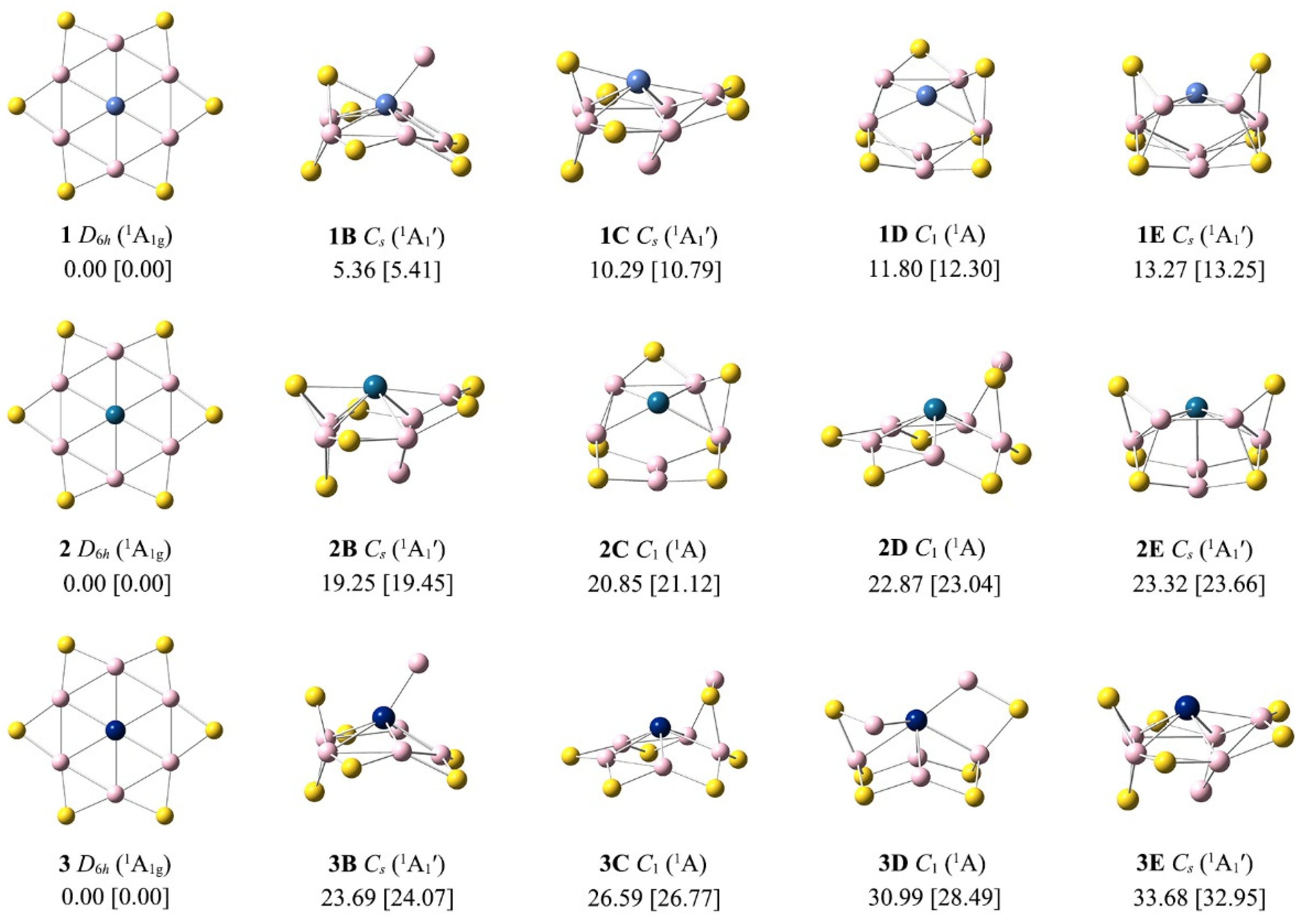
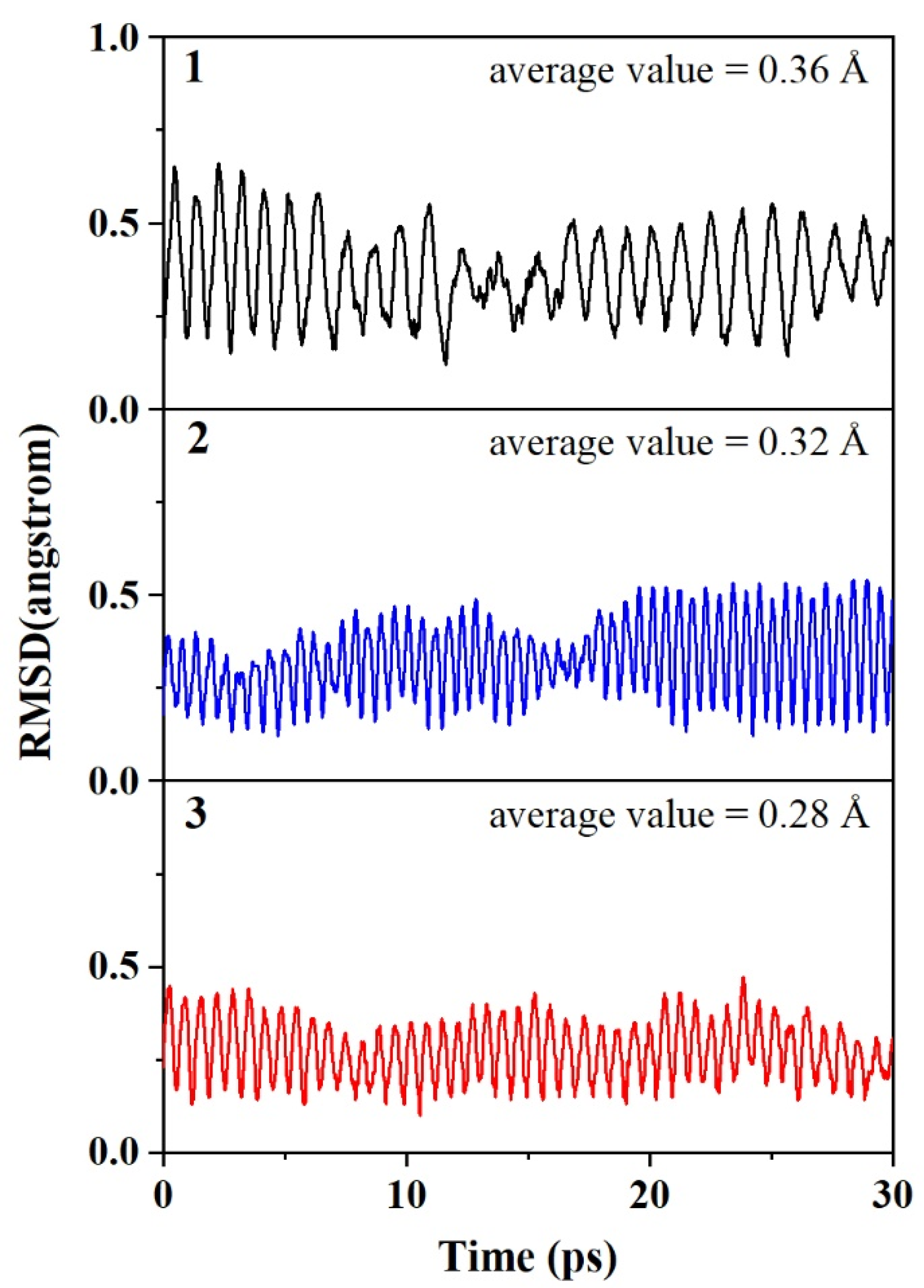
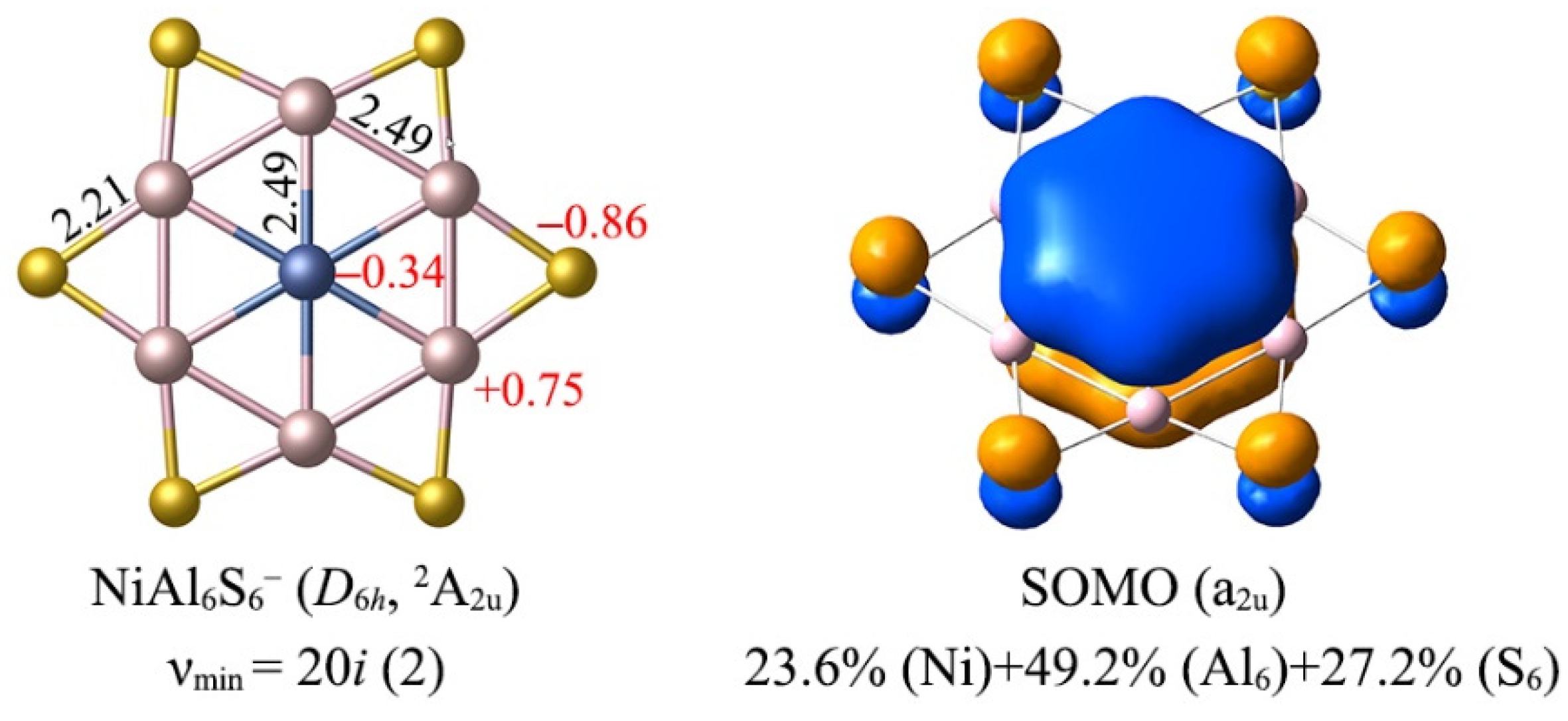
3.1. Structures and Stability

The optimized global minima (GMs) structures of ternary MAl6S6 (M = Ni, Pd, Pt) clusters were depicted in Figure 1, at the PBE0/def2-TZVP level. The phM GMs (1–3) assume the perfect D6h symmetry, which is composed of the M center, Al6 ring, and six S bridges at the periphery. Geometrically, the star-like Al6S6 ring is suitable for hosting these hexacoordinate planar transition metals (phMs) with the high symmetry of D6h, which has good tolerance and can be adjusted according to the size of the central atom. Frequency analyses indicate that the empty D6h Al6S6 ring is unstable, which is only a transition state at PBE0/def2-TZVP level. Introducing a transition metal atom into its center can help to stabilize it. Alternative optimized low-lying structures are shown in Figure 2. To check for consistency in terms of structures and energetics, the corresponding B3LYP/def2-TZVP calculations and vibrational analyses were further done for 1–3 and the low-lying isomers, as well as the single-point CCSD(T)/def2-TZVP//B3LYP/def2-TZVP calculations [61,62]. As shown in Figure 2, the CCSD(T)//B3LYP energetics data (in square brackets) are closely consistent with those at single-point CCSD(T)//PBE0. Thus, we shall only discuss the PBE0 and CCSD(T)//PBE0 data in the following discussion.
At the CCSD(T)//PBE0 level, the GMs 1, 2, 3 lie 5.36, 19.25, and 23.69 kcal mol−1 lower than the second low-lying isomers 1B, 2B, and 3B, respectively. Their optimized Cartesian coordinates for GMs 1–3 and the low-lying isomers 1B–3E are provided in Table S1 (ESI†). In these low-lying isomers, all Al atoms tend to coordinate directly to the M center, whereas most of the S atoms are situated on the periphery and link with Al atoms as the bridges (μ2-S). It should be noted that there is one μ3-S atom is bound to the M center as the face-capping group in 1B/1C/1D/2B/2D/3B/3C/3E. However, there is no terminal μ1-S atom in these low-lying isomers. The central M atom has a coordination number of six/seven, while the coordination number of the Al atom is three/four in 1B–3E. The most stable triplet structures are obviously higher than 1E, 2E, and 3E in energy at the CCSD(T) level, respectively. Thus, the phM 1, 2, and 3 stars are the GMs on the potential energy surfaces.
The bond distances, Wiberg bond indices (WBIs), and natural population analysis (NPA) charges can help us to explore the bonding characters of 1–3, which are shown in Figure 1 and Table 1. As shown in Figure 1, the calculated Ni–Al bond distance in 1 is 2.54 Å, which is longer than the Ni–Al covalent single bond length (2.36 Å) based on covalent atomic radii proposed by Pyykkö [63]. Because of the perfect D6h symmetry, the Al–Al bond distance in 1 is also 2.54 Å, which is close to the recommended single bond (2.52 Å). The Al–S distance 2.18 Å, is between the Al-S single bond (2.29 Å) and Al=S double bonds (2.07 Å). Considering the differences in electronegativity of the elements (Ni:1.9, Al:1.5, S:2.5), Ni-Al and Al-S bonding can be sort of polar in nature. Thus, it is not easy to judge the bond strength just by the bond distances. WBIs and NPA charges offer valuable bonding information. As shown in Table 1, the WBINi–Al 0.22 and WBIAl–Al 0.40, are less than 0.5, indicating their delocalized bonding nature. The WBIAl–S in 1 is 0.88, suggesting that the Al–S bonding is quite strong, which is consistent with the conclusions from the analyses of bond distances. With the increases in the size of central M atoms, the changes in the corresponding bond distances have almost the same trends. Interestingly, the Pd–Al in 2 has exactly equal bond distance with the Pt–Al (2.58 Å) in 3. The WBIPd–Al and WBIPt–Al are 0.23 and 0.25, respectively. It should be noted that the periphery Al–S bond distances in 1–3 seem to be almost unchanged (from 2.18 to 2.19 Å), as well as their WBIs. Indeed, the bridging S atoms can help to make the relatively flexible Al6 ring more rigid to some extent.
Due to the electronegativity differences, there is obvious electron transfer from the Al atoms to the central M and periphery S atoms. As shown in Table 1, the NPA charges on Ni, Al, and S atoms are −0.30, +0.84, and −0.79 |e|, respectively, thus 1 features the negative–positive–negative charge distribution pattern, which favors the stabilization of the species via Coulomb attractions. Since Pd, Pt and Ni are in the same group in the periodic table, the charge distributions in 2 and 3 are basically similar to those of 1. It should be noted that the transition metals carry only a small number of negative charges, making them easier to stabilize. According to NPA charge data, MAl6S6 (M = Ni, Pd, Pt) can approximately be formulated as [MAl6]6+[S6]6−.
For a thermodynamically stable cluster, its kinetic stability is equally important for experimental realization. Are these perfect phM MAl6S6 (M = Ni, Pd, Pt) stars dynamically stable? Born–Oppenheimer molecular dynamics (BOMD) simulations were performed for clusters 1–3, at the PBE0/def2-SVP level, for 30 ps at room temperature (298 K). The root-mean-square deviations (RMSD, relative to the PBE0/def2-SVP optimized structures) of the structures are depicted in Figure 3. The average RMSD values of 1–3 are in the 0.28~0.36 Å range, indicating that their original structures can be maintained during the 30 ps simulations. As a technical note, the major spikes in 1 are due to the inversion vibration of Al/S up and down the molecular planes, suggesting that the Al6 ring is relatively soft. As the size of the central M atom increases, the vibration decreases. The BOMD data suggest that 1–3 species also have reasonable kinetic stability against isomerization and decomposition.

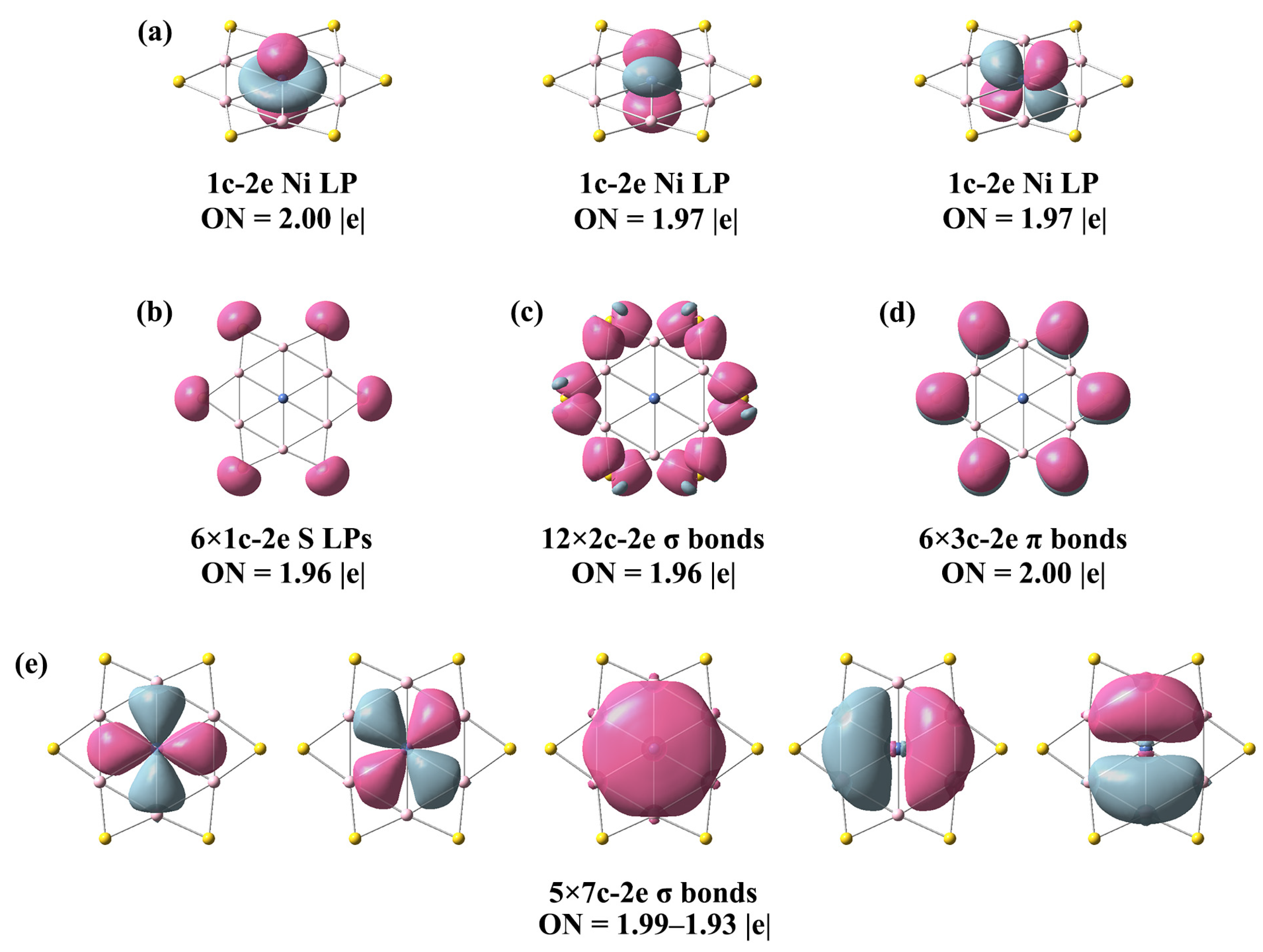
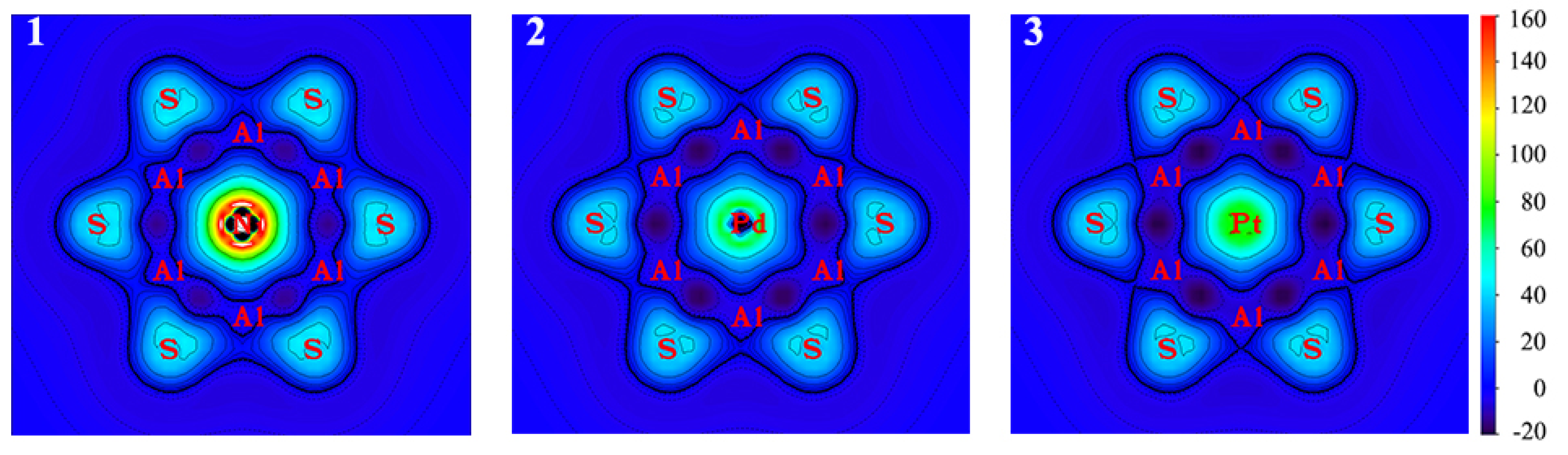
3.2. Chemical Bonding

To further understand the electronic structures and stability of MAl6S6 (M = Ni, Pd, Pt) clusters, it is essential to perform in-depth chemical bonding analyses. Here, we chose to carry out AdNDP analyses for these phM stars. AdNDP is an extension of the NBO analysis, which recovers not only the Lewis bonding elements (lone pairs and 2c-2e bonds) but also delocalized nc-2e bonds. The AdNDP scheme for NiAl6S6 is illustrated in Figure 4, which is relatively straightforward for comprehension. There are 64 valence electrons in NiAl6S6, which can be attributable to five subsets from (a) to (e), according to the CMO orbital composition and structural characteristics. As shown in Figure 4a, there are three 1c-2e lone pairs (LPs) on the central Ni atom, with the occupation numbers (ON) from 2.00 to 1.97 |e|. Subset (b) indicates that there are six 1c-2e LPs of the periphery S atoms (ON = 1.96 |e|). Subset (c) contains 12 typical 2c-2e Al-S localized σ bonds on the peripheral Al6S6 ring (ON = 1.96 |e|). In Subset (d), there are six delocalized 3c-2e π bonds on the Al-S-Al triangles, with the ON 2.00 |e|. The residual 10 electrons can correspond to five 7c-2e delocalized σ bonds on the NiAl6 unit, which are depictured in subset (e). Thus, the phM NiAl6S6 possesses 10σ aromaticity, according to the classical (4n + 2) Hückel rule. The orbital composition of occupied CMOs for 1 is listed in Table S2, which further supports the above AdNDP results. The AdNDP bonding patterns of 2 and 3 are very similar to 1, which are shown in Figure S1 and Figure S2, respectively.
A total of 64 valence electrons are ideal for these σ aromatic phM stars, and even one additional electron can deteriorate their electronic stability. Table S3 listed the LUMOs and atomic composition of 1–3. For such delocalized orbitals, intuitively, adding electrons to them will be beneficial to the stability of the systems. However, the result is counter-intuitive. As depictured in Figure 5, D6h NiAl6S6− (2A2u) is only a second-order saddle point on the potential energy surface, with two small imaginary frequencies at the PBE0/def2-TZVP level. It should be noted that the singly occupied molecular orbital (SOMO) of NiAl6S6− is a typical delocalized π orbital. In general, the electron on π-SOMO should be beneficial to the stability of the system. Even then, the D6h NiAl6S6− anion is not stable. Why is the phM NiAl6S6− star unstable? We briefly answer this question. The electron on SOMO has both positive and negative effects on the stability of the plane structure of NiAl6S6−. On the one hand, π delocalization can help to disperse electrons from the central transition metal Ni atom. However, the charge on Ni is only −0.34 |e|, which makes this effect contribute a little to the stability of the NiAl6S6− star. In addition, although the SOMO is a bonding orbital in general, it has some antibonding components. The π-LPs of S atoms play a crucial role in the anti-bonding characters, which account for 27.2% of the total. The combination of these two factors makes the electrons on SOMO contribute very little to the stability of the system. On the other hand, both Ni-Al and Al-Al bond distances are equal to 2.49 Å, which is obviously shorter than those in NiAl6S6 (2.54 Å). According to the NPA distribution, the charge of the Al atom is +0.75 |e| in NiAl6S6−. The relatively short Al-Al bond distances make the electrostatic repulsion between them increase obviously, which makes the plane structure of D6h NiAl6S6− become unstable. Similarly, D6h NiAl6S62− dianion is the third-order saddle point on the potential energy surface, whose Ni center satisfies the 18ve rule. Thus, 18ve counting is not a prerequisite for the planar hypercoordinate transition metals species.

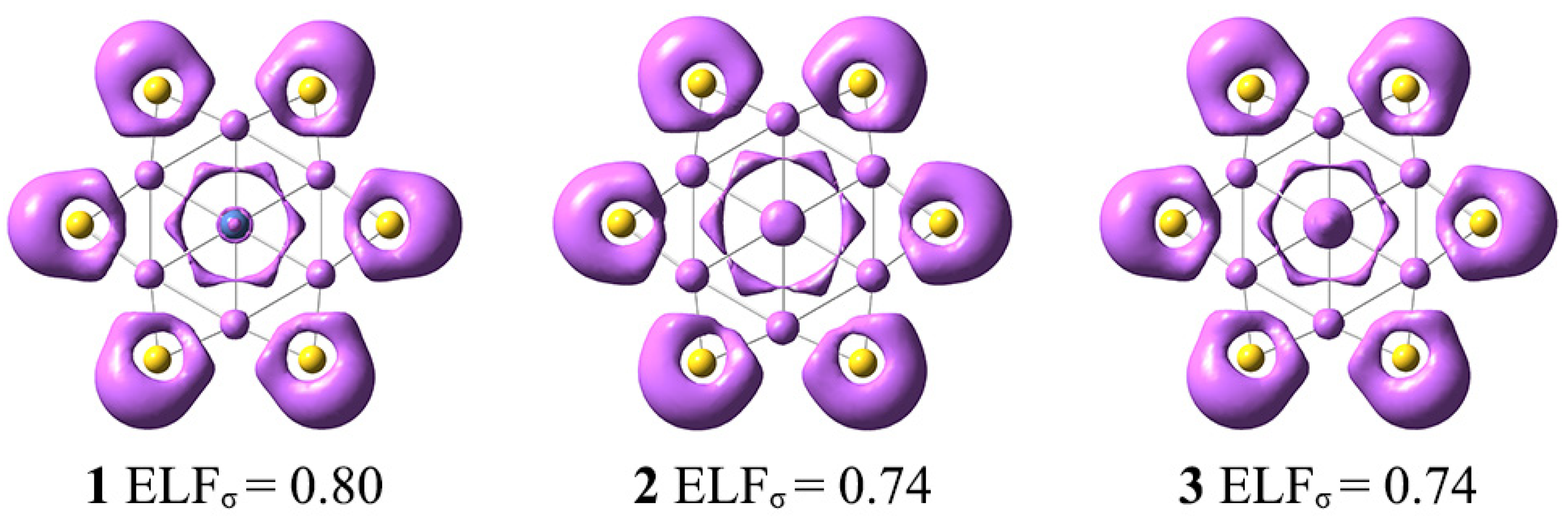
3.3. σ-Aromaticity

In general, many beautiful planar molecules are associated with aromaticity, which is very important for the stability of the system. Aromaticity can be described not only qualitatively but also quantitatively. To further strengthen the AdNDP analyses presented above, detailed ELF analyses were performed for the MAl6S6 (M = Ni, Pd, Pt) stars. As shown in Figure 6, the bifurcation values of ELFσ in 1–3 are 0.80, 0.74, and 0.74, respectively. Thus, the MAl6S6 (M = Ni, Pd, Pt) stars are σ aromatic according to the ELF criteria, which are consistent with our conclusion of AdNDP analyses.
As an independent, semi-quantitative measure of aromaticity in the systems, NICS plays an important role in the characterization of aromaticity. The negative NICS(0) and NICS(1) values can reflect σ and π aromaticity, respectively. As shown in Figure S3, the NICS(0) values at the Al-M-Al triangles are in the range of −32.0~−63.8 ppm for 1–3, suggesting they possess typical σ aromaticity. For the Al-S-Al triangles of 1–3, the NICS(1) values are from −4.0 to −6.5 ppm, indicating they have a certain degree of π aromaticity. However, evaluating NICS values at some point seems to be inadequate. To more intuitively observe the aromaticity, the color-filled maps of ICSSzz(0) of 1–3 are plotted in Figure 7. It should be noted that positive ICSSzz values indicate diatropic ring currents and aromaticity. The calculated ICSSzz data provide a quantitative assessment, fully supporting the idea of σ aromaticity in MAl6S6 (M = Ni, Pd, Pt) stars.

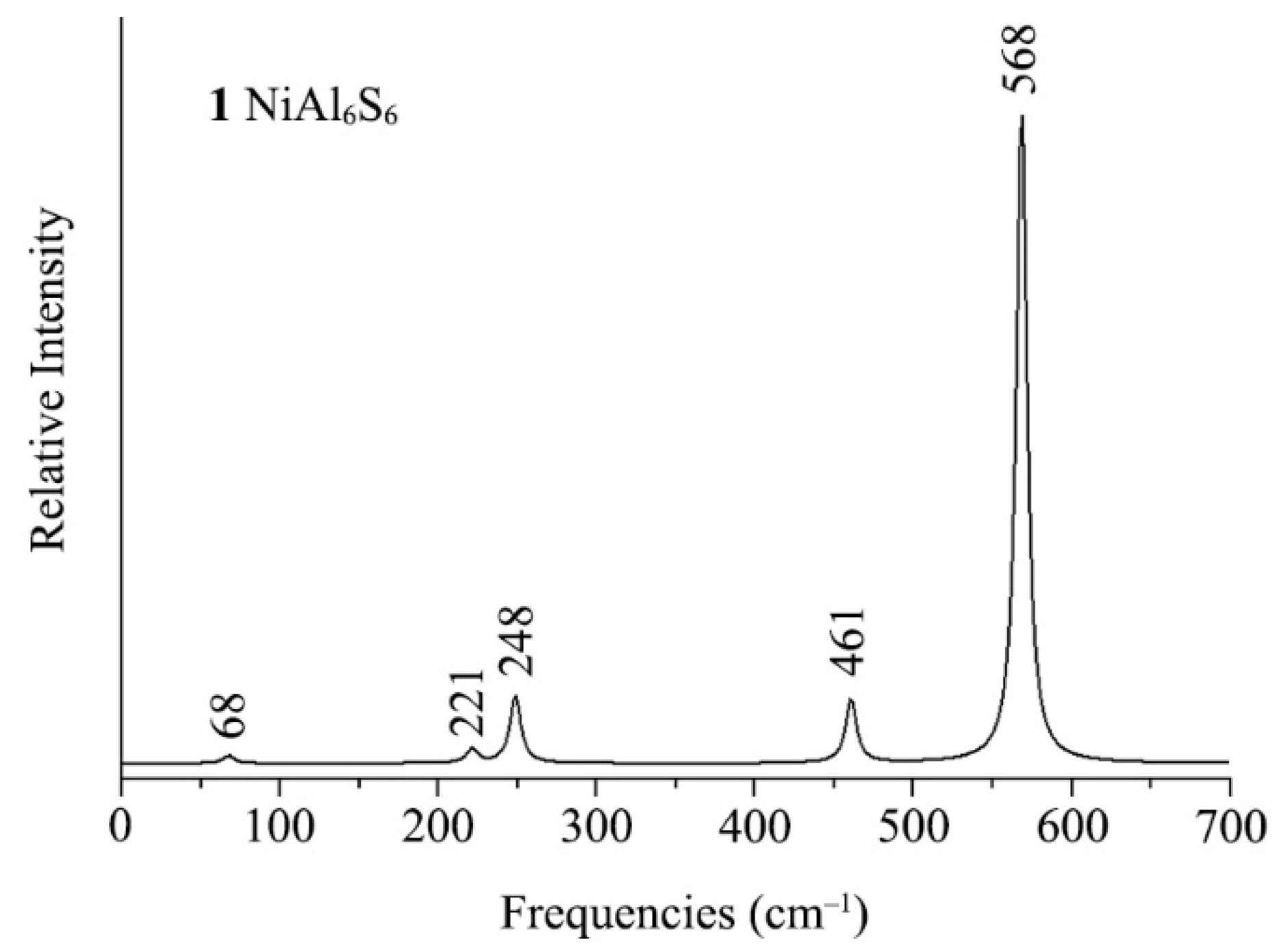
3.4. Simulated IR Spectrums

To facilitate future experimental characterization, the IR spectrums of the phM stars 1, 2, and 3 were simulated at the PBE0/def2-TZVP level. As depictured in Figure 8, the strongest IR absorption peak occurs at 568 cm−1, which mainly originates from inplane asymmetrical Al-S stretching vibrations. The peak at 461 cm−1, is mainly generated by coupled vibrations of Al-S, Al-Ni, and Al-Al in-plane asymmetrical stretching vibrations. The weak peak at 248 cm−1, corresponds to asymmetrical Ni-Al in-plane stretching vibrations. The weak peak at 67 cm−1 is the result of the up-and-down movements of the phNi center within the Al6 ring along the molecular axis. As shown in Figure S4, the locations and intensity of absorption peaks in 2 (PdAl6S6) and 3 (PtAl6S6) are basically like those of 1.

4. Summary

In summary, we have designed the phM MAl6S6 (M = Ni, Pd, Pt) stars. Based on extensive searches and high-level calculations, these perfect phM stars turned out to be the global minima on the potential energy surfaces. In addition, the dynamic simulations revealed that they possess good kinetic stabilities. The formation of peripheral 2c-2e Al-S σ bonds, 3c-2e Al-S-Al π bonds, and the 10σ aromaticity contribute to the stabilization of phM-containing structures in MAl6S6 (M = Ni, Pd, Pt) species. Thus, these phM species may be targeted in future experiments and enrich the planar hypercoordinate transition metals chemistry.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28030942/s1, Table S1: Cartesian coordinates for global-minimum (GM) clusters 1–3 of the MAl6S6 (M = Ni, Pd, Pt) series at the PBE0/def2-TZVP level, along with four lowest-lying nB–nE isomeric structures.; Table S2: Orbital composition analysis for the canonical molecular orbitals (CMOs) of GM NiAl6S6 (1, D6h, 1A1g) cluster. Main components greater than 15% are shown in bold; Table S3: Orbital composition analysis for the lowest unoccupied molecular orbitals (LUMOs) of the MAl6S6 (M = Ni, Pd, Pt) series; Figure S1: The AdNDP bonding pattern of PdAl6S6. Occupation numbers (ONs) are shown; Figure S2: The AdNDP bonding pattern of PtAl6S6. Occupation numbers (ONs) are shown; Figure S3: Nucleus independent chemical shifts (NICSs) for clusters 1–3. Here the NICS(0) data (blue color) are calculated at the center of the Al-M-Al (M = Ni, Pd, Pt) triangle, whereas the NICS(1) values (red color) are at 1 Å above the center of the Al-S-Al triangle; Figure S4: Calculated IR spectrums of PdAl6S6 and PtAl6S6 at the PBE0/def2-TZVP level.

Author Contributions

J.-C.G. designed the works. L.-X.B. performed the global minima searching and the bonding analysis. L.-X.B. wrote the draft. All authors took part in the discussions and approved the final version. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (22173053), and the Natural Science Foundation of Shanxi Province (20210302123439).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigoreva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon film. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Pan, Y.D.; Abazari, R.; Yao, J.M.; Gao, J.K. Recent progress in two-dimensional metal-organic framework photocatalysts: Synthesis, photocatalytic mechanism, and applications. J. Phy. Energy 2021, 3, 032010. [Google Scholar] [CrossRef]
  3. Sanati, S.; Rezvani, Z.; Abazari, R.; Hou, Z.Q.; Dai, H. Hierarchical CuAl-layered double hydroxide/CoWO4 nanocomposites with enhanced efficiency in supercapacitors with long cyclic stability. New J. Chem. 2019, 43, 15240–15248. [Google Scholar] [CrossRef]
  4. Wang, Y.; Li, Y.F.; Chen, Z.F. Planar hypercoordinate motifs in two-diemensional materials. Acc. Chem. Res. 2020, 1, 887–895. [Google Scholar] [CrossRef] [PubMed]
  5. Wang, M.H.; Cui, Z.H.; Wang, S.; Li, Q.; Zhao, J.J.; Chen, Z.F. A two-dimensional Be2Au monolayer with planar hexacoordinate s-block metal atoms: A superconducting global minimum Dirac material with two perfect Dirac node-loops. Chem. Sci. 2022, 13, 11099–11109. [Google Scholar] [CrossRef]
  6. Hoffmann, R.; Alder, R.W.; Wilcox, C.F. Planar tetracoordinate carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
  7. Collins, J.B.; Dill, J.D.; Jemmis, E.D.; Apeloig, Y.; Schleyer, P.V.R.; Seeger, R.; Pople, J.A. Stabilization of planar tetracoordinate carbon. J. Am. Chem. Soc. 1976, 98, 5419–5427. [Google Scholar] [CrossRef]
  8. Schleyer, P.v.R.; Boldyrev, A.I. A new, general strategy for achieving planar tetracoordinate geometries for carbon and other second row periodic elements. J. Chem. Soc. Chem. Commun. 1991, 1536–1538. [Google Scholar] [CrossRef]
  9. Sorger, K.; von Ragué, P. Planar and inherently nontetrahedral tetracoordinate carbon: A status report. J. Mol. Struct. THEOCHEM 1995, 338, 317–346. [Google Scholar] [CrossRef]
  10. Keese, R. Carbon flatland: Planar tetracoordinate carbon and fenestranes. Chem. Rev. 2006, 106, 4787–4808. [Google Scholar] [CrossRef]
  11. Merino, G.; Mendez-Rojas, M.A.; Vela, A.; Heine, T. Recent advances in planar tetracoordinate carbon chemistry. J. Comput. Chem. 2007, 28, 362–372. [Google Scholar] [CrossRef] [PubMed]
  12. Yang, L.M.; Ganz, E.; Chen, Z.F.; Wang, Z.X.; Schleyer, P.V.R. Four decades of the chemistry of planar hypercoordinate compounds. Angew. Chem. Int. Ed. 2015, 54, 9468–9501. [Google Scholar] [CrossRef] [PubMed]
  13. Vassilev-Galindo, V.; Pan, S.J.; Donald, K.; Merino, G. Planar pentacoordinate carbons. Nat. Rev. Chem. 2018, 2, 0114. [Google Scholar] [CrossRef]
  14. Li, X.; Wang, L.S.; Boldyrev, A.I.; Simons, J. Tetracoordinated planar carbon in the Al4C− anion. A combined photoelectron spectroscopy and ab initio study. J. Am. Chem. Soc. 1999, 121, 6033–6038. [Google Scholar] [CrossRef]
  15. Wang, L.S.; Boldyrev, A.I.; Li, X.; Simon, J. Experimental observation of pentaatomic tetracoordinate planar carbon-containing molecules. J. Am. Chem. Soc. 2000, 122, 7681–7687. [Google Scholar] [CrossRef]
  16. Li, X.; Zhang, H.F.; Wang, L.S.; Geske, G.D.; Boldyrev, A.I. Pentaatomic tetracoordinate planar carbon, [CAl4]2–: A new structural unit and its salt complexes. Angew. Chem. Int. Ed. 2000, 39, 3630–3632. [Google Scholar] [CrossRef]
  17. Xu, J.; Zhang, X.X.; Yu, S.; Ding, Y.H.; Bowen, K.H. Identifying the hydrogenated planar tetracoordinate carbon: A combined experimental and theoretical study of CAl4H and CAl4H−. J. Phys. Chem. Lett. 2017, 8, 2263–2267. [Google Scholar] [CrossRef] [Green Version]
  18. Zhang, C.J.; Dai, W.S.; Xu, H.G.; Xu, X.L.; Zheng, W.J. Structural evolution of carbon-doped aluminum clusters AlnC− (n = 6–15): Anion photoelectron spectroscopy and theoretical calculations. J. Phys. Chem. A 2022, 126, 5621–5631. [Google Scholar] [CrossRef]
  19. Wang, Z.X.; Schleyer, P.R. Construction principles of “Hyparenes”: Families of molecules with planar pentacoordinate carbons. Science 2001, 292, 2465–2469. [Google Scholar] [CrossRef]
  20. Pei, Y.; An, W.; Ito, K.; Schleyer, P.V.R.; Zeng, X.C. Planar pentacoordinate carbon in CAl5+: A global minimum. J. Am. Chem. Soc. 2008, 130, 10394–10400. [Google Scholar] [CrossRef]
  21. Cui, Z.H.; Vassilev-Galindo, V.; Cabellos, J.L.; Osorio, E.; Orozco, M.; Pan, S.; Ding, Y.H.; Merino, G. Planar pentacoordinate carbon atoms embedded in a metallocene framework. Chem. Commun. 2017, 53, 138–141. [Google Scholar] [CrossRef]
  22. Guo, J.C.; Feng, L.Y.; Barroso, J.; Merino, G.; Zhai, H.J. Planar or tetrahedral? A ternary 17-electron CBe5H4+ cluster with planar pentacoordinate carbon. Chem. Commun. 2020, 56, 8305–8308. [Google Scholar] [CrossRef] [PubMed]
  23. Exner, K.; Schleyer, P.V.R. Planar hexacoordinate Carbon: A viable possibility. Science 2000, 290, 1937–1940. [Google Scholar] [CrossRef] [PubMed]
  24. Wu, Y.B.; Duan, Y.; Lu, G.; Lu, H.G.; Yang, P.; Schleyer, P.V.R.; Merino, G.; Islas, R.; Wang, Z.X. D3h CN3Be3+ and CO3Li3+: Viable planar hexacoordinate carbon prototypes. Phys. Chem. Chem. Phys. 2012, 14, 14760–14763. [Google Scholar] [CrossRef] [PubMed]
  25. Leyva-Parra, L.; Diego, L.; Yanez, O.; Inostroza, D.; Barroso, J.; Vasquez-Espinal, A.; Merino, G.; Tiznado, W. Planar hexacoordinate carbons: Half covalent, half ionic. Angew. Chem. Int. Ed. 2021, 60, 8700–8704. [Google Scholar] [CrossRef] [PubMed]
  26. Jian, T.; Chen, X.N.; Li, S.D.; Boldyrev, A.I.; Li, J.; Wang, L.S. Probing the structures and bonding of size-selected boron and doped-boron clusters. Chem. Soc. Rev. 2019, 48, 3550–3591. [Google Scholar] [CrossRef] [PubMed]
  27. Barroso, J.; Pan, S.; Merino, G. Structural transformations in boron clusters induced by metal doping. Chem. Soc. Rev. 2022, 51, 1098–1123. [Google Scholar] [CrossRef] [PubMed]
  28. Zhai, H.J.; Alexandrova, A.N.; Birch, K.A.; Boldyrev, A.I.; Wang, L.S. Hepta- and octacoordinate boron in molecular wheels of eight- and nine-atom boron clusters: Observation and confirmation. Angew. Chem. Int. Ed. 2003, 42, 6004–6008. [Google Scholar] [CrossRef] [PubMed]
  29. Yu, H.L.; Sang, R.L.; Wu, Y.Y. Structure and aromaticity of B6H5+ cation: A novel borhydride system containing planar pentacoordinated boron. J. Phys. Chem. A 2009, 113, 3382–3386. [Google Scholar] [CrossRef]
  30. Chen, C.; Liu, Y.Q.; Cui, Z.H. σ-Aromaticity planar pentacoordinate beryllium atoms. Inorg. Chem. 2021, 60, 16053–16058. [Google Scholar] [CrossRef]
  31. Pu, Z.; Ge, M.; Li, Q. MB82– (M = Be, Mg, Ca, Sr, and Ba): Planar octacoordinated alkaline earth metal atoms enclosed by boron rings. Sci. China Chem. 2010, 53, 1737–1745. [Google Scholar] [CrossRef]
  32. Lin, L.; Lievens, P.; Nguyen, M.T. In search of aromatic sevenmembered rings. J. Mol. Struct. THEOCHEM 2010, 943, 23–31. [Google Scholar] [CrossRef]
  33. Kalita, A.J.; Sarmah, K.; Yashmin, F.; Borah, R.R.; Baruah, I.; Deka, R.P.; Guha, A.K. σ-Aromaticity in planar pentacoordinate aluminium and gallium clusters. Sci. Rep. 2022, 12, 10041. [Google Scholar] [CrossRef] [PubMed]
  34. Guo, J.C.; Feng, L.Y.; Zhang, X.Y.; Zhai, H.J. Star-like CBe5Au5+ cluster: Planar pentacoordinate carbon, superalkali cation, and multifold (π and σ) aromaticity. J. Phys. Chem. A 2018, 122, 1138–1145. [Google Scholar] [CrossRef]
  35. Wang, M.H.; Chen, C.; Pan, S.; Cui, Z.H. Planar hexacoordinate gallium. Chem. Sci. 2021, 12, 15067–15076. [Google Scholar] [CrossRef]
  36. Romanescu, C.; Galeev, T.R.; Li, W.L.; Boldyrev, A.I.; Wang, L.S. Transition-metal-centered monocyclic boron wheel clusters (M©Bn): A new class of aromatic borometallic compounds. Acc. Chem. Res. 2013, 46, 350–358. [Google Scholar] [CrossRef]
  37. Romanescu, C.; Galeev, T.R.; Li, W.L.; Boldyrev, A.I.; Wang, L.S. Aromatic metal-centered monocyclic boron rings: Co©B8− and Ru©B9−. Angew. Chem. Int. Ed. 2011, 50, 9334–9337. [Google Scholar] [CrossRef]
  38. Galeev, T.R.; Romanescu, C.; Li, W.L.; Wang, L.S.; Boldyrev, A.I. Observation of the highest coordination number in planar species: Decacoordinated Ta©B10− and Nb©B10− anions. Angew. Chem. Int. Ed. 2012, 51, 2101–2105. [Google Scholar] [CrossRef]
  39. Hou, J.; Duan, Q.; Qin, J.; Shen, X.; Zhao, J.; Liang, Q.; Jiang, D.; Gao, S. Unconventional charge distribution in the planar wheel-type M©B6H6−/0/+ (M = Mn, Fe and Co): Central M with negative charges and peripheral boron ring with positive charges. Phys. Chem. Chem. Phys. 2015, 17, 9644–9650. [Google Scholar] [CrossRef]
  40. Guo, J.C.; Ren, G.M.; Miao, C.Q.; Tian, W.J.; Wu, Y.B.; Wang, X. CBe5Hnn−4 (n = 2–5): Hydrogen-stabilized CBe5 pentagons containing planar or quasi-planar pentacoordinate carbons. J. Phys. Chem. A 2015, 119, 13101–13106. [Google Scholar] [CrossRef]
  41. Zhao, X.F.; Li, J.J.; Li, H.R.; Yuan, C.X.; Tian, X.X.; Li, S.D.; Wu, Y.B.; Guo, J.C.; Wang, Z.X. Viable aromatic BenHn stars enclosing a planar hypercoordinate boron or late transition metal. Phys. Chem. Chem. Phys. 2018, 20, 7217–7222. [Google Scholar] [CrossRef] [PubMed]
  42. Kalita, A.J.; Rohman, S.S.; Kashyap, C.; Ullaha, S.S.; Guha, A.K. Double aromaticity in a BBe6H6+ cluster with a planar hexacoordinate boron structure. Chem. Commun. 2020, 56, 12597–12599. [Google Scholar] [CrossRef] [PubMed]
  43. Ye, Y.H.; Wang, Y.Q.; Zhang, M.; Geng, Y.; Su, Z.M. Sulphur-bridged BAl5S5+ with 17 counting electrons: A regular planar pentacoordinate boron system. Molecules 2021, 26, 5205. [Google Scholar] [CrossRef]
  44. Sun, R.; Zhao, X.F.; Jin, B.; Huo, B.; Bian, J.H.; Guan, X.L.; Yuan, C.X.; Wu, Y.B. Influence of stepwise oxidation on the structure, stability, and properties of planar pentacoordinate carbon species CAl5+. Phys. Chem. Chem. Phys. 2020, 22, 17062–17067. [Google Scholar] [CrossRef] [PubMed]
  45. Sun, R.; Jin, B.; Huo, B.; Yuan, C.; Zhai, H.J.; Wu, Y.B. Planar pentacoordinate carbon in a sulphur-surrounded boron wheel: The global minimum of CB5S5+. Chem. Commun. 2022, 58, 2552–2555. [Google Scholar] [CrossRef]
  46. Jin, B.; Sun, R.; Huo, B.; Yuan, C.X.; Wu, Y.B. M©B7O7+ (M = Ni, Pd, Pt): Aromatic molecular stars with a planar heptacoordinate transition metal. Chem. Commun. 2021, 57, 13716–13719. [Google Scholar] [CrossRef]
  47. Saunders, M. Stochastic search for isomers on a quantum mechanical surface. J. Comput. Chem. 2004, 25, 621–626. [Google Scholar] [CrossRef]
  48. Sergeeva, A.P.; Averkiev, B.B.; Zhai, H.J.; Boldyrev, A.I.; Wang, L.S. All-boron analogues of aromatic hydrocarbons: B17− and B18−. J. Chem. Phys. 2011, 134, 224304. [Google Scholar] [CrossRef] [Green Version]
  49. Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  50. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  51. Purvis, G.D., III; Bartlett, R.J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
  52. Millam, J.M.; Bakken, V.; Chen, W.; Hase, W.L.; Schlegel, H.B. Ab initio classical trajectories on the Born-Oppenheimer surface: Hessian-based integrators using fifth-order polynomial and rational function fits. J. Chem. Phys. 1999, 111, 3800–3805. [Google Scholar] [CrossRef]
  53. Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 6.0: Natural bond orbital analysis program. J. Comput. Chem. 2013, 34, 1429–1437. [Google Scholar] [CrossRef] [PubMed]
  54. Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: Adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef] [PubMed]
  55. Savin, A.; Nesper, R.; Wengert, S.; Fäsler, T.F. ELF: The Electron Localization Function. Angew. Chem. Int. Ed. 1997, 36, 1808–1832. [Google Scholar] [CrossRef]
  56. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  57. Dransfeld, A.; Schleyer, P.R.; Maerker, C.; Jiao, H.; van Eikema Hommes, N.J. Nucleus-independent chemical shifts: A simple and efficient aromaticity probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar]
  58. Kloda, S.; Kleinpeter, E. Ab initio calculation of the anisotropy effect of multiple bonds and the ring current effect of arenes application in conformational and configurational analysis. J. Chem. Soc. Perkin Trans. 2001, 2, 1893–1898. [Google Scholar]
  59. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  60. Legault, C.Y. CYLview, 1.0b.; Universite. de Sherbrooke. 2009. Available online: http://www.cylview.org (accessed on 16 November 2022).
  61. Becke, A.D. Density Functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5659. [Google Scholar] [CrossRef] [Green Version]
  62. Lee, C.; Yang, W.; Parr, R.G. Development of the colle-salvettib correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter Mater. Phys. 1988, 37, 785–791. [Google Scholar] [CrossRef] [Green Version]
  63. Pyykkö, P. Additive covalent radii for single-, double-, and triple-bonded molecules and tetrahedrally bonded crystals: A summary. J. Phys. Chem. A 2015, 119, 2326–2337. [Google Scholar] [CrossRef] [PubMed]
Molecules 28 00942 sch001 550
Scheme 1. Basic idea of designing phM MAl6S6 (M = Ni, Pd, Pt) clusters.
Scheme 1. Basic idea of designing phM MAl6S6 (M = Ni, Pd, Pt) clusters.
Molecules 28 00942 sch001
Molecules 28 00942 g001 550
Figure 1. Optimized global-minimum structures 1–3 of MAl6S6 (M = Ni, Pd, Pt) at the PBE0/def2-TZVP level. The bond distances are labeled in angstroms.
Figure 1. Optimized global-minimum structures 1–3 of MAl6S6 (M = Ni, Pd, Pt) at the PBE0/def2-TZVP level. The bond distances are labeled in angstroms.
Molecules 28 00942 g001
Molecules 28 00942 g002 550
Figure 2. Optimized GM structures 1–3 of the MAl6S6 (M = Ni, Pd, Pt) clusters at the PBE0/def2-TZVP level, along with their four lowest-lying isomers (nB–nE). Relative energies are listed in kcal mol−1 at the single-point CCSD(T) level using their PBE0 geometries, with zero-point energy (ZPE) corrections at PBE0. Shown in square brackets for comparison are the energetics at single-point CCSD(T)/def2-TZVP//B3LYP/def2-TZVP level, including ZPE corrections at B3LYP.
Figure 2. Optimized GM structures 1–3 of the MAl6S6 (M = Ni, Pd, Pt) clusters at the PBE0/def2-TZVP level, along with their four lowest-lying isomers (nB–nE). Relative energies are listed in kcal mol−1 at the single-point CCSD(T) level using their PBE0 geometries, with zero-point energy (ZPE) corrections at PBE0. Shown in square brackets for comparison are the energetics at single-point CCSD(T)/def2-TZVP//B3LYP/def2-TZVP level, including ZPE corrections at B3LYP.
Molecules 28 00942 g002
Molecules 28 00942 g003 550
Figure 3. Calculated root-mean-square deviations (RMSDs) of GM clusters 1–3 during the Born-Oppenheimer molecular dynamics (BOMD) simulations at 298 K.
Figure 3. Calculated root-mean-square deviations (RMSDs) of GM clusters 1–3 during the Born-Oppenheimer molecular dynamics (BOMD) simulations at 298 K.
Molecules 28 00942 g003
Molecules 28 00942 g004 550
Figure 4. The AdNDP bonding pattern of 1. Occupation numbers (ONs) are shown.
Figure 4. The AdNDP bonding pattern of 1. Occupation numbers (ONs) are shown.
Molecules 28 00942 g004
Molecules 28 00942 g005 550
Figure 5. Optimized structures D6h NiAl6S6− at the PBE0/def2-TZVP level. The bond distances (in Å; black color), atomic nature charges ((in |e|; red color), the lowest vibrational frequency νmin (cm−1) and the number of imaginary frequencies are shown. The SOMO and its compositions are also listed.
Figure 5. Optimized structures D6h NiAl6S6− at the PBE0/def2-TZVP level. The bond distances (in Å; black color), atomic nature charges ((in |e|; red color), the lowest vibrational frequency νmin (cm−1) and the number of imaginary frequencies are shown. The SOMO and its compositions are also listed.
Molecules 28 00942 g005
Molecules 28 00942 g006 550
Figure 6. Electron localization function (ELF) of σ electron clouds for 1–3. The approximated bifurcation values are shown.
Figure 6. Electron localization function (ELF) of σ electron clouds for 1–3. The approximated bifurcation values are shown.
Molecules 28 00942 g006
Molecules 28 00942 g007 550
Figure 7. Color-filled maps of ICSSzz (in ppm) at the molecular plane for the 1–3 clusters. Positive values indicate aromaticity.
Figure 7. Color-filled maps of ICSSzz (in ppm) at the molecular plane for the 1–3 clusters. Positive values indicate aromaticity.
Molecules 28 00942 g007
Molecules 28 00942 g008 550
Figure 8. Calculated IR spectrum of NiAl6S6 at the PBE0/def2-TZVP level.
Figure 8. Calculated IR spectrum of NiAl6S6 at the PBE0/def2-TZVP level.
Molecules 28 00942 g008
Table
Table 1. The lowest vibrational frequencies (νmin/cm−1), HOMO-LUMO gaps (Gap/eV), Wiberg bond indices, and atomic nature charges (q, |e|) of MAl6S6 (M = Ni, Pd, Pt) at the PBE0/def2-TZVP level.
Table 1. The lowest vibrational frequencies (νmin/cm−1), HOMO-LUMO gaps (Gap/eV), Wiberg bond indices, and atomic nature charges (q, |e|) of MAl6S6 (M = Ni, Pd, Pt) at the PBE0/def2-TZVP level.
SpeciesνminGapWBIM-AlWBIAl-AlWBIAl-SqMqAlqS
1 NiAl6S6173.240.220.400.88−0.300.84−0.79
2 PdAl6S6273.230.230.380.87−0.420.87−0.80
3 PtAl6S6243.260.250.360.87−0.540.89−0.80
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Bai, L.-X.; Guo, J.-C. σ-Aromatic MAl6S6 (M = Ni, Pd, Pt) Stars Containing Planar Hexacoordinate Transition Metals. Molecules 2023, 28, 942. https://doi.org/10.3390/molecules28030942

AMA Style

Bai L-X, Guo J-C. σ-Aromatic MAl6S6 (M = Ni, Pd, Pt) Stars Containing Planar Hexacoordinate Transition Metals. Molecules. 2023; 28(3):942. https://doi.org/10.3390/molecules28030942

Chicago/Turabian Style

Bai, Li-Xia, and Jin-Chang Guo. 2023. "σ-Aromatic MAl6S6 (M = Ni, Pd, Pt) Stars Containing Planar Hexacoordinate Transition Metals" Molecules 28, no. 3: 942. https://doi.org/10.3390/molecules28030942

APA Style

Bai, L. -X., & Guo, J. -C. (2023). σ-Aromatic MAl6S6 (M = Ni, Pd, Pt) Stars Containing Planar Hexacoordinate Transition Metals. Molecules, 28(3), 942. https://doi.org/10.3390/molecules28030942

Article Metrics

Back to TopTop