Next Article in Journal
Neuroprotective Actions of Different Exogenous Nucleotides in H2O2-Induced Cell Death in PC-12 Cells
Next Article in Special Issue
Rhombohedral Boron Monosulfide as a p-Type Semiconductor
Previous Article in Journal
Targeting Proliferation Signals and the Cell Cycle Machinery in Acute Leukemias: Novel Molecules on the Horizon
Previous Article in Special Issue
Hall Effect Anisotropy in the Paramagnetic Phase of Ho0.8Lu0.2B12 Induced by Dynamic Charge Stripes
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 3
10.3390/molecules28031225
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Prediction of a Cyclic Hydrogenated Boron Molecule as a Promising Building Block for Borophane

by
Yasunobu Ando
1,*,
Takeru Nakashima
1,
Heming Yin
2,
Ikuma Tateishi
3,
Xiaoni Zhang
2,
Yuki Tsujikawa
2,
Masafumi Horio
2,
Nguyen Thanh Cuong
4,
Susumu Okada
4,
Takahiro Kondo
4 and
Iwao Matsuda
2,*
1
CD-FMat, National Institute of Advanced Industrial Science and Technology (AIST), Tsukuba 305-8560, Ibaraki, Japan
2
Institute for Solid State Physics, The University of Tokyo, Kashiwa 277-8581, Chiba, Japan
3
RIKEN Center for Emergent Matter Science, Wako 351-0198, Saitama, Japan
4
Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba 305-8573, Ibaraki, Japan
*
Authors to whom correspondence should be addressed.
Molecules 2023, 28(3), 1225; https://doi.org/10.3390/molecules28031225
Submission received: 20 December 2022 / Revised: 20 January 2023 / Accepted: 21 January 2023 / Published: 26 January 2023
(This article belongs to the Special Issue New Science of Boron Allotropes, Compounds, and Nanomaterials)
Browse Figures
Review Reports Versions Notes

Abstract

:
We have extensively searched for a cyclic hydrogenated boron molecule that has a three-center two-electron bond at the center. Using first-principles calculations, we discovered a stable molecule of 2:4:6:8:-2H-1,5:1,5-μH-B8H10 and propose its existence. This molecule can be regarded as a building block for sheets of topological hydrogen boride (borophane), which was recently theoretically proposed and experimentally discovered. The electronic structure of the cyclic hydrogenated boron molecule is discussed in comparison with that of cyclic hydrogenated carbon molecules.

1. Introduction

The theoretical design of new molecules is a central issue in chemistry. Such methods have led to the syntheses of new functional materials such as catalysts or device components that have become technologically significant [1]. Molecules with unique bonding schemes have attracted academic interest because they often have unexpected chemical properties that violate well-established models and trigger innovations.
Boron is an electron-deficient element, and it has been found to form unique bonding configurations with multi-center atoms. Various boron-based molecules have been designed and synthesized [2]. Some of these molecules have shown anti-Van’t Hoff/Le Bel features [3,4,5,6]. The predicted existence of a 2D or planar boron material, borophene, has triggered vigorous explorations of its molecules or atomic sheets [7]. Researchers have reported growths of various borophene layers on metal substrates [8,9,10]. Theoretical and experimental searches for 2D boron have been extended to seeking low-dimensional materials composed of boron and other elements [7]. An example is the recent synthesis of sheets of hydrogen boride (HB) or borophane [11,12,13], which show intriguing functions such as hydrogen storage [14]. Boron and hydrogen atoms create a three-center two-electron (3c-2e) bond with unique chemical characteristics that allow us to design new 2D HB structures [15,16,17].
In this study, we searched for a possible planar structure of hydrogenated boron molecules (0D HB) through theoretical calculations. On the basis of the well-known boron hydride molecule diborone, shown in Figure 1a, we designed various molecular models by adding cyclic structures with different numbers of member atoms to different types of well-known boron-hydride (borane) molecules [18]. Among the twelve candidates, we found that only the molecule 2:4:6:8:-2H-1,5:1,5-μH-B8H10 was stable both thermodynamically and kinetically. The structural formula and atomic structure of the molecule are drawn in Figure 1b,c, respectively. The molecule has a 3c-2e bond at the center and two five-membered rings on the sides. The nomenclature of the molecule is based on references [19,20]; its atomic structure can be regarded as a building block of a topological borophane layer, discovered recently [12,13,15,17]. This research shows intriguing relationships between the planar molecules and atomic sheets of the hydrogenated boron compound. This cyclic hydrogenated boron molecule provides new perspectives in boron chemistry.

2. Results and Discussion

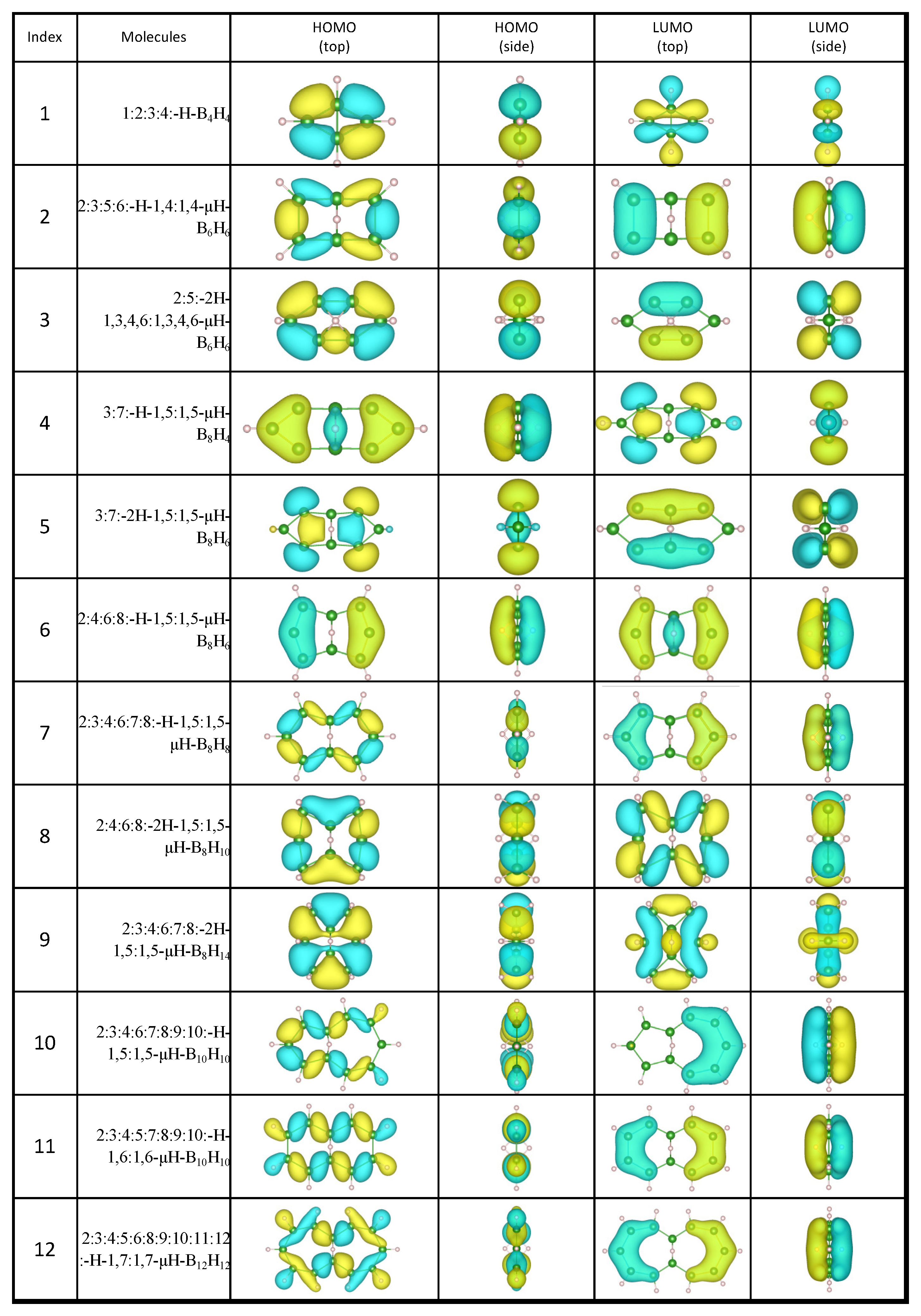
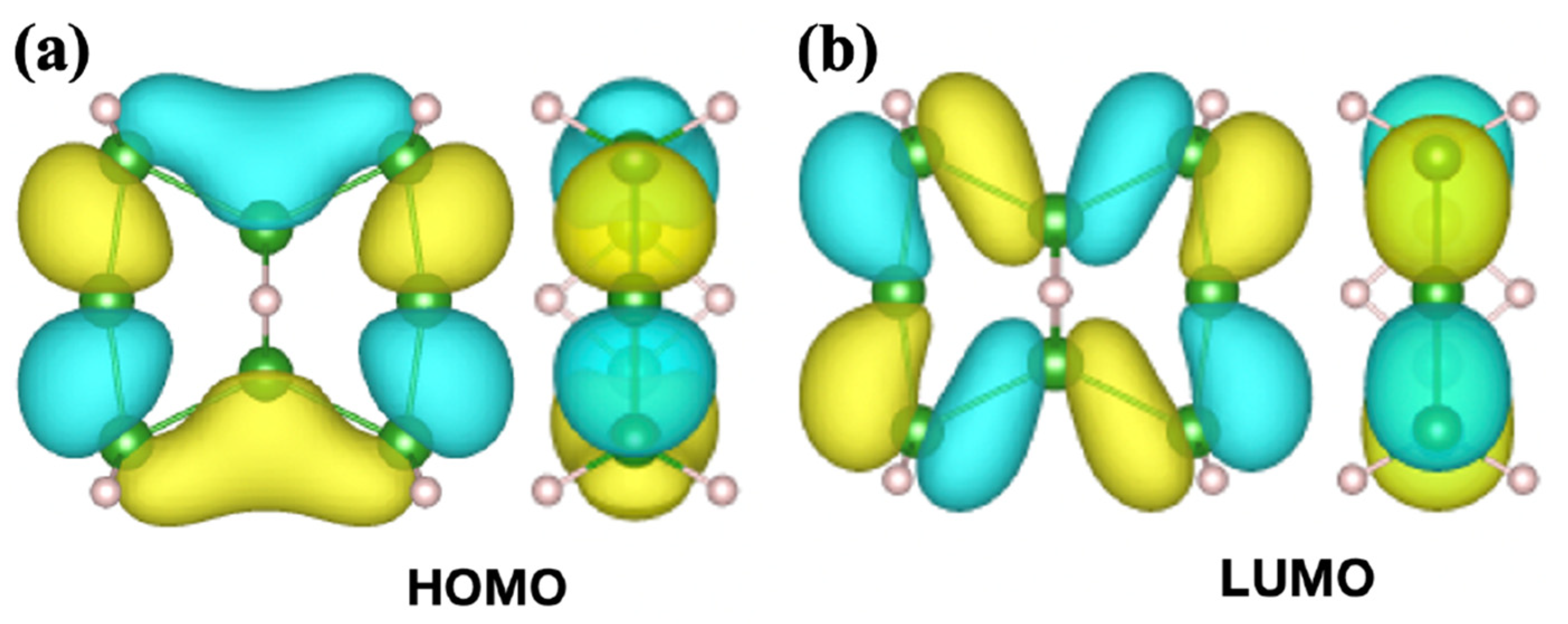
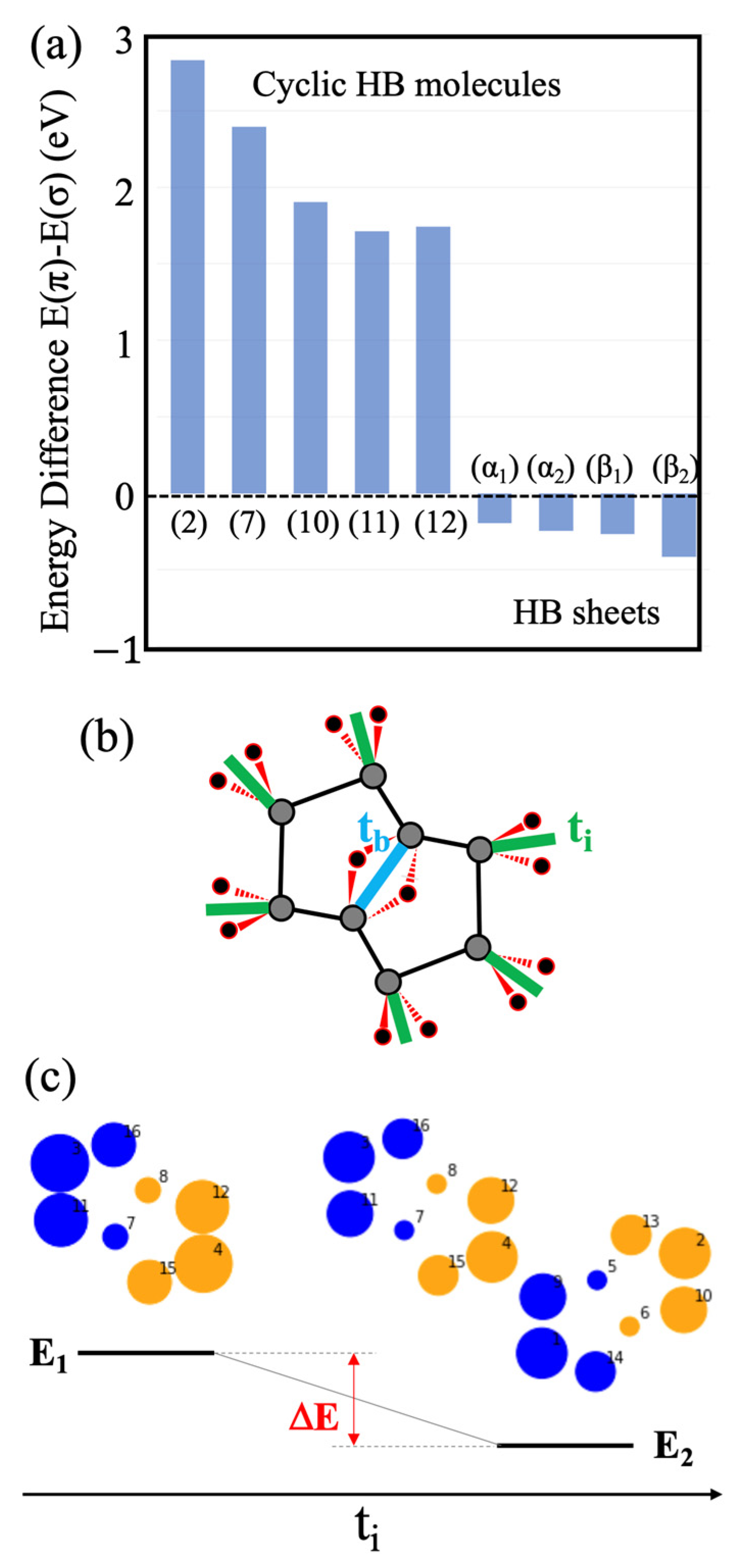
2.1. Candidates from the Cyclic Hydrogenated Boron Compounds

In searching for a new hydrogenated boron molecule, we examined the 12 candidates displayed in Figure 2 and listed in Table 1. We followed the same nomenclature as for the B8H10 molecule [19,20]. The atomic structures of the molecular candidates are schematically presented in Appendix A (Figure A1). The stable molecule was determined by filtering values of cohesive energy and signs of vibration frequency. All the candidates were found to gain cohesive energy during molecular formation. However, most of them were excluded because they had negative phonon energies or imaginary vibrational modes, indicating breakdowns in their molecular structure. It is apparent in Table 1 that only the molecule 2:4:6:8:-2H-1,5:1,5-μH-B8H10 (Figure 1b,c) is stable and could possibly exist in nature. The formation energy of this molecule is Eform = 194.5 kcal/mol, from four molecules of diborane—B2H6 (Table 2). Comparing this with Eform = 156.3 kcal/mol for eight molecules of borane (BH3) shows that the formation energy of the proposed molecule is 38.3 kcal/mol, which is slightly higher than that of the borane molecule.
A molecule of 2:4:6:8:-2H-1,5:1,5-μH-B8H10 has two types of boron atoms: those that make chemical bonds with hydrogen and those that do not. Two boron atoms in the 3c-2e bond at the center share hydrogen atoms. Besides the two boron atoms that connect with their neighbors, the other four boron atoms are individually terminated by two hydrogen atoms. To help understand the electronic states of the molecule, Figure 3 shows the schematics of the highest occupied and the lowest unoccupied molecular orbitals, HOMO and LUMO, respectively. Both orbitals extend inside the cyclic plane and have σ bonds.

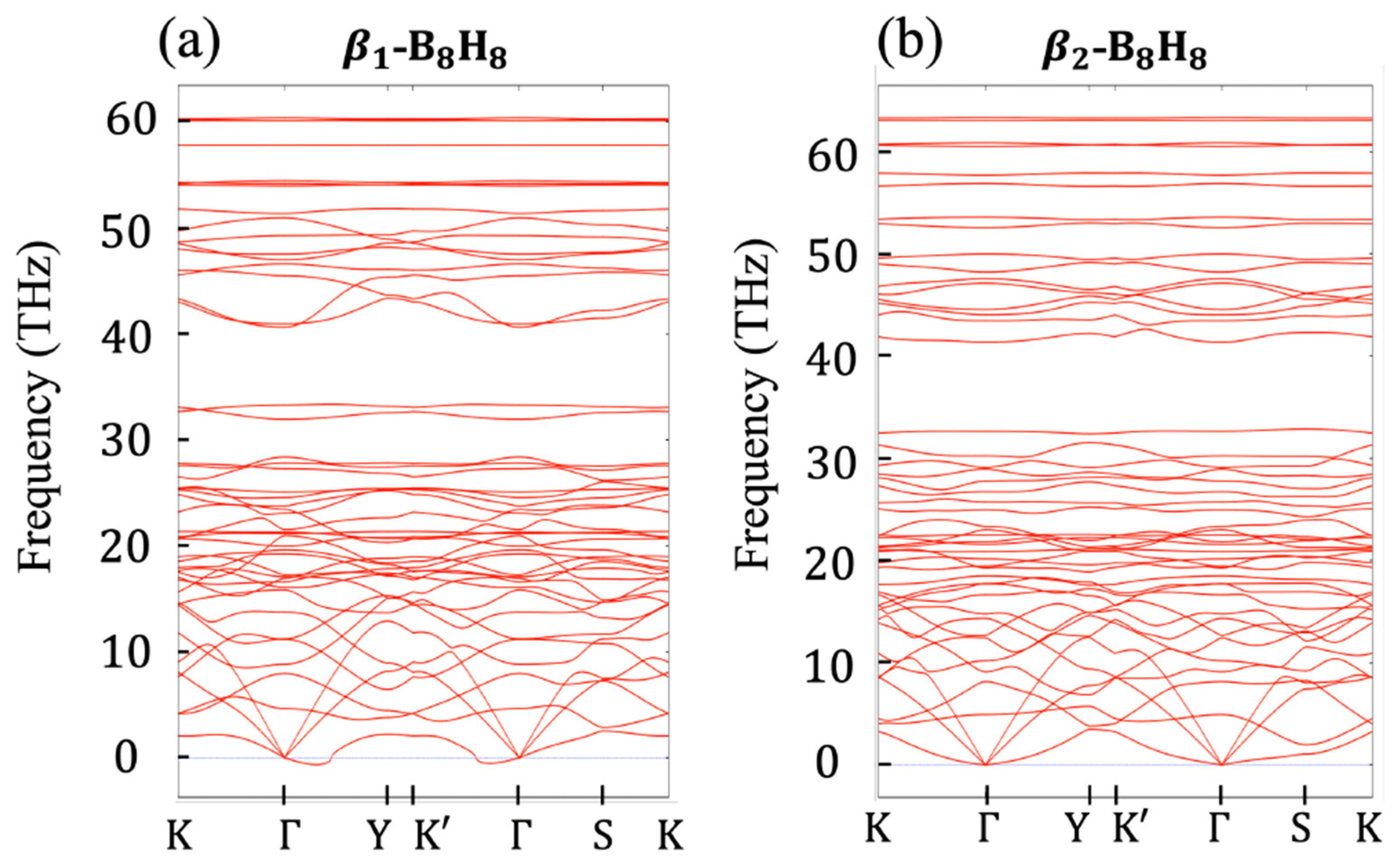
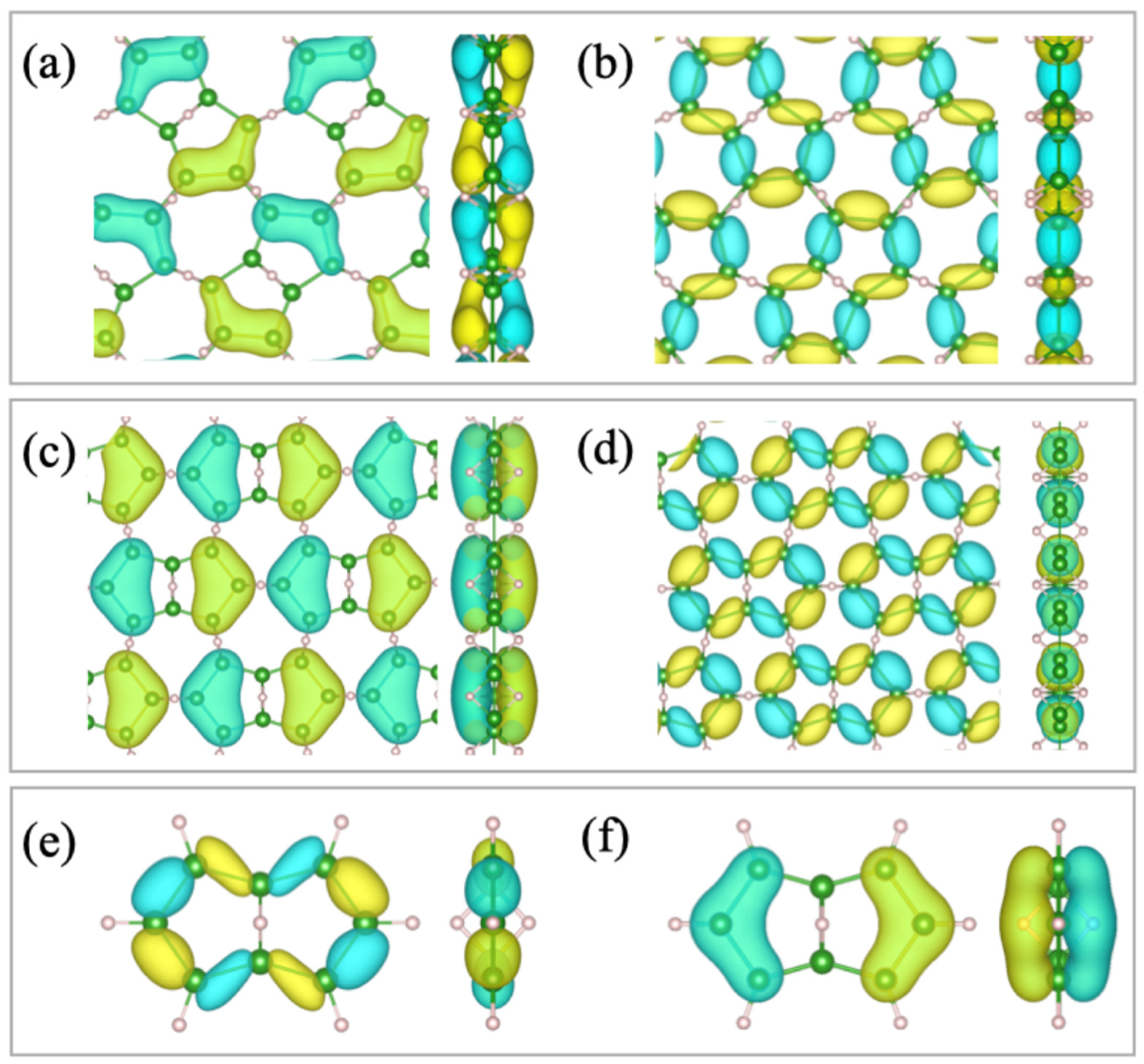
2.2. Relation to the Borophane Layer

The molecule 2:4:6:8:-2H-1,5:1,5-μH-B8H10 has a five-membered boron ring on each of the two sides of the 3c-2e bond, as shown in Figure 1b,c. The topological borophane layer (α-HB sheet) reported recently also has such a pair of five-membered rings in its sheet structure, as shown in Figure 4a,b [12,13]. Among the different arrangements, the pair unit is the tiled β-HB sheet (Figure 4c,d). In this section, we discuss the physical and chemical relationships between the proposed molecule and borophane layers.
The α-HB sheet in Figure 4a,b was predicted by topological band theory and confirmed to be thermodynamically and kinetically stable by first-principles calculations [15,17]. It is noteworthy that its kinetic stability was supported by the positive vibrational energy of the phonon modes. This material was successfully synthesized through an ion-exchange reaction [12,13]. The α-HB sheet is a semimetal, with electronic states of the Dirac nodal loop (DNL) at the Fermi level. X-ray spectroscopic measurements have revealed a gapless electronic structure [12,13]. In Figure 4, the wave functions of (a) the lower and (b) the higher DNL bands at the Г point schematically overlap in the atomic structure model [15]. Focusing on the spatial distributions of the electronic states, one finds that the borophane layer can be described in terms of tiling with the molecular orbitals of the pair of five-membered rings. Wave functions of the energetically higher and lower DNL bands have out-of-plane (π) and in-plane (σ) characteristics, respectively. Instead of the molecular orbitals of 2:4:6:8:-2H-1,5:1,5-μH-B8H10, the shapes match the HOMO and LUMO of 2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8, which is shown in Figure 4e,f.
A case of the β-HB sheet is given in Figure 4c,d; as the electronic structure and stability of the borophane layer have not been derived yet, we present our calculation results in Appendix B. The β sheet is also semimetallic, with a DNL at the Fermi level (Figure A2 in Appendix B). The phonon dispersion diagram for β-type borophane is shown in Figure A3. The phonon dispersion diagrams for β1-borophane show the imaginary phonon, while the one for β2-borophane shows that all the phonon energy is positive. The absence of an imaginary phonon modes implies kinematic stability, but it may not be sufficient to conclude their actual existence, as quadratic phonon bands appear near zero phonon energy. As shown in Appendix B, the electronic states of the β-HB sheet presented in Figure 4c,d are built with blocks of molecular orbitals of the pair of five-membered rings, as in the case of the α-sheet. The wave functions of the energetically higher and lower DNL bands have out-of-plane (π) and in-plane (σ) characteristics, respectively. The molecular orbital shapes are also similar to those of 2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8 in Figure 4e,f.
Comparing Figure 3 and Figure 4 indicates that the electronic states of the borophane layer agree better with the HOMO and LUMO of 2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8 than those of 2:4:6:8:-2H-1,5:1,5-μH-B8H10. The electronic properties can naturally be understood in terms of the bonding scheme between boron and hydrogen atoms. Besides the 3c-2e bond at the center, the rest of the B–H bonds in the B8H8 molecule are associated with one hydrogen atom, while those in B8H10 have two or no hydrogen atoms. The chemical environment of the B8H8 molecule generates the same π/σ LUMO/HOMO states as those of the borophane layer. It is worth mentioning that—in Table 1—2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8 is unstable, although the HB sheets themselves are stable. We infer that the π electronic state is unfavorable for a single molecule of hydrogenated boron and that the molecule 2:4:6:8:-2H-1,5:1,5-μH-B8H10 consists of σ bonding states.
By further comparing wave functions between the B8H8 molecule and the DNL sheets of HB, one finds that the energy levels of the molecular orbitals are reversed between the π and σ types. It is intriguing to find this contrast although the molecule corresponds to a building block of the layer. To systematically investigate their electronic properties, this study calculated the energy difference E(π) − E(σ) for the molecules and the sheets. As shown in Figure 5a, the two types of low-dimensional structures—0D (molecule) and 2D (sheets)—have an opposite sign of energy difference E(π) − E(σ). This difference is apparently due to interactions between the building blocks in the 2D network. To examine the issue quantitatively, the tight-binding model was calculated using the hopping parameters between the composing boron atoms. An α-HB sheet structure was adopted in the simulation. The critical parameters were the transfer integrals—tb and ti—at the two types of inequivalent 3c-2e bonds, where tb and ti correspond to the bonds at the unit center and those at the linkage between the units, respectively (Figure 5b). In the calculation, the transfer integrals at the single bonds between the boron atoms were uniformly set as ts. Under the condition tb/ts = 1, the energy level of the π-orbital decreases by ΔE = −0.114 ts when ti/ts is changed only from 0 to 0.1. The electronic change in the molecular orbital through the ti interaction is shown in Figure 5c. The isolated molecular orbitals (ti/ts. = 0) interact with each other and form a delocalized wave function (ti/ts = 0.1) similar to the one in Figure 4a. The model calculation demonstrates that the energy level of the π molecular orbitals can become lower than that of a σ orbital through interactions between the building units. The development of the delocalized π states is likely responsible for forming the 2D network in the HB sheet.
The calculation results showed a significant role of the 3c-2e bond in the change in molecular orbitals between the cyclic molecule and topological borophane. Besides the electronic structure, it is interesting to consider a possible reaction path for building an HB sheet from HB molecules. Figure 6a recalls the molecular structure of 2:4:6:8:-2H-1,5:1,5-μH-B8H10. There are three types of boron atoms: BC, BH, and BA. The BC atoms take part in the center 3c-2e B–H–B bonds and, thus, are not involved in linkages between molecules. The BH atoms individually bond with two hydrogen atoms, while the BA atoms are absent from the B–H bonding. Thus, we infer that a combination of BH and BA atoms naturally contributes to the two 3c-2e B–H–B bonds that connect the molecules that form the 2D network of the HB sheet.
To build an α-sheet composed of five-membered and seven-membered rings, one can assemble B8H10 molecules to form an intermediate seven-membered ring structure, as shown in Figure 6b. The heptagonal network is associated with two pairs of BH and BA atoms that naturally lead to the formation of 3c-2e bonds. There is also a pair of BH atoms that can induce intermolecular B–H–B bonding by releasing two hydrogen atoms or H2. However, for a β-sheet, the intermediate seven-membered ring is formed by combinations of BH atoms with combinations of BA atoms, as illustrated in Figure 6c. Pairs of BA atoms lack a hydrogen atom and are unlikely to generate a 3c-2e B–H–B bond themselves; thus, the B8H10 molecules cannot be used as blocks for building a β-structure. The argument for B–H–B bond formation favors α-sheet rather than β-sheet formation.
It is intriguing that β-borophane (Figure 4c,d) is not stable according to the calculations (Appendix B). However, the cyclic hydrogenated boron molecule 2:4:6:8:-2H-1,5:1,5-μH-B8H10 in Figure 1b,c and the topological α-borophane in Figure 1a,b were found to be stable. It is coincidental but intriguing to find that the reaction path of the molecular assembly favors a combination of the stable hydrogenated boron species.
Layers of topological borophane have been synthesized by liquid exfoliation associated with an ion-exchange reaction [11,12,13]. This is a top-down approach and typically results in powders of microscopic flakes. However, various 2D materials such as graphene and transition-metal dichalcogenide have been grown by chemical vapor deposition (CVD). This bottom-up approach has led to the synthesis of wide-area and single-crystalline films [21]. The cyclic B8H10 molecule proposed in this research has an atomic structure that corresponds to the building blocks of topological α-borophane. Thus, this molecule is the ideal precursor or CVD reacting gas for preparing single-crystalline topological borophane with a macroscopically wide area.

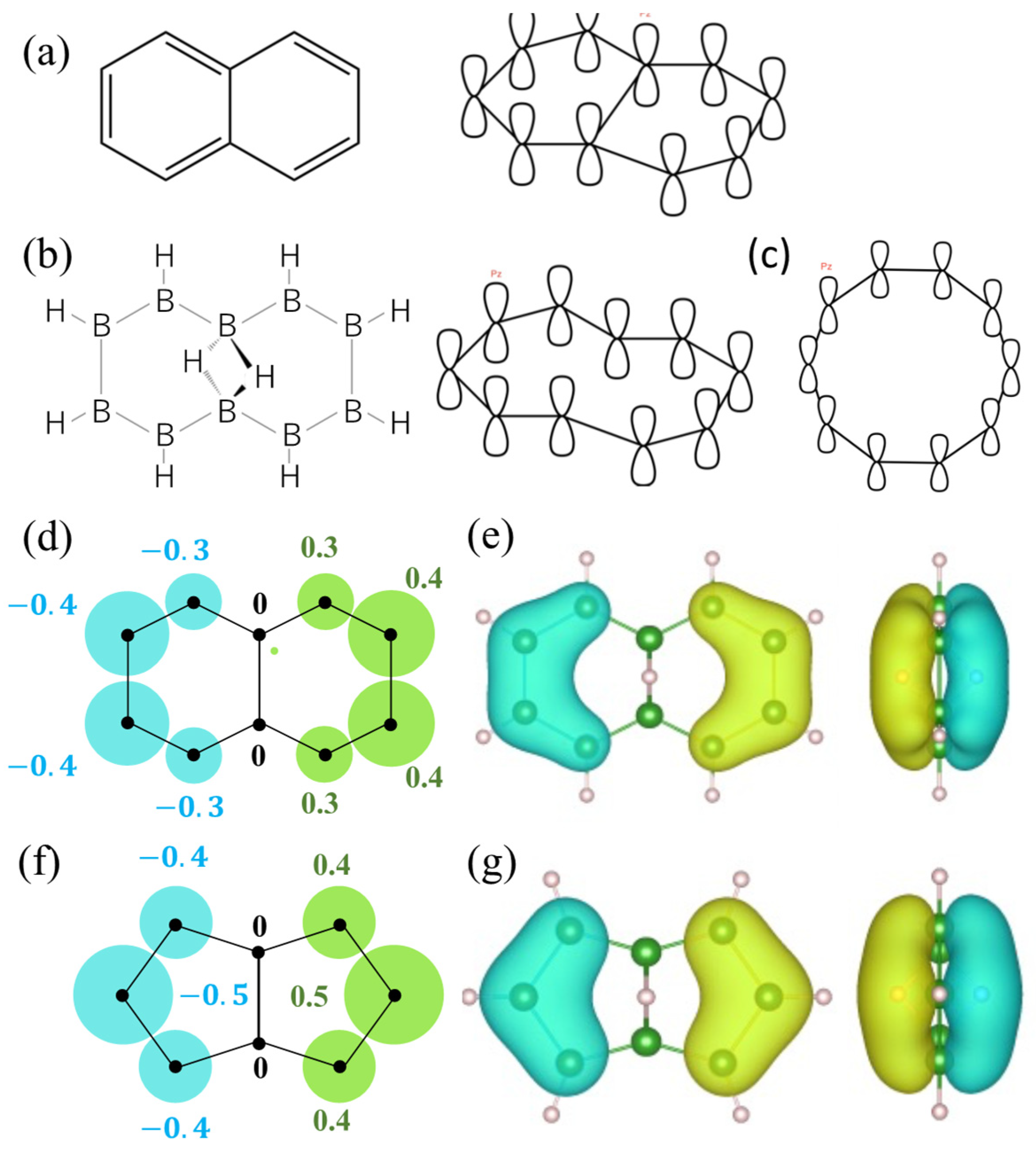
2.3. Orbitals of the Cyclic Boron Molecule in the Hückel Model

To examine the electronic states of a cyclic hydrogenated boron molecule, the classical Hückel model was applied and the results were compared with those for carbon molecules. The Hückel model has been used to simply calculate the energies of the π molecular orbitals in a conjugated carbon system by regarding all molecular orbitals as linear combinations of atomic orbitals [22,23,24,25,26,27]. Figure 7a shows the example of the cyclic conjugated carbon compound naphthalene (C10H8). This molecule consists of two loops of pz-orbitals, and each molecular orbital belongs to the genus-2 topological classification.
For comparison, we prepared a cyclic hydrogenated boron molecule with 10 boron atoms, corresponding to the 10 carbon atoms in naphthalene. The molecule is 1,6-1,6-decadiborane, B10H10, as illustrated in Figure 7b. As the two central boron atoms connect to each other through 3c-2e bonds, the pz-orbitals of the constituent boron atoms formed one molecular orbital loop, as shown in Figure 7b. This loop was topologically equivalent to a circle (genus-1), as illustrated in Figure 6c. This made it simple to calculate the Hückel model of the cyclic hydrogenated boron molecule. In this research, the Hückel model was calculated with a constant onsite Coulomb integral and constant resonance integral between neighboring atoms. The overlap integral was set to zero. A wave function calculated from the Hückel model is shown in Figure 7d for comparison with the LUMO in Figure 7e obtained from first-principles calculations. The molecular orbitals agreed well. Figure 7f,g also compares molecular orbitals between the Hückel model and the first-principles calculations for 2:4:6:8:-2H-1,5:1,5-μH-B8H10. Again, the molecular orbitals of the two models were similar. This similarity could be a theoretical test ground for deepening our understandings of quantum chemistry-based topological structures and electronic states.

3. Calculation Methods

Calculations of optimized atomic structures, molecular orbitals, and vibrational properties were all made via density functional theory (DFT), implemented using the Python package “Psi4 1.5.0” [28]. Becke three-parameter exchange and Lee–Yang–Parr correlations (B3LYP) were selected as an exchange-correlation functional [29,30]. The Gaussian basis set 6-311g(d,p) was applied to describe the electronic structures. Molecular geometry was optimized under Gaussian-level criteria.
For 2D HB or borophane sheets, calculations of wave functions and band diagrams were carried out via “Quantum ESPRESSO 7.1”, which is a first-principles code based on DFT, the plane-wave method, and the pseudopotential method [31]. The present calculations used the GGA–PBE exchange-correlation functional [32] with ultra-soft pseudopotentials in the library of standard solid-state pseudopotentials called “SSSP” [33]. The structure stabilities were evaluated from the phonon dispersion obtained from “Phonopy 2.16.3” [34], which can be used as post-process code for Quantum ESPRESSO.
The atomic structures and wave functions were visualized via Visualization of Electronic and STructural Analysis (VESTA) [35].

4. Conclusions

In summary, we predict the existence of a new cyclic hydrogenated boron molecule, 2:4:6:8:-2H-1,5:1,5-μH-B8H10, on the basis of first-principles calculations. This molecule can be regarded as a building block of topological hydrogen boride (borophane) sheets. This research shows intriguing relationships between the planar molecule and the atomic sheet forms of the hydrogenated boron compound. The cyclic B8H10 molecule provides new perspectives in boron chemistry. This molecule could also be the ideal precursor or CVD reaction gas for preparing wide-area topological borophane, which could lead to technological innovations.

Author Contributions

Conceptualization, Y.A. and I.M.; calculation, Y.A., T.N., H.Y., I.T. and N.T.C.; validation, X.Z., Y.T., M.H., S.O., T.K. and I.M.; writing—original draft preparation, Y.A. and I.M.; writing—review and editing, Y.A. and I.M.; visualization, Y.A., T.N., H.Y. and I.M.; supervision, S.O., T.K. and I.M.; project administration, I.M.; funding acquisition, I.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by JST, CREST Grant Number JPMJCR21O4, Japan, and by JSPS KAKENHI Grant Numbers JP19H04398 and JP18H03874.

Data Availability Statement

The data is contained in the article.

Acknowledgments

We acknowledge M. Sato, T. Sumi, and F. Komori for their discussions with us.

Conflicts of Interest

The authors declare no conflict of interest.

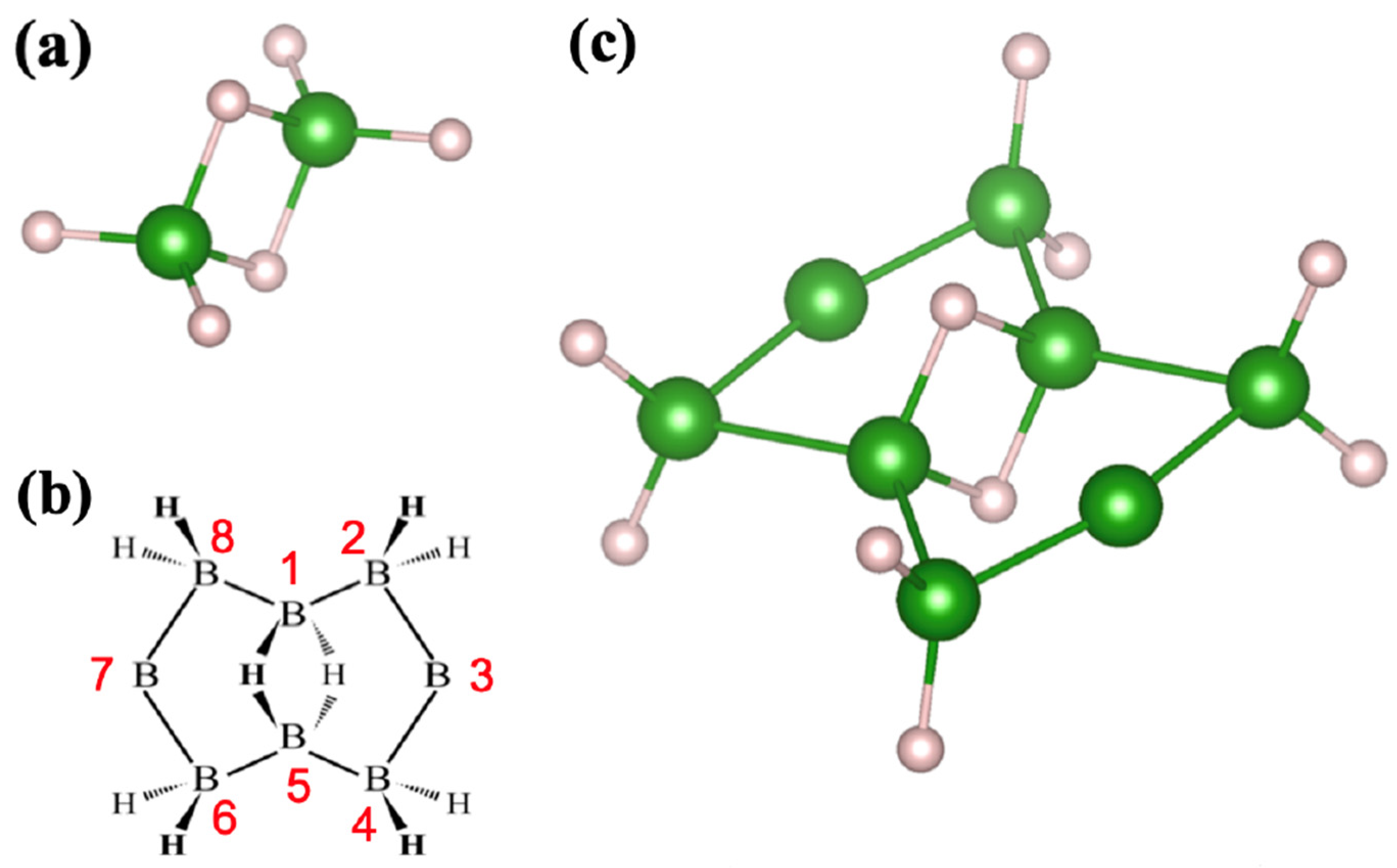
Appendix A

Figure A1 shows candidates for cyclic hydrogen boron molecules that were theoretically examined in this research.
Molecules 28 01225 g0a1 550
Figure A1. Candidates for the cyclic hydrogenated boron molecules. The structures are overlapped with molecular orbitals of HOMOs and LUMOs. The color of each molecular orbitals corresponds to the sign of its wave functions.
Figure A1. Candidates for the cyclic hydrogenated boron molecules. The structures are overlapped with molecular orbitals of HOMOs and LUMOs. The color of each molecular orbitals corresponds to the sign of its wave functions.
Molecules 28 01225 g0a1

Appendix B

Figure A2 summarizes atomic models and electronic structures of the β1- and β2-borophane layers. The phonon dispersion curves of the individual HB sheets are given in Figure A3.
Molecules 28 01225 g0a2 550
Figure A2. The β borophane. The β1-type: (a) atomic structure, (b) band diagram, (c) π wave functions (lower bands of a DNL), and (d) σ wave functions (higher bands of a DNL). The β2-type: (e) atomic structure, (f) band diagram, (g) π wave functions (lower bands of a DNL), and (h) σ wave functions (higher bands of a DNL). The color of each molecular orbitals corresponds to the sign of its wave functions. The unit cell is represented as a rhombus in each subfigure corresponding to the atomic structures and orbitals. The letters shown in (b,f) represent the high symmetry points in the first Brillouin zone shown as insets of (b,f).
Figure A2. The β borophane. The β1-type: (a) atomic structure, (b) band diagram, (c) π wave functions (lower bands of a DNL), and (d) σ wave functions (higher bands of a DNL). The β2-type: (e) atomic structure, (f) band diagram, (g) π wave functions (lower bands of a DNL), and (h) σ wave functions (higher bands of a DNL). The color of each molecular orbitals corresponds to the sign of its wave functions. The unit cell is represented as a rhombus in each subfigure corresponding to the atomic structures and orbitals. The letters shown in (b,f) represent the high symmetry points in the first Brillouin zone shown as insets of (b,f).
Molecules 28 01225 g0a2
Molecules 28 01225 g0a3 550
Figure A3. Phonon dispersion diagrams of the (a) β1- and (b) β2-borophane. The letters shown in (a,b) represent the high symmetry points in the first Brillouin zone shown as insets of Figure A2b,f.
Figure A3. Phonon dispersion diagrams of the (a) β1- and (b) β2-borophane. The letters shown in (a,b) represent the high symmetry points in the first Brillouin zone shown as insets of Figure A2b,f.
Molecules 28 01225 g0a3
The β1-borophane layer is tiled with the pseudo-2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8 structures as shown in Figure A2a which has the 3c-2e bond at a shared edge of pentagons. The band structure of β1-borophane is shown in Figure A2b, which has a DNL. The wave functions that form a DNL are periodic HOMO (σ bonding; Figure A2c) and LUMO (π bonding; Figure A2d) arrangements of the 2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8 molecule (Figure 4e,f). On an isolated molecule, the π bond is at a higher energy level than the σ bond. When the 2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8 molecule is crystallized in 2D by forming intermolecular 3c-2e B–H–B bonds, both molecular orbitals overlap with those on the neighboring molecules, and hopping integrals are introduced. Because of the out-of-plane structure of the 3c-2e bond, the sign of the hopping integral is different for the σ and π bonds, as discussed in reference [16]. The hopping integral for the π (σ) bond is negative (positive), so the band dispersion of the 2D crystal shows a cosine band with a lower (higher) energy at the Г point. These hopping integrals have energy scales comparable with those of the molecular orbitals, and thus the band is inverted at the Г point (Figure A2b). Because the inverted bands have different eigenvalues with respect to the mirror operation about the z = 0 plane, hybridization between them is prohibited and a gapless band crossing is produced, which is the DNL.
The atomics structure of β2-borophane layer is shown in Figure A2e which has a different 3c-2e bonds arrangement from that of β1-borophane layer. The band structure of β2-borophane is shown in Figure A2f, which also has a DNL. The wave functions that form the lower (higher) bands of a DNL is π (σ) bonding states as shown in Figure 4g,h. The π bonding states of β2-borophane has nodes at 3c-2e bonds like that of β1-borophane, though the character of the wave function differs from the isolated 2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8 molecule due to the different 3c-2e bonding arrangement.
The phonon dispersion curves of both β1- and β2-borophane layers are given in Figure A3 to evaluate their stability. The phonon dispersion of the β1-borophane shows the imaginary phonon, which implies that the β1-borophane layers are unstable. On the other hand, the β2-borophane shows that all the band dispersion is positive. Though the absence of imaginary phonon modes implies kinematic stability, but it may not be sufficient to conclude their actual existence because quadratic phonon bands appear near zero phonon energy.

References

  1. Callister, W.D., Jr.; Rethwisch, D.G. Materials Science and Engineering: An Introduction, 10th ed.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
  2. Hagemann, H. Boron Hydrogen Compounds: Hydrogen Storage and Battery Applications. Molecules 2021, 26, 7425. [Google Scholar] [CrossRef] [PubMed]
  3. van’t Hoff, J.H. A suggestion looking to the extension into space of the structural formulas at present used in chemistry, and a note upon the relation between the optical activity and the chemical constitution of organic compounds. Arch. Neerl. Sci. Exactes Nat. 1874, 9, 445–454. [Google Scholar]
  4. Le Bel, J.A. Sur les Relations qui existent entre les Formules atomiques des Corps organiques et le Pouvoir rotatoire de leurs Dissolutions. Bell. Soc. Chim. Fr. 1874, 22, 337–347. [Google Scholar]
  5. Fau, S.; Frenking, G. Anti van’t Hoff/Le Bel geometries of boron compounds. A theoretical study of classical and nonclassical isomers of B2CH4, B2NH3 and B2OH2. J. Mol. Struct. THEOCHEM 1995, 338, 117–130. [Google Scholar] [CrossRef]
  6. Song, B.; Zhou, Y.; Yang, H.-M.; Liao, J.-H.; Yang, L.-M.; Yang, X.-B.; Ganz, E. Two-dimensional anti-Van’t Hoff/Le Bel array AlB6 with high stability, unique motif, triple dirac cones, and superconductivity. J. Am. Chem. Soc. 2019, 141, 3630–3640. [Google Scholar] [CrossRef]
  7. Matsuda, I.; Wu, K. 2D Boron: Boraphene, Borophene, Boronene, 1st ed.; Springer: Cham, Switzerland, 2021. [Google Scholar]
  8. Feng, B.; Zhang, J.; Zhong, Q.; Li, W.; Li, S.; Li, H.; Cheng, P.; Meng, S.; Chen, L.; Wu, K. Experimental Realization of Two-Dimensional Boron Sheets. Nat. Chem. 2016, 8, 563–568. [Google Scholar] [CrossRef] [Green Version]
  9. Feng, B.; Sugino, O.; Liu, R.-Y.; Zhang, J.; Yukawa, R.; Kawamura, M.; Iimori, T.; Kim, H.; Hasegawa, Y.; Li, H.; et al. Dirac Fermions in Borophene. Phys. Rev. Lett. 2017, 118, 096401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  10. Feng, B.; Zhang, J.; Ito, S.; Arita, M.; Cheng, C.; Chen, L.; Wu, K.; Komori, F.; Sugino, O.; Miyamoto, K.; et al. Discovery of 2D anisotropic Dirac cones. Adv. Mater. 2018, 30, 1704025. [Google Scholar] [CrossRef]
  11. Nishino, H.; Fujita, T.; Cuong, N.T.; Tominaka, S.; Miyauchi, M.; Iimura, S.; Hirata, A.; Umezawa, N.; Okada, S.; Nishibori, E.; et al. Formation and Characterization of Hydrogen Boride Sheets Derived from MgB2 by Cation Exchange. J. Am. Chem. Soc. 2017, 139, 13761–13769. [Google Scholar] [CrossRef]
  12. Niibe, M.; Cameau, M.; Cuong, N.T.; Sunday, O.I.; Zhang, X.; Tsujikawa, Y.; Okada, S.; Yubuta, K.; Kondo, T.; Matsuda, I. Electronic structure of a borophene layer in rare-earth aluminum/chromium boride and its hydrogenated derivative borophane. Phys. Rev. Mater. 2021, 5, 084007. [Google Scholar] [CrossRef]
  13. Zhang, X.; Tsujikawa, Y.; Tateishi, I.; Niibe, M.; Wada, T.; Horio, M.; Hikichi, M.; Ando, Y.; Yubuta, K.; Kondo, T.; et al. Electronic Topological Transition of 2D Boron by the Ion Exchange Reaction. J. Phys. Chem. C 2022, 126, 12802–12808. [Google Scholar] [CrossRef]
  14. Kawamura, R.; Cuong, N.T.; Fujita, T.; Ishibiki, R.; Hirabayashi, T.; Yamaguchi, A.; Matsuda, I.; Okada, S.; Kondo, T.; Miyauchi, M. Photoinduced hydrogen release from hydrogen boride sheets. Nat. Commun. 2019, 10, 4880. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  15. Cuong, N.T.; Tateishi, I.; Cameau, M.; Niibe, M.; Umezawa, N.; Slater, B.; Yubuta, K.; Kondo, T.; Ogata, M.; Okada, S.; et al. Topological Dirac Nodal Loops in Nonsymmorphic Hydrogenated Monolayer Boron. Phys. Rev. B 2020, 101, 195412. [Google Scholar] [CrossRef]
  16. Tateishi, I.; Cuong, N.T.; Moura, C.A.S.; Cameau, M.; Ishibiki, R.; Fujino, A.; Okada, S.; Yamamoto, A.; Araki, M.; Ito, S.; et al. Semimetallicity of Free-Standing Hydrogenated Monolayer Boron from MgB2. Phys. Rev. Mater. 2019, 3, 024004. [Google Scholar] [CrossRef]
  17. Tateishi, I.; Zhang, X.; Matsuda, I. Electronic Structures of Polymorphic Layers of Borophane. Molecules 2022, 27, 1808. [Google Scholar] [CrossRef]
  18. Boron Hydride Chemistry; Muetterties, E.L. (Ed.) Academic Press: New York, NY, USA, 2012. [Google Scholar]
  19. Connelly, N.G.; Damhus, T.; Hartshorn, R.M.; Hutton, A.T. Nomenclature of Inorganic Chemistry: IUPAC Recommendations 2005; Royal Society of Chemistry: Cambridge, UK, 2005. [Google Scholar]
  20. Beckett, M.A.; Brellochs, B.; Chizhevsky, I.T.; Damhus, T.; Hellwich, K.-H.; Kennedy, J.D.; Laitinen, R.; Powella, W.H.; Rabinovich, D.; Viñas, C.; et al. Nomenclature for boranes and related species (IUPAC Recommendations 2019). Pure Appl. Chem. 2020, 92, 355–381. [Google Scholar] [CrossRef] [Green Version]
  21. Choi, S.H.; Yun, S.J.; Won, Y.S.; Oh, C.S.; Kim, S.M.; Kim, K.K.; Lee, Y.H. Large-scale synthesis of graphene and other 2D materials towards industrialization. Nat. Commun. 2022, 13, 1484. [Google Scholar] [CrossRef]
  22. Solà, M. Aromaticity rules. Nat. Chem. 2022, 14, 585–590. [Google Scholar] [CrossRef]
  23. Mutai, K. Quantum Chemistry, Ryoshi Kagaku; SHOKODO Co. Ltd.: Tokyo, Japan, 1991. (In Japanese) [Google Scholar]
  24. Hückel, E. Quantum-theoretical contributions to the benzene problem. I. The electron configuration of benzene and related compounds. Z. Phys. 1931, 70, 204–286. [Google Scholar] [CrossRef]
  25. Krygowski, T.M.; Cyrañski, M.K.; Czarnocki, Z.; Häfelinger, G.; Katritzky, A.R. Aromaticity: A Theoretical Concept of Immense Practical Importance. Tetrahedron 2000, 56, 1783–1796. [Google Scholar] [CrossRef]
  26. Hess, B.A., Jr.; Schaad, L.J. Hueckel molecular orbital .pi. resonance energies. Benzenoid hydrocarbons. J. Am. Chem. Soc. 1971, 93, 2413–2416. [Google Scholar] [CrossRef]
  27. Schaad, L.J.; Hess, B.A., Jr. Huckel theory and aromatically. J. Chem. Educ. 1974, 51, 640. [Google Scholar] [CrossRef]
  28. Smith, D.G.A.; Burns, L.A.; Simmonett, A.C.; Parrish, R.M.; Schieber, M.C.; Galvelis, R.; Kraus, P.; Kruse, H.; Remigio, R.D.; Alenaizan, A.; et al. PSI4 1.4: Open-source software for high-throughput quantum chemistry. J. Chem. Phys. 2020, 152, 184108. [Google Scholar] [CrossRef] [PubMed]
  29. Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648. [Google Scholar] [CrossRef] [Green Version]
  30. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [Green Version]
  31. Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
  33. Prandini, G.; Marrazzo, A.; Castelli, I.E.; Mounet, N.; Marzari, N. Precision and efficiency in solid-state pseudopotential calculations. npj Comput. Mater. 2018, 4, 72. [Google Scholar] [CrossRef] [Green Version]
  34. Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
  35. Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Cryst. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
Molecules 28 01225 g001 550
Figure 1. Molecules of hydrogenated boron compounds. (a) Atomic structure of diborane, B2H6. (b) A structural formula and (c) the optimized molecular structure of 2:4:6:8:-2H-1,5:1,5-μH-B8H10. Numbers of the boron atoms for nomenclature are labeled in (b).
Figure 1. Molecules of hydrogenated boron compounds. (a) Atomic structure of diborane, B2H6. (b) A structural formula and (c) the optimized molecular structure of 2:4:6:8:-2H-1,5:1,5-μH-B8H10. Numbers of the boron atoms for nomenclature are labeled in (b).
Molecules 28 01225 g001
Molecules 28 01225 g002 550
Figure 2. Structural formula of 12 candidates for a new cyclic hydrogenated boron molecule. A top-left number of each formula corresponds to the index in Table 1.
Figure 2. Structural formula of 12 candidates for a new cyclic hydrogenated boron molecule. A top-left number of each formula corresponds to the index in Table 1.
Molecules 28 01225 g002
Molecules 28 01225 g003 550
Figure 3. Top and side views of (a) the highest occupied molecular orbitals (HOMO) and (b) the lowest unoccupied molecular orbitals (LUMO) of 2:4:6:8:-2H-1,5:1,5-μH-B8H10. The HOMO and LUMO energy levels were −8.14 eV and −4.05 eV with reference to the vacuum level, respectively. The colors of the molecular orbitals correspond to the sign of their wave functions.
Figure 3. Top and side views of (a) the highest occupied molecular orbitals (HOMO) and (b) the lowest unoccupied molecular orbitals (LUMO) of 2:4:6:8:-2H-1,5:1,5-μH-B8H10. The HOMO and LUMO energy levels were −8.14 eV and −4.05 eV with reference to the vacuum level, respectively. The colors of the molecular orbitals correspond to the sign of their wave functions.
Molecules 28 01225 g003
Molecules 28 01225 g004 550
Figure 4. Atomic structures of the borophane layer (α1, β1), and the molecule (2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8). Wave functions and molecular orbitals at Г point are schematically overlapped in the atomic models. (a) Lower and (b) higher bands of a Dirac nodal loop of the α1-borophane [15,17]. (c) Lower and (d) higher bands of a Dirac nodal loop of the β1-borophane (see Appendix A). (e) HOMO and (f) LUMO of the 2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8 molecule. The color of each molecular orbital corresponds to the sign of its wave functions.
Figure 4. Atomic structures of the borophane layer (α1, β1), and the molecule (2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8). Wave functions and molecular orbitals at Г point are schematically overlapped in the atomic models. (a) Lower and (b) higher bands of a Dirac nodal loop of the α1-borophane [15,17]. (c) Lower and (d) higher bands of a Dirac nodal loop of the β1-borophane (see Appendix A). (e) HOMO and (f) LUMO of the 2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8 molecule. The color of each molecular orbital corresponds to the sign of its wave functions.
Molecules 28 01225 g004
Molecules 28 01225 g005 550
Figure 5. (a) Energy differences E(π) − E(σ) between boron materials, corresponding to the HOMO-LUMO gap (gap between lower-band and higher band of DNL at Г point) for the HB molecules (the HB sheets). Molecules: (2) 2:3:5:6:-H-1,4:1,4-μH-B6H6, (7) 2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8, (10) 2:3:4:6:7:8:9:10:-H-1,5:1,5-μH-B10H10, (11) 2:3:4:5:7:8:9:10:-H-1,6:1,6-μH-B10H10, (12) 2:3:4:5:6:8:9:10:11:12:-H-1,7:1,7-μH-B12H12. The index numbers correspond to those in Figure 2 and Table 1. Sheets (at Г point): (α1) α1-borophane, (α2) α2-borophane, (β1) β1-borophane, (β2) β2-borophane. (b) Descriptions of the tight-binding parameters tb and ti. (c) Energy diagram calculated from the tight-binding model with wave function forms before and after the interaction. Only one of the neighboring molecular orbitals is shown for the case ti/ts = 0.1 for comparison with the results in Figure 4a.
Figure 5. (a) Energy differences E(π) − E(σ) between boron materials, corresponding to the HOMO-LUMO gap (gap between lower-band and higher band of DNL at Г point) for the HB molecules (the HB sheets). Molecules: (2) 2:3:5:6:-H-1,4:1,4-μH-B6H6, (7) 2:3:4:6:7:8:-H-1,5:1,5-μH-B8H8, (10) 2:3:4:6:7:8:9:10:-H-1,5:1,5-μH-B10H10, (11) 2:3:4:5:7:8:9:10:-H-1,6:1,6-μH-B10H10, (12) 2:3:4:5:6:8:9:10:11:12:-H-1,7:1,7-μH-B12H12. The index numbers correspond to those in Figure 2 and Table 1. Sheets (at Г point): (α1) α1-borophane, (α2) α2-borophane, (β1) β1-borophane, (β2) β2-borophane. (b) Descriptions of the tight-binding parameters tb and ti. (c) Energy diagram calculated from the tight-binding model with wave function forms before and after the interaction. Only one of the neighboring molecular orbitals is shown for the case ti/ts = 0.1 for comparison with the results in Figure 4a.
Molecules 28 01225 g005
Molecules 28 01225 g006 550
Figure 6. Construction of the borophane layer with the 2:4:6:8:-2H-1,5:1,5-μH-B8H10 molecules. (a) Molecular structures with labels on the different boron sites. (b) Building the α-borophane. (c) Building the β-borophane. Intermediate seven-membered rings are shaded in green in (b,c).
Figure 6. Construction of the borophane layer with the 2:4:6:8:-2H-1,5:1,5-μH-B8H10 molecules. (a) Molecular structures with labels on the different boron sites. (b) Building the α-borophane. (c) Building the β-borophane. Intermediate seven-membered rings are shaded in green in (b,c).
Molecules 28 01225 g006
Molecules 28 01225 g007 550
Figure 7. Application of the Hückel model to cyclic molecules. (a) Naphthalene molecule and the pz configuration. (b) 1,6-1,6-decadiborane and the pz configuration. (c) pz configuration of a cyclic decagon molecule. (d,e) Molecular orbitals of 1,6-1,6-decadiborane, calculated from (d) the Hückel model and (e) first-principles calculations. (f,g) Molecular orbitals of 1,5-1,5-octadiborane, calculated from the (g) Hückel model and (f) first-principles calculations. The color of each molecular orbital corresponds to the sign of its wave functions.
Figure 7. Application of the Hückel model to cyclic molecules. (a) Naphthalene molecule and the pz configuration. (b) 1,6-1,6-decadiborane and the pz configuration. (c) pz configuration of a cyclic decagon molecule. (d,e) Molecular orbitals of 1,6-1,6-decadiborane, calculated from (d) the Hückel model and (e) first-principles calculations. (f,g) Molecular orbitals of 1,5-1,5-octadiborane, calculated from the (g) Hückel model and (f) first-principles calculations. The color of each molecular orbital corresponds to the sign of its wave functions.
Molecules 28 01225 g007
Table
Table 1. Filtration of the molecule candidates, TRUE or FALSE. Stability is determined by the absence (stability: TRUE) or presence (Stability: FALSE) of an imaginary vibrational mode. Atomic structures of the cyclic hydrogenated boron molecules are shown in Figure 2 and Appendix A.
Table 1. Filtration of the molecule candidates, TRUE or FALSE. Stability is determined by the absence (stability: TRUE) or presence (Stability: FALSE) of an imaginary vibrational mode. Atomic structures of the cyclic hydrogenated boron molecules are shown in Figure 2 and Appendix A.
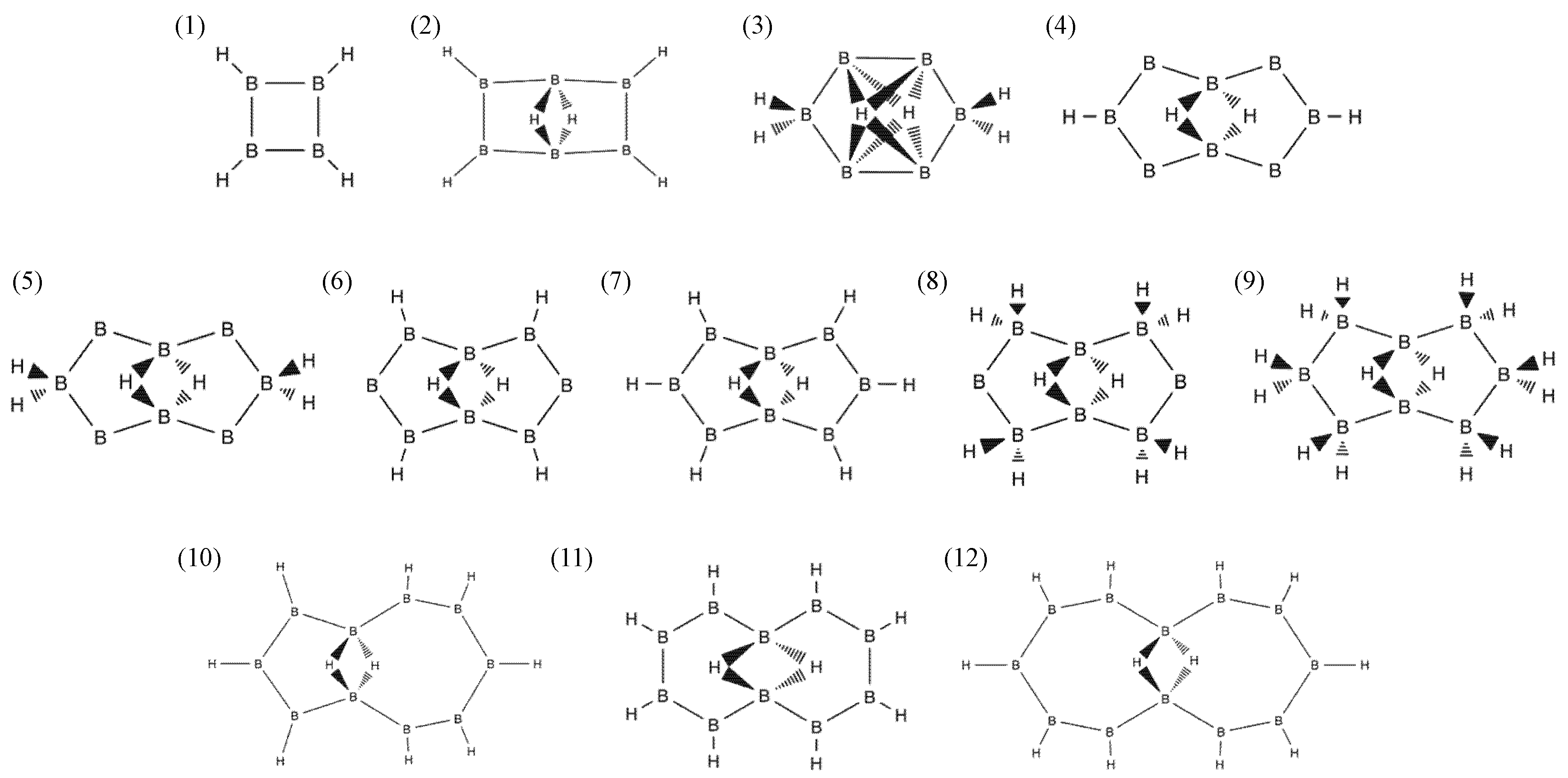
IndexMolecule CandidateTotal Energy (eV)HOMO Level (eV)LUMO Level (eV)Stability
11:2:3:4:-H-B4H4−2768.32−6.64−2.50FALSE
22:3:5:6:-H-1,4:1,4-μH-B6H6−4148.76−6.56−3.73FALSE
32:5:-2H-1,3,4,6:1,3,4,6-μH-B6H6−4149.17−7.65−4.22FALSE
43:7:-H-1,5:1,5-μH-B8H4−5466.93−5.93−4.30FALSE
53:7:-2H-1,5:1,5-μH-B8H6−5499.07−5.20−4.54FALSE
62:4:6:8:-H-1,5:1,5-μH-B8H6−5501.27−5.93−4.16FALSE
72:3:4:6:7:8:-H-1,5:1,5-μH-B8H8−5533.90−6.64−4.24FALSE
82:4:6:8:-2H-1,5:1,5-μH-B8H10−5568.84−8.14−4.05TRUE
92:3:4:6:7:8:-2H-1,5:1,5-μH-B8H14−5635.07−7.10−3.70FALSE
102:3:4:6:7:8:9:10:-H-1,5:1,5-μH-B10H10−6915.86−6.18−4.24FALSE
112:3:4:5:7:8:9:10:-H-1,6:1,6-μH-B10H10−6917.17−6.18−4.46FALSE
122:3:4:5:6:8:9:10:11:12:-H-1,7:1,7-μH-B12H12−8299.69−6.31−4.57FALSE
Table
Table 2. B2H6, 8 BH3, and B8H10 + 7H2. All the systems have 8 boron and 24 hydrogen atoms.
Table 2. B2H6, 8 BH3, and B8H10 + 7H2. All the systems have 8 boron and 24 hydrogen atoms.
SystemTotal Energy
E (Hartree)		E − 4E(B2H6)
(Hartree)		E − 4E(B2H6)
(kcal/mol)
4 B2H6−213.2180.0000.000
8 BH3−212.9690.249156.250
B8H10 + 7H2−212.9080.310194.528
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ando, Y.; Nakashima, T.; Yin, H.; Tateishi, I.; Zhang, X.; Tsujikawa, Y.; Horio, M.; Cuong, N.T.; Okada, S.; Kondo, T.; et al. Prediction of a Cyclic Hydrogenated Boron Molecule as a Promising Building Block for Borophane. Molecules 2023, 28, 1225. https://doi.org/10.3390/molecules28031225

AMA Style

Ando Y, Nakashima T, Yin H, Tateishi I, Zhang X, Tsujikawa Y, Horio M, Cuong NT, Okada S, Kondo T, et al. Prediction of a Cyclic Hydrogenated Boron Molecule as a Promising Building Block for Borophane. Molecules. 2023; 28(3):1225. https://doi.org/10.3390/molecules28031225

Chicago/Turabian Style

Ando, Yasunobu, Takeru Nakashima, Heming Yin, Ikuma Tateishi, Xiaoni Zhang, Yuki Tsujikawa, Masafumi Horio, Nguyen Thanh Cuong, Susumu Okada, Takahiro Kondo, and et al. 2023. "Prediction of a Cyclic Hydrogenated Boron Molecule as a Promising Building Block for Borophane" Molecules 28, no. 3: 1225. https://doi.org/10.3390/molecules28031225

APA Style

Ando, Y., Nakashima, T., Yin, H., Tateishi, I., Zhang, X., Tsujikawa, Y., Horio, M., Cuong, N. T., Okada, S., Kondo, T., & Matsuda, I. (2023). Prediction of a Cyclic Hydrogenated Boron Molecule as a Promising Building Block for Borophane. Molecules, 28(3), 1225. https://doi.org/10.3390/molecules28031225

Article Metrics

Back to TopTop