Hall Effect Anisotropy in the Paramagnetic Phase of Ho0.8Lu0.2B12 Induced by Dynamic Charge Stripes
Abstract
1. Introduction
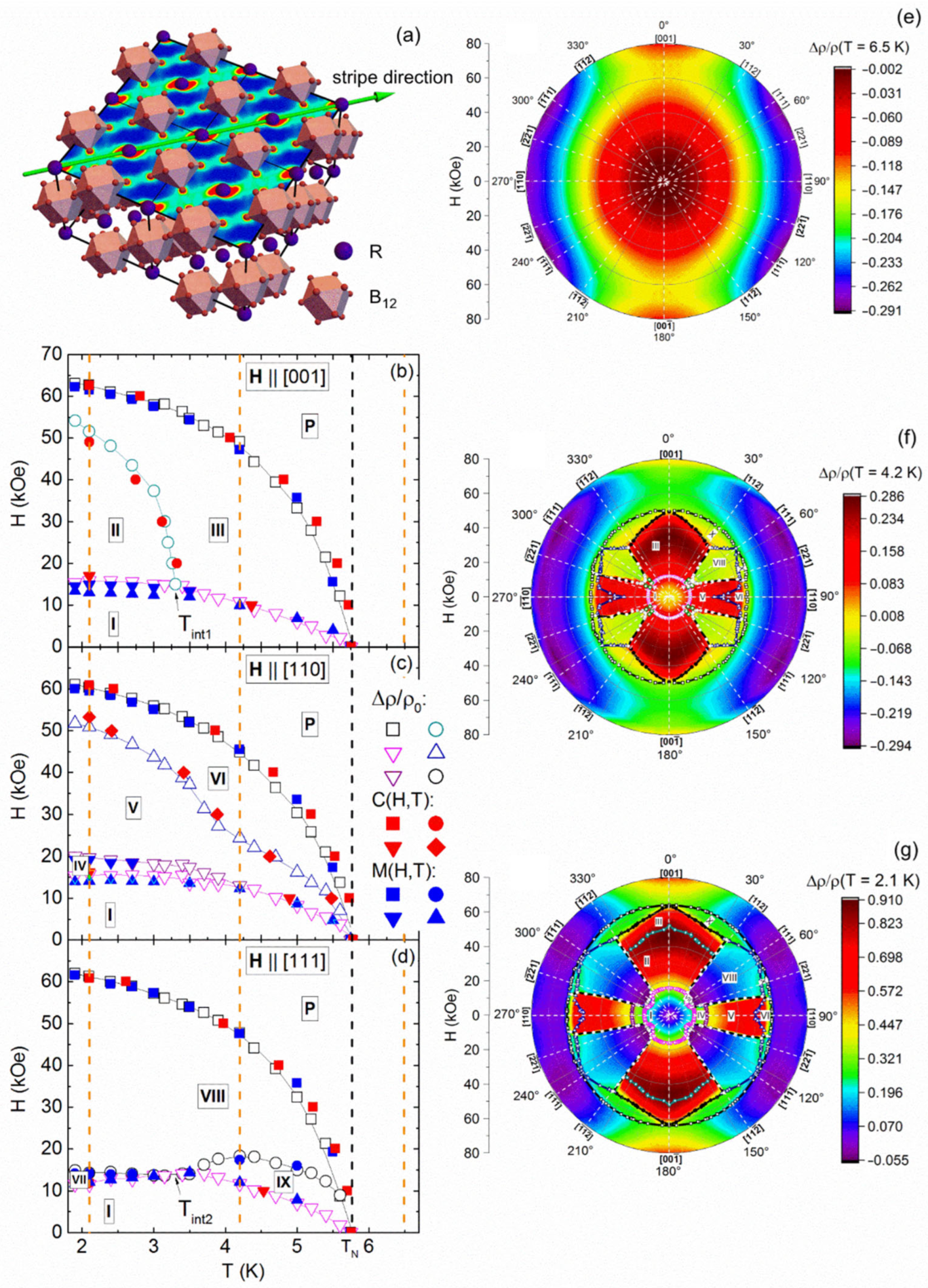
2. Experimental Results and Data Analysis
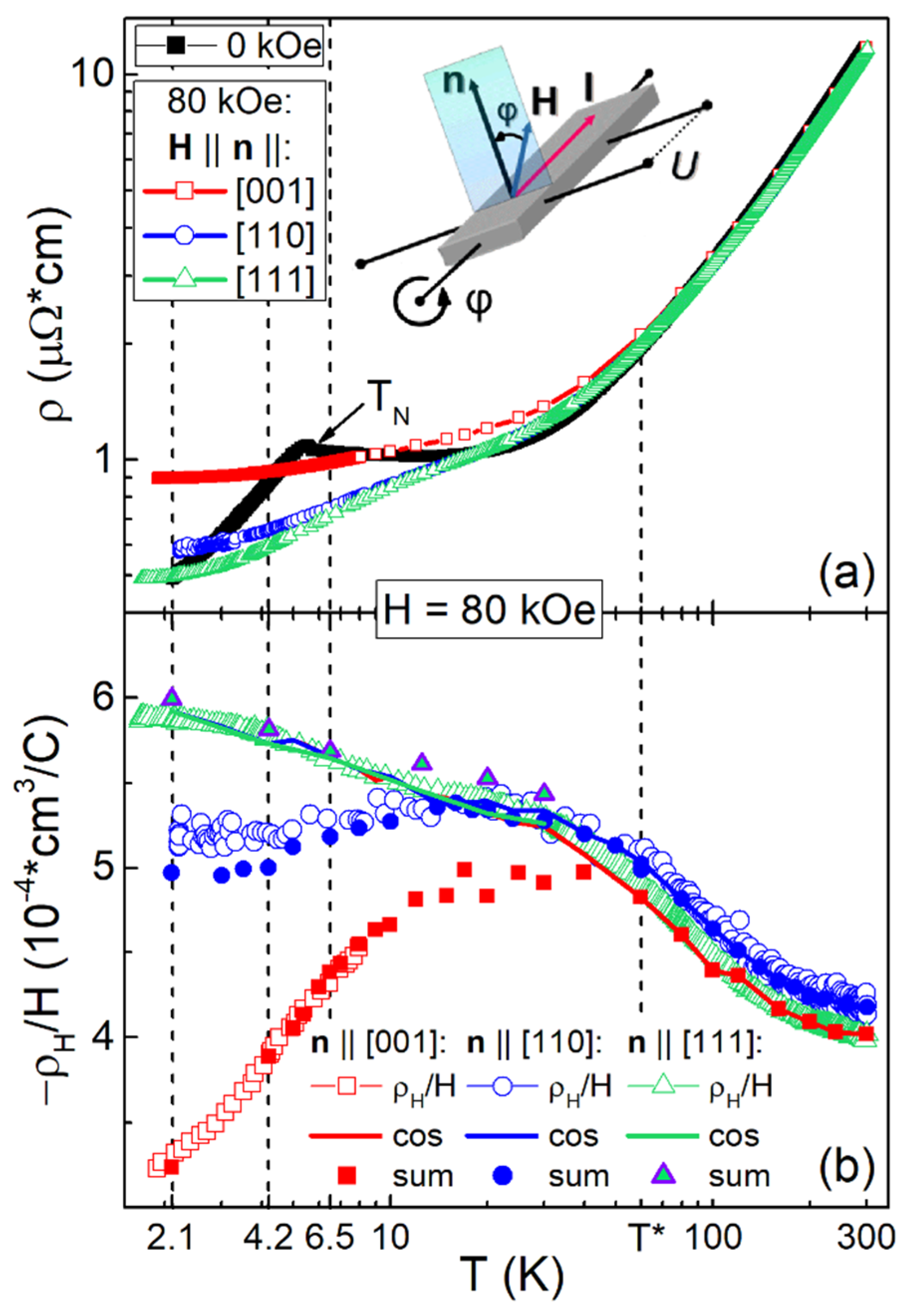
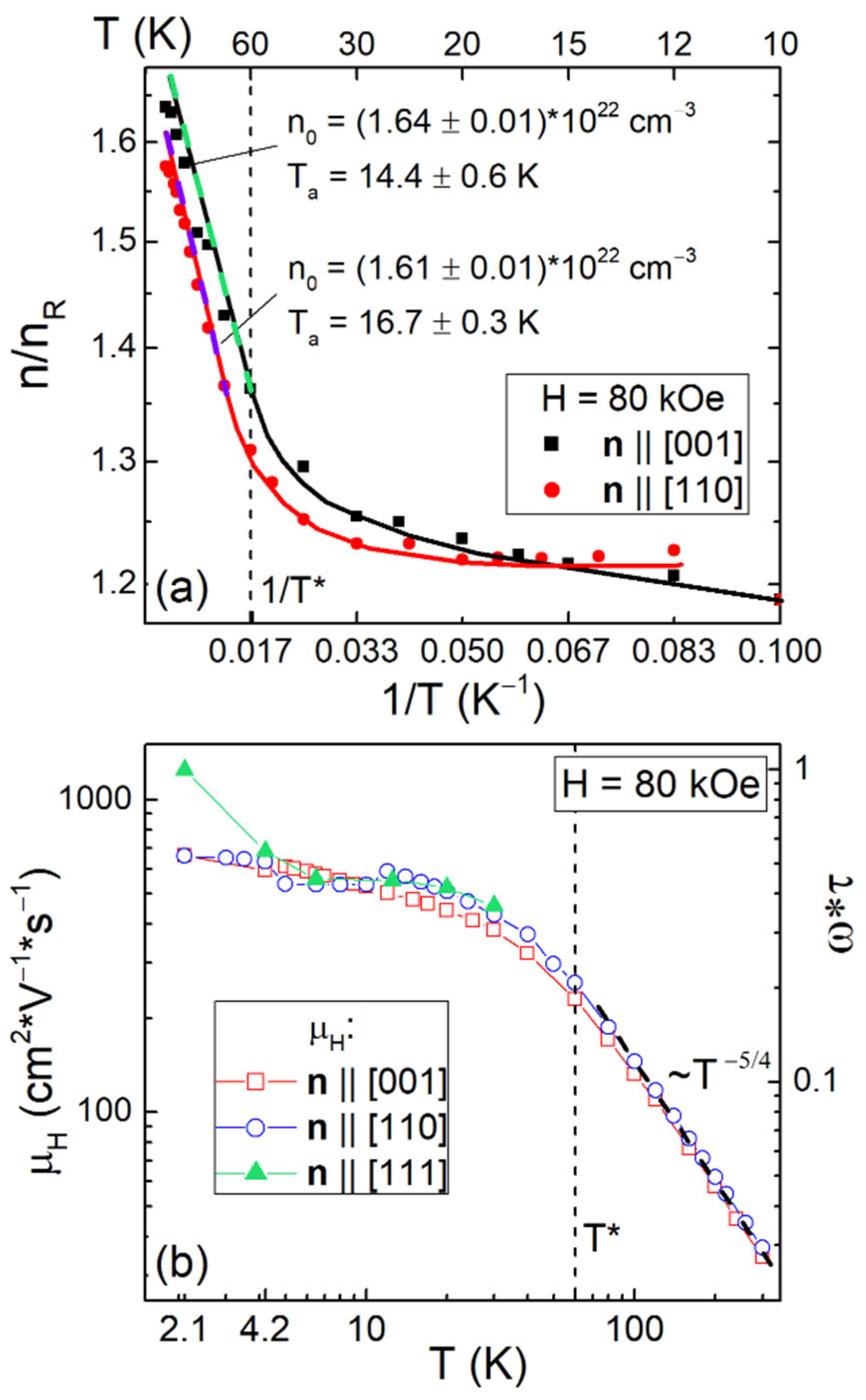
2.1. Temperature Dependences of Resistivity and Hall Resistivity
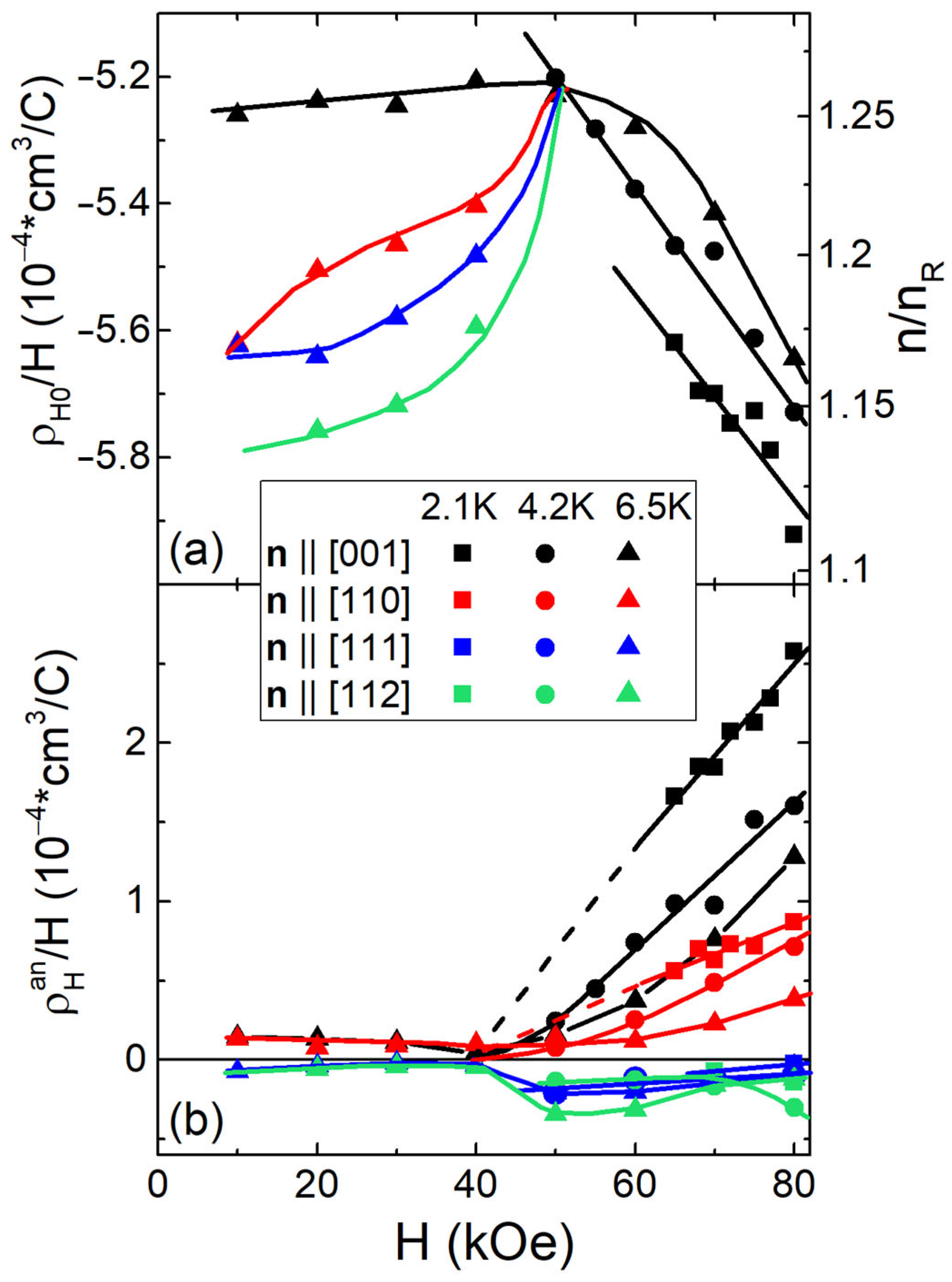
2.2. Field Dependences of Hall Resistivity and Magnetization
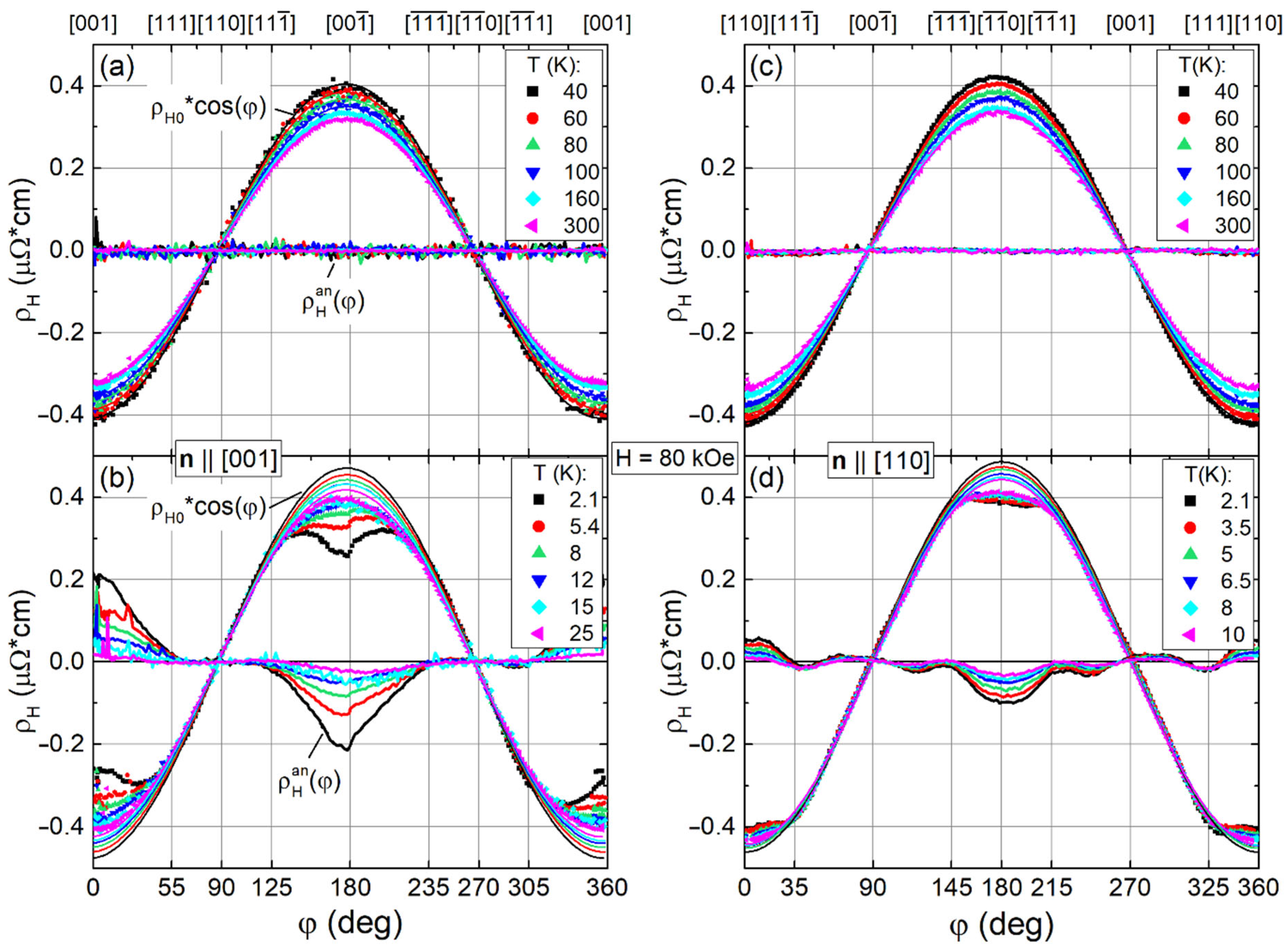
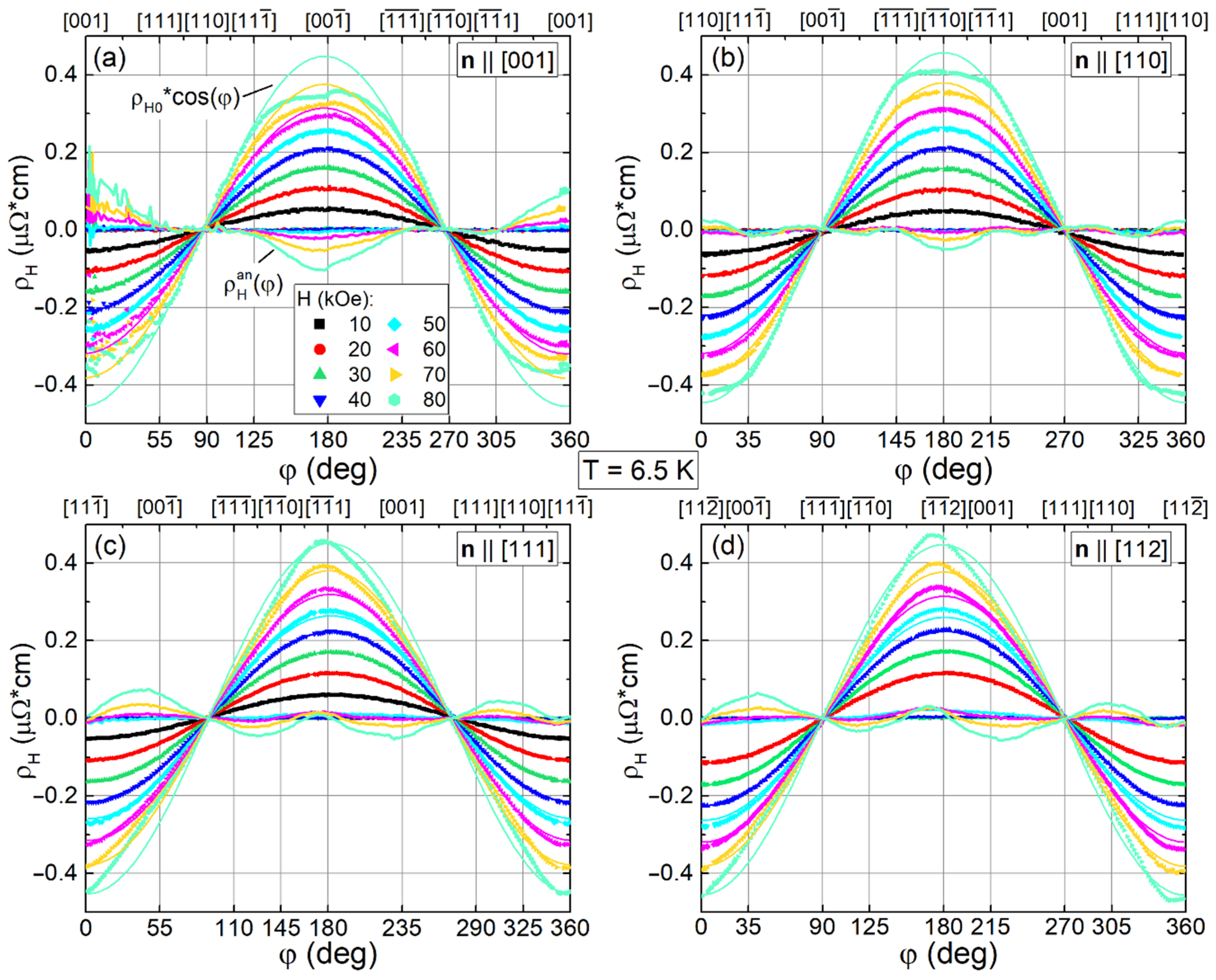
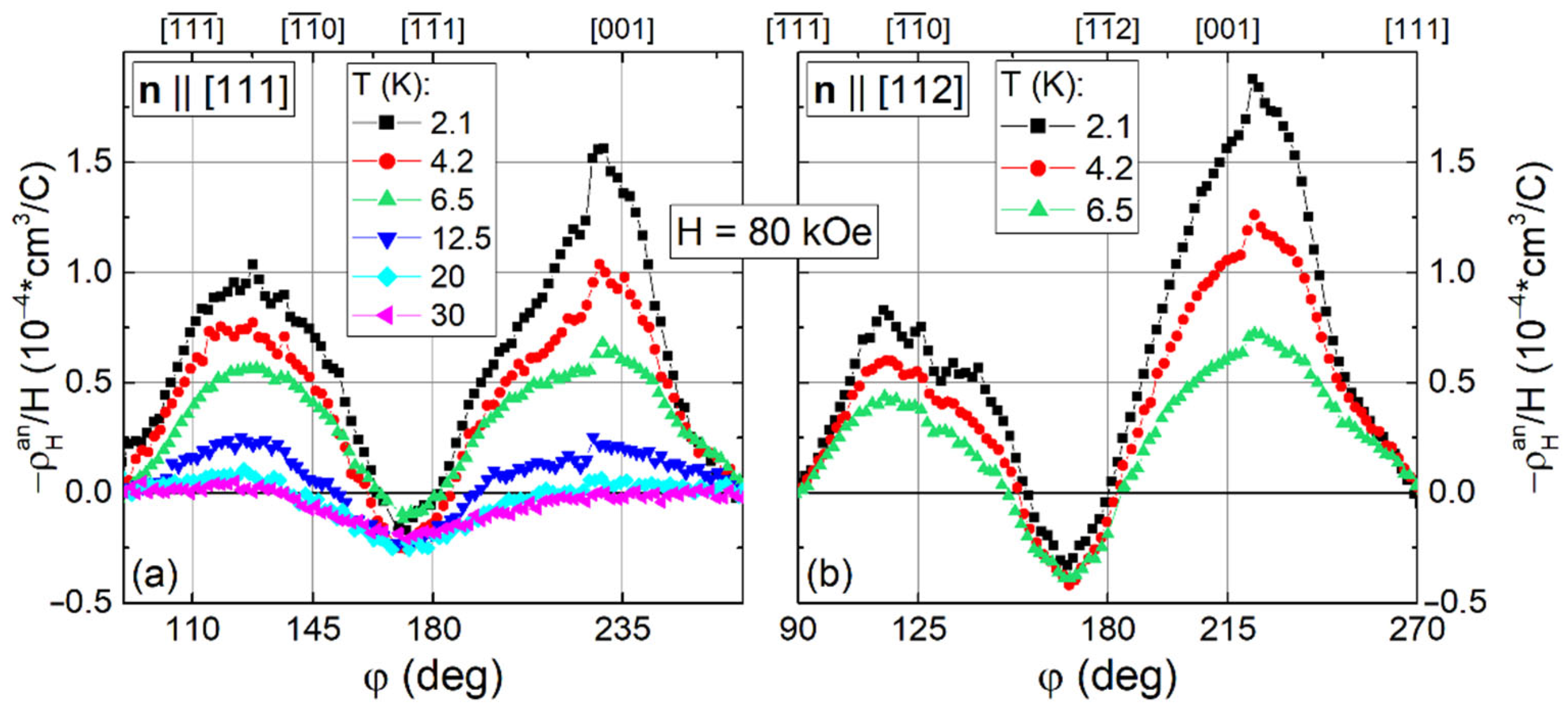
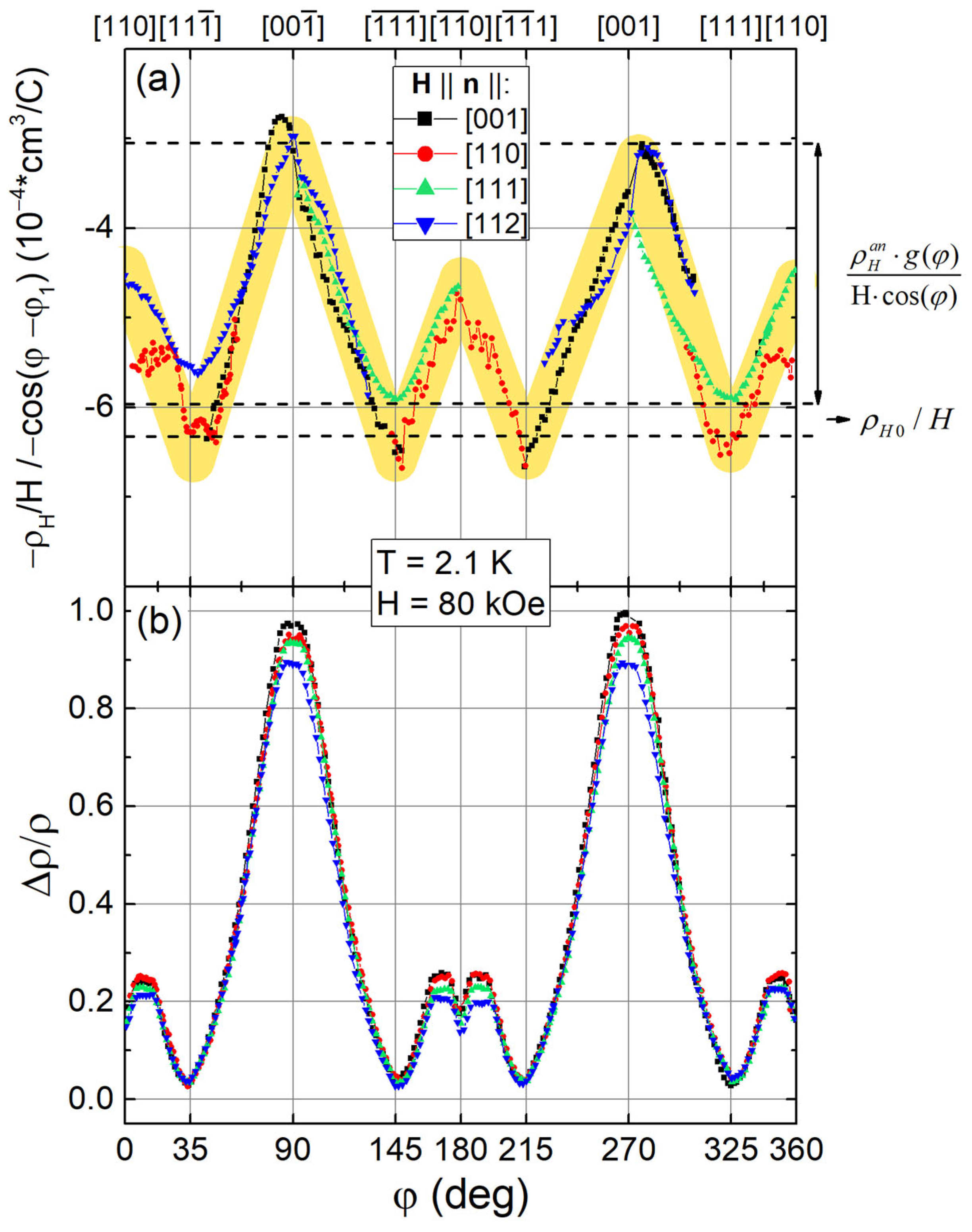
2.3. Angular Dependences of Hall Resistivity in the Paramagnetic State of Ho0.8Lu0.2B12
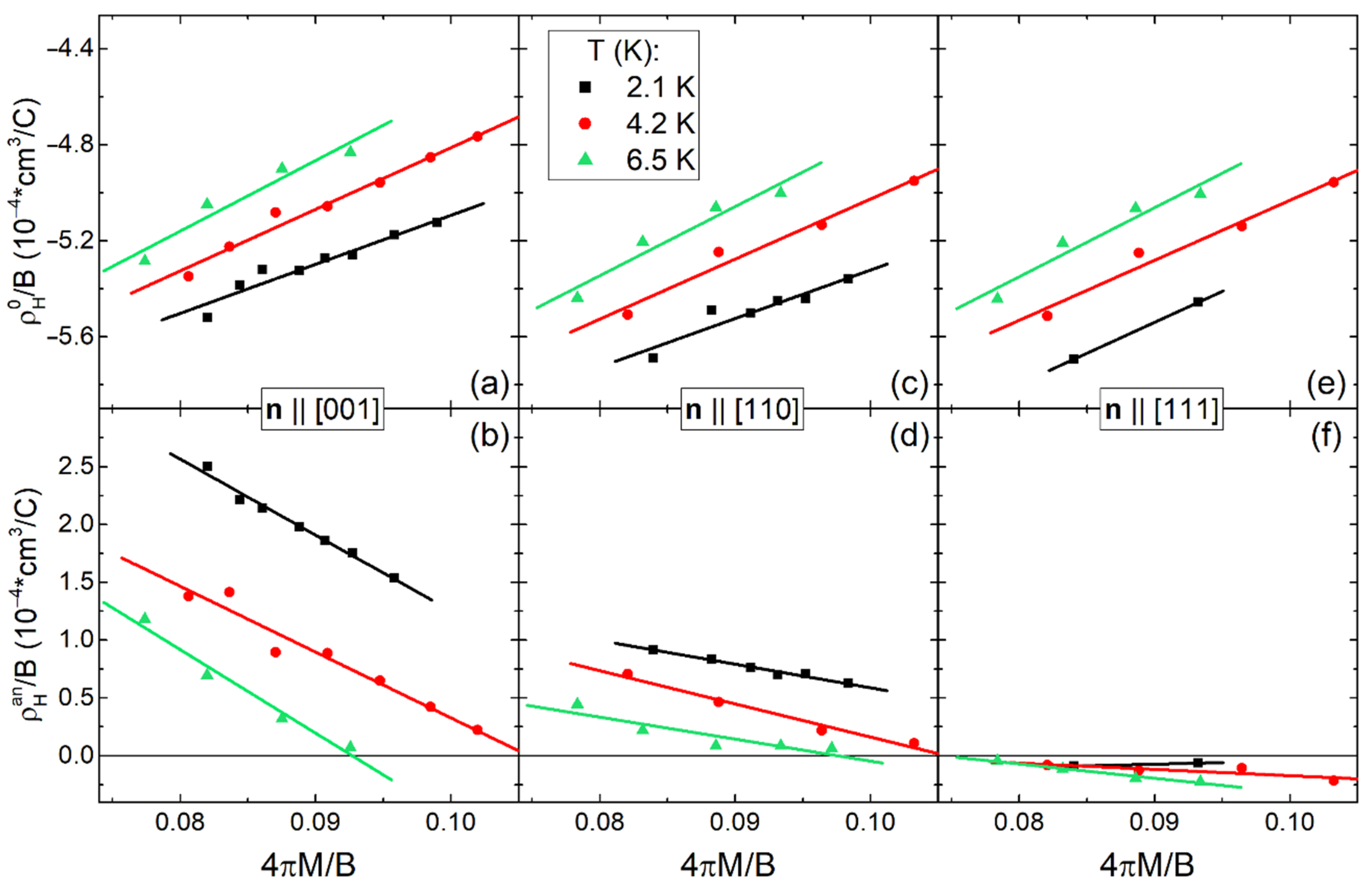
2.4. Analysis of Contributions to Hall Resistivity
3. Discussion
3.1. Multicomponent Analysis of the Contributions to Anomalous Hal Effect (AHE) in the Regime of Ferromagnetic Fluctuations
3.2. Mechanisms of AHE in Ho0.8Lu0.2B12
3.3. AHE Anisotropy and Dynamic Charge Stripes
4. Experimental Details
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Loudon, J.C.; Mathur, N.D.; Midgley, P.A. Charge-ordered ferromagnetic phase in La0.5Ca0.5MnO3. Nature 2002, 420, 797. [Google Scholar] [CrossRef] [PubMed]
- Moreo, A.; Yunoki, S.; Dagotto, E. Phase separation scenario for manganese oxides and related materials. Science 1999, 283, 2034. [Google Scholar] [CrossRef] [PubMed]
- Salamon, M.B.; Jaime, M. Phase separation scenario for manganese oxides and related materials. Rev. Mod. Phys. 2001, 73, 583. [Google Scholar] [CrossRef]
- Bebenin, N.G.; Loshkareva, N.N.; Makhnev, A.A.; Mostovshchikova, E.V.; Nomerovannaya, L.V.; Gan’Shina, E.A.; Vinogradov, A.N.; Mukovskii, Y.M. Optical and magneto-optical properties of ferromagnetic La1−xBaxMnO3 single crystals. J. Phys. Condens. Matter 2010, 22, 096003. [Google Scholar] [CrossRef] [PubMed]
- Rho, H.; Snow, C.S.; Cooper, S.L.; Fisk, Z.; Comment, A.; Ansermet, J.P. Evolution of magnetic polarons and spin-carrier interactions through the metal-insulator transition in Eu1−xGdxO. Phys. Rev. Lett. 2002, 88, 4. [Google Scholar] [CrossRef]
- Hayden, S.M.; Lander, G.H.; Zarestky, J.; Brown, P.J.; Stassis, C.; Metcalf, P.; Honig, J.M. Incommensurate magnetic correlations in La1.8Sr0.2NiO4. Phys. Rev. Lett. 1992, 68, 1061. [Google Scholar] [CrossRef]
- Cheong, S.W.; Aeppli, G.; Mason, T.E.; Mook, H.; Hayden, S.M.; Canfield, P.C.; Fisk, Z.; Clausen, K.N.; Martinez, J.L. Incommensurate magnetic fluctuations in La2−xSrxCuO4. Phys. Rev. Lett. 1991, 67, 1791. [Google Scholar] [CrossRef]
- Tranquada, J.M.; Woo, H.; Perring, T.G.; Goka, H.; Gu, G.D.; Xu, G.; Fujita, M.; Yamada, K. Quantum magnetic excitations from stripes in copper oxide superconductors. Nature 2004, 429, 534. [Google Scholar] [CrossRef]
- Fernandes, R.M.; Chubukov, A.V.; Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 2014, 10, 97. [Google Scholar] [CrossRef]
- Lee, J.J.; Schmitt, F.T.; Moore, R.G.; Johnston, S.; Cui, Y.T.; Li, W.; Yi, M.; Liu, Z.K.; Hashimoto, M.; Zhang, Y.; et al. Interfacial mode coupling as the origin of the enhancement of Tc in FeSe films on SrTiO3. Nature 2014, 515, 245. [Google Scholar] [CrossRef]
- Ge, J.F.; Liu, Z.L.; Liu, C.; Gao, C.L.; Qian, D.; Xue, Q.K.; Liu, Y.; Jia, J.F. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO3. Nat. Mater. 2015, 14, 285. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Shen, Y.; Pan, B.; Hao, Y.; Ma, M.; Zhou, F.; Steffens, P.; Schmalzl, K.; Forrest, T.R.; Abdel-Hafiez, M.; et al. Strong interplay between stripe spin fluctuations, nematicity and superconductivity in FeSe. Nat. Mater. 2016, 15, 159. [Google Scholar] [CrossRef] [PubMed]
- Si, Q.; Yu, R.; Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 2016, 1, 1. [Google Scholar] [CrossRef]
- Sachdev, S.; Keimer, B. Quantum criticality. Phys. Today 2011, 64, 29. [Google Scholar] [CrossRef]
- Dagotto, E.; Hotta, T.; Moreo, A. Colossal magnetoresistant materials: The key role of phase separation. Phys. Rep. 2001, 344, 1. [Google Scholar] [CrossRef]
- Ahn, K.H.; Lookman, T.; Bishop, A.R. Strain-induced metal–insulator phase coexistence in perovskite manganites. Nature 2004, 428, 401. [Google Scholar] [CrossRef]
- Uehara, M.; Mori, S.; Chen, C.H.; Cheong, S.W. Percolative phase separation underlies colossal magnetoresistance in mixed-valent manganites. Nature 1999, 399, 560. [Google Scholar] [CrossRef]
- Alvarez, G.; Mayr, M.; Moreo, A.; Dagotto, E. Areas of superconductivity and giant proximity effects in underdoped cuprates. Phys. Rev. B 2005, 71, 014514. [Google Scholar] [CrossRef]
- Aliaga, H.; Magnoux, D.; Moreo, A.; Poilblanc, D.; Yunoki, S.; Dagotto, E. Theoretical study of half-doped models for manganites: Fragility of CE phase with disorder, two types of colossal magnetoresistance, and charge-ordered states for electron-doped materials. Phys. Rev. B 2003, 68, 104405. [Google Scholar] [CrossRef]
- Tokura, Y.; Kuwahara, H.; Moritomo, Y.; Tomioka, Y.; Asamitsu, A. Competing Instabilities and Metastable States in (N d, S m)1/2Sr1/2MnO3. Phys. Rev. Lett. 1996, 76, 3184. [Google Scholar] [CrossRef]
- Akahoshi, D.; Uchida, M.; Tomioka, Y.; Arima, T.; Matsui, Y.; Tokura, Y. Random potential effect near the bicritical region in perovskite manganites as revealed by comparison with the ordered perovskite analogs. Phys. Rev. Lett. 2003, 90, 4. [Google Scholar] [CrossRef]
- Tomioka, Y.; Tokura, Y. Global phase diagram of perovskite manganites in the plane of quenched disorder versus one-electron bandwidth. Phys. Rev. B 2004, 70, 014432. [Google Scholar] [CrossRef]
- Milward, G.C.; Calderón, M.J.; Littlewood, P.B. Electronically soft phases in manganites. Nature 2005, 433, 607. [Google Scholar] [CrossRef] [PubMed]
- Tranquada, J.M. Spins, Stripes, and Superconductivity in Hole-Doped Cuprates. In AIP Conference Proceedings; American Institute of Physics AIP: College Park, ML, USA, 2013; Volume 1550, pp. 114–187. [Google Scholar]
- Thampy, V.; Chen, X.M.; Cao, Y.; Mazzoli, C.; Barbour, A.M.; Hu, W.; Miao, H.; Fabbris, G.; Zhong, R.D.; Gu, G.D.; et al. Static charge-density-wave order in the superconducting state of La2−xBaxCuO4. Phys. Rev. B 2017, 95, 241111. [Google Scholar] [CrossRef]
- Jacobsen, H.; Holm, S.L.; Lăcătuşu, M.E.; Rømer, A.T.; Bertelsen, M.; Boehm, M.; Toft-Petersen, R.; Grivel, J.C.; Emery, S.B.; Udby, L.; et al. Distinct nature of static and dynamic magnetic stripes in cuprate superconductors. Phys. Rev. Lett. 2018, 120, 037003. [Google Scholar] [CrossRef]
- Anissimova, S.; Parshall, D.; Gu, G.D.; Marty, K.; Lumsden, M.D.; Chi, S.; Fernandez-Baca, J.A.; Abernathy, D.L.; Lamago, D.; Tranquada, J.M.; et al. Direct observation of dynamic charge stripes in La2–xSrxNiO4. Nat. Commun. 2014, 5, 1. [Google Scholar] [CrossRef]
- Abeykoon, A.M.M.; Božin, E.S.; Yin, W.G.; Gu, G.; Hill, J.P.; Tranquada, J.M.; Billinge, S.J.L. Evidence for short-range-ordered charge stripes far above the charge-ordering transition in La1.67Sr0.33NiO4. Phys. Rev. Lett. 2013, 111, 096404. [Google Scholar] [CrossRef]
- Kohsaka, Y.; Taylor, C.; Fujita, K.; Schmidt, A.; Lupien, C.; Hanaguri, T.; Azuma, M.; Takano, M.; Eisaki, H.; Takagi, H.; et al. An intrinsic bond-centered electronic glass with unidirectional domains in underdoped cuprates. Science 2007, 315, 1380. [Google Scholar] [CrossRef]
- Gabani, S.; Flachbart, K.; Siemensmeyer, K.; Mori, T. Magnetism and superconductivity of rare earth borides. J. Alloys Compd. 2020, 821, 153201. [Google Scholar] [CrossRef]
- Paderno, Y.; Shitsevalova, N.; Batko, I.; Flahbart, K.; Misiorek, H.; Mucha, J.; Jeżowski, A. Transition and rare earth element dodecaborides. Transition and rare earth element dodecaborides. J. Alloys Compd. 1995, 219, 215. [Google Scholar] [CrossRef]
- Inosov, D.S. (Ed.) Rare-Earth Borides, 1st ed.; Jenny Stanford Publishing: Singapore, 2021. [Google Scholar]
- Mori, T. Rare Earth Higher Borides. In Handbook on the Physics and Chemistry of Rare-Earths; Bunzli, C., Pecharsky, V., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; pp. 39–154. [Google Scholar]
- Werheit, H.; Filipov, V.; Shirai, K.; Dekura, H.; Shitsevalova, N.; Schwarz, U.; Armbrüster, M. Raman scattering and isotopic phonon effects in dodecaborides. J. Phys. Condens. Matter 2011, 23, 065403. [Google Scholar] [CrossRef] [PubMed]
- Khoroshilov, A.L.; Krasnorussky, V.N.; Krasikov, K.M.; Bogach, A.V.; Glushkov, V.V.; Demishev, S.V.; Samarin, N.A.; Voronov, V.V.; Shitsevalova, N.Y.; Filipov, V.B.; et al. Maltese cross anisotropy in Ho0.8Lu0.2B12 antiferromagnetic metal with dynamic charge stripes. Phys. Rev. B 2019, 99, 174430. [Google Scholar] [CrossRef]
- Bolotina, N.B.; Dudka, A.P.; Khrykina, O.N.; Mironov, V.S. Crystal Structures of Dodecaborides: Complexity in Simplicity. In Rare-Earth Borides, 1st ed.; Inosov, D.S., Ed.; Jenny Stanford Publishing: New York, NY, USA, 2021; Chapter 3; pp. 293–330. [Google Scholar]
- Sluchanko, N.E.; Azarevich, A.N.; Bogach, A.V.; Vlasov, I.I.; Glushkov, V.V.; Demishev, S.V.; Maksimov, A.A.; Tartakovskii, I.I.; Filatov, E.V.; Flachbart, K.; et al. Effects of disorder and isotopic substitution in the specific heat and Raman scattering in LuB12. J. Exp. Theor. Phys. 2011, 113, 468. [Google Scholar] [CrossRef]
- Sluchanko, N.E.; Azarevich, A.N.; Bogach, A.V.; Bolotina, N.B.; Glushkov, V.V.; Demishev, S.V.; Dudka, A.P.; Khrykina, O.N.; Filipov, V.B.; Shitsevalova, N.Y.; et al. Observation of dynamic charge stripes in Tm0.19Yb0.81B12 at the metal–insulator transition. J. Phys. Condens. Matter 2019, 31, 065604. [Google Scholar] [CrossRef]
- Zhukova, E.S.; Gorshunov, B.P.; Komandin, G.A.; Alyabyeva, L.N.; Muratov, A.V.; Aleshchenko, Y.A.; Anisimov, M.A.; Shitsevalova, N.Y.; Polovets, S.E.; Filipov, V.B.; et al. Collective infrared excitation in rare-earth GdxLa 1−xB6 hexaborides. Phys. Rev. B 2019, 100, 104302. [Google Scholar] [CrossRef]
- Krasikov, K.M.; Bogach, A.V.; Bozhko, A.D.; Glushkov, V.V.; Demishev, S.V.; Khoroshilov, A.L.; Shitsevalova, N.Y.; Filipov, V.; Gabáni, S.; Flachbart, K.; et al. Anisotropy of the charge transport in Ho11B12 antiferromagnet with dynamic charge stripes. Solid State Sci. 2020, 104, 106253. [Google Scholar] [CrossRef]
- Khrykina, O.N.; Dudka, A.P.; Bolotina, N.B.; Sluchanko, N.E.; Shitsevalova, N.Y. Structural instability and poorly defined phase transitions in rare-earth dodecaborides RB12 (R = Ho-Lu) at intermediate temperatures. Solid State Sci. 2020, 107, 106273. [Google Scholar] [CrossRef]
- Sluchanko, N.; Khoroshilov, A.; Krasnorussky, V.; Krasikov, K. Maltese Cross Anisotropy in Antiferromagnetic State of Metallic Ho0.5Lu0.5B12 with Dynamic Charge Stripes. Acta Phys. Pol. A 2020, 137, 756. [Google Scholar] [CrossRef]
- Krasikov, K.M.; Azarevich, A.N.; Glushkov, V.V.; Demishev, S.V.; Khoroshilov, A.L.; Bogach, A.V.; Shitsevalova, N.Y.; Filippov, V.B.; Sluchanko, N.E. Breaking of cubic symmetry in rare-earth dodecaborides with dynamic charge stripes. JETP Lett. 2020, 112, 413. [Google Scholar] [CrossRef]
- Krasikov, K.; Glushkov, V.; Demishev, S.; Khoroshilov, A.; Bogach, A.; Voronov, V.; Shitsevalova, N.; Filipov, V.; Gabáni, S.; Flachbart, K. Suppression of indirect exchange and symmetry breaking in the antiferromagnetic metal HoB12 with dynamic charge stripes. Phys. Rev. B 2020, 102, 214435. [Google Scholar] [CrossRef]
- Krasikov, K.M.; Bogach, A.V.; Demishev, S.V.; Voronov, V.V.; Shitsevalova, N.Y.; Filipov, V.B.; Sluchanko, N.E. Magnetoresistance anisotropy in ErB12 antiferromagnetic metal: The evidence for dynamic charge stripes. J. Magn. Magn. Mater. 2022, 545, 168796. [Google Scholar] [CrossRef]
- Azarevich, A.; Glushkov, V.; Demishev, S.; Bogach, A.; Voronov, V.; Gavrilkin, S.; Shitsevalova, N.; Filipov, V.; Gabáni, S.; Kačmarčík, J.; et al. Evidence of symmetry lowering in antiferromagnetic metal TmB12 with dynamic charge stripes. J. Phys. Condens. Matter 2022, 34, 065602. [Google Scholar] [CrossRef] [PubMed]
- Sluchanko, N.E.; Khoroshilov, A.L.; Bogach, A.V.; Voronov, V.V.; Glushkov, V.V.; Demishev, S.V.; Krasnorussky, V.N.; Krasikov, K.M.; Shitsevalova, N.Y.; Filippov, V.B. Magnetoresistance scaling and the anisotropy of charge carrier scattering in the paramagnetic phase of Ho0.8Lu0.2B12 cage glass. JETP Lett. 2018, 107, 30. [Google Scholar] [CrossRef]
- Sluchanko, N.E. Magnetism, Quantum Criticality, and Metal–Insulator Transitions in RB12. In Rare-Earth Borides, 1st ed.; Jenny Stanford Publishing: New York, NY, USA, 2021; Chapter 4; pp. 331–441. [Google Scholar]
- Sluchanko, N.; Azarevich, A.; Bogach, A.; Demishev, S.; Krasikov, K.; Voronov, V.; Filipov, V.; Shitsevalova, N.; Glushkov, V. Hall effect and symmetry breaking in the nonmagnetic metal LuB12 with dynamic charge stripes. Phys. Rev. B 2021, 103, 35117. [Google Scholar] [CrossRef]
- Khoroshilov, A.L.; Azarevich, A.N.; Bogach, A.V.; Glushkov, V.V.; Demishev, S.V.; Krasnorussky, V.N.; Krasikov, K.M.; Kuznetsov, A.V.; Shitsevalova, N.Y.; Filipov, V.B.; et al. Anisotropy of the Hall Effect in the Paramagnetic Phase of Ho0.8Lu0.2B12 Cage Glass. JETP Lett. 2021, 113, 526. [Google Scholar] [CrossRef]
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, N.P. Anomalous hall effect. Rev. Mod. Phys. 2010, 82, 1539. [Google Scholar] [CrossRef]
- Malkin, B.Z.; Goremychkin, E.A.; Siemensmeyer, K.; Gabáni, S.; Flachbart, K.; Rajňák, M.; Khoroshilov, A.L.; Krasikov, K.M.; Shitsevalova, N.Y.; Filipov, V.B.; et al. Crystal-field potential and short-range order effects in inelastic neutron scattering, magnetization, and heat capacity of the cage-glass compound HoB12. Phys. Rev. B 2021, 104, 134436. [Google Scholar] [CrossRef]
- Siemensmeyer, K.; Habicht, K.; Lonkai, T.; Mat’aš, S.; Gabáni, S.; Shitsevalova, N.; Wulf, E.; Flachbart, K. Magnetic properties of the frustrated fcc–antiferromagnet HoB12 above and below TN. J. Low Temp. Phys. 2007, 146, 581. [Google Scholar] [CrossRef]
- Kalvius, G.M.; Noakes, D.R.; Marcano, N.; Wäppling, R.; Iga, F.; Takabatake, T. Dynamics of the internal field in RB12(R = Er, Yb, Lu). Phys. B Condens. Matter 2003, 326, 398. [Google Scholar] [CrossRef]
- Sluchanko, N.E.; Sluchanko, D.N.; Samarin, N.A.; Glushkov, V.V.; Demishev, S.V.; Kuznetsov, A.V.; Burkhanov, G.S.; Chistyakov, O.D. Hall-effect anomalies near the quantum critical point in Ce Cu6−xAux. Low Temp. Phys. 2009, 35, 544. [Google Scholar] [CrossRef]
- Baranovskiy, A.E.; Grechnev, G.E.; Shitsevalova, N.Y.; Sluchanko, D.N.; Glushkov, V.V.; Demishev, S.V.; Sluchanko, N.E. Hall effect and magnetic ordering in RB12. Low Temp. Phys. 2009, 35, 565. [Google Scholar] [CrossRef]
- Rybina, A.V.; Nemkovski, K.S.; Alekseev, P.A.; Mignot, J.M.; Clementyev, E.S.; Johnson, M.; Capogna, L.; Dukhnenko, A.V.; Lyashenko, A.B.; Filippov, V.B. Lattice dynamics in ZrB12 and LuB12: Ab initio calculations and inelastic neutron scattering measurements. Phys. Rev. B 2010, 82, 4. [Google Scholar] [CrossRef]
- Bolotina, N.B.; Dudka, A.P.; Khrykina, O.N.; Krasnorussky, V.N.; Shitsevalova, N.Y.; Filipov, V.B.; Sluchanko, N.E. The lower symmetry electron-density distribution and the charge transport anisotropy in cubic dodecaboride LuB12. J. Phys. Condens. Matter 2018, 30, 265402. [Google Scholar] [CrossRef] [PubMed]
- Bolotina, N.B.; Dudka, A.P.; Khrykina, O.N.; Glushkov, V.V.; Azarevich, A.N.; Krasnorussky, V.N.; Gabani, S.; Shitsevalova, N.Y.; Dukhnenko, A.V.; Filipov, V.B.; et al. On the role of isotopic composition in crystal structure, thermal and charge-transport characteristics of dodecaborides LuNB12 with the Jahn-Teller instability. J. Phys. Chem. Solids 2019, 129, 434. [Google Scholar] [CrossRef]
- Sluchanko, N.E.; Bogach, A.V.; Glushkov, V.V.; Demishev, S.V.; Samarin, N.A.; Sluchanko, D.N.; Dukhnenko, A.V.; Levchenko, A.V. Anomalies of magnetoresistance of compounds with atomic clusters RB12 (R = Ho, Er, Tm, Lu). J. Exp. Theor. Phys. 2009, 108, 668. [Google Scholar] [CrossRef]
- Sluchanko, N.E.; Azarevich, A.N.; Bogach, A.V.; Glushkov, V.V.; Demishev, S.V.; Anisimov, M.A.; Levchenko, A.V.; Filipov, V.B.; Shitsevalova, N.Y. Hall and transverse even effects in the vicinity of a quantum critical point in Tm1−xYbxB12. J. Exp. Theor. Phys. 2012, 115, 509. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Hewener, B.; Hartmann, U.; Wienss, A.; Christoffer, B.; Persch-Schuy, G. Magnetic force microscopy applied in magnetic data storage technology. Appl. Phys. A 2003, 76, 879. [Google Scholar] [CrossRef]
- Krasnorussky, V.; Bogach, A.; Sluchanko, N.; Demishev, S.; Shitsevalova, N.; Filipov, V.; Pristas, G.; Gabani, S.; Flachbart, K.; Glushkov, V.V. Anomalous Magnetic Contributions to Hall Effect in Ho0.5Lu0.5B12. Acta Phys. Pol. A 2020, 137, 767. [Google Scholar] [CrossRef]
- Karplus, R.; Luttinger, J.M. Hall effect in ferromagnetics. Phys. Rev. 1954, 95, 1154. [Google Scholar] [CrossRef]
- Sluchanko, N.E.; Sluchanko, D.N.; Glushkov, V.V.; Demishev, S.V.; Samarin, N.A.; Shitsevalova, N.Y. Anomalous hall effect in HoB12. JETP Lett. 2008, 86, 604. [Google Scholar] [CrossRef]
- Kohout, A.; Batko, I.; Czopnik, A.; Flachbart, K.; Matas, S.; Meissner, M.; Paderno, Y.; Shitsevalova, N.; Siemensmeyer, K. Phase diagram and magnetic structure investigation of the fcc antiferromagnet HoB12. Phys. Rev. B 2004, 70, 224416. [Google Scholar] [CrossRef]
- Siemensmeyer, K.; Flachbart, K.; Gabáni, S.; Maťaš, S.; Paderno, Y.; Shitsevalova, N. Magnetic structure of rare-earth dodecaborides. J. Solid State Chem. 2006, 179, 2748. [Google Scholar] [CrossRef]
- Tennant, D.A.; Nagler, S.E.; Garrett, A.W.; Barnes, T.; Torardi, C.C. Excitation Spectrum and Superexchange Pathways in the Spin Dimer VODPO4˙1/2D2O. Phys. Rev. Lett. 1997, 78, 4998. [Google Scholar] [CrossRef]
- Flachbart, K.; Bauer, E.; Gabáni, S.; Kaldarar, H.; Lonkai, T.; Maťaš, S.; Pavlík, V.; Priputen, P.; Shitsevalova, N.; Siemensmeyer, K.; et al. Magnetic ordering in HoB12 below and above TN. J. Magn. Magn. Mater. 2007, 310, 1727. [Google Scholar] [CrossRef]
- Dyakonov, M. Basics of semiconductor and spin physics. In Spin Physics in Semiconductors; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Batista, C.D.; Lin, S.-Z.; Hayami, S.; Kamiya, Y. Frustration and chiral orderings in correlated electron systems. Rep. Prog. Phys. 2016, 79, 084504. [Google Scholar] [CrossRef]
- Taguchi, Y.; Oohara, Y.; Yoshizawa, H.; Nagaosa, N.; Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 2001, 291, 2573. [Google Scholar] [CrossRef]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall effect in the A phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef]
- Pureur, P.; Fabris, F.W.; Schaf, J.; Campbell, I.A. Chiral susceptibility in canonical spin glass and re-entrant alloys from Hall effect measurements. Europhys. Lett. 2004, 67, 123. [Google Scholar] [CrossRef]
- Machida, Y.; Nakatsuji, S.; Onoda, S.; Tayama, T.; Sakakibara, T. Time-reversal symmetry breaking and spontaneous Hall effect without magnetic dipole order. Nature 2010, 463, 210. [Google Scholar] [CrossRef]
- Liu, Z.H.; Zhang, Y.J.; Liu, G.D.; Ding, B.; Liu, E.K.; Jafri, H.M.; Hou, Z.P.; Wang, W.H.; Ma, X.Q.; Wu, G.H. Transition from anomalous Hall effect to topological Hall effect in hexagonal non-collinear magnet Mn3Ga. Sci. Rep. 2017, 7, 515. [Google Scholar] [CrossRef]
- Smit, J. The spontaneous Hall effect in ferromagnetics II. Physica 1958, 24, 39. [Google Scholar] [CrossRef]
- Jungwirth, T.; Niu, Q.; MacDonald, A.H. Anomalous Hall effect in ferromagnetic semiconductors. Phys. Rev. Lett. 2002, 88, 207208. [Google Scholar] [CrossRef] [PubMed]
- Berger, L. Side-jump mechanism for the Hall effect of ferromagnets. Phys. Rev. B 1970, 2, 4559. [Google Scholar] [CrossRef]
- Gorshunov, B.P.; Zhukova, E.S.; Komandin, G.A.; Torgashev, V.I.; Muratov, A.V.; Aleshchenko, Y.A.; Demishev, S.V.; Shitsevalova, N.Y.; Filipov, V.B.; Sluchanko, N.E. Collective infrared excitation in LuB12 cage-glass. JETP Lett. 2018, 107, 100. [Google Scholar] [CrossRef]




| RH, 10−4 × cm3/C | H||n||[001] | H||n||[110] | H||n||[111] |
|---|---|---|---|
| RH0 | −7.3 | −7.7 | −7.7 |
| RHan | 6.8 | 2.3 | 0 |
| RM0 | 25.2 | 26.9 | 26.5 |
| RMan | −64.9 | −20.9 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoroshilov, A.L.; Krasikov, K.M.; Azarevich, A.N.; Bogach, A.V.; Glushkov, V.V.; Krasnorussky, V.N.; Voronov, V.V.; Shitsevalova, N.Y.; Filipov, V.B.; Gabáni, S.; et al. Hall Effect Anisotropy in the Paramagnetic Phase of Ho0.8Lu0.2B12 Induced by Dynamic Charge Stripes. Molecules 2023, 28, 676. https://doi.org/10.3390/molecules28020676
Khoroshilov AL, Krasikov KM, Azarevich AN, Bogach AV, Glushkov VV, Krasnorussky VN, Voronov VV, Shitsevalova NY, Filipov VB, Gabáni S, et al. Hall Effect Anisotropy in the Paramagnetic Phase of Ho0.8Lu0.2B12 Induced by Dynamic Charge Stripes. Molecules. 2023; 28(2):676. https://doi.org/10.3390/molecules28020676
Chicago/Turabian StyleKhoroshilov, Artem L., Kirill M. Krasikov, Andrey N. Azarevich, Alexey V. Bogach, Vladimir V. Glushkov, Vladimir N. Krasnorussky, Valery V. Voronov, Natalya Y. Shitsevalova, Volodymyr B. Filipov, Slavomir Gabáni, and et al. 2023. "Hall Effect Anisotropy in the Paramagnetic Phase of Ho0.8Lu0.2B12 Induced by Dynamic Charge Stripes" Molecules 28, no. 2: 676. https://doi.org/10.3390/molecules28020676
APA StyleKhoroshilov, A. L., Krasikov, K. M., Azarevich, A. N., Bogach, A. V., Glushkov, V. V., Krasnorussky, V. N., Voronov, V. V., Shitsevalova, N. Y., Filipov, V. B., Gabáni, S., Flachbart, K., & Sluchanko, N. E. (2023). Hall Effect Anisotropy in the Paramagnetic Phase of Ho0.8Lu0.2B12 Induced by Dynamic Charge Stripes. Molecules, 28(2), 676. https://doi.org/10.3390/molecules28020676








