Reliability Characteristics of Metal-Insulator-Semiconductor Capacitors with Low-Dielectric-Constant Materials
Abstract
:1. Introduction
2. Results and Discussion
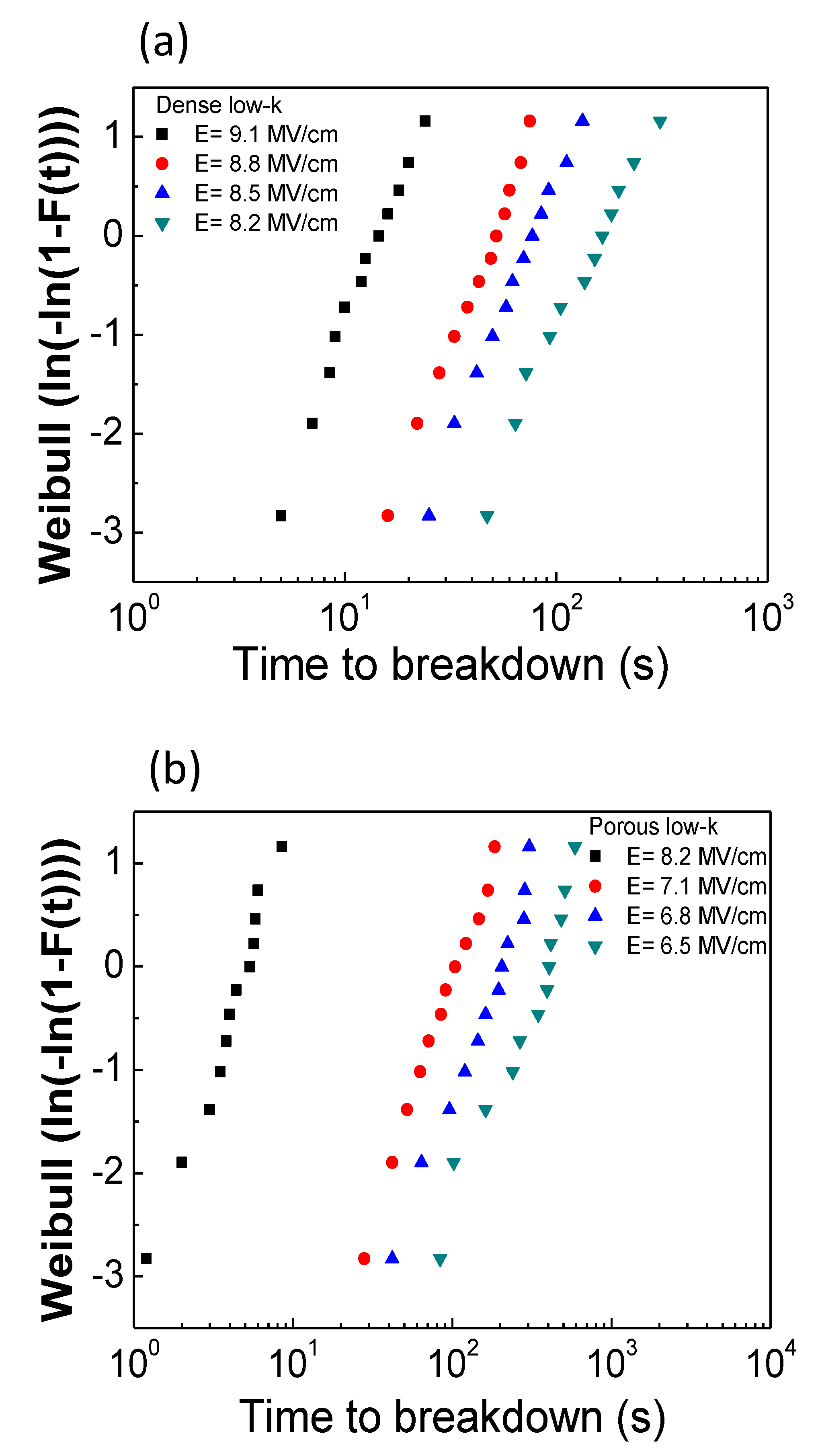
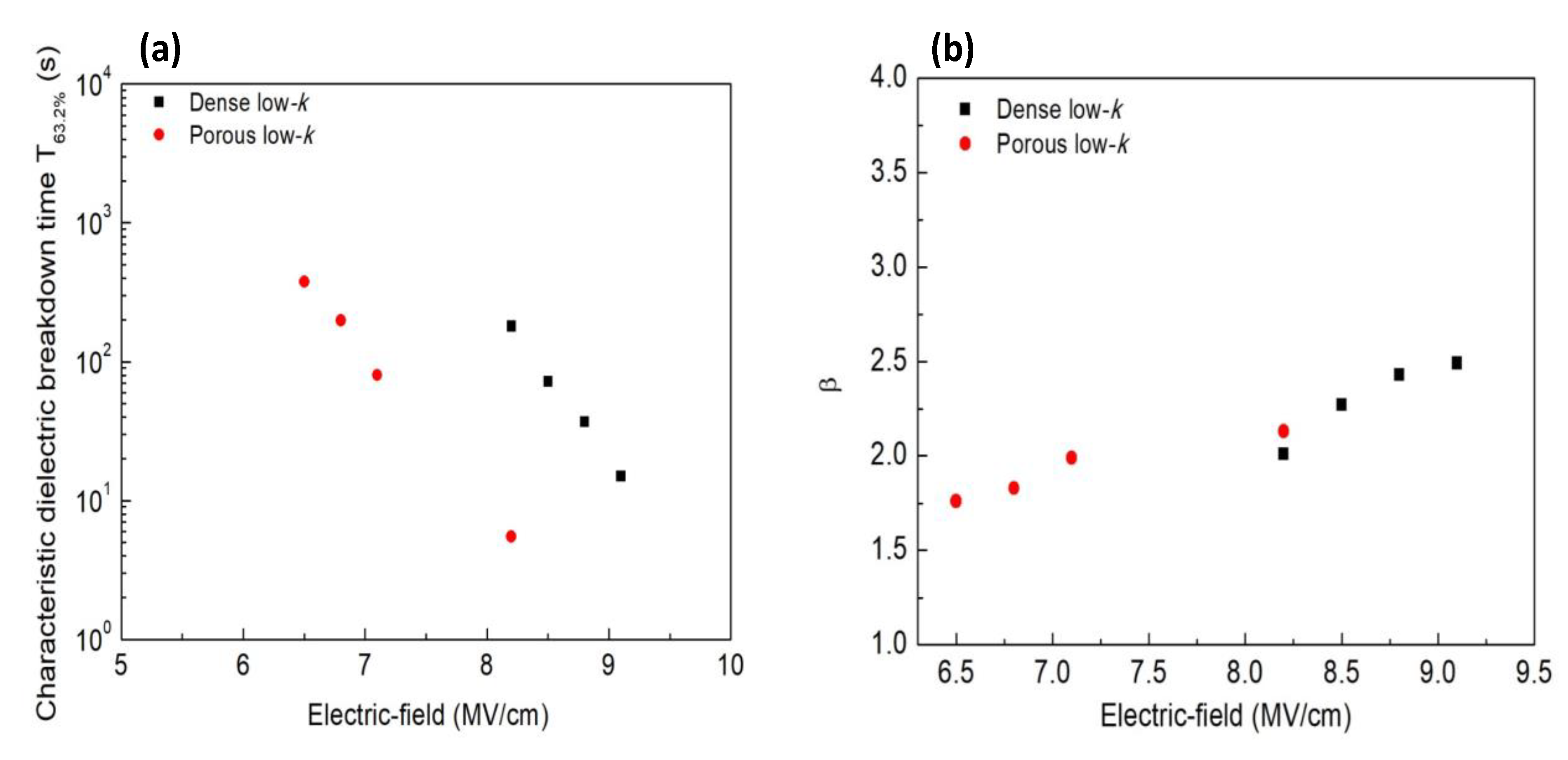
2.1. Low-k Material Effect
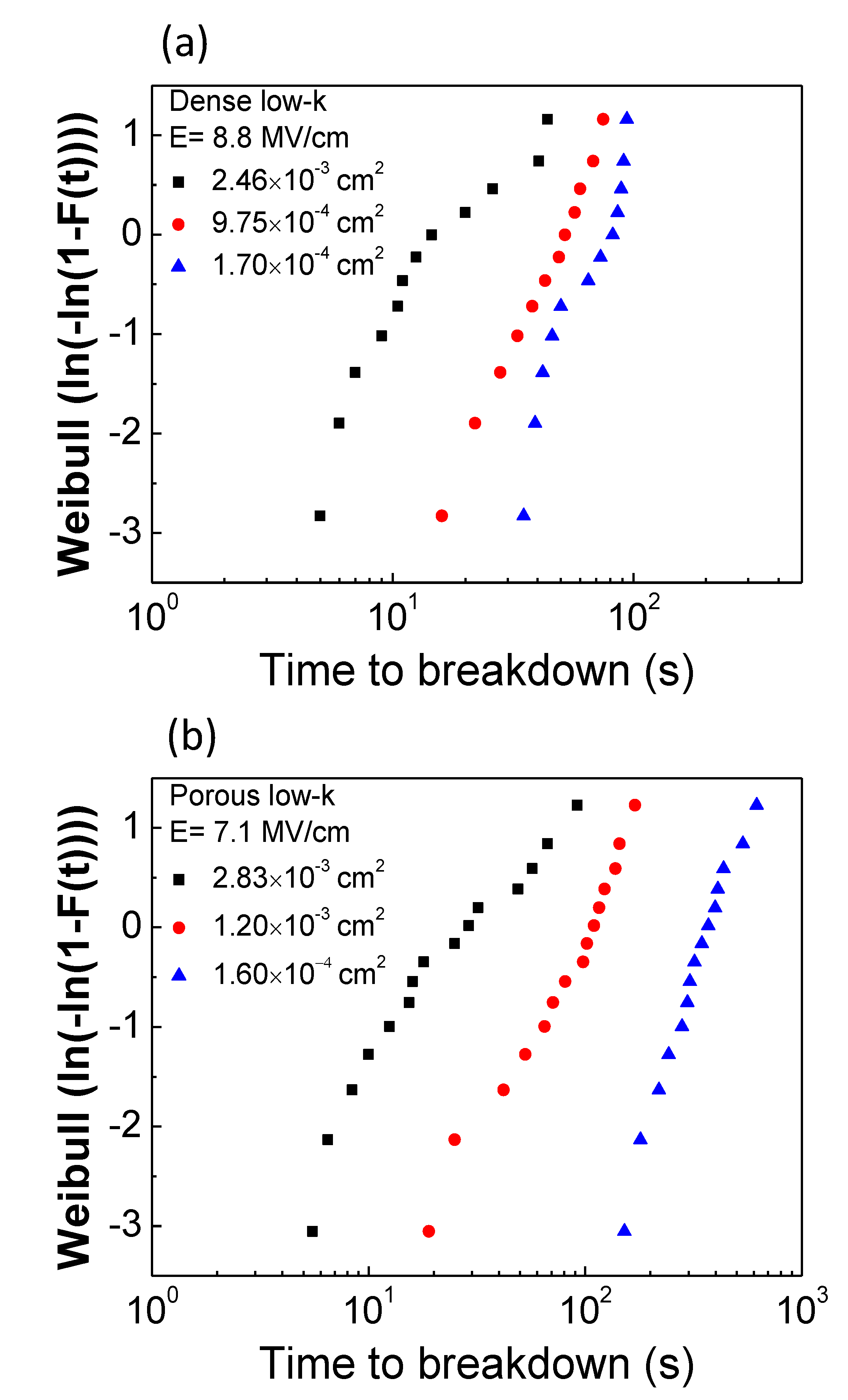
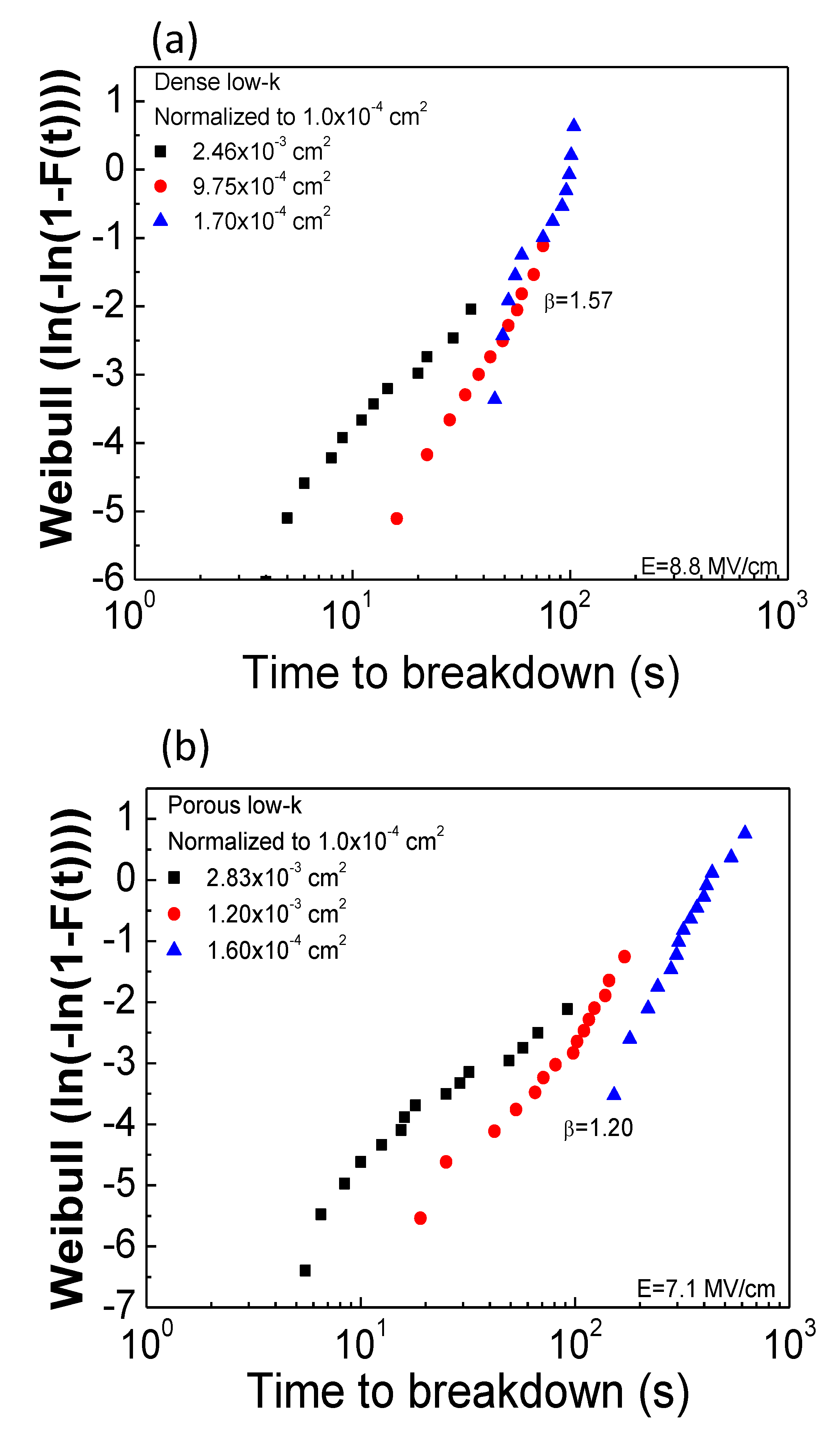
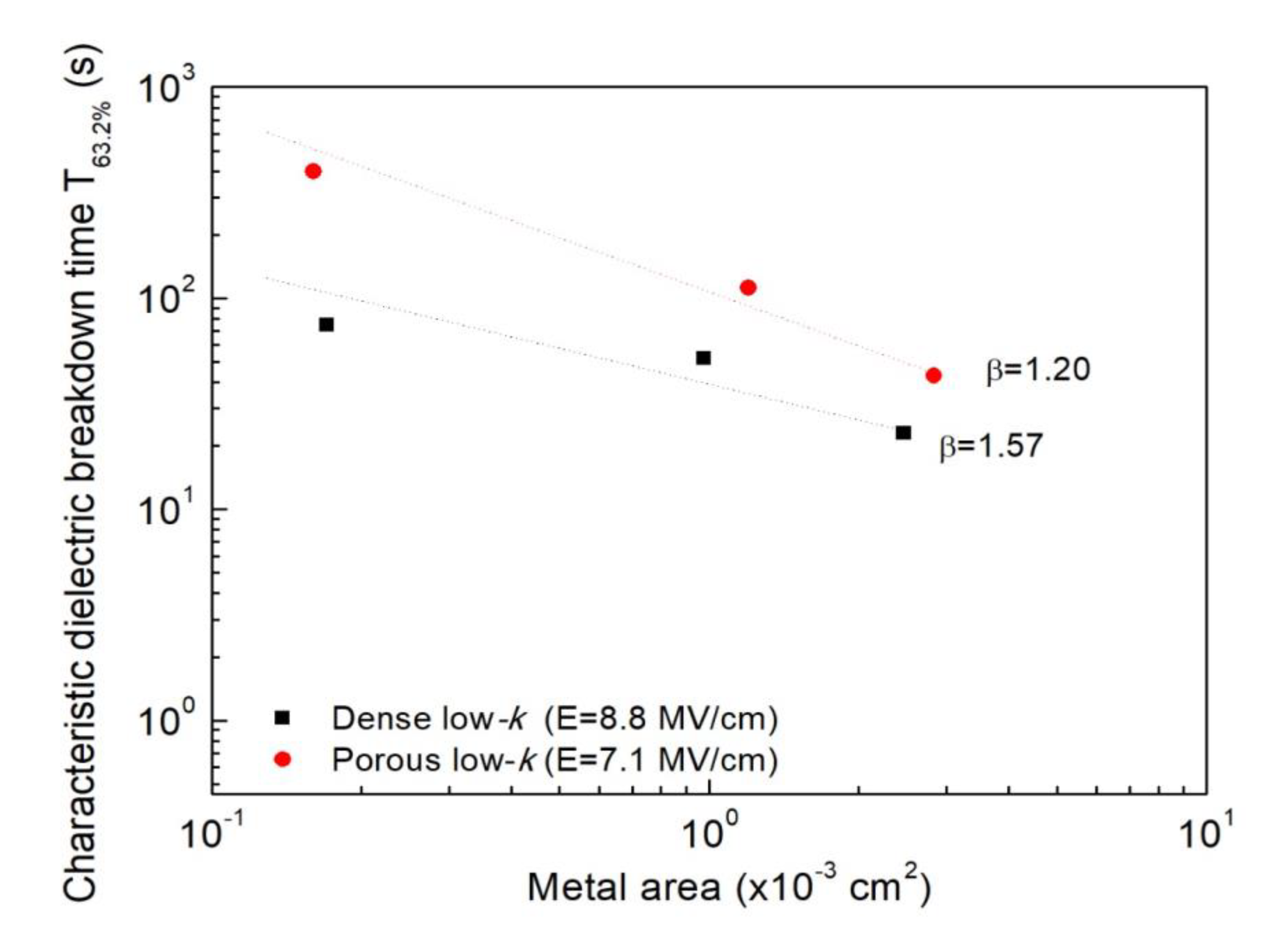
2.2. Metal Gate Area Effect
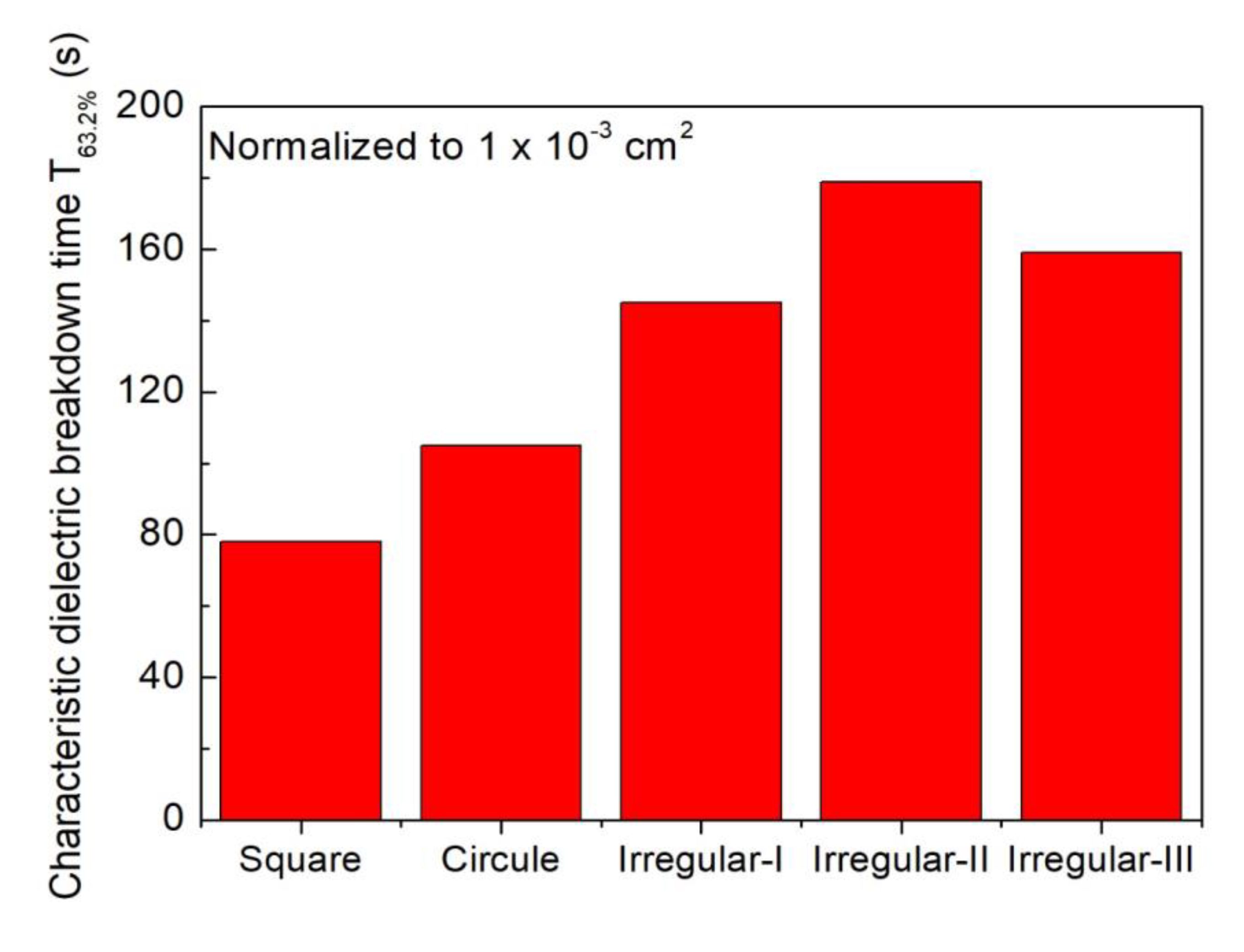
2.3. Metal Gate Geometry Effect
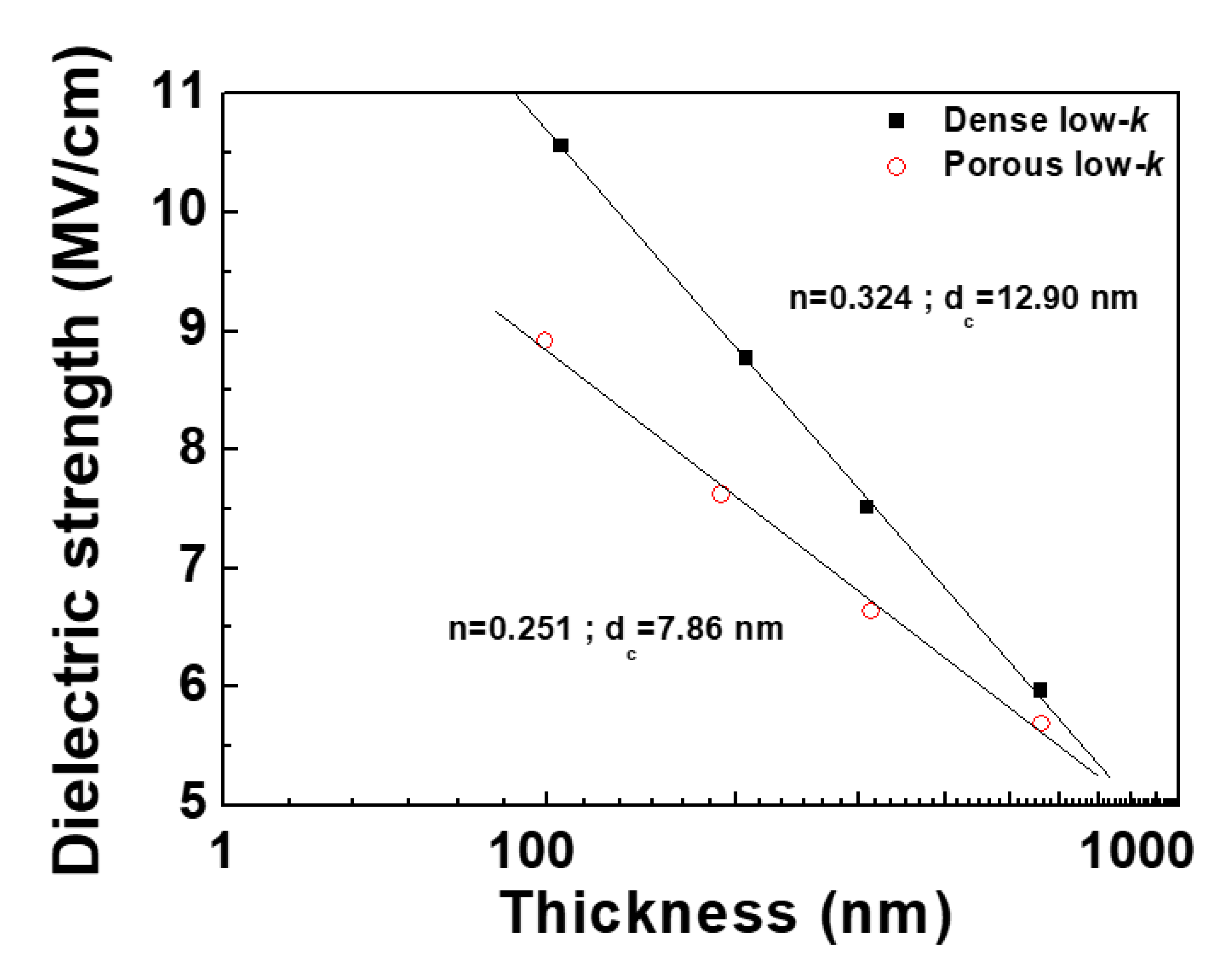
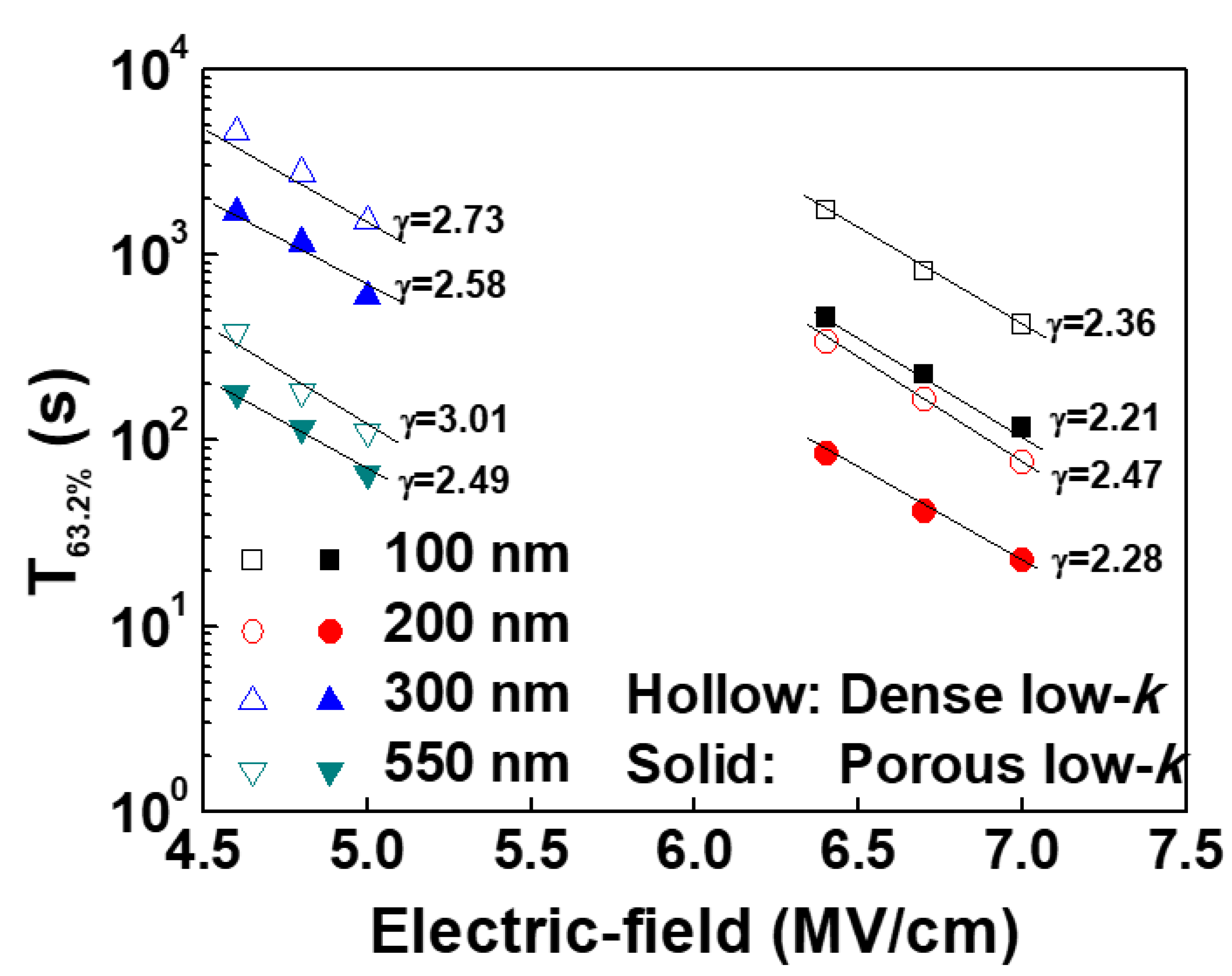
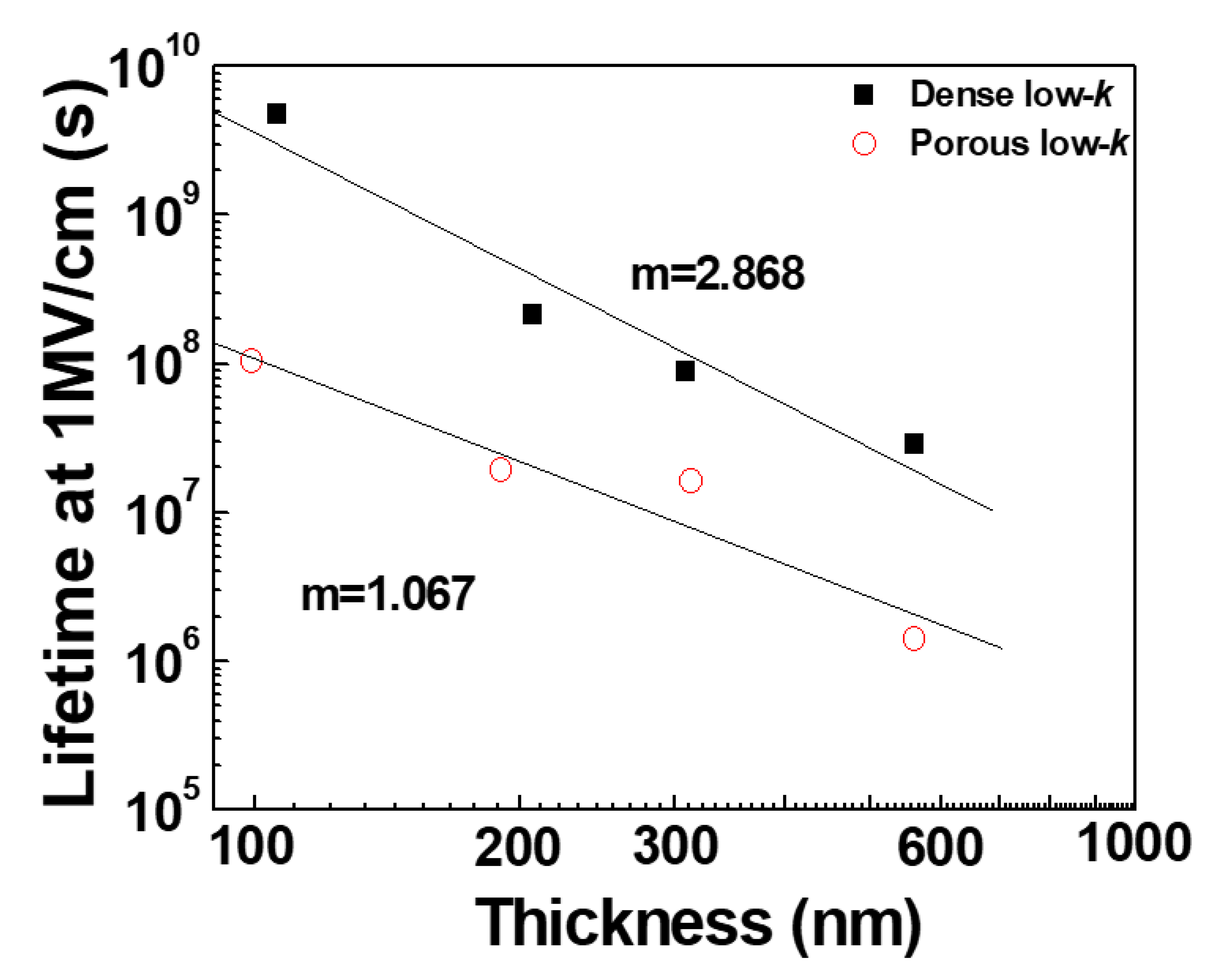
2.4. Dielectric Thickness Effect
3. Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grill, A. Porous pSiCOH ultra low-k dielectrics for chip interconnects prepared by PECVD. Annu. Rev. Mater. Res. 2009, 39, 49. [Google Scholar] [CrossRef]
- Maex, K.; Baklanov, M.; Shamiryan, D.; Lacopi, F.; Brongersma, S.; Yanovitskaya, Z. Low dielectric constant materials for microelectronics. J. Appl. Phys. 2003, 93, 8793. [Google Scholar] [CrossRef]
- Furusawa, T.; Ryuzaki, D.; Yoneyama, R.; Homma, Y.; Hinode, K. Heat and moisture resistance of siloxane-based low-dielectric-constant materials. J. Electrochem. Soc. 2001, 148, F175. [Google Scholar] [CrossRef]
- Uchida, Y.; Hishiya, S.; Fujii, N.; Kohmura, K.; Nakayama, T.; Tanaka, H.; Kikkawa, T. High-voltage SiC and GaN power devices. Microelec. Eng. 2006, 83, 112. [Google Scholar]
- Aoki, H.; Watanabe, D.; Moriyama, R.; Mazumder, M.; Komatsu, N.; Kimura, C.; Sugino, T. Influence of moisture on BCN (low-k) film for interconnection reliability. Dimond Relat. Mater. 2008, 17, 628. [Google Scholar] [CrossRef]
- Kumbhar, A.; Singh, S.; Dusane, R. Enhancement of moisture resistance of spin-on low-k HSQ films by hot wire generated atomic hydrogen treatment. Thin Solid Film 2006, 501, 329. [Google Scholar] [CrossRef]
- Samanta, P.; Zhu, C.; Chan, M. Comparison of electrical stress-induced charge carrier generation/trapping and related degradation of SiO2 and HfO2/SiO2 gate dielectric stacks. Microelectron. Reliab. 2010, 50, 1907. [Google Scholar] [CrossRef]
- Besien, E.; Singh, A.; Barbarin, Y.; Verdinck, P.; Dekkers, H.; Vanstreels, K.; Marneffe, J.; Baklanov, M.; Elshocht, S.V. Low-k a-SiCO:H films as diffusion barriers for advanced interconnects. Microelec. Eng. 2014, 120, 221. [Google Scholar] [CrossRef]
- McPherson, J.; Khamankar, R.; Shanware, A. Complementary model for intrinsic time-dependent dielectric breakdown in SiO2 dielectrics. J. Appl. Phys. 2000, 88, 5351. [Google Scholar] [CrossRef]
- Hong, C.; Milor, L. Modeling of the breakdown mechanisms for porous copper/low-k process flows. Microelec. Reliab. 2007, 47, 1478. [Google Scholar] [CrossRef]
- McPherson, J. Time dependent dielectric breakdown physics–Models revisited. Microelec. Reliab. 2012, 52, 1753. [Google Scholar] [CrossRef]
- Chen, F.; Bravo, O.; Harmon, D.; Shinosky, M.; Aitken, J. Cu/low-k dielectric TDDB reliability issues for advanced CMOS technologies. Microelec. Reliab. 2008, 48, 1375. [Google Scholar] [CrossRef]
- Chen, F.; Shinosky, M. Electron fluence driven, Cu catalyzed, interface breakdown mechanism for BEOL low-k time dependent dielectric breakdown. Microelec. Reliab. 2014, 54, 529. [Google Scholar] [CrossRef]
- Chery, E.; Federspiel, X.; Roy, D.; Volpi, F.; Chaix, J. Identification of the (√ E+ 1/E)-dependence of porous low-k time dependent dielectric breakdown using over one year long package level tests. Microelec. Reliab. 2013, 109, 90. [Google Scholar] [CrossRef]
- Cheng, Y.; Lee, C.; Huang, J.; Chen, G.; Fang, J. Comparison of various low dielectric constant materials. Thin Solid Film. 2018, 660, 871. [Google Scholar] [CrossRef]
- Cheng, Y.; Lee, C.; Hung, W.; Chen, G.; Fang, J. Electrical and reliability characteristics of dielectric stack with low dielectric constant SiCOH and capping SiCNH films. Surf. Coat. Technol. 2018, 350, 57. [Google Scholar] [CrossRef]

| Dielectric | Dense Low-k | Porous Low-k | ||
|---|---|---|---|---|
| Model | E | E1/2 | E | E1/2 |
| γ | 2.70 | 15.9 | 2.51 | 13.61 |
| Error (Error2) | 0.00229 | 0.00225 | 0.00240 | 0.00253 |
| Lifetime at 1 MV/cm (s) | 5.12 × 1010 | 1.36 × 1015 | 3.70 × 108 | 5.82 × 1011 |
| Lifetime at 2 MV/cm (s) | 3.44 × 109 | 2.01 × 1012 | 3.01 × 107 | 2.19 × 109 |
| Sample | Precursor | UV Curing | Dielectric Constant (k) | Leakage Current Density at 1 MV/cm (×10−12) | Breakdown Electric Filed at 25 °C (MV/cm) | Porosity (%) | Pore Size (nm) |
|---|---|---|---|---|---|---|---|
| Dense low-k | DEMS + O2 | No | 3.02 ± 0.05 | 5.66 ± 0.7 | 9.4 ± 0.5 | N/D | N/D |
| Porous low-k | DEMS + O2 + ATRP | Yes | 2.56 ± 0.08 | 2.69 ± 0.33 | 8.2 ± 0.4 | 15.0 ± 0.5 | 1.35 ± 0.14 |
| Mask Geometry | Square | Circle | Irregular | ||
|---|---|---|---|---|---|
 |  |  |  |  | |
| Designed mask area (×10−3cm2) | 0.10~2.50 | 0.90~2.46 | 1.62 | 1.62 | 1.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.-L.; Peng, W.-F.; Huang, C.-J.; Chen, G.-S.; Fang, J.-S. Reliability Characteristics of Metal-Insulator-Semiconductor Capacitors with Low-Dielectric-Constant Materials. Molecules 2023, 28, 1134. https://doi.org/10.3390/molecules28031134
Cheng Y-L, Peng W-F, Huang C-J, Chen G-S, Fang J-S. Reliability Characteristics of Metal-Insulator-Semiconductor Capacitors with Low-Dielectric-Constant Materials. Molecules. 2023; 28(3):1134. https://doi.org/10.3390/molecules28031134
Chicago/Turabian StyleCheng, Yi-Lung, Wei-Fan Peng, Chi-Jia Huang, Giin-Shan Chen, and Jau-Shiung Fang. 2023. "Reliability Characteristics of Metal-Insulator-Semiconductor Capacitors with Low-Dielectric-Constant Materials" Molecules 28, no. 3: 1134. https://doi.org/10.3390/molecules28031134
APA StyleCheng, Y.-L., Peng, W.-F., Huang, C.-J., Chen, G.-S., & Fang, J.-S. (2023). Reliability Characteristics of Metal-Insulator-Semiconductor Capacitors with Low-Dielectric-Constant Materials. Molecules, 28(3), 1134. https://doi.org/10.3390/molecules28031134







