Phosphorus Chemistry at the Roots of Bioenergetics: Ligand Permutation as the Molecular Basis of the Mechanism of ATP Synthesis/Hydrolysis by FOF1-ATP Synthase
Abstract
:1. Introduction

2. Results and Discussion
2.1. Novel Insights from Oxygen Exchange Experiments on Submitochondrial Particles
- (i).
- The energy of the ion gradients is required primarily to induce a conformational change that enables product ATP release from an F1 catalytic site;
- (ii).
- ATP synthesis occurs at a second catalytic site in F1 without external energy input.
2.2. Biological Implications of the Results of Isotope Exchange Experiments on Submitochondrial Particles
2.2.1. Derivation of Limitations on the Rates of Oxygen Exchange
- (i).
- Release of Pi is limiting. In this case, bound ATP can rapidly exchange with 18O in H18OH, which will cause the label to appear in ATP or subsequently in Pi. However, each inorganic phosphate molecule released can contain at most four oxygens from 18O labeled water. Thus, in this case, the rate of ATP–HOH exchange can be high relative to the Pi–ATP exchange, but the rate of Pi–HOH exchange relative to the Pi–ATP exchange cannot be greater than four;
- (ii).
- Release of ATP is limiting. In such a case, tightly bound Pi can rapidly exchange with the oxygens of 18O water, but the γ-phosphate of ATP can contain at most three labeled oxygens. Thus, in this situation, the rate of Pi–HOH exchange can be high relative to the Pi–ATP exchange, but the ratio of the rate of ATP–HOH exchange to that of the Pi–ATP exchange cannot exceed three.
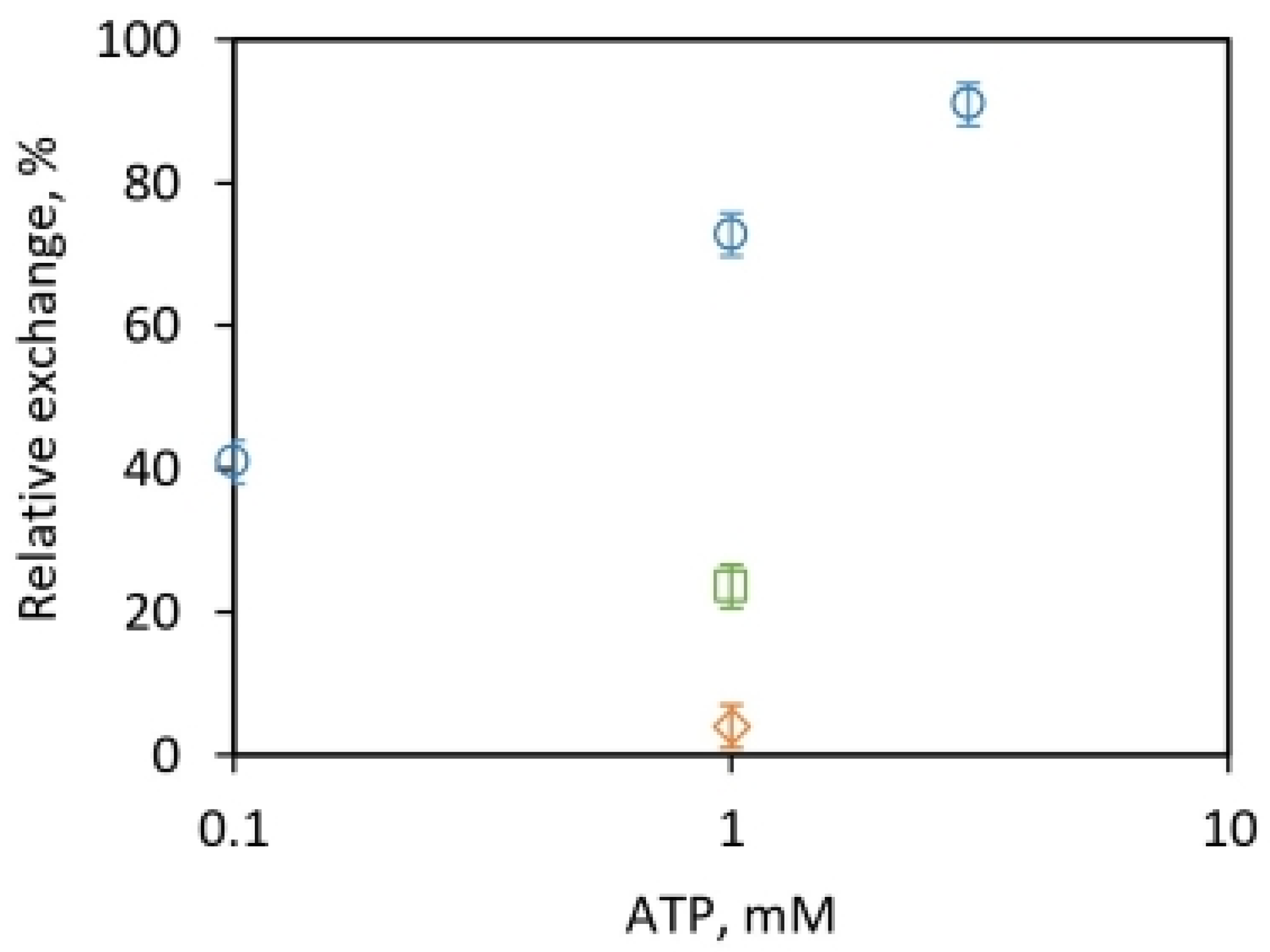
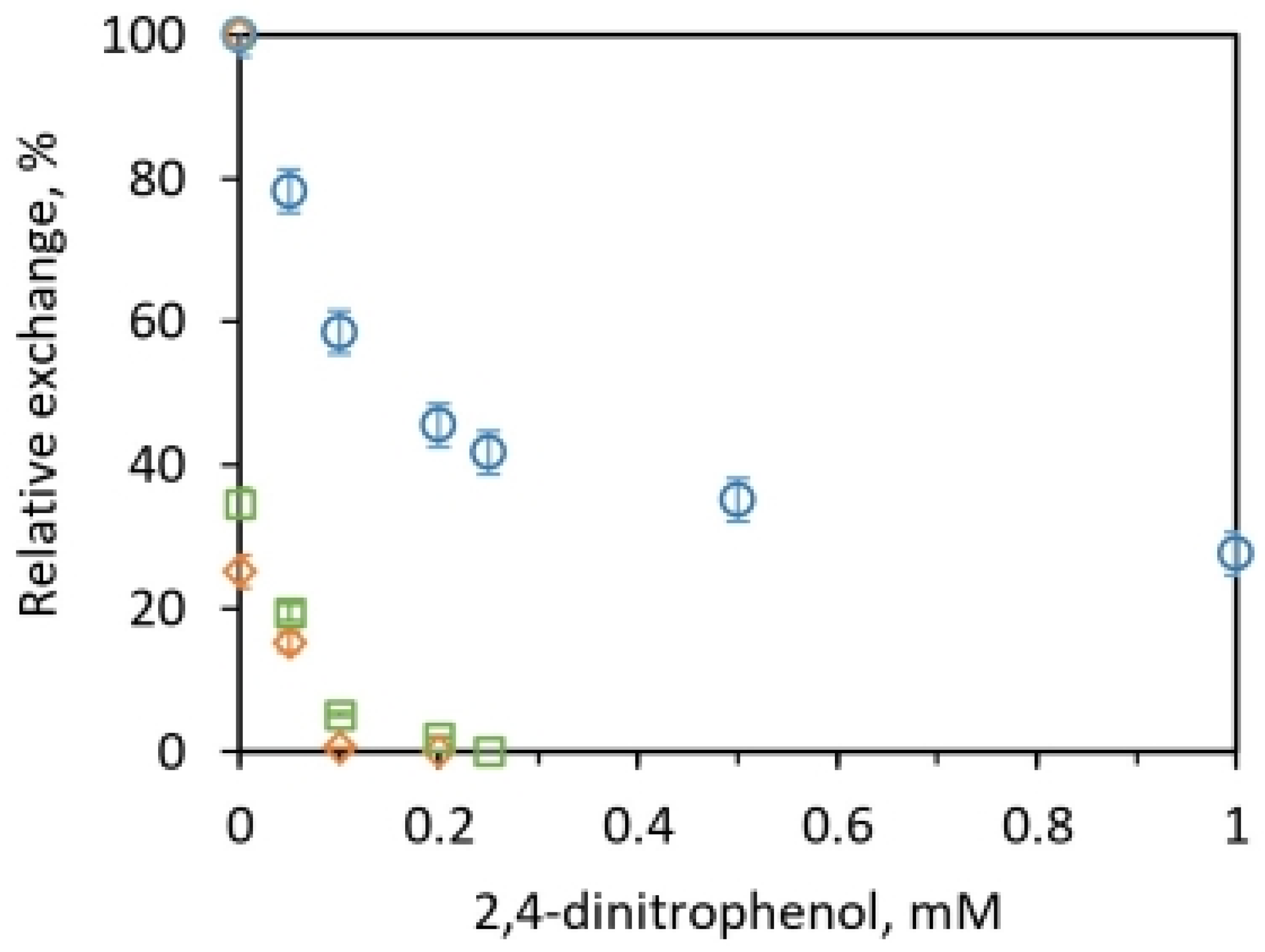
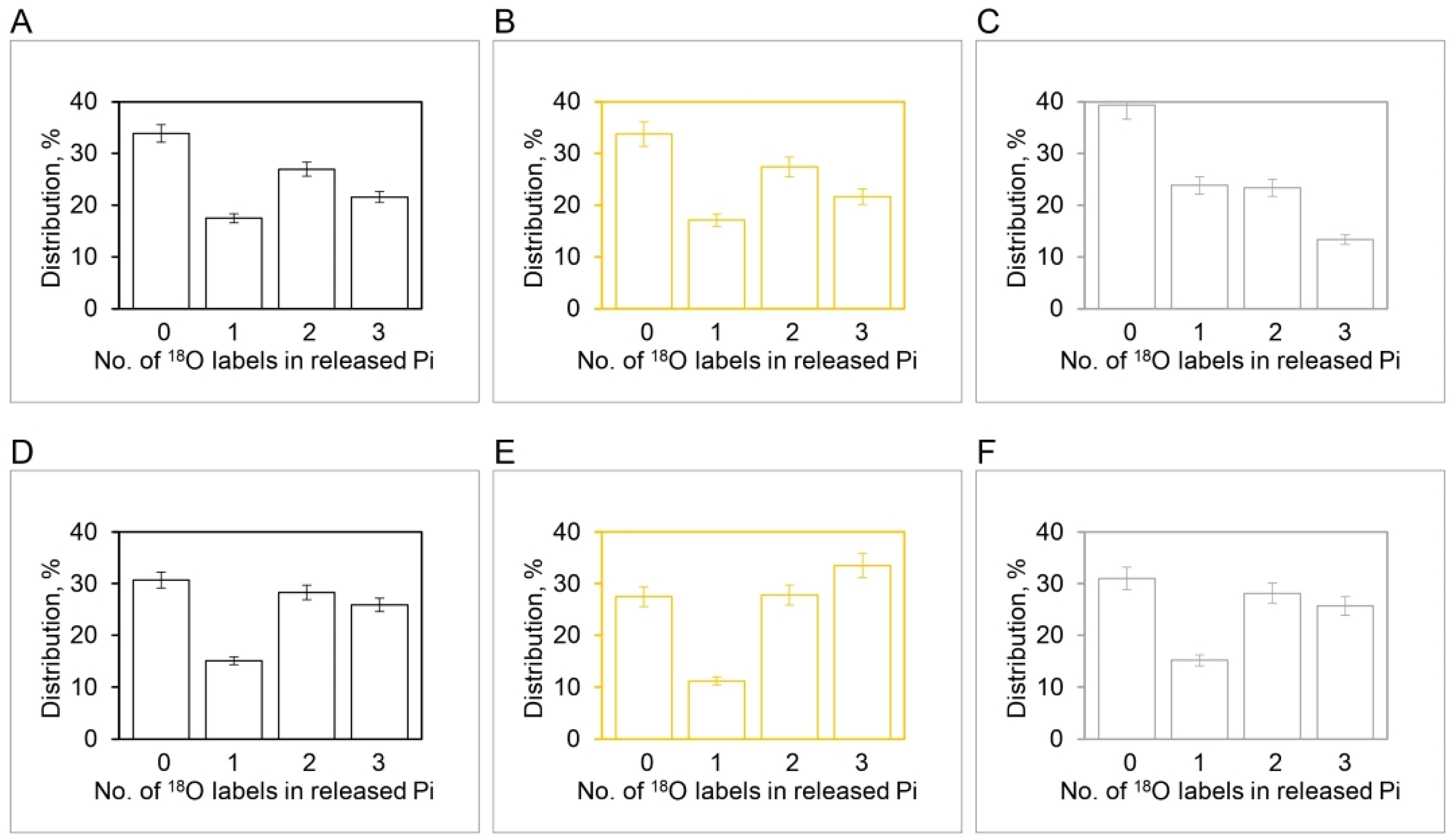
2.2.2. Measurement of the Relative Rates of Isotope Exchanges and Difficulties of Their Rationalization by the Existing Model
2.2.3. Possible Explanation of the Kinetic Data on Relative Rates of Oxygen Exchanges
2.2.4. Resolution of the Apparently Conflicting Experimental Data and Discussion of Other Key Mechanistic Aspects of ATP Synthesis/Hydrolysis
- (i).
- The meeting of the nucleotide requirement for the intermediate Pi–HOH exchange by ATP, but not by ADP, with the latter postulated as an obligatory requirement by the binding change mechanism [81], goes against the mechanism (Section 2.1);
- (ii).
- The concomitant enhancement (Section 2.2.2) above theoretical limits of both the intermediate Pi–HOH and ATP–HOH exchanges with respect to the Pi–ATP exchange (Section 2.2.1) is impossible to explain using Boyer’s simple model containing only a single route of water entry.
- (iii).
- The equations of the binding change mechanism have not been cast in a model-independent way [57,91]. There is no independent verification of the reversals postulated to occur as a result of the mechanism at low substrate concentrations during ATP synthesis/hydrolysis. At physiological ATP, for the F1-ATPase, leading in essence to an irreversible cleavage of ATP. As formulated, has to be an integer, and it is difficult to interpret a non-integer value of in molecular terms;
- (iv).
- For ATP hydrolysis by the FOF1-ATPase, the incorporation of water oxygens into ATP/Pi that arises from the postulated repeated cycles of reversal of the ATP formation reaction has to also be accompanied by a reversal in the direction of H+ translocation across the membrane. However, such a rapid fluctuation/change in direction of the electrochemical ion gradients, and such cycles of bidirectional ion movement, have never been demonstrated in any biochemical system. It was stated by Boyer in 1997 that this “remains an important question” [92], but it has not been addressed, let alone answered, even after the passage of 25 years;
- (v).
- Point (iv) is further exacerbated by the fact that mechanical aspects of the ATP synthase motor also need to be included in the analysis. We stated that, “it is imperative to relate the chemical kinetics (the arrows representing an elementary step in the kinetic scheme) to the mechanical aspects (structure and dynamics of the molecular machine). It is very difficult to conceive how a unidirectional, discrete motion can take place by a reversible mode of catalysis (E.ATP E.ADP.Pi), i.e., how can a subunit of a single enzyme molecule oscillate back and forth in the presence of a driving force in one direction? This irreversibility of operation in a single molecule mode contradicts the fundamental tenet of the binding change mechanism that ATP synthesis occurs reversibly (and spontaneously) in a catalytic site of the enzyme” [33];
- (vi).
- During the operation of a molecular motor at physiological conditions, a species is encouraged to bind to its site on the enzyme mainly to undergo the reaction to the product, and thereafter immediately unbind and release the product. There is no logical explanation as to why it should bind and be released before its conversion to product, or why a reaction should move back and forth numerous times before its product is finally released. Nor can this be considered an efficient mode of operation of the system;
- (vii).
- The binding change mechanism proposed a catalytic site at which during steady-state catalysis by the ATP synthase/F1-ATPase [59]. Later, in one of his last papers on the subject, Boyer acknowledged that “during hydrolysis the quasi-equilibrium may be shifted toward bound ADP so that essentially only ADP will be released” [61]. It further added that “how this could be achieved is not known” [61]. We are none the wiser twenty years on after that statement was made;
- (viii).
- The bisite binding change mechanism revealed fundamental flaws, in that low-affinity F1 catalytic sites were occupied by bound MgATP, while higher-affinity catalytic sites were left unfilled during the catalysis of ATP hydrolysis [33];
- (ix).
- While “unisite” catalysis and its acceleration by chase ATP binding at a second catalytic site has been amply demonstrated [78], there has been no report of “unisite” ATP synthesis. Nor has the acceleration of the rate of ATP synthesis been demonstrated to achieve the physiological catalysis of synthesis. In fact, classical biochemical experiments on the mitochondrial F1 using radioactive probes showed that rapid steady-state ATP synthesis is achieved by the enzyme only after the filling of three catalytic sites [93];
- (x).
- Pioneering biochemical studies by Senior and coworkers [94] using fluorescent probes have conclusively demonstrated that trisite catalysis is the true operating mode of steady-state Vmax hydrolysis by F1-ATPase. The technologically sophisticated single-molecule studies of Kinosita and coworkers on F1-ATPase offer further support to a trisite mode of ATP hydrolysis from nanomolar to millimolar ATP concentrations [95]. Finally, high-resolution X-ray structures of F1-ATPase that visualized the transition state have proven beyond doubt that Mg-nucleotide binds to all three β-catalytic sites of the F1-ATPase during catalysis [76]. It is very difficult, if not impossible, to explain these important findings based on bisite models of catalysis, such as the binding change mechanism;
- (xi).
- It was very important to distinguish between bisite activation and trisite catalysis during the process of ATP hydrolysis. The binding change mechanism did not do that, which, in retrospect, can be considered a major shortcoming. Trisite catalysis with bisite activation in ATP hydrolysis by F1-ATPase has been explained only very recently [77,91];
- (xii).
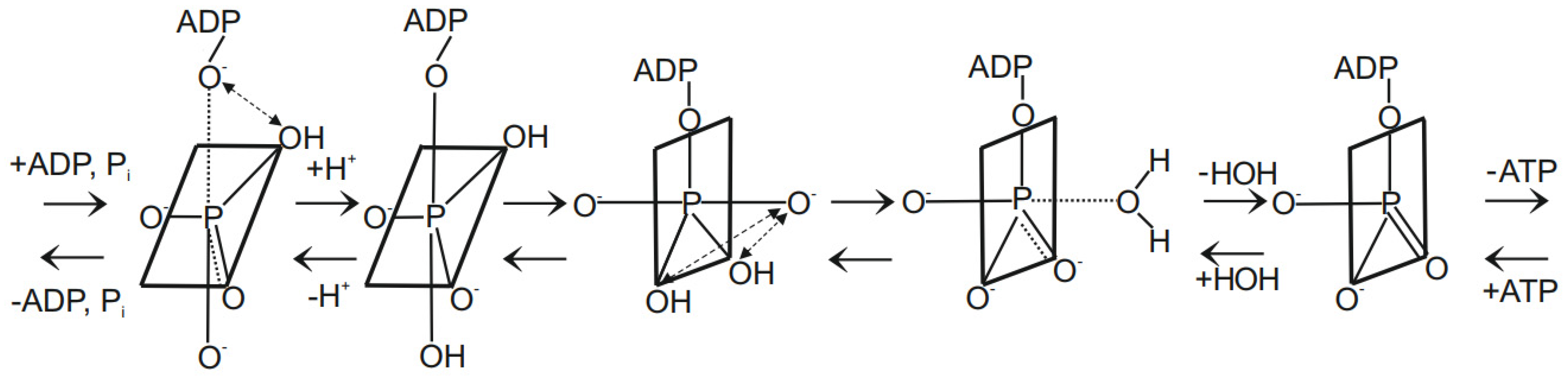
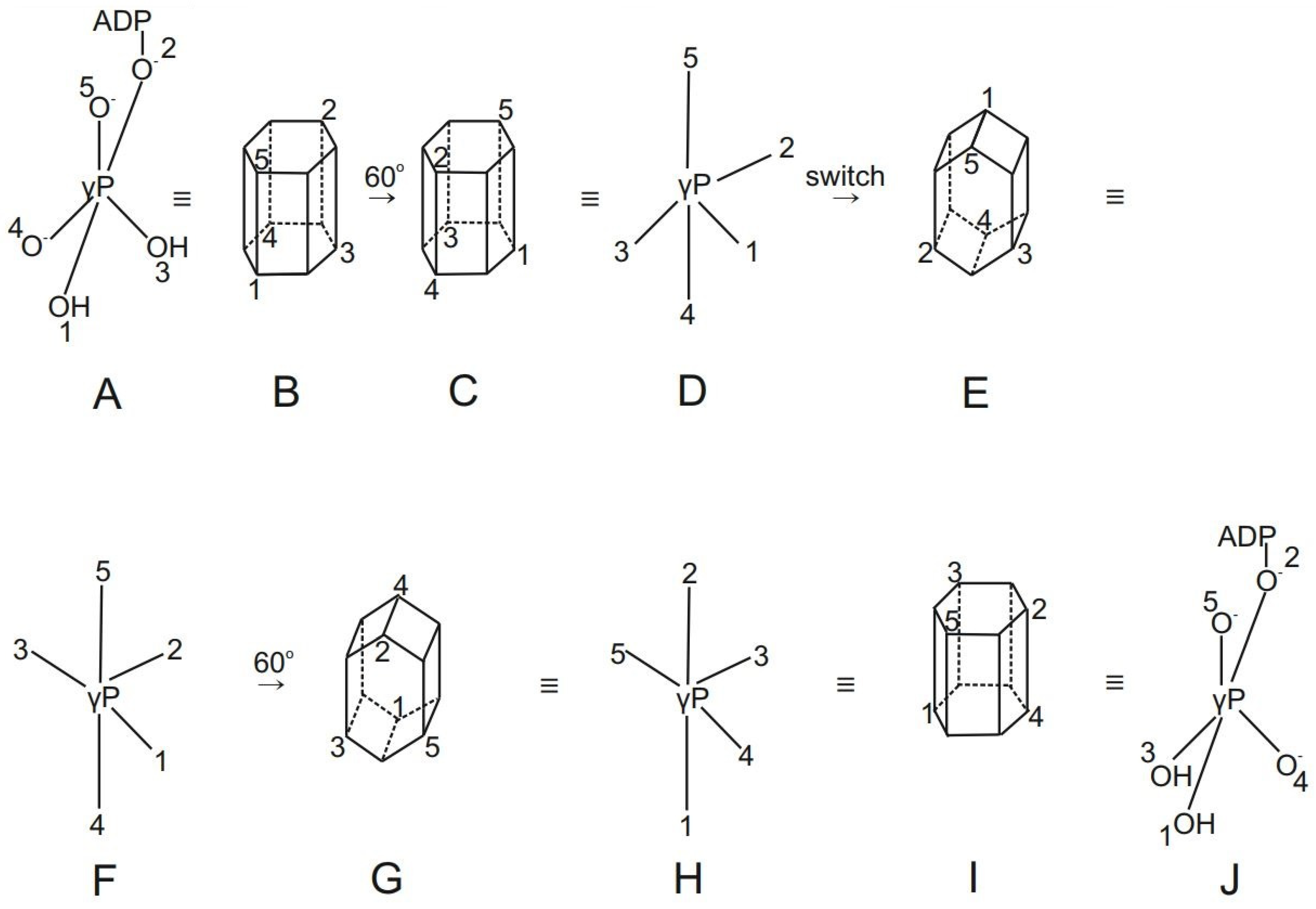
- The cleavage of bonds followed by their re-formation by irregular processes leads to intermediates of lower coordination number. Hence, such processes do not satisfy the general chemical concept of the preservation of coordination number. The latter is only possible if the molecular skeleton is flexible, i.e., the numbered positions on the skeleton (such as the trigonal bipyramid skeleton) can be interconverted with the maintenance of coordination numbers via the deformation of bond angles or rotation about bonds (dynamic skeletal symmetry). Hence there is no chemical necessity to propose mechanisms involving bond breaking and bond re-forming processes as done by the binding change mechanism in order to rationalize the oxygen exchange reactions. We shall further discuss this concept, which is of great importance to phosphorus chemistry, in Section 2.2.5 and Section 2.2.6.
2.2.5. New Concepts for Rationalization and Explanation of Oxygen Exchange in Oxidative Phosphorylation and Photophosphorylation
2.2.6. Stereochemical Consequences
3. Experimental
3.1. Preparation of Submitochondrial Particles
3.2. Determination of Incorporation of the 18O
3.3. Oxygen Exchange
3.4. Experiments on Particles in the Presence of Uncoupler
3.5. Separation of Pi
3.6. Mass Spectroscopic Experiments for Determination of 18O in Pi
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allen, D.W.; Loakes, D.; Tebby, J. Organophosphorus Chemistry; Royal Society of Chemistry: London, UK, 2016. [Google Scholar]
- Adamek, J. (Ed.) Organophosphorus Chemistry: A New Perspective; MDPI: Basel, Switzerland, 2023. [Google Scholar]
- Kolodiazhnyi, O.I. Phosphorus compounds of natural origin: Prebiotic, stereochemistry, application. Symmetry 2021, 13, 889. [Google Scholar] [CrossRef]
- Caminade, A.-M. Phosphorus dendrimers as nanotools against cancers. Molecules 2020, 25, 3333. [Google Scholar] [CrossRef] [PubMed]
- Kuźnik, A.; Kozicka, D.; Hawranek, W.; Socha, K.; Erfurt, K. One-pot and catalyst-free transformation of N-protected 1-amino-1-ethoxyalkylphosphonates into bisphosphonic analogs of protein and non-protein α-amino acids. Molecules 2022, 27, 3571. [Google Scholar] [CrossRef] [PubMed]
- Vassaki, M.; Lazarou, S.; Turhanen, P.; Choquesillo-Lazarte, D.; Demadis, K.D. Drug-inclusive inorganic-organic hybrid systems for the controlled release of the osteoporosis drug zoledronate. Molecules 2022, 27, 6212. [Google Scholar] [CrossRef] [PubMed]
- del Corte, X.; Maestro, A.; Lόpez-Francés, A.; Palacios, F.; Vicario, J. Synthesis of tetrasubstituted phosphorus analogs of aspartic acid as antiproliferative agents. Molecules 2022, 27, 8024. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, R.; Howell, J.M.; Muetterties, E.L. Molecular orbital theory of pentacoordinate phosphorus. J. Am. Chem. Soc. 1972, 94, 3047–3058. [Google Scholar] [CrossRef]
- Seeman, J.I. The ways of science through the lens of the Woodward-Hoffmann rules. Chem. Rec. 2022, 22, e202100211. [Google Scholar] [CrossRef]
- Nath, S. Modern theory of energy coupling and ATP synthesis. Violation of Gauss’s law by the chemiosmotic theory and validation of the two-ion theory. Biophys. Chem. 2019, 255, 106271, Corrigendum. Biophys. Chem. 2022, 286, 106826. [Google Scholar] [CrossRef]
- Nath, S. Two-ion theory of energy coupling in ATP synthesis rectifies a fundamental flaw in the governing equations of the chemiosmotic theory. Biophys. Chem. 2017, 230, 45–52. [Google Scholar] [CrossRef]
- Nath, S. Integration of demand and supply sides in the ATP energy economics of cells. Biophys. Chem. 2019, 252, 106208. [Google Scholar] [CrossRef]
- Nath, S. Network representation and analysis of energy coupling mechanisms in cellular metabolism by a graph-theoretical approach. Theory Biosci. 2022, 141, 249–260. [Google Scholar] [CrossRef] [PubMed]
- Holmes-Cerfon, M.; Gortler, S.J.; Brenner, M.P. A geometrical approach to computing free-energy landscapes from short-ranged potentials. Proc. Natl. Acad. Sci. USA 2012, 109, E5–E14. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. Energy landscapes and dynamics of ion translocation through membrane transporters: A meeting ground for physics, chemistry, and biology. J. Biol. Phys. 2021, 47, 401–433. [Google Scholar] [CrossRef] [PubMed]
- Wadhwa, N.; Berg, H.C. Bacterial motility: Machinery and mechanism. Nat. Rev. Microbiol. 2021, 20, 161–173. [Google Scholar] [CrossRef] [PubMed]
- Trybus, K.M. Myosin V from head to tail. Cell Mol. Life Sci. 2008, 65, 1378–1389. [Google Scholar] [CrossRef] [PubMed]
- Burgess, S.; Walker, M.; Wang, F.; Sellers, J.R.; White, H.D.; Knight, P.J.; Trinick, J. The prepower stroke conformation of myosin V. J. Cell Biol. 2002, 159, 983–991. [Google Scholar] [CrossRef] [PubMed]
- Rastogi, K.; Puliyakodan, M.S.; Pandey, V.; Nath, S.; Elangovan, R. Maximum limit to the number of myosin II motors participating in processive sliding of actin. Sci. Rep. 2016, 6, 32043. [Google Scholar] [CrossRef]
- Okazaki, K.; Takada, S. Structural comparison of F1-ATPase: Interplay among enzyme structures, catalysis, and rotations. Structure 2011, 19, 588–598. [Google Scholar] [CrossRef]
- Forsyth, A.M.; Wan, J.; Owrutsky, P.D.; Abkarian, M.; Stone, H.A. Multiscale approach to link red blood cell dynamics, shear viscosity, and ATP release. Proc. Natl. Acad. Sci. USA 2011, 108, 10986–10991. [Google Scholar] [CrossRef]
- Singharoy, A.; Chipot, C. Methodology for the simulation of molecular motors at different scales. J. Phys. Chem. B 2017, 121, 3502–3514. [Google Scholar] [CrossRef]
- Nath, S. A thermodynamic principle for the coupled bioenergetic processes of ATP synthesis. Pure Appl. Chem. 1998, 70, 639–644. [Google Scholar] [CrossRef]
- Nath, S. The thermodynamic efficiency of ATP synthesis in oxidative phosphorylation. Biophys. Chem. 2016, 219, 69–74. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. Optimality principle for the coupled chemical reactions of ATP synthesis and its molecular interpretation. Chem. Phys. Lett. 2018, 699, 212–217. [Google Scholar] [CrossRef]
- Nath, S. Entropy production and its application to the coupled nonequilibrium processes of ATP synthesis. Entropy 2019, 21, 746. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. Coupling mechanisms in ATP synthesis: Rejoinder to “Response to molecular-level understanding of biological energy coupling and transduction”. Biophys. Chem. 2021, 272, 106579. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. Charge transfer across biomembranes: A solution to the conundrum of high desolvation free energy penalty in ion transport. Biophys. Chem. 2021, 275, 106604. [Google Scholar] [CrossRef] [PubMed]
- Štrajbl, M.; Shurki, A.; Warshel, A. Converting conformational changes to electrostatic energy in molecular motors: The energetics of ATP synthase. Proc. Natl. Acad. Sci. USA 2013, 100, 14834–14839. [Google Scholar] [CrossRef]
- Nath, S.S.; Nath, S. Energy transfer from adenosine triphosphate: Quantitative analysis and mechanistic insights. J. Phys. Chem. B 2009, 113, 1533–1537. [Google Scholar] [CrossRef]
- Nath, S. The new unified theory of ATP synthesis/hydrolysis and muscle contraction, its manifold fundamental consequences and mechanistic implications and its applications in health and disease. Int. J. Mol. Sci. 2008, 9, 1784–1840. [Google Scholar] [CrossRef]
- Nath, S. Molecular mechanisms of energy transduction in cells: Engineering applications and biological implications. Adv. Biochem. Eng. Biotechnol. 2003, 85, 125–180. [Google Scholar]
- Nath, S. The molecular mechanism of ATP synthesis by F1F0-ATP synthase: A scrutiny of the major possibilities. Adv. Biochem. Eng. Biotechnol. 2002, 74, 65–98. [Google Scholar] [PubMed]
- Senior, A.E.; Nadanaciva, S.; Weber, J. The molecular mechanism of ATP synthesis by F1F0-ATP synthase. Biochim. Biophys. Acta 2002, 1553, 188–211. [Google Scholar] [CrossRef]
- Xu, L.; Liu, F. The chemo-mechanical coupled model for F1F0-motor. Prog. Biophys. Mol. Biol. 2012, 108, 139–148. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. Analysis of molecular mechanisms of ATP synthesis from the standpoint of the principle of electrical neutrality. Biophys. Chem. 2017, 224, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Kell, D.B. A protet-based, protonic charge transfer model of energy coupling in oxidative and photosynthetic phosphorylation. Adv. Microb. Physiol. 2021, 78, 1–35. [Google Scholar] [PubMed]
- Frasch, W.D.; Bukhari, Z.A.; Yanagisawa, S. F1FO ATP synthase molecular motor mechanisms. Front. Microbiol. 2022, 13, 965620. [Google Scholar] [CrossRef] [PubMed]
- Bruns, K.; Studtrucker, N.; Sharma, A.; Fossen, T.; Mitzner, D.; Eissman, A.; Tessmer, U.; Roder, R.; Henklein, P.; Wray, V.; et al. Structural characterization and oligomerization of PB1–F2, a proapoptotic influenza A virus protein. J. Biol. Chem. 2007, 282, 353–363. [Google Scholar] [CrossRef]
- Hards, K.; McMillan, D.G.G.; Schurig-Briccio, L.A.; Gennis, R.B.; Lill, H.; Bald, D.; Cook, G.M. Ionophoric effects of the antitubercular drug bedaquiline. Proc. Natl. Acad. Sci. USA 2018, 115, 7326–7331. [Google Scholar] [CrossRef]
- Nath, S. Interpretation of the mechanism of action of antituberculosis drug bedaquiline based on a novel two-ion theory of energy coupling in ATP synthesis. Bioeng. Transl. Med. 2019, 4, 164–170. [Google Scholar] [CrossRef]
- Sarathy, J.P.; Grüber, G.; Dick, T. Re-understanding the mechanisms of action of the anti-mycobacterial drug bedaquiline. Antibiotics 2019, 8, 261. [Google Scholar] [CrossRef]
- Niedzwiecka, K.; Baranowska, E.; Panja, C.; Kucharczyk, R. ATP synthase subunit a supports permeability transition in yeast lacking dimerization subunits and modulates yPTP conductance. Cell Physiol. Biochem. 2020, 54, 211–229. [Google Scholar] [PubMed]
- Nath, S. A novel conceptual model for the dual role of FOF1-ATP synthase in cell life and cell death. Biomol. Concepts 2020, 11, 143–152. [Google Scholar] [CrossRef] [PubMed]
- Bernardi, P.; Carraro, M.; Lippe, G. The mitochondrial permeability transition: Recent progress and open questions. FEBS J. 2022, 289, 7051–7074. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. Supercomplex supercomplexes: Raison d’etre and functional significance of supramolecular organization in oxidative phosphorylation. Biomol. Concepts 2022, 13, 272–288. [Google Scholar] [CrossRef] [PubMed]
- Chu, X.-Y.; Xu, Y.-Y.; Tong, X.-Y.; Wang, G.; Zhang, H.-Y. The legend of ATP: From origin of life to precision medicine. Metabolites 2022, 12, 461. [Google Scholar] [CrossRef] [PubMed]
- Callender, R.; Dyer, R.B. Advances in time-resolved approaches to characterize the dynamical nature of enzymatic catalysis. Chem. Rev. 2006, 106, 3031–3042. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Moerner, W.E. An adaptive anti-Brownian electrokinetic trap with real-time information on single-molecule diffusivity and mobility. ACS Nano 2011, 5, 5792–5799. [Google Scholar] [CrossRef]
- Rob, T.; Wilson, D.J. Time-resolved mass spectrometry for monitoring millisecond time-scale solution-phase processes. Eur. J. Mass. Spectrom. 2012, 18, 205–214. [Google Scholar] [CrossRef]
- Clark, T.B.; Ziółkowski, M.; Schatz, G.C.; Goodson, T. Two-photon and time-resolved fluorescence spectroscopy as probes for structural determination in amyloid β-peptides and aggregates. J. Phys. Chem. B 2014, 118, 2351–2359. [Google Scholar] [CrossRef]
- Sielaff, H.; Börsch, M. Twisting and subunit rotation in single FOF1-ATP synthase. Trans. R. Soc. B 2013, 368, 20120024. [Google Scholar] [CrossRef]
- Krah, A.; Vogelaar, T.; De Jong, S.I.; Claridge, J.K.; Bond, P.J.; McMillan, D. ATP binding by an F1Fo ATP synthase ε subunit is pH subunit, suggesting a diversity of ε subunit functional regulation in bacteria. Front. Mol. Biosci. 2023, 10, 1059673. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, B.; Diez, M.; Zarrabi, N.; Gräber, P.; Börsch, M. Movements of the ε-subunit during catalysis and activation in single membrane-bound H+-ATP synthase. EMBO J. 2005, 24, 2053–2063. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. A novel systems biology/engineering approach solves fundamental molecular mechanistic problems in bioenergetics and motility. Process Biochem. 2006, 41, 2218–2235. [Google Scholar] [CrossRef]
- Huang, H.-L.; Brudwig, G.W. Kinetic modeling of substrate-water exchange in Photosystem II. BBA Adv. 2021, 1, 100014. [Google Scholar] [CrossRef] [PubMed]
- Mehta, R.; Singh, J.; Nath, S. Time-resolved oxygen exchange measurements offer novel mechanistic insights into enzyme-catalyzed ATP synthesis during photophosphorylation. J. Phys. Chem. B 2020, 124, 5139–5148. [Google Scholar] [CrossRef] [PubMed]
- O’Neal, C.C.; Boyer, P.D. Assessment of the rate of bound substrate interconversion and of ATP acceleration of product release during catalysis by mitochondrial adenosine triphosphatase. J. Biol. Chem. 1984, 259, 5761–5767. [Google Scholar] [CrossRef] [PubMed]
- Boyer, P.D.; Cross, R.L.; Momsen, W. A new concept for energy coupling in oxidative phosphorylation based on a molecular explanation of the oxygen exchange reactions. Proc. Natl. Acad. Sci. USA 1973, 70, 2837–2839. [Google Scholar] [CrossRef]
- Boyer, P.D. The binding change mechanism for ATP synthase—Some probabilities and possibilities. Biochim. Biophys. Acta 1993, 1140, 215–250. [Google Scholar] [CrossRef]
- Boyer, P.D. Catalytic site occupancy during ATP synthase catalysis. FEBS Lett. 2002, 512, 29–32. [Google Scholar] [CrossRef]
- Nath, S.; Rohatgi, H.; Saha, A. The torsional mechanism of energy transfer in ATP synthase. Curr. Sci. 1999, 77, 167–169. [Google Scholar]
- Nath, S.; Rohatgi, H.; Saha, A. The catalytic cycle of ATP synthesis by means of a torsional mechanism. Curr. Sci. 2000, 78, 23–27. [Google Scholar]
- Nath, S.; Jain, S. BREAKTHROUGHS AND VIEWS: Kinetic modeling of ATP synthesis by ATP synthase and its mechanistic implications. Biochem. Biophys. Res. Commun. 2000, 272, 629–633. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Murugavel, R.; Hansen, L.D. ATP synthase and the torsional mechanism: Resolving a 50-year-old mystery. Curr. Sci. 2004, 87, 16–19. [Google Scholar]
- Villadsen, J.; Nielsen, J.; Lidén, G. Bioreaction Engineering Principles, 3rd ed.; Springer: New York, NY, USA, 2011; Chapter 4. [Google Scholar]
- Channakeshava, C. New paradigm for ATP synthesis and consumption. J. Biosci. 2011, 36, 3–4. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, B. A role for anions in ATP synthesis and its molecular mechanistic interpretation. J. Bioenerg. Biomembr. 2011, 43, 299–310. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, B. Revisiting the ‘chemiosmotic theory’: Coupled transport of anion and proton for ATP synthesis. Bioenergetics 2013, 2, e116. [Google Scholar] [CrossRef]
- Rao, N.M. Medical Biochemistry, 2nd ed.; New Age International: New Delhi, India, 2014; pp. 280–281. [Google Scholar]
- Wray, V. Commentary on “Oxidative phosphorylation revisited”. Biotechnol. Bioeng. 2015, 112, 1984–1985. [Google Scholar] [CrossRef] [PubMed]
- Ji, S. The Cell Language Theory: Connecting Mind and Matter; World Scientific: Singapore, 2018; Chapter 3. [Google Scholar]
- Levy, W.B.; Calvert, V.G. Communication consumes 35 times more energy than computation in the human cortex, but both costs are needed to predict synapse number. Proc. Natl. Acad. Sci. USA 2021, 118, e2008173118. [Google Scholar] [CrossRef]
- Juretić, D. Bioenergetics: A Bridge across Life and Universe; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Hill, R.D.; Boyer, P.D. Inorganic orthophosphate activation and adenosine diphosphate as the primary phosphoryl acceptor in oxidative phosphorylation. J. Biol. Chem. 1967, 242, 4320–4323. [Google Scholar] [CrossRef]
- Menz, R.I.; Walker, J.E.; Leslie, A.G.W. Structure of bovine mitochondrial F1-ATPase with nucleotide bound to all three catalytic sites: Implication for the mechanism of rotary catalysis. Cell 2001, 106, 331–341. [Google Scholar] [CrossRef]
- Nath, S. Beyond binding change: The molecular mechanism of ATP hydrolysis by F1-ATPase and its biochemical consequences. Front. Chem. 2023, 11, 1058500. [Google Scholar] [CrossRef] [PubMed]
- Wray, V. Elucidating a complex mechanism: Perspective on “Beyond binding change: The molecular mechanism of ATP hydrolysis by F1-ATPase and its biochemical consequences”. Function 2023, 4, zqad051. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. Consolidation of Nath’s torsional mechanism of ATP synthesis and two-ion theory of energy coupling in oxidative phosphorylation and photophosphorylation. Biophys. Chem. 2020, 257, 106279. [Google Scholar] [CrossRef] [PubMed]
- Allison, W.S. F1-ATPase: A molecular motor that hydrolyzes ATP with sequential opening and closing of catalytic sites coupled to rotation of its γ-subunit. Acc. Chem. Res. 1998, 31, 819–826. [Google Scholar] [CrossRef]
- Jones, D.H.; Boyer, P.D. The apparent absolute requirement of adenosine diphosphate for the inorganic phosphate-water exchange of oxidative phosphorylation. J. Biol. Chem. 1969, 24, 5767–5772. [Google Scholar] [CrossRef]
- Hinkle, P.C.; Penefsky, H.S.; Racker, E. Partial resolution of the enzymes catalyzing oxidative phosphorylation. XII. The H218O-inorganic phosphate and H218O-adenosine triphosphate exchange reactions in submitochondrial particles from beef heart. J. Biol. Chem. 1967, 242, 1788–1792. [Google Scholar] [CrossRef]
- Lee, C.P.; Ernster, L. Studies of the energy-transfer system of submitochondrial particles. 2. Effects of oligomycin and aurovertin. Eur. J. Biochem. 1968, 3, 391–400. [Google Scholar] [CrossRef]
- Boyer, P.D.; Luchsinger, W.W.; Falcone, A.B. O18 and P32 exchange reactions of mitochondria in relation to oxidative phosphorylation. J. Biol. Chem. 1956, 223, 405–421. [Google Scholar] [CrossRef]
- Chan, P.C.; Lehninger, A.L.; Enns, T. The phosphate-water oxygen exchange reaction of oxidative phosphorylation in submitochondrial preparations. J. Biol. Chem. 1960, 235, 1790–1795. [Google Scholar] [CrossRef]
- DeMaster, E.G.; Mitchell, R.A. A comparison of arsenate and vanadate as inhibitors or uncouplers of mitochondrial and glycolytic energy metabolism. Biochemistry 1973, 12, 3616–3621. [Google Scholar] [CrossRef]
- Kayalar, C.; Rosing, J.; Boyer, P.D. An alternating site sequence for oxidative phosphorylation suggested by measurement of substrate binding patterns and exchange reaction inhibitions. J. Biol. Chem. 1977, 252, 2486–2491. [Google Scholar] [CrossRef] [PubMed]
- Drysdale, G.R.; Cohn, M. On the mode of action of 2,4-dinitrophenol in uncoupling oxidative phosphorylation. J. Biol. Chem. 1958, 233, 1574–1577. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. Molecular mechanistic insights into coupling of ion transport to ATP synthesis. Biophys. Chem. 2018, 241, 20–26. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. Molecular mechanistic insights into uncoupling of ion transport from ATP synthesis. Biophys. Chem. 2018, 242, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. Elucidating events within the black box of enzyme catalysis in energy metabolism: Insights into the molecular mechanism of ATP hydrolysis by F1-ATPase. Biomolecules 2023, 13, 1596. [Google Scholar] [CrossRef]
- Boyer, P.D. The ATP synthase—A splendid molecular machine. Annu. Rev. Biochem. 1997, 66, 717–749. [Google Scholar] [CrossRef] [PubMed]
- Matsuno-Yagi, A.; Hatefi, Y. Studies on the mechanism of oxidative phosphorylation. J. Biol. Chem. 1990, 265, 82–88. [Google Scholar] [CrossRef]
- Weber, J.; Senior, A.E. Bi-site catalysis in F1-ATPase: Does it exist? J. Biol. Chem. 2001, 276, 35422–35428. [Google Scholar] [CrossRef]
- Sakaki, N.; Shimo-Kon, R.; Adachi, K.; Itoh, H.; Furuike, S.; Muneyuki, E.; Yoshida, M.; Kinosita, K. One rotary mechanism for F1-ATPase over ATP concentrations from millimolar down to nanomolar. Biophys. J. 2005, 88, 2047–2056. [Google Scholar] [CrossRef]
- Hackney, D.D. Theoretical analysis of distribution of [18O]Pi species during exchange with water: Application to exchanges catalyzed by yeast inorganic pyrophosphatase. J. Biol. Chem. 1980, 255, 5320–5328. [Google Scholar] [CrossRef]
- Smirnova, I.N.; Kasho, V.N.; Volk, S.E.; Ivanov, A.H.; Baykov, A.A. Rates of elementary steps catalyzed by rat liver cytosolic and mitochondrial inorganic pyrophosphatases in both directions. Arch. Biochem. Biophys. 1995, 318, 340–348. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.-M.; Tsai, J.-Y.; Hsiao, C.-D.; Huang, Y.-T.; Chiu, C.-L.; Liu, M.-H.; Tung, J.-Y.; Liu, T.-H.; Pan, R.-L.; Sun, Y.-J. Crystal structure of a membrane-embedded H+–translocating pyrophosphatase. Nature 2012, 484, 399–403. [Google Scholar] [CrossRef] [PubMed]
- Kellosalo, J.; Kajander, T.; Kogan, K.; Pokharel, K.; Goldman, A. The structure and catalytic cycle of a sodium-pumping pyrophosphatase. Science 2012, 337, 473–476. [Google Scholar] [CrossRef] [PubMed]
- Baykov, A.A. Energy coupling in cation-pumping pyrophosphatase—Back to Mitchell. Front. Plant Sci. 2020, 11, 107. [Google Scholar] [CrossRef]
- Ebel, R.E.; Lardy, H.A. Stimulation of rat liver mitochondrial adenosine triphosphatase by anions. J. Biol. Chem. 1975, 250, 191–196. [Google Scholar] [CrossRef] [PubMed]
- Nath, S.; Villadsen, J. Oxidative phosphorylation revisited. Biotechnol. Bioeng. 2015, 112, 429–437. [Google Scholar] [CrossRef] [PubMed]
- Ko, Y.H.; Hong, S.; Pedersen, P.L. Chemical mechanism of ATP synthase. J. Biol. Chem. 1999, 274, 28853–28856. [Google Scholar] [CrossRef]
- Chen, C.; Saxena, A.K.; Simcoke, W.N.; Garboczi, D.N.; Pedersen, P.L.; Ko, Y.H. Mitochondrial ATP synthase: Crystal structure of the catalytic F1 unit in a vanadate-induced transition-like state and implications for mechanism. J. Biol. Chem. 2006, 281, 13777–13783. [Google Scholar] [CrossRef]
- Sebők-Nagy, K.; Blastyák, A.; Juhász, G.; Páli, T. Reversible binding of divalent cations to Ductin protein assemblies—A putative new regulatory mechanism of membrane traffic processes. Front. Mol. Biosci. 2023, 10, 1195010. [Google Scholar] [CrossRef]
- Mildvan, A.S. Role of magnesium and other divalent cations in ATP-utilizing enzymes. Magnesium 1987, 6, 28–33. [Google Scholar]
- Longuet-Higgins, H.C. The symmetry groups of non-rigid molecules. Mol. Phys. 1963, 6, 445–460. [Google Scholar] [CrossRef]
- Muetterties, E.L. Topological representation of stereoisomerism. I. Polytopal rearrangements. J. Am. Chem. Soc. 1969, 91, 1636–1643. [Google Scholar] [CrossRef]
- Berry, R.S. Correlation of rates of intramolecular tunneling processes, with application to some group V compounds. J. Chem. Phys. 1960, 32, 933–938. [Google Scholar] [CrossRef]
- Webb, M.R.; Grubmeyer, C.; Penefsky, H.S.; Trentham, D.R. The stereochemical course of phosphoric residue transfer catalyzed by beef heart mitochondrial ATPase. J. Biol. Chem. 1980, 255, 11637–11639. [Google Scholar] [CrossRef]
- Senter, P.; Eckstein, F.; Kagawa, Y. Substrate metal-adenosine 5′-triphosphate chelate structure and stereochemical course of reaction catalyzed by the adenosine triphosphatase from the thermophilic bacterium PS3. Biochemistry 1983, 22, 5514–5518. [Google Scholar] [CrossRef]
- Neumann, J.; Schwierz, N. Artificial intelligence resolves kinetic pathways of magnesium binding to RNA. J. Chem. Theory Comput. 2022, 18, 1202–1212. [Google Scholar] [CrossRef] [PubMed]
- Westheimer, F.H. Why nature chose phosphates. Science 1985, 235, 1173–1178. [Google Scholar] [CrossRef]
- Kamerlin, S.C.L.; Sharma, P.K.; Prasad, R.B.; Warshel, A. Why nature really chose phosphate. Q. Rev. Biophys. 2013, 46, 1–132. [Google Scholar] [CrossRef]
- Nath, S. Beyond the chemiosmotic theory: Analysis of key fundamental aspects of energy coupling in oxidative phosphorylation in the light of a torsional mechanism of energy transduction and ATP synthesis—Invited review part 1. J. Bioenerg. Biomembr. 2010, 42, 293–300. [Google Scholar] [CrossRef]
- Nath, S. Beyond the chemiosmotic theory: Analysis of key fundamental aspects of energy coupling in oxidative phosphorylation in the light of a torsional mechanism of energy transduction and ATP synthesis—Invited review part 2. J. Bioenerg. Biomembr. 2010, 42, 301–309. [Google Scholar] [CrossRef]
- Nath, S. The torsional mechanism of energy transduction and ATP synthesis as a breakthrough in our understanding of the mechanistic, kinetic and thermodynamic details. Thermochim. Acta 2004, 422, 5–17. [Google Scholar] [CrossRef]
- Nath, S.; Elangovan, R. New perspectives on photosynthetic phosphorylation in the light of a torsional mechanism of energy transduction and ATP synthesis. J. Bioenerg. Biomembr. 2011, 43, 601–610. [Google Scholar] [CrossRef] [PubMed]
- Nath, S. The need for consistency with physical laws and logic in choosing between competing molecular mechanisms in biological processes: A case study in modeling ATP synthesis. Function 2022, 3, zqac054. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, I.A.; Skulachev, V.P. H+-adenosine triphosphatase and membrane energy coupling. Biochim. Biophys. Acta 1977, 463, 29–89. [Google Scholar] [CrossRef] [PubMed]
- Mislow, K. Role of pseudorotation in the stereochemistry of nucleophilic displacement reactions. Acc. Chem. Res. 1970, 3, 321–331. [Google Scholar] [CrossRef]
- Ugi, I.; Marquarding, D.; Klusacek, H.; Gillespie, P.; Ramirez, F. Berry pseudorotation and turnstile rotation. Acc. Chem. Res. 1971, 4, 288–296. [Google Scholar] [CrossRef]
- Windus, T.L.; Gordon, M.S.; Burggraf, L.W.; Davis, L.P. A new twist on pseudorotation. J. Am. Chem. Soc. 1991, 113, 4356–4357. [Google Scholar] [CrossRef]
- Emsley, J.; Hall, D. The Chemistry of Phosphorus: Environmental, Organic, Inorganic, Biochemical, and Spectroscopic Aspects; Harper & Row: London, UK, 1976. [Google Scholar]
- Knowles, J.R. Enzyme-catalyzed phosphoryl transfer reactions. Annu. Rev. Biochem. 1980, 49, 877–919. [Google Scholar] [CrossRef]
- Elias, A.J. The Chemistry of the p-Block Elements: Syntheses, Reactions and Applications; The Orient Blackswan: Hyderabad, India, 2019. [Google Scholar]
- Walsh, C.T. The Chemical Biology of Phosphorus; Royal Society of Chemistry: Cambridge, UK, 2021. [Google Scholar]
- Smith, A.L.; Hansen, M. Preservation of coupling capacity in submitochondrial particles. Biochem. Biophys. Res. Commun. 1962, 8, 33–37. [Google Scholar] [CrossRef]
- Martin, J.B.; Doty, D.M. Determination of inorganic phosphate. Anal. Chem. 1949, 21, 965–967. [Google Scholar] [CrossRef]
- Penefsky, H.S. Preparation of beef heart mitochondrial ATPase. Methods Enzymol. 1979, 55, 304–308. [Google Scholar]
- Hackney, D.D.; Stempel, K.E.; Boyer, P.D. Oxygen–18 probes of enzymic reactions of phosphate compounds. Methods Enzymol. 1980, 64, 60–83. [Google Scholar]
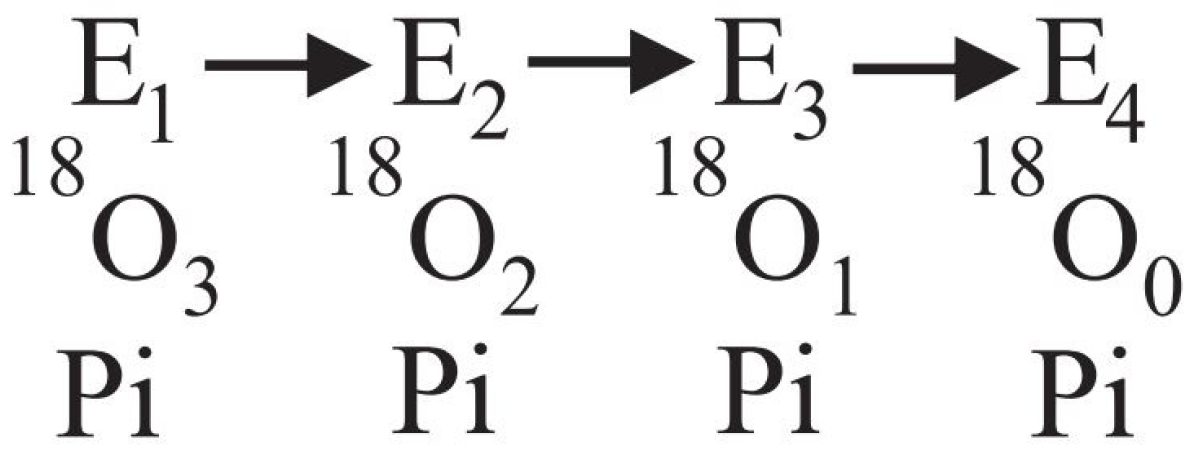
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nath, S. Phosphorus Chemistry at the Roots of Bioenergetics: Ligand Permutation as the Molecular Basis of the Mechanism of ATP Synthesis/Hydrolysis by FOF1-ATP Synthase. Molecules 2023, 28, 7486. https://doi.org/10.3390/molecules28227486
Nath S. Phosphorus Chemistry at the Roots of Bioenergetics: Ligand Permutation as the Molecular Basis of the Mechanism of ATP Synthesis/Hydrolysis by FOF1-ATP Synthase. Molecules. 2023; 28(22):7486. https://doi.org/10.3390/molecules28227486
Chicago/Turabian StyleNath, Sunil. 2023. "Phosphorus Chemistry at the Roots of Bioenergetics: Ligand Permutation as the Molecular Basis of the Mechanism of ATP Synthesis/Hydrolysis by FOF1-ATP Synthase" Molecules 28, no. 22: 7486. https://doi.org/10.3390/molecules28227486
APA StyleNath, S. (2023). Phosphorus Chemistry at the Roots of Bioenergetics: Ligand Permutation as the Molecular Basis of the Mechanism of ATP Synthesis/Hydrolysis by FOF1-ATP Synthase. Molecules, 28(22), 7486. https://doi.org/10.3390/molecules28227486





