Impact of Nd Doping on Electronic, Optical, and Magnetic Properties of ZnO: A GGA + U Study
Abstract
:1. Introduction
2. Results and Discussion
2.1. Analysis of System Structure and Stability
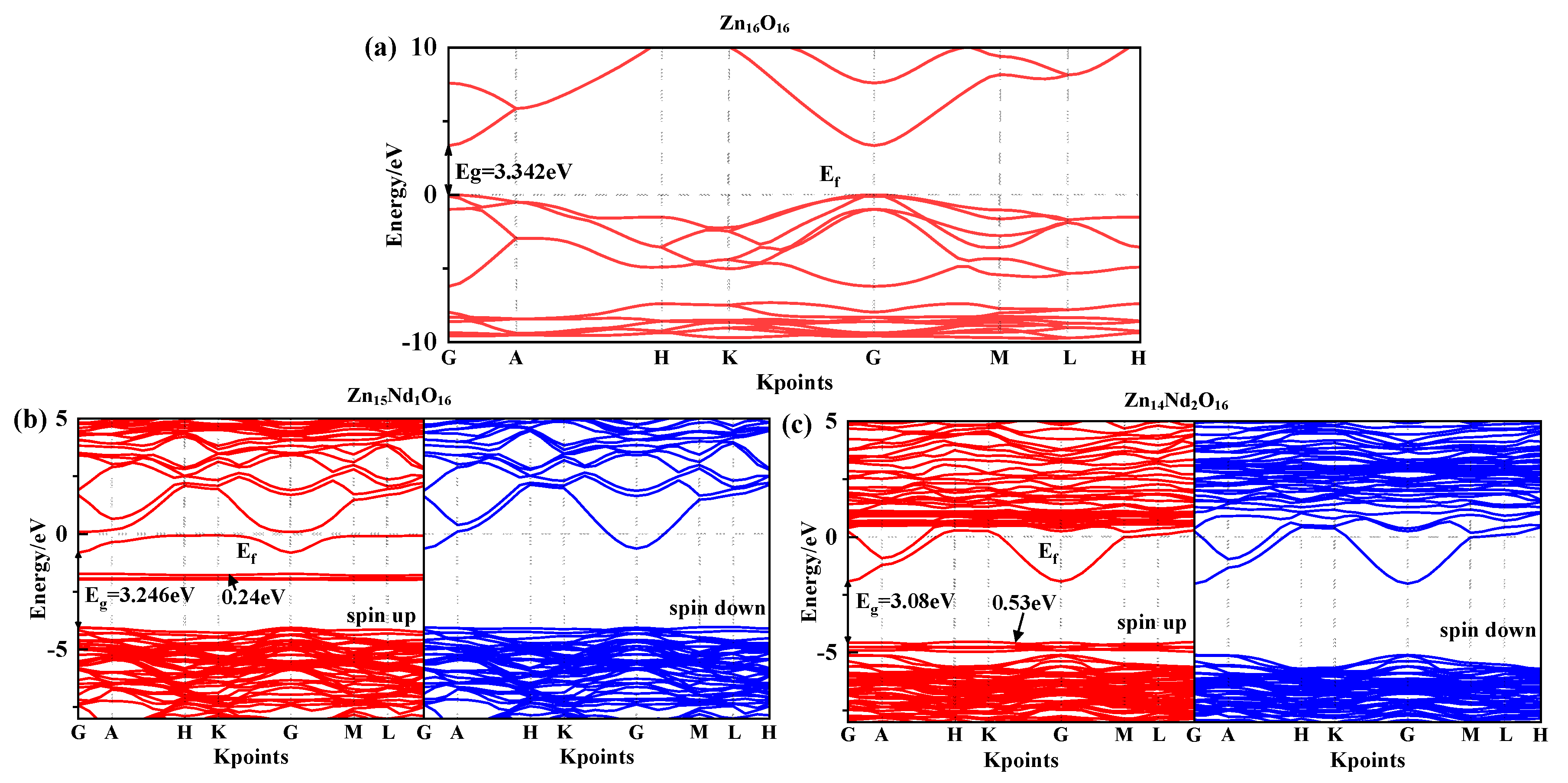
2.2. Analysis of Energy Band Structure
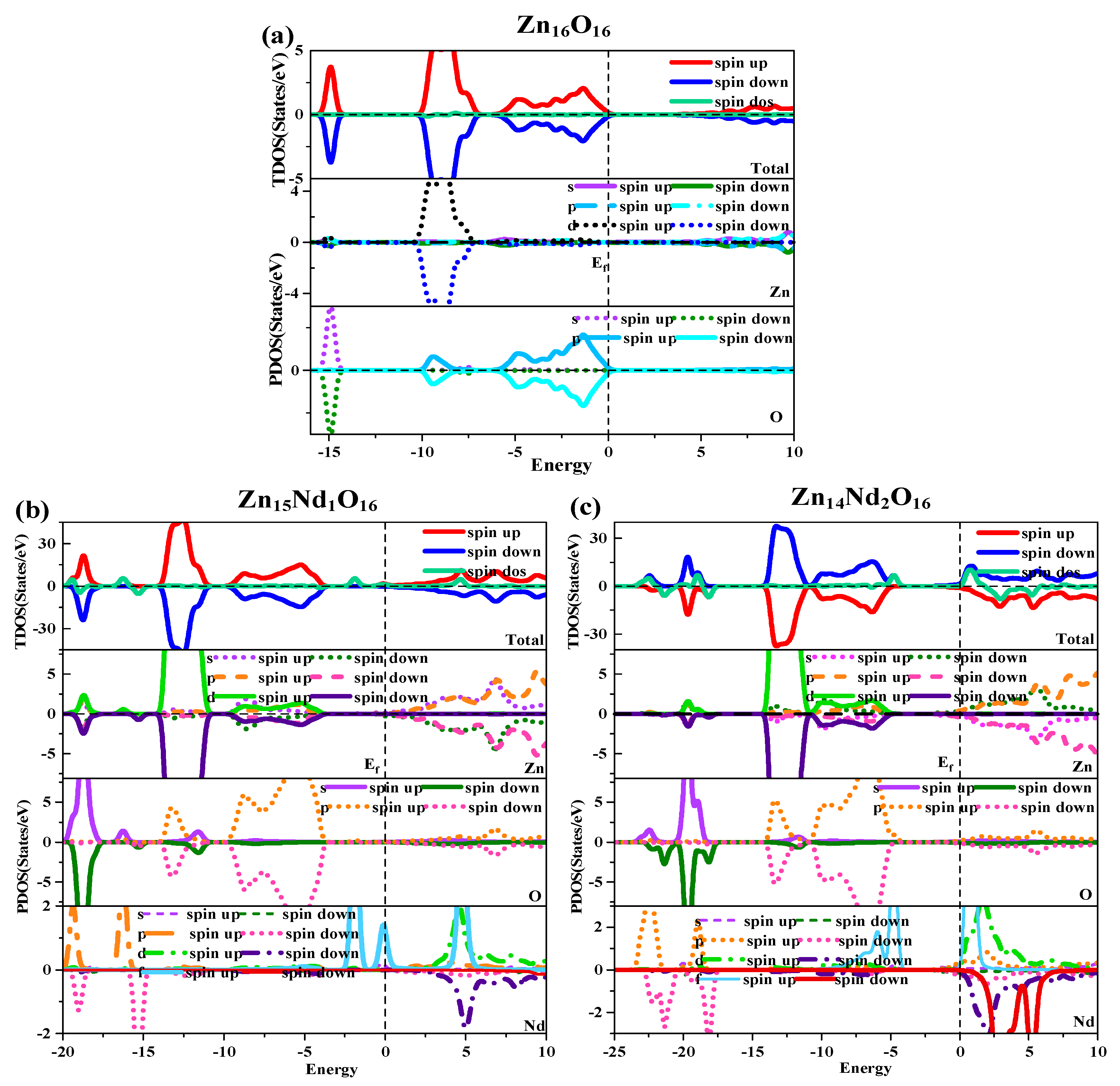
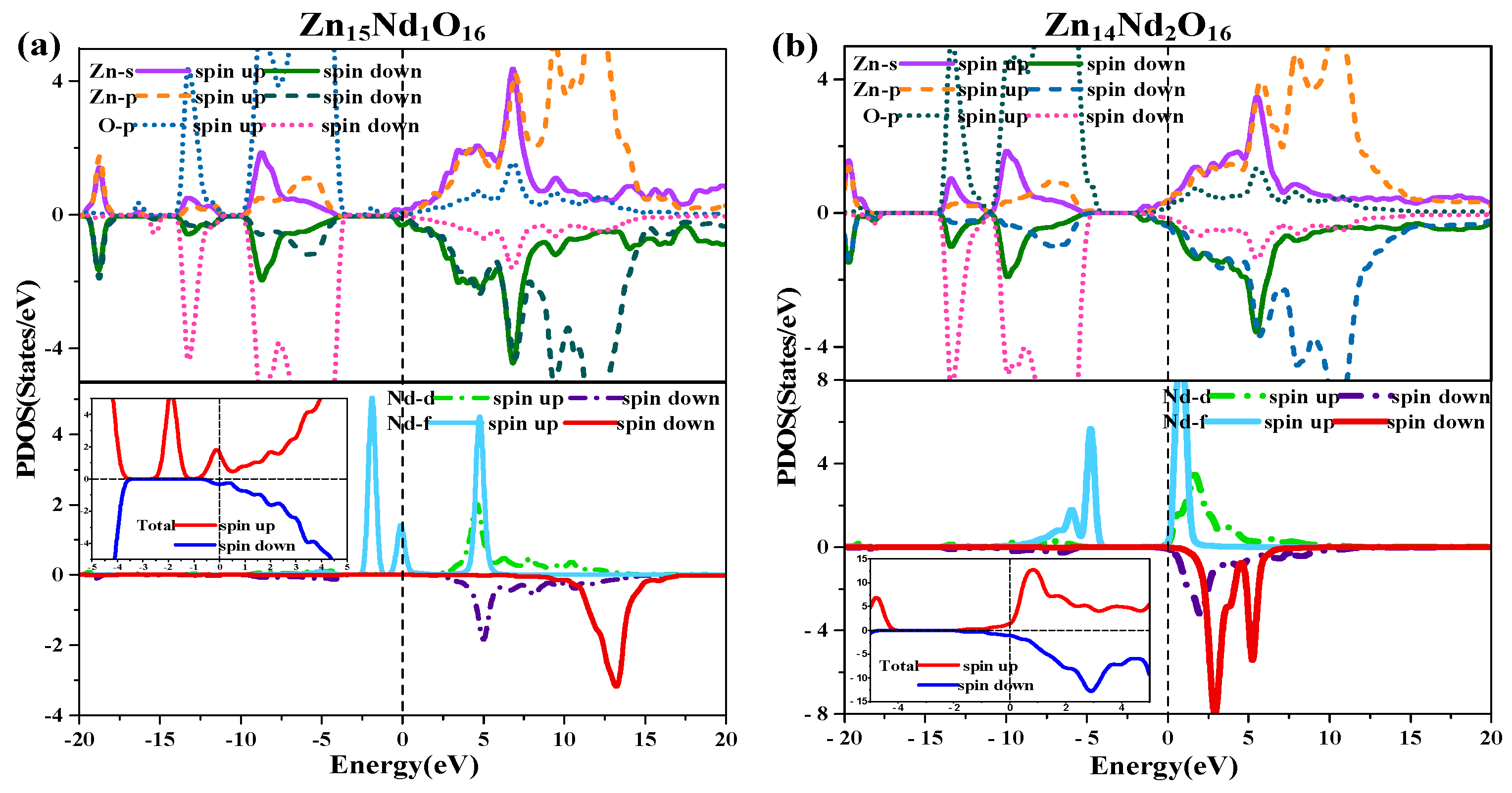
2.3. Analysis of Density of States
2.4. Analysis of Orbital Charges
2.5. Analysis of Population Value and Bond Length
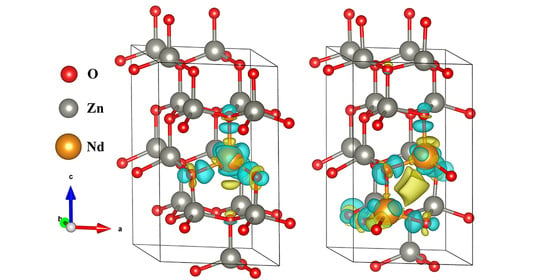
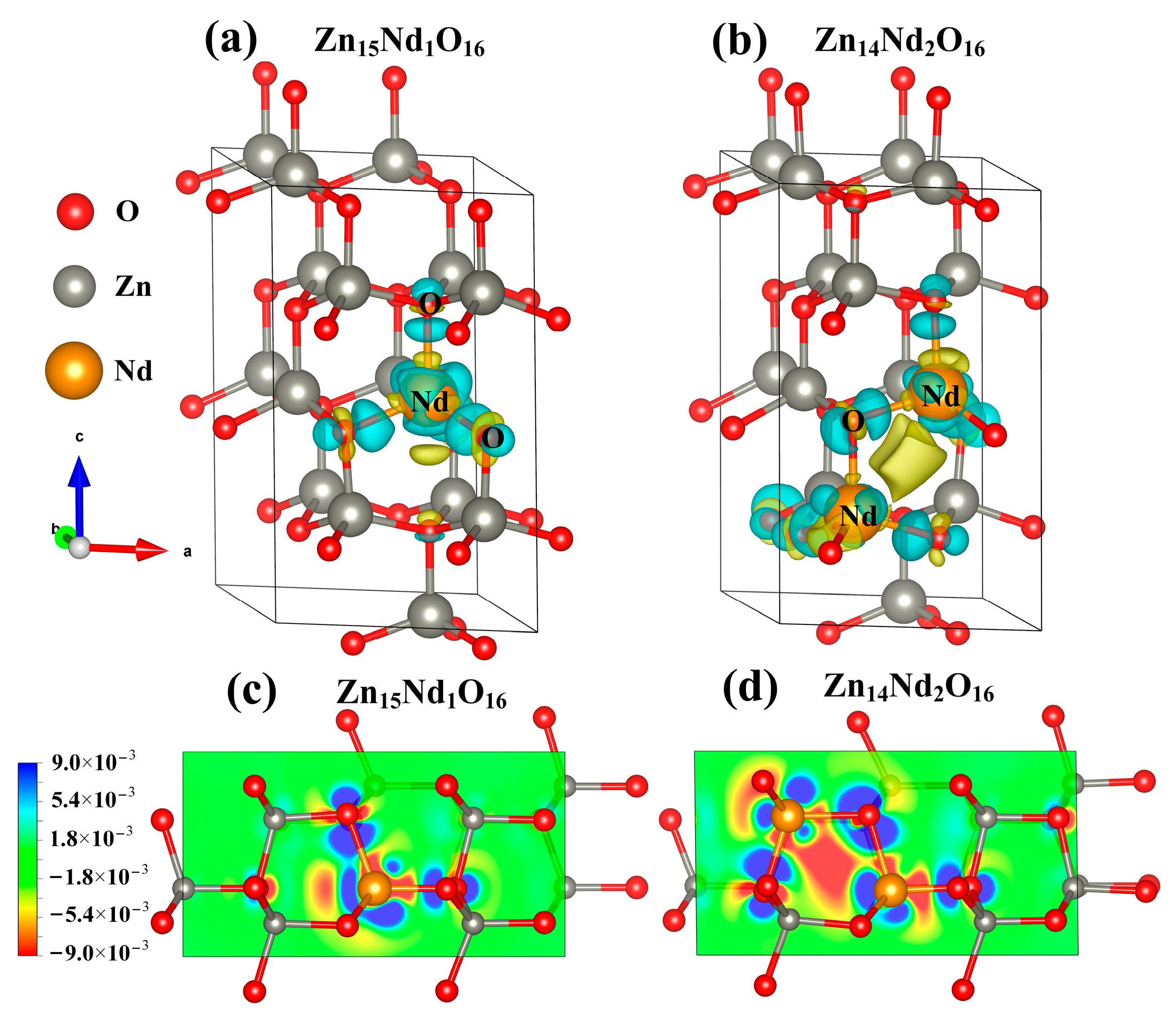
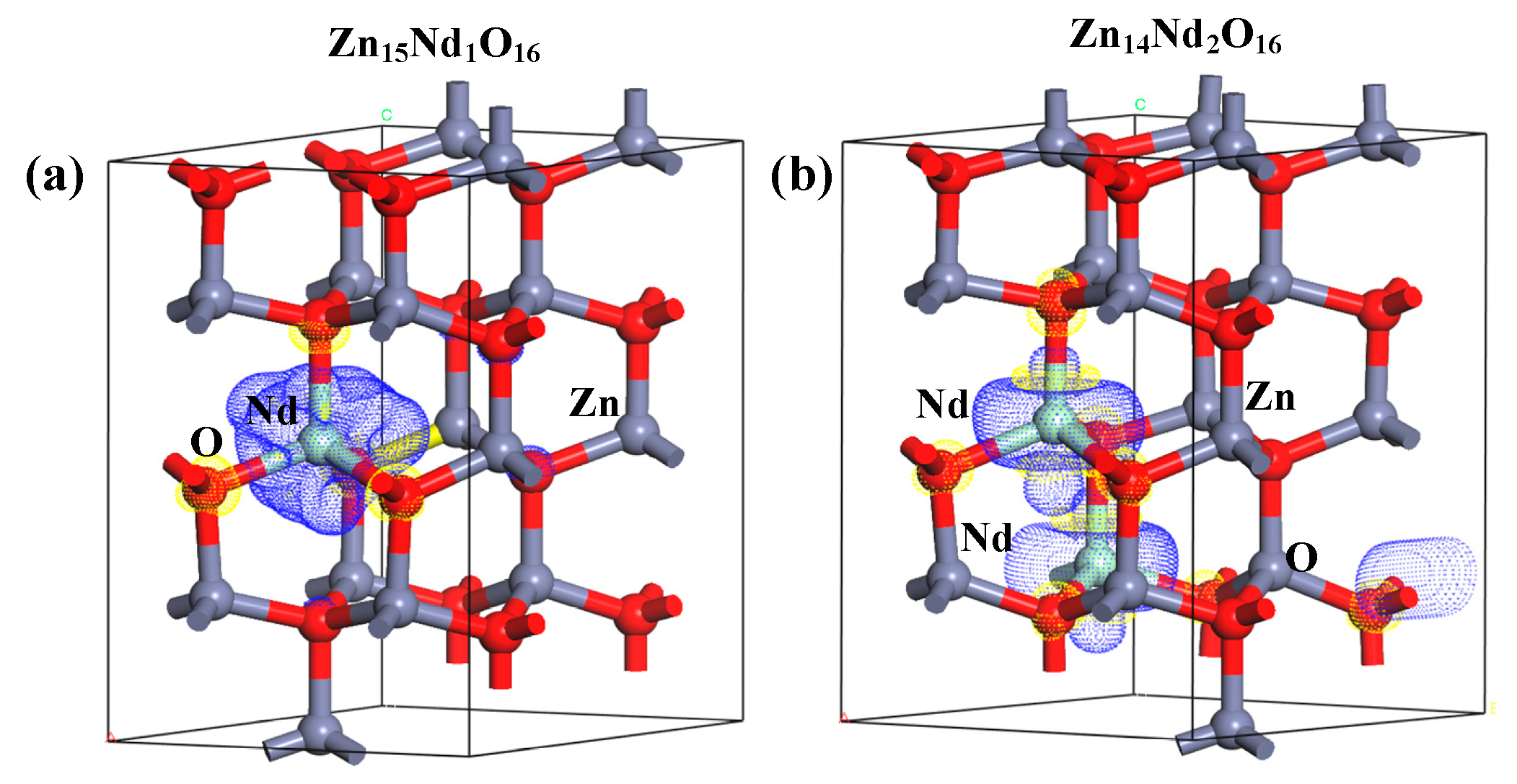
2.6. Analysis of Differential Charge Density
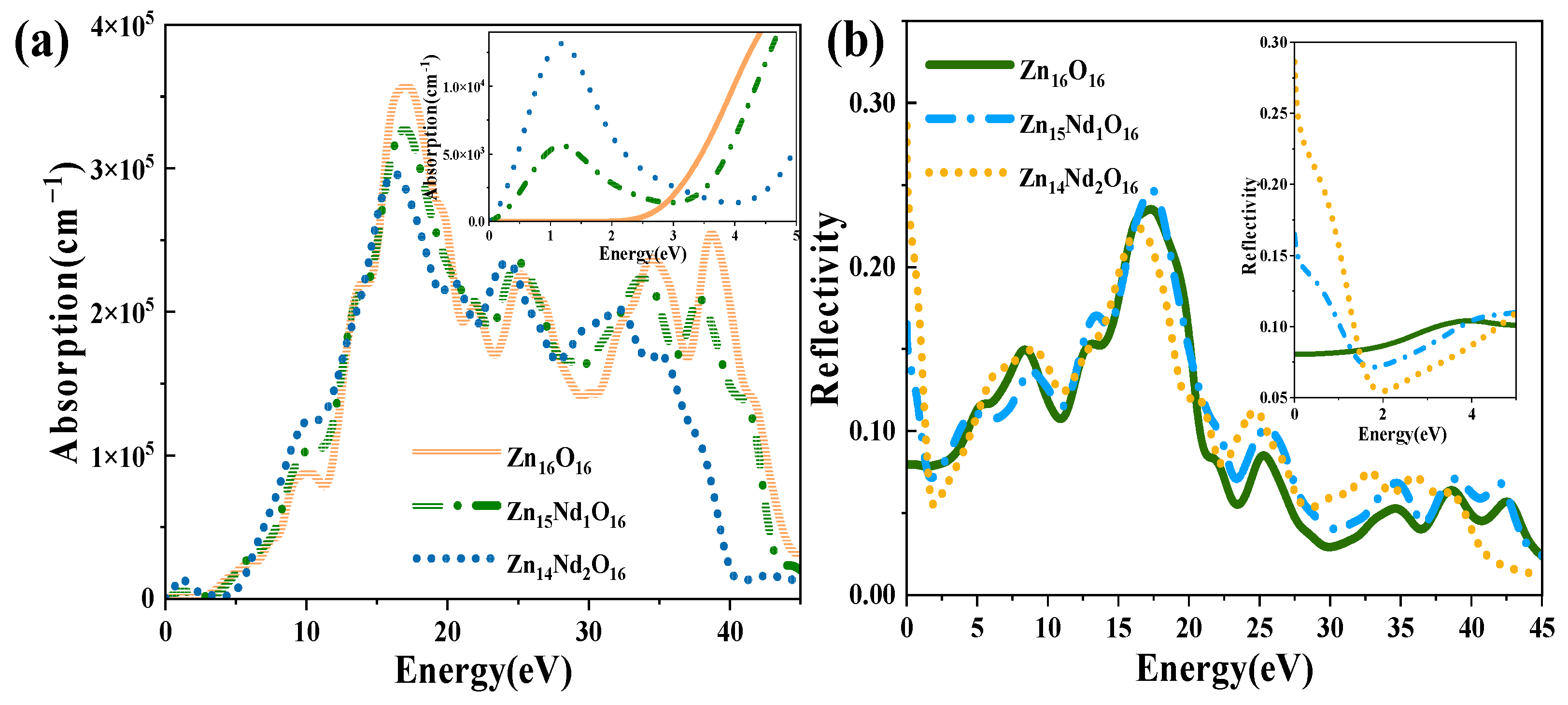
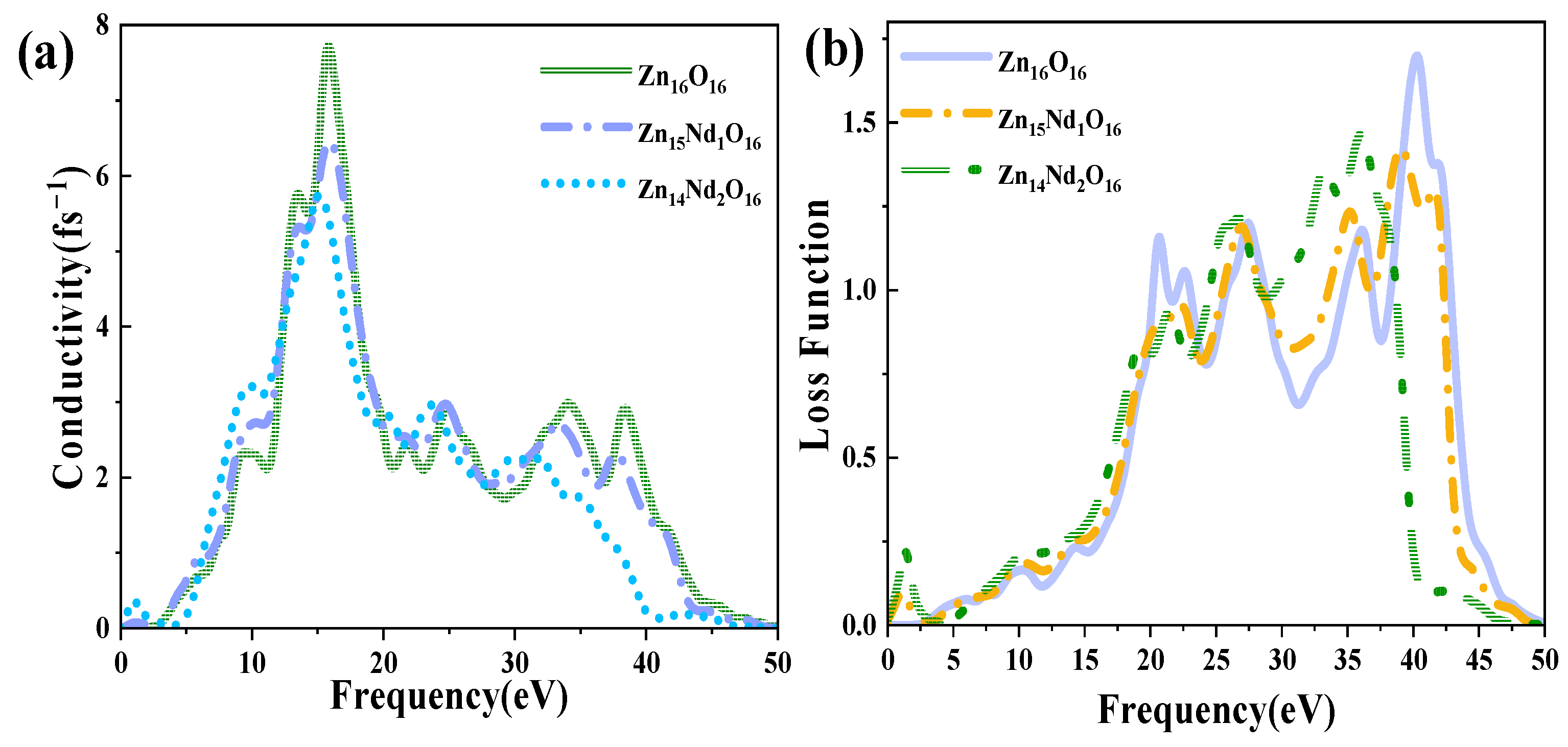
2.7. Optical Properties
2.8. Magnetic Properties
3. Computational Methodology and Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, C.; Yun, F.; Morkoc, H. Ferromagnetism of ZnO and GaN: A Review. Sci. Mater. Electron. 2005, 16, 555. [Google Scholar] [CrossRef]
- Zutic, I.; Fabian, J.; Sarma, S.D. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323. [Google Scholar] [CrossRef]
- Dietl, T.; Ohno, O.H.; Matsukura, A.F.; Cibert, J.; Ferrand, E.D. Zener model description of ferromagnetism in zinc–blende magnetic semiconductors. Science 2000, 287, 1019. [Google Scholar] [CrossRef]
- Larabi, A.; Mebarki, M.; Sari, A.; Merad, G. Chromium and hydrogen doping effects on magnetic and electronic properties of ZnO. J. Magn. Magn. Mater. 2018, 446, 192. [Google Scholar] [CrossRef]
- Foster, G.M.; Faber, G.; Yao, Y.-F.; Yang, C.C.; Heller, E.R.; Look, D.C.; Brillson, L.J. Direct measurement of defect and dopant abruptness at high electron mobility ZnO homojunctions. Appl. Phys. Lett. 2016, 109, 143506. [Google Scholar] [CrossRef]
- Saadi, H.; Benzarti, Z.; Sanguino, P.; Pina, J.; Abdelmoula, N.; de Melo, J.S.S. Enhancing the electrical conductivity and the dielectric features of ZnO nanoparticles through Co doping effect for energy storage applications. J. Mater. Sci. Mater. Electron. 2023, 34, 116. [Google Scholar] [CrossRef]
- Ozgür, Ü.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M.A.; Doğan, S.; Avrutin, V.; Cho, S.-J.; Morkoç, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 041301. [Google Scholar] [CrossRef]
- Zhang, X.J.; Mi, W.B.; Wang, X.C.; Bai, H.L. First–principles prediction of electronic structure and magnetic ordering of rare–earth metals doped ZnO. J. Alloys Compd. 2014, 617, 828. [Google Scholar] [CrossRef]
- Kayani, Z.N.; Sahar, M.; Riaz, S.; Naseem, S.; Saddiqe, Z. Enhanced magnetic, antibacterial and optical properties of Sm doped ZnO thin films: Role of Sm doping. Opt. Mater. 2020, 108, 110457. [Google Scholar] [CrossRef]
- Wang, Y.; Piao, J.; Lu, Y.; Li, S.; Yi, J. Intrinsic ferromagnetism in Sm doped ZnO. Mater. Res. Bull. 2016, 83, 408. [Google Scholar] [CrossRef]
- Xu, X.Y.; Wang, L.M.; Fu, J.J.; Xu, Y.Y.; Shao, J.W. Preparation and doping of flower–like nano ZnO and its photocatalytic degradation of reactive dye. China Dye. Finish. 2021, 47, 47. [Google Scholar]
- Sharma, D.K.; Sharma, K.K.; Kumar, V.; Sharma, A. Effect of Ce doping on the structural, optical and magnetic properties of ZnO nanoparticles. J. Mater. Sci. Mater. Electron. 2016, 27, 10330. [Google Scholar] [CrossRef]
- Wen, J.Q.; Zhang, J.M.; Qiu, Z.G.; Yang, X.; Li, Z.Q. The investigation of Ce doped ZnO crystal: The electronic, optical and magnetic properties. Phys. B Condens. Matter. 2018, 534, 44. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, Q.; Sha, S.; Xu, Z. Electronic structure, optical and ferromagnetic properties of ZnO co–doped with Ag and Co according to First–principles calculations. Vacuum 2020, 173, 109127. [Google Scholar] [CrossRef]
- Khuili, M.; Fazouan, N.; Abou El Makarim, H.; Atmani, E.H.; Rai, D.P.; Houmad, M. First–principles calculations of rare earth (RE=Tm, Yb, Ce) doped ZnO: Structural, optoelectronic, magnetic, and electrical properties. Vacuum 2020, 181, 109603. [Google Scholar] [CrossRef]
- Yuonesi, M.; Pakdel, A. Effect of low concentration of nickel on structural and optical properties of ZnO nanofilms. Phys. B Condens. Matter. 2010, 405, 2083. [Google Scholar] [CrossRef]
- Wagner, M.R.; Callsen, G.; Reparaz, J.S.; Kirste, R.; Hoffmann, A.; Rodina, A.V.; Schleife, A.; Phillips, M.R. Effects of strain on the valence band structure and exciton-polariton energies in ZnO. Phys. Rev. B 2013, 88, 235210. [Google Scholar] [CrossRef]
- Pham, A.; Assadi, M.H.N.; Yu, A.B.; Li, S. Critical role of Fock exchange in characterizing dopant geometry and magnetic interaction in magnetic semiconductors. Phys. Rev. B 2014, 89, 155110. [Google Scholar] [CrossRef]
- Chauhan, S.; Kumar, M.; Chhoker, S.; Katyal, S.C.; Awana, V.P.S. Structural, vibrational, optical and magnetic properties of sol–gel derived Nd doped ZnO nanoparticles. J. Mater. Sci. Mater. Electron. 2013, 24, 5102. [Google Scholar] [CrossRef]
- Moeller, T. The Chemistry of the Lanthanides; Pergamon Press: Oxford, UK, 1973. [Google Scholar]
- Greenwood, N.N.; Earnshaw, A. Chemistry of the Elements; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Reeber, R.R. Lattice parameters of ZnO from 4.2 to 296 K. J. Appl. Phys. 1970, 41, 5063. [Google Scholar] [CrossRef]
- Ma, X.; Miao, L.; Bie, S.; Jiang, J. Synergistic effect of V/N–codoped anatase TiO2 photocatalysts. Solid State Commun 2010, 150, 689. [Google Scholar] [CrossRef]
- Long, R.; English, N.J. First–principles calculation of nitrogen–tungsten codoping effects on the band structure of anatase–titania. Appl. Phys. Lett. 2009, 94, 132102. [Google Scholar] [CrossRef]
- Srikant, V.; Clarke, D.R. On the optical band gap of zinc oxide band gap of zinc oxide. J. Appl. Phys. 1998, 83, 5447. [Google Scholar] [CrossRef]
- Hou, Q.Y.; Guo, S.Q.; Zhao, C.W. First–principle study of the effects of oxygen vacancy on the electronic structure and the absorption spectrum of ZnO. Acta Phys. Sin. 2014, 63, 1. [Google Scholar]
- Shahmoradi, B.; Soga, K.; Ananda, S.; Somashekar, R.; Byrappa, K. Modification of neodymium–doped ZnO hybrid nanoparticles under mild hydrothermal conditions. Nanoscale 2010, 2, 1160. [Google Scholar] [CrossRef]
- Divya, N.K.; Pradyumnan, P.P. Enhancement of photocatalytic activity in Nd doped ZnO with an increase in dielectric constant. J. Mater. Sci. Mater. Electron. 2016, 28, 2147. [Google Scholar] [CrossRef]
- Wu, H.C.; Chen, H.H.; Zhu, R. Effects of Al–impurity type on formation energy, crystal structure, electronic structure, and optical properties of ZnO by using density functional theory and the hubbard–U method. Materials 2016, 9, 647. [Google Scholar] [CrossRef]
- Sun, C.Q. Oxidation electronics: Bond–band–barrier correlation and its applications. Prog. Mater. Sci. 2003, 48, 521. [Google Scholar] [CrossRef]
- Segall, M.D.; Pickard, C.J.; Shah, R.; Payne, M.C. Population analysis in plane wave electronic structure calculations. Mol. Phys. 1996, 2, 571. [Google Scholar] [CrossRef]
- Huang, K. Solid Physics; Higher Education Press: Beijing, China, 2002. (In Chinese) [Google Scholar]
- Fang, R.C. Solid State Spectroscopy; University of Science and Technology of China Press: Hefei, China, 2001. (In Chinese) [Google Scholar]
- Shen, X.C. Spectra and Optical Properties of Semiconductors Second Edition; Science Press: Beijing, China, 2002. (In Chinese) [Google Scholar]
- Shen, X.C. Semiconductor Spectroscopy and Optical Properties; Science Press: Beijing, China, 2002; pp. 140–141. [Google Scholar]
- Dhar, S.; Brandt, O.; Ramsteiner, M.; Sapega, V.F.; Ploog, K.H. Colossal magnetic moment of Gd in GaN. Phys. Rev. Lett. 2005, 94, 037205. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Kittel, C. Indirect exchange coupling of nuclear magnetic moments by conduction electrons. Phys. Rev. 1954, 96, 99. [Google Scholar] [CrossRef]
- Kasuya, T. A theory of metallic ferro–and antiferromagnetism on Zener’s model. Prog. Theor. Phys. 1956, 16, 45. [Google Scholar] [CrossRef]
- Miyazaki, M.; Sato, K.; Mitsui, A.; Nishimura, H. Properties of Ga–doped ZnO films. J. Non–Cryst. Solids 1997, 218, 323. [Google Scholar] [CrossRef]
- Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 1959, 10, 87. [Google Scholar] [CrossRef]
- Goodenough, J.B. An interpretation of the magnetic properties of the erovskite–type mixed crystals La1−xSrxCoO3−λ. J. Phys. Chem. Solids 1958, 6, 287. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Q.; Douglas, J.F.; Lin, H.; Sahrakorpi, S.; Barbiellini, B.; Markiewicz, R.S.; Bansil, A.; Fedorov, A.V.; Dessau, D.S.; et al. Minority–spin t2g states and the degree of spin polarization in ferromagnetic metallic La2–2xSr1 + 2xMn2O7 (x = 0.38). Sci. Rep. 2013, 3, 3167. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First–principles simulation: Ideas, illustrations and the CASTEP code. Phys. Condens. Matter. 2002, 14, 2717. [Google Scholar] [CrossRef]
- Hamann, D.R.; Schlüter, M.; Chiang, C. Norm–Conserving Pseudopotentials. Phys. Rev. Lett. 1979, 43, 1494. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA + U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]


| Model | a/Å | c/Å | c/a |
|---|---|---|---|
| This work | 3.269 | 5.272 | 1.613 |
| Experimental [22] | 3.248 | 5.220 | 1.607 |
| DFT [8] | 3.20 | 5.15 | 1.609 |
| Model | a/Å | c/Å | c/a | α | β | γ | V/Å3 | Ef/eV |
|---|---|---|---|---|---|---|---|---|
| Zn15Nd1O16 | 6.544 | 10.556 | 1.613 | 90.00° | 90.00° | 120.00° | 391.442 | −1.83 |
| Zn14Nd2O16 a1 | 6.625 | 10.668 | 1.610 | 90.00° | 90.00° | 120.00° | 405.471 | −3.63 |
| Zn14Nd2O16 a2 | 6.670 | 10.643 | 1.596 | 89.36° | 90.00° | 120.38° | 403.919 | −3.60 |
| Zn14Nd2O16 a3 | 6.594 | 10.645 | 1.614 | 90.66° | 89.34° | 119.21° | 403.918 | −3.60 |
| Zn14Nd2O16 a4 | 6.612 | 10.674 | 1.614 | 90.00° | 89.43° | 120.09° | 404.854 | −3.59 |
| Model | Atom | S | p | d | f | Total/eV | Net Charge/e |
|---|---|---|---|---|---|---|---|
| Zn16O16 | Zn (SU) | 0.20 | 0.34 | 4.99 | 0.00 | 5.54 | 0.93 |
| Zn (SD) | 0.20 | 0.34 | 4.99 | 0.00 | 5.54 | - | |
| O (SU) | 0.92 | 2.55 | 0.00 | 0.00 | 3.46 | −0.93 | |
| O (SD) | 0.92 | 2.55 | 0.00 | 0.00 | 3.46 | - | |
| Zn15Nd1O16 | Zn (SU) | 0.20 | 0.38 | 4.99 | 0.00 | 5.57 | 0.88 |
| Zn (SD) | 0.20 | 0.37 | 4.99 | 0.00 | 5.55 | - | |
| O (SU) | 0.90 | 2.54 | 0.00 | 0.00 | 3.44 | −0.91 | |
| O (SD) | 0.91 | 2.56 | 0.00 | 0.00 | 3.46 | - | |
| Nd (SU) | 1.21 | 2.90 | 0.56 | 3.70 | 8.37 | 1.05 | |
| Nd (SD) | 1.14 | 2.90 | 0.50 | 0.03 | 4.58 | - | |
| Zn14Nd2O16 | Zn (SU) | 0.19 | 0.35 | 4.99 | 0.00 | 5.53 | 0.92 |
| Zn (SD) | 0.20 | 0.35 | 4.99 | 0.00 | 5.54 | - | |
| O (SU) | 0.91 | 2.51 | 0.00 | 0.00 | 3.42 | −0.88 | |
| O (SD) | 0.91 | 2.54 | 0.00 | 0.00 | 3.46 | - | |
| Nd1 (SU) | 1.29 | 3.02 | 0.71 | 3.01 | 8.03 | 1.01 | |
| Nd1 (SD) | 1.26 | 3.01 | 0.64 | 0.05 | 4.97 | - | |
| Nd2 (SU) | 1.31 | 3.05 | 0.72 | 3.01 | 8.10 | 0.87 | |
| Nd2 (SD) | 1.29 | 3.04 | 0.64 | 0.05 | 5.03 | - |
| Model | Bond | Population Value | Bond Length/Å |
|---|---|---|---|
| Zn16O16 | Zn-Omax | 1.08 | 1.966 |
| Zn-Omin | 0.12 | 1.975 | |
| Zn15Nd1O16 | Zn-Omax | 0.35 | 1.985 |
| Zn-Omin | 0.40 | 1.967 | |
| Nd-O(//c) | 0.22 | 2.238 | |
| Nd-O(⊥c) | 0.34 | 2.191 | |
| Zn14Nd2O16 | Zn-Omax | 0.33 | 1.982 |
| Zn-Omin | 0.41 | 1.985 | |
| Nd1-O(//c) | 0.27 | 2.260 | |
| Nd1-O(⊥c) | 0.43 | 2.195 | |
| Nd2-O(//c) | 0.35 | 2.230 | |
| Nd2-O(⊥c) | 0.46 | 2.223 |
| Model | Coupling Mode | Total Magnetic Moment (µB) | ||
|---|---|---|---|---|
| Zn15Nd1O16 | 3.75 | 3.92 | FM | 3.75 |
| Zn14Nd2O16 | 5.97 | 6.29 | FM | 5.97 |
| Model | Atoms | Magnetic Moment (µB) | Orbital Magnetic Moment (µB) | |||
|---|---|---|---|---|---|---|
| s | p | d | f | |||
| Zn15Nd1O16 | O2 | −0.03 | −0.01 | −0.02 | ||
| O4 | −0.03 | −0.01 | −0.02 | |||
| O8 | −0.03 | −0.01 | −0.02 | |||
| O11 | −0.01 | 0.00 | −0.01 | |||
| Zn6 | −0.02 | –0.02 | 0.00 | 0.00 | ||
| Zn9 | 0.01 | 0.00 | 0.01 | 0.00 | ||
| Zn12 | 0.01 | 0.00 | 0.01 | 0.00 | ||
| Zn13 | −0.01 | −0.01 | 0.00 | 0.00 | ||
| Zn14 | 0.01 | 0.00 | 0.01 | 0.00 | ||
| Nd | 3.79 | 0.07 | 0.00 | 0.06 | 3.67 | |
| Zn14Nd2O16 | O1 | −0.02 | 0.00 | −0.02 | ||
| O2 | −0.03 | 0.00 | −0.03 | |||
| O3 | −0.02 | −0.01 | −0.01 | |||
| O4 | −0.02 | −0.01 | −0.01 | |||
| O5 | −0.02 | 0.00 | −0.02 | |||
| O8 | −0.02 | −0.01 | −0.01 | |||
| O11 | −0.02 | 0.00 | −0.02 | |||
| Zn9 | −0.01 | −0.01 | 0.00 | 0.00 | ||
| Nd1 | 3.06 | 0.03 | 0.01 | 0.07 | 2.96 | |
| Nd2 | 3.08 | 0.02 | 0.01 | 0.08 | 2.96 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Liu, G.; Shi, H.; Zhang, B.; Ning, J.; Shao, T.; Xue, S.; Zhang, F. Impact of Nd Doping on Electronic, Optical, and Magnetic Properties of ZnO: A GGA + U Study. Molecules 2023, 28, 7416. https://doi.org/10.3390/molecules28217416
Wu Q, Liu G, Shi H, Zhang B, Ning J, Shao T, Xue S, Zhang F. Impact of Nd Doping on Electronic, Optical, and Magnetic Properties of ZnO: A GGA + U Study. Molecules. 2023; 28(21):7416. https://doi.org/10.3390/molecules28217416
Chicago/Turabian StyleWu, Qiao, Gaihui Liu, Huihui Shi, Bohang Zhang, Jing Ning, Tingting Shao, Suqin Xue, and Fuchun Zhang. 2023. "Impact of Nd Doping on Electronic, Optical, and Magnetic Properties of ZnO: A GGA + U Study" Molecules 28, no. 21: 7416. https://doi.org/10.3390/molecules28217416
APA StyleWu, Q., Liu, G., Shi, H., Zhang, B., Ning, J., Shao, T., Xue, S., & Zhang, F. (2023). Impact of Nd Doping on Electronic, Optical, and Magnetic Properties of ZnO: A GGA + U Study. Molecules, 28(21), 7416. https://doi.org/10.3390/molecules28217416