Exploring the Relationship between the Structural Characteristics and Mechanical Behavior of Multicomponent Fe-Containing Phases: Experimental Studies and First-Principles Calculations
Abstract
:1. Introduction
2. Experimental Method and Calculation Details
2.1. Experimental Method
2.2. Calculation Details
2.2.1. Thermodynamic Properties
2.2.2. Mechanical Modulus
2.2.3. Stacking Fault Energy
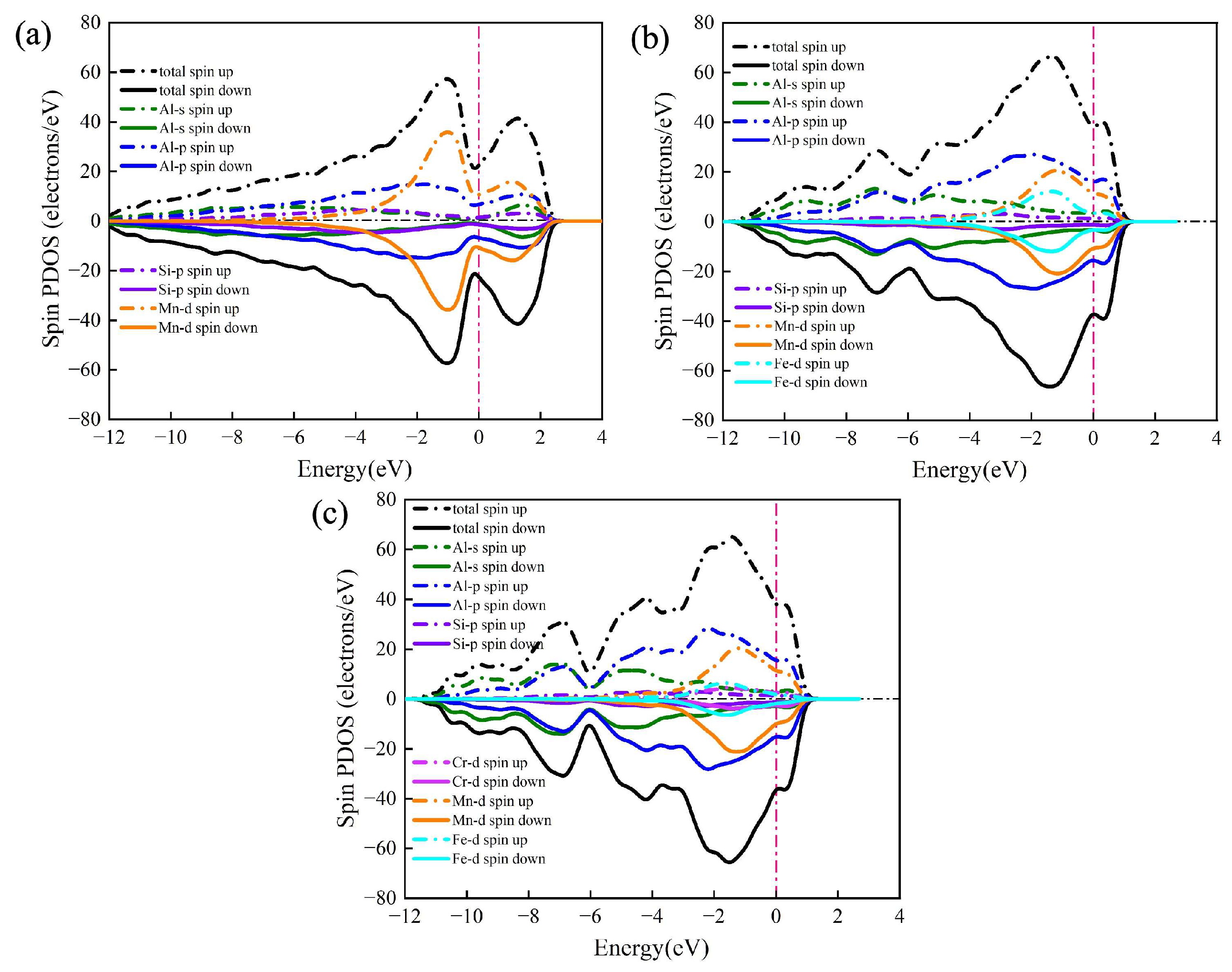
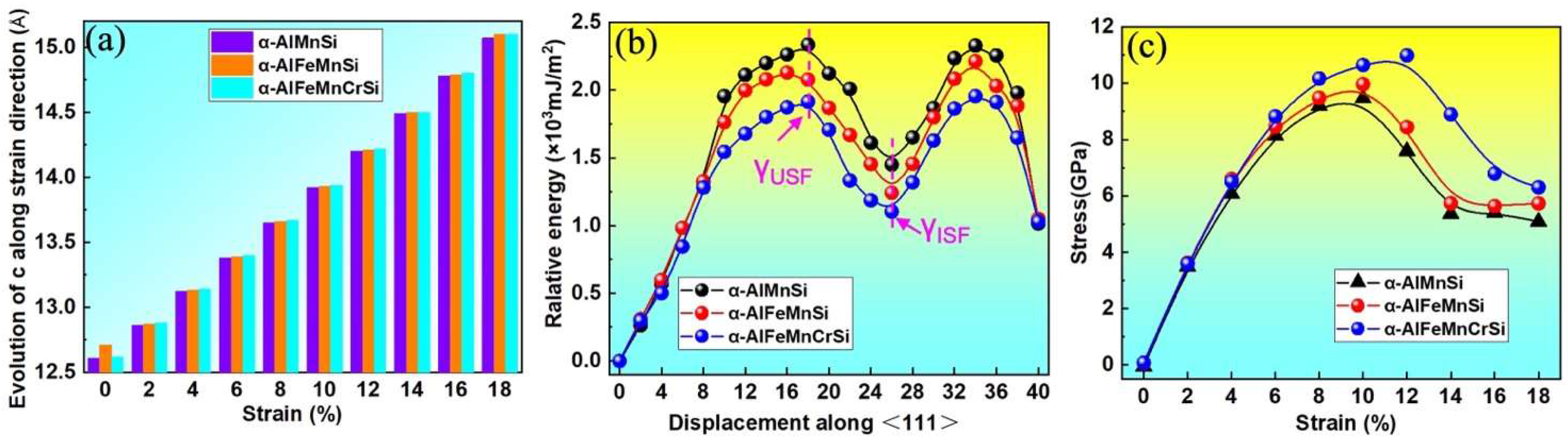
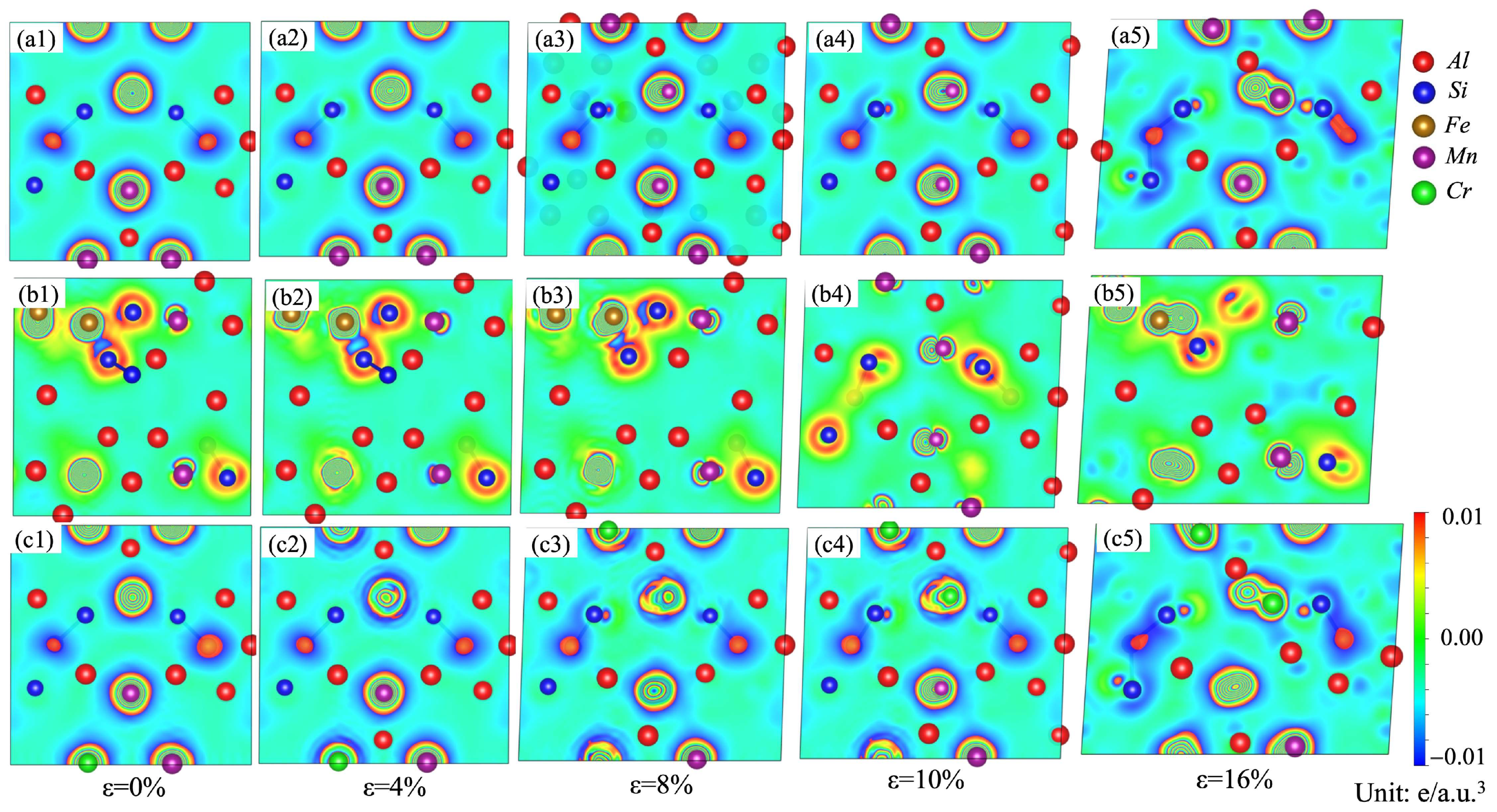
3. Results and Discussion
3.1. Characteristics of Fe-Containing Phases by Experimental Studies
3.2. Crystal Structure Models of DFT Calculations
3.3. Thermodynamic Properties and Mechanical Modulus
3.4. Stacking Fault Energy and Tensile Properties
4. Conclusions
- (1)
- The substitution of Mn atoms by Fe and Cr in α-AlMnSi are confirmed by structural determination, composition analysis and formation enthalpy calculation; Fe and Cr prefer to occupy Mn-12j sites in the α-AlMnSi phase to form the α-AlFeMnCrSi phase.
- (2)
- The energetically favored structures of α-AlFeMnSi and α-AlFeMnCrSi show an improved stability, mechanical modulus and hardness, both in calculation and experimental results, which is attributed to the stronger bonding strength of Si-Fe and Si-Cr. The stronger chemical bonds of Si-Fe and Si-Cr lead to a decrease in the thermal expansion coefficient and an increment in the stacking fault energy and ideal strength.
- (3)
- The mechanical modulus and hardness of the α-AlMnSi, α-AlFeMnSi and α-AlFeMnCrSi phases decrease with increasing temperature, which is validated by nanoindentation. The thermal expansion coefficient exhibits the opposite trend.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rømming, C.; Hasen, V.; Gjønnes, J. Crystal Structure of β-Al4.5FeSi. Acta Crystallogr. B 1994, 50, 307–312. [Google Scholar] [CrossRef]
- Taghaddos, E.; Hejazi, M.M. Effect of iron-intermetallics on the fluidity of 413 aluminum alloy. J. Alloys Compd. 2009, 468, 539–545. [Google Scholar] [CrossRef]
- Dietrich, B.G.; Becker, H.; Smolka, M. Intermetallic sludge formation in Fe containing secondary Al-Si alloys influenced by Cr and Mn as preparative tool for metal melt filtration. Adv. Eng. Mater. 2017, 19, 201700161. [Google Scholar] [CrossRef]
- Song, D.F.; Wang, S.C.; Zhao, Y.L. Effect of melt holding on morphological evolution and sedimentation behavior of iron-rich intermetallic phases in Al-Si-Fe-Mn-Mg alloy. Trans. Nonferrous Met. Soc. China 2020, 30, 1–13. [Google Scholar] [CrossRef]
- Shabestari, S.G.; Gruzleski, J.E. Gravity segregation of complex intermetallic compounds in liquid aluminum-silicon alloy. Metall. Mater. Trans. A 1995, 26, 999–1006. [Google Scholar] [CrossRef]
- Becker, H.; Thum, A.B.; Kriegel, D.M.; Leineweber, A. Effect of melt conditioning on removal of Fe from secondary Al-Si alloys containing Mg, Mn, and Cr. Metall. Mater. Trans. A 2018, 49, 6375–6389. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Wang, D.T.; Li, X.Z.; Zhang, H.T.; Nagaumi, H. Exploring crystal structures, stability and mechanical properties of Fe, Mn-containing intermetallics in Al-Si Alloy by experiments and first-principles calculations. J. Alloys Compd. 2021, 876, 160022. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Wang, D.T.; Nagaumi, H.; Zhou, Y.X.; Yu, W.; Chong, X.Y.; Li, X.Z.; Zhang, H.T. Morphology, thermal stability, electron structure and mechanical properties of α-AlFeMnSi phases with varying Mn/Fe atomic ratios: Experimental studies and DFT calculations. J. Alloys Compd. 2022, 901, 163523. [Google Scholar] [CrossRef]
- Li, T.X.; Da, S.; Ming, X.Z.; Sun, B.D.; Zhou, Y.H. Physical simulation and theoretical analysis of migrating rate of inclusions in aluminum melt in electromagnetic field. Trans. Nonferrous Met. Soc. China 2001, 1, 30–34. [Google Scholar] [CrossRef]
- Kim, H.Y.; Park, T.Y. Effects of Mn on the crystal structure of α-Al(Mn,Fe)Si particles in A356 alloys. J. Cryst. Growth 2006, 291, 207–211. [Google Scholar] [CrossRef]
- Tibballs, J.E.; Horst, J.A.; Simensen, C.J. Precipitation of α-Al(Fe,Mn)Si from the melt. J. Mater. Sci. 2001, 36, 937–941. [Google Scholar] [CrossRef]
- Ferraro, S.; Fabrizi, A.; Timelli, G. Evolution of sludge particles in secondary die-cast aluminum alloys as function of Fe, Mn and Cr contents. Mater. Chem. Phys. 2015, 153, 168–179. [Google Scholar] [CrossRef]
- Cai, Y.H.; Liang, R.; Hou, L.; Zhang, S. Effect of Cr and Mn on the microstructure of spray-formed Al–25Si–5Fe–3Cu alloy. Mater. Sci. Eng. A 2011, 528, 4248–4254. [Google Scholar] [CrossRef]
- Hou, L.G.; Cui, H.; Cai, Y.H.; Zhang, J.S. Effect of (Mn+Cr) addition on the microstructure and thermal stability of spray-formed hypereutectic Al–Si alloys. Mater. Sci. Eng. A 2009, 527, 85–92. [Google Scholar] [CrossRef]
- Zee, M.; Khalid, S. DFT calculations based insight into bonding character and strength of Fe2Al5 and Fe4Al13 intermetallics at Al-Fe joints. Procedia Manuf. 2018, 15, 1407–1415. [Google Scholar] [CrossRef]
- Dinsdale, A.; Fang, C.M. Understanding the thermodynamics and crystal structure of complex Fe containing intermetallic phases formed on solidification of aluminium alloys. JOM 2019, 71, 1731–1736. [Google Scholar] [CrossRef]
- Amirkhanyan, L.; Weissbach, T.; Gruber, T.; Zienert, T.; Fabrichnaya, O.; Kortus, J. Thermodynamic investigation of the τ4-Al–Fe–Si intermetallic ternary phase: A density-functional theory study. J. Alloys Compd. 2014, 598, 137–141. [Google Scholar] [CrossRef]
- Zienert, T.; Amirkhanyan, L.; Seidel, J.; Wirnata, R.; Weissbach, T.; Gruber, T.; Fabrichnaya, O.; Kortus, J. Heat capacity of η-AlFe (Fe2Al5). Intermetallics 2016, 77, 14–22. [Google Scholar] [CrossRef]
- Zienert, T.; Leineweber, A.; Fabrichnaya, O. Heat capacity of Fe-Al intermetallics: B2-FeAl, FeAl2, Fe2Al5 and Fe4Al13. J. Alloys Compd. 2017, 725, 848–859. [Google Scholar] [CrossRef]
- Shabestari, S.G. The effect of iron and manganese on the formation of intermetallic compounds in aluminum-silicon alloys. Mater. Sci. Eng. A 2004, 383, 289–298. [Google Scholar] [CrossRef]
- Timelli, G.; Bonollo, F. The influence of Cr content on the microstructure and mechanical properties of AlSi9Cu3(Fe) die-casting alloys. Mater. Sci. Eng. A 2010, 528, 273–282. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Wang, D.T.; Li, X.Z. Understanding crystal structure and morphology evolution of Fe, Mn, Cr-containing phases in Al-Si cast alloy. Intermetallics 2021, 131, 107103. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.; Probert, D.M.; Pickard, J.; Hasnip, C.J.; Clark, S.J. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B Condens. Matter. 1990, 41, 7892–7895. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989; Volume 16. [Google Scholar] [CrossRef]
- Baroni, S.; Giannozzi, P.; Isaev, E. Density-Functional perturbation theory for quasi-harmonic calculations. Rev. Miner. Geochem. 2010, 71, 39–57. [Google Scholar] [CrossRef]
- Davies, G.F. Effective elastic moduli under hydrostatic stress i.quasi- harmonic theory. J. Phys. Chem. Solids 1974, 35, 1513–1520. [Google Scholar] [CrossRef]
- Zhou, Y.X.; Gan, M.D.; Yu, W.; Chong, X.Y.; Feng, J. First-principles study of thermophysical properties of polymorphous YTaO4 ceramics. J. Am. Ceram. Soc. 2021, 104, 6467–6480. [Google Scholar] [CrossRef]
- Chong, X.Y.; Jiang, Y.H.; Zhou, R.; Feng, J. Elastic properties and electronic structures of CrxBy as superhard compounds. J. Alloys Compd. 2014, 610, 684–694. [Google Scholar] [CrossRef]
- Edström, D.; Sangiovanni, D.G.; Hultman, L.; Petrov, I.; Greene, J.E.; Chirita, V. Elastic properties and plastic deformation of TiC- and VC-based alloys. Acta Mater. 2018, 144, 376. [Google Scholar] [CrossRef]
- Hill, R.W. The elastic behavior of a crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
- Zhou, Y.X.; Wang, H.L.; Dong, Q.; Tan, J.; Chen, X.H.; Jiang, B.; Pan, F.S.; Eckert, J. Probing the stability, adhesion strength, and fracture mechanism of Mg/Al2Y interfaces via first-principles calculations. Mater. Today Commun. 2022, 33, 104612. [Google Scholar] [CrossRef]
- Emmanuel, C. Screw dislocation in zirconium: An ab initio study. Phys. Rev. B 2012, 86, 144104. [Google Scholar] [CrossRef]
- Tian, L.Y.; Lizárraga, R.; Larsson, H.; Holmström, E.; Vitos, L. A first principles study of the stacking fault energies for fcc Co-based binary alloys. Acta Mater. 2017, 136, 215. [Google Scholar] [CrossRef]
- Simensen, C.J.; Bjorneklett, A. A Model for α-Al(Mn,Fe)Si Crystals; The Minerals, Metals & Materials Society: San Diego, CA, USA, 2017; pp. 197–203. [Google Scholar] [CrossRef]
- Que, Z.P.; Mendis, C.L. Heterogeneous nucleation and phase transformation of Fe-rich intermetallic compounds in Al-Mg-Si alloys. J. Alloys Compd. 2020, 836, 155515. [Google Scholar] [CrossRef]
- Chen, C.L.; Richter, A.; Thomson, R.C. Investigation of mechanical properties of intermetallic phases in multi-component Al–Si alloys using hot-stage nanoindentation. Intermetallics 2010, 18, 499–508. [Google Scholar] [CrossRef]
- Cooper, M. The crystal structure of ternary alpha-(Al Fe Si). Acta Crystallogr. 1967, 23, 1106–1107. [Google Scholar] [CrossRef]
- Chong, X.Y.; Guan, P.W.; Hu, M.Y.; Jiang, Y.H.; Li, Z.L.; Feng, J. Exploring accurate structure, composition and thermophysical properties of η carbides in 17.90 wt%W-4.15wt% Cr-1.10wt%V-0.69wt%C steel. Scr. Mater. 2018, 154, 149–153. [Google Scholar] [CrossRef]
- Connolly, J.W.D.; Williams, A.R. Density-functional theory applied to phase transformations in transition-metal alloys. Phys. Rev. B Condens. Matter 1983, 27, 5169. [Google Scholar] [CrossRef]
- Van De Walle, A. Multicomponent multisublattice alloys, nonconfigurational entropy and other additions to the Alloy Theoretic Automated Toolkit. Calphad 2009, 33, 266–278. [Google Scholar] [CrossRef]
- Wu, P.; Zhou, Y.X.; Wu, F.S.; Hu, M.Y.; Chong, X.Y.; Feng, J. Theoretical and experimental investigations of mechanical properties for polymorphous YTaO4 ceramics. J. Am. Ceram. Soc. 2019, 102, 7656–7664. [Google Scholar] [CrossRef]
- Tibballs, J.E.; Davis, R.L.; Parker, B.A. Al-Si substitution in α-phase AlMnSi. J. Mater. Sci. 1989, 24, 2177–2182. [Google Scholar] [CrossRef]
- Chong, X.Y.; Jiang, Y.H.; Zhou, R.; Feng, J. Multialloying effect on thermophysical properties of Cr7C3-type carbides. J. Am. Ceram. Soc. 2017, 100, 1588–1597. [Google Scholar] [CrossRef]
- Chong, X.Y.; Hu, M.Y.; Wu, P.; Shan, Q.; Jiang, Y.H.; Li, Z.L.; Feng, J. Tailoring the anisotropic mechanical properties of hexagonal M7X3 (M=Fe, Cr, W, Mo; X=C, B) by multialloying. Acta Mater. 2019, 169, 193–208. [Google Scholar] [CrossRef]
- Chong, X.Y.; Palma, P.S.P.; Wang, Y.; Shang, S.L.; Drymiotis, F.; Ravi, V.A.; Star, K.E.; Fleurial, J.P.; Liu, Z.K. Thermodynamic properties of the Yb-Sb system predicted from first-principles calculations. Acta Mater. 2021, 217, 117169. [Google Scholar] [CrossRef]
- Chong, X.Y.; Jiang, Y.H.; Hu, M.Y.; Feng, J. Elaborating the phases and mechanical properties of multiphase alloy: Experimental two-dimensional mapping combined with theoretical calculations. Mater. Charact. 2017, 134, 347–353. [Google Scholar] [CrossRef]
- Chong, X.Y.; Jiang, Y.H.; Feng, J. Exploring the intrinsic ductile metastable Fe-C compounds: Complex chemical bonds, anisotropic elasticity and variable thermal expansion. J. Alloys Compd. 2018, 745, 196–211. [Google Scholar] [CrossRef]
- Goyal, A.; Li, Y.Z.; Chernatynskiy, A.; Jayashankar, J.S.; Kautzky, M.C.; Sinnott, S.B.; Phillpot, S.R. The influence of alloying on the stacking fault energy of gold from density functional theory calculations. Comput. Mater. Sci. 2021, 188, 110236. [Google Scholar] [CrossRef]
- Lai, S.; Gan, M.D.; Xu, L.J.; Tan, Z.L.; Li, Z.L.; Wei, S.Z.; Jiang, Y.H.; Feng, J.; Chong, X.Y. Stability and fracture mechanism of α-Fe/V6C5 interface in high vanadium Fe-based alloys by first-principles calculations. Surf. Interfaces 2023, 36, 102573. [Google Scholar] [CrossRef]
- Xia, F.F.; Xu, W.W.; Shi, Z.C.; Xie, W.; Chen, L.J. Exploring the alloying effects on generalized stacking fault energy and ideal strength of Ni and Ni3Al phases in Ni-based superalloys. Mech. Mater. 2022, 165, 104183. [Google Scholar] [CrossRef]
- Chong, X.Y.; Shang, S.L.; Krajewski, A.M.; Shimanek, J.D.; Du, W.; Wang, Y.; Feng, J.; Shin, D.; Beese, A.M.; Liu, Z.K. Correlation analysis of materials properties by machine learning: Illustrated with stacking fault energy from first-principles calculations in dilute fcc-based alloys. J. Phys. Condens. Matter 2021, 33, 295702. [Google Scholar] [CrossRef] [PubMed]


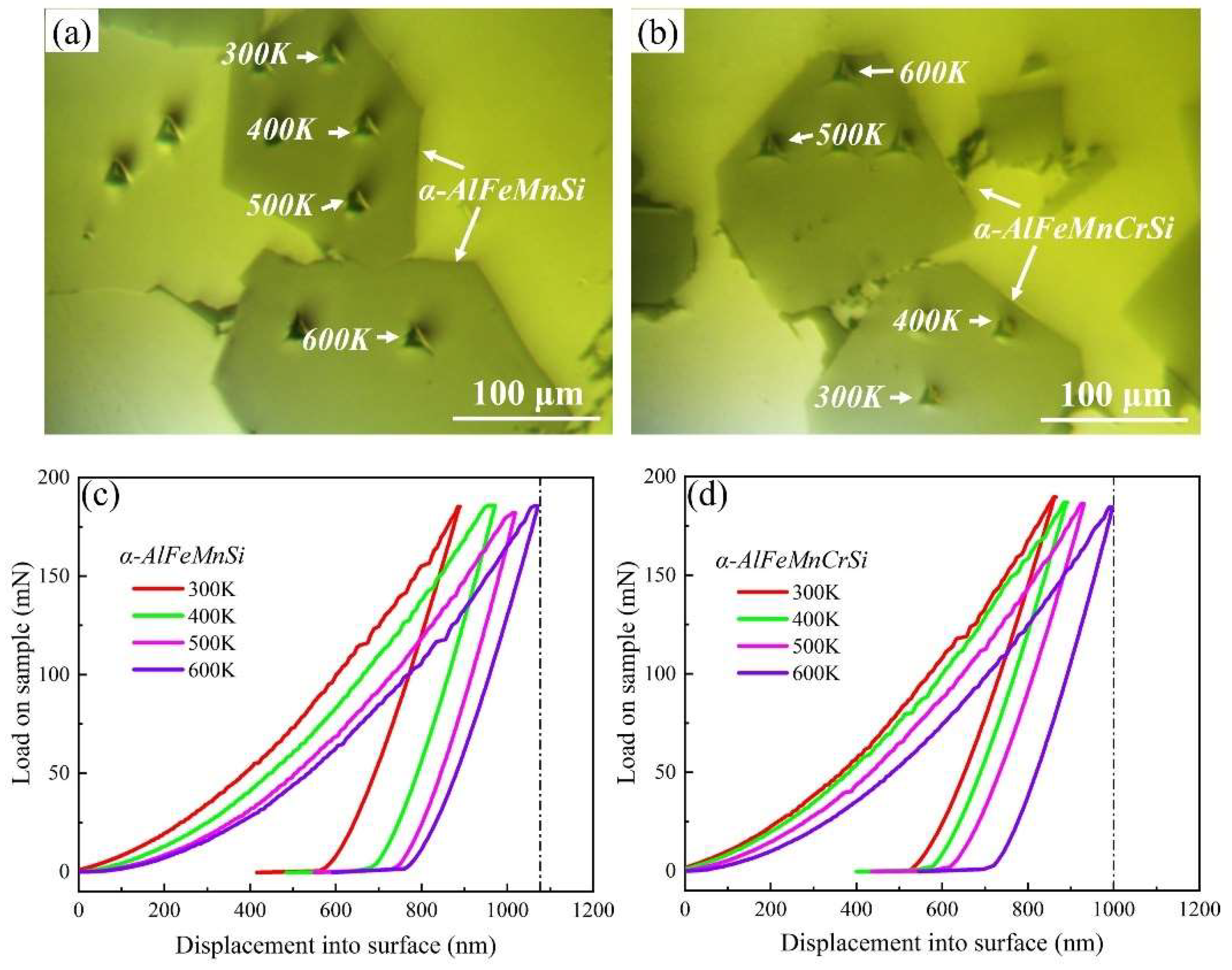
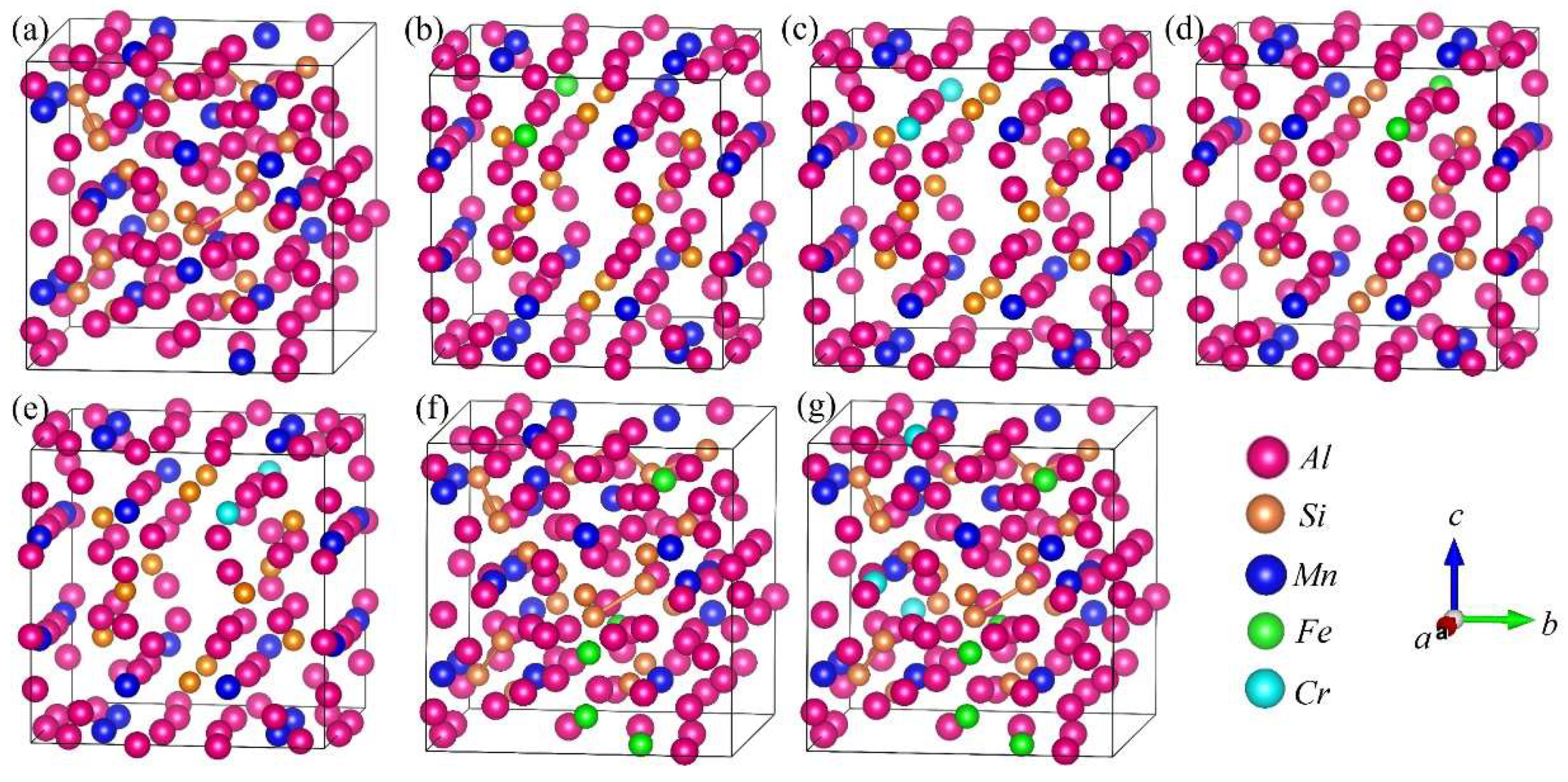
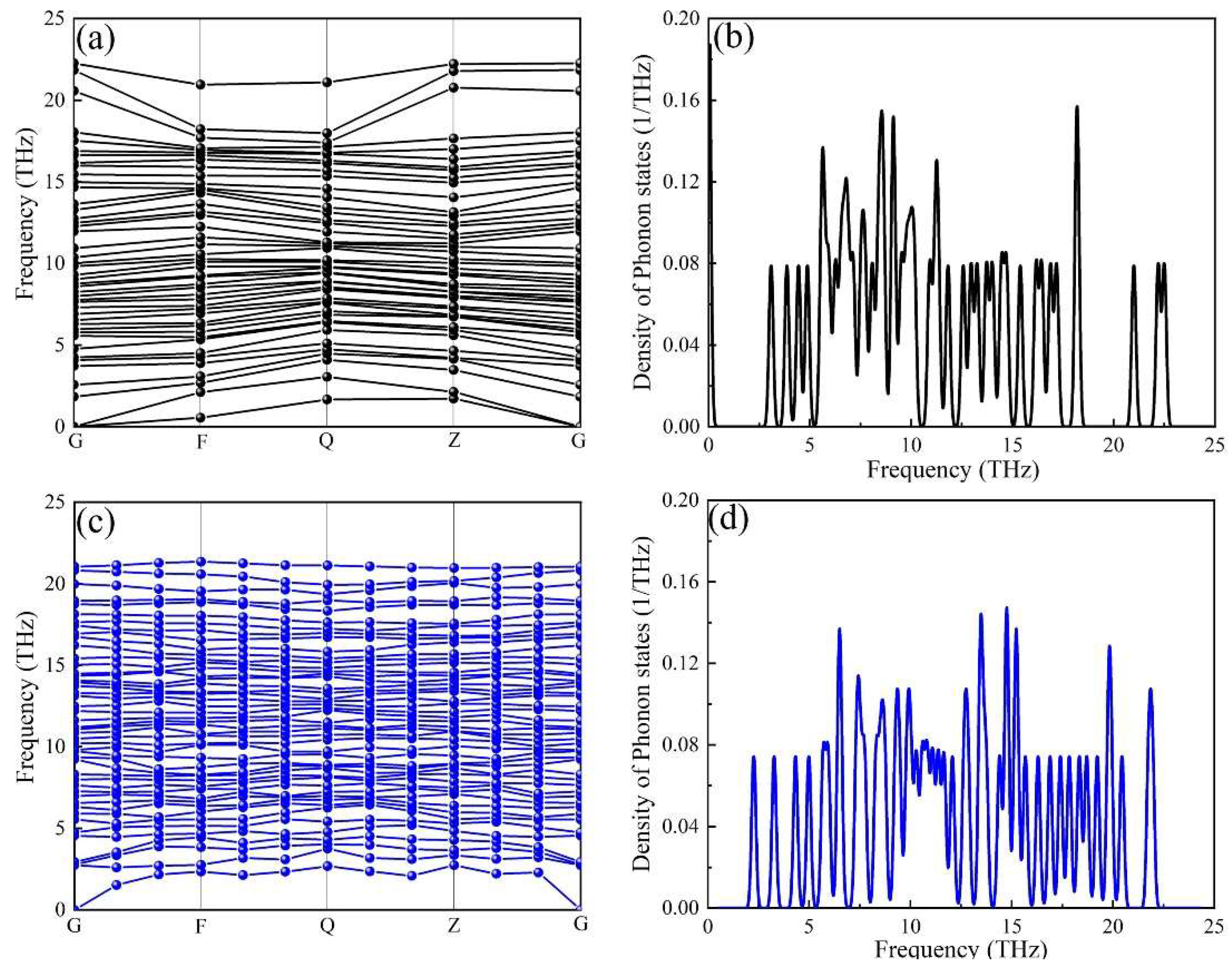

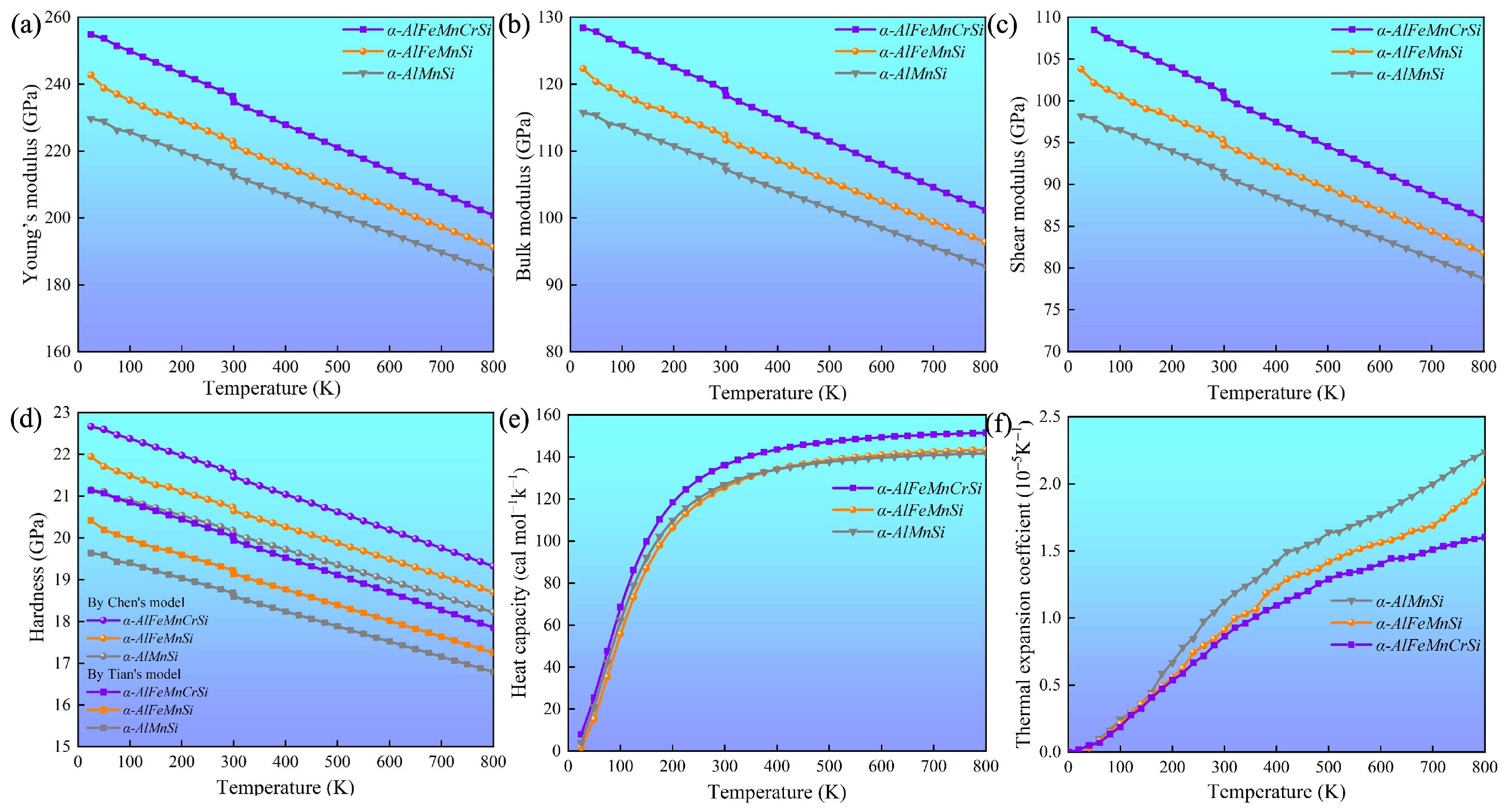


| Si | Fe | Mn | Cr | Al | |
|---|---|---|---|---|---|
| A1 | 6.99 | 0.49 | 1.56 | 0.01 | Bal. |
| A2 | 7.03 | 0.54 | 1.49 | 0.61 | Bal. |
| α-AlFeMnSi | α-AlFeMnCrSi | |||
|---|---|---|---|---|
| E (GPa) | H (GPa) | E (GPa) | H (GPa) | |
| 300 K | 215.9 | 14.2 | 224.8 | 16.98 |
| 400 K | 205.2 | 13.3 | 218.5 | 15.84 |
| 500 K | 199.1 | 12.8 | 210.6 | 14.7 |
| 600 K | 192.6 | 11.9 | 201.5 | 13.1 |
| Crystal Structures | Atom Coordinates | a | b | c | V (Å3) | Ef |
|---|---|---|---|---|---|---|
| α-AlMnSi | - | 12.64 | 12.60 | 12.69 | 2021.1 | −1.292 |
| α-AlFeMn-12jMnSi | Mn-12j (0.328, 0.197, 0) | 12.71 | 12.70 | 12.70 | 2050.0 | −2.166 |
| α-AlFeMn-12kMnSi | Mn-12k (0.18, 0.308, 0.5) | 12.69 | 12.71 | 12.70 | 2048.4 | −1.795 |
| α-AlCrMn-12jMnSi | Mn-12j (0.328, 0.197, 0) | 12.69 | 12.71 | 12.71 | 2050.0 | −2.502 |
| α-AlCrMn-12kMnSi | Mn-12k (0.18, 0.308, 0.5) | 12.71 | 12.69 | 12.70 | 2048.4 | −2.346 |
| α-AlFeMnSi | - | 12.65 | 12.62 | 12.71 | 2029.1 | −2.722 |
| α-AlFeMnCrSi | - | 12.62 | 12.58 | 12.68 | 2013.1 | −3.531 |
| Species | C11 | C12 | C13 | C22 | C23 | C33 | C44 | C55 | C66 | 11 | 12 | 44 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α-AlMnSi | 296.4 | 94 | 105.2 | 210.7 | 102.1 | 129.2 | 132.2 | 50.1 | 29.2 | 212.1 | 100.4 | 70.5 |
| α-AlFeMnSi | 312.7 | 103.6 | 113.2 | 220.6 | 105.4 | 120.6 | 164.4 | 52.6 | 31.3 | 218 | 107.4 | 67.1 |
| α-AlFeMnCrSi | 325.5 | 106.5 | 112.2 | 223.4 | 105.9 | 133.8 | 168.7 | 57.9 | 38.6 | 227.6 | 108.2 | 88.4 |
| Phases | x-y Bonds | Mean Bond Lengths (Å) at Different Temperatures | ||||
|---|---|---|---|---|---|---|
| 0 K | 200 K | 400 K | 600 K | 800 K | ||
| α-AlMnSi | Al-Si | 2.83 | 2.85 | 2.86 | 2.87 | 2.87 |
| Al-Mn | 2.67 | 2.68 | 2.68 | 2.68 | 2.69 | |
| Si-Mn | 2.59 | 2.60 | 2.59 | 2.60 | 2.63 | |
| α-AlFeMnSi | Al-Si | 2.85 | 2.86 | 2.88 | 2.90 | 2.92 |
| Al-Mn | 2.68 | 2.70 | 2.72 | 2.73 | 2.75 | |
| Si-Mn | 2.60 | 2.60 | 2.61 | 2.64 | 2.67 | |
| Al-Fe | 2.75 | 2.79 | 2.78 | 2.80 | 2.79 | |
| Si-Fe | 2.52 | 2.53 | 2.55 | 2.57 | 2.59 | |
| α-AlFeMnCrSi | Al-Si | 2.83 | 2.85 | 2.86 | 2.87 | 2.88 |
| Al-Mn | 2.68 | 2.69 | 2.70 | 2.71 | 2.71 | |
| Si-Mn | 2.65 | 2.66 | 2.66 | 2.70 | 2.71 | |
| Al-Fe | 2.73 | 2.75 | 2.78 | 2.78 | 2.79 | |
| Si-Fe | 2.65 | 2.65 | 2.65 | 2.66 | 2.67 | |
| Al-Cr | 2.65 | 2.66 | 2.67 | 2.71 | 2.71 | |
| Si-Cr | 2.56 | 2.58 | 2.58 | 2.64 | 2.65 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Zhang, X.; Nagaumi, H.; Zhang, M.; Zhou, P.; Wang, R.; Zhang, B. Exploring the Relationship between the Structural Characteristics and Mechanical Behavior of Multicomponent Fe-Containing Phases: Experimental Studies and First-Principles Calculations. Molecules 2023, 28, 7141. https://doi.org/10.3390/molecules28207141
Wang D, Zhang X, Nagaumi H, Zhang M, Zhou P, Wang R, Zhang B. Exploring the Relationship between the Structural Characteristics and Mechanical Behavior of Multicomponent Fe-Containing Phases: Experimental Studies and First-Principles Calculations. Molecules. 2023; 28(20):7141. https://doi.org/10.3390/molecules28207141
Chicago/Turabian StyleWang, Dongtao, Xiaozu Zhang, Hiromi Nagaumi, Minghe Zhang, Pengfei Zhou, Rui Wang, and Bo Zhang. 2023. "Exploring the Relationship between the Structural Characteristics and Mechanical Behavior of Multicomponent Fe-Containing Phases: Experimental Studies and First-Principles Calculations" Molecules 28, no. 20: 7141. https://doi.org/10.3390/molecules28207141
APA StyleWang, D., Zhang, X., Nagaumi, H., Zhang, M., Zhou, P., Wang, R., & Zhang, B. (2023). Exploring the Relationship between the Structural Characteristics and Mechanical Behavior of Multicomponent Fe-Containing Phases: Experimental Studies and First-Principles Calculations. Molecules, 28(20), 7141. https://doi.org/10.3390/molecules28207141





