Next Article in Journal
Comparative Study of Planar Octahedron Molecular Structure via Eccentric Invariants
Next Article in Special Issue
Chemistry of CS2 and CS3 Bridged Decaborane Analogues: Regular Coordination Versus Cluster Expansion
Previous Article in Journal
Pharmacokinetic Study of Triptolide Nanocarrier in Transdermal Drug Delivery System—Combination of Experiment and Mathematical Modeling
Previous Article in Special Issue
Structural Evolution and Electronic Properties of Selenium-Doped Boron Clusters SeBn0/− (n = 3–16)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 2
10.3390/molecules28020554
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

F2BMF (M = B and Al) Molecules: A Matrix Infrared Spectra and Theoretical Calculations Investigation

by
Juanjuan Cheng
1,
Liyan Cai
1,
Zhen Pu
2,
Bing Xu
1,* and
Xuefeng Wang
1,*
1
Shanghai Key Lab of Chemical Assessment and Sustainability, School of Chemical Science and Engineering, Tongji University, Shanghai 200092, China
2
China Academy of Engineering and Physics, Mianyang 621900, China
*
Authors to whom correspondence should be addressed.
Molecules 2023, 28(2), 554; https://doi.org/10.3390/molecules28020554
Submission received: 23 October 2022 / Revised: 31 December 2022 / Accepted: 2 January 2023 / Published: 5 January 2023
(This article belongs to the Special Issue New Boron Chemistry: Current Advances and Future Prospects)
Browse Figures
Review Reports Versions Notes

Abstract

:
Reactions of laser-ablated B and Al atoms with BF3 have been explored in the 4 K excess neon through the matrix isolation infrared spectrum, isotopic substitutions and quantum chemical calculations. The inserted complexes F2BMF (M = B, Al) were identified by anti-symmetric and symmetric stretching modes of F-B-F, and the F-11B-F stretch modes are at 1336.9 and 1202.4 cm−1 for F211B11BF and at 1281.5 and 1180.8 cm−1 for F211BAlF. The CASSCF analysis, EDA-NOCV calculation and the theory of atoms-in-molecules (AIM) are applied to investigate the bonding characters of F2BBF and F2BAlF molecules. The bonding difference between boron and aluminum complexes reveals interesting chemistries, and the FB species stabilization by a main group atom was first observed in this article.

1. Introduction

B2 species, comprising electron-precise B-B bonds, have witnessed swift developments in the past twenty years, in which B2Xn (X = F, Cl, Br, n = 2,4) molecules are important precursors for synthesizing boron-containing compounds, which garnered much attention from scientists [1]. As for B2F4, Trefonas and Lipscomb showed that B2F4 has a planar structure in the solid phase by X-ray diffraction [2], while several earlier Raman and infrared spectroscopic studies suggested a staggered structure [3,4,5]. In 1977, Danielson, Patton, and Hedberg confirmed that the gaseous B2F4 molecule has a D2h symmetry by electron diffraction [6]. Fan and Li also found that the ground state of B2F4 has an eclipsed conformation (in D2h symmetry) [6]. Later, Danielson, Patton, and Hedberg demonstrated that the experimental difficulties in determining the structure of B2F4 were probably due to its very low internal rotation barrier around the B-B bond (0.42 kcal⋅mol) [7]. For F2B2, the linear singlet structure FBBF (D∞h, 3Σ−) is a second-order stationary point at MBPT(2), and it could convert into a bent structure (C2h, 1Ag), which is 5.0 kcal/mol higher in energy than a linear structure at MBPT(2) [8]. The double-bond character for the bent structure is suggested by the NBO analysis (WBI-[BB] = 1.432 Å), involving two highest occupied ag and bu MO’s, which can be visualized as a donor-acceptor complex formed by the delocalization of σ lone pairs into empty pπ orbitals lying in the molecular plane. The association of two ground-state BF molecules into the C2h bent structure has a very low barrier (<1.0 kcal/mol) via a loose C2h symmetric transition state (RBB = 2.434 Å) [8]. Recently, our assignment of the experimentally observed B-F stretching frequencies at 1327 cm−1 to the trans-bent isomer FBBF is therefore very tentative due to similarity in the calculated anti-symmetric B-F stretching frequencies of the linear and bent isomers [9].
Although B2F4 and B2F2 have already been known well, there seems to be no relevant report on the B2F3 molecule. As we know, B2F3 should possesse FB2 and FB fragments, having significant differences from B2F4 and B2F2 molecules, but its structure and properties have not yet been understood. Boron is the main group element in the periodic table, and bonding between boron and main group elements has also been an attractive subject [10,11,12,13,14]. For example, by laser vaporization of a mixed B/Bi target, the Bi ≡ B and Bi = B multiple bonds in BiB2O2− and Bi2B− are observed and are characterized by photoelectron spectroscopy and ab initio calculations [15]. Several years ago, we reported some boryl complexes F2BMF (M = C, Si, Ge, Sn, Pb) [14], and DFT and CCSD(T) calculations demonstrate that triplet F2BCF is the most stable isomer with two singly occupied molecular orbitals, while singlet F2BMF (M = Si, Ge, Sn and Pb) molecules possess a near right angle B-M-F moiety with lone pair electrons on the M atom. In this paper, the laser-ablated B and Al were demonstrated to react with BF3 to produce the fluoroboryl complexes F2BBF and F2BAlF, which have been identified by boron isotopic substitution and theoretical frequency calculations. The bonding formation for B-B as well as B-Al in fluoroboryl complexes of F2BMF was investigated by EDA-NOCV and CASSCF calculations. The active molecular orbital and NBO analysis, and the bonding difference, were analyzed in detail.

2. Results and Discussion

The assignment of absorptions was based on the behavior of the products’ absorptions upon stepwise annealing and photolysis behavior and will be discussed below. The typical infrared spectra in the selected regions and the absorption bands are shown in Figure 1, Figure 2 and Figure 3 and Table 1, respectively. In addition, the calculated frequencies based on DFT are listed in the same tables for comparison.

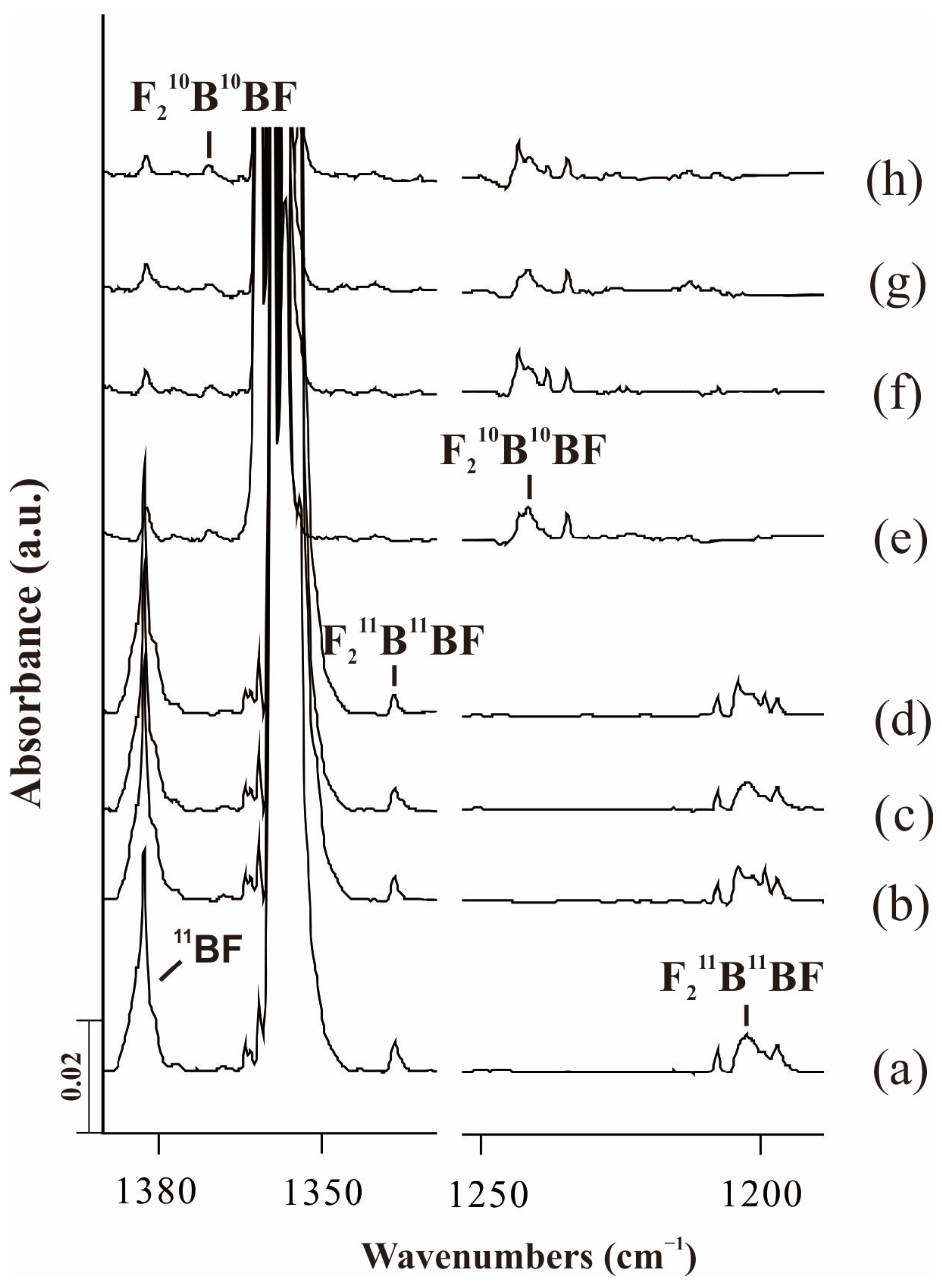
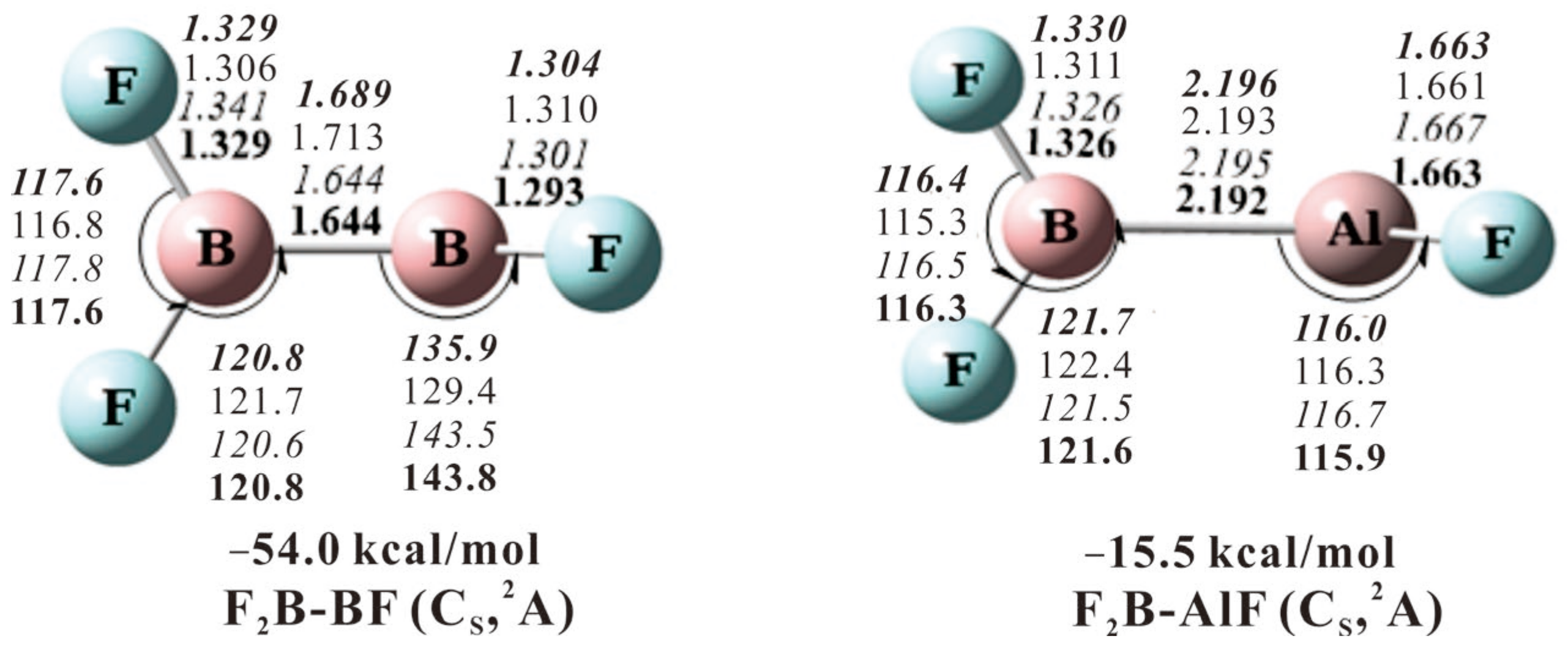
2.1. F2BBF

In the reaction of laser-ablated 11B with 11BF3 in excess neon, as shown in the Figure 1, the new product absorptions upon co-deposition appeared at 1336.9 and 1202.4 cm−1. These two bands decreased slightly after annealing to 8 K and 12 K. These two bands shifted to 1370.6 and 1241.6 cm−1 in the reaction of 10BF3 with the 10B target, which showed the similar behavior to that of the counterparts produced with 11B + 11BF3.
The 1336.9 cm−1 appeared at the BF2 stretching region and shifted to 1370.6 cm−1 with 10BF3 + 10B, giving the 1.0252 10B/11B isotopic frequency ratio, which are in good agreement with the isotopic frequency ratio of 1.0280 in the B2F4 molecule [3]. The 1202.4 cm−1 shifted to 1241.6 cm−1, giving the 10B/11B isotopic frequency ratio of 1.0326 that was close to the calculated ratio of 1.0350 and fit in the previously reported values of the F-B-F vibration mode [16]. Unfortunately, the BBF stretching mode was covered by precursor bands in our experiments. These bands are appropriate for the F2B-BF molecule based on the isotopic shifts and photochemical behavior.
In the reaction of 11BF3 with 10B target (Figure 2a–d), two new bands appeared at 1338.7 and 1200.8 cm−1 in the BF2 stretching region, which decreased slightly after annealing to 8 K and λ > 300 nm photolysis, and decreased obviously after λ > 220 nm irradiation. In addition, the other new group bands appeared at 1369.4 and 1223.8 cm−1 after λ > 220 nm irradiation. In the reaction of 10BF3 with 11B (Figure 2e–h), 1369.4 and 1223.8 cm−1 bands appeared on deposition, which decreased largely upon λ > 220 nm irradiation. Meanwhile, new group bands were located at 1338.7 and 1200.8 cm−1 after λ > 220 nm photolysis. Obviously, we obtained the same two isomers in 10BF3 + 11B and 11BF3 + 10B experiments.
It is very interesting to observe that in the reaction of 11BF3 with 10B (Figure 2a–d), F211B10BF was produced at first, but decreased with the emergence of F210B11BF on >220 nm irradiation. Similarly, in Figure 2e–h, F210B11BF was observed firstly and then F211B10BF appeared accompanied with no obvious change of F210B11BF on the >220 nm irradiation. Apparently, α-F transfer happened between the two species due to the photo irradiation.
This assignment is supported by our DFT frequency calculations (Table 1). The F2BBF molecule is predicted to have Cs symmetry with 2A ground state (Figure 4). The anti-symmetric and symmetric B-F stretching modes of the F211B(10B)-11BF molecule were predicted at 1332.3 (1378.8) and 1188.9 (1221.3) cm−1 using the B3LYP functional, very close to our observed values of 1336.9 (1369.4) and 1202.4 (1223.8) cm−1. Furthermore, the anti-symmetric and symmetric B-F stretching modes of the F211B(10B)-10BF molecule were predicted at 1332.3 (1378.9) and 1192.3 (1226.3) cm−1, which are in good agreement with our observed values at 1338.7 (1370.6) and 1200.8 (1241.6) cm−1. The results of BPW91 and CCSD(T) are consistent with that of B3LYP.

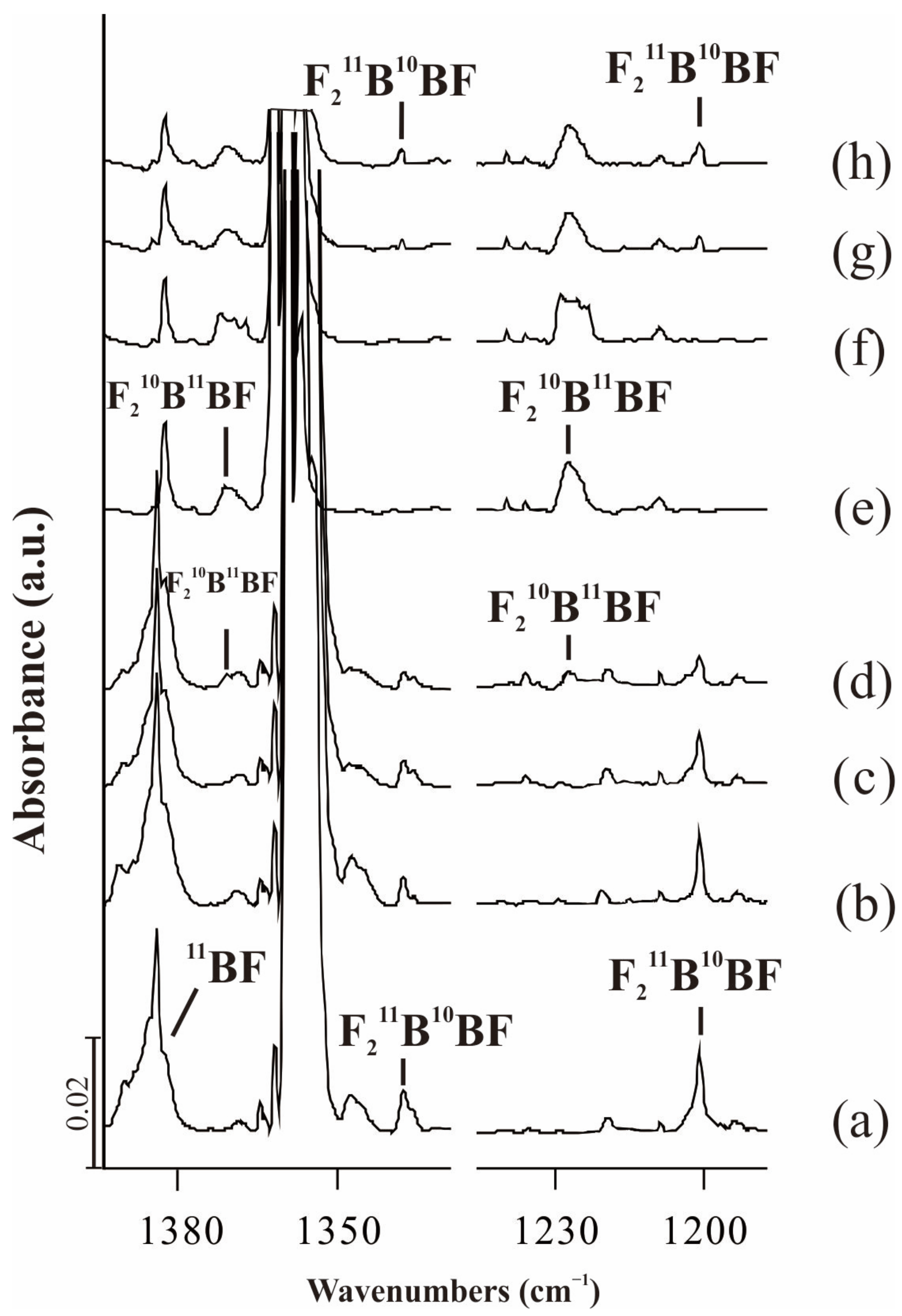
2.2. F2BAlF

As shown in Figure 3 and Table 1, the new product absorptions located at 1281.5, 1180.8 and 819.6 cm−1 in the reaction of 11BF3 with laser-ablated Al atoms, increased on annealing to 8 K, but decreased sharply on the λ = 450 nm irradiation and increased again on annealing to 12 K. These bands shifted to 1324.6, 1217.1 and 819.6 cm−1 in the reaction of 10BF3 with Al atoms, which showed a similar response to kinds of photolysis and annealing.
The absorption bands at 1281.5 and 1180.8 cm−1 shifted to 1324.6 and 1217.1 cm−1, giving 1.0336 and 1.0307 of 10B/11B isotopic frequency ratio, which match very well with the F-B-F radical vibration mode [16]. The absorption bands at 819.6 cm−1 showed no 10B/11B isotopic frequency ratio shift, indicating that only Al and F are involved in this mode. It is most likely that this absorption arises from terminal Al–F stretching vibrations. All these indicate that this group band is attributable to the F2BAlF molecular.
The B3LYP calculations predict the F2BAlF molecule to have CS symmetry with 2A ground state. The calculated BF2 anti-symmetric and symmetric mode using B3LYP is 1312.0 and 1172.2 cm−1, being overestimated by about 2.3% and underestimated by about 0.7%, respectively. The calculated Al-F stretching vibration is overestimated by about 1.6%, which fits the observed values very well.

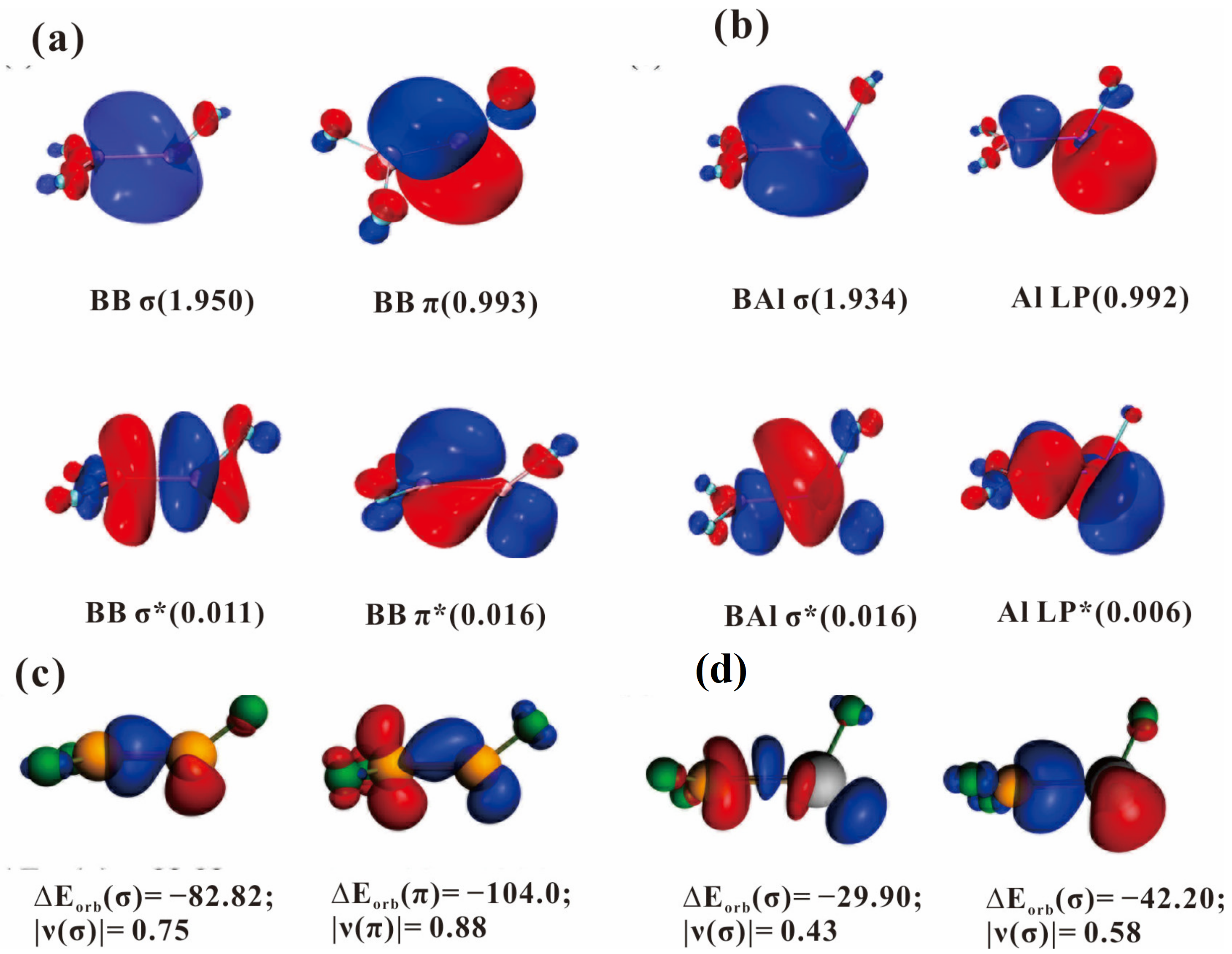
3. Reaction Product Comparison and Bonding Consideration

Two stable complexes, F2BBF and F2BAlF, were calculated by the B3LYP functional and parameters are illustrated in Figure 4. The reaction of laser-ablated B atoms with BF3 to produce inserted complex F2BBF is exothermic by 54.0 kcal/mol at CCSD(T) level. The subsequent α-F transfer reaction to give FBBF2 requires an energy barrier of 31.7 kcal/mol. In our experiments of 11BF3 with 10B or 10BF3 with 11B, only one inserted species was observed first and then α-F transfer occurs upon 220 nm photolysis. In the reaction of BF3 with Al atom, the F2BAlF molecule is produced with an exothermic 15.5 kcal/mol−1 reaction at the CCSD(T) level. However, the FB-AlF2 produced by a-F transfer from F2B-AlF is endothermic by 6.8 kcal/mol−1, which could not be observed in our experiments (Figure 5).
The bond angle of B-B-F for the F2B-BF molecule is 142°, which is quite different from the 116° of B-Al-F angle for F2B-AlF (Figure 4). As shown in Figure 6a, for the F2BBF molecule, the B = B bond is composed of one σ bond with an occupation of 1.94 e and one (p-p) π bond with an occupation of 1.00 e in the plane, which leads to a larger B-B-F bond angle. The effective bond order (EBO) of B-B bond is 1.32 calculated by natural bond orbital (NBO) population analysis. The calculated 1.644 Å of B = B bond length is shorter than that of B-B single bond between 1.819 and 1.859 Å, but longer than 1.561 and 1.590 Å of the B = B double bond length in R(H)B = B(H)R (R = :C{N(2,6- Pri2C6H3)CH}2) [17], and in OC(H)B = B(H)CO [18], respectively, affirming that B-B bond order in F2B-BF is between one and two. Notice that for the F2BAlF molecule, the effective bond order (EBO) of B-Al is 0.96 with an occupation of 1.93 e in the σ character (Figure 6b). The Al atom possesses a single electron (mostly from the s orbital) which does not participate in bonding. Although B and Al atom are in the same group, their bonding situation is very different. As shown in Table S1, for the F2BBF molecule, both boron atoms have a good hybridization with the s and p orbital, while little hybridization occurs between the s and p orbital for the B-Al σ bond in the F2BAlF molecule.
The energy decomposition analysis (EDA) can be used in quantitative interpretation of chemical bonds’ formation in terms of three major components (Table 2) [19]. For the F2BBF molecule, the EDA shows that the total interaction energy of −148.3 kcal/mol between the F2B and BF fragments consists of an attractive electrostatic energy of −53.0 kcal/mol, an orbital interaction energy of −193.9 kcal/mol and a large Pauli repulsion of 97.5 kcal/mol. This interaction energy is bigger than that of the H-H single bond (−112.9 kcal/mol), but smaller than the N-N triple bond’s (−232.2 kcal/mol) [19]. Surprisingly, this interaction between B and B is bigger than that of the triple bond between B and heavier transition metal atom that we observed previously [20]. It is possible to breakdown the orbital term ΔEorb into pairwise orbital contributions of the interacting fragments by EDA–Natural Orbitals for the Chemical Valence (NOCV) method [21,22,23]. Figure 6c clearly depicted the natural orbitals for the chemical valence of F2BBF. The σ bond between B and B is mainly caused by the outflow of electrons (most 2s electron of B) from FB to B of BF2 and then the (p-p) π bond is formed by the outflow of one 2p electrons of B of BF2 to 2p vacant orbital of B of BF. The decomposition of the orbital interaction shows that 42.7% (−82.8 kcal/mol) come from the σ bond, while 53.6% (−104.0 kcal/mol) come from the π bonds, respectively.
For the F2BAlF molecular, only one σ bond existed between B and Al and both B and Al atom contribute to this σ bond together (Figure 6d). From Figure 6b, we can observe that the occupation of the σ bond is 1.93 e. Moreover, the Al atom possesses a single electron (most from the s orbital) which did not participate in bonding. Although B and Al atoms are in the same group, their bonding situation is very different. In Table S1, for the F2BBF molecule, both two boron atoms have good hybridization with the s and p orbital. While for the B-Al σ bond, the bonding electron is either from the s orbital or from the p orbital of the Al atom in a different phase and little hybridization happening between the s and p orbital. Thus, the 3s electrons of aluminum barely participates in bonding with other atoms and no π bond formed in the F2BAlF molecule.
Although the FBAlF2 molecule was not observed in the experiment by the α-F transfer, a similar bonding composition could be demonstrated to that of FBBF2 (Figure S1). The B-Al is also caused by the outflow of electrons (most 2s electron of B) from FB to Al, and then the (p-p) π bond is formed by the inflow of one 3p electrons of Al to the 2p vacant orbital of B. The total interaction energy of −122.0 kcal/mol between BF and AlF2 is very strong, and 29.3% (−39.5 kcal/mol) come from the σ bond and 68.3% (−91.9 kcal/mol) from π bond; thus, compounds with σ-donor and π-acceptor bonding modes formed [20].
For further analyzing the bond character, the atoms in the molecule theory (AIM) analysis were performed (Figure S2). The negative value of local energy density H(r) = −0.12656 and −0.02651 for B-B and B-Al was obtained, respectively. The bond critical point between the B and B atom locates in the negative value of the Laplacian value (∇2ρcp = −0.426); however, this value is slightly positive (∇2ρcp = 0.058) and close to zero between the B and Al atom. Figure S3 displayed the color-filled maps of the localized orbital locator (LOL) on the F2BM (B, Al) plane. It demonstrated that there are high electron localization regions between boron and metal (B and Al), which indicates the covalent bond character. From B to Al, the BF2 antisymmetric and symmetric stretch mode can red-shift from 1336.9 and 1202.4 cm−1 to 1281.5 and 1180.8 cm−1.

4. Experimental and Computational Methods

Laser-ablated B and Al atoms react with 11BF3 and 10BF3 in excess neon during condensation at 4 K using a closed-cycle helium refrigerator (Sumitomo Heavy Industries Model SRDK-408D2, Japan). A Nd:YAG laser fundamental (1064 nm, 10 Hz repetition rate with 10 ns pulse width) was focused onto the rotating B, or Al target, and typically 20–30 mJ/pulse was used. The laser-ablated enriched 10B (Eagle Pitcher, America, 93.8% 10B, 6.2% 11B), enriched 11B (Eagle Pitcher, 97.5% 11B, 2.5% 10B), and Al (Alfa Aesar, America, 99.999%) atoms were reacted with 11BF3 and 10BF3 purchased from Jinglin (Shanghai, China) Chemical Industry Limited Liability Company (Shanghai, China, chemical purity, ≥99.99%) in excess neon spread uniformly onto the CsI window. Infrared spectra were recorded at a resolution of 0.5 cm−1 between 4000 and 400 cm−1 using a HgCdTe range B detector. Selected samples were irradiated by a mercury lamp (175 W, without globe) with the aid of glass filters to permit the allowed wavelengths to pass.
All structures were optimized at the BPW91/def2-TZVPP and B3LYP/def2-TZVPP [24,25] basis set via the Gaussian 09 program [26] and CAS(9e, 11o)/def2-TZVP [27,28] and CCSD(T)/def2-TZVP(-f) [29,30,31] basis set via the ORCA 4.0.1 program [32,33]. The single point energy calculations were performed with the correlated molecular orbital theory coupled cluster CCSD(T) [29,30,31] theory. Transition states were optimized with the Rational Function Optimization (RFO) method and were verified to link the desired reactant and product through the intrinsic reaction coordinate (IRC) calculations. Atoms in molecules’ (AIM) [34] analysis was performed to elicit detailed information on the bonding characters with the Multiwfn code [35]. The orbital composition and effective bond order and Wiberg bond order were calculated by a natural bond orbital (NBO) population analysis [26,36]. In addition, ab initio calculations based on the high-level multi-configurational wavefunction method were also performed to obtain the accurate electronic structure information of BF2-MF compounds by the ORCA 4.0.1 program [32,33]. CASSCF [27] calculations including three active electrons in eight active orbitals [CAS(3e, 8o)], and NEVPT2 [37,38,39] calculations including three active electrons in four active orbitals [CAS(3e, 4o)] were performed with the def2-TZVP [28] basis set for all atoms. The effect of the dynamic correlation was taken into account by NEVPT2 [37,38,39] on top of the wavefunctions at CASSCF level to obtain more accurate energies. The energy decomposition analysis with the natural orbitals of the chemical valence (EDA-NOCV) method [21,22,23] were carried out with the ADF 2017 program [40] package to study the chemical bonding between the B and Al atoms with the B atom.

5. Conclusions

The reaction of laser-ablated B and Al atoms with BF3 has been studied by the matrix isolation infrared spectrum and theoretical calculations. The structure and properties of the B2F3 molecule, which can be drawn as F2B-BF, have been investigated. The F-B-F stretching mode was located at 1336.9 and 1202.4 cm−1. For comparison, the F2BAlF molecule was also investigated and the F-B-F stretching mode was at 1281.5 and 1180.8 cm−1. The CASSCF analysis, EDA-NOCV calculation, the theory of atoms-in-molecules (AIM) and localized orbital locator (LOL) are applied to investigate the bonding characters of the B-B and B-Al bond in F2BBF and F2BAlF molecules. The B-B bond in F2BBF favors the one and half bond order, in which two boron atoms have a good hybridization between s and p orbital. Meanhile, due to little hybridization between s and p orbital, 3s electrons of aluminum barely participate in bonding with other atoms, thus one bond order is formed for the B-Al bond.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28020554/s1, Figure S1: Plot of the deformation densities Δρ of the BF→AlF2 σ donation and AlF2→BF π back-donation in FBAlF2 with the associated interaction energy ∆Eorb and charge eigenvalues |νn|(in e).; Figure S2: Contour line diagrams of the Laplacian of the electronic density of F2BMF (M = B, Al).; Figure S3: Color-filled maps of localized orbital locator of F2BMF molecules (M = B, Al).; Table S1: Compositions of Natural Bond Orbitals from NBO Analysis of F2BMF molecules (M = B, Al).; Table S2: Effective Bond Order Computed at B3LYP/def2-TZVPP level of F2BMF molecules (M = B, Al).; Table S3: Calculated Fundamental Frequencies of F2BBF and F2AlBF isotopomers in the Ground 2A State.

Author Contributions

Conceptualization, B.X. and X.W.; methodology, J.C.; software, Z.P.; validation, J.C., L.C. and B.X.; formal analysis, B.X.; investigation, B.X.; resources, B.X and X.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (nos. 21371136 and 21873070).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

If you interested in our article and could not find some other data, please contact us from email.

Conflicts of Interest

The authors have declared no conflict of interest.

References

  1. Borthakur, R.; Saha, K.; Kar, S.; Ghosh, S. Recent advances in transition metal diborane(6), diborane(4) and diborene(2) chemistry. Coord. Chem. Rev. 2019, 399, 213021. [Google Scholar] [CrossRef]
  2. Trefonas, L.; Lipscomb, W.N. Crystal and Molecular Structure of Diboron Tetrafluoride, B2F4. J. Chem. Phys. 1958, 28, 54–55. [Google Scholar] [CrossRef]
  3. Nimon, L.A.; Seshadri, K.S.; Taylor, R.C.; White, D. Infrared Spectra and Geometry of Matrix-Isolated Diboron Tetrachloride and Tetrafluoride; Raman Spectra of the Liquids. J. Chem. Phys. 1970, 53, 2416–2427. [Google Scholar] [CrossRef]
  4. Finch, A.; Hyams, I.; Steele, D. The vibrational spectra of diboron compounds—I. Infrared spectra of diboron tetrafluoride. Spectrochim. Acta 1965, 21, 1423–1431. [Google Scholar] [CrossRef]
  5. Gayles, J.N.; Self, J. Infrared Spectrum of Diboron Tetrafluoride in the Gaseous and Solid States. J. Chem. Phys. 1964, 40, 3530–3539. [Google Scholar] [CrossRef]
  6. Li, Z.H.; Fan, K.N. B2F4 molecule: A challenge for theoretical calculations. J. Phys. Chem. A 2002, 106, 6659–6664. [Google Scholar] [CrossRef]
  7. Danielson, D.D.; Patton, J.V.; Hedberg, K. The effect of Temperature on Structure of Gaseous Molecules. 3. Molecular-Structure and Barrier to Internal-Rotation for Diboron Tetrafluoride. J. Am. Chem. Soc. 1977, 99, 6484–6487. [Google Scholar] [CrossRef]
  8. Korkin, A.A.; Balkova, A.; Bartlett, R.J.; Boyd, R.J.; Schleyer, P.v.R. The 28-Electron Tetraatomic Molecules:  N4, CN2O, BFN2, C2O2, B2F2, CBFO, C2FN, and BNO2. Challenges for Computational and Experimental Chemistry. J. Phys. Chem. 1996, 100, 5702–5714. [Google Scholar] [CrossRef]
  9. Xu, B.; Beckers, H.; Ye, H.Y.; Lu, Y.; Cheng, J.J.; Wang, X.F.; Riede, l.S. Cleavage of the N identical withN Triple Bond and Unpredicted Formation of the Cyclic 1,3-Diaza-2,4-Diborete (FB)2N2 from N2 and Fluoroborylene BF. Angew. Chem. Int. Ed. Engl. 2021, 60, 17205–17210. [Google Scholar] [CrossRef]
  10. Andrews, L.; Lanzisera, D.V.; Hassanzadeh, P. Reactions of Laser-Ablated Boron Atoms with Ethylene and Ethane. Infrared Spectra and DFT Calculations for Several Novel BC2Hx (x = 1, 2, 3, 4, 5) Molecules. J. Phys. Chem. A 1998, 102, 3259. [Google Scholar] [CrossRef]
  11. Lanzisera, D.V.; Andrews, L. Reactions of laser-ablated boron atoms with methylamines. Matrix infrared spectra and MP2 frequency calculations for isotopic product molecules. J. Phys. Chem. A 1997, 101, 824–830. [Google Scholar] [CrossRef]
  12. Lanzisera, D.V.; Andrews, L. Reactions of laser-ablated boron atoms with methanol. Infrared spectra and ab initio calculations of CH3BO, CH2BOH, and CH2BO in solid argon. J. Phys. Chem. A 1997, 101, 1482–1487. [Google Scholar] [CrossRef]
  13. Lanzisera, D.V.; Andrews, L. Reactions of Laser-Ablated Boron Atoms with Methyl Halides in Excess Argon. Infrared Spectra and Density Functional Theory Calculations on CH3BX, CH2BX, and CHBX (X = F, Cl, Br). J. Phys. Chem. A 2000, 104, 9295–9301. [Google Scholar] [CrossRef]
  14. Xu, B.; Li, L.; Yu, W.J.; Huang, T.F.; Wang, X.F. Matrix Infrared Spectra and Theoretical Calculations of Fluoroboryl Complexes F2B-MF (M = C, Si, Ge, Sn and Pb). J. Phys. Chem. A 2018, 122, 7301–7311. [Google Scholar] [CrossRef]
  15. Apeloig, Y.; Pauncz, R.; Karni, M.; West, R.; Steiner, W.; Chapman, D. Why Is Methylene a Ground State Triplet while Silylene Is a Ground State Singlet? Organometallics 2003, 22, 3250–3256. [Google Scholar] [CrossRef]
  16. Hassanzadeh, P.; Andrews, L. Reaction of halogens with laser-ablated boron: Infrared spectra of BXn (X = F, Cl, Br, I; n = 1, 2, 3) in solid argon. J. Phys. Chem. 1993, 97, 4910–4915. [Google Scholar] [CrossRef]
  17. Wang, Y.; Quillian, B.; Wei, P.; Wannere, C.S.; Xie, Y.; King, R.B.; Schaefer, H.F., 3rd; Schleyer, P.V.; Robinson, G.H. A stable, neutral diborene containing a B=B double bond. J. Am. Chem. Soc. 2007, 129, 12412–12413. [Google Scholar] [CrossRef]
  18. Wang, Z.X.; Chen, Z.F.; Jiao, H.J.; Schleyer, P.V. Isolobal boron carbonyl carbocation analogs. J. Theor. Comput. Chem. 2005, 4, 669–688. [Google Scholar] [CrossRef]
  19. Zhao, L.; von Hopffgarten, M.; Andrada, D.M.; Frenking, G. Energy decomposition analysis. WIREs Comput. Mol. Sci. 2017, 8, e1345. [Google Scholar] [CrossRef]
  20. Xu, B.; Li, W.J.; Yu, W.J.; Pu, Z.; Tan, Z.; Cheng, J.J.; Wang, X.F.; Andrews, L. Boron-Transition-Metal Triple-Bond FB identical with MF2 Complexes. Inorg. Chem. 2019, 58, 13418–13425. [Google Scholar] [CrossRef]
  21. Mitoraj, M.P.; Michalak, A.; Ziegler, T. A Combined Charge; Energy Decomposition Scheme for Bond Analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef] [PubMed]
  22. Mitoraj, M.; Michalak, A. Donor–Acceptor Properties of Ligands from the Natural Orbitals for Chemical Valence. Organometallics 2007, 26, 6576–6580. [Google Scholar] [CrossRef]
  23. Michalak, A.; Mitoraj, M.; Ziegler, T. Bond Orbitals from Chemical Valence Theory. J. Phys. Chem. A 2008, 112, 1933–1939. [Google Scholar] [CrossRef] [PubMed]
  24. Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
  25. Lee, C.T.; Yang, W.T.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron-Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
  26. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A. Gaussian 09; Carnegie Mellon University: Pittsburgh, PA, USA, 2009. [Google Scholar]
  27. Roos, B.O. Advances in Chemical Physics. In Ab Initio Methods in Quantum Chemistry-II; Lawley, K.P., Ed.; John Wiley & Sons Ltd.: New York, NY, USA, 1987; Chapter 69; pp. 399–445. [Google Scholar]
  28. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  29. Purvis, G.D.; Bartlett, R.J. A Full Coupled-Cluster Singles and Doubles Model-the Inclusion of Disconnected Triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
  30. Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A Fifth-Order Perturbation Comparison of Electron Correlation Theories. Chem. Phys. Lett. 1989, 157, 479. [Google Scholar] [CrossRef]
  31. Bartlett, R.J.; Musial, M. Coupled-Cluster Theory in Quantum Chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef] [Green Version]
  32. Neese, F. Software update: The ORCA program system, version 4.0. Wiley Interdiscip. Rev.-Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
  33. Neese, F. The ORCA program system. Wiley Interdiscip. Rev.-Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  34. Bader, R.F.W. Atoms in Molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
  35. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  36. Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural-Population Analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
  37. Angeli, C.; Cimiraglia, R.; Malrieu, J.P. N-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants. J. Chem. Phys. 2002, 117, 9138–9153. [Google Scholar] [CrossRef]
  38. Angeli, C.; Cimiraglia, R.; Malrieu, J.P. N-electron valence state perturbation theory: A fast implementation of the strongly contracted variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
  39. Pastore, M.; Angeli, C.; Cimiraglia, R. A multireference perturbation theory study on the vertical electronic spectrum of thiophene. Theor. Chem. Acc. 2007, 118, 35–46. [Google Scholar] [CrossRef]
  40. ADF; SCM. Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands, 2017. [Google Scholar]
Molecules 28 00554 g001 550
Figure 1. Infrared spectra of the laser-ablated B atoms’ reactions with BF3 in excess solid neon. (a) co-deposition of 11B + 1.0% 11BF3 for 60 min; (b) after annealing to 8 K; (c) after λ > 300 nm irradiation for 6 min; (d) after annealing to 12 K; (e) co-deposition of 10B + 0.5% 10BF3 for 60 min; (f) after annealing to 8 K; (g) after λ > 300 nm irradiation for 6 min; (h) after annealing to 12 K.
Figure 1. Infrared spectra of the laser-ablated B atoms’ reactions with BF3 in excess solid neon. (a) co-deposition of 11B + 1.0% 11BF3 for 60 min; (b) after annealing to 8 K; (c) after λ > 300 nm irradiation for 6 min; (d) after annealing to 12 K; (e) co-deposition of 10B + 0.5% 10BF3 for 60 min; (f) after annealing to 8 K; (g) after λ > 300 nm irradiation for 6 min; (h) after annealing to 12 K.
Molecules 28 00554 g001
Molecules 28 00554 g002 550
Figure 2. Infrared spectra of the laser-ablated B react with BF3 in excess solid neon. (a) co-deposition of 10B + 1.0% 11BF3 for 60 min; (b) after annealing to 8 K; (c) after λ > 300 nm irradiation for 6 min; (d) λ > 220 nm irradiation for 6 min; (e) co-deposition of 11B + 0.5% 10BF3 for 60 min; (f) after annealing to 8 K; (g) after λ > 300 nm irradiation for 6 min; (h) λ > 220 nm for irradiation for 6 min.
Figure 2. Infrared spectra of the laser-ablated B react with BF3 in excess solid neon. (a) co-deposition of 10B + 1.0% 11BF3 for 60 min; (b) after annealing to 8 K; (c) after λ > 300 nm irradiation for 6 min; (d) λ > 220 nm irradiation for 6 min; (e) co-deposition of 11B + 0.5% 10BF3 for 60 min; (f) after annealing to 8 K; (g) after λ > 300 nm irradiation for 6 min; (h) λ > 220 nm for irradiation for 6 min.
Molecules 28 00554 g002
Molecules 28 00554 g003 550
Figure 3. Infrared spectra of the laser-ablated Al atoms reactions with BF3 in excess solid neon. (a) co-deposition of Al + 0.5% 11BF3 for 60 min; (b) after annealing to 8 K; (c) after λ = 450 nm irradiation for 6 min; (d) after annealing to 12 K; (e) co-deposition of Al + 0.5% 10BF3 for 60 min; (f) after annealing to 8 K; (g) after λ = 450 nm irradiation for 6 min; (h) after annealing to 12 K.
Figure 3. Infrared spectra of the laser-ablated Al atoms reactions with BF3 in excess solid neon. (a) co-deposition of Al + 0.5% 11BF3 for 60 min; (b) after annealing to 8 K; (c) after λ = 450 nm irradiation for 6 min; (d) after annealing to 12 K; (e) co-deposition of Al + 0.5% 10BF3 for 60 min; (f) after annealing to 8 K; (g) after λ = 450 nm irradiation for 6 min; (h) after annealing to 12 K.
Molecules 28 00554 g003
Molecules 28 00554 g004 550
Figure 4. Structures of the product F2BMF (M = B, Al) optimized using the CCSD(T)/def2-TZVP(-f) (bold and italic), CAS(9e, 11o)/def2-TZVP, BPW91/def2-TZVPP (italic) and B3LYP/def2-TZVPP (bold) functionals/basis set. The def2-TZVP(-f), def2-TZVP and def2-TZVPP basis are set for all atoms. Bond lengths are in Å and angles in degrees. The energies are in kcal/mol and relative to corresponding M + BF3 calculated by CCSD(T)/def2-TZVPP.
Figure 4. Structures of the product F2BMF (M = B, Al) optimized using the CCSD(T)/def2-TZVP(-f) (bold and italic), CAS(9e, 11o)/def2-TZVP, BPW91/def2-TZVPP (italic) and B3LYP/def2-TZVPP (bold) functionals/basis set. The def2-TZVP(-f), def2-TZVP and def2-TZVPP basis are set for all atoms. Bond lengths are in Å and angles in degrees. The energies are in kcal/mol and relative to corresponding M + BF3 calculated by CCSD(T)/def2-TZVPP.
Molecules 28 00554 g004
Molecules 28 00554 g005 550
Figure 5. Potential energy surface of group 13 atoms (B and Al) and BF3 reaction products calculated at CCSD (T)/def2-TZVPP level. Energies were given in kcal/mol.
Figure 5. Potential energy surface of group 13 atoms (B and Al) and BF3 reaction products calculated at CCSD (T)/def2-TZVPP level. Energies were given in kcal/mol.
Molecules 28 00554 g005
Molecules 28 00554 g006 550
Figure 6. (a) The active molecular orbitals of F2BBF at CASSCF (3e, 8o)/def2-TZVP level. The isosurface value is 0.04 a.u. MO occupation numbers are given with each orbital; (b) The active molecular orbitals of F2BAlF at CASSCF (3e, 8o)/def2-TZVP level. The isosurface value is 0.04 a.u. MO occupation numbers are given with each orbital; (c) Plot of the deformation densities Δρ of the F2B→BF σ donation and BF→BF2 π back-donation in F2BBF with the associated interaction energy ∆Eorb and charge eigenvalues |νn|(in e). The charge flow is from red → blue; (d) Plot of the deformation densities Δρ of the F2B→AlF σ donation and AlF→BF2 σ back-donation in F2BAlF with the associated interaction energy ∆Eorb and charge eigenvalues |νn|(in e). The charge flow is from red → blue.
Figure 6. (a) The active molecular orbitals of F2BBF at CASSCF (3e, 8o)/def2-TZVP level. The isosurface value is 0.04 a.u. MO occupation numbers are given with each orbital; (b) The active molecular orbitals of F2BAlF at CASSCF (3e, 8o)/def2-TZVP level. The isosurface value is 0.04 a.u. MO occupation numbers are given with each orbital; (c) Plot of the deformation densities Δρ of the F2B→BF σ donation and BF→BF2 π back-donation in F2BBF with the associated interaction energy ∆Eorb and charge eigenvalues |νn|(in e). The charge flow is from red → blue; (d) Plot of the deformation densities Δρ of the F2B→AlF σ donation and AlF→BF2 σ back-donation in F2BAlF with the associated interaction energy ∆Eorb and charge eigenvalues |νn|(in e). The charge flow is from red → blue.
Molecules 28 00554 g006
Table
Table 1. Observed and calculated fundamental frequencies of F2BBF and F2AlBF isotopomers in the ground 2A state.
Table 1. Observed and calculated fundamental frequencies of F2BBF and F2AlBF isotopomers in the ground 2A state.
Approximate DescriptionObs(Ne)Cal(int) aCal(int) bCal(int) cObs(Ne)Cal(int) aCal(int) bCal(int) c
BBFantisymstr/1491.2(52)1461.7(50)1466.2/1501.4(41)1471.7(37)1477.8
BF2antisymstr1336.91332.3(294)1286.7(265)1376.31369.41378.8(317)1331.6(284)1425.1
BF2symstr1202.41188.9(465)1150.9(427)1213.61223.81221.3(505)1182.6(465)1245.4
F211B10BF F210B10BF
BBFantisymstr/1538.6(70)1508.0(63)1511.4/1546.82(56)1516.6(49)1520.8
BF2antisymstr1338.71332.3(294)1286.7(265)1376.31370.61378.90(324)1331.6(284)1425.1
BF2symstr1200.81192.3(462)1154.2(424)1217.91241.61226.32(505)1187.3(463)1251.9
F211BAlF F210BAlF
BF2antisymmstr1281.51312.0(277)1270.9(257)1342.11324.61357.4(299)1314.9(275)1389.1
BF2symstr1180.81172.2(320)1133.9(309)1190.31217.11208.2(378)1168.8(336)1227.4
AlFstr819.6806.7(106)780.1(98)814.5819.6806.8(106)780.2(98)814.6
The vibrational frequencies (cm−1) and intensities (km/mol, in parentheses) are calculated using: a B3LYP/def2-TZVPP; b BPW91/def2-TZVPP; c CCSD(T)/def2-TZVP(-f) functionals/basis set.
Table
Table 2. The results of EDA-NOCV theory for F2BMF at B3LYP/TZ2P.
Table 2. The results of EDA-NOCV theory for F2BMF at B3LYP/TZ2P.
OrbitalsF2BBF (2A)OrbitalsF2BAlF (2A)
ΔEint−148.3ΔEint−28.84
ΔEPauli97.5ΔEPauli111.5
ΔEelstat−53.0 (21.5%)ΔEelstat−60.4 (42.8%)
ΔEorb−193.9 (78.5%)ΔEorb−80.7 (57.2%)
ΔEσ−82.82 (42.7%)ΔEσ−29.9 (37.1%)
ΔEπ−104.0 (53.6%)ΔEσ−42.2 (52.3%)
ΔEorb(rest)−7.1 (3.7%)ΔEorb(rest)−8.6 (15.6%)
ΔEdist1.1ΔEdist0.76
Energy values are given in kcal/mol.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Cheng, J.; Cai, L.; Pu, Z.; Xu, B.; Wang, X. F2BMF (M = B and Al) Molecules: A Matrix Infrared Spectra and Theoretical Calculations Investigation. Molecules 2023, 28, 554. https://doi.org/10.3390/molecules28020554

AMA Style

Cheng J, Cai L, Pu Z, Xu B, Wang X. F2BMF (M = B and Al) Molecules: A Matrix Infrared Spectra and Theoretical Calculations Investigation. Molecules. 2023; 28(2):554. https://doi.org/10.3390/molecules28020554

Chicago/Turabian Style

Cheng, Juanjuan, Liyan Cai, Zhen Pu, Bing Xu, and Xuefeng Wang. 2023. "F2BMF (M = B and Al) Molecules: A Matrix Infrared Spectra and Theoretical Calculations Investigation" Molecules 28, no. 2: 554. https://doi.org/10.3390/molecules28020554

APA Style

Cheng, J., Cai, L., Pu, Z., Xu, B., & Wang, X. (2023). F2BMF (M = B and Al) Molecules: A Matrix Infrared Spectra and Theoretical Calculations Investigation. Molecules, 28(2), 554. https://doi.org/10.3390/molecules28020554

Article Metrics

Back to TopTop