Investigating the Influence of Diffusion on the Cohesive Zone Model of the SiC/Al Composite Interface
Abstract
:1. Introduction
2. Simulation Results and Discussion
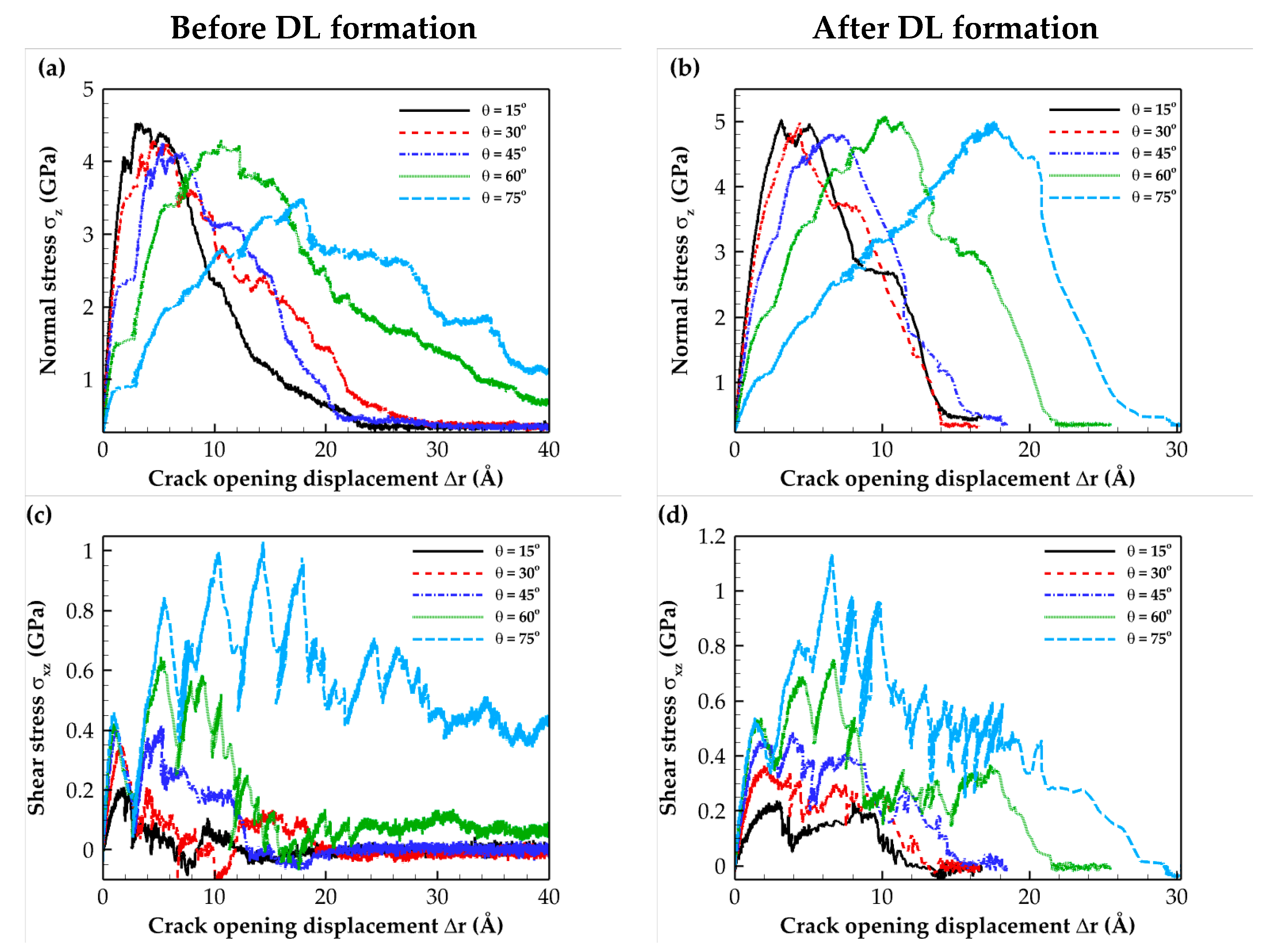
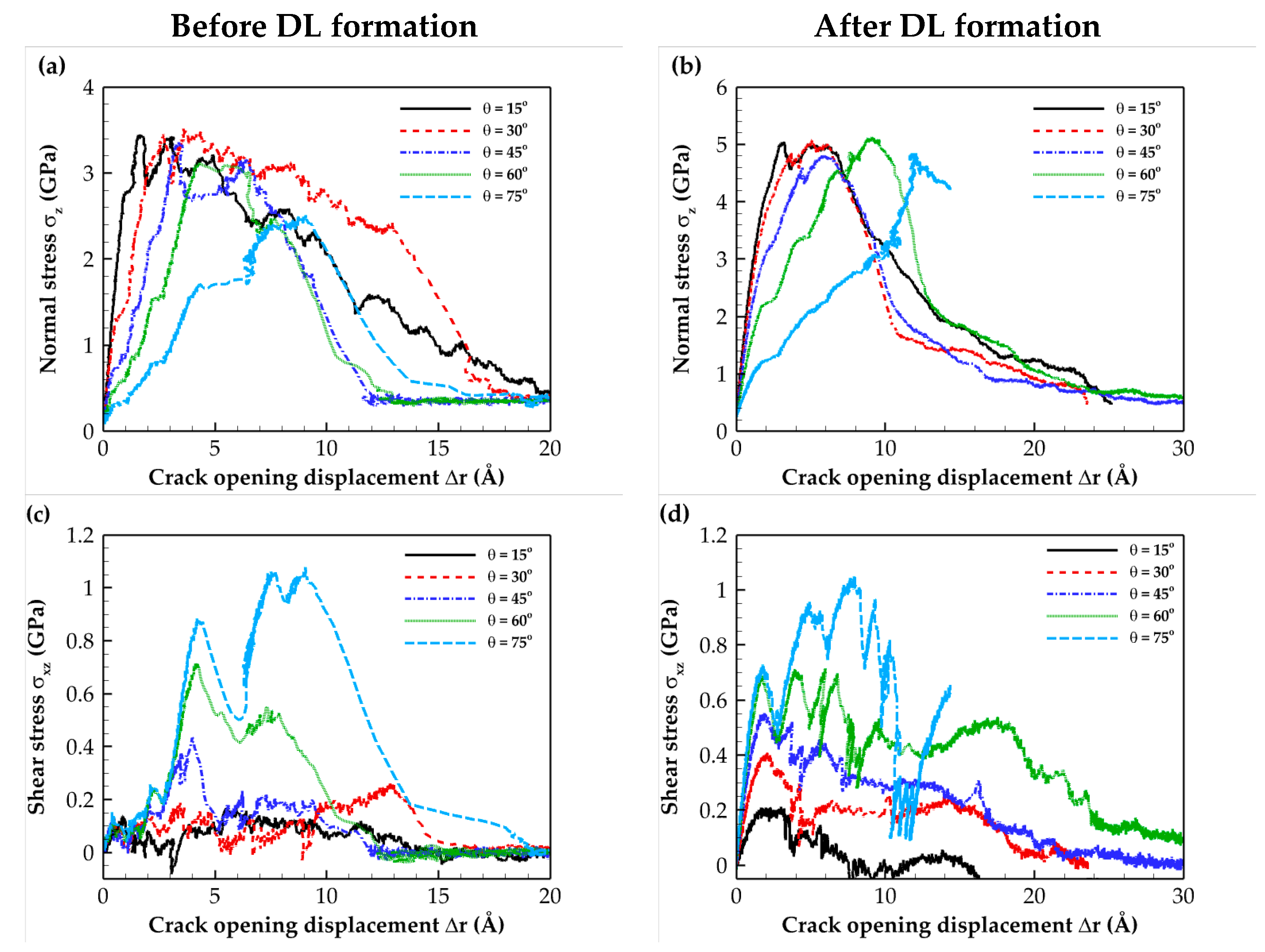
2.1. Crack Growth Process
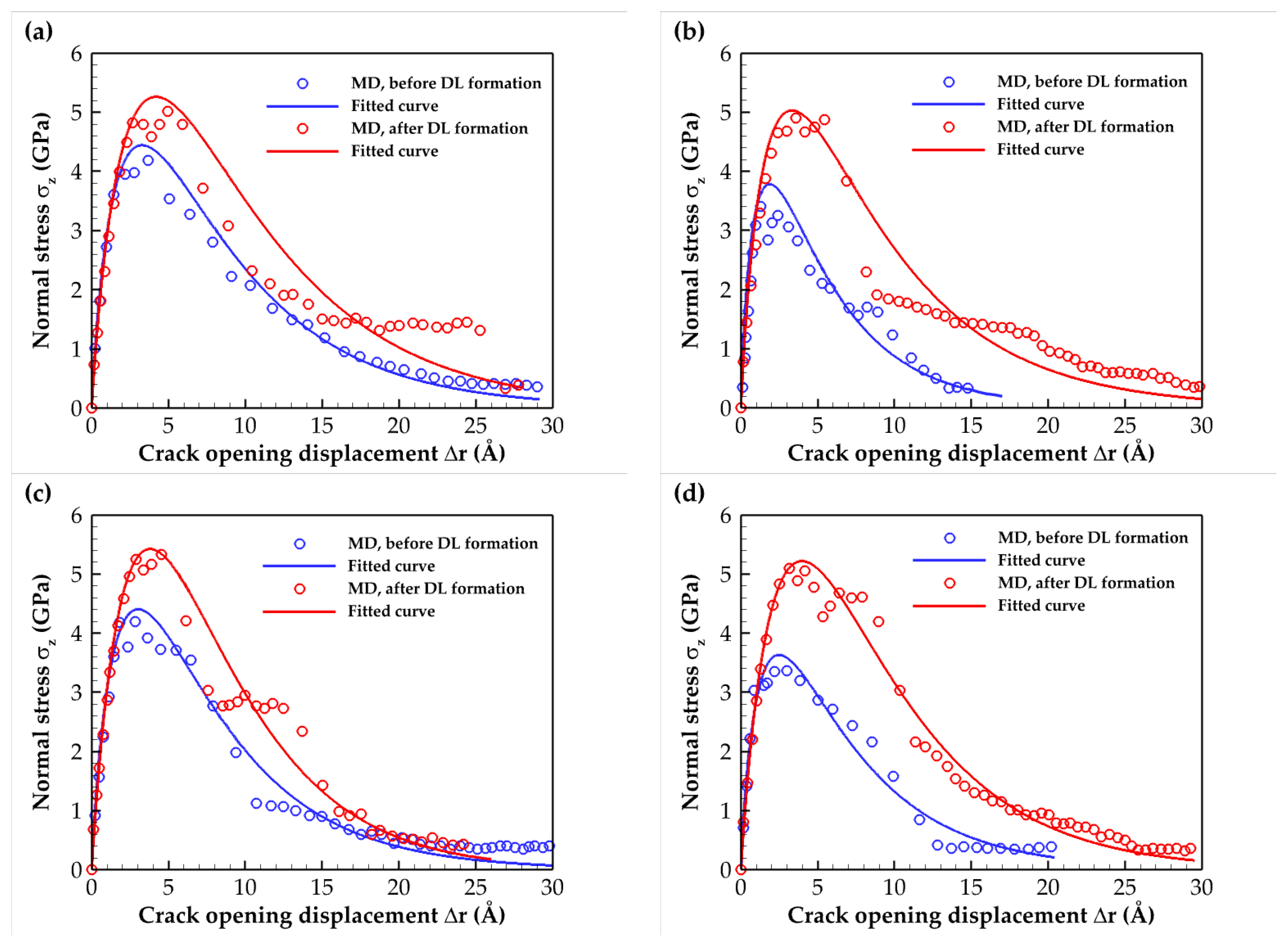
2.2. Traction–Separation Response
2.3. Cohesive Zone Model
3. Simulation Methodology
3.1. Potential Functions
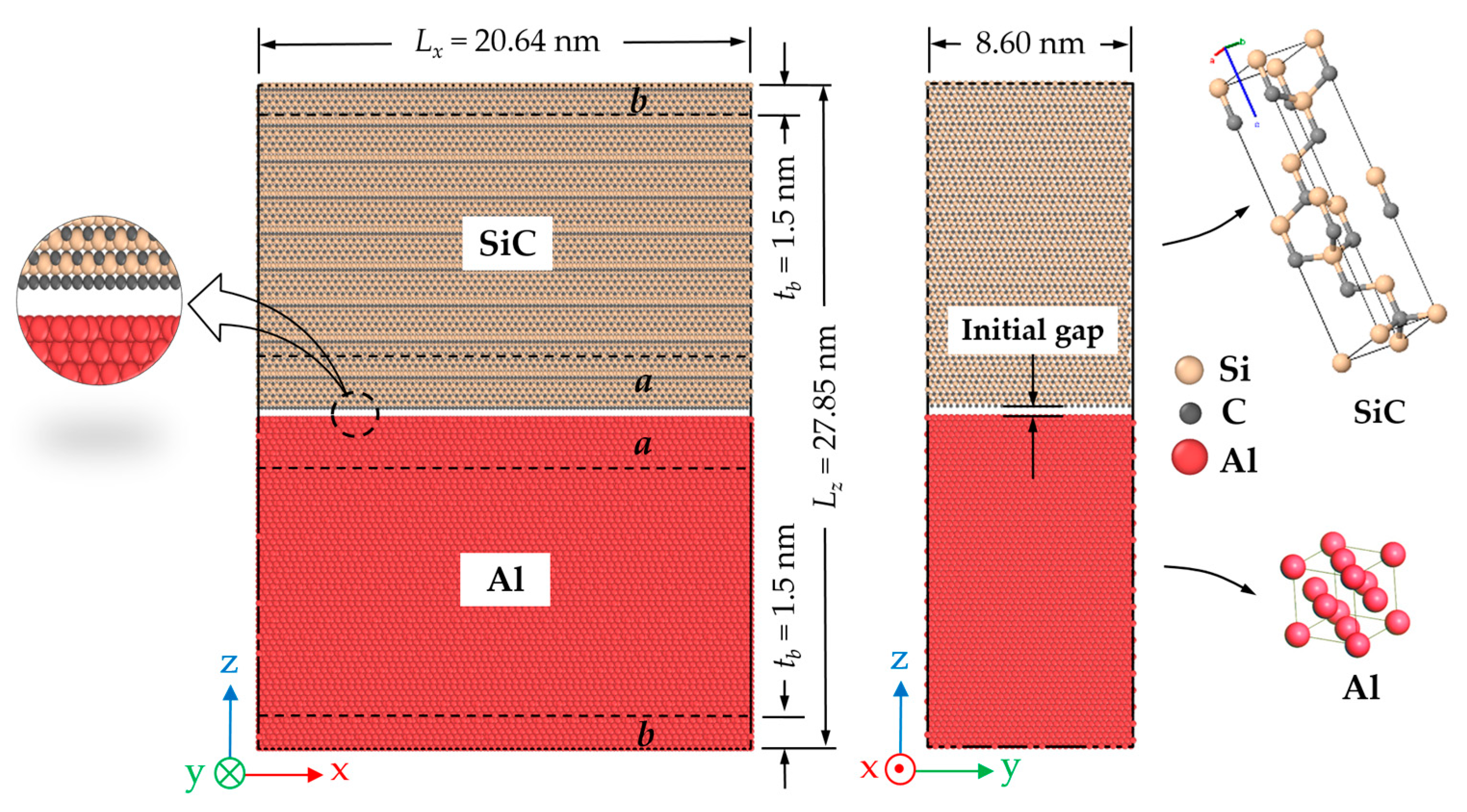
3.2. Molecular Dynamics Model
3.3. Loading Conditions
4. Conclusions
- The formation of the diffusion layer did not cause a significant effect on the elastic and shear moduli.
- The tensile and shear strengths of the Si-terminated interfaces were lower than those of their C-terminated counterparts before heat treatment. However, after heat treatment, the strengths of the two interfaces approached each other.
- The formation of a diffusion layer increased the tensile strength of the C- and Si-terminated interfaces by about 20% and 40%, respectively, compared with the interfaces before heat treatment.
- Following heat treatment, the work of separation increased by approximately 30% and 100% for the C- and Si-terminated interfaces, respectively.
- The shear strength was significantly lower than the tensile strength at the 6H-SiC(0001)/Al(111) and 3C-SiC(111)/Al(111) interfaces. Therefore, there was no direct correlation between shear and tensile strengths for these interfaces, unlike isotropic materials, where the shear strength was about half that of the tensile strength.
- The existing continuum-based cohesive zone model was consistent with the proposed traction–separation law based on the MD results.
- The hierarchical multiscale modeling of the interface in finite element software can be done using the cohesive zone model obtained from the MD simulations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Rajan, T.P.D.; Pillai, R.M.; Pai, B.C. Reinforcement coatings and interfaces in aluminium metal matrix composites. J. Mater. Sci. 1998, 33, 3491–3503. [Google Scholar] [CrossRef]
- Kim, J.-K.; Tjong, S.C.; Mai, Y.-W. Effect of interface strength on metal matrix composites properties. In Comprehensive Composite Materials II; Beaumont, P.W.R., Zweben, C.H., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 4, pp. 22–59. [Google Scholar]
- Postek, E.; Sadowski, T. Dynamic pulse sensitivity of WC/Co composite. Comp. Struct. 2018, 203, 498–512. [Google Scholar] [CrossRef]
- Postek, E.; Sadowski, T. Distributed microcracking process of WC/Co cermet under dynamic impulse compressive loading. Comp. Struct. 2018, 194, 494–508. [Google Scholar] [CrossRef]
- Zhou, X.W.; Moody, N.R.; Jones, R.E.; Zimmerman, J.A.; Reedy, E.D. Molecular-dynamics-based cohesive zone law for brittle interfacial fracture under mixed loading conditions: Effects of elastic constant mismatch. Acta Mater. 2009, 57, 4671–4686. [Google Scholar] [CrossRef]
- Noreyan, A.; Qi, Y.; Stoilov, V. Critical shear stresses at aluminum–silicon interfaces. Acta Mater. 2008, 56, 3461–3469. [Google Scholar] [CrossRef]
- Dandekar, C.R.; Shin, Y.C. Molecular dynamics based cohesive zone law for describing Al–SiC interface mechanics. Compos. Part A Appl. Sci. 2011, 42, 355–363. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, Y.; Wang, T.; Liu, Q.; Lu, Z. Crack propagation behaviors at Cu/SiC interface by molecular dynamics simulation. Comput. Mater. Sci. 2014, 82, 17–25. [Google Scholar] [CrossRef]
- Zhou, X.; Bu, W.; Song, S.; Sansoz, F.; Huang, X. Multiscale modeling of interfacial mechanical behaviours of SiC/Mg nanocomposites. Mater. Des. 2019, 182, 108093. [Google Scholar] [CrossRef]
- Fathalian, M.; Postek, E.; Sadowski, T. Mechanical and electronic properties of Al(111)/6H-SiC interfaces: A DFT study. Molecules 2023, 28, 4345. [Google Scholar] [CrossRef]
- Chang, H.C.; Le May, C.Z.; Wallace, L.F. Use of silicon carbide in high temperature transistors. In Proceedings of the Conference of Silicon Carbide, Boston, MA, USA; 1960; pp. 496–507. [Google Scholar]
- Tajima, Y.; Kijima, K.; Kingery, W.D. Diffusion of ion implanted aluminum in silicon carbide. Chem. Phys. 1982, 77, 2592–2598. [Google Scholar] [CrossRef]
- Sozhamannan, G.G.; Prabu, S.B. Influence of interface compounds on interface bonding characteristics of aluminium and silicon carbide. Mater. Charact. 2009, 60, 986–990. [Google Scholar] [CrossRef]
- Müting, J.; Bobal, V.; Willinger, M.G.; Zadeh, A.B.; Reidt, S.; Vines, L.; Grossner, U. Spatially resolved diffusion of aluminum in 4H-SiC during postimplantation annealing. IEEE Trans. Electron. Devices 2020, 67, 4360–4365. [Google Scholar] [CrossRef]
- Tahani, M.; Postek, E.; Sadowski, T. Molecular dynamics study of interdiffusion for cubic and hexagonal SiC/Al interfaces. Crystals 2023, 13, 46. [Google Scholar] [CrossRef]
- Tahani, M.; Postek, E.; Motevalizadeh, L.; Sadowski, T. Effect of vacancy defect content on the interdiffusion of cubic and hexagonal SiC/Al interfaces: A molecular dynamics study. Molecules 2023, 28, 744. [Google Scholar] [CrossRef]
- Luo, M.; Liang, L.; Lang, L.; Xiao, S.; Hu, W.; Deng, H. Molecular dynamics simulations of the characteristics of Mo/Ti interfaces. Comput. Mater. Sci. 2018, 141, 293–301. [Google Scholar] [CrossRef]
- Ouyang, Y.; Wu, J.; Wen, J.; Chen, H.; Zhou, Y.; Tao, X.; Du, Y. Molecular dynamics simulation of diffusion for Ni–Zr interface. Int. J. Mod. Phys. B 2020, 34, 2050217. [Google Scholar] [CrossRef]
- Zhu, Y.; Liao, G.; Shi, T.; Tang, Z.; Li, M. Interdiffusion cross crystal-amorphous interface: An atomistic simulation. Acta Mater. 2016, 112, 378–389. [Google Scholar] [CrossRef]
- Tahani, M.; Postek, E.; Sadowski, T. Diffusion and interdiffusion study at Al- and O-terminated Al2O3/AlSi12 interface using molecular dynamics simulations. Materials 2023, 16, 4324. [Google Scholar] [CrossRef]
- Feldman, D.W.; Parker, J.H.; Choyke, W.J.; Patrick, L. Phonon dispersion curves by Raman scattering in SiC, Polytypes 3C, 4H, 6H, 15R, and 21R. Phys. Rev. 1968, 173, 787–793. [Google Scholar] [CrossRef]
- Vallin, J.; Mongy, M.; Salama, K.; Beckman, O. Elastic constants of aluminum. J. Appl. Phys. 1964, 35, 1825–1826. [Google Scholar] [CrossRef]
- Hoekstra, J.; Kohyama, M. Ab initio calculations of the β-SiC(001)/Al interface. Phys. Rev. B 1998, 57, 2334–2341. [Google Scholar] [CrossRef]
- Wang, C.; Chen, W.; Jia, Y.; Xie, J. Calculating study on properties of Al (111)/6H-SiC (0001) interfaces. Metals 2020, 10, 1197. [Google Scholar] [CrossRef]
- Paliwal, B.; Cherkaoui, M. An improved atomistic simulation based mixed-mode cohesive zone law considering non-planar crack growth. Int. J. Solids Struct. 2013, 50, 3346–3360. [Google Scholar] [CrossRef]
- Santhosh Kumar, S.; Seshu Bai, V.; Rajkumar, K.V.; Sharma, G.K.; Jayakumar, T.; Rajasekharan, T. Elastic modulus of Al–Si/SiC metal matrix composites as a function of volume fraction. J. Phys. D Appl. Phys. 2009, 42, 175504. [Google Scholar] [CrossRef]
- Ren, S.; Qu, X.; Guo, J.; He, X.; Qin, M.; Shen, X. Net-shape forming and properties of high volume fraction SiCp/Al composites. J. Alloys Compd. 2009, 484, 256–262. [Google Scholar] [CrossRef]
- Griffith, A.A.; Taylor, G.I., VI. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. Ser. A 1921, 221, 163–198. [Google Scholar] [CrossRef]
- Izumi, S.; Hara, S.; Kumagai, T.; Sakai, S. A method for calculating surface stress and surface elastic constants by molecular dynamics: Application to the surface of crystal and amorphous silicon. Thin Solid Films 2004, 467, 253–260. [Google Scholar] [CrossRef]
- Rohatgi, P. Nucleation phenomenon during solidification of metal matrix composites. Mater. Sci. Eng. A 1993, 162, 163–174. [Google Scholar] [CrossRef]
- Bakshi, S.R.; Keshri, A.K.; Singh, V.; Seal, S.; Agarwal, A. Interface in carbon nanotube reinforced aluminum silicon composites: Thermodynamic analysis and experimental verification. J. Alloys Compd. 2009, 481, 207–213. [Google Scholar] [CrossRef]
- Needleman, A. An analysis of tensile decohesion along an interface. J. Mech. Phys. Solids 1990, 38, 289–324. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mat. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Kramer, M.J.; Becker, C.A.; Asta, M. Analysis of semi-empirical interatomic potentials appropriate for simulation of crystalline and liquid Al and Cu. Philos. Mag. 2008, 88, 1723–1750. [Google Scholar] [CrossRef]
- Mishin, Y.; Farkas, D.; Mehl, M.J.; Papaconstantopoulos, D.A. Interatomic potentials for monoatomic metals from experimental data and ab initio calculations. Phys. Rev. B 1999, 59, 3393–3407. [Google Scholar] [CrossRef]
- Erhart, P.; Albe, K. Analytical potential for atomistic simulations of silicon, carbon, and silicon carbide. Phys. Rev. B 2005, 71, 035211. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, N. An inverse adhesion problem for extracting interfacial pair potentials for the Al(0 0 1)/3C SiC(0 0 1) interface. Inverse Probl. 2008, 24, 035019. [Google Scholar] [CrossRef]
- Purja Pun, G.P.; Yamakov, V.; Mishin, Y. Interatomic potential for the ternary Ni–Al–Co system and application to atomistic modeling of the B2–L10 martensitic transformation. Model. Simul. Mat. Sci. Eng. 2015, 23, 065006. [Google Scholar] [CrossRef]
- Vashishta, P.; Kalia, R.K.; Nakano, A.; Rino, J.P. Interaction potential for silicon carbide: A molecular dynamics study of elastic constants and vibrational density of states for crystalline and amorphous silicon carbide. J. Appl. Phys. 2007, 101, 103515. [Google Scholar] [CrossRef]
- Li, S.; Arsenault, R.J.; Jena, P. Quantum chemical study of adhesion at the SiC/Al interface. J. Appl. Phys. 1988, 64, 6246–6253. [Google Scholar] [CrossRef]
- Geng, L.; Zhang, J.; Meng, Q.-C.; Yao, C.-K. Side-surface structure of a commercial β-silicon carbide whisker. J. Am. Ceram. 2002, 85, 2864–2866. [Google Scholar] [CrossRef]
- Vedeneyev, V.T. Bond Energies Ionization Potentials and Electron Affinities; Edward Arnold Publishers: London, UK, 1966. [Google Scholar]
- Hou, Z.Y.; Dong, K.J.; Tian, Z.A.; Liu, R.S.; Wang, Z.; Wang, J.G. Cooling rate dependence of solidification for liquid aluminium: A large-scale molecular dynamics simulation study. Phys. Chem. Chem. Phys. 2016, 18, 17461–17469. [Google Scholar] [CrossRef] [PubMed]


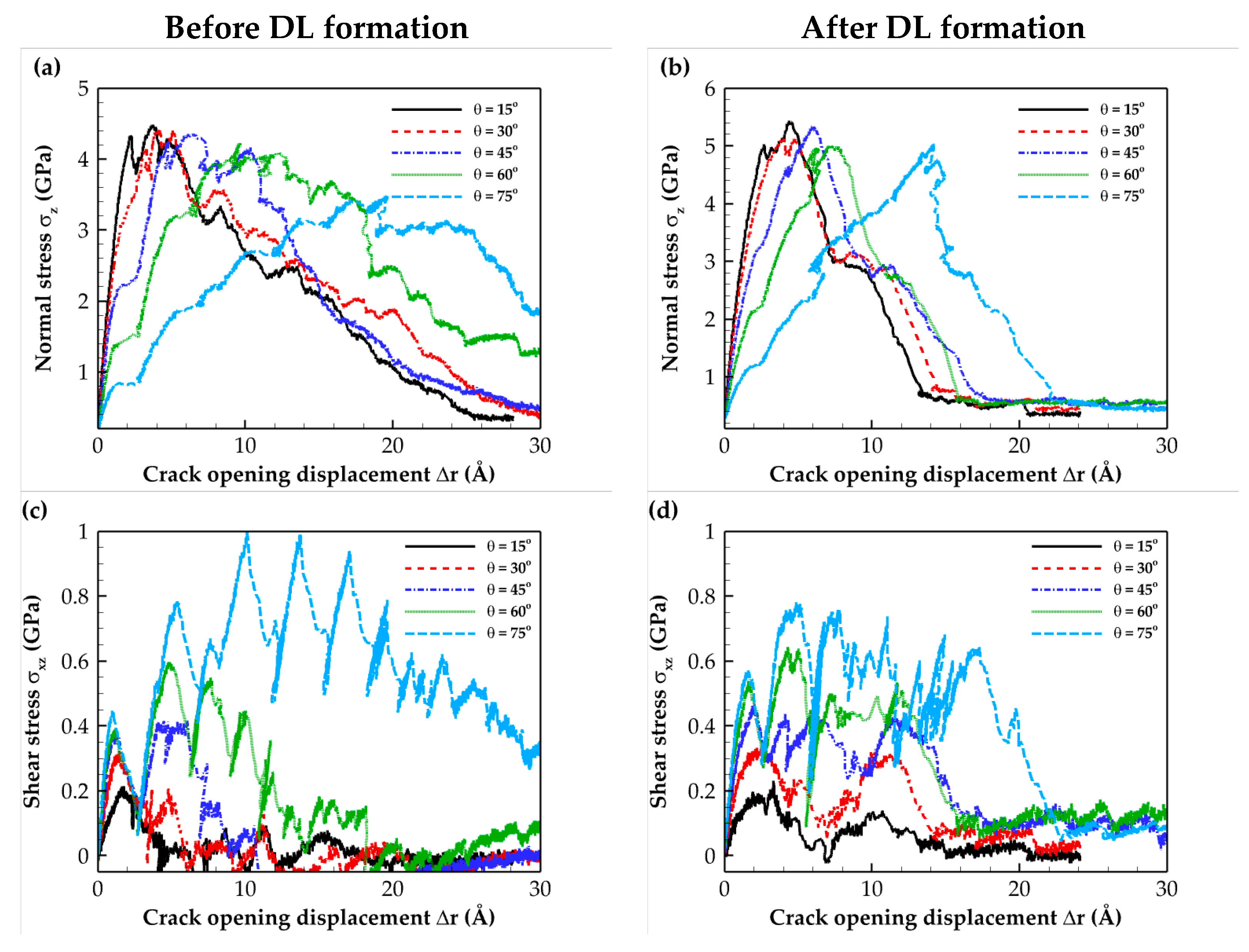
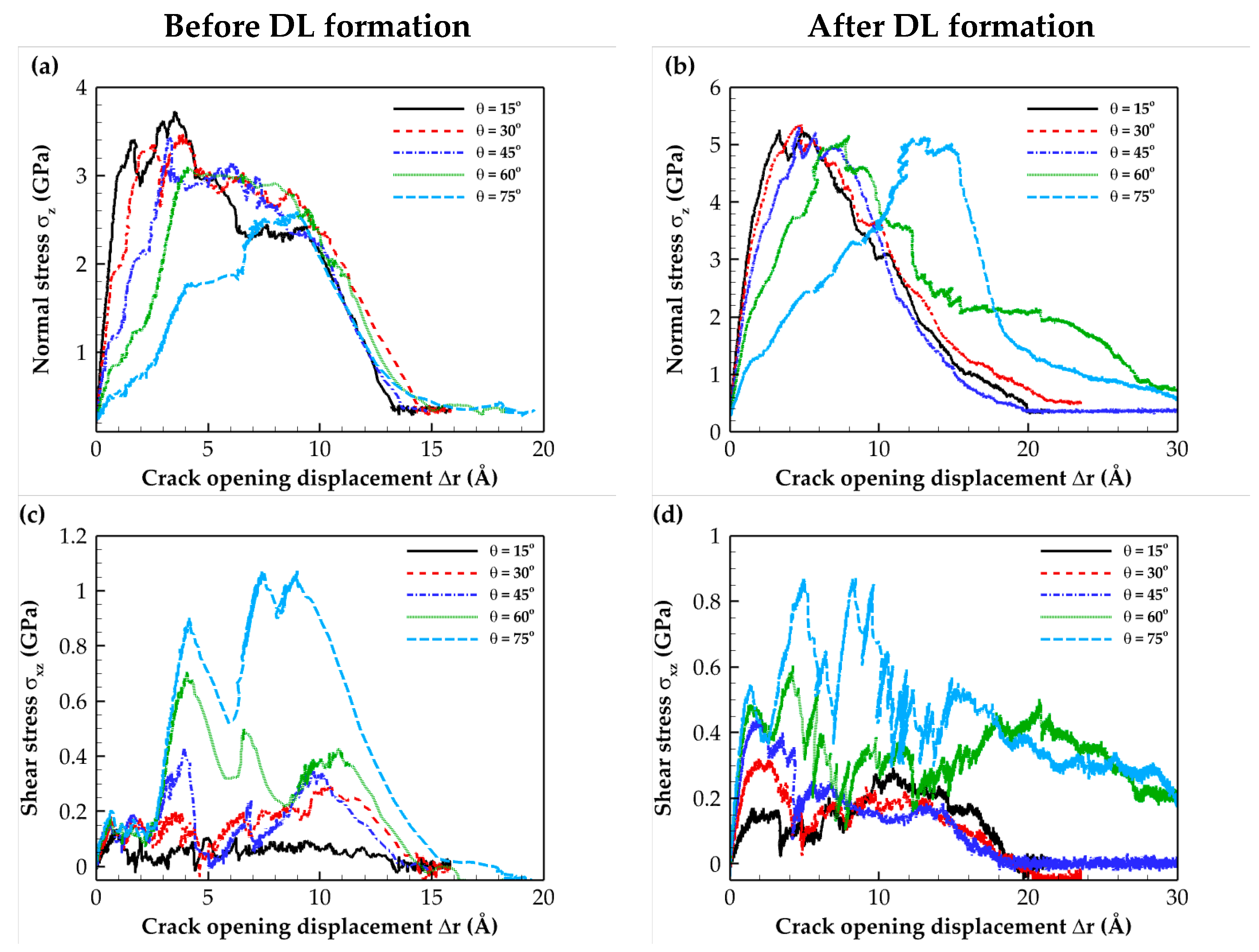
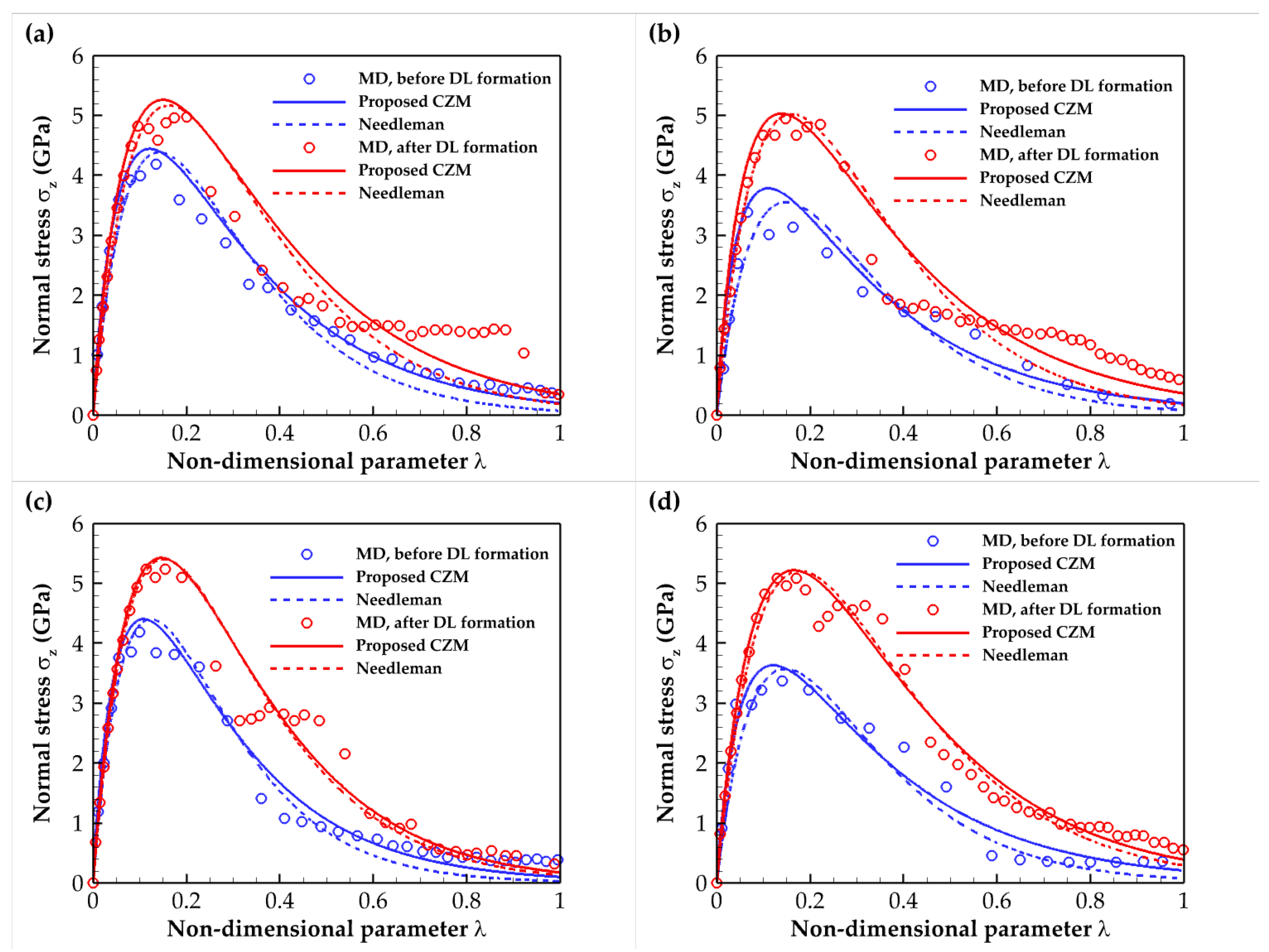
| Composite Material | Annealing Condition | E (GPa) | σmax (GPa) | Toughness (109 J/m3) | Work of Separation (J/m2) |
|---|---|---|---|---|---|
| C-terminated 6H-SiC/Al | Before DL formation | 161.7 | 4.39 | 0.174 | 4.81 |
| After DL formation | 163.5 | 5.17 | 0.231 | 6.41 | |
| Si-terminated 6H-SiC/Al | Before DL formation | 162.9 | 3.55 | 0.052 | 2.49 |
| After DL formation | 164.7 | 5.02 | 0.217 | 5.59 | |
| C-terminated 3C-SiC/Al | Before DL formation | 165.5 | 4.40 | 0.164 | 4.50 |
| After DL formation | 167.4 | 5.40 | 0.183 | 5.71 | |
| Si-terminated 3C-SiC/Al | Before DL formation | 163.7 | 3.57 | 0.071 | 3.17 |
| After DL formation | 166.0 | 5.21 | 0.232 | 6.21 |
| 6H-SiC/Al | 3C-SiC/Al | |||
|---|---|---|---|---|
| C-Terminated | Si-Terminated | C-Terminated | Si-Terminated | |
| woa (J/m2) | 1.09 | 0.74 | 1.12 | 0.86 |
| σmax (GPa) (Equation (2)) | 5.24 | 4.38 | 5.43 | 4.73 |
| Composite Material | Annealing Condition | G (GPa) | τmax (GPa) |
|---|---|---|---|
| C-terminated 6H-SiC/Al | Before DL formation | 36.9 | 1.71 |
| After DL formation | 36.5 | 1.80 | |
| Si-terminated 6H-SiC/Al | Before DL formation | 39.2 | 1.12 |
| After DL formation | 35.2 | 1.82 | |
| C-terminated 3C-SiC/Al | Before DL formation | 39.8 | 1.72 |
| After DL formation | 32.2 | 1.60 | |
| Si-terminated 3C-SiC/Al | Before DL formation | 33.1 | 1.39 |
| After DL formation | 30.7 | 1.65 |
| θ (°) | vx (Å/ps) | vz (Å/ps) |
|---|---|---|
| 0 | 0 | 0.01225 |
| 15 | 0.00317 | 0.01183 |
| 30 | 0.00612 | 0.01060 |
| 45 | 0.00866 | 0.00866 |
| 60 | 0.01060 | 0.00612 |
| 75 | 0.01183 | 0.00317 |
| 90 | 0.01225 | 0 |
| Composite Material | Annealing Condition | σmax | δn (Å) | α | β |
|---|---|---|---|---|---|
| C-terminated 6H-SiC/Al | Before DL formation | 4.39 | 27 | 0.759 | 0.663 |
| After DL formation | 5.17 | 28 | 0.703 | 0.414 | |
| Si-terminated 6H-SiC/Al | Before DL formation | 3.55 | 17 | 0.689 | 0.939 |
| After DL formation | 5.02 | 24 | 0.764 | 0.732 | |
| C-terminated 3C-SiC/Al | Before DL formation | 4.40 | 28 | 0.783 | 0.816 |
| After DL formation | 5.40 | 28 | 0.932 | 0.859 | |
| Si-terminated 3C-SiC/Al | Before DL formation | 3.57 | 20 | 0.724 | 0.621 |
| After DL formation | 5.21 | 24 | 0.880 | 0.829 |
| Material | Method | C11 (GPa) | C12 (GPa) | C44 (GPa) | K (GPa) | E (GPa) | G (GPa) | ν |
|---|---|---|---|---|---|---|---|---|
| Al | Present a | 107.03 | 61.06 | 31.05 | 76.38 | 62.67 | 22.99 | 0.363 |
| Present b | 105.09 | 59.46 | 30.66 | 74.67 | 62.12 | 22.82 | 0.361 | |
| MD c | 107.21 | 60.60 | 32.88 | 76.14 | 63.44 | 23.31 | 0.361 | |
| Experiment d | 107.3 | 60.08 | 28.3 | 75.7 | 63.83 | 23.48 | 0.359 | |
| 3C-SiC | Present | 383.78 | 144.41 | 239.75 | 224.20 | 304.81 | 119.68 | 0.273 |
| MD e | 390.1 | 142.7 | 191.0 | 225.1 | 313.6 | 123.7 | 0.268 | |
| Experiment f | 390 | 142 | 256 | 225 | 314.2 | 124 | 0.267 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tahani, M.; Postek, E.; Sadowski, T. Investigating the Influence of Diffusion on the Cohesive Zone Model of the SiC/Al Composite Interface. Molecules 2023, 28, 6757. https://doi.org/10.3390/molecules28196757
Tahani M, Postek E, Sadowski T. Investigating the Influence of Diffusion on the Cohesive Zone Model of the SiC/Al Composite Interface. Molecules. 2023; 28(19):6757. https://doi.org/10.3390/molecules28196757
Chicago/Turabian StyleTahani, Masoud, Eligiusz Postek, and Tomasz Sadowski. 2023. "Investigating the Influence of Diffusion on the Cohesive Zone Model of the SiC/Al Composite Interface" Molecules 28, no. 19: 6757. https://doi.org/10.3390/molecules28196757
APA StyleTahani, M., Postek, E., & Sadowski, T. (2023). Investigating the Influence of Diffusion on the Cohesive Zone Model of the SiC/Al Composite Interface. Molecules, 28(19), 6757. https://doi.org/10.3390/molecules28196757








