Exploring the Mechanism of the Intramolecular Diels–Alder Reaction of (2E,4Z,6Z)-2(allyloxy)cycloocta-2,4,6-trien-1-one Using Bonding Evolution Theory
Abstract
:1. Introduction
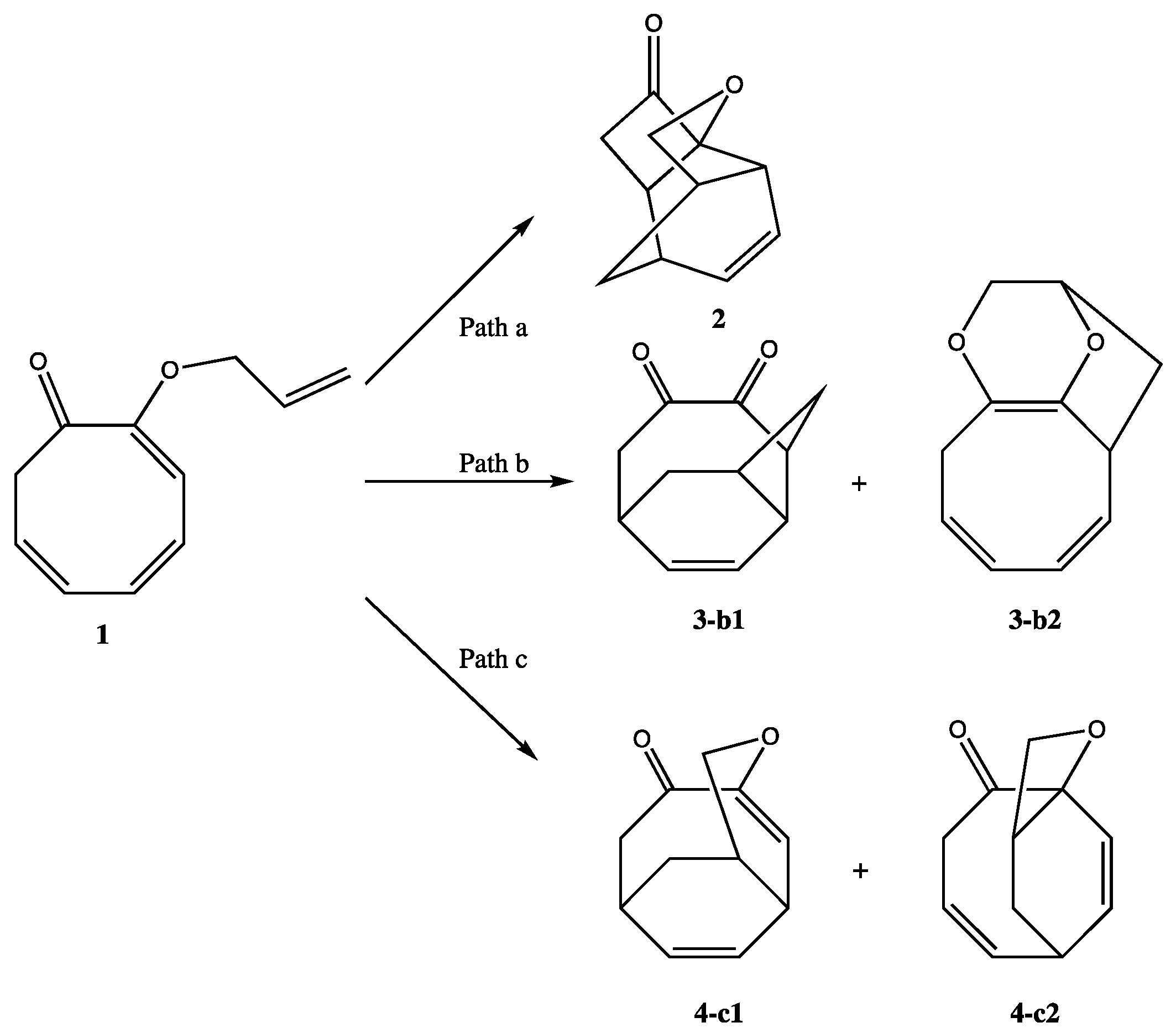
2. Results and Discussion
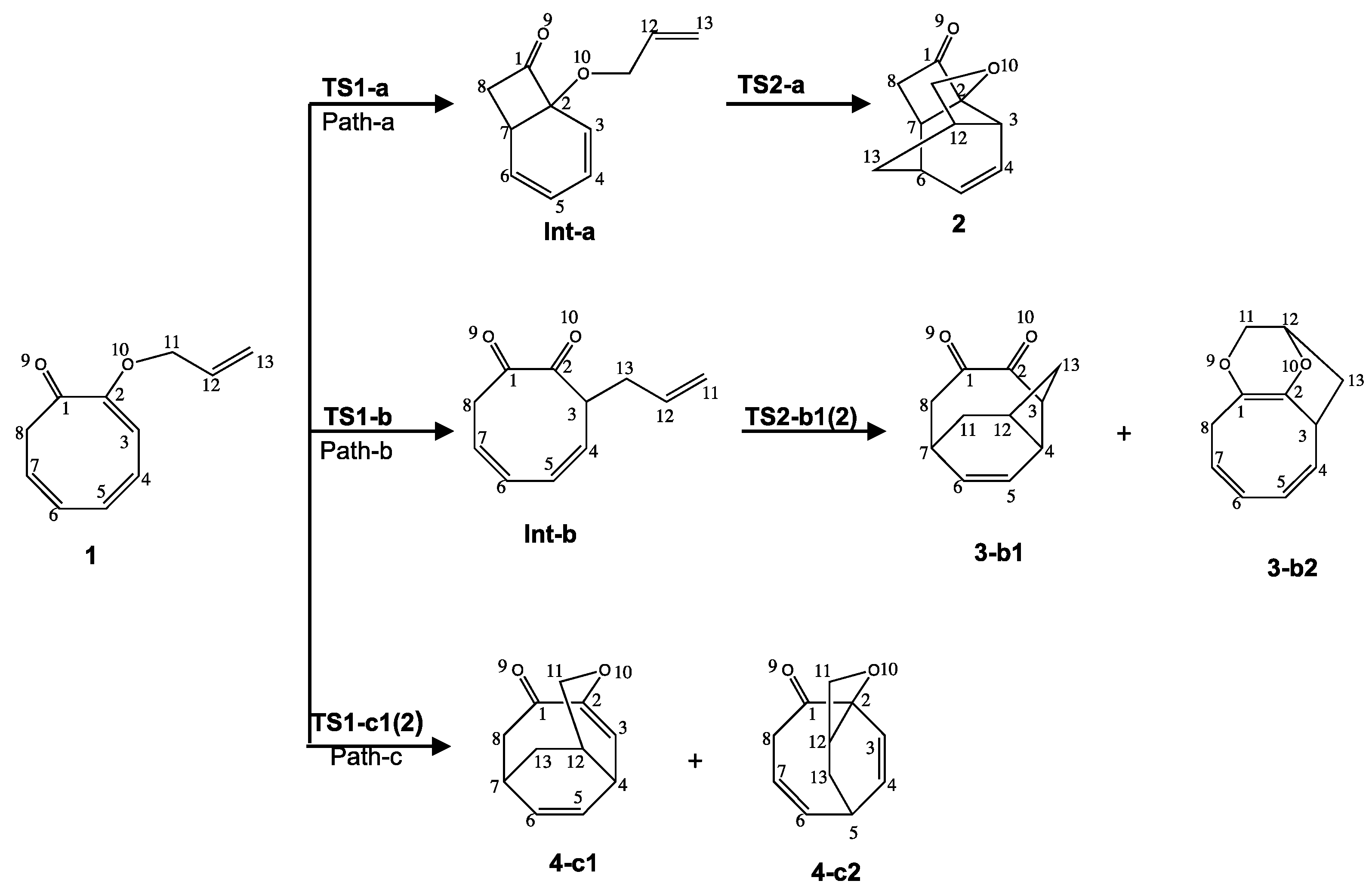
2.1. Thermodynamic and Geometrical Aspects
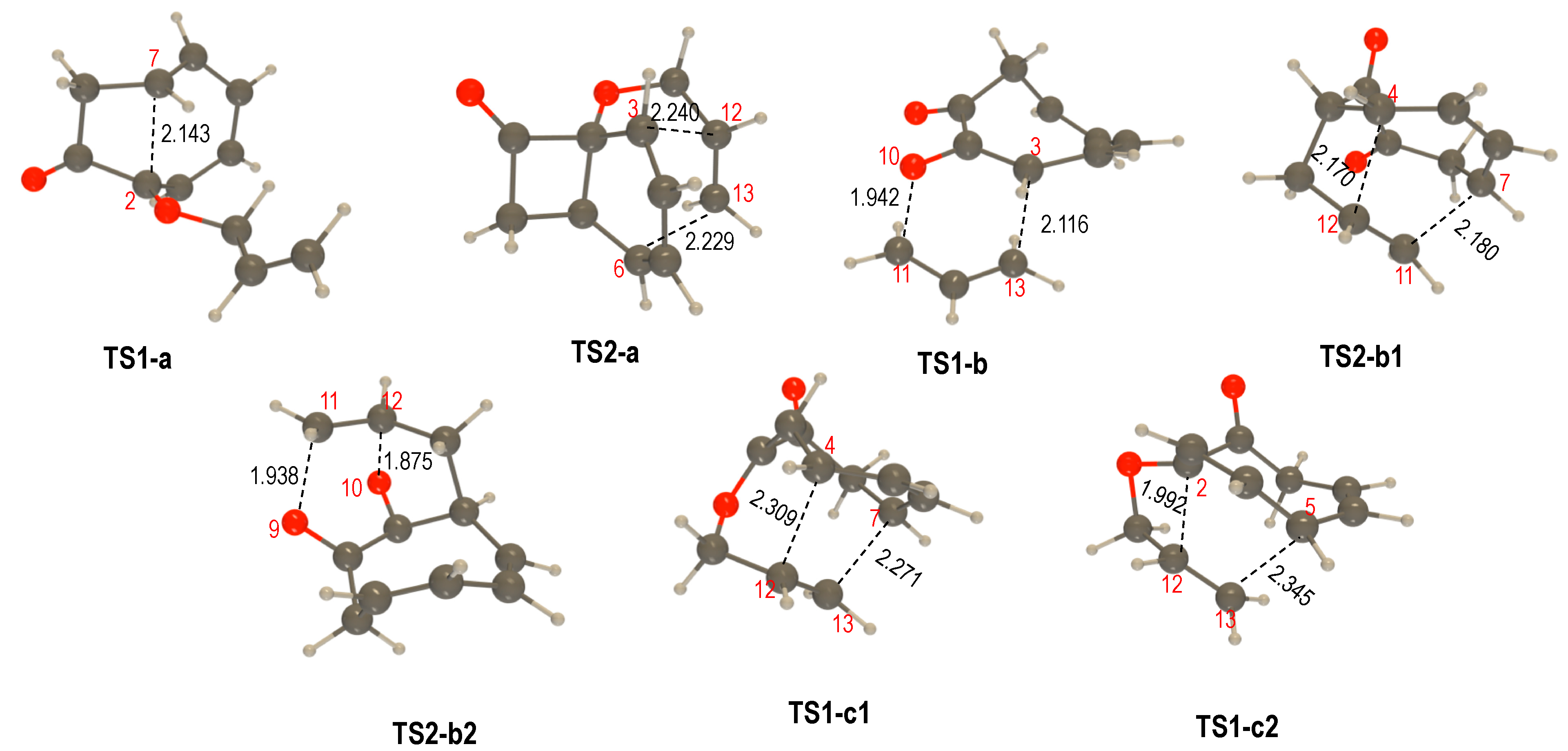
2.2. QTAIM Analysis of the Transition State Structures
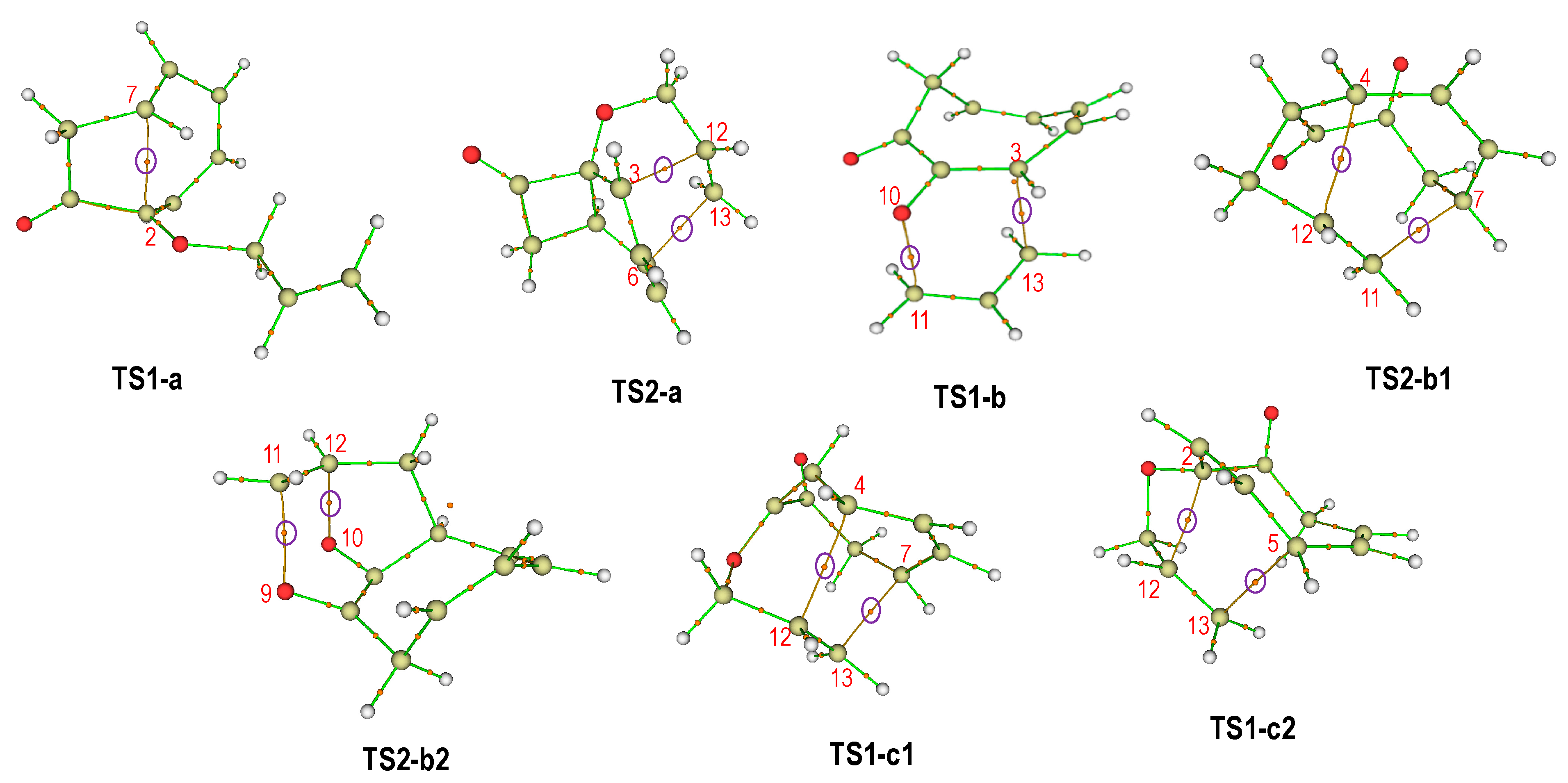
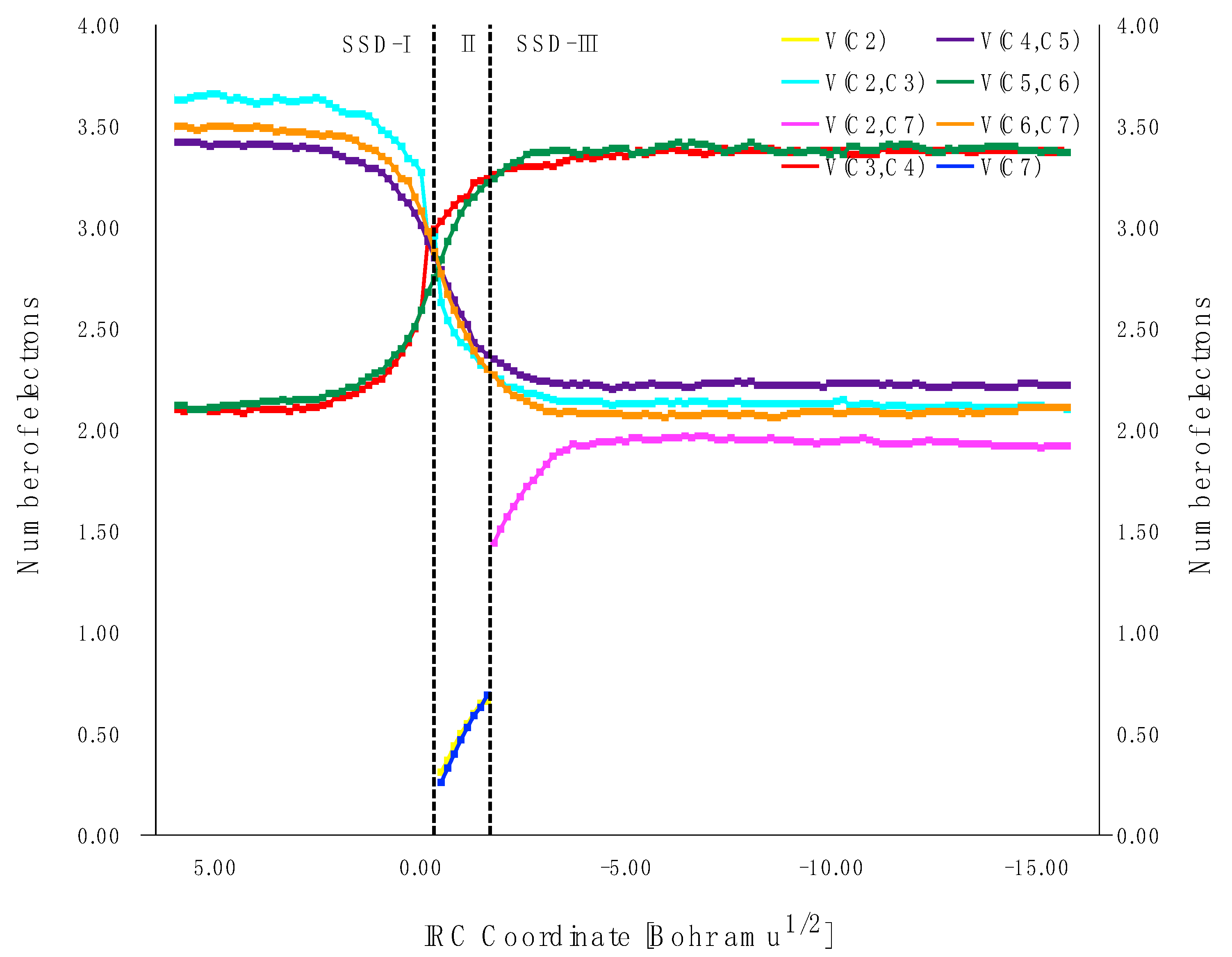
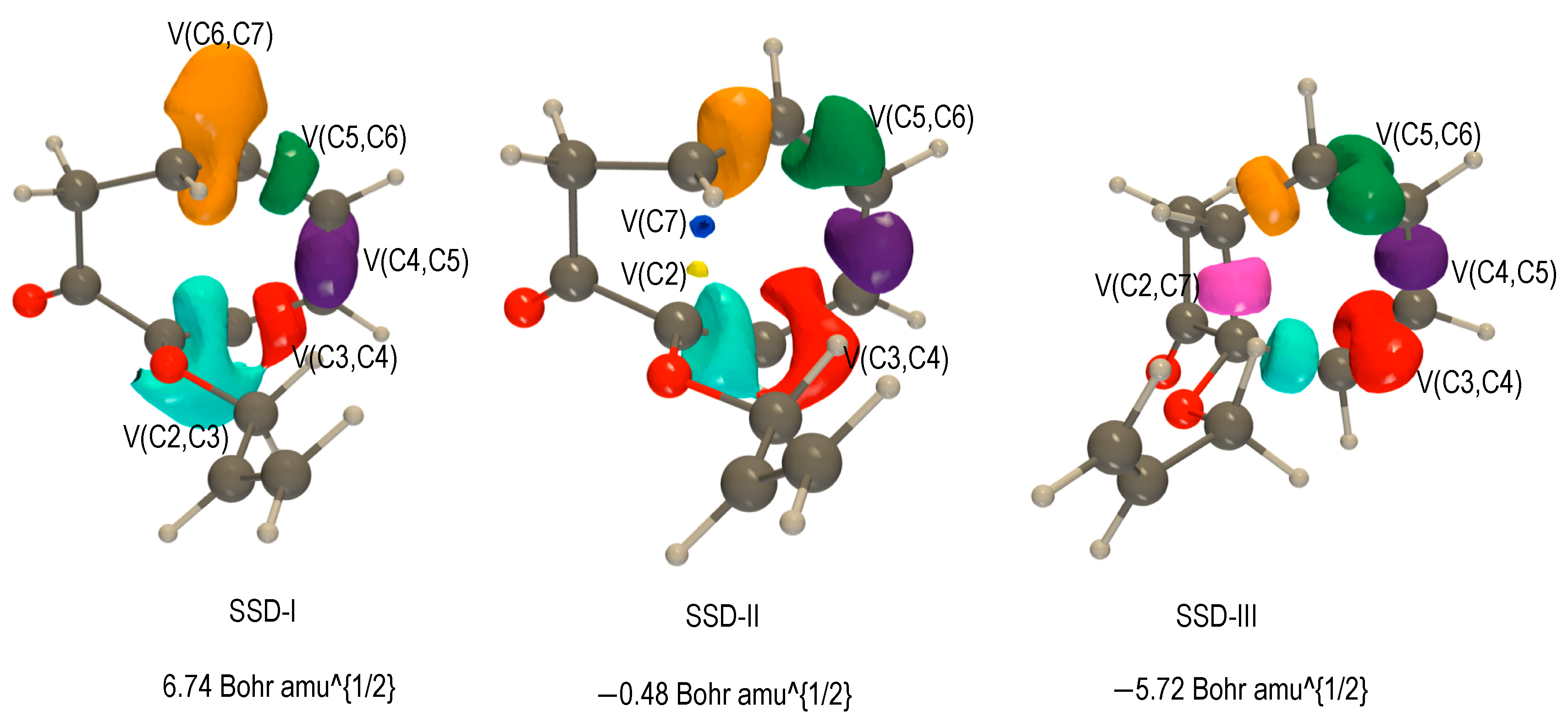
2.3. BET Analysis along Different Reaction Paths
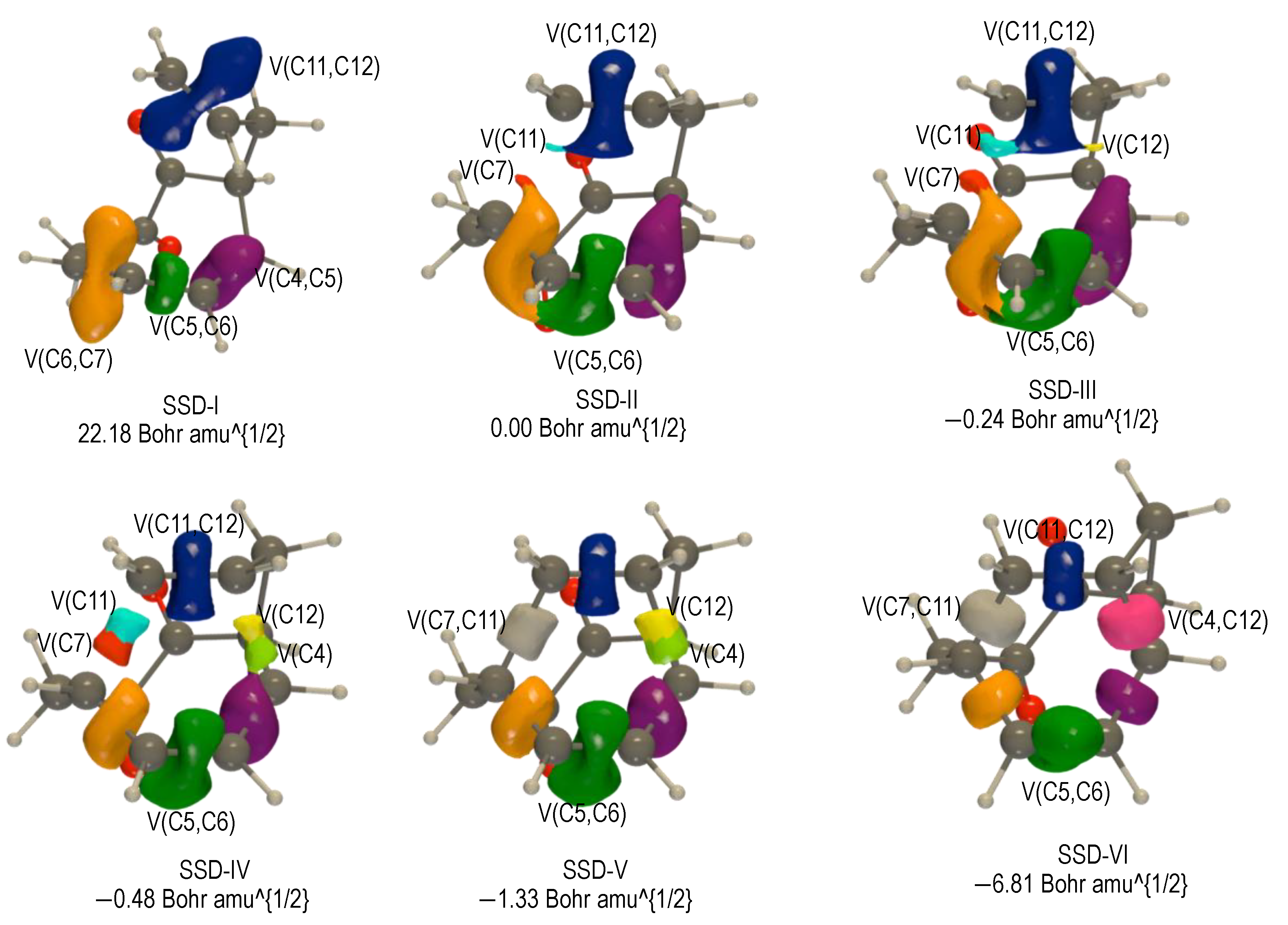
2.3.1. BET Analysis within Path a
First Step: Tautomerization Process Yielding Int1-a
Second Step: Diels–Alder Reaction of the Intermediate Int-a Yielding to 2
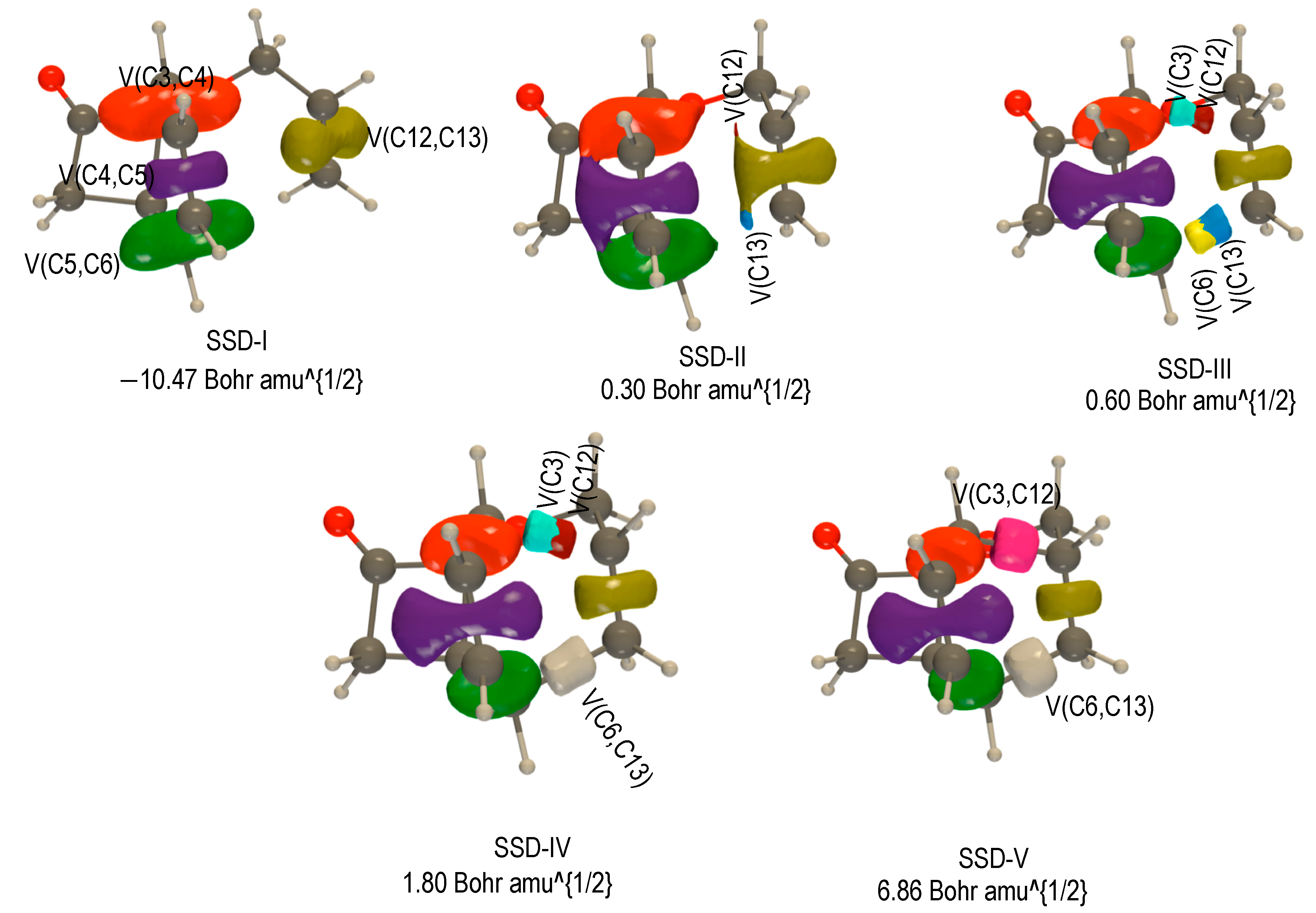
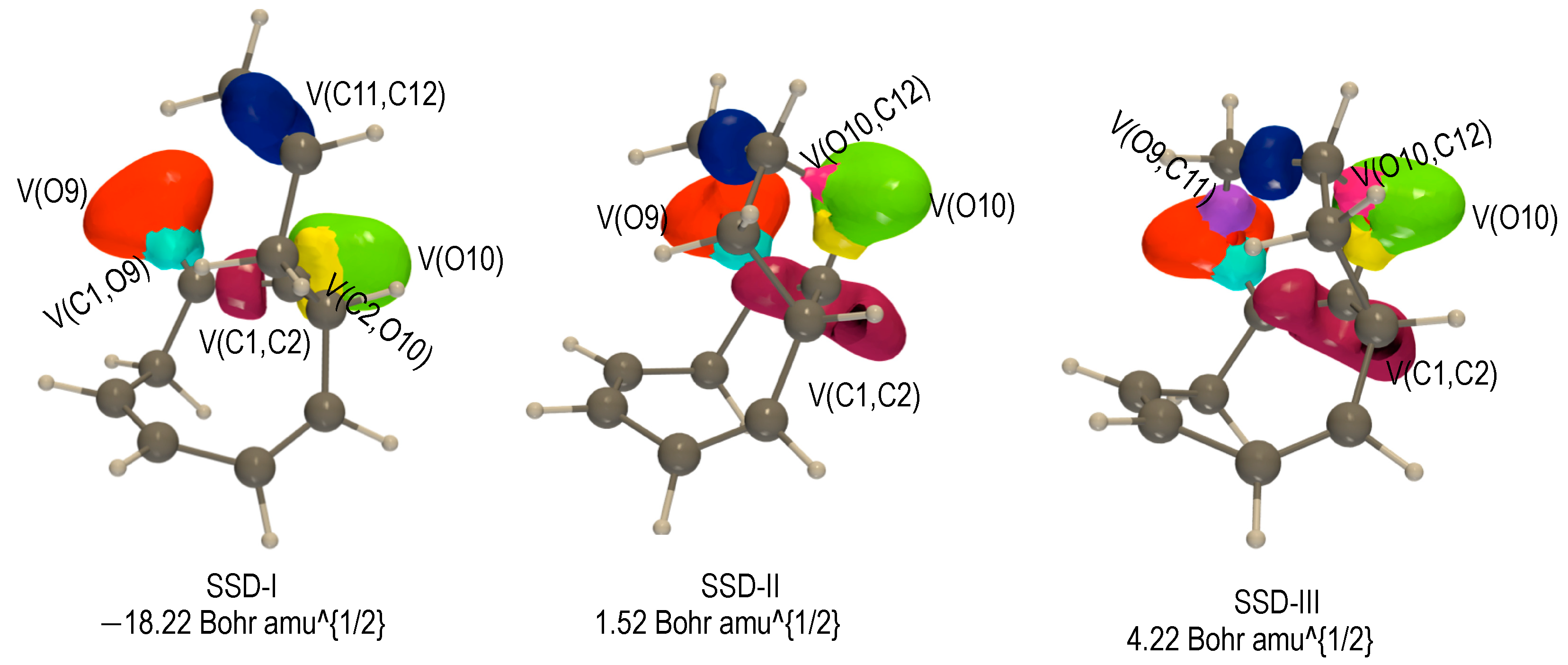
2.3.2. BET Analysis within Path b
First Step: [3,3] Sigmatropic Rearrangement of 1 Yielding to Int-b
Second Step: Diels—Alder Reaction of Intermediate Int-b Yielding 3-b1 and 3-b2
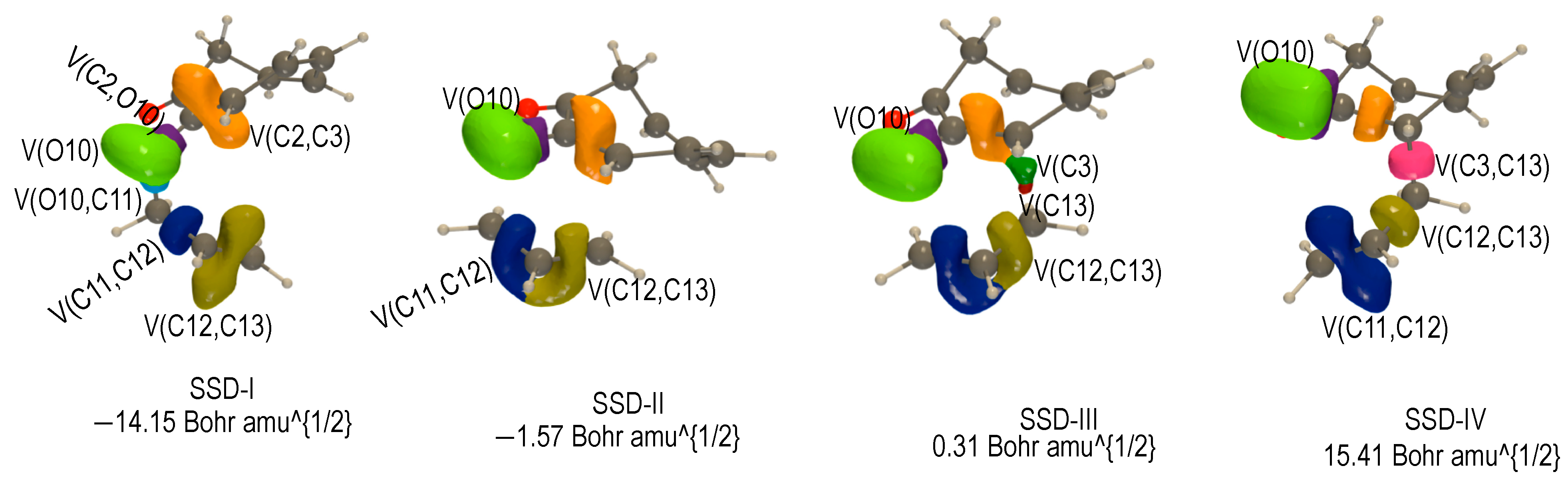
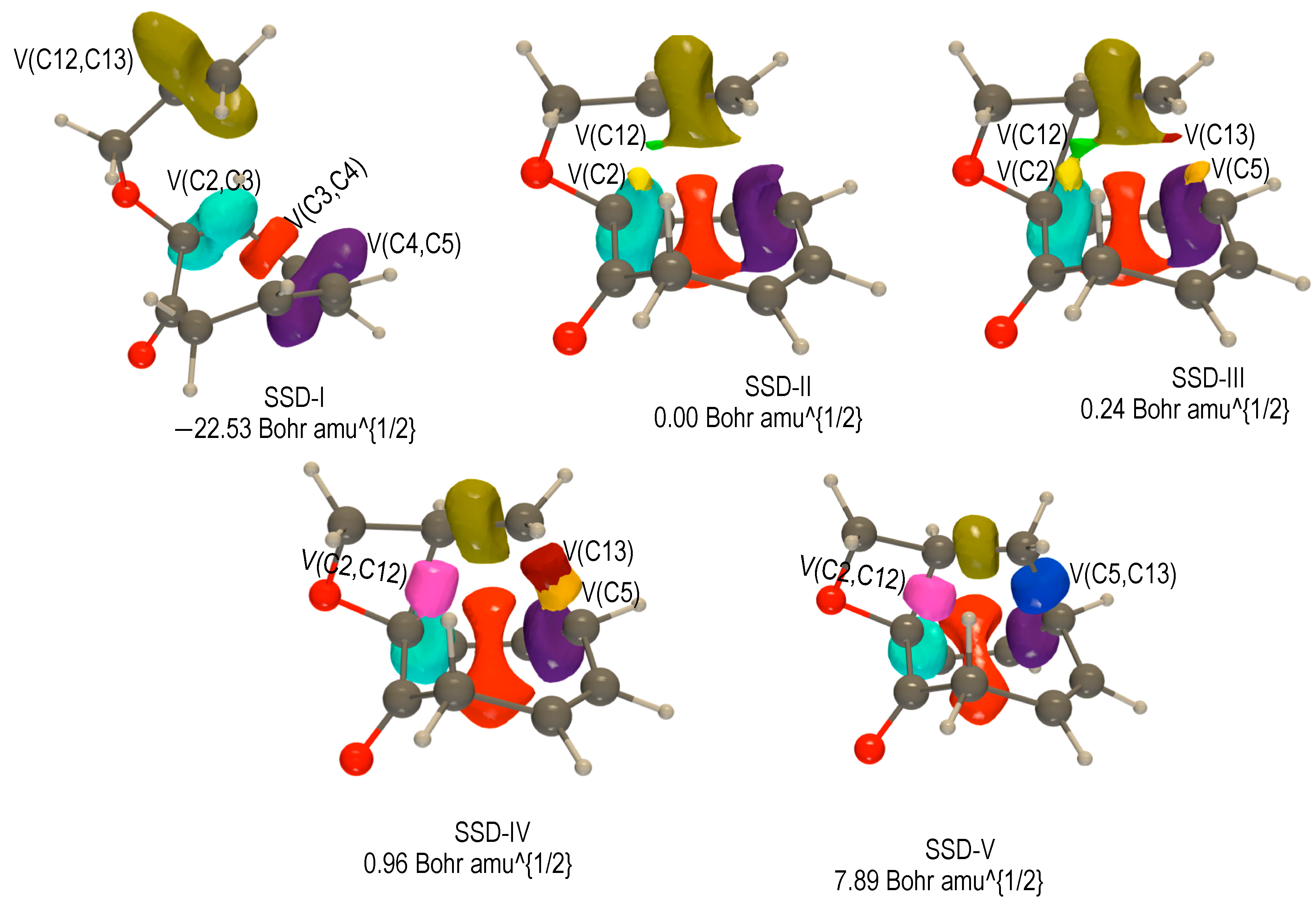
2.3.3. BET Analysis within Path c
3. Computational Method
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Nicolaou, K.C.; Snyder, S.; Montagnon, A.T.; Vassilikogiannakis, G. The Diels–Alder reaction in total synthesis. Angew. Chem. Int. Ed. 2002, 41, 1668–1698. [Google Scholar] [CrossRef]
- Funel, J.A.; Abele, S. Industrial Applications of the Diels–Alder Reaction. Angew. Chem. Int. Ed. 2013, 52, 3822–3863. [Google Scholar] [CrossRef] [PubMed]
- Brieger, G.; Bennett, J.N. The intramolecular Diels–Alder reaction. Chem. Rev. 1980, 80, 63–97. [Google Scholar] [CrossRef]
- Smith, M.B. March’s Advanced Organic Chemistry: Reactions, Mechanisms, and Structure; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Kitahara, Y.; Oda, M.; Miyakoshi, S.; Nakanishi, S. The chemistry of 2-hydroxy-2,4,6-cyclooctatrienone (1,7-π-homotropolone). Tetrahedron Lett. 1976, 25, 2149–2152. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules—A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Biegler-König, F.W.; Bader, R.F.W.; Tang, T.-H. Calculation of the average properties of atoms in molecules. II. J. Comput. Chem. 1982, 3, 317–328. [Google Scholar] [CrossRef]
- Popelier, P.L.A.; Brémond, E.A.G. Geometrically faithful homeomorphisms between the electron density and the bare nuclear potential. Int. J. Quantum. Chem. 2009, 109, 2542–2553. [Google Scholar] [CrossRef]
- Pendás, A.M.; Francisco, E. Quantum chemical topology as a theory of open quantum systems. J. Chem. Theory Comput. 2019, 15, 1079–1088. [Google Scholar] [CrossRef]
- Andrés, J.; Berski, S.; Contreras-Garcia, J.; Gonzalez-Navarrete, P. Following the molecular mechanism for the NH3 + LiH → LiNH2 + H2 chemical reaction: A Study based on the joint use of the quantum theory of atoms in molecules (QTAIM) and noncovalent interaction (NCI) index. J. Phys. Chem. A 2014, 118, 1663–1672. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Navarrete, P.; Andrés, J.; Berski, S. How a quantum chemical topology analysis enables prediction of electron density transfers in chemical reactions. The degenerated cope rearrangement of semibullvalene. J. Phys. Chem. Lett. 2012, 3, 2500–2505. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.S.-V.; Raghavendra, V.; Subramanian, V. Bader’s theory of atoms in molecules (aim) and its applications to chemical bonding. J. Chem. Sci. 2016, 128, 1527–1536. [Google Scholar] [CrossRef]
- Thom, R. Structural Stability and Morphogenesis, an Outline of a General Theory of Models; Benjamin/Cummings Publishing Co. Reading, Mass.: San Francisco, CA, USA, 1980. [Google Scholar]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Krokidis, X.; Noury, S.; Silvi, B. Characterization of elementary chemical processes by catastrophe theory. J. Phys. Chem. A 1997, 101, 7277–7282. [Google Scholar] [CrossRef]
- Andrés, J.; Gracia, L.; González-Navarrete, P.; Safont, V.S. Applications of Topological Methods in Molecular Chemistry; Chauvin, R., Lepetit, C., Silvi, B., Alikhani, E., Eds.; Springer International Publishing: Cham, Switzerland, 2016; Chapter 10; pp. 257–294. [Google Scholar]
- Andrés, J.; Berski, S.; Domingo, L.R.; González-Navarrete, P. Nature of the ring-closure process along the rearrangement of octa-1,3,5,7-tetraene to cycloocta-1,3,5-triene from the perspective of the electron localization function and catastrophe theory. J. Comput. Chem. 2012, 33, 748–756. [Google Scholar] [CrossRef]
- Adjieufack, A.I.; Andrés, J.; Oliva, M.; Safont, V.S. Deciphering the molecular mechanism of intramolecular reactions from the perspective of bonding evolution theory. Physchem 2022, 2, 207–223. [Google Scholar] [CrossRef]
- Adjieufack, A.I.; Gaudel-Siri, A.; Gingras, M.; Siri, D. Unraveling the reaction mechanism of AlCl3 Lewis acid catalyzed acylation reaction of pyrene from the perspective of the molecular electron density theory. New J. Chem. 2022, 47, 1925–1934. [Google Scholar] [CrossRef]
- Adjieufack, A.I.; Liégeois, V.; Champagne, B. Investigating the mechanism of the catalytic intramolecular aza-wittig reaction involved in the synthesis of 2-methylbenzothiazole from the perspective of bonding evolution theory. Synthesis 2023, 44, 2070–2082. [Google Scholar] [CrossRef]
- Adjieufack, A.I.; Liégeois, V.; Mbouombouo Ndassa, I.; Champagne, B. Topological investigation of the reaction mechanism of glycerol carbonate decomposition by bond evolution theory. RSC Adv. 2021, 11, 10083–10093. [Google Scholar] [CrossRef]
- Adjieufack, A.I.; Mbah Bake, M.; Nguemo Nguimkeu, C.; Pilmé, J.; Ndassa Mbouombouo, I. Exploring the sequence of electron density along the chemical reactions between carbonyl oxides and ammonia/water using bond evolution theory. Chem. Phys. Chem. 2021, 22, 1792–1801. [Google Scholar] [CrossRef]
- Poston, T.; Stewart, I. Catastrophe Theory and Its Applications; Pitman Publishing Limited: London, UK, 1978. [Google Scholar]
- Castrigiano, D.P.L.; Hayes, S.A. Catastrophe Theory, 2nd ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gilmore, R. Catastrophe Theory for Scientists and Engineers; Dover Publications: Mineola, NY, USA, 1993. [Google Scholar]
- Andrés, J.; Gracia, L.; González-Navarrete, P.; Safont, V.S. Chemical structure and reactivity by means of quantum chemical topology analysis. Comput. Theor. Chem. 2015, 1053, 17–30. [Google Scholar] [CrossRef]
- Benallou, A.; El Abdallaoui, H.E.A.; Garmes, H. C–C bond formation in the intramolecular Diels–Alder reaction of triene amides. Heliyon 2018, 4, e00504. [Google Scholar] [CrossRef] [PubMed]
- Hallooman, D.; Cudian, D.; Ríos-Gutiérrez, M.; Rhyman, L.; Alswaidan, I.A.; Elzagheid, M.I.; Domingo, L.R.; Ramasami, P. Understanding the intramolecular Diels–Alder reactions of N-substituted N-allyl-furfurylamines: An MEDT study. ChemistrySelect 2017, 2, 9736–9743. [Google Scholar] [CrossRef]
- Moto Ongagna, J.; Tamafo Fouegue, A.D.; Ateba Amana, B.; Mouzong D’ambassa, G.; Zobo Mfomo, J.; Mbaze Meva’A, L.; Bikele, D. B3LYP, M06 and B3PW91 DFT assignment of nd8 metal-bis-(N-heterocyclic carbene) complexes. J. Mol. Model. 2020, 26, 246. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R.; Sáez, J.A. Understanding the electronic reorganization along the nonpolar [3+2] cycloaddition reactions of carbonyl ylides. J. Org. Chem. 2011, 76, 373–379. [Google Scholar] [CrossRef]
- Domingo, L.R. A new C–C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415–32428. [Google Scholar] [CrossRef]
- Adjieufack, A.I.; Mbouombouo Ndassa, I.; Patouossa, I.; Ketcha Mbadcam, J.; Safont, V.S.; Oliva, M.; Andrés, J. On the outside looking in: Rethinking the molecular mechanism of 1,3-dipolar cycloadditions from the perspective of bonding evolution theory. The reaction between cyclic nitrones and ethyl acrylate. Phys. Chem. Chem. Phys. 2017, 19, 18288–18302. [Google Scholar] [CrossRef]
- Adjieufack, A.I.; Maraf Mbah, B.; Ketcha Madcap, J.; Mbouombouo Ndassa, I.; Andrés, J.; Oliva, M.; Safont, V.S. How effectively bonding evolution theory retrieves and visualizes curly arrows: The cycloaddition reaction of cyclic nitrones. Int. J. Quantum Chem. 2019, 119, e25985. [Google Scholar] [CrossRef]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions. J. Chem. Theory Comput. 2006, 2, 364–382. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision A. 03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Tomasi, J.; Menucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Fukui, K. Formulation of the Reaction Coordinate. J. Phys. Chem. 1970, 74, 4161–4163. [Google Scholar] [CrossRef]
- Gonzalez, C.; Schlegel, H.B. Reaction path following in mass-weighted internal coordinates. J. Phys. Chem. 1990, 94, 5523–5527. [Google Scholar] [CrossRef]
- Gonzalez, C.; Schlegel, H.B. Improved algorithms for reaction path following: Higher-order implicit algorithms. J. Chem. Phys. 1991, 95, 5853–5860. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational tools for the electron localization function topological analysis. Comput. Chem. 1999, 23, 597–604. [Google Scholar] [CrossRef]
- Liégeois, V. DrawProfile. Unamur. Available online: www.unamur.be/drawprofile (accessed on 24 July 2023).


| Species | ∆E | ∆H | ∆S | ∆G |
|---|---|---|---|---|
| 1 | 0.0 | 0.0 | 0.0 | 0.0 |
| TS1-a | 58.3 | 55.7 | −1.9 | 56.6 |
| Int-a | 4.3 | 4.9 | −18.0 | 13.3 |
| TS2-a | 20.2 | 18.5 | −14.5 | 25.3 |
| 2 | −26.4 | −27.0 | −0.5 | −26.8 |
| TS1-b | 29.2 | 27.7 | −7.6 | 31.3 |
| Int-b | −4.0 | −4.2 | 3.0 | −5.6 |
| TS2-b1 | 36.8 | 35.2 | −11.5 | 40.5 |
| TS2-b2 | 53.0 | 51.5 | −14.7 | 58.4 |
| 3-b1 | −22.6 | −21.9 | −13.4 | −15.7 |
| 3-b2 | 16.7 | 17.6 | −17.2 | 25.6 |
| TS1-c1 | 58.9 | 57.4 | −14.1 | 63.9 |
| TS1-c2 | 66.0 | 64.5 | −11.7 | 70.0 |
| 4-c1 | −9.4 | −8.3 | −19.2 | 0.7 |
| 4-c2 | 13.1 | 13.9 | −14.4 | 20.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adjieufack, A.I.; Ongagna, J.M.; Essomba, J.S.; Ewonkem, M.B.; Oliva, M.; Safont, V.S.; Andrés, J. Exploring the Mechanism of the Intramolecular Diels–Alder Reaction of (2E,4Z,6Z)-2(allyloxy)cycloocta-2,4,6-trien-1-one Using Bonding Evolution Theory. Molecules 2023, 28, 6755. https://doi.org/10.3390/molecules28196755
Adjieufack AI, Ongagna JM, Essomba JS, Ewonkem MB, Oliva M, Safont VS, Andrés J. Exploring the Mechanism of the Intramolecular Diels–Alder Reaction of (2E,4Z,6Z)-2(allyloxy)cycloocta-2,4,6-trien-1-one Using Bonding Evolution Theory. Molecules. 2023; 28(19):6755. https://doi.org/10.3390/molecules28196755
Chicago/Turabian StyleAdjieufack, Abel Idrice, Jean Moto Ongagna, Jean Serge Essomba, Monique Bassomo Ewonkem, Mónica Oliva, Vicent Sixte Safont, and Juan Andrés. 2023. "Exploring the Mechanism of the Intramolecular Diels–Alder Reaction of (2E,4Z,6Z)-2(allyloxy)cycloocta-2,4,6-trien-1-one Using Bonding Evolution Theory" Molecules 28, no. 19: 6755. https://doi.org/10.3390/molecules28196755
APA StyleAdjieufack, A. I., Ongagna, J. M., Essomba, J. S., Ewonkem, M. B., Oliva, M., Safont, V. S., & Andrés, J. (2023). Exploring the Mechanism of the Intramolecular Diels–Alder Reaction of (2E,4Z,6Z)-2(allyloxy)cycloocta-2,4,6-trien-1-one Using Bonding Evolution Theory. Molecules, 28(19), 6755. https://doi.org/10.3390/molecules28196755







