Novel Mechanism-Based Descriptors for Extreme Ultraviolet-Induced Photoacid Generation: Key Factors Affecting Extreme Ultraviolet Sensitivity
Abstract
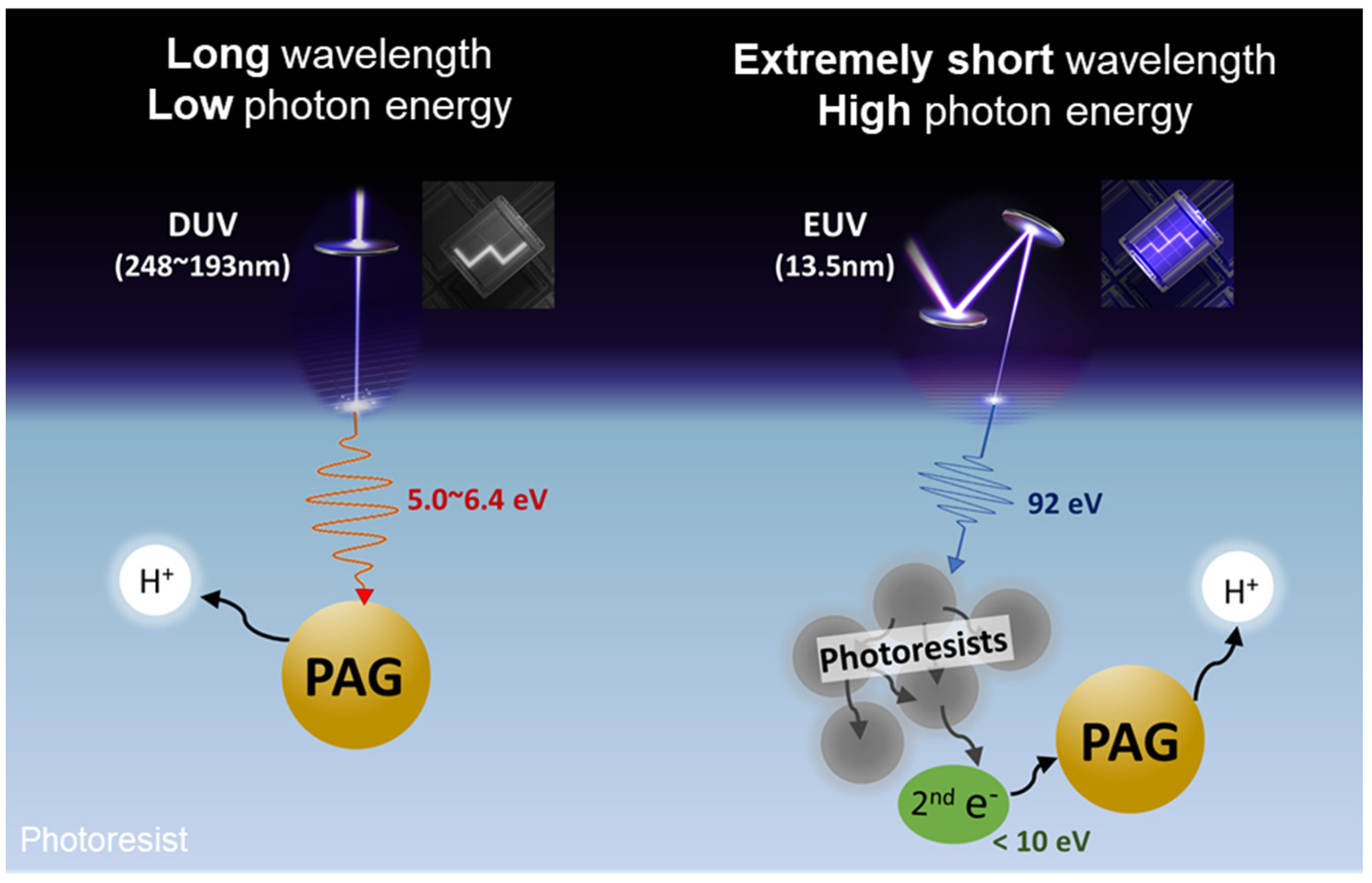
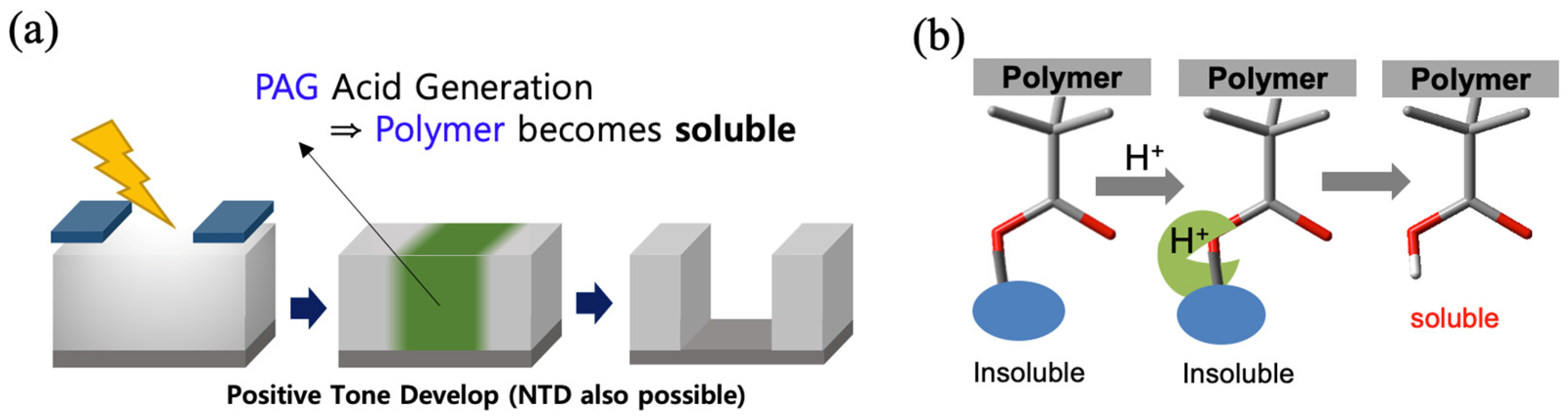
1. Introduction
2. Results and Discussion
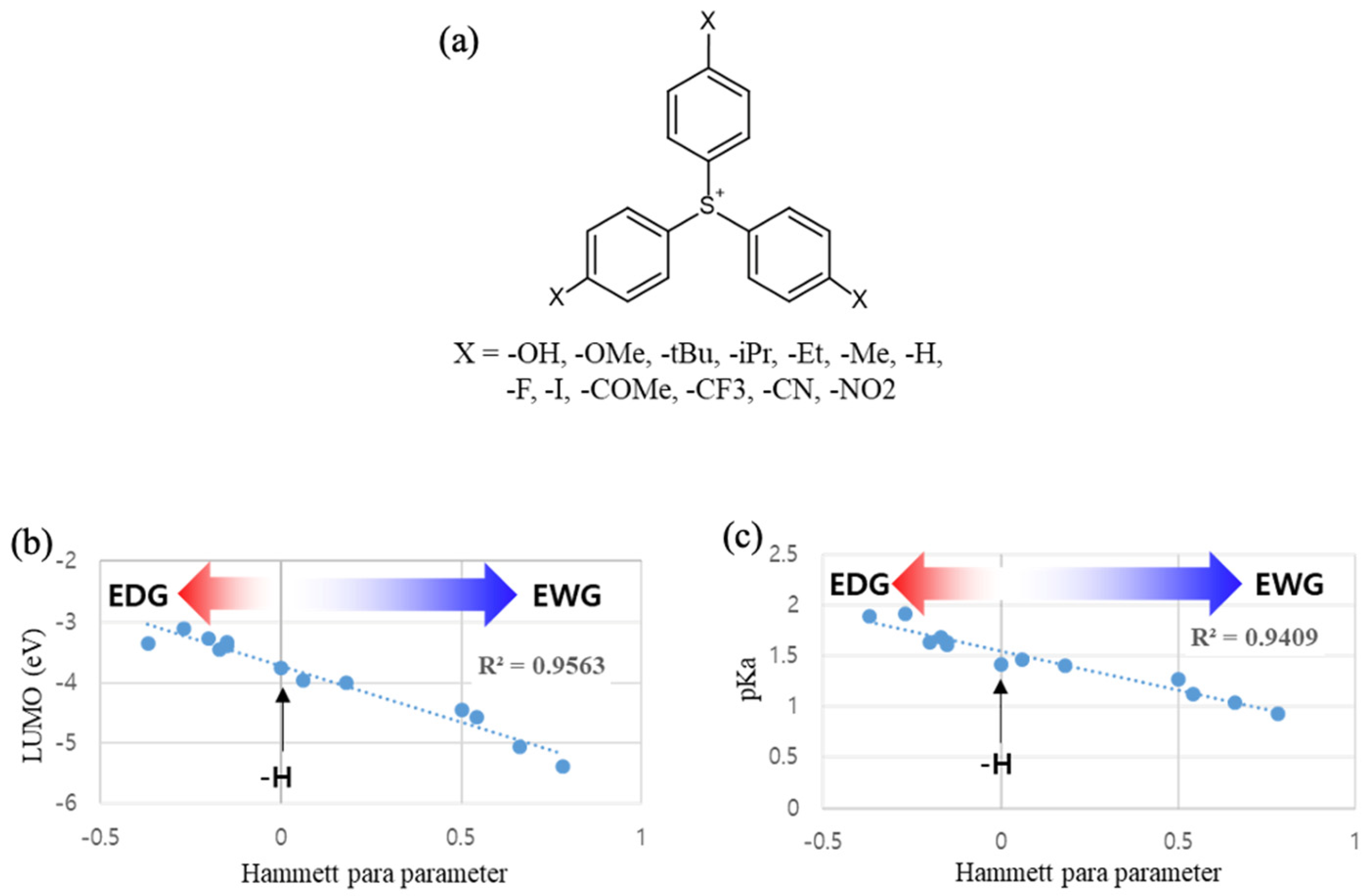
2.1. Linear Correlation Analysis for DUV(ArF) and EUV Sensitivity
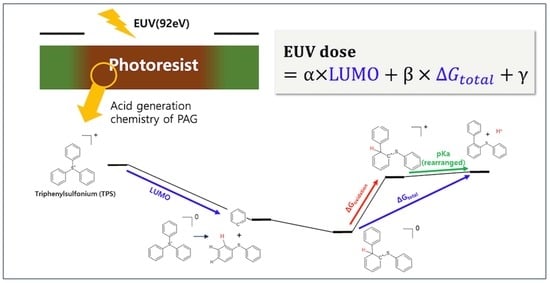
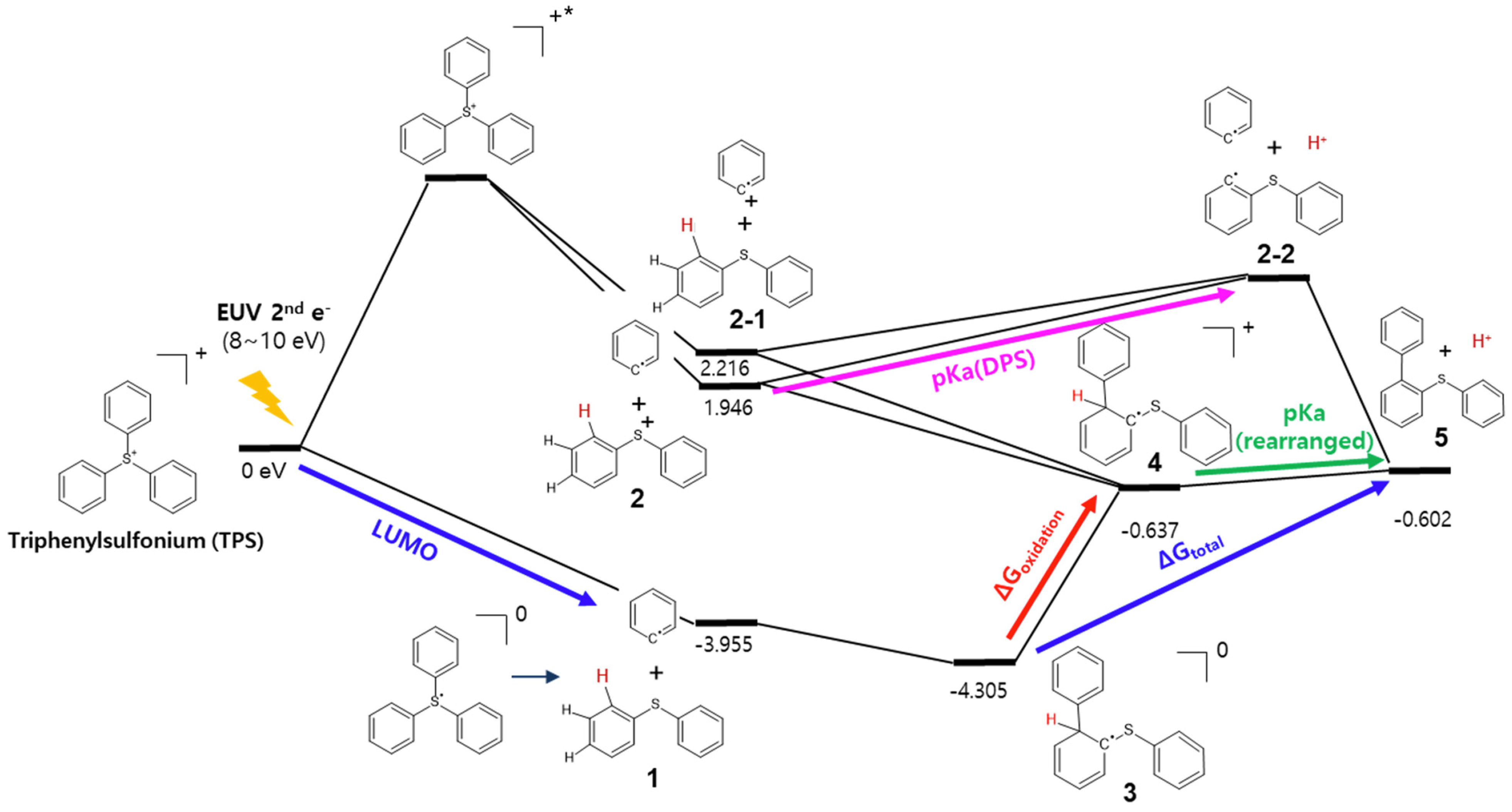
2.2. Simulation Study for the Photochemical Reaction Profile of TPS Cation
2.3. Two-Parameter Dose-Prediction Model (for TPS Cations from Ref. [10])
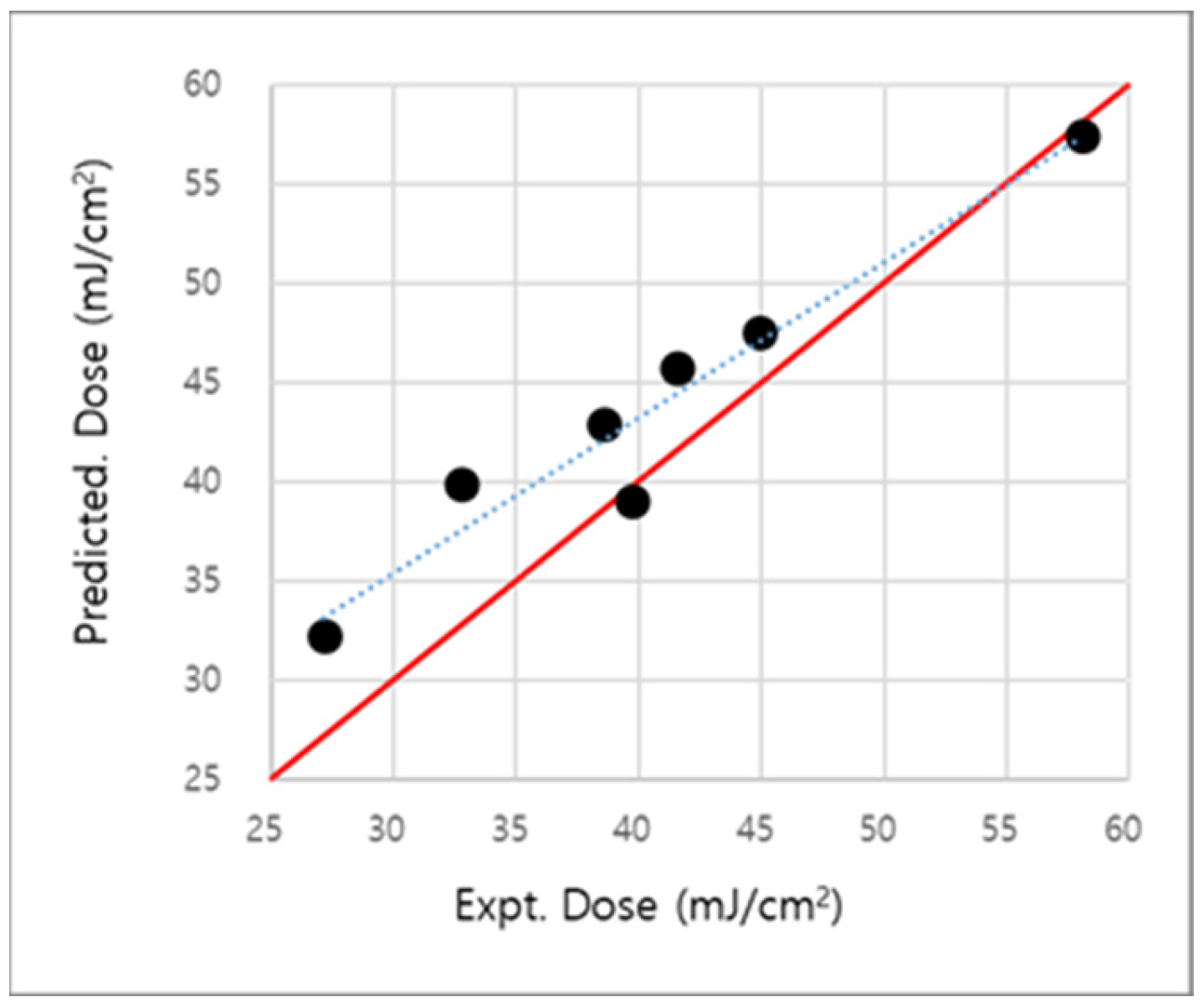
2.4. Extension and Validation of the Two-Parameter Dose-Prediction Model
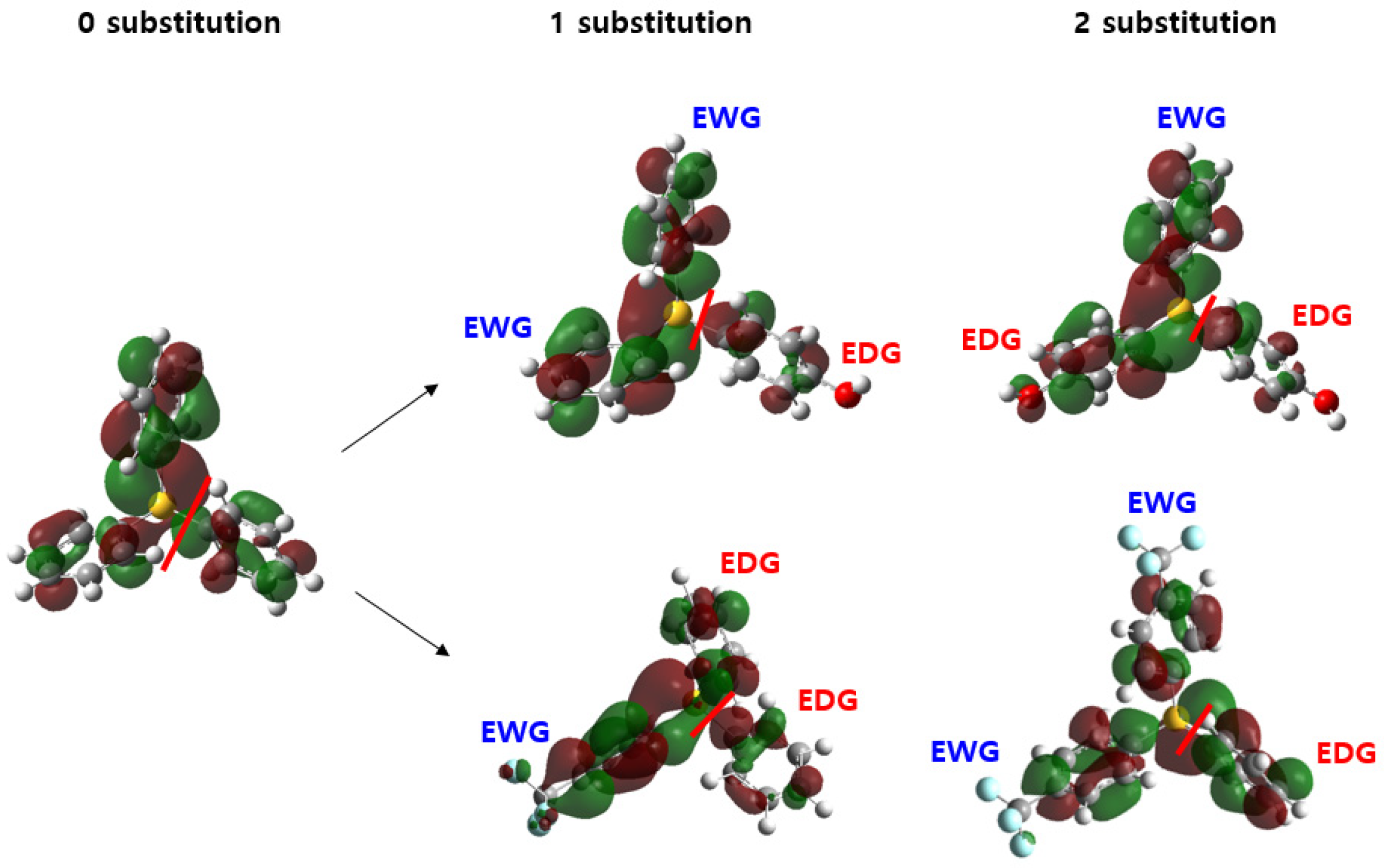
2.5. Insights on the Design Strategy of the New PAG Molecule
- (1)
- α and β >0. As we discussed previously, satisfying both low LUMO (electron-withdrawing substituents) and low ΔGtotal (electron-donating substituents) will be frustrated by the trade-off. One might suggest hybrid-type TPS cations with both electron-withdrawing and donating substituents;
- (2)
- α < 0 and β > 0. For this photoresist system, electron-donating substituents will be preferred in both LUMO and ΔGtotal-related terms. In this situation, lowering the oxidation potential barrier of rearranged TPS intermediates might be more critical than lowering the LUMO of TPS cations (deprotonation-dominated system);
- (3)
- α >0 and β < 0. In this photoresist system, electron-withdrawing substituents could be beneficial to lower the EUV dose by lowering LUMO without significant deterioration of deprotonation efficiency. In this situation, lowering LUMO is more effective than lowering ΔGtotal (electron-trapping-dominated system).
3. Computational Details
- (1)
- pKa of diphenylsulfide (DPS, for structure 2 to 2-2):
- (2)
- pKa of rearranged triphenylsulfonium (TPS, for structures 4 to 5):
- (3)
- Oxidation potential (for structures 3 to 4):
- (4)
- Overall energy change (for structures 3 to 5):
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Lord Rayleigh, F.R.S. On the Stability, or Instability of Certain Fluid Motions. Proc. Lond. Math. Soc. 1880, s1–s11, 57–72. [Google Scholar] [CrossRef]
- Pirati, A.; van Schoot, J.; Troost, K.; van Ballegoij, R.; Krabbendam, P.; Stoeldraijer, J.; Loopstra, E.; Benschop, J.; Finders, J.; Meiling, H.; et al. The Future of EUV Lithography: Enabling Moore’s Law in the Next Decade. In Proceedings of the SPIE Advanced Lithography, San Johe, CA, USA, 26 February–2 March 2017; p. 101430G. [Google Scholar]
- Ito, H.; Willson, C.G. Chemical amplification in the design of dry developing resist materials. Polym. Eng. Sci. 1983, 23, 1012–1018. [Google Scholar] [CrossRef]
- Ito, H. Chemical Amplification Resists for Microlithography. In Advances in Polymer Science Series; Springer: Berlin/Heidelberg, Germany, 2005; Volume 172, pp. 137–138. [Google Scholar] [CrossRef]
- Buitrago, E.; Yildirim, O.; Verspaget, C.; Tsugama, N.; Hoefnagels, R.; Rispens, G.; Ekinci, Y. Evaluation of EUV Resist Performance Using Interference Lithography. In Proceedings of the SPIE Advanced Lithography, San Johe, CA, USA, 22–26 February 2015; Volume 9422, p. 94221S. [Google Scholar] [CrossRef]
- Wang, X.; Tasdemir, Z.; Mochi, I.; Vockenhuber, M.; van Lent-Protasova, L.; Meeuwissen, M.; Custers, R.; Rispens, G.; Hoefnagels, R.; Ekinci, Y. Progress in EUV Resists towards high-NA EUV Lithography. In Proceedings of the SPIE Advanced Lithography, San Johe, CA, USA, 24–28 February 2019; Volume 10957, p. 109570A. [Google Scholar]
- Kozawa, T. Theoretical study on trade-off relationships between resolution, line edge roughness, and sensitivity in resist processes for semiconductor manufacturing by extreme ultraviolet lithography. Jpn. J. Appl. Phys. 2019, 58, 096502. [Google Scholar] [CrossRef]
- Kozawa, T.; Tagawa, S. Radiation Chemistry in Chemically Amplified Resists. Jpn. J. Appl. Phys. 2010, 49, 030001. [Google Scholar] [CrossRef]
- Grzeskowiak, S.; Narasimhan, A.; Rebeyev, E.; Joshi, S.; Brainard, R.L.; Denbeaux, G. Acid Generation Efficiency of EUV PAGs via Low Energy Electron Exposure. J. Photopolym. Sci. Technol. 2016, 29, 453–458. [Google Scholar] [CrossRef]
- Asakura, T.; Yamamoto, H.; Nishimae, Y.; Okada, K.; Ohwa, M. PAG Study in EUV Lithography. J. Photopolym. Sci. Technol. 2009, 22, 89–95. [Google Scholar] [CrossRef][Green Version]
- Komuro, Y.; Yamamoto, H.; Kobayashi, K.; Utsumi, Y.; Ohomori, K.; Kozawa, T. Acid generation mechanism in anion-bound chemically amplified resists used for extreme ultraviolet lithography. Jpn. J. Appl. Phys. 2014, 53, 116503. [Google Scholar] [CrossRef]
- Despagnet-Ayoub, E.; Kramer, W.W.; Sattler, W.; Sattler, A.; LaBeaume, P.J.; Thackeray, J.W.; Cameron, J.F.; Cardolaccia, T.; Rachford, A.A.; Winkler, J.R.; et al. Triphenylsulfonium topophotochemistry. Photochem. Photobiol. Sci. 2018, 17, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Tagawa, S.; Nagahara, S.; Iwamoto, T.; Wakita, M.; Kozawa, T.; Yamamoto, Y.; Werst, D.; Trifunac, A.D. Radiation and Photochemistry of Onium Salt Acid Generators in Chemically Amplified Resists. In Proceedings of the Advances in Resist Technology and Processing XVII, Santa Clara, CA, USA, 28 February–1 March 2000; Volume 3999, pp. 204–213. [Google Scholar]
- Hansch, C.; Leo, A. Substituent Constants for Correlation Analysis in Chemistry and Biology; Wiley-Interscience: New York, NY, USA, 1979. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular Orbital Methods. 9. Extended Gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 1971, 54, 724. [Google Scholar] [CrossRef]
- Caricato, M.; Mennucci, B.; Tomasi, J.; Ingrosso, F.; Cammi, R.; Corni, S.; Scalmani, G. Formation and relaxation of excited states in solution: A new time dependent polarizable continuum model based on time dependent density functional theory. J. Chem. Phys. 2006, 124, 124520–124532. [Google Scholar] [CrossRef] [PubMed]
- Zhan, C.-G.; Dixon, D.A. Absolute Hydration Free Energy of the Proton from First-Principles Electronic Structure Calculations. J. Phys. Chem. A 2001, 105, 11534–11540. [Google Scholar] [CrossRef]
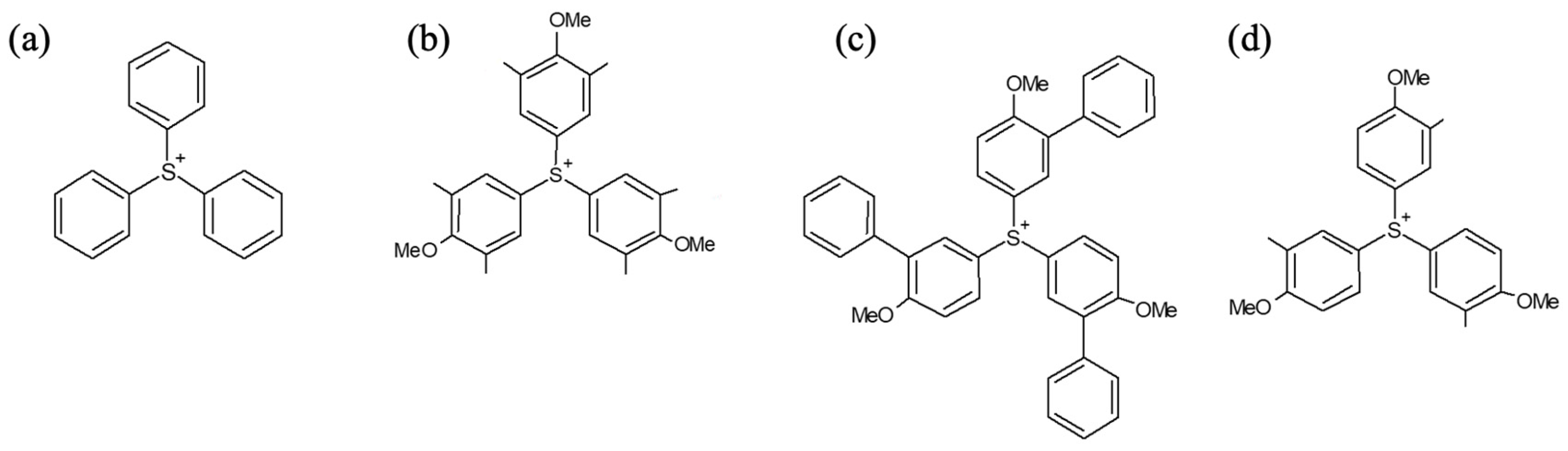
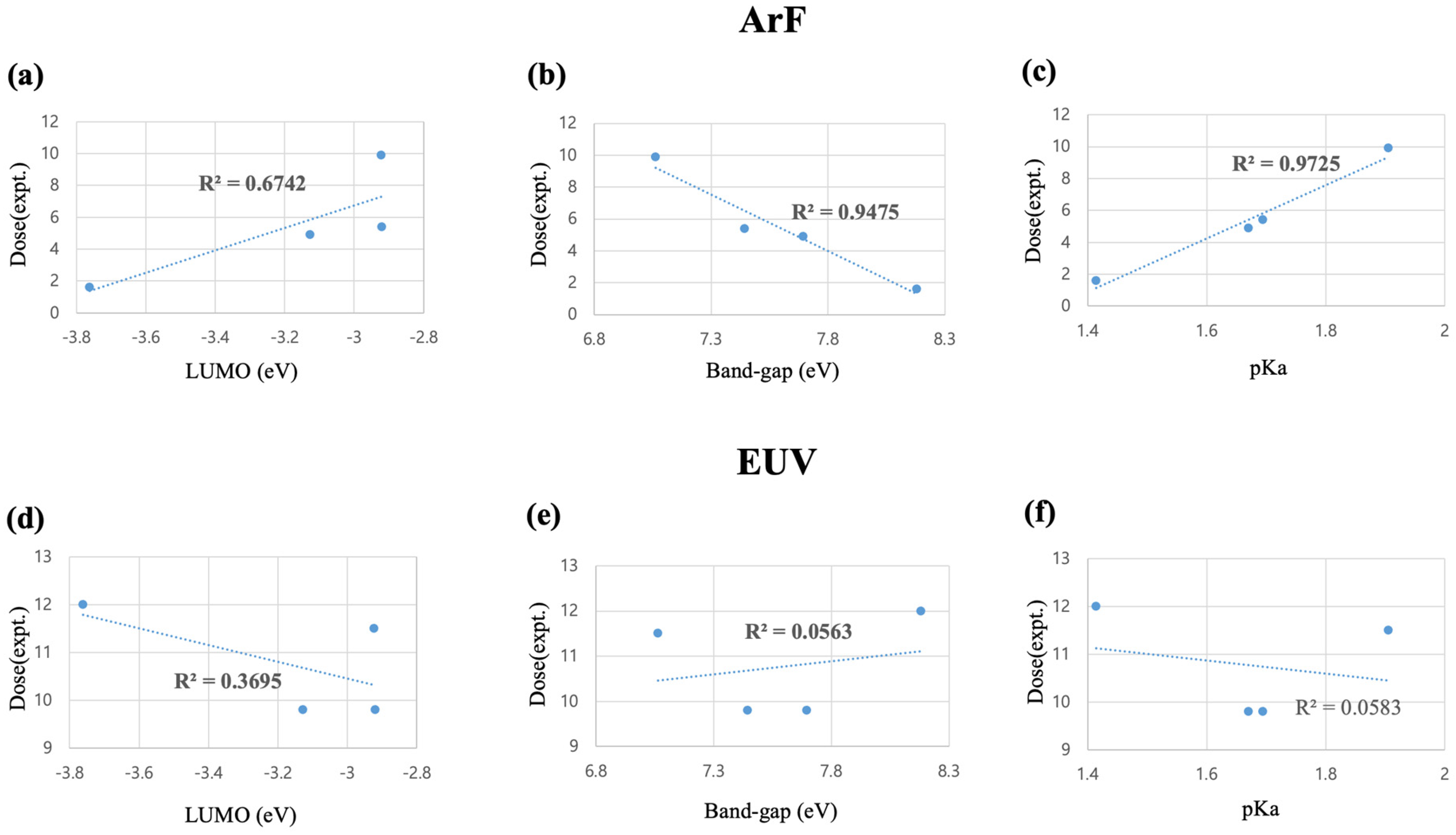
| PAG Cations | HOMO (eV) | LUMO (eV) | Band Gap (eV) | pKa (DPS) | Dose (mJ/cm2) | |
|---|---|---|---|---|---|---|
| ArF (E0) | EUV (Esize) | |||||
| TPS | −11.942 | −3.761 | 8.181 | 1.414 | 1.6 | 12 |
| MDP | −10.822 | −3.127 | 7.695 | 1.670 | 4.9 | 9.8 |
| MMP | −10.364 | −2.920 | 7.444 | 1.694 | 5.4 | 9.8 |
| MPP | −9.985 | −2.922 | 7.063 | 1.905 | 9.9 | 11.5 |
| LUMO with | pKa (DPS) | pKa (Rearranged) | ΔGoxidation | ΔGtotal |
|---|---|---|---|---|
| R2 | 0.85 | 0.95 | 0.52 | 0.99 |
| Experimental Sets | Ref. [10] | Set 1 | Set 2 | Set 3 | Validation Set |
|---|---|---|---|---|---|
| Number of PAG cations | 4 | 9 | 9 | 8 | 7 |
| PAG concentration | 4% (polymer:100) | Condition 1 | Condition 1 | Condition 2 | Condition 2 |
| PDQ type | N-1-adamantyl lacetamine | Type1 | Type2 | Type1 | Type1 |
| PDQ concentration | 0.27% (polymer:100) | Condition 1 | Condition 1 | Condition 2 | Condition 2 |
| Polymer | PHS/poly(methacrylates) co-polymer | Condition 1 | Condition 1 | Condition 1 | Condition 1 |
| Solvent | PGMEA:Ethyl acetate (7:3) | PGMEA:Ethyl acetate (7:3) | PGMEA:Ethyl acetate (7:3) | PGMEA:Ethyl acetate (7:3) | PGMEA:Ethyl acetate (7:3) |
| LUMO Single-Parameter Correlation with EUV Dose | ||||||
|---|---|---|---|---|---|---|
| Sets of PAG | Ref. [10] | Set 1 | Set 2 | Set 3 | Validation Set | |
| R2(LUMO vs experimental EUV dose) | 0.49 | 0.07 | 0.63 | 0.83 | 0.42 | |
| LUMO and ΔGtotal based regression model for EUV dose prediction | ||||||
| R2(experimental vs predicted EUV dose) | 0.518 | 0.66 | 0.67 | 0.91 | 0.94 | |
| Maximum difference in dose (experimental—predicted) | 11.33 | 5.70 | 8.00 | 5.15 | 7.15 | |
| Correlation between LUMO and ΔGtotal | 0.42 | 0.38 | 0.55 | 0.34 | 0.03 | |
| Regression Model Coefficient | α | −2.69 | 17.86 | −16.18 | 18.56 | 18.56 |
| β | 12.63 | −133.86 | −251.49 | −194.58 | −194.58 | |
| γ | −37.63 | 528.78 | 788.71 | 717.87 | 717.87 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.Y.; Song, H.-J.; Nguyen, T.C.; Son, W.-J.; Kim, D.; Song, G.; Hong, S.-K.; Go, H.; Park, C.; Jang, I.; et al. Novel Mechanism-Based Descriptors for Extreme Ultraviolet-Induced Photoacid Generation: Key Factors Affecting Extreme Ultraviolet Sensitivity. Molecules 2023, 28, 6244. https://doi.org/10.3390/molecules28176244
Park JY, Song H-J, Nguyen TC, Son W-J, Kim D, Song G, Hong S-K, Go H, Park C, Jang I, et al. Novel Mechanism-Based Descriptors for Extreme Ultraviolet-Induced Photoacid Generation: Key Factors Affecting Extreme Ultraviolet Sensitivity. Molecules. 2023; 28(17):6244. https://doi.org/10.3390/molecules28176244
Chicago/Turabian StylePark, Ji Young, Hyun-Ji Song, Thanh Cuong Nguyen, Won-Joon Son, Daekeon Kim, Giyoung Song, Suk-Koo Hong, Heeyoung Go, Changmin Park, Inkook Jang, and et al. 2023. "Novel Mechanism-Based Descriptors for Extreme Ultraviolet-Induced Photoacid Generation: Key Factors Affecting Extreme Ultraviolet Sensitivity" Molecules 28, no. 17: 6244. https://doi.org/10.3390/molecules28176244
APA StylePark, J. Y., Song, H.-J., Nguyen, T. C., Son, W.-J., Kim, D., Song, G., Hong, S.-K., Go, H., Park, C., Jang, I., & Kim, D. S. (2023). Novel Mechanism-Based Descriptors for Extreme Ultraviolet-Induced Photoacid Generation: Key Factors Affecting Extreme Ultraviolet Sensitivity. Molecules, 28(17), 6244. https://doi.org/10.3390/molecules28176244