Spatial Balance of Photogenerated Charge Carriers in Active Layers of Polymer Solar Cells
Abstract
1. Introduction
2. Results
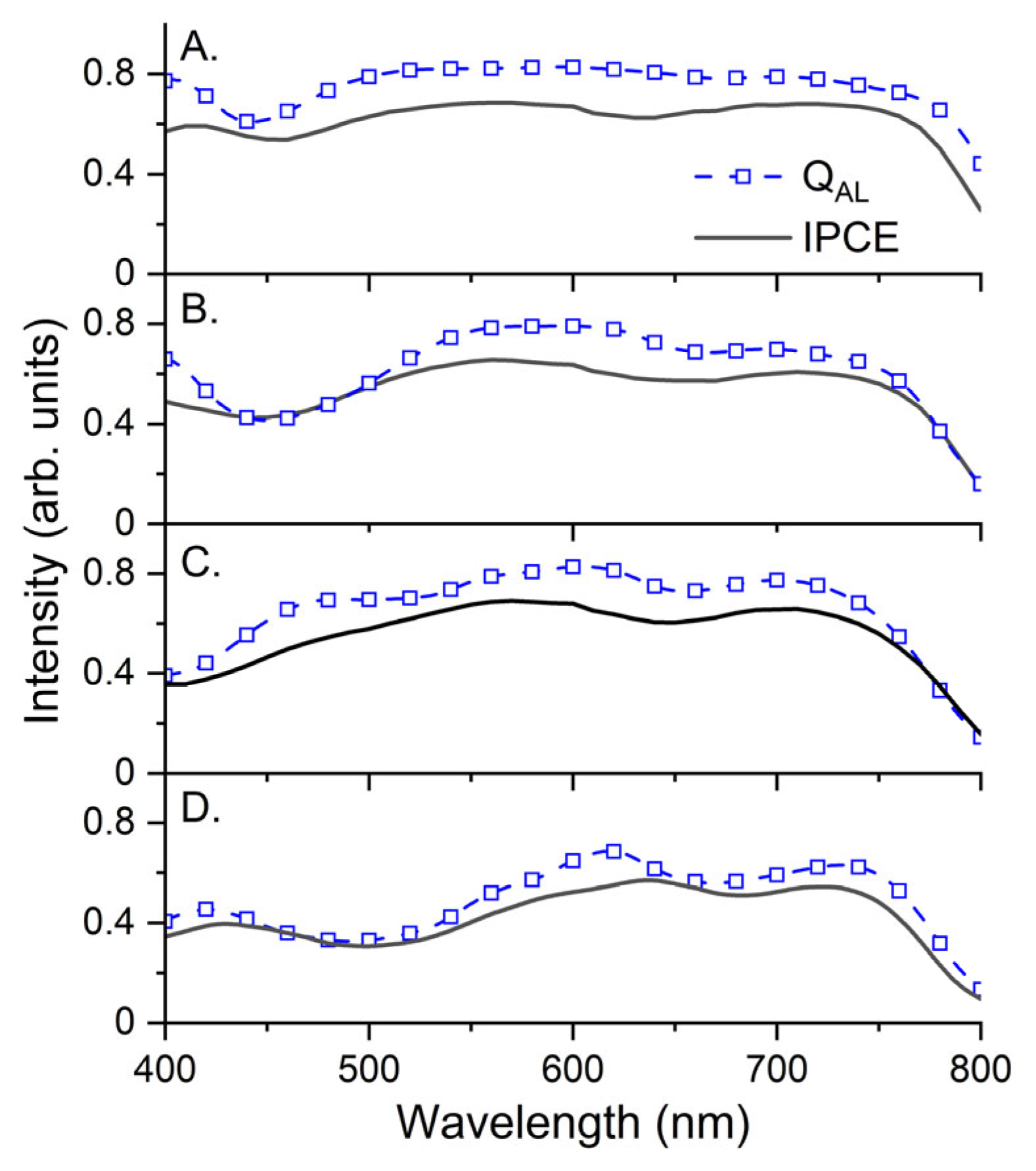
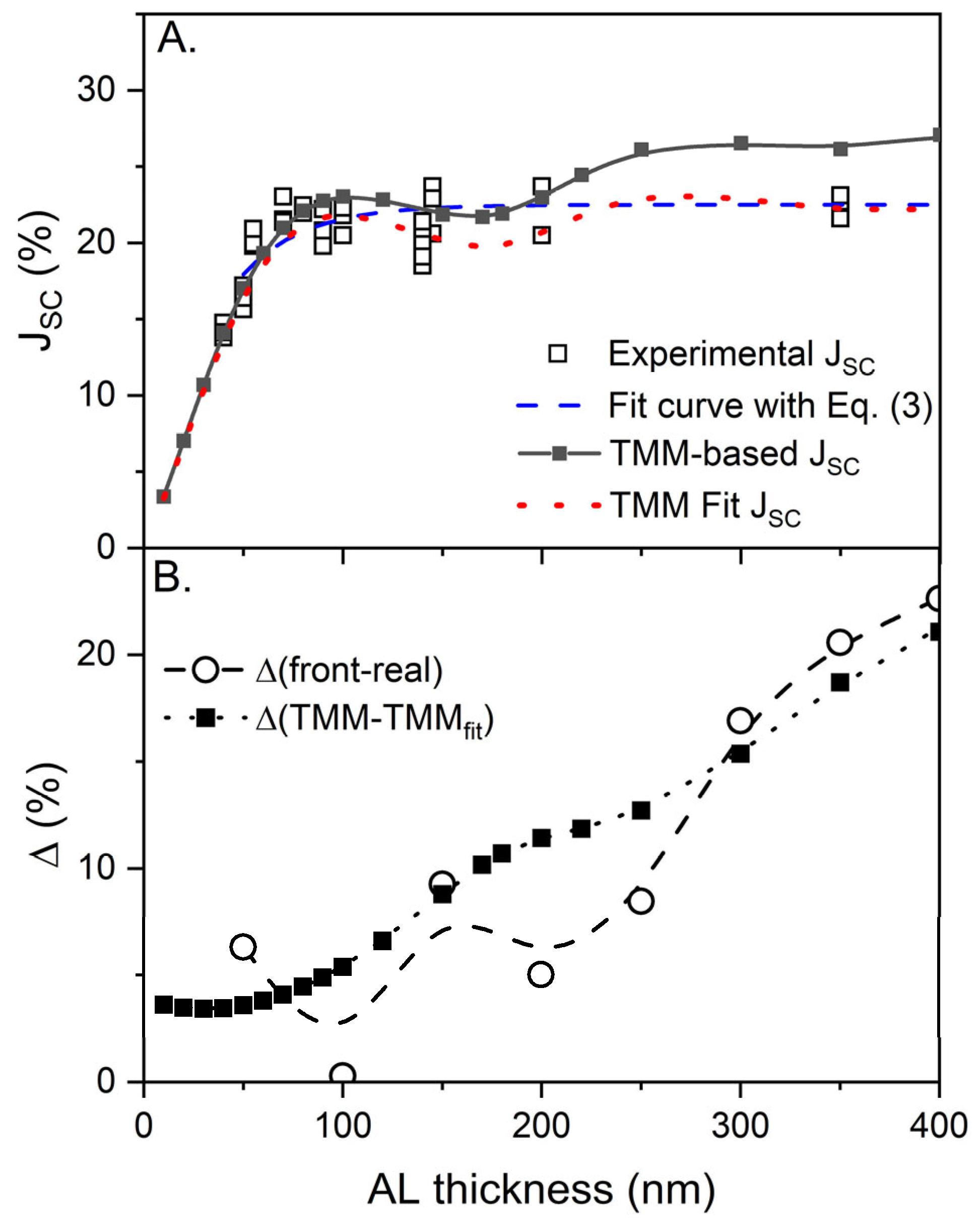
2.1. Thickness-Dependent PSC Properties
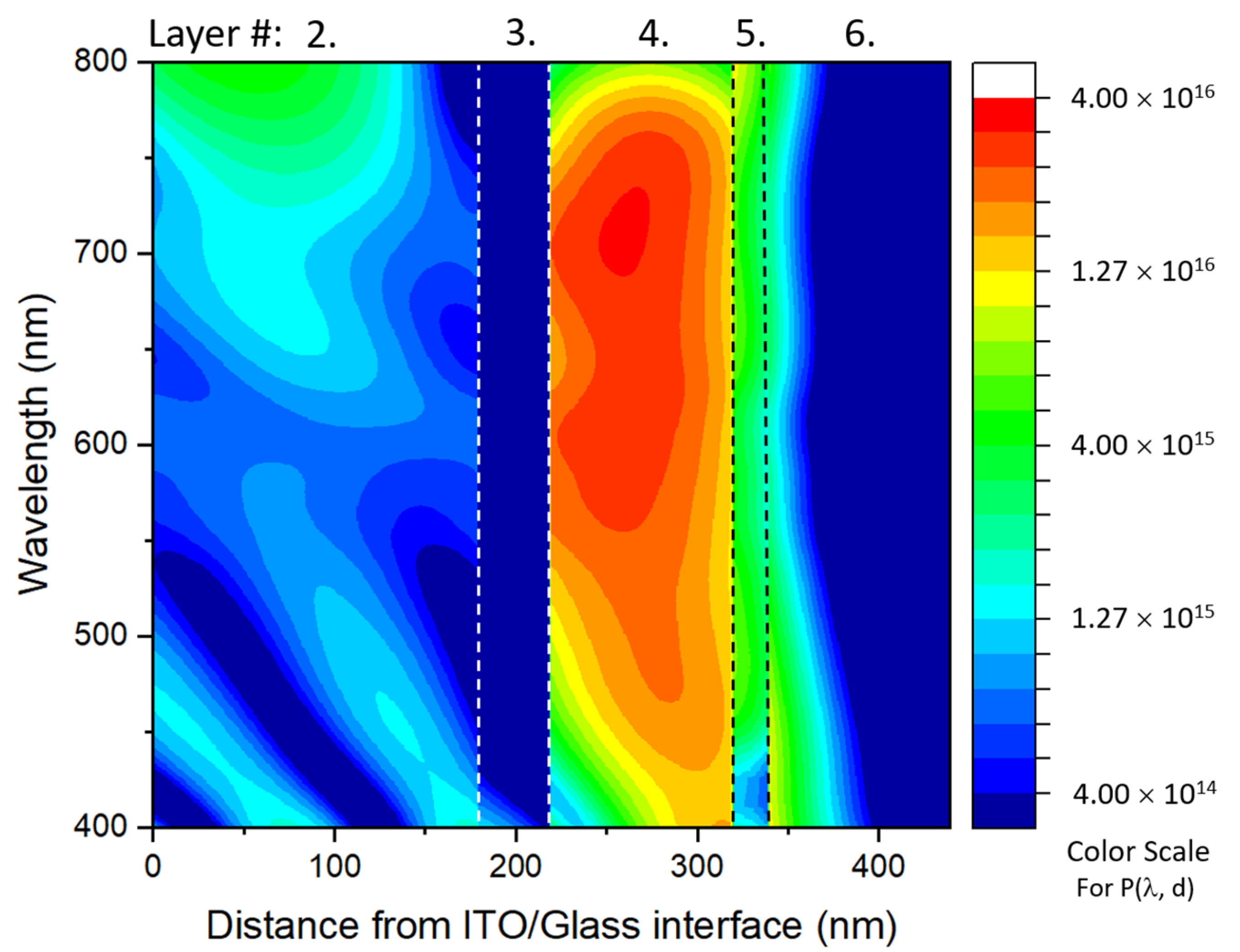
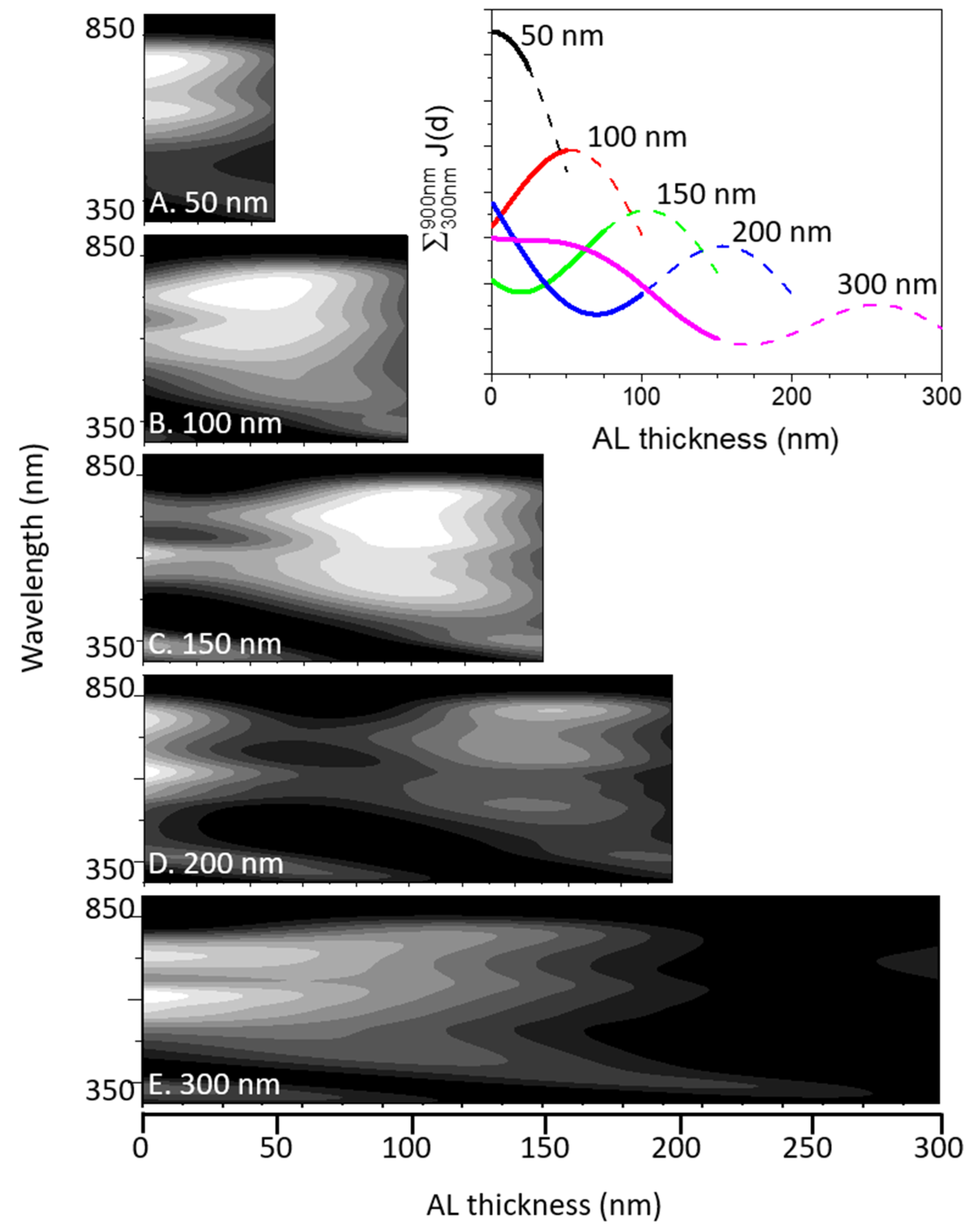
2.2. TMM Analysis of Photon Absorption in an AL
3. Discussion
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Zhan, L.; Li, S.; Lau, T.K.; Cui, Y.; Lu, X.; Shi, M.; Li, C.Z.; Li, H.; Hou, J.; Chen, H. Over 17% efficiency ternary organic solar cells enabled by two non-fullerene acceptors working in an alloy-like model. Energy Environ. Sci. 2020, 13, 635–645. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, Y.; Jin, K.; Qin, J.; Xu, J.; Li, W.; Xiong, J.; Liu, J.; Xiao, Z.; Sun, K.; et al. 18% Efficiency organic solar cells. Sci. Bull. 2020, 65, 272–275. [Google Scholar] [CrossRef]
- Firdaus, Y.; Le Corre, V.M.; Khan, J.I.; Kan, Z.; Laquai, F.; Beaujuge, P.M.; Anthopoulos, T.D. Key Parameters Requirements for Non-Fullerene-Based Organic Solar Cells with Power Conversion Efficiency >20%. Adv. Sci. 2019, 6, 1802028. [Google Scholar] [CrossRef] [PubMed]
- Sun, R.; Wu, Q.; Guo, J.; Wang, T.; Wu, Y.; Qiu, B.; Luo, Z.; Yang, W.; Hu, Z.; Guo, J.; et al. A Layer-by-Layer Architecture for Printable Organic Solar Cells Overcoming the Scaling Lag of Module Efficiency. Joule 2020, 4, 407–419. [Google Scholar] [CrossRef]
- Bergqvist, J.; Österberg, T.; Melianas, A.; Ever Aguirre, L.; Tang, Z.; Cai, W.; Ma, Z.; Kemerink, M.; Gedefaw, D.; Andersson, M.R.; et al. Asymmetric Photocurrent Extraction in Semitransparent Laminated Flexible Organic Solar Cells. NPJ Flex. Electron. 2018, 2, 4. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, G.; Liu, J.; Yao, H.; Zhang, J.; Ma, T.; Li, Z.; Yan, H. An All-Solution Processed Recombination Layer with Mild Post-Treatment Enabling Efficient Homo-Tandem Non-fullerene Organic Solar Cells. Adv. Mater. 2017, 29, 1604231–1604237. [Google Scholar] [CrossRef]
- Karki, A.; Gillett, A.J.; Friend, R.H.; Nguyen, T.Q. The path to 20% power conversion efficiencies in nonfullerene acceptor organic solar cells. Adv. Energy Mater. 2021, 11, 2003441. [Google Scholar] [CrossRef]
- Pettersson, L.A.A.; Roman, L.S.; Inganäs, O. Modeling photocurrent action spectra of photovoltaic devices based on organic thin films. J. Appl. Phys. 1999, 86, 487–496. [Google Scholar] [CrossRef]
- Krückemeier, L.; Kaienburg, P.; Flohre, J.; Bittkau, K.; Zonno, I.; Krogmeier, B.; Kirchartz, T. Developing design criteria for organic solar cells using well-absorbing non-fullerene acceptors. Commun. Phys. 2018, 1, 27. [Google Scholar] [CrossRef]
- Shoaee, S.; Stolterfoht, M.; Neher, D. The Role of Mobility on Charge Generation, Recombination, and Extraction in Polymer-Based Solar Cells. Adv. Energy Mater. 2018, 8, 1703355. [Google Scholar] [CrossRef]
- Park, H.; An, J.; Song, J.; Lee, M.; Ahn, H.; Jahnel, M.; Im, C. Thickness-dependent internal quantum efficiency of narrow band-gap polymer-based solar cells. Sol. Energy Mater. Sol. Cells 2015, 143, 242–249. [Google Scholar] [CrossRef]
- Szymanski, R.; Henry, R.; Stuard, S.H.; Vongsaysy, U.; Courtel, S.; Vellutini, L.; Bertrand, M.; Ade, H. Balanced charge transport optimizes industry-relevant ternary polymer solar cells. Solar RRL 2020, 4, 2000538. [Google Scholar] [CrossRef]
- Gavim, A.E.X.; Rosa, E.H.S.; Viana, E.R.; Coutinho, D.J.; Rodrigues, P.C.; Gonzalez, J.C.; Faria, R.M.; Silva, W.J.; Macedo, A.G. Modelling the electric field in non-fullerene organic solar cells: The effect of 1-chloronaphthalene additive. Sol. Energy 2022, 247, 286–294. [Google Scholar] [CrossRef]
- Guo, B.; Li, W.; Guo, X.; Meng, X.; Ma, W.; Zhang, M.; Li, Y. High Efficiency Nonfullerene Polymer Solar Cells with Thick Active Layer and Large Area. Adv. Mater. 2017, 29, 1702291. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Fan, B.; Ying, L.; Li, N.; Brabec, C.J.; Huang, F.; Cao, Y. Recent Progress in Thick-Film Organic Photovoltaic Devices: Materials, Devices, and Processing. SusMat 2021, 1, 4–23. [Google Scholar] [CrossRef]
- Jung, S.; Kim, K.Y.; Lee, Y.I.; Youn, J.H.; Moon, H.T.; Jang, J.; Kim, J. Optical Modeling and Analysis of Organic Solar Cells with Coherent Multilayers and Incoherent Glass Substrate Using Generalized Transfer Matrix Method. Jpn. J. Appl. Phys. 2011, 50, 122301–1223019. [Google Scholar] [CrossRef]
- Moulé, A.J.; Bonekamp, J.B.; Meerholz, K. The effect of active layer thickness and composition on the performance of bulk-heterojunction solar cells. J. Appl. Phys. 2006, 100, 094503. [Google Scholar] [CrossRef]
- Klein, M.F.G.; De Medeiros, G.Q.G.; Kapetana, P.; Lemmer, U.; Colsmann, A. Modeling Approach to Derive the Anisotropic Complex Refractive Index of Polymer: Fullerene Blends for Organic Solar Cells Utilizing Spectroscopic Ellipsometry. J. Photon. Energy 2015, 5, 057204. [Google Scholar] [CrossRef]
- Jones, A.L.; Ho, C.H.Y.; Riley, P.R.; Angunawela, I.; Ade, H.; So, F.; Reynolds, J.R. Investigating the Active Layer Thickness Dependence of Non-Fullerene Organic Solar Cells Based on PM7 Derivatives. J. Mater. Chem. C 2020, 8, 15459–15469. [Google Scholar] [CrossRef]
- Zonno, I.; Krogmeier, B.; Katte, V.; Lübke, D.; Martinez-Otero, A.; Kirchartz, T. Discriminating between Surface and Bulk Recombination in Organic Solar Cells by Studying the Thickness Dependence of the Open-Circuit Voltage. Appl. Phys. Lett. 2016, 109, 183301. [Google Scholar] [CrossRef]
- Cui, Y.; Yao, H.; Hong, L.; Zhang, T.; Tang, Y.; Lin, B.; Xian, K.; Gao, B.; An, C.; Bi, P.; et al. Organic Photovoltaic Cell with 17% Efficiency and Superior Processability. Natl. Sci. Rev. 2020, 7, 1239–1246. [Google Scholar] [CrossRef]
- Blakesley, J.C.; Neher, D. Relationship between Energetic Disorder and Open-Circuit Voltage in Bulk Heterojunction Organic Solar Cells. Phys. Rev. B 2011, 84, 075210. [Google Scholar] [CrossRef]
- Upreti, T.; Wilken, S.; Zhang, H.; Kemerink, M. Slow Relaxation of Photogenerated Charge Carriers Boosts Open-Circuit Voltage of Organic Solar Cells. J. Phys. Chem. Lett. 2021, 12, 9874–9881. [Google Scholar] [CrossRef] [PubMed]
- Gueymard, C.A. The sun’s total and spectral irradiance for solar energy applications and solar radiation models. Sol. Energy 2004, 76, 423–453. [Google Scholar] [CrossRef]
- Islam, S. In-Depth Analysis of Organic Solar Cells Using Transport Equation and Optical Transfer Matrix Method with Detailed Analytical Derivations. Energies 2021, 14, 735. [Google Scholar] [CrossRef]
- Tamai, Y.; Fan, Y.; Kim, V.O.; Ziabrev, K.; Rao, A.; Barlow, S.; Marder, S.R.; Friend, R.H.; Menke, S.M. Ultrafast long-range charge separation in non-fullerene organic solar cells. ACS Nano 2017, 11, 12473–12481. [Google Scholar] [CrossRef]
- Song, J.; Lee, Y.; Jin, B.; An, J.; Park, H.; Park, H.; Lee, M.; Im, C. Connecting charge transfer kinetics to device parameters of a narrow-bandgap polymer-based solar cell. Phys. Chem. Chem. Phys. 2016, 18, 26550–26561. [Google Scholar] [CrossRef]
- Zhao, W.; Qian, D.; Zhang, S.; Li, S.; Inganäs, O.; Gao, F.; Hou, J. Fullerene-free polymer solar cells with over 11% efficiency and excellent thermal stability. Adv. Mater. 2016, 28, 4734–4739. [Google Scholar] [CrossRef]
- Bin, H.; Gao, L.; Zhang, Z.G.; Yang, Y.; Zhang, Y.; Zhang, C.; Chen, S.; Xue, L.; Yang, C.; Xiao, M.; et al. 11.4% Efficiency non-fullerene polymer solar cells with trialkylsilyl substituted 2D-conjugated polymer as donor. Nat. Commun. 2016, 7, 13651. [Google Scholar] [CrossRef]
- Zhao, W.; Li, S.; Yao, H.; Zhang, S.; Zhang, Y.; Yang, B.; Hou, J. Molecular optimization enables over 13% efficiency in organic solar cells. J. Am. Chem. Soc. 2017, 139, 7148–7151. [Google Scholar] [CrossRef]
- Gupta, R.K.; Garai, R.; Hossain, M.; Afroz, M.A.; Kalita, D.; Iyer, P.K. Engineering Polymer Solar Cells: Advancement in Active Layer Thickness and Morphology. J. Mater. Chem. C 2021, 9, 8746–8775. [Google Scholar] [CrossRef]
- Gupta, R.K.; Garai, R.; Afroz, M.A.; Iyer, P.K. Regulating active layer thickness and morphology for high performance hot-casted polymer solar cells. J. Mater. Chem. C 2020, 8, 8191–8198. [Google Scholar] [CrossRef]
- Im, C.; Kang, S.W.; Choi, J.Y.; An, J. Comparing donor- and acceptor-originated excitons of non-fullerene acceptor blend polymeric system. Polymers 2021, 13, 1770. [Google Scholar] [CrossRef] [PubMed]
- Larouche, S.; Martinu, L. OpenFilters: Open-source software for the design, optimization, and synthesis of optical filters. Appl. Opt. 2008, 47, C219. [Google Scholar] [CrossRef] [PubMed]

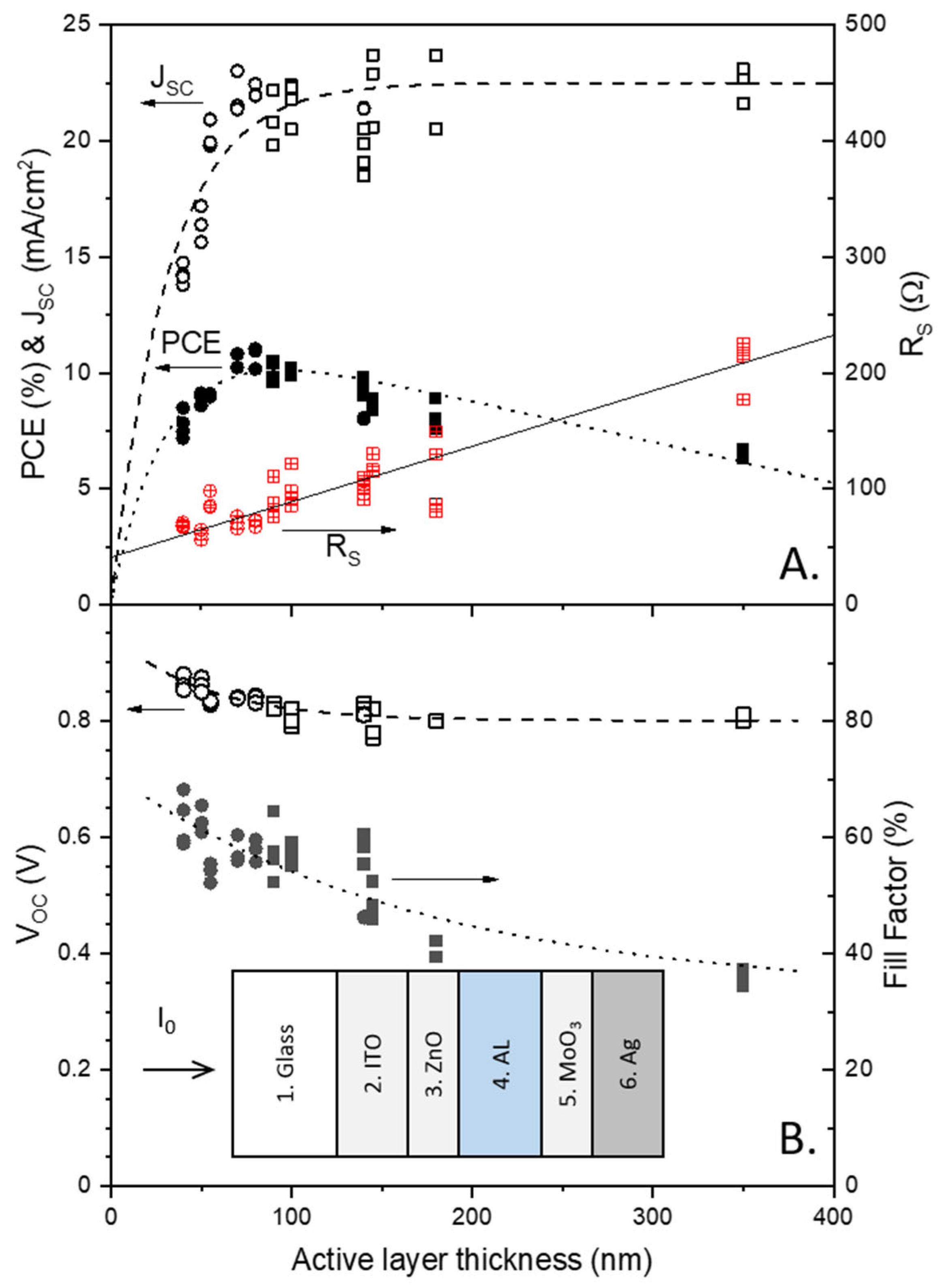
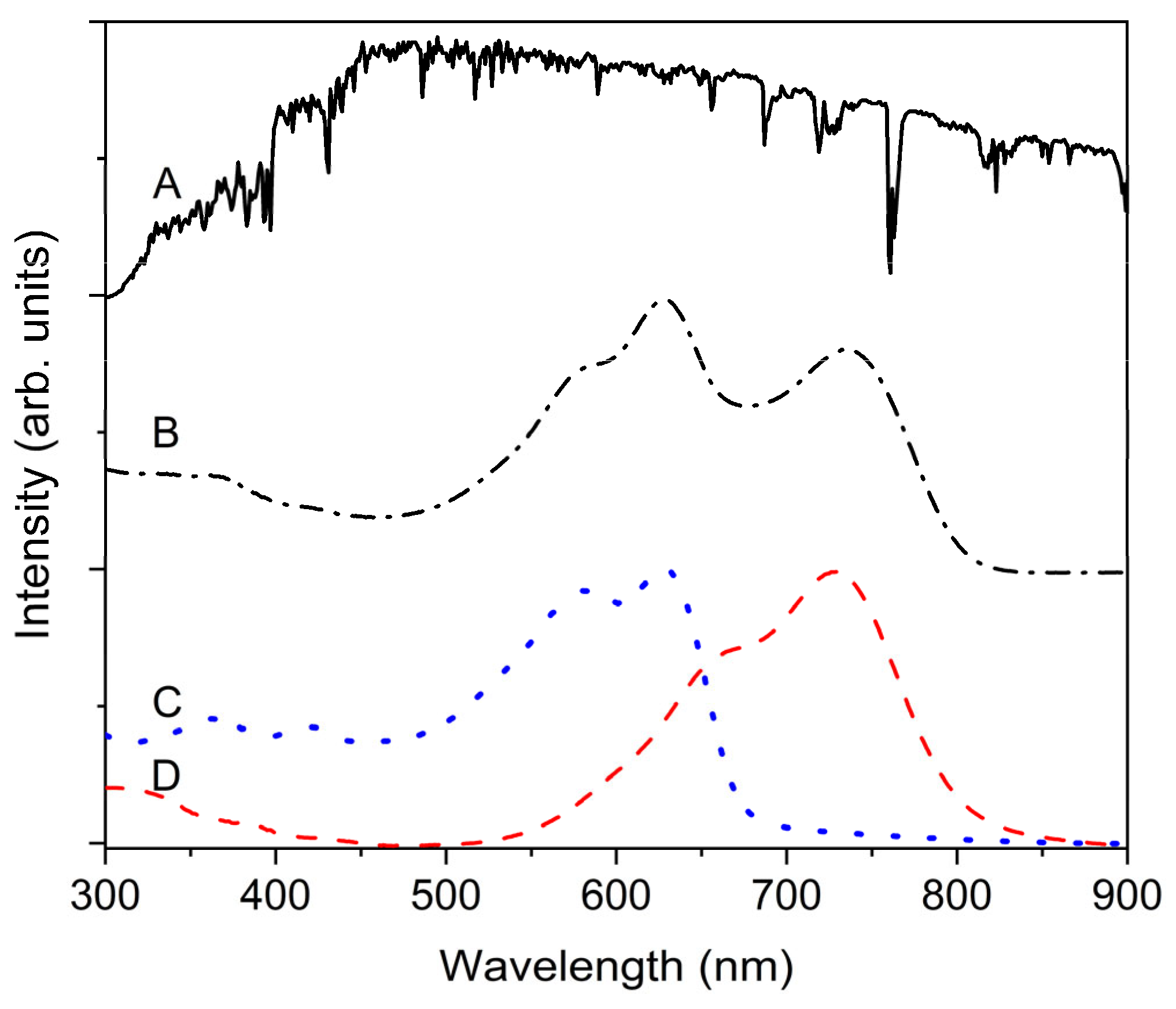
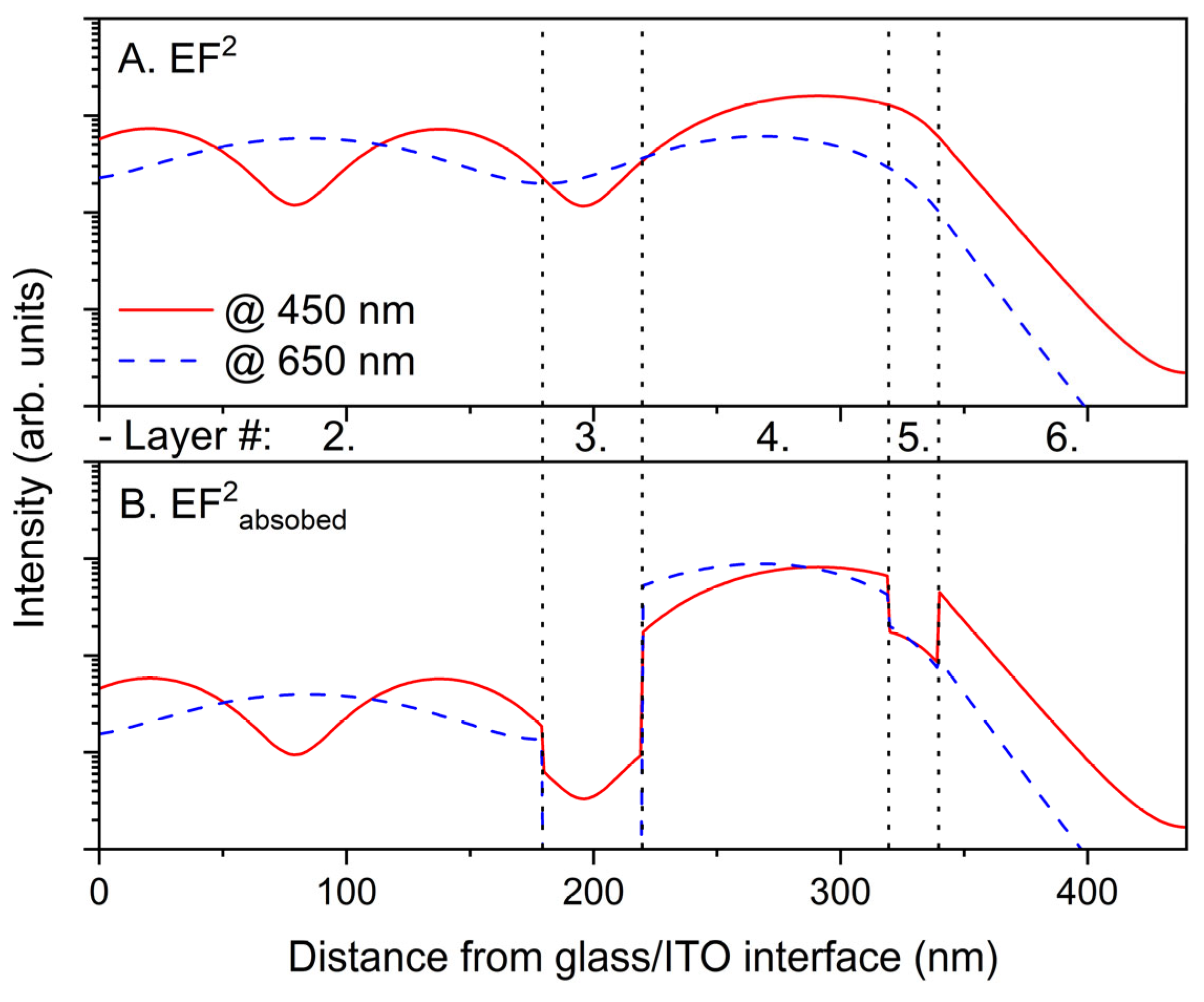
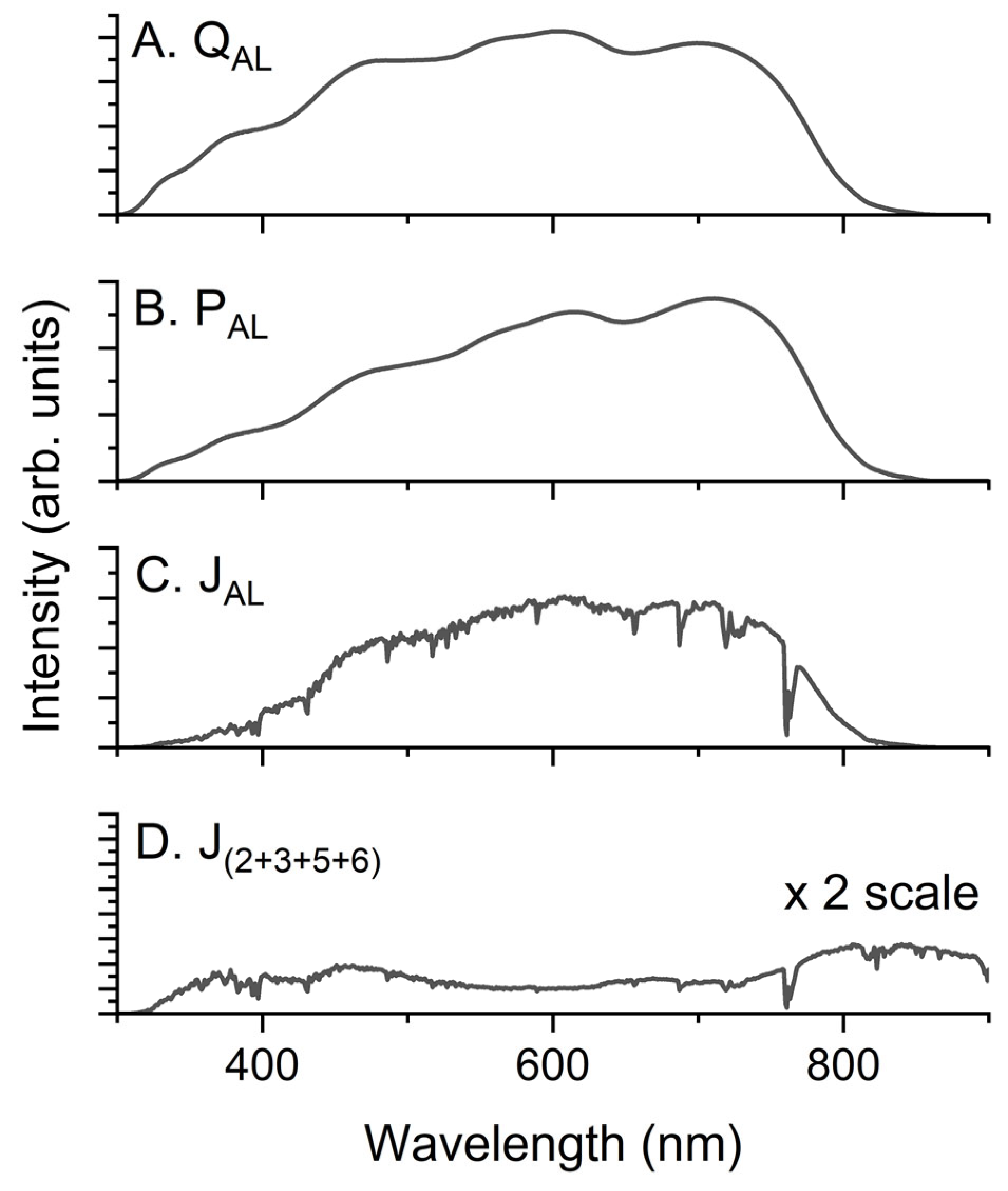
| AL Thickness (nm) | FF (%) | VOC (V) | JSC (mA/cm2) | PCE (%) |
|---|---|---|---|---|
| 50 | 62.5 | 0.85 | 17.2 | 9.1 |
| 80 | 60.4 | 0.84 | 21.4 | 10.8 |
| 100 | 57.3 | 0.80 | 22.3 | 10.0 |
| 140 | 60.4 | 0.81 | 19.1 | 9.2 |
| 200 | 42.1 | 0.80 | 23.7 | 8.0 |
| 350 | 35.1 | 0.81 | 23.1 | 6.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Im, C.; Kang, S.W.; Choi, J.Y.; An, J.; Mičová, J.; Remeš, Z. Spatial Balance of Photogenerated Charge Carriers in Active Layers of Polymer Solar Cells. Molecules 2023, 28, 5823. https://doi.org/10.3390/molecules28155823
Im C, Kang SW, Choi JY, An J, Mičová J, Remeš Z. Spatial Balance of Photogenerated Charge Carriers in Active Layers of Polymer Solar Cells. Molecules. 2023; 28(15):5823. https://doi.org/10.3390/molecules28155823
Chicago/Turabian StyleIm, Chan, Sang Woong Kang, Jeong Yoon Choi, Jongdeok An, Júlia Mičová, and Zdeněk Remeš. 2023. "Spatial Balance of Photogenerated Charge Carriers in Active Layers of Polymer Solar Cells" Molecules 28, no. 15: 5823. https://doi.org/10.3390/molecules28155823
APA StyleIm, C., Kang, S. W., Choi, J. Y., An, J., Mičová, J., & Remeš, Z. (2023). Spatial Balance of Photogenerated Charge Carriers in Active Layers of Polymer Solar Cells. Molecules, 28(15), 5823. https://doi.org/10.3390/molecules28155823








