Evaluation of the Usefulness of Topological Indices for Predicting Selected Physicochemical Properties of Bioactive Substances with Anti-Androgenic and Hypouricemic Activity
Abstract
1. Introduction
2. Results and Discussion
3. Materials and Methods
3.1. Calculation of Topological Indices
3.2. Chromatographic Parameters of Lipophilicity (RMW)
3.3. Calculated Parameters
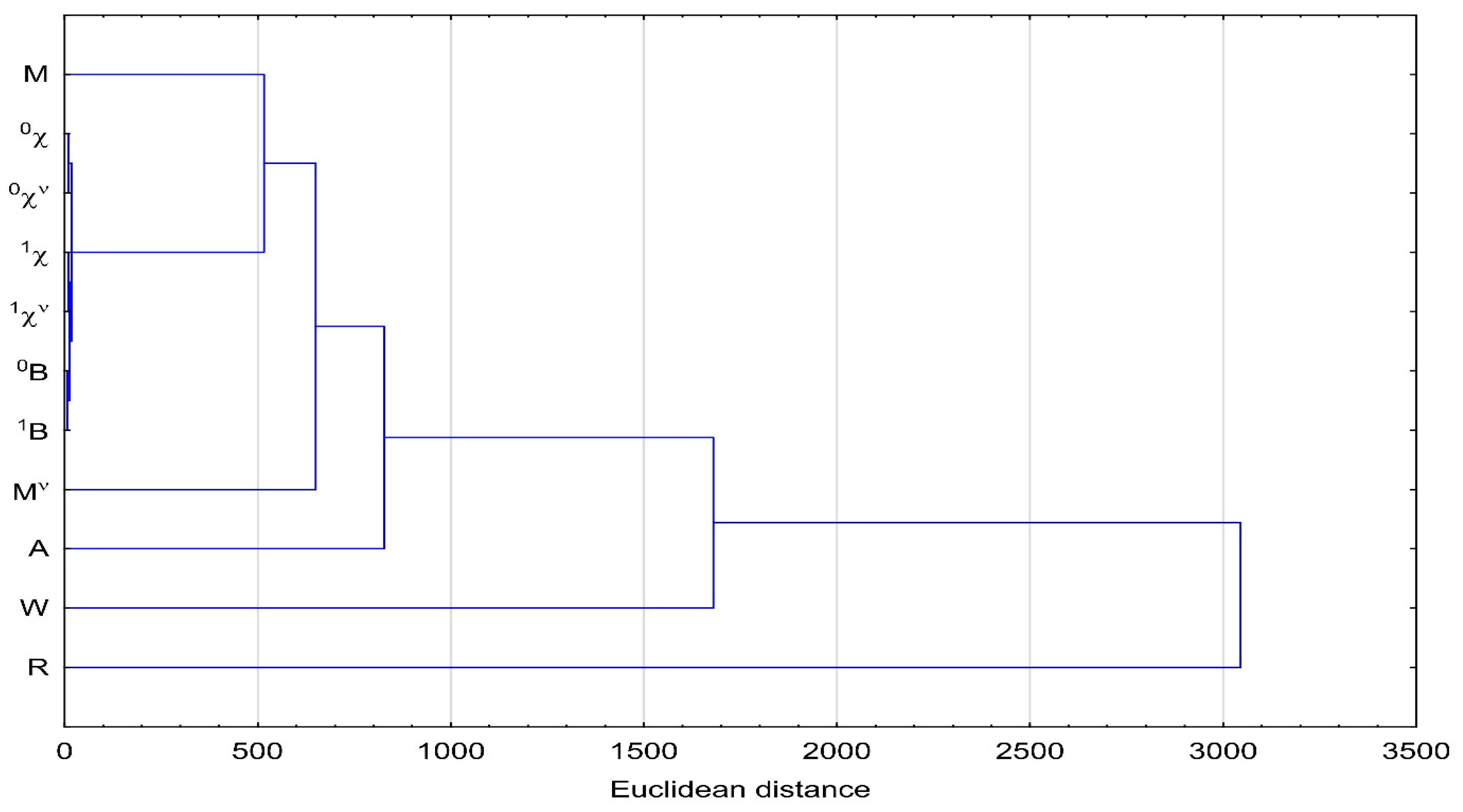
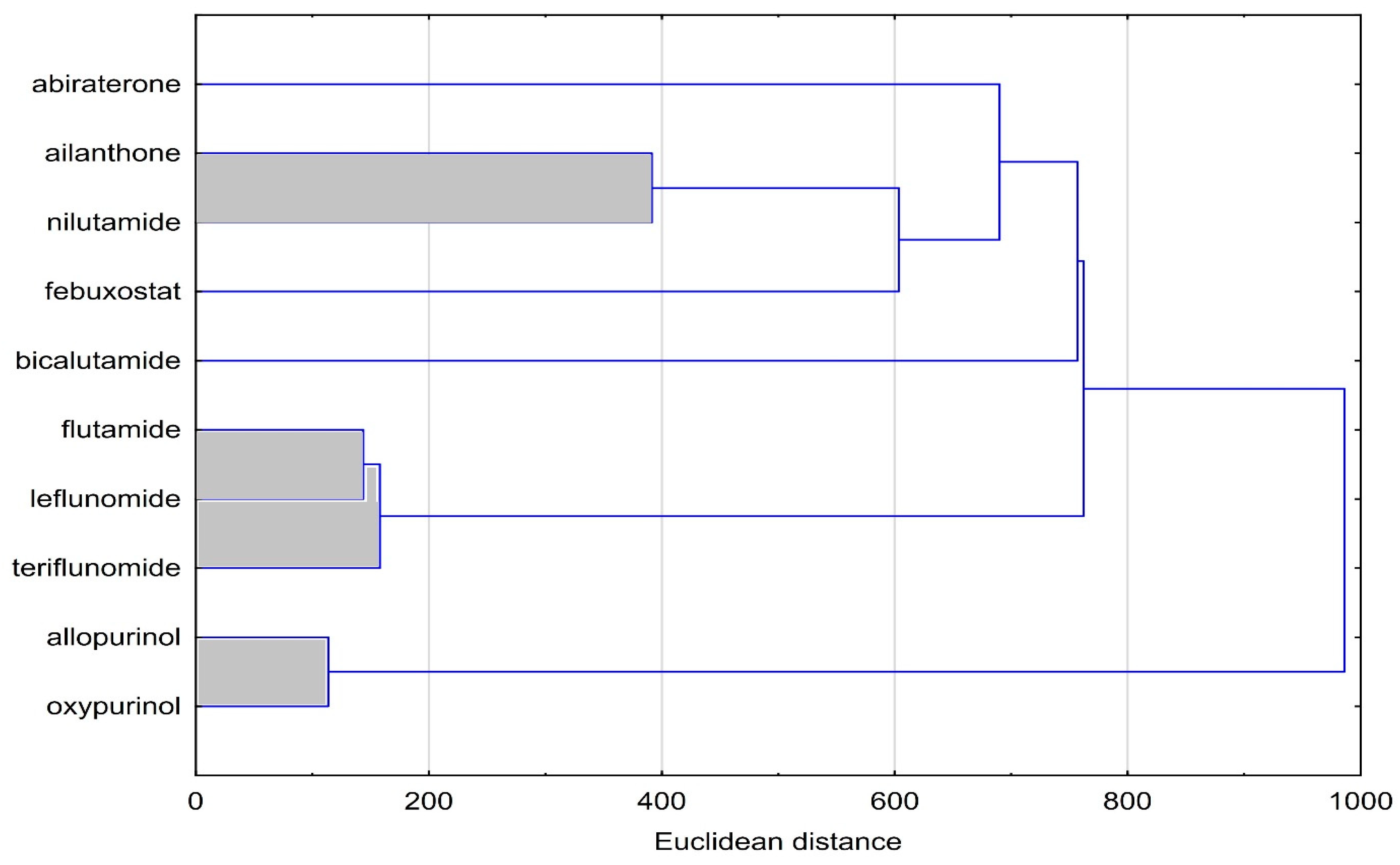
3.4. Cluster Analysis (CA)
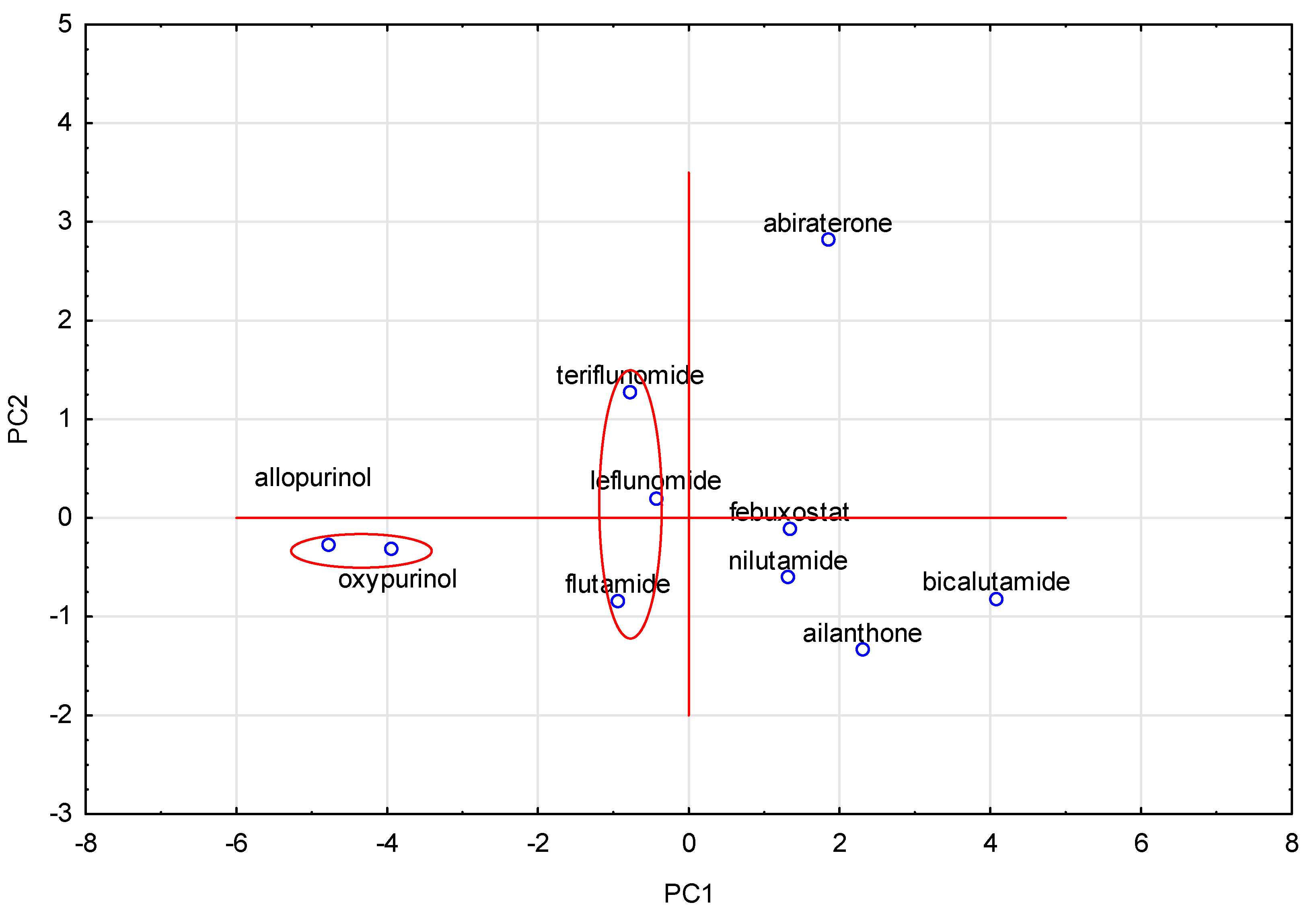
3.5. Principal Component Analysis (PCA)
3.6. Linear Regression
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Guan, L.; Yang, H.; Cai, Y.; Sun, L.; Di, P.; Li, W.; Liu, G.; Tang, Y. ADMET-score—A comprehensive scoring function for evaluation of chemical drug-likeness. MedChemComm 2018, 10, 148–157. [Google Scholar] [CrossRef] [PubMed]
- Haque, S.K.M.; Ratemi, E.S. Drug development and analysis review. Pharm. Chem. J. 2017, 50, 837–850. [Google Scholar] [CrossRef]
- Shou, W.Z. Current status and future directions of high-throughput ADME screening in drug discovery. J. Pharm. Anal. 2020, 10, 201–208. [Google Scholar] [CrossRef]
- Kar, S.; Leszczynski, J. Open access in silico tools to predict the ADMET profiling of drug candidates. Expert Opin. Drug Discov. 2020, 15, 1473–1487. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xing, J.; Xu, Y.; Zhou, N.; Peng, J.; Xiong, Z.; Liu, X.; Luo, X.; Luo, C.; Chen, K.; et al. In silico ADME/T modelling for rational drug design. Q. Rev. Biophys. 2015, 48, 488–515. [Google Scholar] [CrossRef] [PubMed]
- Jia, C.-Y.; Li, J.-Y.; Hao, G.-F.; Yang, G.-F. A drug-likeness toolbox facilitates ADMET study in drug discovery. Drug Discov. Today 2020, 25, 248–258. [Google Scholar] [CrossRef]
- Kiriiri, G.K.; Njogu, P.M.; Mwangi, A.N. Exploring different approaches to improve the success of drug discovery and development projects: A review. Future J. Pharm. Sci. 2020, 6, 27. [Google Scholar] [CrossRef]
- Dong, J.; Wang, N.-N.; Yao, Z.-J.; Zhang, L.; Cheng, Y.; Ouyang, D.; Lu, A.-P.; Cao, D.-S. ADMETlab: A platform for systematic ADMET evaluation based on a comprehensively collected ADMET database. J. Cheminform. 2018, 10, 29. [Google Scholar] [CrossRef]
- Muratov, E.N.; Bajorath, J.; Sheridan, R.P.; Tetko, I.V.; Filimonov, D.; Poroikov, V.; Oprea, T.I.; Baskin, I.I.; Varnek, A.; Roitberg, A.; et al. QSAR without borders. Chem. Soc. Rev. 2020, 49, 3525–3564. [Google Scholar] [CrossRef]
- Roy, K.; Kar, S.; Das, R.N. Newer directions in QSAR/QSPR. In A Primer on QSAR/QSPR Modeling; Springer Briefs in Molecular Science; Springer: Cham, Switzerland, 2015; pp. 105–121. [Google Scholar] [CrossRef]
- Dastmalchi, S.; Hamzeh-Mivehroud, M.; Sokouti, B. A Practical Approach. In Quantitative Structure–Activity Relationship; CRC Press: Boca Raton, FL, USA, 2018; p. 115. [Google Scholar] [CrossRef]
- Gozalbes, R.; Doucet, J.P.; Derouin, F. Application of topological descriptors in QSAR and drug design: History and new trends. Curr. Drug Targets Infect. Disord. 2022, 2, 93–102. [Google Scholar] [CrossRef]
- Grover, M.; Singh, B.; Bakshi, M.; Singh, S. Quantitative structure-property relationships in pharmaceutical research—Part 1. Pharm. Sci. Technol. Today 2000, 3, 28–35. [Google Scholar] [CrossRef]
- Amos, R.; Haddad, P.R.; Szucs, R.; Dolan, J.W.; Pohl, C.A. Molecular modelling and prediction accuracy in quantitative structure-retention relationship calculations for chromatography. Trends Anal. Chem. 2008, 105, 352–359. [Google Scholar] [CrossRef]
- Yuanita, E.; Sudirman; Dharmayani, N.K.T.; Ulfa, M.; Syahri, J. uantitative structure-activity relationship (QSAR) and molecular docking of xanthone derivatives as anti-tuberculosis agents. J. Clin. Tuberc. Other Mycobact Dis. 2020, 21, 100203. [Google Scholar] [CrossRef]
- Rodríguez-Lozada, J.; Tovar-Gudiño, E.; Guevara-Salazar, J.A.; Razo-Hernández, R.S.; Santiago, Á.; Pastor, N.; Fernández-Zertuche, M. QSAR and molecular docking studies of the inhibitory activity of novel heterocyclic GABA analogues over GABA-AT. Molecules 2018, 23, 2984. [Google Scholar] [CrossRef]
- Sridhar, J.; Liu, J.; Foroozesh, M.; Stevens, C.L.K. Insights on cytochrome P450 enzymes and inhibitors obtained through QSAR studies. Molecules 2012, 17, 9283–9305. [Google Scholar] [CrossRef]
- Valencia, J.; Rubio, V.; Puerto, G.; Vasquez, L.; Bernal, A.; Mora, J.R.; Cuesta, S.A.; Paz, J.L.; Insuasty, B.; Abonia, R.; et al. QSAR studies, molecular docking, molecular dynamics, synthesis, and biological evaluation of novel quinolinone-based thiosemicarbazones against Mycobacterium tuberculosis. Antibiotics 2022, 12, 61. [Google Scholar] [CrossRef] [PubMed]
- Guha, R.; Jurs, P.C. Development of QSAR models to predict and interpret the biological activity of artemisinin analogues. J. Chem. Inf. Comput. Sci. 2004, 44, 1440–1449. [Google Scholar] [CrossRef] [PubMed]
- Thai, K.-M.; Bui, Q.-H.; Tran, T.-D.; Huynh, T.-N.-P. QSAR modeling on benzo[c]phenanthridine analogues as topoisomerase I inhibitors and anti-cancer agents. Molecules 2012, 17, 5690–5712. [Google Scholar] [CrossRef]
- Paritala, J.; Peraman, R.; Kondreddy, V.K.; Subrahmanyam, C.V.S.; Ravichandiran, V. Quantitative structure retention relationship (QSRR) approach for assessment of chromatographic behavior of antiviral drugs in the development of liquid chromatographic method. J. Liq. Chromatogr. Relat. Technol. 2021, 44, 637–648. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, M.; Sun, F.; Li, S.; Hse, C.-Y.; Jin, C. Screening, synthesis, and QSAR research on cinnamaldehyde-amino acid schiff base compounds as antibacterial agents. Molecules 2018, 23, 3027. [Google Scholar] [CrossRef] [PubMed]
- Santos-Garcia, L.; De Mecenas Filho, M.A.; Musilek, K.; Kuca, K.; Ramalho, T.C.; Da Cunha, E.F.F. QSAR study of N-myristoyltransferase inhibitors of antimalarial agents. Molecules 2018, 23, 2348. [Google Scholar] [CrossRef] [PubMed]
- Narasimhan, B.; Belsare, D.; Pharande, D.; Mourya, V.; Dhake, A. Esters, amides and substituted derivatives of cinnamic acid: Synthesis, antimicrobial activity and QSAR investigations. Eur. J. Med. Chem. 2004, 39, 827–834. [Google Scholar] [CrossRef]
- Wang, Q.S.; Zhang, L. Review of research on quantitative structure-retention relationships in thin-layer chromatography. J. Liq. Chromatogr. Relat. Technol. 1999, 22, 1–14. [Google Scholar] [CrossRef]
- Sobańska, A.W. Application of planar chromatographic descriptors to the prediction of physicochemical properties and biological activity of compounds. J. Liq. Chromatogr. Relat. Technol. 2018, 41, 255–271. [Google Scholar] [CrossRef]
- Kadela-Tomanek, M.; Jastrzębska, M.; Chrobak, E.; Bębenek, E.; Boryczka, S. Chromatographic and computational screening of lipophilicity and pharmacokinetics of newly synthesized betulin-1,4-quinone hybrids. Processes 2021, 9, 376. [Google Scholar] [CrossRef]
- Bębenek, E.; Bober-Majnusz, K.; Siudak, S.; Chrobak, E.; Kadela-Tomanek, M.; Wietrzyk, J.; Boryczka, S. Application of TLC to evaluate the lipophilicity of newly synthesized betulin derivatives. J. Chromatogr. Sci. 2020, 58, 323–333. [Google Scholar] [CrossRef]
- Apostolov, S.; Vastag, G.; Matijevi’c, B.; Ðakovi´c-Sekuli´c, T.; Marinkovi´c, A. Thin-layer chromatography on reversed phase in the characterization of retention behaviour, lipophilicity, and pharmacokinetics of cyanoacetamide derivatives. J. Chil. Chem. Soc. 2020, 65, 4654–4660. [Google Scholar] [CrossRef]
- Ginex, T.; Vazquez, J.; Gilbert, E.; Herrero, E.; Luque, F.J. Lipophilicity in drug design: An overview of lipophilicity descriptors in 3D-QSAR studies. Futur. Med. Chem. 2019, 11, 1177–1193. [Google Scholar] [CrossRef]
- Awasthi, A.K.; Jain, S.; Piplode, S.; Pandey, S. QSPR modeling of the lipophilicity of aziridine derivatives. Der Pharma Chem. 2014, 6, 380–387. [Google Scholar]
- Starek, M.; Plenis, A.; Zagrobelna, M.; Dąbrowska, M. Assessment of lipophilicity descriptors of selected NSAIDs obtained at different TLC stationary phases. Pharmaceutics 2021, 13, 440. [Google Scholar] [CrossRef] [PubMed]
- Pyka, A.; Kępczyńska, E.; Bojarski, J. Application of selected traditional structural descriptors to QSRR and QSAR analysis of barbiturates. Indian J. Chem. 2003, 42A, 1405–1413. [Google Scholar]
- Dołowy, M.; Bober, K.; Pyka-Pajak, A. Topological indices in modeling of chromatographic retention. In Chemometrics in Chromatography; Komsta, L., Vander Heyden, Y., Sherma, J., Eds.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Boca Raton, FL, USA, 2018; pp. 319–350. [Google Scholar]
- Ośmiałowski, K.; Kaliszan, R. Studies of performance on graph theoretical indices in QSAR analysis. Quant. Struct. Act. Relat. 1991, 10, 125–134. [Google Scholar] [CrossRef]
- Estrada, E.; Uriarte, E. Recent advances on the role of topological indices in drug discovery research. Curr. Med. Chem. 2001, 8, 1573–1588. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; Patlewicz, G.; Uriarte, E. From molecular graphs to drugs. A review on the use of topological indices in drug design and discovery. Indian J. Chem. 2003, 42A, 1315–1329. [Google Scholar]
- Pyka, A. Indeksy topologiczne i ich znaczenie w badaniach chromatograficznych. Część I. Wiad. Chem. 1997, 51, 783–802. [Google Scholar]
- Barysz, M.; Jashari, G.; Lall, R.S.; Srivastava, V.K.; Trinajstić, N. Studies in Physical and Theoretical Chemistry, Chemical Application of Topology and Graph Theory; King, R.B., Ed.; Elsevier: Amsterdam, The Netherlands, 1983; p. 222. [Google Scholar]
- Balaban, A.T.; Motoc, I.; Bonchev, D.; Mekenyan, O. Topological indices for structure—Activity correlations. Top. Curr. Chem. 1983, 114, 21–55. [Google Scholar]
- Randić, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Pyka, A.; Dołowy, M. Application of structural descriptors for the evaluation of some physicochemical properties of selected bile acids. Acta Pol. Pharm. 2004, 61, 407–413. [Google Scholar]
- Pyka, A. Topological indexes and QSRR methodology in pharmaceutical and chemical analysis. J. AOAC Int. 2012, 95, 673–690. [Google Scholar] [CrossRef]
- Pyka, A.; Kazimierczak, A.; Gurak, D. Utilization of reversed-phase TLC and topological indices to the lipophilicity investigations of naproxen. Pharm. Methods 2013, 4, 16–20. [Google Scholar] [CrossRef]
- Pyka, A. Use of selected topological indexes for evaluation of lipophilicity of steroid compounds investigated by RP-HPTLC. J. Liq. Chromatogr. Relat. Technol. 2009, 32, 3056–3065. [Google Scholar] [CrossRef]
- Dołowy, M.; Pyka, A. Lipophilicity assessment of spironolactone by means of reversed phase liquid chromatography and by newly developed calculation procedures. Acta Pol. Pharm. 2015, 72, 235–244. [Google Scholar] [PubMed]
- Pyka, A. Chromatographic data-topological index dependence for selected steroids. J. Liq. Chromatogr. Relat. Technol. 2001, 24, 453–460. [Google Scholar] [CrossRef]
- Liu, J.; Arockiaraj, M.; Arulperumjothi, M.; Prabhu, S. Distance based and bond additive topological indices of certain repurposed antiviral drug compounds tested for treating COVID-19. Int. J. Quantum Chem. 2021, 121, e26617. [Google Scholar] [CrossRef]
- Kirmani, S.A.K.; Ali, P.; Azam, F.; Alvi, P.A. On ve-degree and ev-degree topological properties of hyaluronic acid-anticancer drug conjugates with QSPR. J. Chem. 2021, 2021, 3860856. [Google Scholar] [CrossRef]
- Dołowy, M.; Jampilek, J.; Bober-Majnusz, K. A Comparative study of the lipophilicity of metformin and phenformin. Molecules 2021, 26, 6613. [Google Scholar] [CrossRef] [PubMed]
- Pyka, A.; Dołowy, M.; Gurak, D. Use of selected structural descriptors for evaluation of the lipophilicity of bile acids investigated by RPHPTLC. JPC—J. Planar Chromatogr. 2005, 18, 465–470. [Google Scholar] [CrossRef]
- Wardecki, D.; Dołowy, M.; Bober-Majnusz, K.; Jampilek, J. Comparative study of the lipophilicity of selected anti-androgenic and blood uric acid lowering compounds. Molecules 2023, 28, 166. [Google Scholar] [CrossRef]
- Jóźwiak, K.; Szumilo, H.; Soczewinski, E. Lipophilicity, methods of determination and its role in biological effect of chemical substances. Wiad. Chem. 2001, 55, 1047–1074. [Google Scholar]
- Stanisz, A. Przystępny Kurs Statystyki z Zastosowaniem Statistica PL na Przykładach Medycyny; Analizy Wielowymiarowe; Stat Soft Polska: Krakow, Poland, 2007; Volume 3. [Google Scholar]
- Jolliffe, J.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. 2016, 374, 20150202. [Google Scholar] [CrossRef]
| Compound | Topological Indices Based on Adjacency Matrix | Topological Indices Based on Distance Matrix | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| M | Mν | 0χ | 1χ | 0χν | 1χν | W | R | A | 0B | 1B | |
| Blood Uric Acid-Lowering Compounds | |||||||||||
| Allopurinol | 96 | 184 | 5.9309 | 3.6481 | 4.9574 | 2.7451 | 76.804 | 152.786 | 48.6479 | 2.5718 | 0.7468 |
| Oxypurinol | 102 | 218 | 6.6903 | 4.0423 | 5.3410 | 2.9328 | 101.248 | 201.424 | 61.1606 | 2.5845 | 0.6837 |
| Febuxostat | 190 | 342 | 14.499 | 8.3593 | 14.6247 | 6.7450 | 810.546 | 1619.431 | 955.8462 | 2.6186 | 0.3456 |
| Anti-Androgens | |||||||||||
| Abiraterone | 210 | 246 | 16.8011 | 1.5871 | 16.1181 | 9.4695 | 1447.587 | 2893.781 | 577.6900 | 2.4969 | 0.2531 |
| Bicalutamide | 287 | 573 | 19.0629 | 10.1215 | 14.7881 | 7.8966 | 1749.234 | 3495.225 | 661.7294 | 2.6786 | 0.2656 |
| Flutamide | 135 | 399 | 13.9309 | 7.5186 | 10.1154 | 2.0128 | 526.913 | 1051.791 | 246.1452 | 2.5929 | 0.3781 |
| Nilutamide | 160 | 462 | 15.1280 | 7.8722 | 11.3934 | 5.9729 | 1067.496 | 2132.563 | 786.2401 | 2.6346 | 0.3388 |
| Leflunomide | 166 | 402 | 12.5823 | 7.0160 | 9.7846 | 4.3595 | 588.241 | 1174.697 | 274.7566 | 2.4525 | 0.3471 |
| Teriflunomide | 170 | 298 | 12.8012 | 6.6709 | 9.7462 | 5.0397 | 640.855 | 1278.586 | 297.3176 | 2.3403 | 0.3003 |
| Ailanthone | 204 | 404 | 17.2760 | 10.9384 | 14.4220 | 9.0418 | 1152.250 | 2302.750 | 456.6286 | 2.7868 | 0.3619 |
| Partition Coefficient (logP) | Topological Index | Linear Equation | Correlation Coefficient (r) | No. Eq. |
|---|---|---|---|---|
| Blood Uric Acid-Lowering Compounds | ||||
| AlogPs | W | AlogPs = −1.060 + 0.00599 × W | 0.9970 | (1) |
| AlogPs | R | AlogPs = −1.057 + 0.00300 × R | 0.9970 | (2) |
| AlogPs | A | AlogPs = −0.7926 + 0.00480 × A | 0.9982 | (3) |
| AClogP | W | AClogP = −0.8596 + 0.00610 × W | 0.9971 | (4) |
| AClogP | R | AClogP = −0.8570 + 0.00305 × R | 0.9971 | (5) |
| AClogP | A | AClogP = −0.5875 + 0.00489 × A | 0.9983 | (6) |
| XlogP2 | Mν | XlogP2 = −5.144 + 0.02257 × Mν | 0.9984 | (7) |
| XlogP2 | 0χ | XlogP2 = −3.122 + 0.39545 × 0χ | 0.9976 | (8) |
| XlogP2 | 1χ | XlogP2 = −3.384 + 0.71734 × 1χ | 0.9973 | (9) |
| XlogP2 | 1B | XlogP2 = 5.6126 − 8.714 × 1B | −1.0000 | (10) |
| ACD/logP | M | ACD/logP = −112.3 + 1.1217 × M | 0.9984 | (11) |
| ACD/logP | 1χ | ACD/logP = −87.95 + 22.558 × 1χ | 0.9972 | (12) |
| ACD/logP | 0χν | ACD/logP = −56.95 + 10.794 × 0χν | 0.9994 | (13) |
| ACD/logP | 1χν | ACD/logP = −75.65 + 26.173 × 1χν | 0.9992 | (14) |
| ACD/logP | W | ACD/logP = −14.00 + 0.14181 × W | 0.9996 | (15) |
| ACD/logP | R | ACD/logP = −13.94 + 0.07094 × R | 0.9996 | (16) |
| ACD/logP | A | ACD/logP = −7.640 + 0.11365 × A | 0.9999 | (17) |
| Anti-Androgens | ||||
| AlogPs | 1χ | AlogPs = 5.6093 − 0.4320 × 1χ | −0.8667 | (18) |
| AClogP | 1χ | AClogP = 5.0751 − 0.3574 × 1χ | −0.8910 | (19) |
| mlogP | 1χ | mlogP = 4.6684 − 0.2898 × 1χ | −0.7764 | (20) |
| XlogP3 | 1χ | XlogP3 = 5.9902 − 0.4834 × 1χ | −0.8154 | (21) |
| logPavg | 1χ | logPavg = 5.1783 − 0.3768 × 1χ | −0.8425 | (22) |
| logPKOWWIN | 1χ | logPKOWWIN = 6.9299 − 0.5693 × 1χ | −0.9099 | (23) |
| Chromatographic Parameter of Lipophilicity (RMW) | Topological Index | Linear Equation | Correlation Coefficient (r) | No. Eq. |
|---|---|---|---|---|
| Blood Uric Acid-Lowering Compounds | ||||
| RP18 (EtOH/H2O) | M | RP18 (EtOH/H2O) = −2.520 + 0.02750 × M | 0.9976 | (24) |
| RP18 (EtOH/H2O) | 0χν | RP18 (EtOH/H2O) = −1.163 + 0.26467 × 0χν | 0.9989 | (25) |
| RP18 (EtOH/H2O) | 1χν | RP18 (EtOH/H2O) = −1.621 + 0.64167 × 1χν | 0.9985 | (26) |
| RP18 (EtOH/H2O) | W | RP18 (EtOH/H2O) = −0.1099 + 0.00348 × W | 0.9991 | (27) |
| RP18 (EtOH/H2O) | R | RP18 (EtOH/H2O) = −0.1085 + 0.00174 × R | 0.9991 | (28) |
| RP18 (EtOH/H2O) | A | RP18 (EtOH/H2O) = 0.04581 + 0.00279 × A | 0.9997 | (29) |
| RP18 (ACN/H2O) | Mν | RP18 (ACN/H2O) = −2.358 + 0.01248 × Mν | 0.9999 | (30) |
| RP18 (ACN/H2O) | 0B | RP18 (ACN/H2O) = −110.3 + 42.834 × 0B | 0.9989 | (31) |
| RP18 (ACN/H2O) | 1B | RP18 (ACN/H2O) = 3.5769 − 4.798 × 1B | −0.9974 | (32) |
| RP18W (ACN/H2O) | W | RP18W (ACN/H2O) = −0.4364 + 0.00245 × W | 0.9973 | (33) |
| RP18W (ACN/H2O) | R | RP18W (ACN/H2O) = −0.4354 + 0.00122 × R | 0.9973 | (34) |
| RP18W (ACN/H2O) | A | RP18W (ACN/H2O) = −0.3272 + 0.00196 × A | 0.9984 | (35) |
| Anti-Androgens | ||||
| RP18 (P-2-ol/H2O) | 1B | RP18 (P-2-ol/H2O) = 4.5928 − 7.182 × 1B | −0.7581 | (36) |
| RP18W (P-2-ol/H2O) | 0B | RP18W (P-2-ol/H2O) = 9.8338 − 3.232 × 0B | −0.8043 | (37) |
| Physicochemical Parameter | Topological Index | Linear Equation | Correlation Coefficient (r) | No. Eq. |
|---|---|---|---|---|
| MR | M | MR = −15.89 + 0.52076 × M | 0.9997 | (38) |
| MR | 0χ | MR = −0.7278 + 5.7737 × 0χ | 0.9990 | (39) |
| MR | 1χ | MR = −4.596 + 10.479 × 1χ | 0.9992 | (40) |
| MR | 0χν | MR = 9.8652 + 5.0076 × 0χν | 1.0000 | (41) |
| MR | 1χν | MR = 1.1774 + 12.144 × 1χν | 1.0000 | (42) |
| MR | W | MR = 29.792 + 0.06577 × W | 1.0000 | (43) |
| MR | R | MR = 29.820 + 0.03290 × R | 1.0000 | (44) |
| MR | A | MR = 32.753 + 0.05268 × A | 0.9997 | (45) |
| P | M | P = −6.211 + 0.20575 × M | 0.9997 | (46) |
| P | 0χ | P = −0.2209 + 2.2811 × 0χ | 0.9989 | (47) |
| P | 1χ | P = −1.749 + 4.1401 × 1χ | 0.9991 | (48) |
| P | 0χν | P = 3.9624 + 1.9786 × 0χν | 1.0000 | (49) |
| P | 1χν | P = 0.53001 + 4.7984 × 1χν | 1.0000 | (50) |
| P | W | P = 11.836 + 0.02599 × W | 1.0000 | (51) |
| P | R | P = 11.847 + 0.01300 × R | 1.0000 | (52) |
| P | A | P = 13.006 + 0.02082 × A | 0.9998 | (53) |
| MV | M | MV = −95.86 + 1.7703 × M | 0.9978 | (54) |
| MV | 0χν | MV = −8.455 + 17.039 × 0χν | 0.9990 | (55) |
| MV | 1χν | MV = −37.97 + 41.311 × 1χν | 0.9987 | (56) |
| MV | W | MV = 59.330 + 0.22386 × W | 0.9993 | (57) |
| MV | R | MV = 59.426 + 0.11199 × R | 0.9993 | (58) |
| MV | A | MV = 69.362 + 0.17943 × A | 0.9998 | (59) |
| Physicochemical Parameter | Topological Index | Linear Equation | Correlation Coefficient | No. Eq. |
|---|---|---|---|---|
| BP | M | BP = 103.44 + 1.9858 × M | 0.7560 | (60) |
| BP | 0χ | BP = −286.5 + 49.958 × 0χ | 0.9324 | (61) |
| BP | 0χν | BP = 8.4148 + 38.328 × 0χν | 0.7902 | (62) |
| BP | W | BP = 244.79 + 0.23084 × W | 0.8231 | (63) |
| BP | R | BP = 245.04 + 0.11542 × R | 0.8230 | (64) |
| IR | 0χν | IR = 1.4038 + 0.01315 × 0χν | 0.7992 | (65) |
| IR | 1χν | IR = 1.4775 + 0.01415 × 1χν | 0.8622 | (66) |
| MR | 0χ | MR = −26.99 + 6.7763 × 0χ | 0.8675 | (67) |
| MR | 0χν | MR = −9.561 + 7.0284 × 0χν | 0.9940 | (68) |
| MR | 1χν | MR = 37.344 + 6.3639 × 1χν | 0.9024 | (69) |
| MR | W | MR = 40.612 + 0.03567 × W | 0.8724 | (70) |
| MR | R | MR = 40.636 + 0.01784 × R | 0.8727 | (71) |
| PSA | Mν | PSA = −9.044 + 0.22389 × Mν | 0.7852 | (72) |
| PSA | 1χ | PSA = 11.136 + 9.3195 × 1χ | 0.9273 | (73) |
| P | 0χν | P = −49.99 + 7.1096 × 0χν | 0.7836 | (74) |
| ST | 0χ | ST = −2.977 + 3.3866 × 0χ | 0.7761 | (75) |
| ST | 1χν | ST = 29.281 + 3.1633 × 1χν | 0.8029 | (76) |
| MV | M | MV = 99.569 + 0.71158 × M | 0.7679 | (77) |
| MV | 0χ | MV = −21.71 + 16.701 × 0χ | 0.8834 | (78) |
| MV | 0χν | MV = 26.659 + 16.883 × 0χν | 0.9865 | (79) |
| MV | 1χν | MV = 143.81 + 14.571 × 1χν | 0.8537 | (80) |
| MV | W | MV = 142.43 + 0.09032 × W | 0.9128 | (81) |
| MV | R | MV = 142.49 + 0.04518 × R | 0.9131 | (82) |
| Binding Type | kr Value |
|---|---|
| C-C | 1.000 |
| C-O | 0.750 |
| C=O | 0.375 |
| C=C | 1.500 |
| C-Cl | 0.353 |
| C-N | 0.857 |
| C=N | 0.428 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wardecki, D.; Dołowy, M.; Bober-Majnusz, K. Evaluation of the Usefulness of Topological Indices for Predicting Selected Physicochemical Properties of Bioactive Substances with Anti-Androgenic and Hypouricemic Activity. Molecules 2023, 28, 5822. https://doi.org/10.3390/molecules28155822
Wardecki D, Dołowy M, Bober-Majnusz K. Evaluation of the Usefulness of Topological Indices for Predicting Selected Physicochemical Properties of Bioactive Substances with Anti-Androgenic and Hypouricemic Activity. Molecules. 2023; 28(15):5822. https://doi.org/10.3390/molecules28155822
Chicago/Turabian StyleWardecki, Dawid, Małgorzata Dołowy, and Katarzyna Bober-Majnusz. 2023. "Evaluation of the Usefulness of Topological Indices for Predicting Selected Physicochemical Properties of Bioactive Substances with Anti-Androgenic and Hypouricemic Activity" Molecules 28, no. 15: 5822. https://doi.org/10.3390/molecules28155822
APA StyleWardecki, D., Dołowy, M., & Bober-Majnusz, K. (2023). Evaluation of the Usefulness of Topological Indices for Predicting Selected Physicochemical Properties of Bioactive Substances with Anti-Androgenic and Hypouricemic Activity. Molecules, 28(15), 5822. https://doi.org/10.3390/molecules28155822









