Next Article in Journal
The Anticancer Effect of Napabucasin (BBI608), a Natural Naphthoquinone
Previous Article in Journal
Chemical and Sensory Properties of Waffles Supplemented with Almond Skins
Previous Article in Special Issue
New Insights into Adsorption Properties of the Tubular Au26 from AIMD Simulations and Electronic Interactions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 15
10.3390/molecules28155676
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Communication

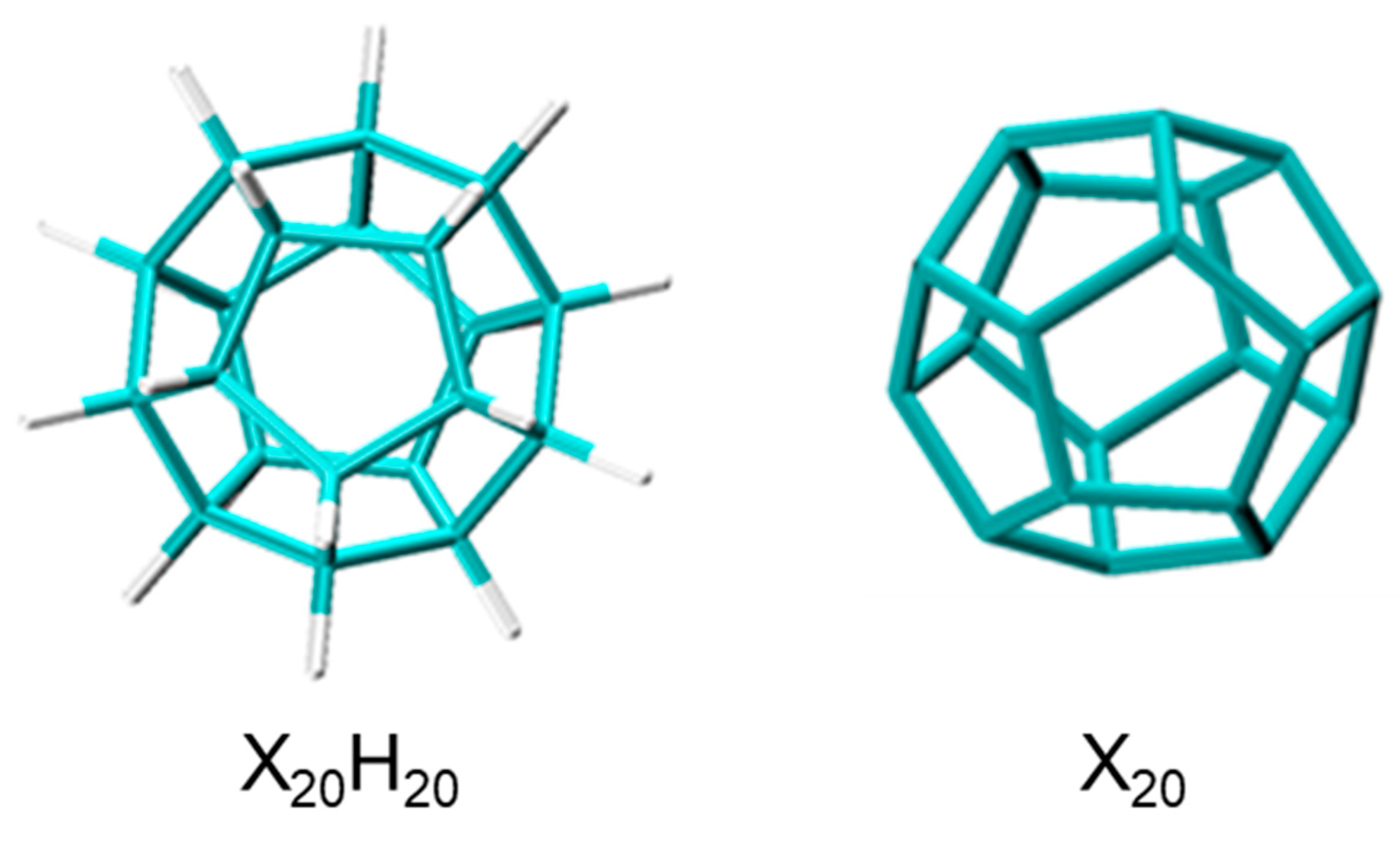
Selective Noble Gas Inclusion in Pentagon-Dodecahedral X20-Cages †

by
Christopher Weinert
1,
Dušan Ćoćić
2,
Ralph Puchta
1,3,4,5,* and
Rudi van Eldik
3,6,*
1
Fakultät Angewandte Mathematik, Physik und Allgemeinwissenschaften, Technische Hochschule Nuremberg Georg Simon Ohm, Keßlerplatz 12, 90489 Nuremberg, Germany
2
Department of Chemistry, Faculty of Science, University of Kragujevac, Radoja Domanovića 12, P.O. Box 60, 34000 Kragujevac, Serbia
3
Inorganic Chemistry, Department of Chemistry and Pharmacy, University of Erlangen-Nuremberg, Egerlandstr. 1, 91058 Erlangen, Germany
4
Central Institute for Scientific Computing (CISC), University of Erlangen-Nuremberg, Martensstr. 5a, 91058 Erlangen, Germany
5
Computer Chemistry Center, Department of Chemistry and Pharmacy, University of Erlangen-Nuremberg, Nägelsbachstr. 25, 91052 Erlangen, Germany
6
Faculty of Chemistry, Nicolaus Copernicus University in Toruń, Gagarina 7, 87-100 Toruń, Poland
*
Authors to whom correspondence should be addressed.
†
Dedicated to Prof. Dr. Thomas Lauterbach on the Occasion of his 60th birthday.
Molecules 2023, 28(15), 5676; https://doi.org/10.3390/molecules28155676
Submission received: 26 May 2023 / Revised: 12 July 2023 / Accepted: 14 July 2023 / Published: 27 July 2023
(This article belongs to the Special Issue Computational Investigation on Molecular Design, Structure, and Solvation)
Browse Figures
Versions Notes

Abstract

Using DFT-based computational chemistry calculations (ωB97XD/def2-tzvp//ωB97XD/def2-svp/svpfit + ZPE(ωB97XD/def2-svp/svpfit)), binding energies of noble gases encapsulated in a series of dodecahedrane molecules (general formula: X20H20 where X = C, Si, Ge, Sn and Pb, and X20 where X = N, P, As, Sb and Bi) were calculated to learn about the noble gas selectivity. Based on calculated binding energies, the Sn20H20 cage can best accommodate noble gases with a medium size radius (Ar and Kr), while the Pb20H20 dodecahedrane cage is best suited for noble gases with the larger radii (Xe and Rn). On the other hand, from the elements of the V main group of the periodic table, the Bi20 cage has shown the best results to selectively encapsulate Ar and Kr, with the amounts of energy being released being −5.24 kcal/mol and −6.13 kcal/mol, respectively. By monitoring the geometric changes of all here-reported host cages upon encapsulating the noble gas guest, the host has shown minor to no flexibility, testifying to the high rigidity of the dodecahedrane structure which was further reflected in very high encapsulating energies.

1. Introduction

Discovery of the C60 molecule, better known as fullerene [1], attracted much attention to further investigate the icosahedral molecules. The icosahedral dodecahedrane with its Ih symmetry, C20H20 (see Scheme 1) was synthesized, and its IR and Raman active frequencies were reported in 1982 [2,3], later on followed by X-ray structural analysis [4]. Structural and stability investigations for a series of dodecahedrane molecules followed [5,6,7,8,9], which suggested that the interior diameter of dodecahedranes (of about ~5 Å) can be exploited for accommodating smaller-size guest species. Special attention was given to the potential applications of icosahedral dodecahedranes as host molecules for encapsulating noble gas molecules, i.e., to act as a preferential absorbent of a hydrophobic guests with applications in purification [10], separation [11], storage [12], catalysis [13,14], and intact transportation [15] of a target solute. Prinzbach et al. [16] have successfully “shot” a helium atom into C20H20 by using an experimental procedure developed for fullerenes [17]. This encapsulated species is fascinating because the steric compression within the cavity is severe and the barrier to penetrating intact C20H20 must be very high. Nevertheless, investigating encapsulating properties of small species by dodecahedrane molecules (see Scheme 1) remains experimental and still very challenging.
Therefore, approaching this field by applying computational chemistry can give a wider picture on the capability and tendency of dodecahedrane molecules as hosts for small molecules [18,19]. The resulting supramolecular structures reminds one of the well-known hydrogen model according to Niels Bohr with one proton (here noble gas atom) in the center and a shell around.
In this article, the focus is on investigating the selective encapsulation capabilities of noble gases by molecules of dodecahedrane structures which molecular skeleton is formed by atoms of the group IV (general formula X20H20, where X = C, Si, Ge, Sn and Pb) and group V (general formula X20, where X = N, P, As, Sb and Bi) of the periodic table.

2. Computational Details

All computational calculations were performed using the ωB97XD [20] theory level. Structures of the investigated systems were optimized by applying the def2-svp/[21,22] svpfit [23] basis set (optimized coordinates of the structures reported here are given in Table S1 ESI) with calculations of the vibration frequencies at the same theory level. We selected dispersion corrected DFT to overcome the well-documented shortcomings of MP2 based methods. For obvious reasons the systems were too big for reliable Coupled Cluster calculations. [21,22] The obtained structures were characterized as minima, transition states or saddle points of higher order by examining the vibrational frequencies (number of imaginary frequencies for the systems reported in the manuscript are listed in Tables S2–S4 ESI) together with the BSSE energies. Suitability of the used theory level has been reported elsewhere [24,25,26,27,28]. For comparison reasons, encapsulation capabilities of cages Pb20H20 and Bi20 were examined using APFD [29] functional and B3LYP [30,31,32] functional in combination with Grimme’s dispersion correction with Becke–Johnson Damping [33] in both cases with def2-svp/svpfit functional for structure optimization. Afterwards, single point calculations at the ωB97XD/def2-svp/svpfit structures were performed at the ωB97XD/def2-tzvp [34] theory level, the energies of which have further been used in discussing the encapsulation affinities of the investigated systems, corrected to zero-point vibration energies from ωB97XD/def2-svp/svpfit calculations (ωB97XD/def2-tzvp//ωB97XD/def2-svp/svpfit + ZPE(ωB97XD/def2-svp/svpfit). The same procedure was performed in a case of two other sample theory levels (APFD and B3LYP-GD3BJ). The GAUSSIAN suite of programs was used with the input templates provided in Table S5 ESI [35]. Non-covalent interactions (NCI) [36] taking place between the dodecahedrane cage hosts and the noble gases were investigated using the Multiwfn program (http://sobereva.com/multiwfn/ (accessed on 20 July 2023)) [37] at the ωB97XD/def2tzvp theory level.

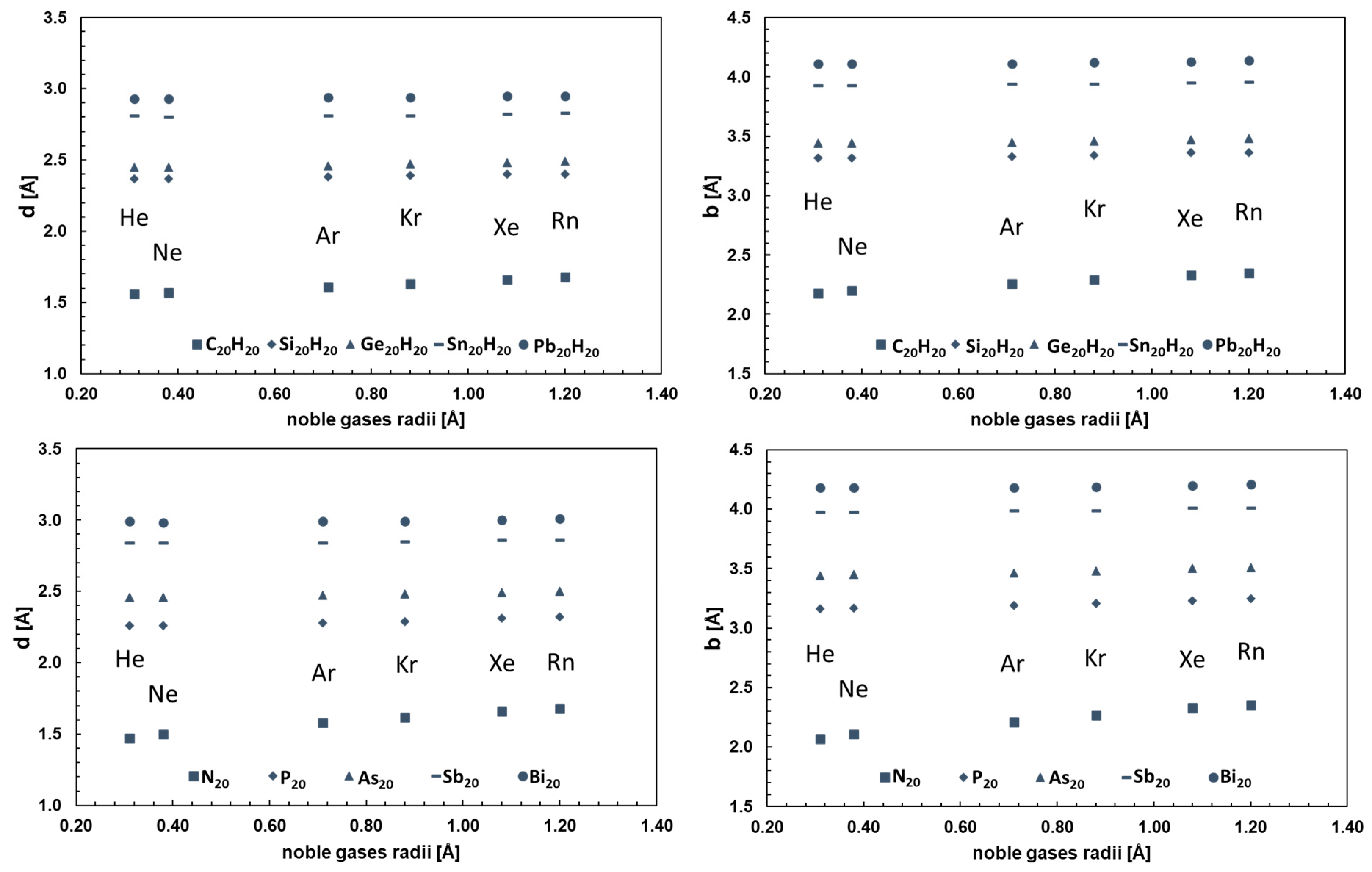
3. Results and Discussion

The investigation of favorable selective complexation properties can be defined by two criteria, viz. comparison of the geometric changes of the host upon encapsulation the guest and an appropriated reaction energy, 23c [26,38,39]. For the purpose of monitoring the energy change of an encapsulation process, constructing a model reaction (1) as follows is a most suitable approach, where Ng represents a noble gas and the host is a selected dodecahedrane:
Ng + Host → [Ng ⊂ Host]
The results of the computed complexation energies for dodecahedranes of a general formula X20H20 are reported in Table 1, whereas for dodecahedrane X20 in Table 2, they are presented with regard to the noble gas radii [40].
As can be seen in Table 1, carbon-based dodecahedranes exhibit very large (unreasonable) amounts of encapsulation energy ranging from 36.94–709.69 kcal/mol. Going down the IV main group along the periodic table, the silicon dodecahedrane cage has a significantly lower encapsulation energy for noble gases, which are linearly increasing with the increasing size of the noble gases radii (Figure 1). The germanium-based dodecahedrane cage has encapsulation energy for He and Ne of ~0 kcal/mol, with a further linear increase in the encapsulation energy going from Ar to Rn (from 7.64 kcal/mol to 39.28 kcal/mol, respectively). The tin cage releases energy upon hosting all noble gases, with the largest amount of energy released for hosting Ar and Kr (−5.63 kcal/mol and −6.41 kcal/mol, respectively), where He and Ne can be considered too small and Xe and Rn too large for the selected Sn20H20 cavity size. Noble gases with the smaller radii (He and Ne) are rather small for the tin cage cavity, while the ones with the larger radii (Xe and Rn) exhibit lower energy released due to their volume. The lead dodecahedrane cage better accommodates noble gases with larger atomic radii (Figure 1), ranging from −1.31 kcal/mol for He to the largest amount of energy released for Rn (−10.55 kcal/mol).
In Table 2, complexation (encapsulation) energies are presented for the dodecahedrane cages based on elements of the V main group of the periodic table. The nitrogen-based cage exhibits very high encapsulation energies, going from 57.18 kcal/mol to 989.41 kcal/mol for the largest noble gas Rn. The phosphorus cage accommodates noble gases with significantly lower encapsulation energies, but still unreasonably large amounts for the noble gases with larger radii (Kr, Xe and Rn). The arsenic-based dodecahedrane cage has encapsulation energy for He of ~0 kcal/mol, with a further linear increase (Figure 1) of the encapsulation energy going from Ne to Rn (from 3.34 kcal/mol to 73.03 kcal/mol, respectively). In the case of antimony cage noble gases, He, Ne, Ar and Kr have an error margin of ~0 kcal/mol, while Xe and Rn have encapsulation energies of 10.22 kcal/mol and 12.90 kcal/mol, respectively. The bismuth cage, like the previously described tin cage, releases energy upon hosting all noble gases, with the largest amount of energy released for hosting the noble gases Ar and Kr (−5.24 kcal/mol and −6.13 kcal/mol, respectively). Noble gases with the smaller radii (He and Ne) are rather small for the bismuth cage cavity, while the ones with the larger radii (Xe and Rn) exhibit lower energy released due to their volume.
If we compare the encapsulation energies between the elements of the same period (Figure 1), we can see that in general elements of the IV main group of the periodic table have shown lower encapsulation energies compared to the elements of the V main group. This difference is very small for the noble gases with smaller radii, but this difference increases with the increasing size of the noble gases’ radii. Our suggestion for these phenomena is that the reverse side of a XH-group in X20H20 cages has less electron density compared to the reverse side of a X20 cages and that larger noble gases can therefore stabilize better. That suggestion can be supported by a color-filled contour line map of charge density for the investigated hosts X20H20 and X20 (Figure 2 and Figure 3). Whereby, examining the cavity for the selected hosts, in a case of X20H20, there is less electron density inside the cavity in comparison to the X20 cages cavities.
Some optimized host–cage complexes (Ne ⊂ Si20H20, Pb20H20, Ng ⊂ Pb20H20, Kr ⊂ N20, Xe ⊂ N20, Rh ⊂ N20 and Ne ⊂ As20) show a relevant number of imaginary frequencies (Tables S2 and S3 ESI), and thus could not be trusted, while those that mention specific results are still herein reported for continuality reasons, they should be treated with a caution.
Additionally, for reason of comparison, encapsulation capabilities of two selected cages (Pb20H20 and Bi20) were tested on two more functionals, with the results presented in Table 3. Comparing these values with energies presented in Table 1 and Table 2 for the same systems there is an obvious difference in quantifying the encapsulation energy depending on the theory level used. While in the case of the smaller noble gases He and Ne, the difference is in the error margin (~1 kcal/mol); for the Ar noble gas this difference becomes significant, and gradually increases with the increasing of the noble gases’ radii. Also notable is that in the case of Bi20, the host ωB97XD functional reproduced a minimum of energies for the noble gases’ series (Ar and Kr), this minimum is absent in the case of APFD and B3LYP-GD3BJ functionals, where with the increasing of the noble gases radii we have a gradual increase of the complexation energy release upon encapsulation.
Geometric changes upon hosting a guest species can reveal insight into the flexibility of a host and its adaptability to accommodate a noble gas. In the case of the here selected dodecahedrane cages due to their symmetry, we selected two relevant structural parameters to describe their conformational change: bond distance between the atoms that are making a host (d; distance between the X adjacent atoms of a representative host) and the distance between one atom of the host to the hosted noble gas (b—distance between the X atom of the host and the hosted Ng atom). These geometric properties for the investigated hosts X20H20 and X20 are summarized in Table 4 and Table 5, and are plotted against the noble gas radii in Figure 4, respectively.
The results summarized in Table 4 and Table 5 and displayed in Figure 4 show very high rigidity for all investigated dodecahedrane hosts upon encapsulating noble gases. Basically, there is no adjustment of the host to the size (radii) of a guest noble gas, even if the noble gas with its size is right for a certain cavity of the dodecahedrane cage or not, which on the other hand is reflected in very large complexation energies (as, for example, in the case of C20H20 and N20, where we have Ecom up to 709.69 kcal/mol or 989.41 kcal/mol for the Rn).
A common practice for examining non-covalent interactions (NCIs) is based on the electron density (ρ), the reduced gradient of the density, and the Laplacian of the density (∇2ρ) [28]. This approach enables the identification of the interactions in real space, and thus the graphical visualization of regions in which non-covalent interactions occur [40,41]. The regions of dispersion–interaction in which non-covalent interactions occur are displayed in Figure 5 and Figures S1–S9 (Supplementary Materials).
The large spatial interaction zones are in agreement with the complexation energies shown in Table 1 and Table 2, according to which the non-covalent interactions control the stabilization of the host–guest complex. The main stabilization energies are predominantly van der Waals by origin, while there is a strong repulsion in cases where the noble gases are too large for a cavity of the selected dodecahedrane cage.

4. Conclusions

Based on encapsulation energies gained by applying a constructed model reaction, by monitoring geometrical changes and investigating the non-covalent interactions between the studied hosts and noble gases, the size of the host plays a decisive role in the selective encapsulation of the noble gas guests. All the selected cages have proven to be very rigid with no room for adjustability upon hosting a guest species, which is reflected in energy extremes depending on the noble gas radii. From dodecahedrane cages based on the IV group of the periodic table, the Sn20H20 cage can best accommodate noble gases with a medium size radius (Ar and Kr), while the Pb20H20 dodecahedrane host is best suited for noble gases with larger radii (Xe and Rn). On the other hand, from the elements of the V main group of the periodic table, the Bi20 cage has shown the best results to selectively encapsulate Ar and Kr with the amount of energy released, −5.24 kcal/mol and −6.13 kcal/mol, respectively.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28155676/s1, Figure S1. Structure of C20H20 with displayed non-covalent interactions according to the color bar (isoval = 0.18). Top row: He and Rn. Bottom row: Ne, Ar, Kr and Xe; Figure S2. Structure of Si20H20 with displayed non-covalent interactions according to the color bar (isoval = 0.22). Top row: He and Rn. Bottom row: Ne, Ar, Kr and Xe; Figure S3. Structure of Ge20H20 with displayed non-covalent interactions according to the color bar (isoval = 0.3). Top row: Ne and Rn. Bottom row: He, Ar, Kr and Xe; Figure S4. Structure of Sn20H20 with displayed non-covalent interactions according to the color bar (isoval = 0.35). Top row: Kr and He. Bottom row: Ne, Ar, Xe and Rn; Figure S5. Structure of Pb20H20 with displayed non-covalent interactions according to the color bar (isoval = 0.35). Top row: Rn and He. Bottom row: Ne, Ar, Kr and Xe; Figure S6. Structure of N20 with displayed non-covalent interactions according to the color bar (isoval = 0.25). Top row: He and Rn. Bottom row: Ne, Ar, Kr and Xe; Figure S7. Structure of P20 with displayed non-covalent interactions according to the color bar (isoval = 0.3). Top row: He and Rn. Bottom row: Ne, Ar, Kr and Xe; Figure S8. Structure of As20 with displayed non-covalent interactions according to the color bar (isoval = 0.35). Top row: He and Rn. Bottom row: Ne, Ar, Kr and Xe; Figure S9. Structure of Sb20 with displayed non-covalent interactions according to the color bar (isoval = 0.37). Top row: Ne and Rn. Bottom row: He, Ar, Kr and Xe; Table S1. Optimized (ωB97XD/def2-svp/svpfit) XYZ coordinates of the structures reported in the manuscript; Table S2. Number of imaginary frequencies calculated at the ωB97XD/def2-svp/svpfit theory level for X20H20 host; Table S3. Number of imaginary frequencies calculated at the ωB97XD/def2-svp/svpfit theory level for X20 host; Table S4. Number of imaginary frequencies calculated on different theory levels for the Pb20H20 and Bi20 hosts; Table S5. Gaussian keywords input templates for the performed calculations.

Author Contributions

Conceptualization, D.Ć., C.W. and R.P.; method selection, D.Ć. and R.P.; validation, C.W., D.Ć. and R.P.; formal analysis, C.W.; investigation, C.W.; data curation, C.W.; writing—original draft preparation, D.Ć.; writing—review and editing, R.P. and R.v.E.; visualization, C.W.; supervision, R.v.E.; project administration, R.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Ministry of Education, Science and Technological Development of the Republic of Serbia grant number No. 451-03-47/2023-01/200122.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data relevant for this study are provided in the SI or can be obtained from the authors upon request.

Acknowledgments

We acknowledge financial support by Deutsche Forschungsgemeinschaft and Friedrich-Alexander-Universität Erlangen-Nürnberg within the funding programme “Open Access Publication Funding”. We thank Johannes Endres, TH Nuremberg for technical support, Tim Clark and Petra Imhof for hosting this work at the CCC and the Regionales Rechenzentrum Erlangen (RRZE) for a generous allotment of computer time.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
  2. Ternansky, R.J.; Balogh, D.W.; Paquette, L.A. Dodecahedrane. J. Am. Chem. Soc. 1982, 104, 4503–4504. [Google Scholar] [CrossRef]
  3. Paquette, L.A.; Ternansky, R.J.; Balogh, D.W.; Kentgen, G. Total synthesis of dodecahedrane. J. Am. Chem. Soc. 1983, 105, 5446–5450. [Google Scholar] [CrossRef]
  4. Gallucci, J.C.; Taylor, R.T.; Kobayashi, T.; Weber, J.C.; Krause, J.; Paquette, L.A. X-ray crystallographic analysis of the structural distortions induced by substitution and annulation of the dodecahedrane nucleus. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1989, 45, 893–898. [Google Scholar] [CrossRef]
  5. Strout, D.L.J. Why Isn’t the N20 Dodecahedron Ideal for Three-Coordinate Nitrogen? Phys. Chem. A 2005, 109, 1478–1480. [Google Scholar] [CrossRef]
  6. Wang, Y.; Xu, J.; Cao, Z.; Zhang, Q.J. Spherical double electric layer structure and unprecedented high stability of the P20O20 cage and its anionic endohedral complex Na-@ P20O20. Phys. Chem. B 2004, 108, 4579–4581. [Google Scholar] [CrossRef]
  7. Baruah, T.; Zope, R.R.; Richardson, S.L.; Pederson, M.R. Electronic structure and rebonding in the onionlike As@Ni12@As20 cluster. Phys. Rev. B 2003, 68, 241404. [Google Scholar] [CrossRef]
  8. Wang, Y.; Moses-DeBusk, M.; Stevens, L.; Hu, J.; Zavalij, P.; Bowen, K.; Dunlap, B.I.; Glaser, E.R.; Eichhorn, B.J. Sb@Ni12@Sb20−/+ and Sb@Pd12@Sb20n cluster anions, where n = +1,− 1,− 3,− 4: Multi-oxidation-state clusters of interpenetrating platonic solids. J. Am. Chem. Soc. 2017, 139, 619–622. [Google Scholar] [CrossRef]
  9. Zdetsis, A.D.J. Theoretical predictions of a new family of stable bismuth and other group 15 fullerenes. Phys. Chem. C 2010, 114, 10775–10781. [Google Scholar] [CrossRef]
  10. Alsbaiee, A.; Smith, B.J.; Xiao, L.; Ling, Y.; Helbling, D.E.; Dichtel, W.R. Rapid removal of organic micropollutants from water by a porous β-cyclodextrin polymer. Nature 2016, 529, 190–194. [Google Scholar] [CrossRef]
  11. Chaix, A.; Mouchaham, G.; Shkurenko, A.; Hoang, P.; Moosa, B.; Bhatt, P.M.; Adil, K.; Salama, K.N.; Eddaoudi, M.; Khashab, N.M.J. Trianglamine-based supramolecular organic framework with permanent intrinsic porosity and tunable selectivity. J. Am. Chem. Soc. 2018, 140, 14571–14575. [Google Scholar] [CrossRef]
  12. Yang, W.; Greenaway, A.; Lin, X.; Matsuda, R.; Blake, A.J.; Wilson, C.; Lewis, W.; Hubberstey, P.; Kitagawa, S.; Champness, N.R.; et al. Exceptional thermal stability in a supramolecular organic framework: Porosity and gas storage. J. Am. Chem. Soc. 2010, 132, 14457–14469. [Google Scholar] [CrossRef]
  13. Yang, J.-M.; Yu, Y.; Rebek, J.J. Selective macrocycle formation in cavitands. J. Am. Chem. Soc. 2021, 143, 2190–2193. [Google Scholar] [CrossRef]
  14. Li, F.; Yang, H.; Zhuo, Q.; Zhou, D.; Wu, X.; Zhang, P.; Yao, Z.; Sun, L. A cobalt@ cucurbit [5] uril complex as a highly efficient supramolecular catalyst for electrochemical and photoelectrochemical water splitting. Angew. Chem. Int. Ed. Engl. 2021, 60, 1976–1985. [Google Scholar] [CrossRef] [PubMed]
  15. Hettiarachchi, G.; Nguyen, D.; Wu, J.; Lucas, D.; Ma, D.; Isaacs, L.; Briken, V. Toxicology and drug delivery by cucurbit [n] uril type molecular containers. PLoS ONE 2010, 5, e10514. [Google Scholar] [CrossRef]
  16. Cross, R.J.; Saunders, M.; Prinzbach, H. Putting helium inside dodecahedrane. Org. Lett. 1999, 1, 1479–1481. [Google Scholar] [CrossRef]
  17. Saunders, M.; Cross, R.J.; Jiménez-Vázquez, H.A.; Shimshi, R.; Khong, A. Noble gas atoms inside fullerenes. Science 1996, 271, 1693–1697. [Google Scholar] [CrossRef]
  18. Jimenez-Vazquez, H.A.; Tamariz, J. Binding energy in and equilibrium constant of formation for the dodecahedrane compounds He@C20H20 and Ne@C20H20. J. Phys. Chem. A 2001, 105, 1315–1319. [Google Scholar] [CrossRef]
  19. Puchta, R.; Walther, D.; März, M.; Begel, S.; van Eldik, R.Z. Host-Guest Complexes of Dodeka (ethylene) octamine: Prediction of Ion Selectivity by Quantum Chemical Calculations IX. Z. Anorg. Allg. Chem. 2019, 645, 701–705. [Google Scholar] [CrossRef]
  20. Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
  21. Řezáč, J.; Greenwell, C.; Beran, G.J.O. Accurate noncovalent interactions via dispersion-corrected second-order Møller–Plesset perturbation theory. J. Chem. Theory Comput. 2018, 14, 4711–4721. [Google Scholar] [CrossRef]
  22. Jan Řezáč, J.; Hobza, P. Benchmark calculations of interaction energies in noncovalent complexes and their applications. Chem. Rev. 2016, 116, 5038–5071. [Google Scholar] [CrossRef]
  23. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  24. Eichkorn, K.; Treutler, O.; Ohm, H.; Haser, M.; Ahlrichs, R. Auxiliary basis sets to approximate Coulomb potentials. Chem. Phys. Lett. 1995, 240, 283–290. [Google Scholar] [CrossRef]
  25. Eichkorn, K.; Weigend, F.; Treutler, O.; Ahlrichs, R. Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials. Theor. Chem. Acc. 1997, 97, 119–124. [Google Scholar] [CrossRef]
  26. Biswas, B.; Singh, P.C. Effect of hydration on the organo-noble gas molecule HKrCCH: Role of krypton in the stabilization of hydrated HKrCCH complexes. Phys. Chem. Chem. Phys. 2015, 17, 30632–30641. [Google Scholar] [CrossRef]
  27. Wu, L.-Y.; Li, J.-F.; Zhao, R.-F.; Luo, L.; Wang, Y.-C.; Yin, B. Exploring the structure, bonding and stability of noble gas compounds promoted by superhalogens. A case study on HNgMX 3 (Ng = Ar–Rn, M = Be–Ca, X = F–Br) via combined high-level ab initio and DFT calculations. Phys. Chem. Chem. Phys. 2019, 21, 19104–19114. [Google Scholar] [CrossRef] [PubMed]
  28. Ćoćić, D.; Puchta, R.; van Eldik, R. Noble guests in organic cages—Encapsulation of noble gases by cryptophane. J. Coord. Chem. 2020, 73, 2602–2613. [Google Scholar] [CrossRef]
  29. Austin, A.; Petersson, G.; Frisch, M.J.; Dobek, F.J.; Scalmani, G.; Throssell, K. A density functional with spherical atom dispersion terms. J. Chem. Theory Comput. 2012, 8, 4989–5007. [Google Scholar] [CrossRef]
  30. Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  31. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
  32. Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11629. [Google Scholar] [CrossRef]
  33. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  34. Weigend, F.; Haser, M.; Patzelt, H.; Anlrichs, R. RI-MP2: Optimized auxiliary basis sets and demonstration of efficiency. Chem. Phys. Lett. 1998, 294, 143–152. [Google Scholar] [CrossRef]
  35. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2010.
  36. Johnson, E.R.; Keinan, S.; Mori− Sánchez, P.; Contreras−García, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
  37. Tian, L.; Feiwu, C.J. Multiwfn: A multifunctional wavefunction analyzer. Comput. Chem. 2012, 33, 580–592. [Google Scholar]
  38. Puchta, R.; Cocic, D.; Michel, M.; van Eldik, R. Host-guest complexes of the Beer-Can-cryptand: Prediction of ion selectivity by quantum chemical calculations XI. J. Coord. Chem. 2019, 72, 2106–2114. [Google Scholar] [CrossRef]
  39. Puchta, R.; Begel, S.; van Eldik, R. Prediction of ion selectivity by quantum chemical calculations X: A recent (personal) review. Adv. Inorg. Chem. 2019, 73, 445–505. [Google Scholar]
  40. Aylward, G.H.; Findlay, T.J.V. Datensammlung Chemie in SI-Einheiten; Wiley-VCH: Weinheim, Germany, 1986. [Google Scholar]
  41. Dubost, E.; Dognon, J.-P.; Rousseau, B.; Milanole, G.; Dugave, C.; Boulard, Y.; Leonce, E.; Boutin, C.; Berthault, P. Understanding a Host–Guest Model System through 129Xe NMR Spectroscopic Experiments and Theoretical Studies. Angew. Chem. Int. Ed. Engl. 2014, 53, 9837–9840. [Google Scholar] [CrossRef] [PubMed]
Molecules 28 05676 sch001
Scheme 1. General structural representation of X20H20 and X20 investigated hosts.
Scheme 1. General structural representation of X20H20 and X20 investigated hosts.
Molecules 28 05676 sch001
Molecules 28 05676 g001
Figure 1. Calculated complexation energies (Ecom) of X20 and X20H20 plotted against the noble gas radii.
Figure 1. Calculated complexation energies (Ecom) of X20 and X20H20 plotted against the noble gas radii.
Molecules 28 05676 g001
Molecules 28 05676 g002
Figure 2. Color-filled contour line map along the XY plane of the X20H20 cages containing the center of the host molecules (blue line representing the van der Waals surface of the host).
Figure 2. Color-filled contour line map along the XY plane of the X20H20 cages containing the center of the host molecules (blue line representing the van der Waals surface of the host).
Molecules 28 05676 g002
Molecules 28 05676 g003
Figure 3. Color-filled contour line map along the XY plane of the X20 cages containing the center of the host molecules (blue line representing the van der Waals surface of the host).
Figure 3. Color-filled contour line map along the XY plane of the X20 cages containing the center of the host molecules (blue line representing the van der Waals surface of the host).
Molecules 28 05676 g003
Molecules 28 05676 g004
Figure 4. Calculated (ωB97XD/def2-SVP/SVPfit) geometric properties (d and b) in [Ng ⊂ Host] complexes plotted against the noble gas radii.
Figure 4. Calculated (ωB97XD/def2-SVP/SVPfit) geometric properties (d and b) in [Ng ⊂ Host] complexes plotted against the noble gas radii.
Molecules 28 05676 g004
Molecules 28 05676 g005
Figure 5. Structure of Bi20 with displayed non-covalent interactions according to the color bar (isoval = 0.35). Top row: Kr and He. Bottom row: Ne, Ar, Xe and Rn.
Figure 5. Structure of Bi20 with displayed non-covalent interactions according to the color bar (isoval = 0.35). Top row: Kr and He. Bottom row: Ne, Ar, Xe and Rn.
Molecules 28 05676 g005
Table 1. Calculated complexation energies (Ecom) and the BSSE energies for the X20H20 hosts based on reaction (1).
Table 1. Calculated complexation energies (Ecom) and the BSSE energies for the X20H20 hosts based on reaction (1).
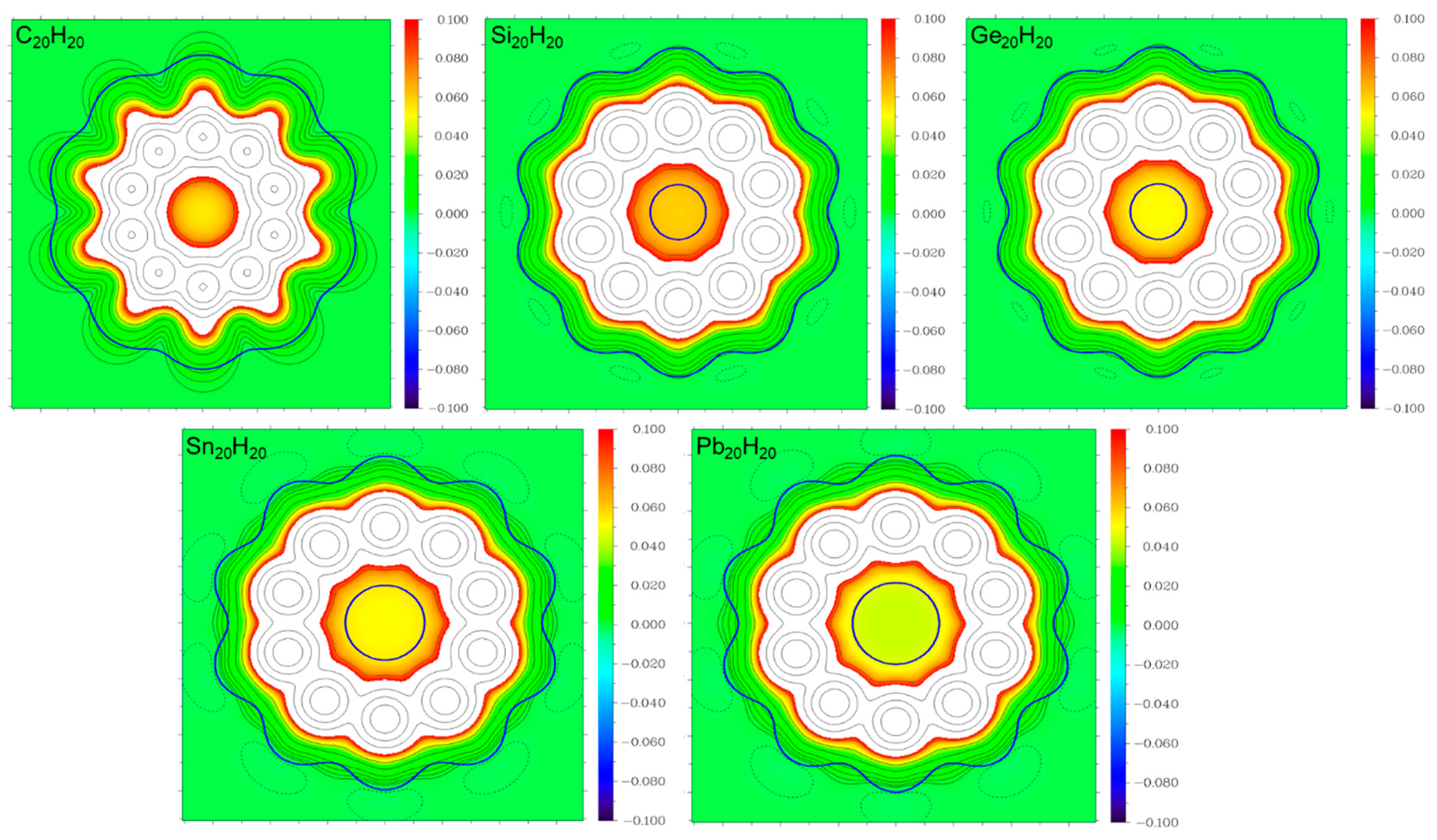
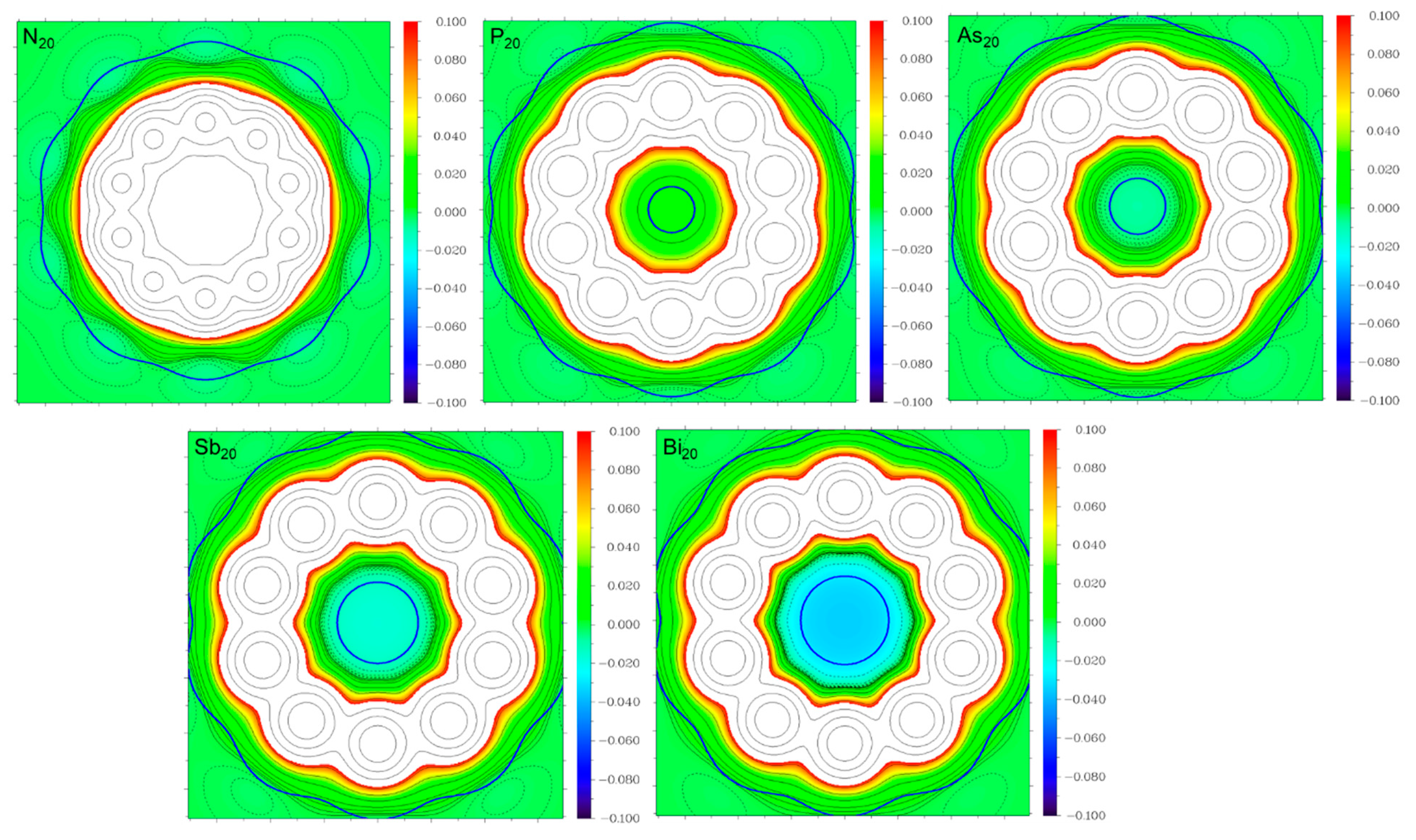
Host/Ecom (BSSE) a [kcal/mol]
Noble GasR [Å]CSiGeSnPb
He0.3136.94 (0.54)0.72 (0.37)−0.01 (0.53)−1.09 (0.29)−1.31 (0.27)
Ne0.38103.50 (1.33)3.31 (0.93)−0.29 (1.24)−3.86 (0.72)−4.34 (0.65)
Ar0.71311.71 (1.59)14.86 (1.07)7.64 (1.59)−5.63 (0.66)−7.69 (0.59)
Kr0.88437.35 (1.71)24.34 (1.14)14.94 (1.83)−6.41 (0.63)−9.68 (0.51)
Xe1.08623.12 (0.58)42.88 (0.62)32.43 (1.45)−2.20 (0.27)−8.65 (0.18)
Rn1.20709.69 (0.70)49.80 (0.57)39.28 (1.49)−2.34 (0.26)−10.55 (0.17)
a Ecom: ωB97XD/def2-tzvp//ωB97XD/def2-svp/svpfit + ZPE(ωB97XD/def2-svp/svpfit).
Table 2. Calculated complexation energies (Ecom) and the BSSE energies for the X20 hosts based on reaction (1).
Table 2. Calculated complexation energies (Ecom) and the BSSE energies for the X20 hosts based on reaction (1).
Host/Ecom (BSSE) a [kcal/mol]
Noble GasR [Å]NPAsSbBi
He0.3157.18 (1.47)5.62 (0.39)0.66 (0.41)−0.57 (0.27)−0.73 (0.26)
Ne0.38165.05 (2.47)12.70 (0.94)3.34 (1.32)−1.64 (0.66)−2.78 (0.63)
Ar0.71474.46 (2.55)46.16 (1.25)17.13 (2.14)−0.76 (0.74)−5.24 (0.69)
Kr0.88659.58 (2.77)72.46 (1.47)30.57 (2.86)1.36 (0.83)−6.13 (0.69)
Xe1.08907.21 (1.80)120.56 (1.06)59.43 (2.78)10.22 (0.71)−2.50 (0.60)
Rn1.20989.41 (1.62)143.90 (1.05)73.03 (2.81)12.90 (0.70)−2.72 (0.61)
a Ecom: ωB97XD/def2-tzvp//ωB97XD/def2-svp/svpfit + ZPE(ωB97XD/def2-svp/svpfit).
Table 3. Calculated complexation energies (Ecom) for the Pb20H20 and Bi20 hosts based on reaction (1) on different theory levels.
Table 3. Calculated complexation energies (Ecom) for the Pb20H20 and Bi20 hosts based on reaction (1) on different theory levels.
Host/Ecom [kcal/mol]
Noble GasR [Å]Pb20H20 a Bi20 aPb20H20 bBi20 b
He0.31−1.62−1.25−1.09−0.78
Ne0.38−4.51−3.51−3.66−3.06
Ar0.71−12.34−10.28−10.77−9.01
Kr0.88−16.14−13.45−13.65−11.08
Xe1.08−20.32−16.46−16.42−11.86
Rn1.20−21.52−17.06−16.93−11.35
a Ecom: APFD/def2-tzvp//APFD/def2-svp/svpfit + ZPE(APFD/def2-svp/svpfit); b Ecom: B3LYP-GD3BJ/def2-tzvp//B3LYP-GD3BJ/def2-svp/svpfit + ZPE(B3LYP-GD3BJ/def2-svp/svpfit).
Table 4. Geometric properties extracted from optimized structures at ωB97XD/def2-SVP/SVPfit theory level for X20H20 dodecahedrane cages.
Table 4. Geometric properties extracted from optimized structures at ωB97XD/def2-SVP/SVPfit theory level for X20H20 dodecahedrane cages.
X20H20 Cage
Noble Gas CSiGeSnPb
R [Å]d [Å]b [Å]d [Å]b [Å]d [Å]b [Å]d [Å]b [Å]d [Å]b [Å]
He0.311.562.182.373.322.453.442.813.932.934.11
Ne0.381.572.202.373.322.453.442.803.932.934.11
Ar0.711.612.262.383.332.463.452.813.942.944.11
Kr0.881.632.292.393.342.473.462.813.942.944.12
Xe1.081.662.332.403.362.483.472.823.952.954.13
Rn1.201.682.352.403.362.493.482.833.962.954.14
Empty host1.55 2.37 2.45 2.81 2.93
Table 5. Geometric properties extracted from optimized structures at ωB97XD/def2-SVP/SVPfit theory level for X20 dodecahedrane cages.
Table 5. Geometric properties extracted from optimized structures at ωB97XD/def2-SVP/SVPfit theory level for X20 dodecahedrane cages.
X20 Cage
Noble Gas NPAsSbBi
R [Å]d [Å]b [Å]d [Å]b [Å]d [Å]b [Å]d [Å]b [Å]d [Å]b [Å]
He0.311.472.072.263.162.463.442.843.982.994.18
Ne0.381.502.112.263.172.463.452.843.982.994.18
Ar0.711.582.212.283.192.473.462.843.992.984.18
Kr0.881.622.272.293.212.483.482.853.992.994.19
Xe1.081.662.332.313.232.493.502.864.012.994.20
Rn1.201.682.352.323.252.503.512.864.013.004.21
Empty host1.47 2.25 2.46 2.84 2.99
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Weinert, C.; Ćoćić, D.; Puchta, R.; van Eldik, R. Selective Noble Gas Inclusion in Pentagon-Dodecahedral X20-Cages. Molecules 2023, 28, 5676. https://doi.org/10.3390/molecules28155676

AMA Style

Weinert C, Ćoćić D, Puchta R, van Eldik R. Selective Noble Gas Inclusion in Pentagon-Dodecahedral X20-Cages. Molecules. 2023; 28(15):5676. https://doi.org/10.3390/molecules28155676

Chicago/Turabian Style

Weinert, Christopher, Dušan Ćoćić, Ralph Puchta, and Rudi van Eldik. 2023. "Selective Noble Gas Inclusion in Pentagon-Dodecahedral X20-Cages" Molecules 28, no. 15: 5676. https://doi.org/10.3390/molecules28155676

APA Style

Weinert, C., Ćoćić, D., Puchta, R., & van Eldik, R. (2023). Selective Noble Gas Inclusion in Pentagon-Dodecahedral X20-Cages. Molecules, 28(15), 5676. https://doi.org/10.3390/molecules28155676

Article Metrics

Back to TopTop