Photoswitchable Molecular Units with Tunable Nonlinear Optical Activity: A Theoretical Investigation
Abstract
1. Introduction
- (i)
- The relationship between the molecular (hyper)polarizabilities of several derivatives consisting of two DTE units, with and without different substituents, and connected by different conjugated linkers, and the changes induced by photochromism on these properties. It is a major objective to find those structures and linkers, in particular, that lead to a significant contrast between the hyperpolarizabilities of the “open” and the “closed” isomers.
- (ii)
- The effect of the linker on the electronic communication of the DTE units and the photochromism as well as the intramolecular EET. A series of linkers has been selected in order to tune EET and eventually to minimize it, to attain full photochromism.
2. Results and Discussion
2.1. (Hyper)polarizabilities
2.2. Two-Photon Absorption
2.3. Excitation Energy Transfer
2.3.1. Intra-Molecular Excited Energy Transfer
2.3.2. Overlap of the Emission Spectrum of the Donor and the Absorption Spectrum of the Acceptor
3. Methods
3.1. Definitions
3.2. Functionals and Basis Sets
3.3. Two-Photon Absorption
3.4. Computation of the Electronic Coupling
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fihey, A.; Russo, R.; Cupellini, L.; Jacquemin, D.; Mennucci, B. Is energy transfer limiting multiphotochromism? answers from ab initio quantifications. Phys. Chem. Chem. Phys. 2017, 19, 2044–2052. [Google Scholar] [CrossRef]
- Galanti, A.; Santoro, J.; Mannancherry, R.; Duez, Q.; Diez-Cabanes, V.; Valasek, M.; De Winter, J.; Cornil, J.; Gerbaux, P.; Mayor, M.; et al. A New Class of Rigid Multi(azobenzene) Switches Featuring Electronic Decoupling: Unravelling the Isomerization in Individual Photochromes. J. Am. Chem. Soc. 2019, 141, 9273–9283. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.P. The Electronic Couplings in Electron Transfer and Excitation Energy Transfer. Acc. Chem. Res. 2009, 42, 509–518. [Google Scholar] [CrossRef]
- Nakamura, Y.; Aratani, N.; Osuka, A. Cyclic porphyrin arrays as artificial photosynthetic antenna: Synthesis and excitation energy transfer. Chem. Soc. Rev. 2007, 36, 831–845. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.Y.; Friesner, R.A.; Murphy, R.B. Ab initio quantum chemical calculation of electron transfer matrix elements for large molecules. J. Chem. Phys. 1997, 107, 450–459. [Google Scholar] [CrossRef]
- Headgordon, M.; Grana, A.M.; Maurice, D.; White, C.A. Analysis of Electronic-Transitions as the Difference of Electron-Attachment and Detachment Densities. J. Phys. Chem. 1995, 99, 14261–14270. [Google Scholar] [CrossRef]
- You, Z.Q.; Hsu, C.P.; Fleming, G.R. Triplet-triplet energy-transfer coupling: Theory and calculation. J. Chem. Phys. 2006, 124, 044506. [Google Scholar] [CrossRef] [PubMed]
- Iozzi, M.F.; Mennucci, B.; Tomasi, J.; Cammi, R. Excitation energy transfer (EET) between molecules in condensed matter: A novel application of the polarizable continuum model (PCM). J. Chem. Phys. 2004, 120, 7029–7040. [Google Scholar] [CrossRef]
- Scholes, G.D. Long-range resonance energy transfer in molecular systems. Annu. Rev. Phys. Chem. 2003, 54, 57–87. [Google Scholar] [CrossRef]
- Kaieda, T.; Kobatake, S.; Miyasaka, H.; Murakami, M.; Iwai, N.; Nagata, Y.; Itaya, A.; Irie, M. Efficient photocyclization of dithienylethene dimer, trimer, and tetramer: Quantum yield and reaction dynamics. J. Am. Chem. Soc. 2002, 124, 2015–2024. [Google Scholar] [CrossRef]
- Chen, H.C.; You, Z.Q.; Hsu, C.P. The mediated excitation energy transfer: Effects of bridge polarizability. J. Chem. Phys. 2008, 129, 084708. [Google Scholar] [CrossRef] [PubMed]
- Scholes, G.D.; Ghiggino, K.P.; Oliver, A.M.; Paddonrow, M.N. Through-Space and through-Bond Effects on Exciton Interactions in Rigidly Linked Dinaphthyl Molecules. J. Am. Chem. Soc. 1993, 115, 4345–4349. [Google Scholar] [CrossRef]
- Oevering, H.; Paddonrow, M.N.; Heppener, M.; Oliver, A.M.; Cotsaris, E.; Verhoeven, J.W.; Hush, N.S. Long-Range Photoinduced through-Bond Electron-Transfer and Radiative Recombination via Rigid Nonconjugated Bridges—Distance and Solvent Dependence. J. Am. Chem. Soc. 1987, 109, 3258–3269. [Google Scholar] [CrossRef]
- Pettersson, K.; Kyrychenko, A.; Ronnow, E.; Ljungdahl, T.; Martensson, J.; Albinsson, B. Singlet energy transfer in porphyrin-based donor-bridge-acceptor systems: Interaction between bridge length and bridge energy. J. Phys. Chem. A 2006, 110, 310–318. [Google Scholar] [CrossRef] [PubMed]
- Cho, H.S.; Jeong, D.H.; Yoon, M.C.; Kim, Y.H.; Kim, Y.R.; Kim, D.; Jeoung, S.C.; Kim, S.K.; Aratani, N.; Shinmori, H.; et al. Excited-state energy transfer processes in phenylene- and biphenylene-linked and directly-linked Zinc(II) and free-base hybrid diporphyrins. J. Phys. Chem. A 2001, 105, 4200–4210. [Google Scholar] [CrossRef]
- Smith, T.A.; Lokan, N.; Cabral, N.; Davies, S.R.; Paddon-Row, M.N.; Ghiggino, K.P. Photophysics of novel donor-{saturated rigid hydrocarbon bridge}-acceptor systems exhibiting efficient excitation energy transfer. J. Photochem. Photobiol. A Chem. 2002, 149, 55–69. [Google Scholar] [CrossRef]
- Kroon, J.; Oliver, A.M.; Paddonrow, M.N.; Verhoeven, J.W. Observation of a Remarkable Dependence of the Rate of Singlet Singlet Energy-Transfer on the Configuration of the Hydrocarbon Bridge in Bichromophoric Systems. J. Am. Chem. Soc. 1990, 112, 4868–4873. [Google Scholar] [CrossRef]
- El-ghayoury, A.; Harriman, A.; Khatyr, A.; Ziessel, R. Intramolecular triplet energy transfer in metal polypyridine complexes bearing ethynylated aromatic groups. J. Phys. Chem. A 2000, 104, 1512–1523. [Google Scholar] [CrossRef]
- McConnell, H.M. Intramolecular Charge Transfer in Aromatic Free Radicals. J. Chem. Phys. 1961, 35, 508–515. [Google Scholar] [CrossRef]
- Kudernac, T.; van der Molen, S.J.; van Wees, B.J.; Feringa, B.L. Uni- and bi-directional light-induced switching of diarylethenes on gold nanoparticles. Chem. Commun. 2006, 3597–3599. [Google Scholar] [CrossRef]
- Chen, J.X.; Wang, J.Y.; He, J.R.; Peng, X.F. Photochromic properties of ruthenium complexes with dithienylethene-ethynylthiophene. Dye. Pigment. 2021, 184, 108750. [Google Scholar] [CrossRef]
- Chergui, M. Ultrafast molecular photophysics in the deep-ultraviolet. J. Chem. Phys. 2019, 150, 070901. [Google Scholar] [CrossRef]
- Munoz-Losa, A.; Curutchet, C.; Krueger, B.P.; Hartsell, L.R.; Mennucci, B. Fretting about FRET: Failure of the Ideal Dipole Approximation. Biophys. J. 2009, 96, 4779–4788. [Google Scholar] [CrossRef] [PubMed]
- Beljonne, D.; Curutchet, C.; Scholes, G.D.; Silbey, R.J. Beyond Forster Resonance Energy Transfer in Biological and Nanoscale Systems. J. Phys. Chem. B 2009, 113, 6583–6599. [Google Scholar] [CrossRef]
- Kenny, E.P.; Kassal, I. Benchmarking Calculations of Excitonic Couplings between Bacteriochlorophylls. J. Phys. Chem. B 2016, 120, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Sauer, K.; Cogdell, R.J.; Prince, S.M.; Freer, A.; Isaacs, N.W.; Scheer, H. Structure-based calculations of the optical spectra of the LH2 bacteriochlorophyll-protein complex from Rhodopseudomonas acidophila. Photochem. Photobiol. 1996, 64, 564–576. [Google Scholar] [CrossRef]
- Krueger, B.P.; Scholes, G.D.; Fleming, G.R. Calculation of couplings and energy-transfer pathways between the pigments of LH2 by the Ab initio transition density cube method. J. Phys. Chem. B 1998, 102, 5378–5386. [Google Scholar] [CrossRef]
- Kistler, K.A.; Spano, F.C.; Matsika, S. A Benchmark of Excitonic Couplings Derived from Atomic Transition Charges. J. Phys. Chem. B 2013, 117, 2032–2044. [Google Scholar] [CrossRef]
- Scholes, G.D.; Ghiggino, K.P. Electronic Interactions and Interchromophore Excitation Transfer. J. Phys. Chem. 1994, 98, 4580–4590. [Google Scholar] [CrossRef]
- Moerner, W.E. Viewpoint: Single Molecules at 31: What’s Next? Nano Lett. 2020, 20, 8427–8429. [Google Scholar] [CrossRef]
- Yang, M.; Fleming, G.R. Third-order nonlinear optical response of energy transfer systems. J. Chem. Phys. 1999, 111, 27–39. [Google Scholar] [CrossRef]
- Coe, B.J. Molecular Materials Possessing Switchable Quadratic Nonlinear Optical Properties. Chem. Eur. J. 1999, 5, 2464–2471. [Google Scholar] [CrossRef]
- Castet, F.; Rodriguez, V.; Pozzo, J.-L.; Ducasse, L.; Plaquet, A.; Champagne, B. Design and Characterization of Molecular Nonlinear Optical Switches. Acc. Chem. Res. 2013, 46, 2656–2665. [Google Scholar] [CrossRef] [PubMed]
- Beaujean, P.; Sanguinet, L.; Rodriguez, V.; Castet, F.; Champagne, B. Multi-State Second-Order Nonlinear Optical Switches Incorporating One to Three Benzazolo-Oxazolidine Units: A Quantum Chemistry Investigation. Molecules 2022, 27, 2770. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.J.; Zou, Q.; Tian, H. Photochromic Materials: More than Meets the Eye. Adv. Mater. 2013, 25, 378–399. [Google Scholar] [CrossRef] [PubMed]
- Boixel, J.; Colombo, A.; Fagnani, F.; Matozzo, P.; Dragonetti, C. Intriguing Second-Order NLO Switches Based on New DTE Compounds. Eur. J. Inorg. Chem. 2022, 2022, e202200034. [Google Scholar] [CrossRef]
- Areephong, J.; Hurenkamp, J.H.; Milder, M.T.W.; Meetsma, A.; Herek, J.L.; Browne, W.R.; Feringa, B.L. Photoswitchable Sexithiophene-Based Molecular Wires. Org. Lett. 2009, 11, 721–724. [Google Scholar] [CrossRef]
- Oliver, S.; Winter, C. Metal Dithiolene Complexes for All-Optical Switching Devices. Adv. Mater. 1992, 4, 119–121. [Google Scholar] [CrossRef]
- Matsuoka, R.; Sakamoto, R.; Kambe, T.; Takada, K.; Kusamoto, T.; Nishihara, H. Ordered alignment of a one-dimensional pi-conjugated nickel bis(dithiolene) complex polymer produced via interfacial reactions. Chem. Commun. 2014, 50, 8137–8139. [Google Scholar] [CrossRef]
- Dirk, C.W.; Kuzyk, M.G. Damping corrections and the calculation of optical nonlinearities in organic molecules. Phys. Rev. B 1990, 41, 1636–1639. [Google Scholar] [CrossRef]
- Zhang, L.; Peslhebre, G.H.; Muchall, H.M. A general measure of conjugation in biphenyls and their radical cations. Can. J. Chem. 2010, 88, 1175–1185. [Google Scholar] [CrossRef]
- Serrano-Andres, L.; Avramopoulos, A.; Li, J.; Labeguerie, P.; Begue, D.; Kello, V.; Papadopoulos, M.G. Linear and nonlinear optical properties of a series of Ni-dithiolene derivatives. J. Chem. Phys. 2009, 131, 134312. [Google Scholar] [CrossRef] [PubMed]
- Avramopoulos, A.; Zaleśny, R.; Reis, H.; Papadopoulos, M.G. A Computational Strategy for the Design of Photochromic Derivatives Based on Diarylethene and Nickel Dithiolene with Large Contrast in Nonlinear Optical Properties. J. Phys. Chem. C 2020, 124, 4221–4241. [Google Scholar] [CrossRef]
- Dobrowolski, J.C.; Ostrowski, S. On the HOMA index of some acyclic and conducting systems. RSC Adv. 2015, 5, 9467–9471. [Google Scholar] [CrossRef]
- Kauczor, J.; Norman, P.; Christiansen, O.; Coriani, S. Communication: A reduced-space algorithm for the solution of the complex linear response equations used in coupled cluster damped response theory. J. Chem. Phys. 2013, 139, 211102. [Google Scholar] [CrossRef]
- Thanh Phuc, N.; Ishizaki, A. Control of Excitation Energy Transfer in Condensed Phase Molecular Systems by Floquet Engineering. J. Phys. Chem. Lett. 2018, 9, 1243–1248. [Google Scholar] [CrossRef]
- Escudero, D.; Veys, K. Anti-Kasha Fluorescence in Molecular Entities: Central Role of Electron-Vibrational Coupling. Acc. Chem. Res. 2022, 55, 2698–2707. [Google Scholar] [CrossRef]
- Veys, K.; Escudero, D. Computational Protocol To Predict Anti-Kasha Emissions: The Case of Azulene Derivatives. J. Phys. Chem. A 2020, 124, 7228–7237. [Google Scholar] [CrossRef]
- Escudero, D. Revising Intramolecular Photoinduced Electron Transfer (PET) from First-Principles. Acc. Chem. Res. 2016, 49, 1816–1824. [Google Scholar] [CrossRef]
- Rohrs, M.; Escudero, D. Multiple Anti-Kasha Emissions in Transition-Metal Complexes. J. Phys. Chem. Lett. 2019, 10, 5798–5804. [Google Scholar] [CrossRef]
- Blasiak, B.; Maj, M.; Cho, M.; Gora, R.W. Distributed Multipolar Expansion Approach to Calculation of Excitation Energy Transfer Couplings. J. Chem. Theory Comput. 2015, 11, 3259–3266. [Google Scholar] [CrossRef]
- Buckingham, A.D. Permanent and Induced Molecular Moments and Long-Range Intermolecular Forces. Adv. Chem. Phys. 1967, 12, 107–142. [Google Scholar] [CrossRef]
- Cohen, H.D.; Roothaan, C.C. Electric Dipole Polarizability of Atoms by Hartree-Fock Method. I. Theory for Closed-Shell Systems. J. Chem. Phys. 1965, 43, S34–S39. [Google Scholar] [CrossRef]
- Romberg, W. Vereinfachte numerische Intergration. K. Nor. Vidensk. Selsk. Forsk 1955, 28, 30–36. [Google Scholar]
- Rutishauser, H. Ausdehnung des Rombergschen Prinzips. Num. Math. 1963, 5, 48–54. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Numerical Intergration; Blaisdell: London, UK, 1967. [Google Scholar]
- Takamuku, S.; Nakano, M. Theoretical Study on Second Hyperpolarizabilities of Intramolecular Pancake-Bonded Diradicaloids with Helical Scaffolds. ACS Omega 2019, 4, 2741–2749. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. A New Mixing of Hartree-Fock and Local Density-Functional Theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Avramopoulos, A.; Reis, H.; Mousdis, G.A.; Papadopoulos, M.G. Ni Dithiolenes—A Theoretical Study on Structure-Property Relationships. Eur. J. Inorg. Chem. 2013, 2013, 4839–4850. [Google Scholar] [CrossRef]
- Avramopoulos, A.; Reis, H.; Otero, N.; Karamanis, P.; Pouchan, C.; Papadopoulos, M.G. A Series of Novel Derivatives with Giant Second Hyperpolarizabilities, Based on Radiaannulenes, Tetrathiafulvalene, Nickel Dithiolene, and Their Lithiated Analogues. J. Phys. Chem. C 2016, 120, 9419–9435. [Google Scholar] [CrossRef]
- Sutradhar, T.; Misra, A. The role of pi-linkers and electron acceptors in tuning the nonlinear optical properties of BODIPY-based zwitterionic molecules. RSC Adv. 2020, 10, 40300–40309. [Google Scholar] [CrossRef]
- Cao, L.L.; Ryde, U. Influence of the protein and DFT method on the broken-symmetry and spin states in nitrogenase. Int. J. Quantum Chem. 2018, 118, e25627. [Google Scholar] [CrossRef]
- Garcia-Borras, M.; Sola, M.; Luis, J.M.; Kirtman, B. Electronic and Vibrational Nonlinear Optical Properties of Five Representative Electrides. J. Chem. Theory Comput. 2012, 8, 2688–2697. [Google Scholar] [CrossRef]
- Jacquemin, D.; Femenias, A.; Chermette, H.; Ciofini, I.; Adamo, C.; André, J.-M.; Perpète, E.A. Assessment of Several Hybrid DFT Functionals for the Evaluation of Bond Length Alternation of Increasingly Long Oligomers. J. Phys. Chem. A 2006, 110, 5952–5959. [Google Scholar] [CrossRef] [PubMed]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Francl, M.M.; Pietro, W.J.; Hehre, W.J.; Gordon, M.S.; DeFrees, D.J.; Pople, J.A. Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements. J. Chem. Phys. 1982, 77, 3654–3665. [Google Scholar] [CrossRef]
- Hariharan, P.C.; Pople, J.A. The influence of polarization functions on molecular orbital hydrogenation energies. Theor. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian-Basis Sets for Use in Correlated Molecular Calculations. 1. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian-Basis Sets for Use in Correlated Molecular Calculations. 3. The Atoms Aluminum through Argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Dolg, M.; Wedig, U.; Stoll, H.; Preuss, H. Energy-Adjusted Abinitio Pseudopotentials for the 1st-Row Transition-Elements. J. Chem. Phys. 1987, 86, 866–872. [Google Scholar] [CrossRef]
- Bachler, V.; Olbrich, G.; Neese, F.; Wieghardt, K. Theoretical evidence for the singlet diradical character of square planar nickel complexes containing two omicron-semiquinonato type ligands. Inorg. Chem. 2002, 41, 4179–4193. [Google Scholar] [CrossRef]
- Tzeli, D.; Theodorakopoulos, G.; Petsalakis, I.D.; Ajami, D.; Rebek, J., Jr. Conformations and Fluorescence of Encapsulated Stilbene. J. Am. Chem. Soc. 2012, 134, 4346–4354. [Google Scholar] [CrossRef] [PubMed]
- Tzeliou, C.E.; Tzeli, D. 3-Input AND Molecular Logic Gate with Enhanced Fluorescence Output: The Key Atom for the Accurate Prediction of the Spectra. J. Chem. Inf. Model. 2022, 62, 6436–6448. [Google Scholar] [CrossRef] [PubMed]
- Peach, M.J.G.; Benfield, P.; Helgaker, T.; Tozer, D.J. Excitation energies in density functional theory: An evaluation and a diagnostic test. J. Chem. Phys. 2008, 128, 044118. [Google Scholar] [CrossRef] [PubMed]
- Dreuw, A.; Head-Gordon, M. Single-reference ab initio methods for the calculation of excited states of large molecules. Chem. Rev. 2005, 105, 4009–4037. [Google Scholar] [CrossRef]
- Casida, M.E.; Huix-Rotllant, M. Progress in Time-Dependent Density-Functional Theory. Annu. Rev. Phys. Chem. 2012, 63, 287–323. [Google Scholar] [CrossRef]
- Jacquemin, D.; Perpete, E.A.; Scuseria, G.E.; Ciofini, I.; Adamo, C. TD-DFT performance for the visible absorption spectra of organic dyes: Conventional versus long-range hybrids. J. Chem. Theory Comput. 2008, 4, 123–135. [Google Scholar] [CrossRef]
- Jacquemin, D.; Planchat, A.; Adamo, C.; Mennucci, B. TD-DFT Assessment of Functionals for Optical 0-0 Transitions in Solvated Dyes. J. Chem. Theory Comput. 2012, 8, 2359–2372. [Google Scholar] [CrossRef]
- Mahr, H. Two-Photon Absorption Spectroscopy. In Quantum Electronics; Rabin, H., Tang, C.L., Eds.; Academic Press: New York, NY, USA, 1975; Volume 1, p. 494. [Google Scholar]
- Swofford, R.L.; Albrecht, A.C. Nonlinear Spectroscopy. Annu. Rev. Phys. Chem. 1978, 29, 421–440. [Google Scholar] [CrossRef]
- Bloembergen, N. Nonlinear Optics; World Scientific: Singapore, 1996. [Google Scholar]
- Olsen, J.; Jorgensen, P. Linear and nonlinear response functions for an exact state and for an MCSCF state. J. Chem. Phys. 1985, 82, 3235–3264. [Google Scholar] [CrossRef]
- Monson, P.R.; McClain, W.M. Polarization Dependence of the Two-Photon Absorption of Tumbling Molecules with Application to Liquid 1-Chloronaphthalene and Benzene. J. Chem. Phys. 1970, 53, 29–37. [Google Scholar] [CrossRef]
- Beerepoot, M.T.P.; Friese, D.H.; List, N.H.; Kongsted, J.; Ruud, K. Benchmarking two-photon absorption cross sections: Performance of CC2 and CAM-B3LYP. Phys. Chem. Chem. Phys. 2015, 17, 19306–19314. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Zahariev, F.; Gordon, M.S. Nonlinear response time-dependent density functional theory combined with the effective fragment potential method. J. Chem. Phys. 2014, 140, 18A523. [Google Scholar] [CrossRef]
- Zaleśny, R.; Murugan, N.A.; Tian, G.; Medved’, M.; Ågren, H. First-Principles Simulations of One- and Two-Photon Absorption Band Shapes of the Bis(BF2) Core Complex. J. Phys. Chem. B 2016, 120, 2323–2332. [Google Scholar] [CrossRef] [PubMed]
- Beerepoot, M.T.P.; Alam, M.M.; Bednarska, J.; Bartkowiak, W.; Ruud, K.; Zaleśny, R. Benchmarking the Performance of Exchange-Correlation Functionals for Predicting Two-Photon Absorption Strengths. J. Chem. Theory Comput. 2018, 14, 3677–3685. [Google Scholar] [CrossRef] [PubMed]
- Choluj, M.; Alam, M.M.; Beerepoot, M.T.P.; Sitkiewicz, S.P.; Matito, E.; Ruud, K.; Zalesny, R. Choosing Bad versus Worse: Predictions of Two-Photon-Absorption Strengths Based on Popular Density Functional Approximations. J. Chem. Theory Comput. 2022, 18, 1046–1060. [Google Scholar] [CrossRef]
- Förster, T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Ann. Phys. 1948, 437, 55–75. [Google Scholar] [CrossRef]
- Stone, A.J. Distributed multipole analysis, or how to describe a molecular charge distribution. Chem. Phys. Lett. 1981, 83, 233–239. [Google Scholar] [CrossRef]
- Stone, A. The Theory of Intermolecular Forces; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Stone, A.J. Distributed Multipole Analysis: Stability for Large Basis Sets. J. Chem. Theory Comput. 2005, 1, 1128–1132. [Google Scholar] [CrossRef] [PubMed]
- Petsalakis, I.D.; Tzeli, D.; Kerkines, I.S.K.; Theodorakopoulos, G. Theoretical study on the electronic structure and the absorption spectra of complexes of C60 and C59N with π-extended derivatives of tetrathiafulvalene. Comp. Theor. Chem. 2011, 965, 168–175. [Google Scholar] [CrossRef]
- Tzeli, D.; Petsalakis, I.; Theodorakopoulos, G. Computational Insight into the Electronic Structure and Absorption Spectra of Lithium Complexes of N-confused Tetraphenylporphyrin. J. Phys. Chem. A 2011, 115, 11749–11760. [Google Scholar] [CrossRef] [PubMed]
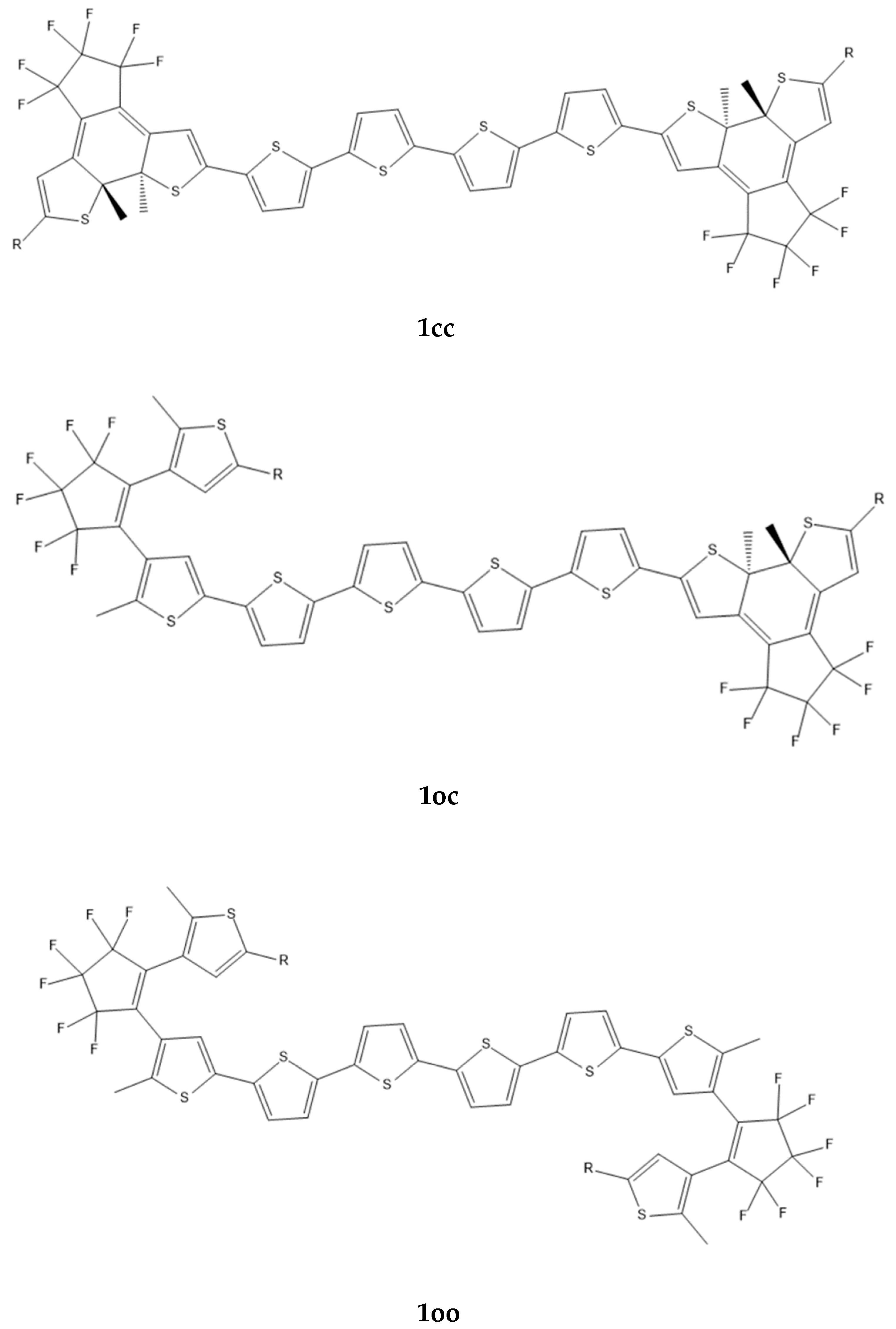
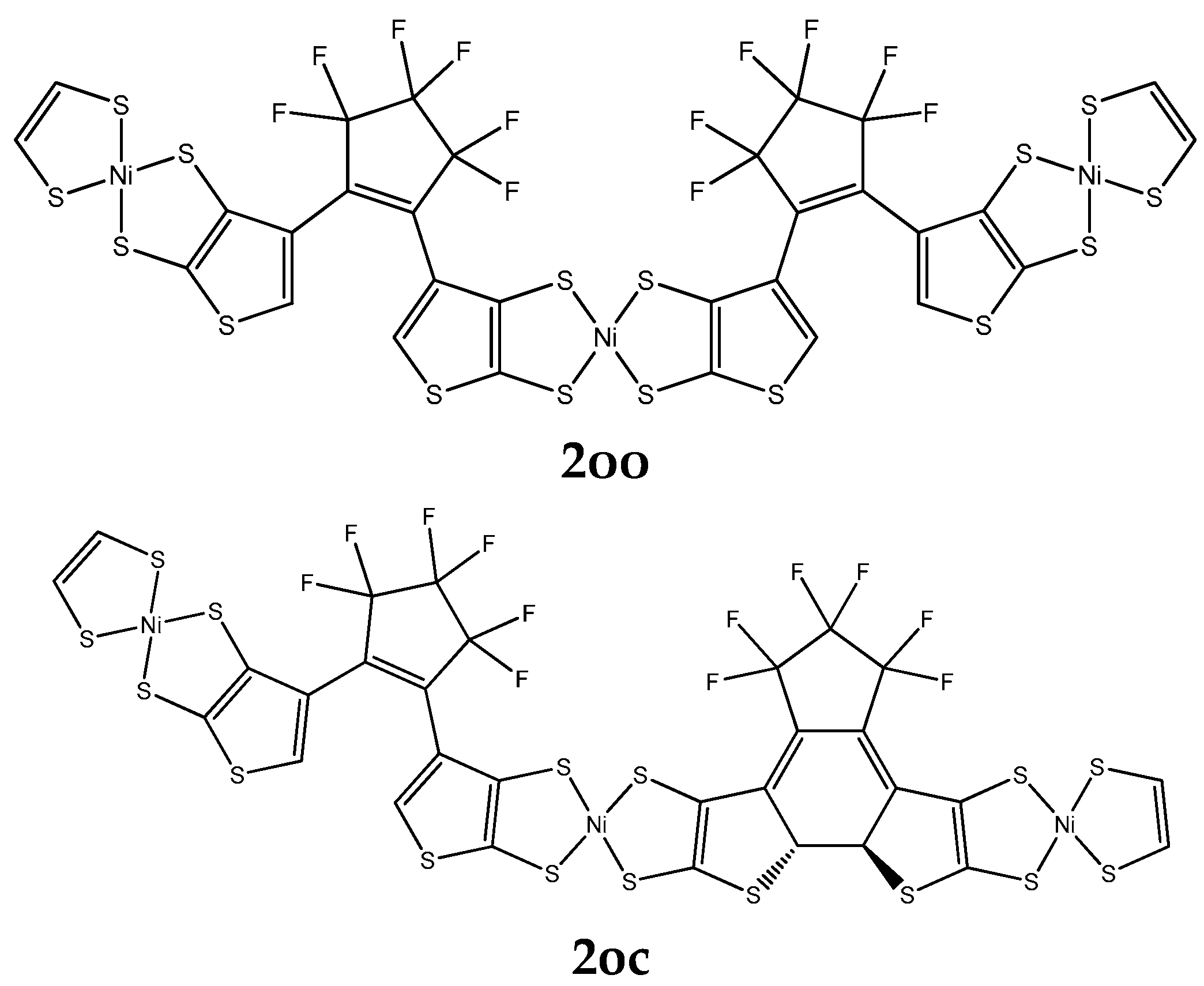



| α | β | γ (×103) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R | 1cc | 1co | 1oo | 1cc | 1co | 1oo | 1cc | 1co | 1oo |
| H | 972.6 1049.5 3 | 882.3 | 796.9 | 680 790 3 | 14,860 | 150 | 14,111 14,660 3 | 8476 | 4078 |
| Cl | 1025.4 | 926.0 | 827.2 | 1200 | 20,860 | 243 | 15,635 | 9299 | 4185 |
| 1108.0 3 | 1250 3 | 16,270 3 | |||||||
| 914.0 4 | 824.6 4 | 776.7 4 | 1960 4 | 11,700 4 | 144 4 | 8654 4 | 4719 4 | 2837 4 | |
| NO2 | 1123.8 | 988.8 | 842.5 | 257 | 48,040 | 773 | 22,841 | 13,260 | 4284 |
| NH2 | 1024.4 | 918.9 | 822.2 | 530 | 401 | 486 | 16,212 | 8949 | 4208 |
| Ph | 1239.1 | 1096.1 | 960.8 | −310 | 10,140 | 150 | 23,611 | 12,378 | 4692 |
| NO2/ NH2 1 | 1094 | 930.0 | 832.4 | 71,350 | 2950 | 4950 | 25,370 | 9049 | 4272 |
| NO2/NH2 2 | 988.0 | 61,260 | 14,861 | ||||||
| Derivative | λ | α | β | γ (×103) |
|---|---|---|---|---|
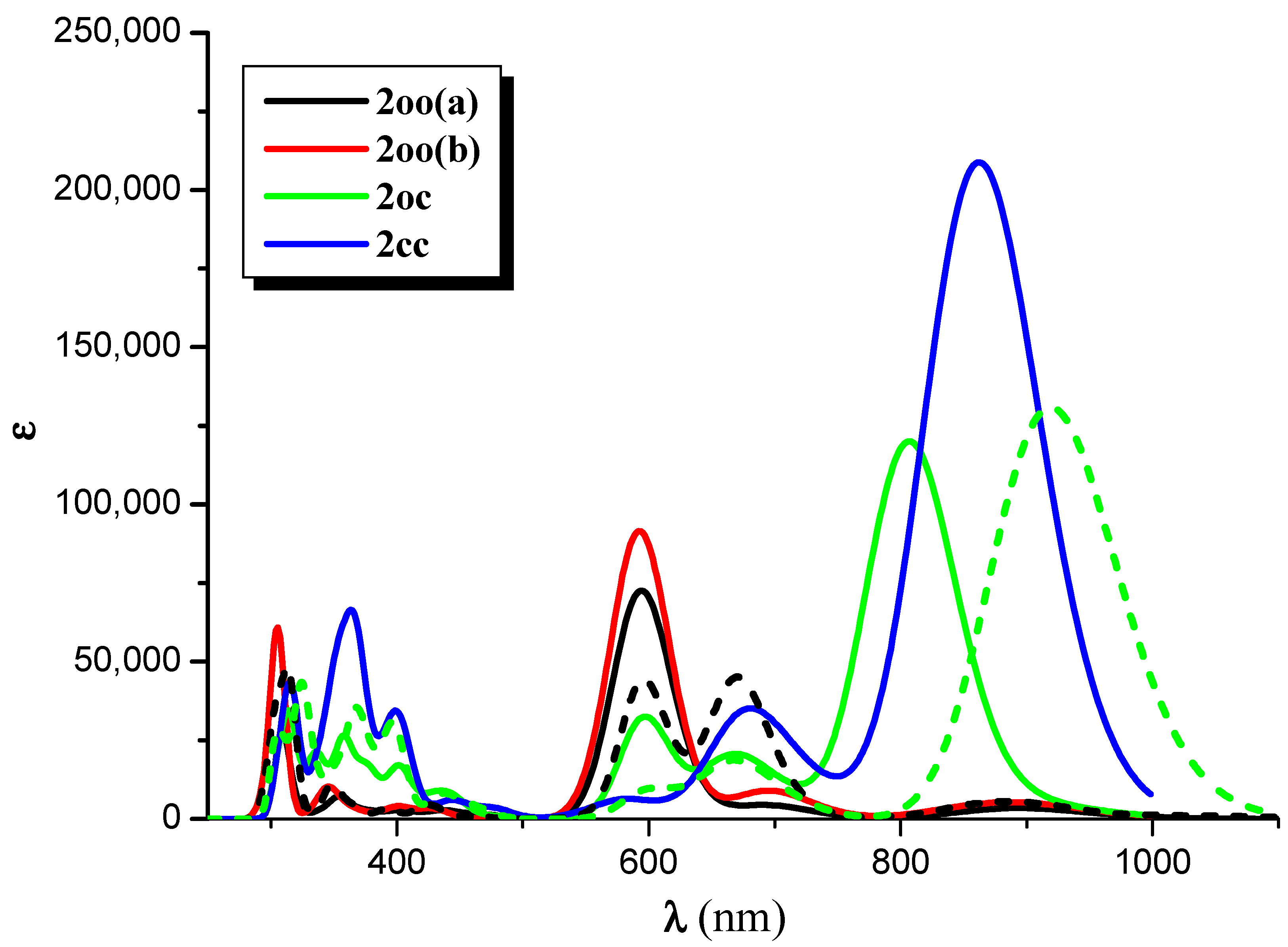
| 2oo | 622.3 1 | 880.3 1 | −410 1 | 2741 1 |
| 2oc | 884.1 1 | 1163 1 1225 2 | 1349 1 1330 2 | 17,400 1 19,236 2 |
| 2cc | 994.3 1 | 1576.9 1 1652.5 2 | −14,076 1 −13,080 2 | 67,870 1 68,890 2 |
| 3oo | 614.01 | 792.9 1 | 432 1 | 1416 1 |
| 3cc | 878.9 1 | 1129.6 1 | 5800 1 | 13,971 1 |
| NO2 -1AB-NH2 | H-1AB-H | ||||||
|---|---|---|---|---|---|---|---|
| cc | co | oc | oo | cc | oc | oo | |
| IHOMA | 0.827 | 0.806 | 0.807 | 0.778 | 0.843 | 0.812 | 0.790 |
| Dimer | VDA | Vc | Vxc |
|---|---|---|---|
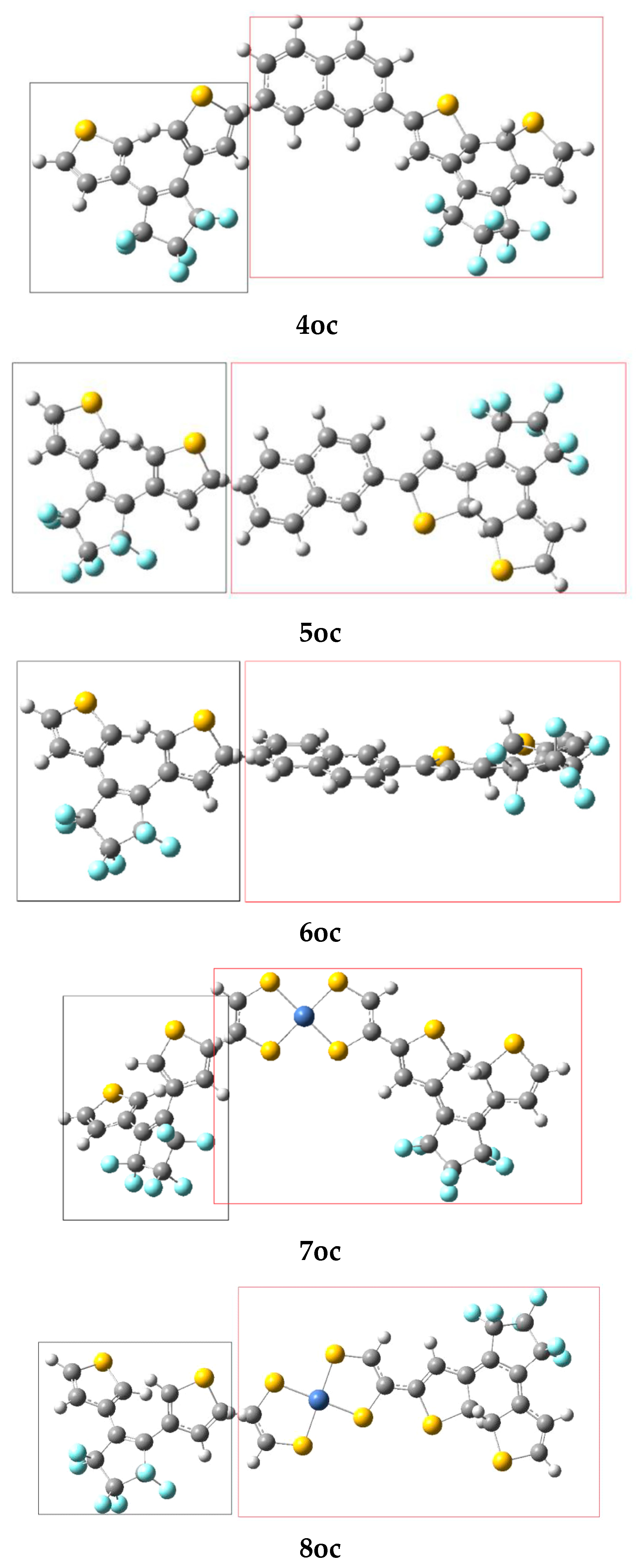
| 1oc a | 8.3 | 8.1 9.7 b | 0.2 0.25 b |
| 2oc | 10.3 | 9.7 | 0.6 |
| 4oc | 101.5 | 101.6 | −0.1 |
| 5oc | 113.0 | 111.3 | 1.7 |
| 6oc | 120.4 | 120.9 | −0.5 |
| 7oc | 32.3 | 30.9 | 1.4 |
| 8oc | 12.8 | 12.1 | 0.7 |
| l + l′ Bridge | 0 | 1 | 2 | 3 | 4 | Analyt. Coulomb a | Analyt. EET a. |
|---|---|---|---|---|---|---|---|
| Naphthalene | 82.3 | 137.1 | 143.6 | 127.4 | 117.8 | 111.3 | 112.9 |
| NiBDT | 4.8 | 8.1 | 13.7 | 12.1 | 15.3 | 12.1 | 12.9 |
| Struct | ΔΕ | λmax | f | Excitations |
|---|---|---|---|---|
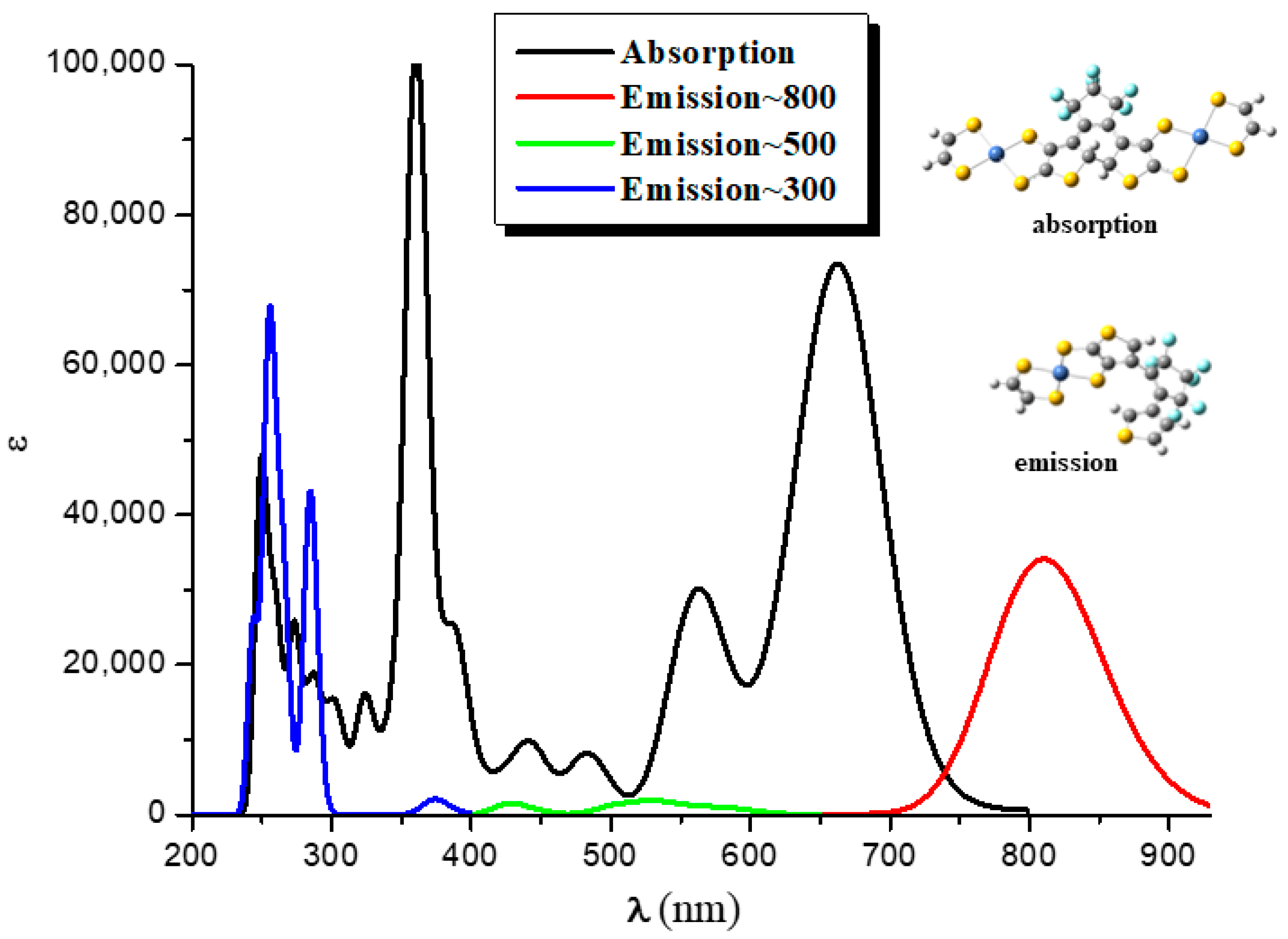
| Absorption | ||||
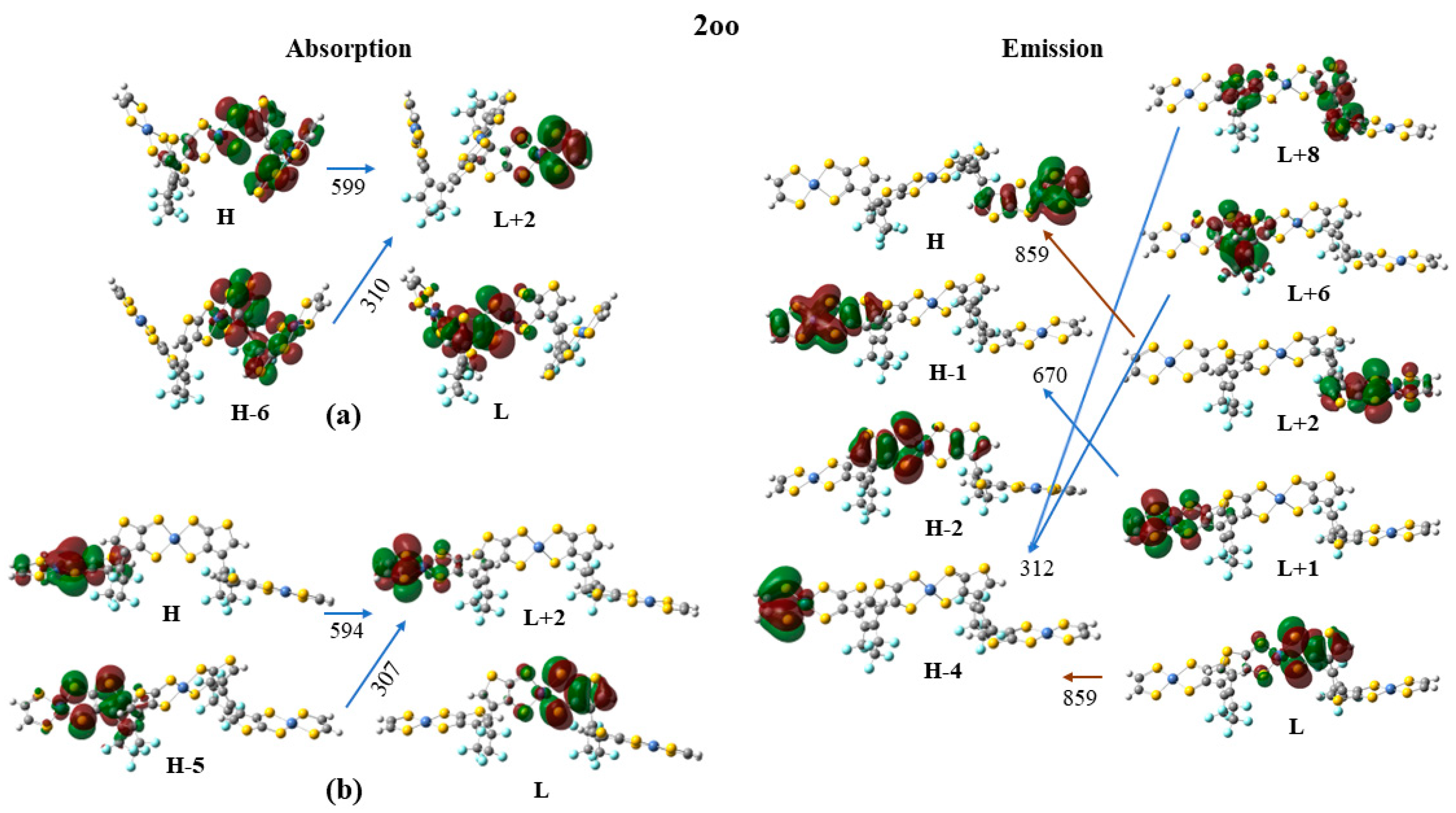
| 2oo(a) | 1.805 | 686.9 | 0.0115 | 0.35|H-2 → L + 1> − 0.29|H → L + 2 > + 0.28|H-1 → L + 1 > + 0.26|H-2 → L> |
| 2.071 | 598.7 | 0.1141 | 0.20|H → L + 2 > + 0.16|H-1 → L + 2 > − 0.21|H-10 → L + 5> | |
| 4.006 | 309.5 | 0.1252 | 0.19|H-0 → L + 2 > − 0.13|H-1 → L + 6> | |
| 2oo(b) | 1.791 | 692.2 | 0.0447 | 0.56|H-1 → L + 1 > − 0.36|H → L + 2> |
| 2.088 | 593.7 | 0.4031 | 0.42|H → L + 2 > + 0.23|H-1 → L + 1> − 0.18|H-2 → L> | |
| 4.044 | 306.6 | 0.2014 | 0.18|H-2 → L + 8 > + 0.20|H-5 → L + 2 > − 0.22|H-35 → L> − 0.20|H-19 → L + 3> | |
| 2oc | 1.537 | 806.9 | 0.7112 | 0.58|H → L > − 0.23|H-5 → L> |
| 1.868 | 663.7 | 0.0926 | 0.38|H-2 → L > − 0.27|H-5 → L> | |
| 3.925 | 315.9 | 0.0983 | 0.39|H-17 → L > + 0.22|H-20 → L > + 0.31|H-20 → L + 2> | |
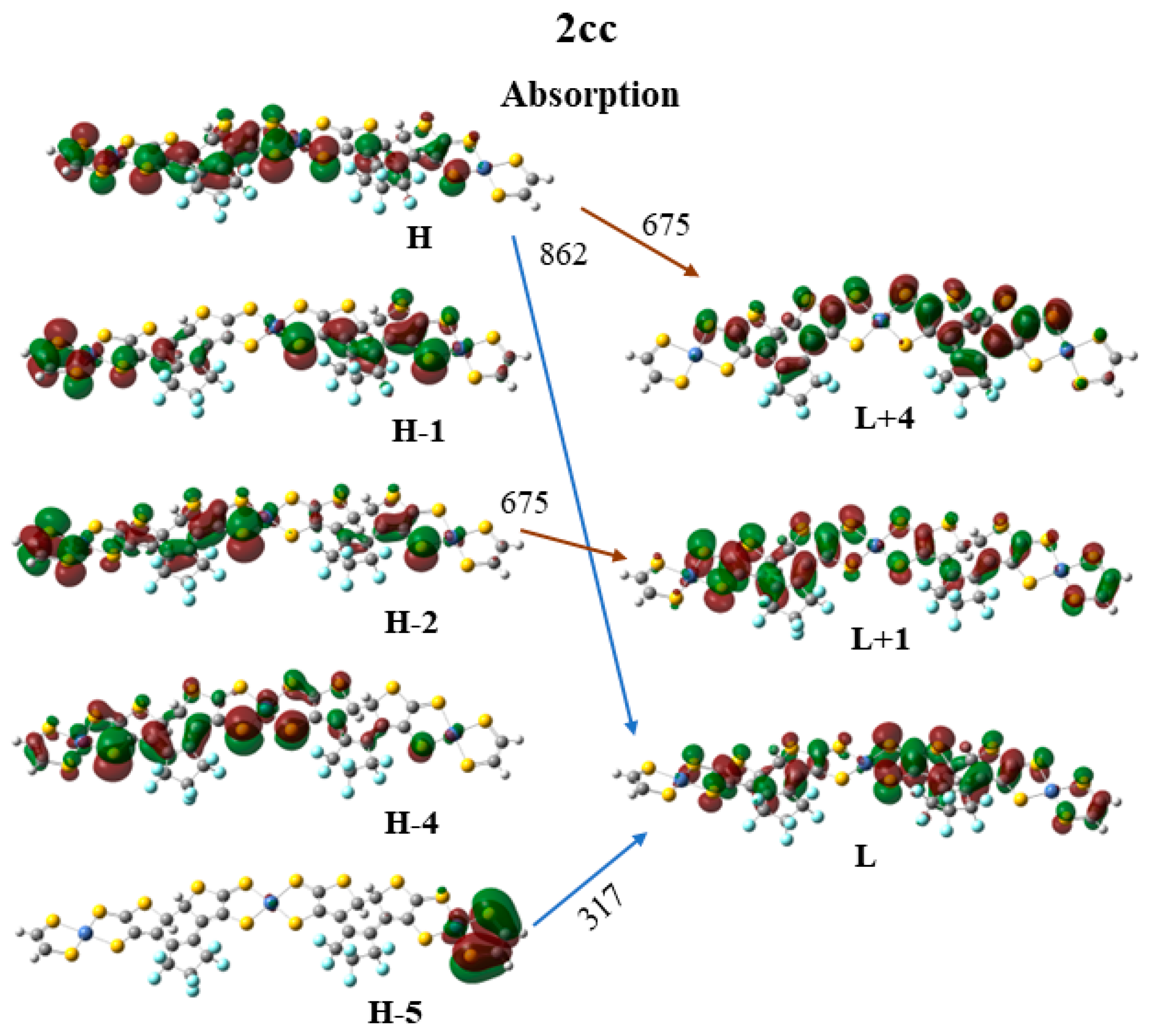
| 2cc | 1.438 | 862.3 | 1.3931 | 0.51|H → L > + 0.30|H-1 → L + 1> |
| 1.837 | 675.1 | 0.1866 | 0.23|H → L + 4 > + 0.20|H-4 → L > − 0.23|H-2 → L + 1> + 0.18|H-1 → L> | |
| 3.107 | 399.0 | 0.1077 | 0.28|H-1 → L + 1 > + 0.21|H → L + 4 > − 0.21|H-4 → L + 1> − 0.18|H-0 → L> | |
| 3.369 | 368.0 | 0.1701 | 0.29|H-17 → L > − 0.16|H-18 → L > + 0.15|H-8 → L> | |
| 3.519 | 352.4 | 0.1073 | 0.27|H-19 → L + 1 > + 0.19|H-19 → L > − 0.18|H-9 → L + 1> − 0.11|H-2 → L + 1> | |
| 3.917 | 316.5 | 0.1402 | 0.27|H-10 → L + 1 > + 0.21|H-10 → L >− 0.19|H-13 → L> + 0.26|H-5 → L> | |
| Emission | ||||
| 2oo | 1.444 | 858.7 | 0.0170 | 0.65|H-0 → L > − 0.15|H-2 → L> |
| 1.851 | 669.7 | 0.1938 | 0.47|H-1 → L + 2> − 0.51|H-1 → L + 1 > − 0.39|H-10 → L + 2 > + 0.27|H-12 → L + 2 > + 0.21|H-10 → L + 1> | |
| 2.074 | 597.8 | 0.1588 | 0.52|H → L + 2 > + 0.40|H-9 → L + 4> | |
| 3.966 | 312.6 | 0.2401 | 0.33|H-2 → L + 8 > + 0.14|H-2 → L + 6> − 0.36|H-30 → L> | |
| 2oc | 1.353 | 916.5 | 0.7071 | 0.57|H → L > − 0.24|H-4 → L> |
| 1.874 | 661.6 | 0.0774 | 0.32|H-5 → L > + 0.29|H → L + 1 > − 0.43|H-2 → L> − 0.25|H → H-19> | |
| 3.806 | 325.8 | 0.0748 | 0.31|H-15 → L > + 0.23|H-4 → L + 4 > − 0.25|H-5 → L + 5> | |
| 2oo | 2oc | 2cc | 2oo | 2oc | 2oo | 2oc |
|---|---|---|---|---|---|---|
| S0 → Si a | Si → S0 b | S0 → Si c | ||||
| 1.81 (1.79) d | 1.54 | 1.44 | 1.44 | 1.35 | 1.67 | 1.40 |
| 2.07 (2.09) d | 1.87 | 1.84 | 1.85 | 1.86 | 1.98 | 1.87 |
| 4.01 (4.04) d | 3.92 | 3.11 | 3.97 | 3.81 | 4.00 | 3.88 |
| 3.37 | ||||||
| 3.52 | ||||||
| 3.92 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avramopoulos, A.; Reis, H.; Tzeli, D.; Zaleśny, R.; Papadopoulos, M.G. Photoswitchable Molecular Units with Tunable Nonlinear Optical Activity: A Theoretical Investigation. Molecules 2023, 28, 5646. https://doi.org/10.3390/molecules28155646
Avramopoulos A, Reis H, Tzeli D, Zaleśny R, Papadopoulos MG. Photoswitchable Molecular Units with Tunable Nonlinear Optical Activity: A Theoretical Investigation. Molecules. 2023; 28(15):5646. https://doi.org/10.3390/molecules28155646
Chicago/Turabian StyleAvramopoulos, Aggelos, Heribert Reis, Demeter Tzeli, Robert Zaleśny, and Manthos G. Papadopoulos. 2023. "Photoswitchable Molecular Units with Tunable Nonlinear Optical Activity: A Theoretical Investigation" Molecules 28, no. 15: 5646. https://doi.org/10.3390/molecules28155646
APA StyleAvramopoulos, A., Reis, H., Tzeli, D., Zaleśny, R., & Papadopoulos, M. G. (2023). Photoswitchable Molecular Units with Tunable Nonlinear Optical Activity: A Theoretical Investigation. Molecules, 28(15), 5646. https://doi.org/10.3390/molecules28155646








