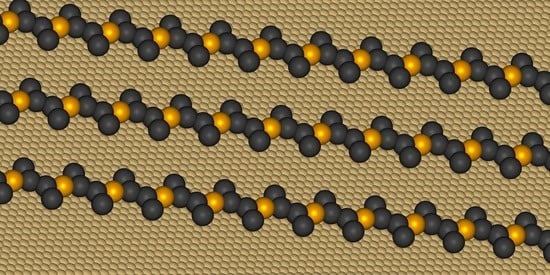
Structural Quantification of the Surface-Confined Metal-Organic Precursors Simulated with the Lattice Monte Carlo Method
Abstract
1. Introduction
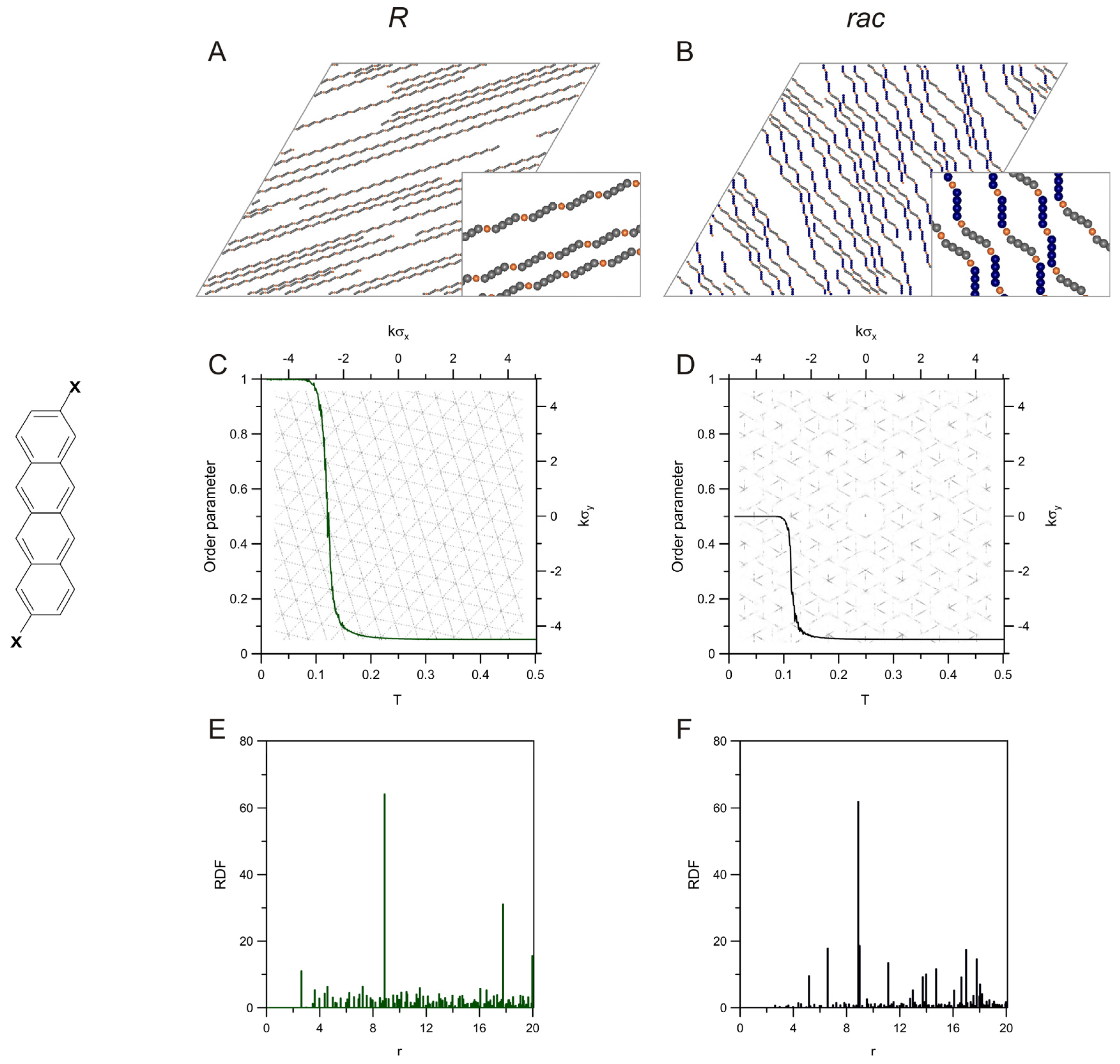
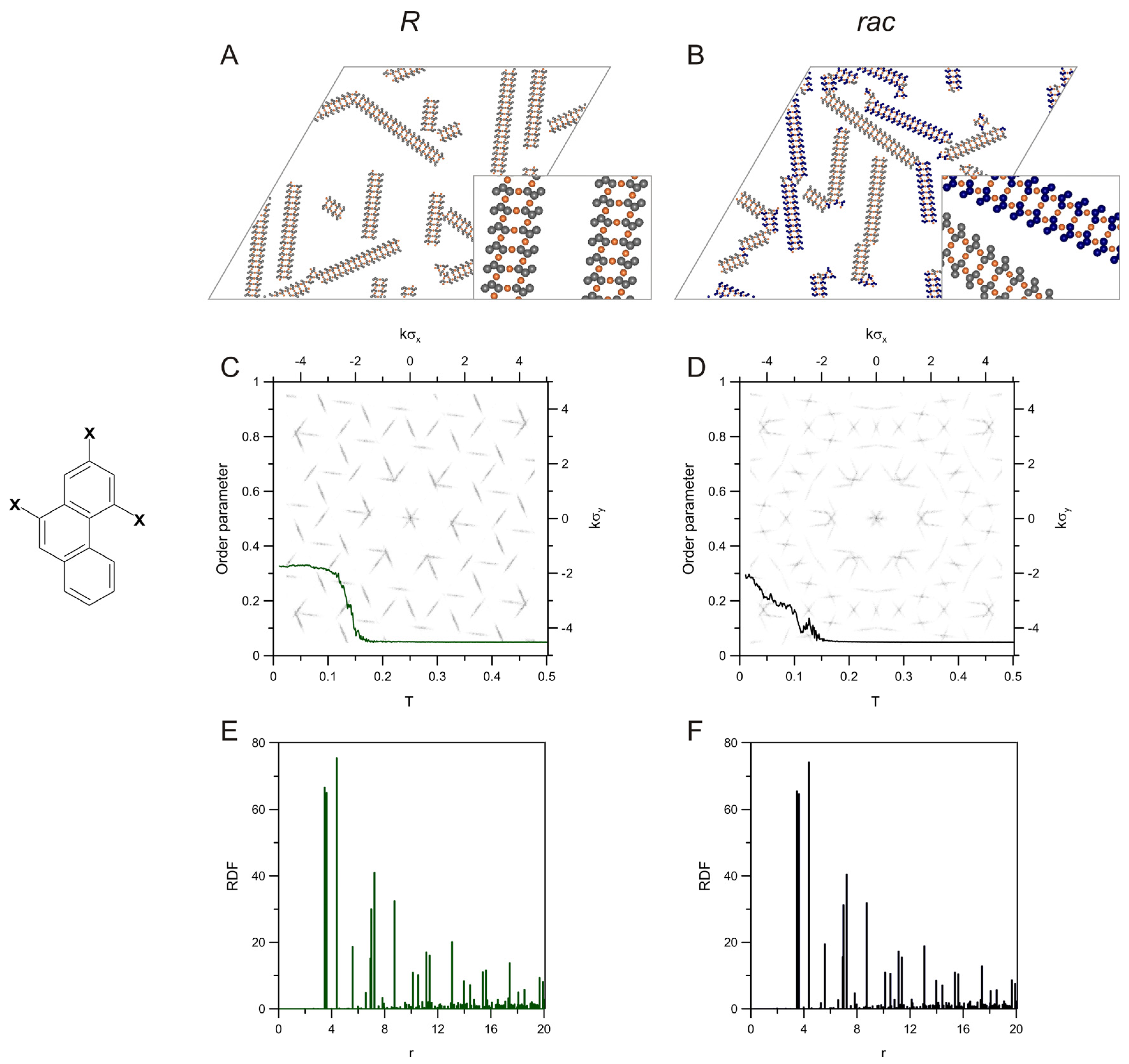
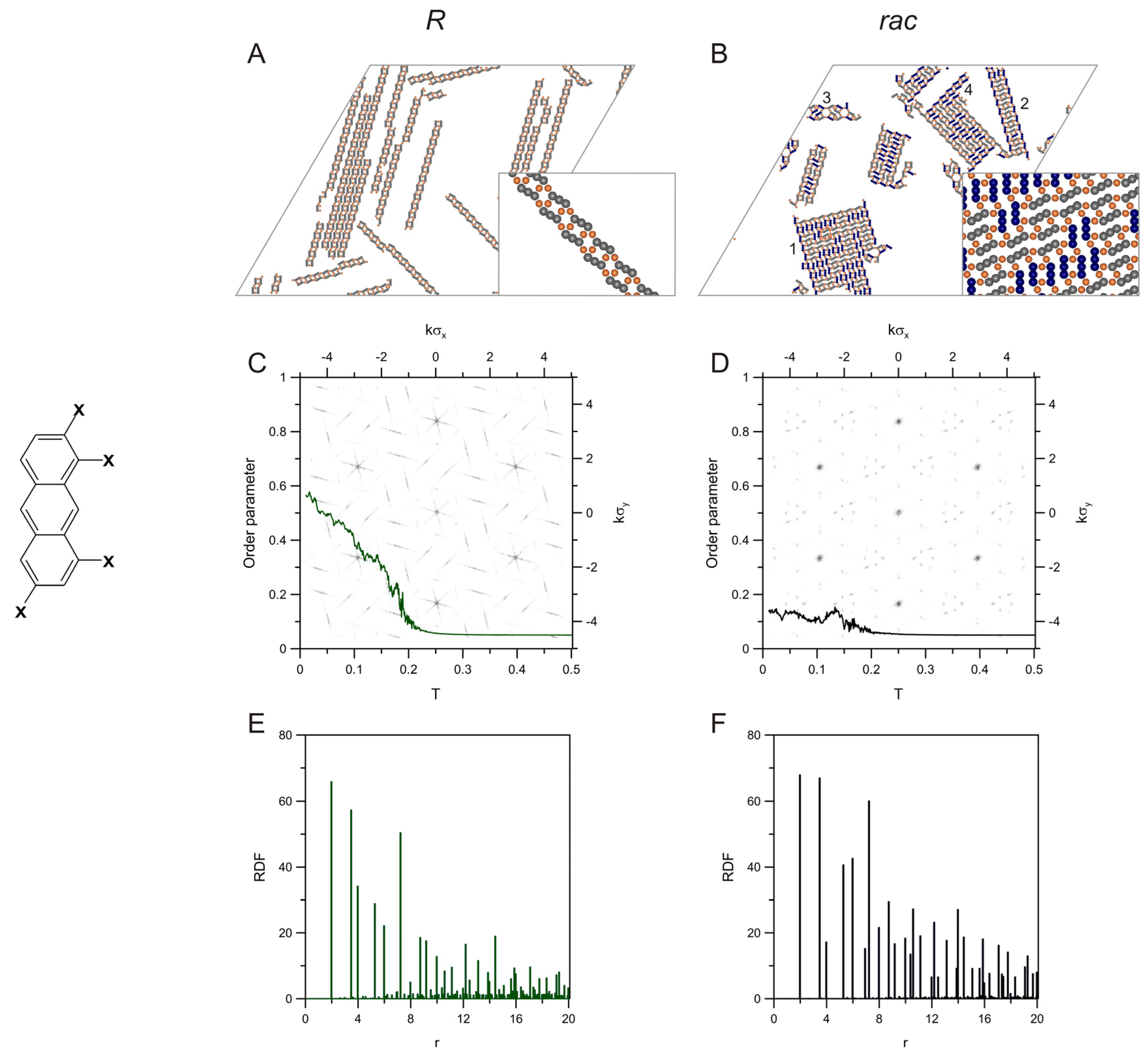
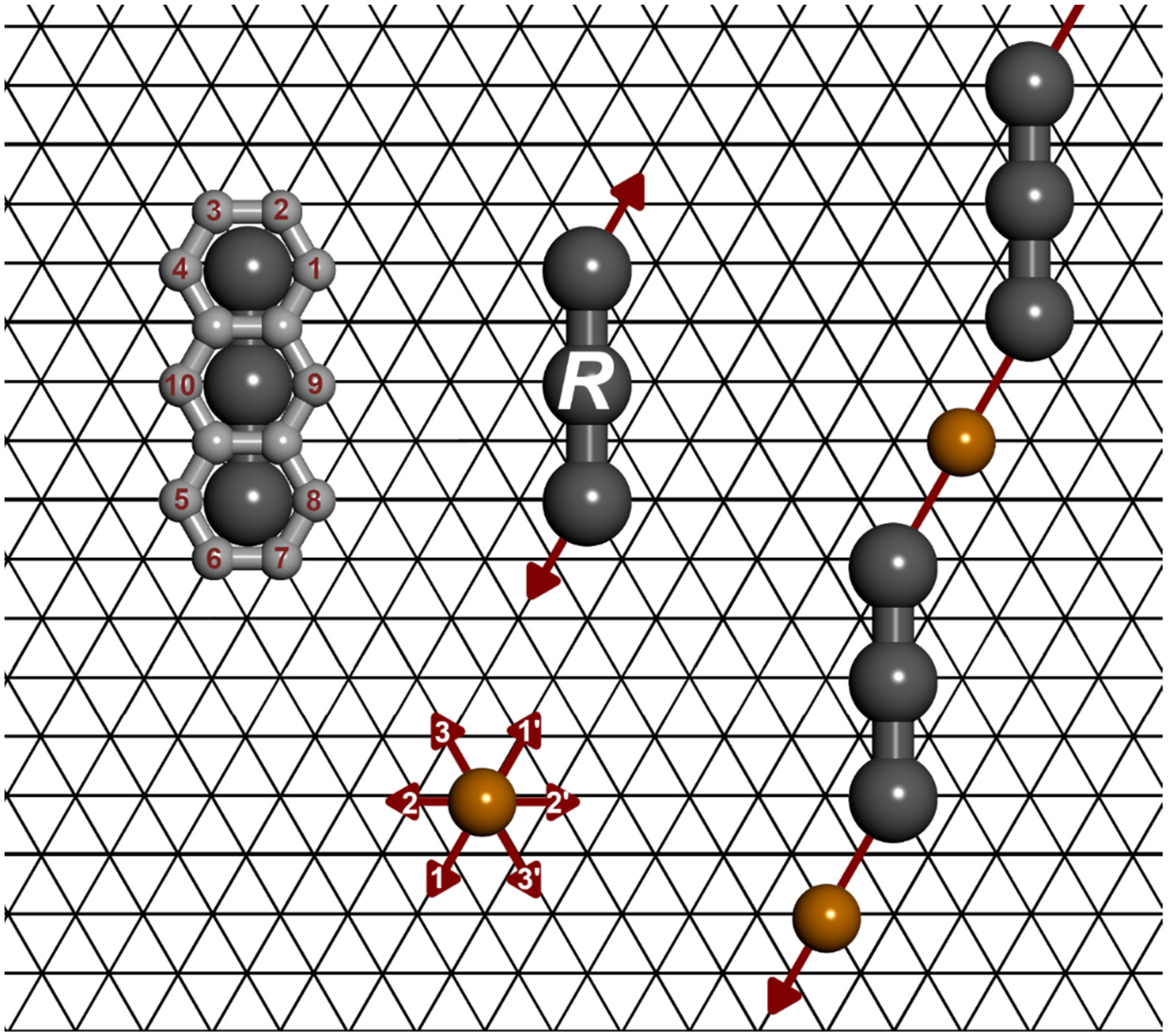
2. Results and Discussion
3. The Model and Calculations
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grzelczak, M.; Vermant, J.; Furst, E.M.; Luis, M.; Liz-Marzán, L.M. Directed Self-Assembly of Nanoparticles. ACS Nano 2010, 4, 3591–3605. [Google Scholar] [CrossRef] [PubMed]
- Moores, A. Bottom up, Solid-Phase Syntheses of Inorganic Nanomaterials by Mechanochemistry and Aging. Curr. Opin. Green Sustain. Chem. 2018, 12, 33–37. [Google Scholar] [CrossRef]
- Sealy, C. Bottom-up Approach Yields 2D Nanomaterials by the Kilo. Mater. Today 2022, 54, 5–6. [Google Scholar] [CrossRef]
- Abid, N.; Khan, A.M.; Shujait, S.; Chaudhary, K.; Ikram, M.; Imran, M.; Haider, J.; Khan, M.; Khan, Q.; Maqbool, M. Synthesis of Nanomaterials Using Various Top-down and Bottom-up Approaches, Influencing Factors, Advantages, and Disadvantages: A Review. Adv. Colloid Interface Sci. 2022, 300, 102597. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Cao, X.; Wu, X.J.; He, Q.; Yang, J.; Zhang, X.; Chen, J.; Zhao, W.; Han, S.; Nam, G.-H.; et al. Recent Advances in Ultrathin Two-Dimensional Nanomaterials. Chem. Rev. 2017, 117, 6225–6331. [Google Scholar] [CrossRef] [PubMed]
- Erol, O.; Uyan, I.; Hatip, M.; Yilmaz, C.; Tekinay, A.B.; Guler, M.O. Recent Advances in Bioactive 1D and 2D Carbon Nanomaterials for Biomedical Applications. Nanomed. Nanotechnol. Biol. Med. 2018, 14, 2433–2454. [Google Scholar] [CrossRef] [PubMed]
- Shen, Q.; Gao, H.Y.; Fuchs, H. Frontiers of On-Surface Synthesis: From Principles to Applications. Nano Today. April 2017, 13, 77–96. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Zou, Y.; Xu, W.; Zhu, D. PPN (Poly-: Peri-Naphthalene) Film as a Narrow-Bandgap Organic Thermoelectric Material. J. Mater. Chem. A 2017, 5, 9891–9896. [Google Scholar] [CrossRef]
- Klappenberger, F.; Hellwig, R.; Du, P.; Paintner, T.; Uphoff, M.; Zhang, L.; Lin, T.; Moghanaki, B.A.; Paszkiewicz, M.; Vobornik, I.; et al. Functionalized Graphdiyne Nanowires: On-Surface Synthesis and Assessment of Band Structure, Flexibility, and Information Storage Potential. Small 2018, 14, e1704321. [Google Scholar] [CrossRef] [PubMed]
- Kong, J.; Franklin, N.R.; Zhou, C.; Chapline, M.G.; Peng, S.; Cho, K.; Dai, H. Nanotube Molecular Wires as Chemical Sensors. Science 2000, 287, 622–625. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Zhang, L.; Lee, S.; Dai, H. Chemically Derived, Ultrasmooth Graphene Nanoribbon Semiconductors. Science 2008, 319, 1229–1232. [Google Scholar] [CrossRef] [PubMed]
- Mallada, B.; Błoński, P.; Langer, R.; Jelínek, P.; Otyepka, M.; de la Torre, B. On-Surface Synthesis of One-Dimensional Coordination Polymers with Tailored Magnetic Anisotropy. ACS Appl. Mater. Interfaces 2021, 13, 32393–32401. [Google Scholar] [CrossRef] [PubMed]
- Eichhorn, J.; Nieckarz, D.; Ochs, O.; Samanta, D.; Schmittel, M.; Szabelski, P.J.; Lackinger, M. On-Surface Ullmann Coupling: The Influence of Kinetic Reaction Parameters on the Morphology and Quality of Covalent Networks. ACS Nano 2014, 8, 7880–7889. [Google Scholar] [CrossRef] [PubMed]
- Lackinger, M. Surface-Assisted Ullmann Coupling. Chem. Commun. 2017, 53, 7872–7885. [Google Scholar] [CrossRef] [PubMed]
- Moreno, C.; Panighel, M.; Vilas-Varela, M.; Sauthier, G.; Tenorio, M.; Ceballos, G.; Peña, D.; Mugarza, A. Critical Role of Phenyl Substitution and Catalytic Substrate in the Surface-Assisted Polymerization of Dibromobianthracene Derivatives. Chem. Mater. 2019, 31, 331–341. [Google Scholar] [CrossRef]
- Wei, S.; Zhang, F.; Zhang, W.; Qiang, P.; Yu, K.; Fu, X.; Wu, D.; Bi, S. Semiconducting 2D Triazine-Cored Covalent Organic Frameworks with Unsubstituted Olefin Linkages. J. Am. Chem. Soc. 2019, 141, 14272–14279. [Google Scholar] [CrossRef]
- Zhang, T.; Grazioli, C.; Yang, H.; Jiang, K.; Brumboiu, I.E.; Jia, L.; Liu, L.; Puglia, C.; Zhuang, X.; Wang, Y. Spectroscopic Evidence of New Low-Dimensional Planar Carbon Allotropes Based on Biphenylene via On-Surface Ullmann Coupling. Chemistry 2021, 3, 1057–1062. [Google Scholar] [CrossRef]
- Hussein, F.; Pigot, C.; Romero Lairado, F.; Minissale, M.; Salomon, E.; Angot, T.; Dumur, F.; Nechab, M.; Gigmes, D.; Clair, S.; et al. On-Surface Homocoupling Reactivity of a Chiral Bifunctional Bromoindanone Molecule on Cu(111). New J. Chem. 2022, 46, 22869–22876. [Google Scholar] [CrossRef]
- Su, J.; Fan, W.; Mutombo, P.; Peng, X.; Song, S.; Ondráček, M.; Golub, P.; Brabec, J.; Veis, L.; Telychko, M.; et al. On-Surface Synthesis and Characterization of [7]Triangulene Quantum Ring. Nano Lett. 2021, 21, 861–867. [Google Scholar] [CrossRef]
- Scheibel, T.; Parthasarathy, R.; Sawicki, G.; Lin, X.-M.; Jaeger, H.; Lindquist, S.L. Conducting Nanowires Built by Controlled Self-Assembly of Amyloid Fibers and Selective Metal Deposition. Proc. Natl. Acad. Sci. USA 2003, 100, 4527–4532. [Google Scholar] [CrossRef]
- Kaltenpoth, G.; Himmelhaus, M.; Slansky, L.; Caruso, F.; Grunze, M. Conductive Core-Shell Particles: An Approach to Self-Assembled Mesoscopic Wires. Adv. Mater. 2003, 15, 1113–1118. [Google Scholar] [CrossRef]
- Kraft, D.J.; Ni, R.; Smallenburg, F.; Hermes, M.; Yoon, K.; Weitz, D.A.; van Blaaderen, A.; Groenewold, J.; Dijkstra, M.; Kegel, W.K. Surface Roughness Directed Self-Assembly of Patchy Particles into Colloidal Micelles. Proc. Natl. Acad. Sci. USA 2012, 109, 10787–10792. [Google Scholar] [CrossRef] [PubMed]
- Baek, K.; Hwang, I.; Roy, I.; Shetty, D.; Kim, K. Self-Assembly of Nanostructured Materials through Irreversible Covalent Bond Formation. Acc. Chem. Res. 2015, 48, 2221–2229. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Lin, H.; Sun, K.; Chen, L.; Zagranyarski, Y.; Aghdassi, N.; Duhm, S.; Li, Q.; Zhong, D.; Li, Y.; et al. On-Surface Synthesis of Rylene-Type Graphene Nanoribbons. J. Am. Chem. Soc. 2015, 137, 4022–4025. [Google Scholar] [CrossRef]
- Wang, W.; Shi, X.; Wang, S.; Van Hove, M.A.; Lin, N. Single-Molecule Resolution of an Organometallic Intermediate in a Surface-Supported Ullmann Coupling Reaction. J. Am. Chem. Soc. 2011, 133, 13264–13267. [Google Scholar] [CrossRef]
- Fan, Q.; Wang, C.; Han, Y.; Zhu, J.; Hieringer, P.-D.D.W.; Kuttner, J.; Hilt, G.; Gottfried, J.M. Surface-Assisted Organic Synthesis of Hyperbenzene Nanotroughs. Angew. Chemie. Int. Ed. 2013, 52, 4668–4672. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, R.; Qiu, J.; Liu, R.; Xu, W. On-Surface Synthesis of Carbon Nanostructures. Adv. Mater. 2018, 30, 1705630. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, Q.; Chen, Q.; Wang, J. Molecular Self-Assembly on Two-Dimensional Atomic Crystals: Insights from Molecular Dynamics Simulations. J. Phys. Chem. Lett. 2015, 6, 4518–4524. [Google Scholar] [CrossRef]
- John, A.S.; Roth, M.W.; Firlej, L.; Kuchta, B.; Charra, F.; Wexler, C. Self-Assembled Two-Dimensional Nanoporous Crystals as Molecular Sieves: Molecular Dynamics Studies of 1,3,5-Tristyrilbenzene-C n Superstructures. J. Chem. Inf. Model. 2020, 60, 2155–2168. [Google Scholar] [CrossRef]
- Baran, Ł. Coarse-Grained Modelling of On-Surface Self-Assembly of Mixtures Comprising Di-Substituted Polyphenyl-Like Compounds and Metal Atoms of Different Sizes. ACS Omega 2021, 6, 25193–25200. [Google Scholar] [CrossRef]
- Baran, Ł.; Dyk, K.; Kamiński, D.M.; Stankevič, M.; Rżysko, W.; Tarasewicz, D.; Zientarski, T. Influence of the substitution position in the tetratopic building blocks on the self-assembly process. J. Mol. Liq. 2022, 346, 117074. [Google Scholar] [CrossRef]
- Nieckarz, D.; Rżysko, W.; Szabelski, P. On-Surface Self-Assembly of Tetratopic Molecular Building Blocks. Phys. Chem. Chem. Phys. 2018, 20, 23363–23377. [Google Scholar] [CrossRef] [PubMed]
- Szabelski, P.; De Feyter, S.; Drach, M.; Lei, S. Computer Simulation of Chiral Nanoporous Networks on Solid Surfaces. Langmuir 2010, 26, 9506–9515. [Google Scholar] [CrossRef] [PubMed]
- Gdula, K.; Nieckarz, D. On-Surface Self-Assembly of Metal-Organic Architectures: Insights from Computer Simulations. J. Phys. Chem. C 2020, 124, 20066–20078. [Google Scholar] [CrossRef]
- Nieckarz, K.; Nieckarz, D. Monte Carlo Simulations of the Metal-Directed Self-Assembly of Y-Shaped Positional Isomers. Crystals 2022, 12, 492. [Google Scholar] [CrossRef]
- Li, L.; Li, X.; Duan, Z.; Meyer, R.J.; Carr, R.; Raman, S.; Koziol, L.; Henkelman, G.; Carr, R. Adaptive Kinetic Monte Carlo Simulations of Surface Segregation in PdAu Nanoparticles. Nanoscale 2019, 11, 10524–10535. [Google Scholar] [CrossRef]
- Maguire, J.B.; Boyken, S.E.; Baker, D.; Kuhlman, B. Rapid Sampling of Hydrogen Bond Networks for Computational Protein Design. J. Chem. Theory Comput. 2018, 14, 2751–2760. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, N.; Li, R.; Wu, T.; Li, N.; Hou, S.; Wang, Y. Construction and Properties of Sierpiński Triangular Fractals on Surfaces. ChemPhysChem 2019, 20, 2262–2270. [Google Scholar] [CrossRef]
- Nieckarz, D.; Szabelski, P. Simulation of the Self-Assembly of Simple Molecular Bricks into Sierpiński Triangles. Chem. Commun. 2014, 50, 6843–6845. [Google Scholar] [CrossRef]
- Nieckarz, K.; Szabelski, P.; Nieckarz, D. Monte Carlo Simulations of the Self-Assembly of Hierarchically Organized Metal-Organic Networks on Solid Surfaces. Surf. Sci. 2022, 719, 122041. [Google Scholar] [CrossRef]
- Benali, A.; Shulenburger, L.; Romero, N.A.; Kim, J.; von Lilienfeld, O.A. Application of Diffusion Monte Carlo to Materials Dominated by van Der Waals Interactions. J. Chem. Theory Comput. 2014, 10, 3417–3422. [Google Scholar] [CrossRef] [PubMed]
- Lisiecki, J.; Szabelski, P. Surface-Confined Metal–Organic Precursors Comprising Naphthalene-Like Derivatives with Differently Distributed Halogen Substituents: A Monte Carlo Model. J. Phys. Chem. C 2020, 124, 20280–20293. [Google Scholar] [CrossRef]
- Lisiecki, J.; Szabelski, P. Designing 2D Covalent Networks with Lattice Monte Carlo Simulations: Precursor Self-Assembly. Phys. Chem. Chem. Phys. 2021, 23, 5780–5796. [Google Scholar] [CrossRef] [PubMed]
- Lisiecki, J.; Szabelski, P. Halogenated Anthracenes as Building Blocks for the On-Surface Synthesis of Covalent Polymers: Structure Prediction with the Lattice Monte Carlo Method. J. Phys. Chem. C 2021, 125, 15934–15949. [Google Scholar] [CrossRef]
- Lisiecki, J.; Szabelski, P. Theoretical Modelling of the Metal-organic Precursors of Anthracene-based Covalent Networks on Surfaces. ChemPhysChem 2022, 23, e202100877. [Google Scholar] [CrossRef] [PubMed]
- Lisiecki, J.; Szabelski, P. Monte Carlo Simulation of the Surface-Assisted Self-Assembly of Metal-Organic Precursors Comprising Phenanthrene Building Blocks. Colloids Surfaces A Physicochem. Eng. Asp. 2022, 648, 129177. [Google Scholar] [CrossRef]
- Zeng, Z.; Huang, J.; Han, D.; Li, X.; Xu, Q.; Wang, T.; Zhu, J. Substrate-Directed Chiral Selectivity of Molecular Self-Assembled and Covalent Structures. Surf. Sci. 2023, 733, 122306. [Google Scholar] [CrossRef]
- Wang, H.; Hu, J.; Liang, Z.; Zhang, H.; Huang, C.; Xie, L.; Jiang, Z.; Huang, H.; Song, F. Chirality Variation from Self-Assembly on Ullmann Coupling for the DBCh Adsorbate on Au(111) and Ag(111). Nanoscale Adv. 2023, 5, 1368–1377. [Google Scholar] [CrossRef]
- Du, Q.; Pu, W.; Sun, Z.; Yu, P. On-Surface Synthesis of All-Cis Standing Phenanthrene Polymers upon Selective C-H Bond Activation. J. Phys. Chem. Lett. 2020, 11, 5022–5028. [Google Scholar] [CrossRef]
- Lin, T.; Shang, X.S.; Adisoejoso, J.; Yu, P. Steering On-Surface Polymerization with Metal-Directed Template. J. Am. Chem. Soc. 2013, 135, 3576–3582. [Google Scholar] [CrossRef]
- De Oteyza, D.G.; García-Lekue, A.; Vilas-Varela, M.; Merino-Díez, N.; Carbonell-Sanromà, E.; Corso, M.; Vasseur, G.; Rogero, C.; Guitián, E.; Pascual, J.I.; et al. Substrate-Independent Growth of Atomically Precise Chiral Graphene Nanoribbons. ACS Nano 2016, 10, 9000–9008. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Luo, X.; Bao, Y.; Liu, Y.P.; Ning, G.-H.; Abdelwahab, I.; Li, L.; Nai, C.T.; Hu, Z.G.; Zhao, D.; et al. A Two-Dimensional Conjugated Aromatic Polymer via C-C Coupling Reaction. Nat. Chem. 2017, 9, 563–570. [Google Scholar] [CrossRef] [PubMed]
- Bieri, M.; Blankenburg, S.; Kivala, M.; Pignedoli, C.A.; Ruffieux, P.; Müllen, K.; Fasel, R. Surface-Supported 2D Heterotriangulene Polymers. Chem. Commun. 2011, 47, 10239–10241. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Ruffieux, P.; Jaafar, R.; Bieri, M.; Braun, T.; Blankenburg, S.; Muoth, M.; Seitsonen, A.P.; Saleh, M.; Feng, X.; et al. Atomically Precise Bottom-up Fabrication of Graphene Nanoribbons. Nature 2010, 466, 470–473. [Google Scholar] [CrossRef] [PubMed]
- Clair, S.; de Oteyza, D.G. Controlling a Chemical Coupling Reaction on a Surface: Tools and Strategies for On-Surface Synthesis. Chem. Rev. 2019, 119, 4717–4776. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation; Elsevier: San Diego, CA, USA, 2002; pp. 23–61, 111–137. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisiecki, J.; Szabelski, P. Structural Quantification of the Surface-Confined Metal-Organic Precursors Simulated with the Lattice Monte Carlo Method. Molecules 2023, 28, 4253. https://doi.org/10.3390/molecules28104253
Lisiecki J, Szabelski P. Structural Quantification of the Surface-Confined Metal-Organic Precursors Simulated with the Lattice Monte Carlo Method. Molecules. 2023; 28(10):4253. https://doi.org/10.3390/molecules28104253
Chicago/Turabian StyleLisiecki, Jakub, and Paweł Szabelski. 2023. "Structural Quantification of the Surface-Confined Metal-Organic Precursors Simulated with the Lattice Monte Carlo Method" Molecules 28, no. 10: 4253. https://doi.org/10.3390/molecules28104253
APA StyleLisiecki, J., & Szabelski, P. (2023). Structural Quantification of the Surface-Confined Metal-Organic Precursors Simulated with the Lattice Monte Carlo Method. Molecules, 28(10), 4253. https://doi.org/10.3390/molecules28104253