A DFT Study of Alkaline Earth Metal-Doped FAPbI3 (111) and (100) Surfaces
Abstract
1. Introduction
2. Results and Discussion
2.1. Surface Structures
2.1.1. Stability of the Plain Surfaces
2.1.2. Stability of Doped Surfaces
2.2. Electronic Properties
2.2.1. Electronic Properties of Bulk and Plain Surfaces
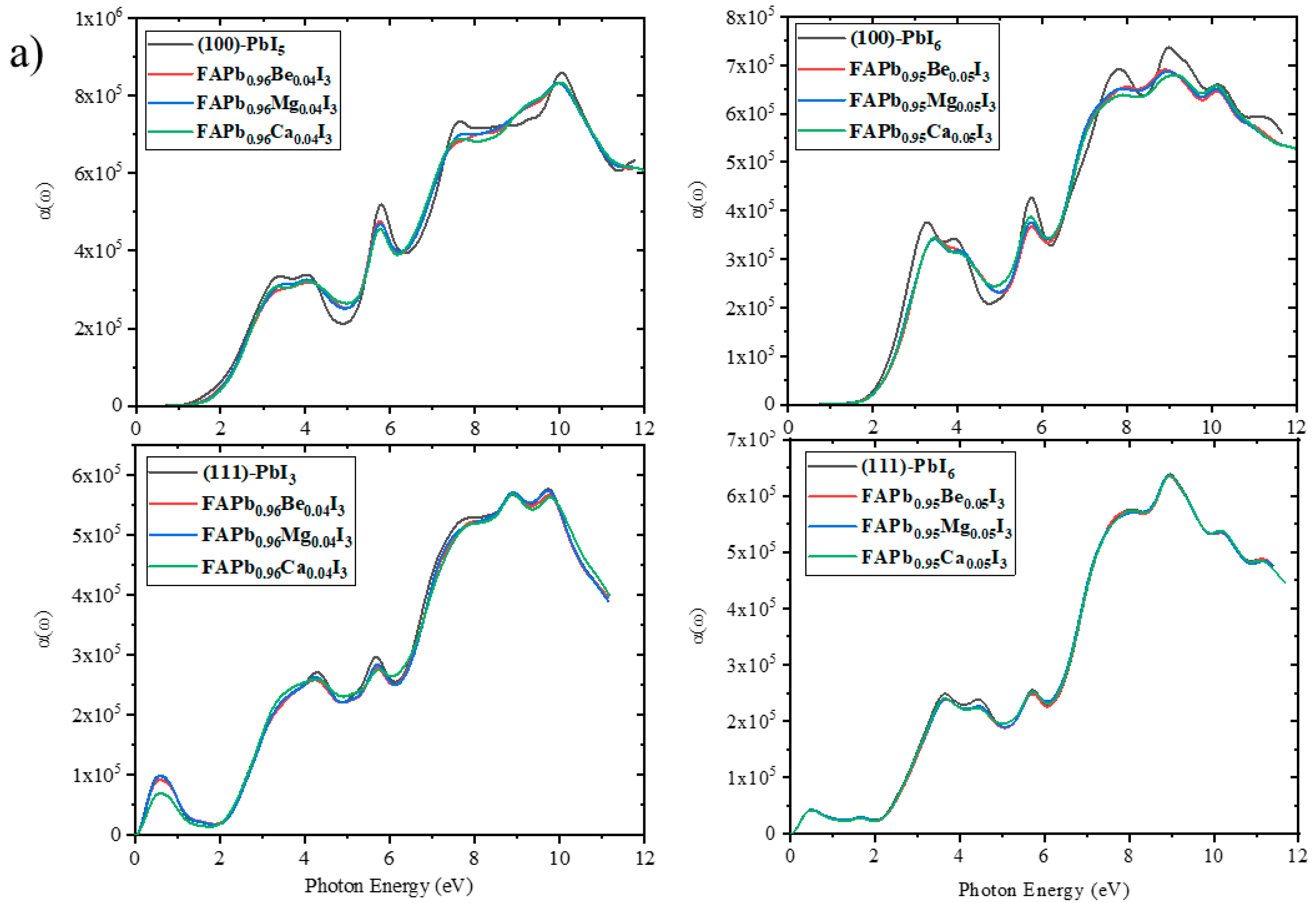
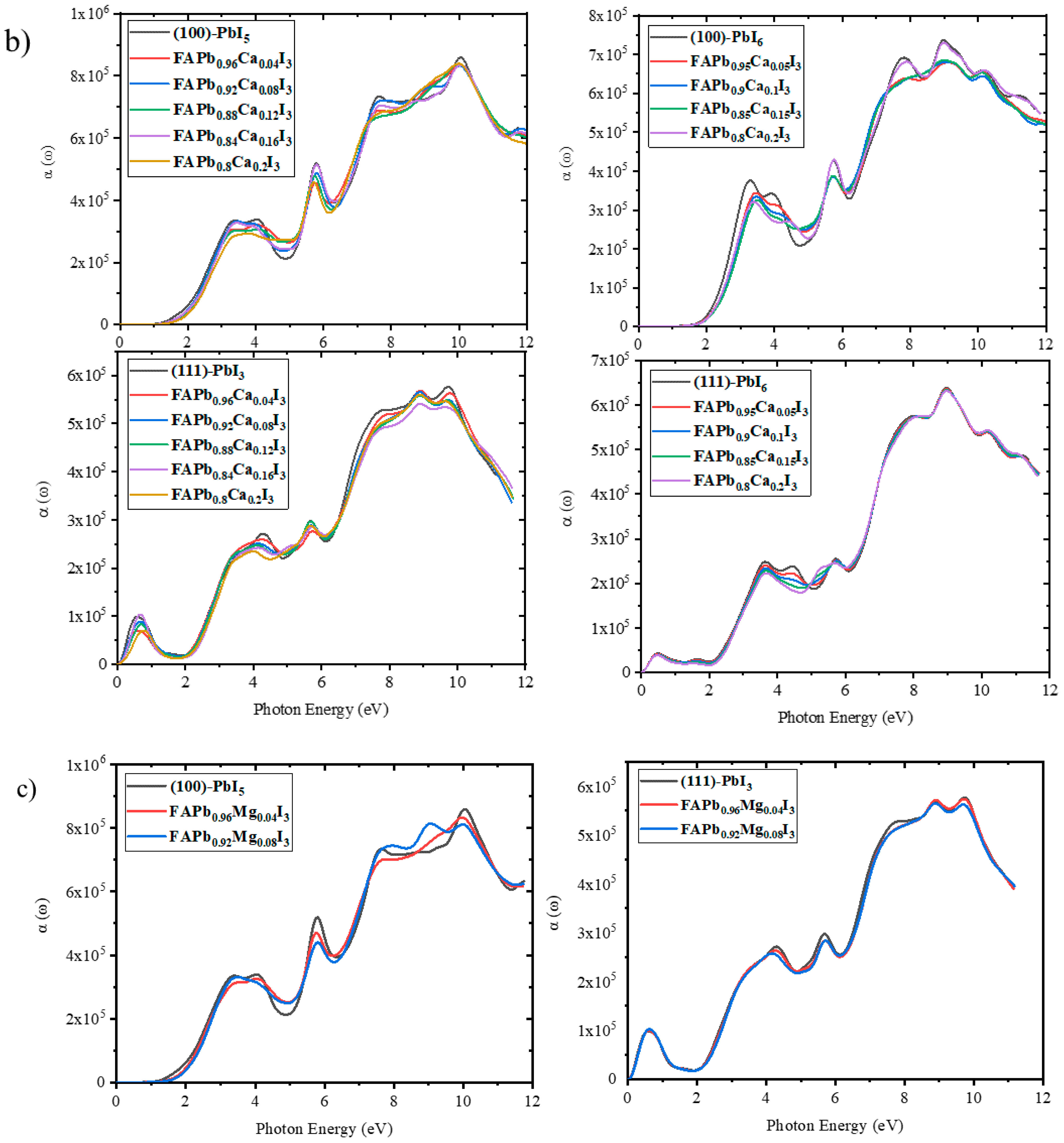
2.2.2. Electronic Properties of Doped Surfaces
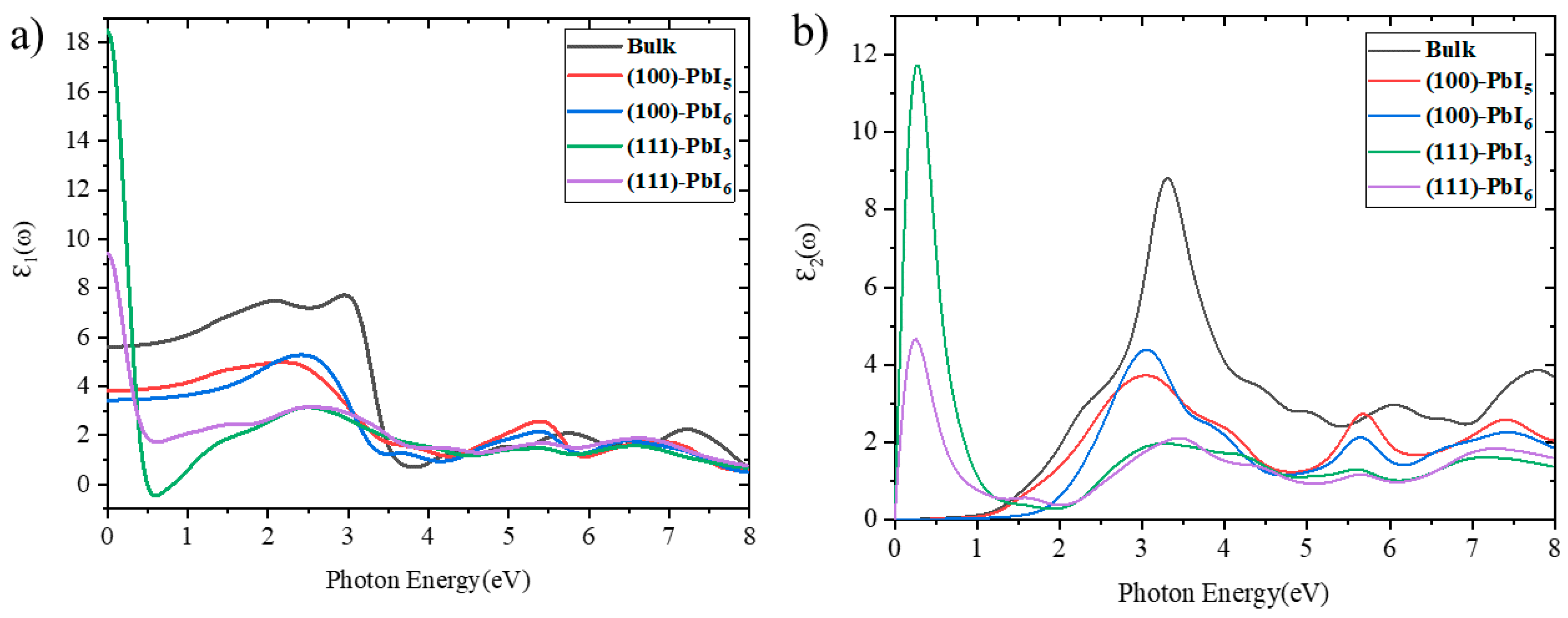
2.3. Optical Properties of Bulk, Plain and Doped Surfaces
2.3.1. Dielectric Functions
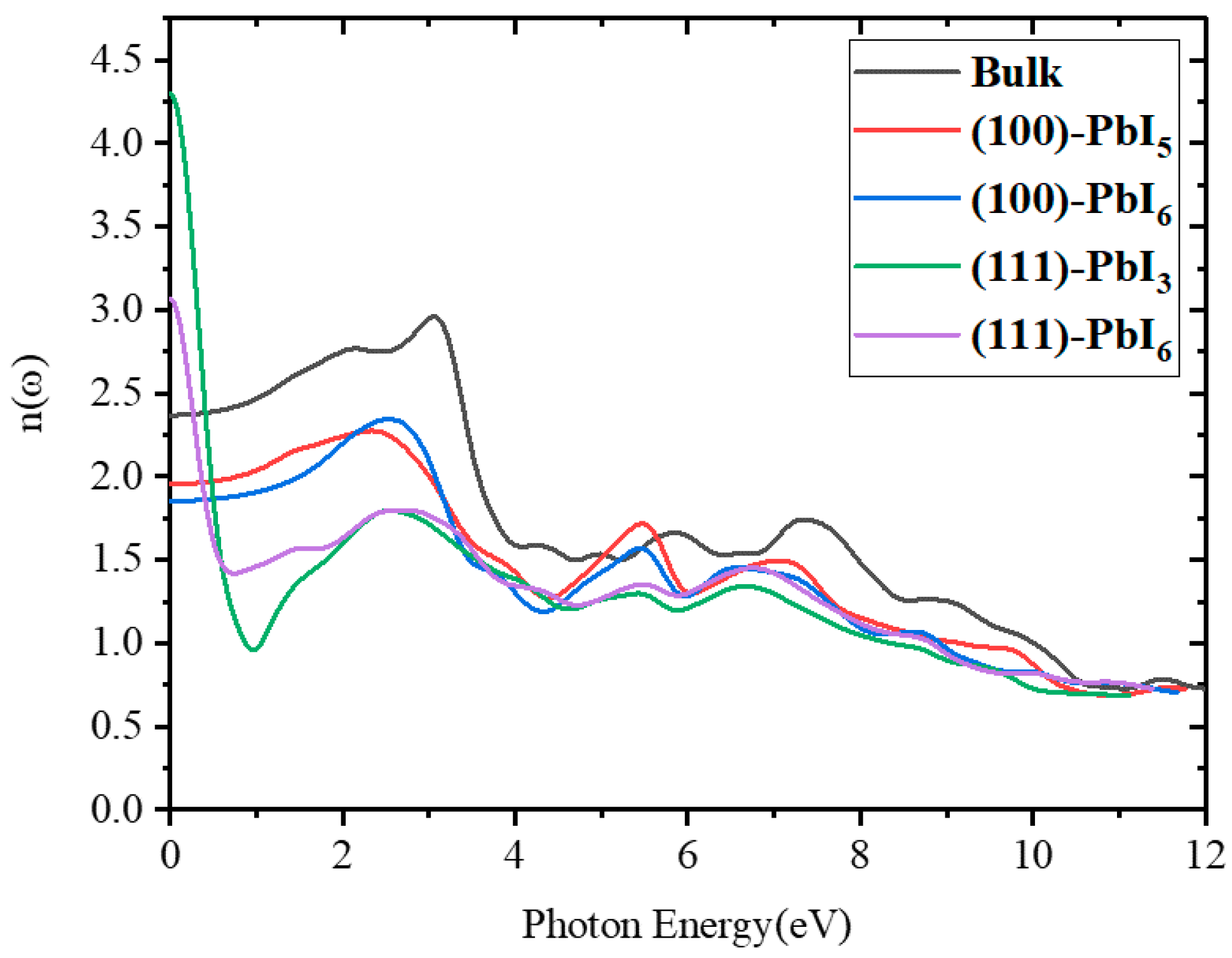
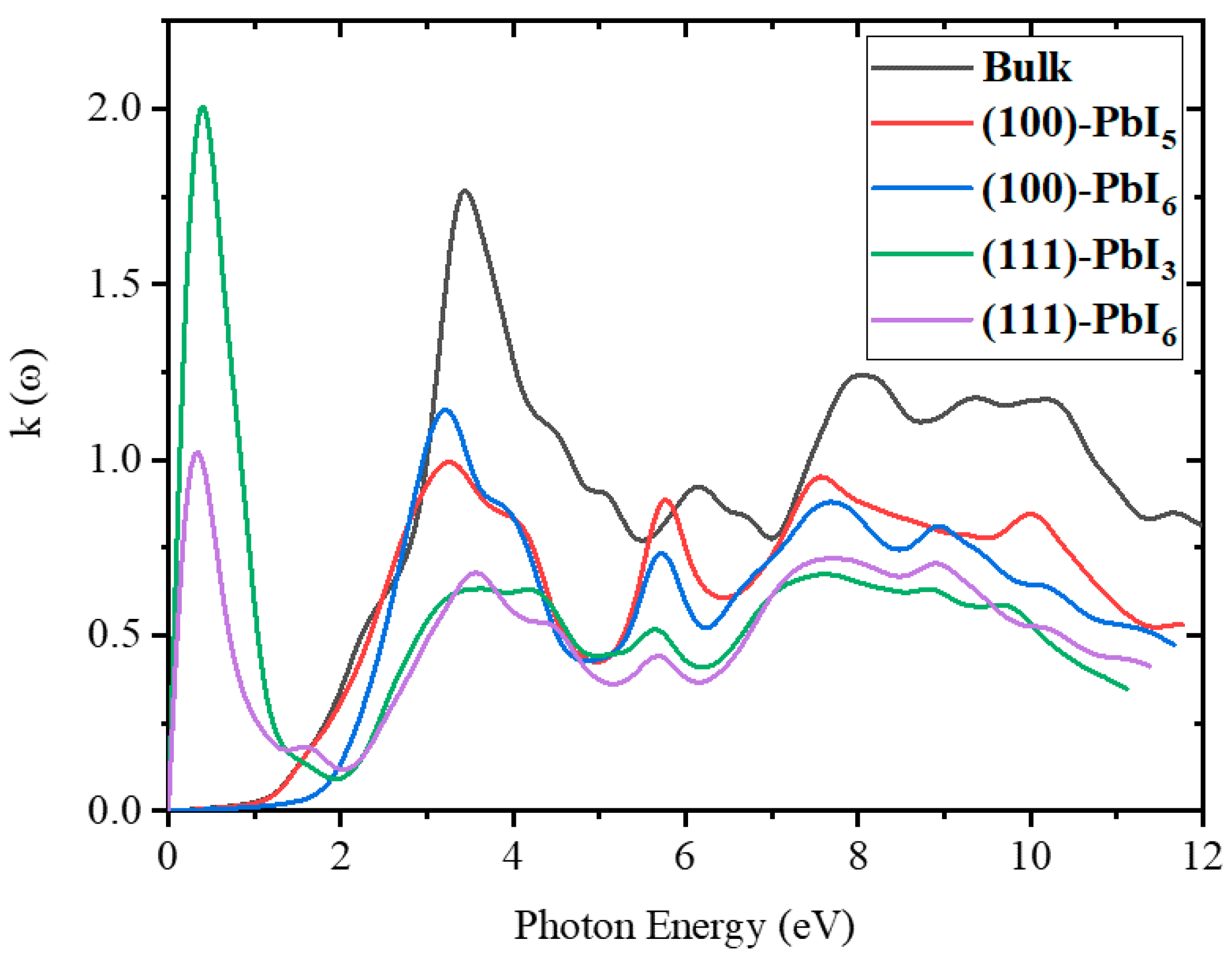
2.3.2. Refractive Index and Extinction Coefficient
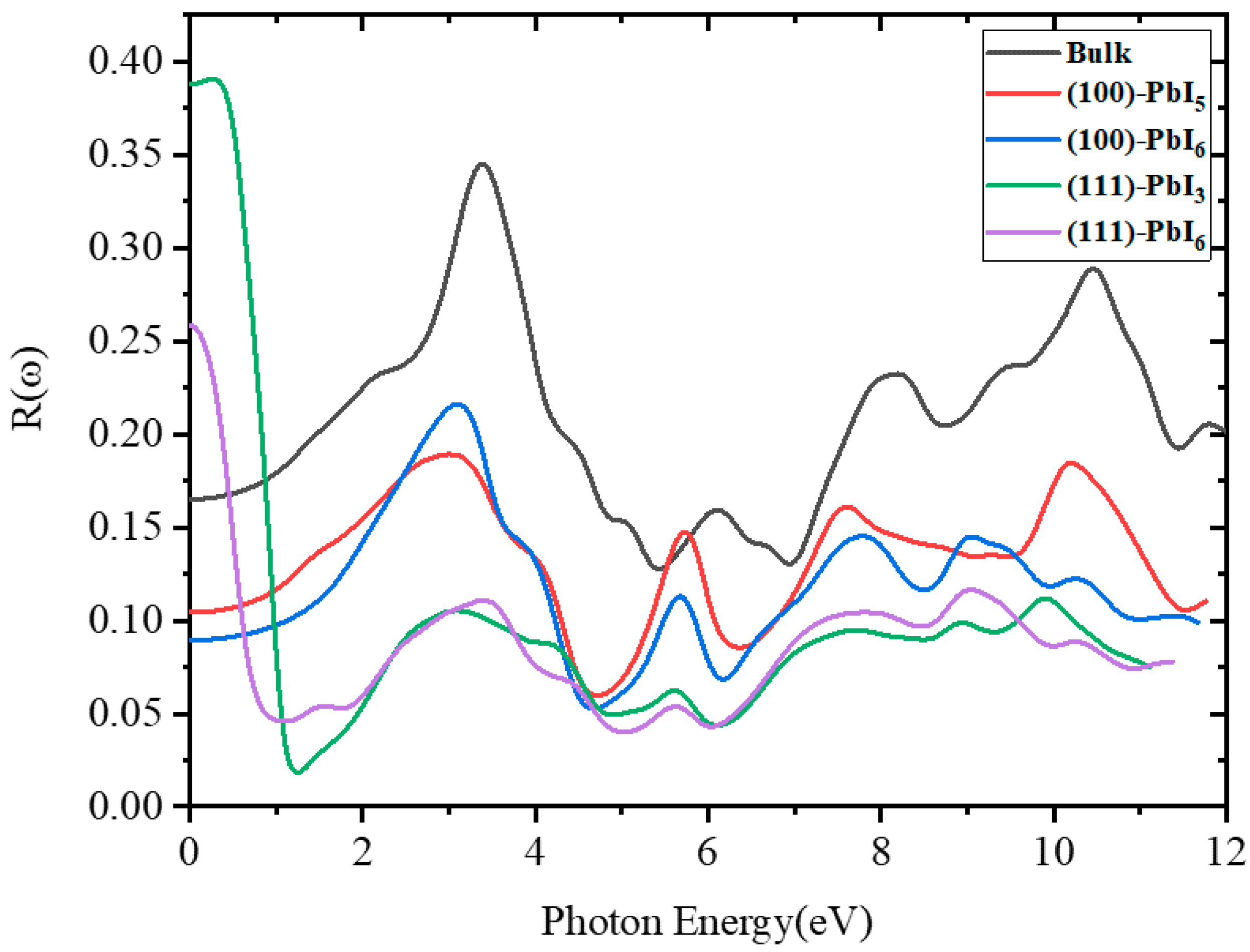
2.3.3. Reflectivity
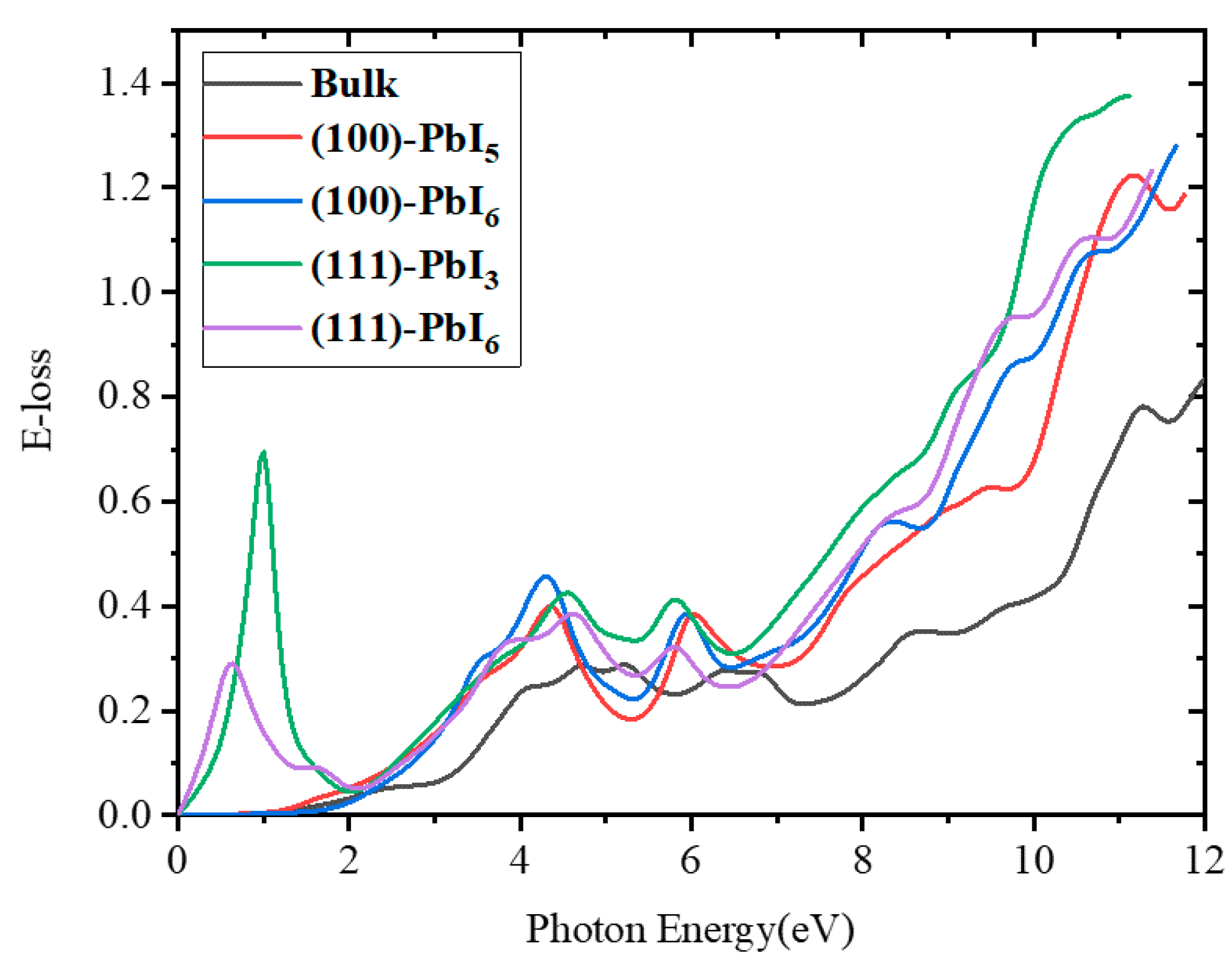
2.3.4. Energy Loss Spectrum
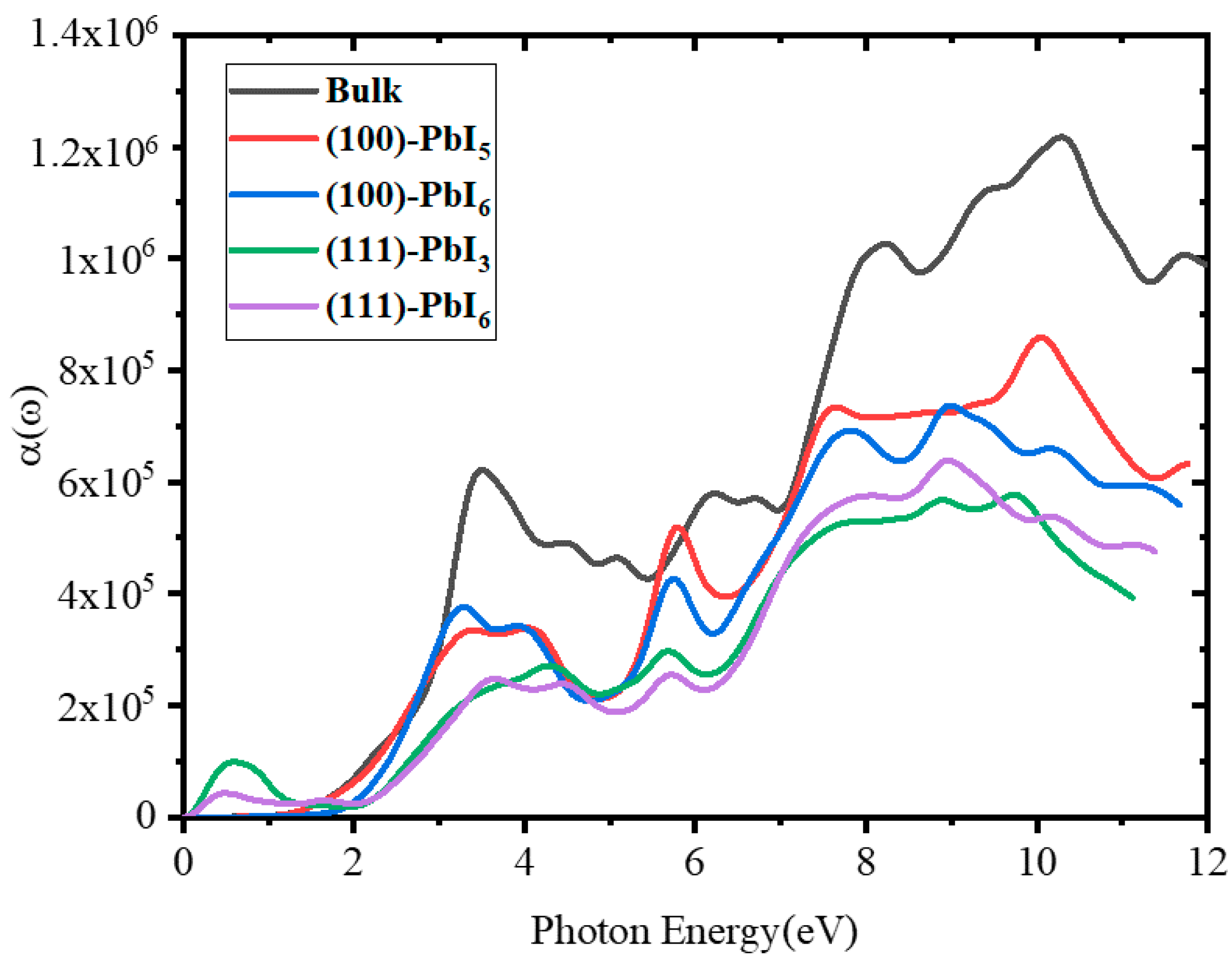
2.3.5. Absorption Coefficient
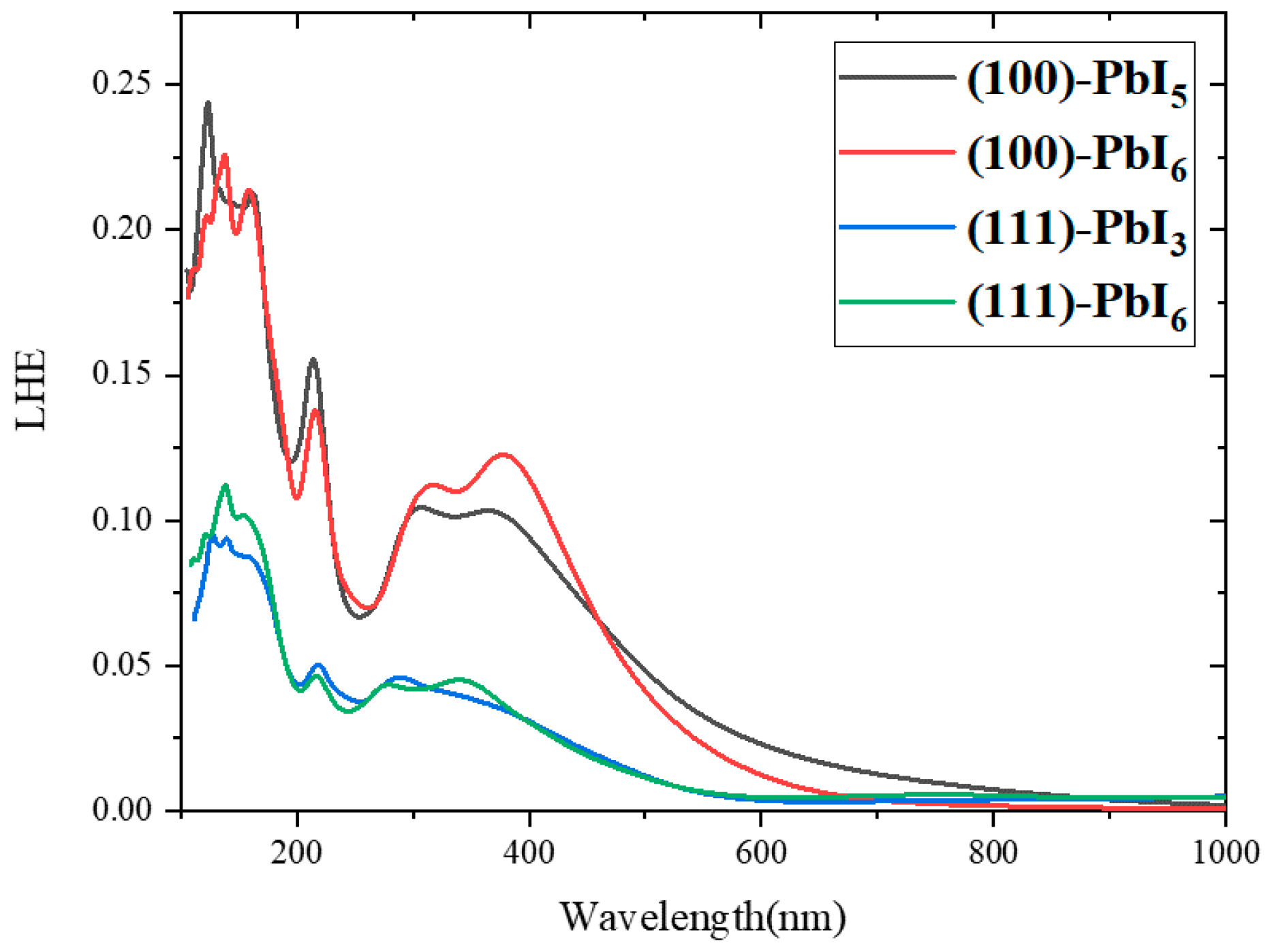
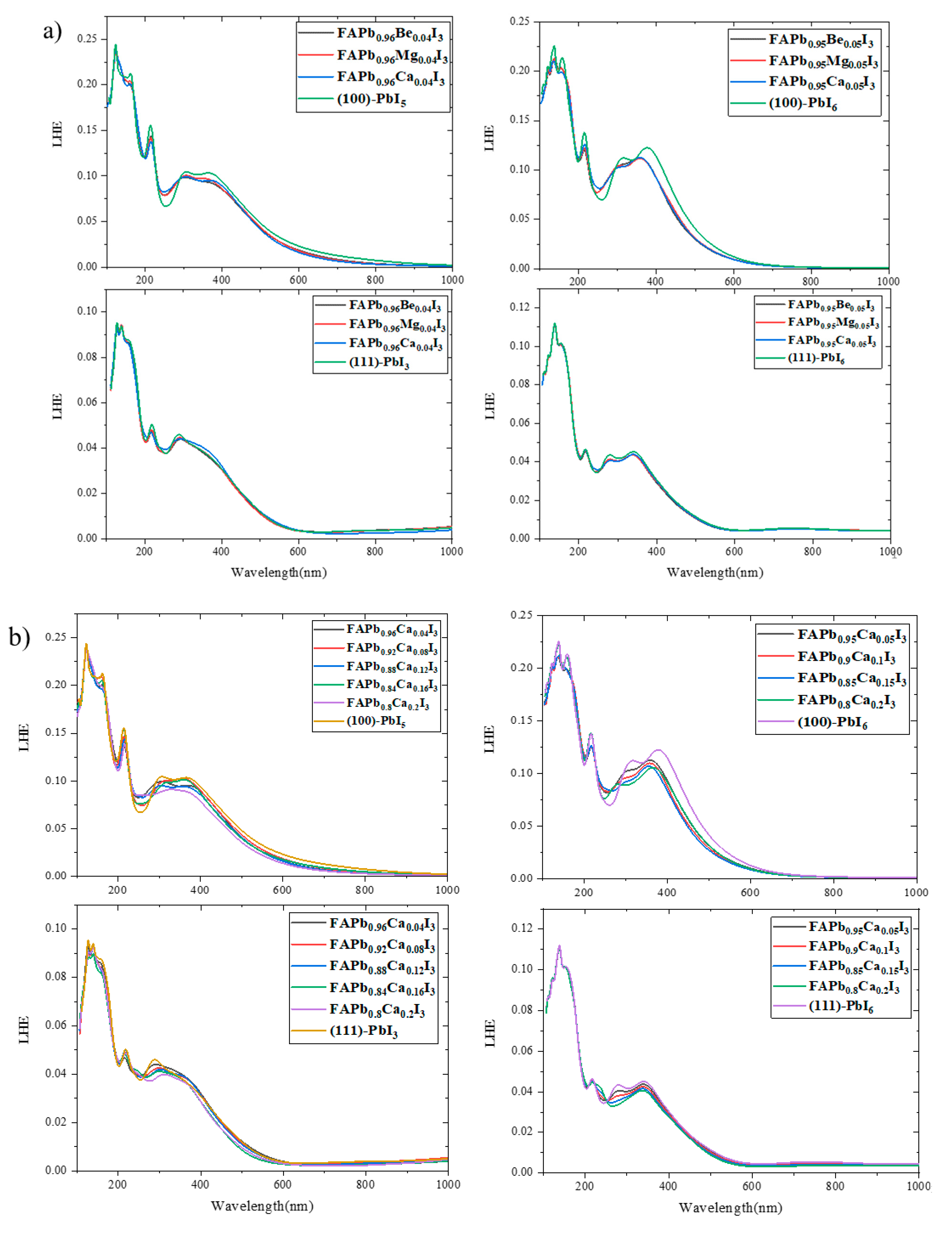
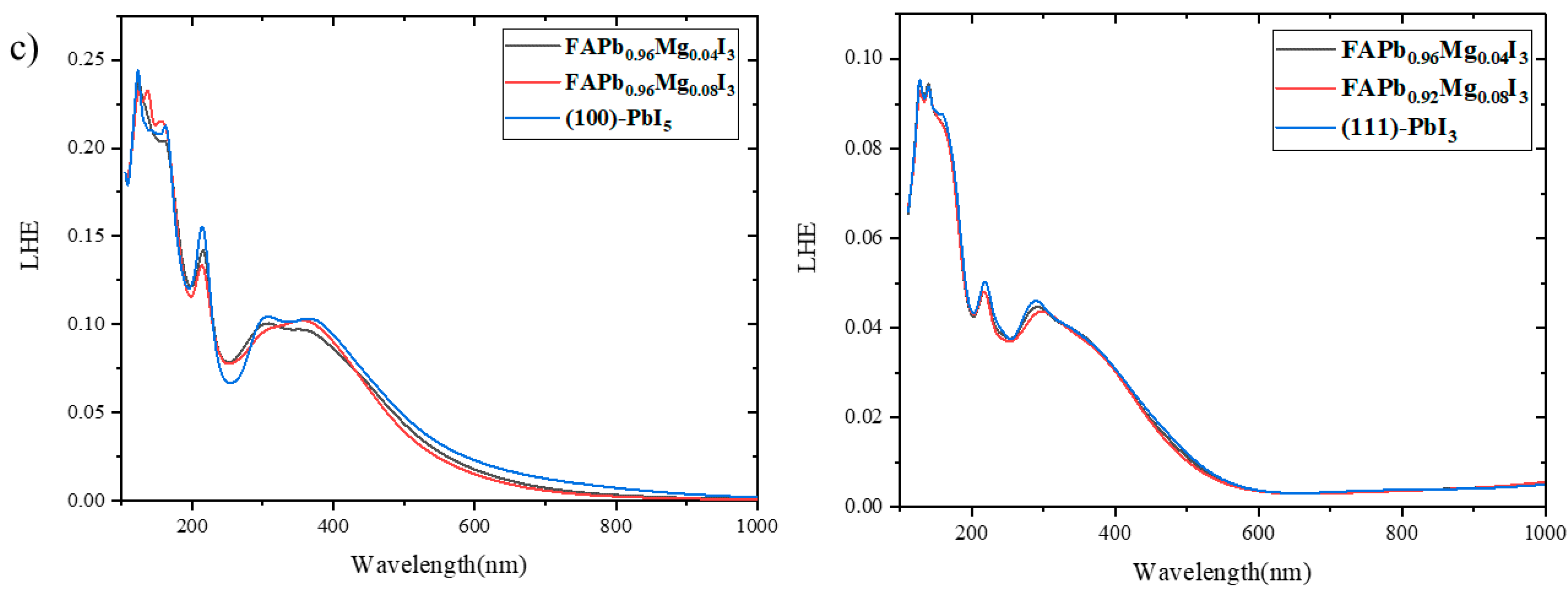
2.4. Light Harvesting Efficiency (LHE)
3. Computational Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Zhao, Y.; Zhu, K. Charge transport and recombination in perovskite (CH3NH3)PbI3 sensitized TiO2 solar cells. J. Phys. Chem. Lett. 2013, 4, 2880–2884. [Google Scholar] [CrossRef]
- O’Regan, B.C.; Barnes, P.R.; Li, X.; Law, C.; Palomares, E.; Marin-Beloqui, J.M. Optoelectronic studies of methylammonium lead iodide perovskite solar cells with mesoporous TiO2: Separation of electronic and chemical charge storage, understanding two recombination lifetimes, and the evolution of band offsets during J–V hysteresis. J. Am. Chem. Soc. 2015, 137, 5087–5099. [Google Scholar] [CrossRef]
- Stoumpos, C.C.; Malliakas, C.D.; Kanatzidis, M.G. Semiconducting tin and lead iodide perovskites with organic cations: Phase transitions, high mobilities, and near-infrared photoluminescent properties. Inorg. Chem. 2013, 52, 9019–9038. [Google Scholar] [CrossRef] [PubMed]
- Efficiencies, B.R.C. National Renewable Energy Laboratory. (NREL) Publication Database. 2022. Available online: http://www.nrel.gov/pv/cell-efficiency.html (accessed on 24 November 2022).
- Yin, W.J.; Shi, T.; Yan, Y. Unique properties of halide perovskites as possible origins of the superior solar cell performance. Adv. Mater. 2014, 26, 4653–4658. [Google Scholar] [CrossRef]
- Lee, M.M.; Teuscher, J.; Miyasaka, T.; Murakami, T.N.; Snaith, H.J. Efficient hybrid solar cells based on meso-superstructured organometal halide perovskites. Science 2012, 338, 643–647. [Google Scholar] [CrossRef] [PubMed]
- Dong, Q.; Fang, Y.; Shao, Y.; Mulligan, P.; Qiu, J.; Cao, L.; Huang, J. Electron-hole diffusion lengths> 175 μm in solution-grown CH3NH3PbI3 single crystals. Science 2015, 347, 967–970. [Google Scholar] [CrossRef] [PubMed]
- Etgar, L.; Gao, P.; Xue, Z.; Peng, Q.; Chandiran, A.K.; Liu, B.; Nazeeruddin, M.K.; Grätzel, M. Mesoscopic CH3NH3PbI3/TiO2 heterojunction solar cells. J. Am. Chem. Soc. 2012, 134, 17396–17399. [Google Scholar] [CrossRef] [PubMed]
- Stranks, S.D.; Eperon, G.E.; Grancini, G.; Menelaou, C.; Alcocer, M.J.; Leijtens, T.; Herz, L.M.; Petrozza, A.; Snaith, H.J. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 2013, 342, 341–344. [Google Scholar] [CrossRef]
- Xing, G.; Mathews, N.; Sun, S.; Lim, S.S.; Lam, Y.M.; Grätzel, M.; Mhaisalkar, S.; Sum, T.C. Long-range balanced electron-and hole-transport lengths in organic-inorganic CH3NH3PbI3. Science 2013, 342, 344–347. [Google Scholar] [CrossRef]
- Liu, M.; Johnston, M.B.; Snaith, H.J. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 2013, 501, 395–398. [Google Scholar] [CrossRef]
- Rehman, W.; Milot, R.L.; Eperon, G.E.; Wehrenfennig, C.; Boland, J.L.; Snaith, H.J.; Johnston, M.B.; Herz, L.M. Charge-carrier dynamics and mobilities in formamidinium lead mixed-halide perovskites. Adv. Mater. 2015, 27, 7938–7944. [Google Scholar] [CrossRef] [PubMed]
- Eperon, G.E.; Stranks, S.D.; Menelaou, C.; Johnston, M.B.; Herz, L.M.; Snaith, H.J. Formamidinium lead trihalide: A broadly tunable perovskite for efficient planar heterojunction solar cells. Energy Environ. Sci. 2014, 7, 982–988. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Prochowicz, D.; Franckevičius, M.; Cieślak, A.; Zakeeruddin, S.; Grätzel, M.; Lewiński, J. Mechanosynthesis of the hybrid perovskite CH3NH3PbI3: Characterization and the corresponding solar cell efficiency. J. Mater. Chem. A 2015, 3, 20772–20777. [Google Scholar] [CrossRef]
- Yakunin, S.; Sytnyk, M.; Kriegner, D.; Shrestha, S.; Richter, M.; Matt, G.J.; Azimi, H.; Brabec, C.J.; Stangl, J.; Kovalenko, M.V. Detection of X-ray photons by solution-processed lead halide perovskites. Nat. Photonics 2015, 9, 444–449. [Google Scholar] [CrossRef]
- Bi, D.; Moon, S.-J.; Häggman, L.; Boschloo, G.; Yang, L.; Johansson, E.M.; Nazeeruddin, M.K.; Grätzel, M.; Hagfeldt, A. Using a two-step deposition technique to prepare perovskite (CH3NH3PbI3) for thin film solar cells based on ZrO2 and TiO2 mesostructures. RSC Adv. 2013, 3, 18762–18766. [Google Scholar] [CrossRef]
- Shirayama, M.; Kadowaki, H.; Miyadera, T.; Sugita, T.; Tamakoshi, M.; Kato, M.; Fujiseki, T.; Murata, D.; Hara, S.; Murakami, T.N. Optical transitions in hybrid perovskite solar cells: Ellipsometry, density functional theory, and quantum efficiency analyses for CH3NH3PbI3. Phys. Rev. Appl. 2016, 5, 014012. [Google Scholar] [CrossRef]
- Niu, G.; Guo, X.; Wang, L. Review of recent progress in chemical stability of perovskite solar cells. J. Mater. Chem. A 2015, 3, 8970–8980. [Google Scholar] [CrossRef]
- Conings, B.; Drijkoningen, J.; Gauquelin, N.; Babayigit, A.; D’Haen, J.; D’Olieslaeger, L.; Ethirajan, A.; Verbeeck, J.; Manca, J.; Mosconi, E. Intrinsic thermal instability of methylammonium lead trihalide perovskite. Adv. Energy Mater. 2015, 5, 1500477. [Google Scholar] [CrossRef]
- Leijtens, T.; Eperon, G.E.; Noel, N.K.; Habisreutinger, S.N.; Petrozza, A.; Snaith, H.J. Stability of metal halide perovskite solar cells. Adv. Energy Mater. 2015, 5, 1500963. [Google Scholar] [CrossRef]
- Berhe, T.A.; Su, W.-N.; Chen, C.-H.; Pan, C.-J.; Cheng, J.-H.; Chen, H.-M.; Tsai, M.-C.; Chen, L.-Y.; Dubale, A.A.; Hwang, B.-J. Organometal halide perovskite solar cells: Degradation and stability. Energy Environ. Sci. 2016, 9, 323–356. [Google Scholar] [CrossRef]
- Noh, J.H.; Im, S.H.; Heo, J.H.; Mandal, T.N.; Seok, S.I. Chemical management for colorful, efficient, and stable inorganic–organic hybrid nanostructured solar cells. Nano Lett. 2013, 13, 1764–1769. [Google Scholar] [CrossRef] [PubMed]
- Murugadoss, G.; Tanaka, S.; Mizuta, G.; Kanaya, S.; Nishino, H.; Umeyama, T.; Imahori, H.; Ito, S. Light stability tests of methylammonium and formamidinium Pb-halide perovskites for solar cell applications. Jpn. J. Appl. Phys. 2015, 54, 08KF08. [Google Scholar] [CrossRef]
- Leguy, A.M.; Hu, Y.; Campoy-Quiles, M.; Alonso, M.I.; Weber, O.J.; Azarhoosh, P.; Van Schilfgaarde, M.; Weller, M.T.; Bein, T.; Nelson, J. Reversible hydration of CH3NH3PbI3 in films, single crystals, and solar cells. Chem. Mater. 2015, 27, 3397–3407. [Google Scholar] [CrossRef]
- Yadav, P.; Prochowicz, D.; Alharbi, E.A.; Zakeeruddin, S.M.; Grätzel, M. Intrinsic and interfacial kinetics of perovskite solar cells under photo and bias-induced degradation and recovery. J. Mater. Chem. C 2017, 5, 7799–7805. [Google Scholar] [CrossRef]
- Baikie, T.; Fang, Y.; Kadro, J.M.; Schreyer, M.; Wei, F.; Mhaisalkar, S.G.; Graetzel, M.; White, T.J. Synthesis and crystal chemistry of the hybrid perovskite (CH3NH3)PbI3 for solid-state sensitised solar cell applications. J. Mater. Chem. A 2013, 1, 5628–5641. [Google Scholar] [CrossRef]
- Masi, S.; Echeverría-Arrondo, C.; Salim, K.M.M.; Ngo, T.T.; Mendez, P.F.; López-Fraguas, E.; Macias-Pinilla, D.F.; Planelles, J.; Climente, J.I.; Mora-Seró, I. Chemi-Structural Stabilization of Formamidinium Lead Iodide Perovskite by Using Embedded Quantum Dots. ACS Energy Lett. 2020, 5, 418–427. [Google Scholar] [CrossRef]
- Rühle, S. Tabulated values of the Shockley–Queisser limit for single junction solar cells. Sol. Energy 2016, 130, 139–147. [Google Scholar] [CrossRef]
- Koh, T.M.; Fu, K.; Fang, Y.; Chen, S.; Sum, T.; Mathews, N.; Mhaisalkar, S.G.; Boix, P.P.; Baikie, T. Formamidinium-containing metal-halide: An alternative material for near-IR absorption perovskite solar cells. J. Phys. Chem. C 2014, 118, 16458–16462. [Google Scholar] [CrossRef]
- Smecca, E.; Numata, Y.; Deretzis, I.; Pellegrino, G.; Boninelli, S.; Miyasaka, T.; La Magna, A.; Alberti, A. Stability of solution-processed MAPbI 3 and FAPbI 3 layers. Phys. Chem. Chem. Phys. 2016, 18, 13413–13422. [Google Scholar] [CrossRef]
- Lee, J.W.; Seol, D.J.; Cho, A.N.; Park, N.G. High-efficiency perovskite solar cells based on the black polymorph of HC(NH2)2PbI3. Adv. Mater. 2014, 26, 4991–4998. [Google Scholar] [CrossRef]
- Pang, S.; Hu, H.; Zhang, J.; Lv, S.; Yu, Y.; Wei, F.; Qin, T.; Xu, H.; Liu, Z.; Cui, G. NH2CH=NH2PbI3: An alternative organolead iodide perovskite sensitizer for mesoscopic solar cells. Chem. Mater. 2014, 26, 1485–1491. [Google Scholar] [CrossRef]
- Travis, W.; Glover, E.N.K.; Bronstein, H.; Scanlon, D.O.; Palgrave, R.G. On the application of the tolerance factor to inorganic and hybrid halide perovskites: A revised system. Chem. Sci. 2016, 7, 4548–4556. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Yang, M.; Park, J.S.; Wei, S.H.; Berry, J.J.; Zhu, K. Stabilizing Perovskite Structures by Tuning Tolerance Factor: Formation of Formamidinium and Cesium Lead Iodide Solid-State Alloys. Chem. Mater. 2016, 28, 284–292. [Google Scholar] [CrossRef]
- Targhi, F.F.; Jalili, Y.S.; Kanjouri, F. MAPbI3 and FAPbI3 perovskites as solar cells: Case study on structural, electrical and optical properties. Results Phys. 2018, 10, 616–627. [Google Scholar] [CrossRef]
- Ma, F.; Li, J.; Li, W.; Lin, N.; Wang, L.; Qiao, J. Stable α/δ phase junction of formamidinium lead iodide perovskites for enhanced near-infrared emission. Chem. Sci. 2016, 8, 800–805. [Google Scholar] [CrossRef]
- Gholipour, S.; Ali, A.M.; Correa-Baena, J.P.; Turren-Cruz, S.H.; Tajabadi, F.; Tress, W.; Taghavinia, N.; Grätzel, M.; Abate, A.; De Angelis, F.; et al. Globularity-Selected Large Molecules for a New Generation of Multication Perovskites. Adv. Mater. 2017, 29, 1702005. [Google Scholar] [CrossRef]
- Yi, C.; Luo, J.; Meloni, S.; Boziki, A.; Ashari-Astani, N.; Grätzel, C.; Zakeeruddin, S.M.; Röthlisberger, U.; Grätzel, M. Entropic stabilization of mixed A-cation ABX3 metal halide perovskites for high performance perovskite solar cells. Energy Environ. Sci. 2016, 9, 656–662. [Google Scholar] [CrossRef]
- Saliba, M.; Matsui, T.; Seo, J.Y.; Domanski, K.; Correa-Baena, J.P.; Nazeeruddin, M.K.; Zakeeruddin, S.M.; Tress, W.; Abate, A.; Hagfeldt, A.; et al. Cesium-containing triple cation perovskite solar cells: Improved stability, reproducibility and high efficiency. Energy Environ. Sci. 2016, 9, 1989–1997. [Google Scholar] [CrossRef]
- Fabini, D.H.; Stoumpos, C.C.; Laurita, G.; Kaltzoglou, A.; Kontos, A.G.; Falaras, P.; Kanatzidis, M.G.; Seshadri, R. Reentrant Structural and Optical Properties and Large Positive Thermal Expansion in Perovskite Formamidinium Lead Iodide. Angew. Chem. Int. Ed. 2016, 55, 15392–15396. [Google Scholar] [CrossRef]
- Wang, J.T.F.; Fu, X.N.; Wang, J.T.F. First-principles analysis of the structural, electronic, and elastic properties of cubic organic-inorganic perovskite HC(NH2)2PbI3. Chin. Phys. B 2017, 26, 106301. [Google Scholar] [CrossRef]
- Guo, L.; Tang, G.; Hong, J. Mechanical Properties of Formamidinium Halide Perovskites FABX3 (FA=CH(NH2)2; B=Pb, Sn; X=Br, I) by First-Principles Calculations. Chin. Phys. Lett. 2019, 36, 056201. [Google Scholar] [CrossRef]
- Weller, M.T.; Weber, O.J.; Frost, J.M.; Walsh, A. Cubic Perovskite Structure of Black Formamidinium Lead Iodide, α-[HC(NH2)2]PbI3, at 298 K. J. Phys. Chem. Lett. 2015, 6, 3209–3212. [Google Scholar] [CrossRef]
- Han, Q.; Bae, S.; Sun, P.; Hsieh, Y.Y.; Yang, M.; Rim, Y.S.; Zhao, H.; Chen, Q.; Shi, W.; Li, G.; et al. Single crystal formamidinium lead iodide (FAPbI3); insight into the stuctural, optical and electrical properties. Adv. Mater 2016, 28, 2253–2258. [Google Scholar] [CrossRef]
- Pellet, N.; Gao, P.; Gregori, G.; Yang, T.Y.; Nazeeruddin, M.K.; Maier, J.; Grätzel, M. Mixed-organic-cation Perovskite photovoltaics for enhanced solar-light harvesting. Angew. Chem. 2014, 126, 3215–3221. [Google Scholar] [CrossRef]
- Yang, W.S.; Noh, J.H.; Jeon, N.J.; Kim, Y.C.; Ryu, S.; Seo, J.; Seok, S.I. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science 2015, 348, 1234–1237. [Google Scholar] [CrossRef]
- Xu, Z.; Zhao, Y.; Zhang, J.; Chen, K.; Brabec, C.J.; Feng, Y. Phase diagram and stability of mixed-cation lead iodide perovskites: A theory and experiment combined study. Phys. Rev. Mater. 2020, 4, 095401. [Google Scholar] [CrossRef]
- Charles, B.; Dillon, J.; Weber, O.J.; Islam, M.S.; Weller, M.T. Understanding the stability of mixed A-cation lead iodide perovskites. J. Mater. Chem. A 2017, 5, 22495–22499. [Google Scholar] [CrossRef]
- Syzgantseva, O.A.; Saliba, M.; Grätzel, M.; Rothlisberger, U. Stabilization of the perovskite phase of formamidinium lead triiodide by methylammonium, Cs, and/or Rb doping. J. Phys. Chem. Lett. 2017, 8, 1191–1196. [Google Scholar] [CrossRef]
- Kim, M.; Kim, G.-H.; Lee, T.K.; Choi, I.W.; Choi, H.W.; Jo, Y.; Yoon, Y.J.; Kim, J.W.; Lee, J.; Huh, D. Methylammonium chloride induces intermediate phase stabilization for efficient perovskite solar cells. Joule 2019, 3, 2179–2192. [Google Scholar] [CrossRef]
- Liu, T.; Zhou, Y.; Li, Z.; Zhang, L.; Ju, M.G.; Luo, D.; Yang, Y.; Yang, M.; Kim, D.H.; Yang, W. Stable formamidinium-based perovskite solar cells via in situ grain encapsulation. Adv. Energy Mater. 2018, 8, 1800232. [Google Scholar] [CrossRef]
- Chen, Y.; Li, N.; Wang, L.; Li, L.; Xu, Z.; Jiao, H.; Liu, P.; Zhu, C.; Zai, H.; Sun, M. Impacts of alkaline on the defects property and crystallization kinetics in perovskite solar cells. Nat. Commun. 2019, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Eom, T.; Ha, Y.-S.; Hong, K.-H.; Kim, H. Thermodynamics of Multicomponent Perovskites: A Guide to Highly Efficient and Stable Solar Cell Materials. Chem. Mater. 2020, 32, 4265–4272. [Google Scholar] [CrossRef]
- Monika; Pachori, S.; Kumari, S.; Verma, A.S. An emerging high performance photovoltaic device with mechanical stability constants of hybrid (HC(NH2)2PbI3) perovskite. J. Mater. Sci. Mater. Electron. 2020, 31, 18004–18017. [Google Scholar] [CrossRef]
- Filip, M.R.; Giustino, F. Computational screening of homovalent lead substitution in organic–inorganic halide perovskites. J. Phys. Chem. C 2016, 120, 166–173. [Google Scholar] [CrossRef]
- Suzuki, A.; Oku, T. Effects of mixed-valence states of Eu-doped FAPbI3 perovskite crystals studied by first-principles calculation. Mater. Adv. 2021, 2, 2609–2616. [Google Scholar] [CrossRef]
- Huang, H.-M.; Cao, M.-L.; Jiang, Z.-Y.; Xiong, Y.-C.; Zhang, X.; Luo, S.-J.; Laref, A. High spin polarization in formamidinium transition metal iodides: First principles prediction of novel half-metals and spin gapless semiconductors. Phys. Chem. Chem. Phys. 2019, 21, 16213–16222. [Google Scholar] [CrossRef]
- Gualdrón-Reyes, A.F.; Macias-Pinilla, D.F.; Masi, S.; Echeverría-Arrondo, C.; Agouram, S.; Muñoz-Sanjosé, V.; Rodríguez-Pereira, J.; Macak, J.M.; Mora-Seró, I. Engineering Sr-doping for enabling long-term stable FAPb1−xSrxI3quantum dots with 100% photoluminescence quantum yield. J. Mater. Chem. C 2021, 9, 1555–1566. [Google Scholar] [CrossRef]
- Zhao, W.; Shi, J.; Tian, C.; Wu, J.; Li, H.; Li, Y.; Yu, B.; Luo, Y.; Wu, H.; Xie, Z. CdS Induced Passivation toward High Efficiency and Stable Planar Perovskite Solar Cells. ACS Appl. Mater. Interfaces 2021, 13, 9771–9780. [Google Scholar] [CrossRef]
- Qian, J.; Xu, B.; Tian, W. A comprehensive theoretical study of halide perovskites ABX3. Org. Electron. 2016, 37, 61–73. [Google Scholar] [CrossRef]
- Roknuzzaman, M.; Alarco, J.A.; Wang, H.; Du, A.; Tesfamichael, T.; Ostrikov, K.K. Ab initio atomistic insights into lead-free formamidinium based hybrid perovskites for photovoltaics and optoelectronics. Comput. Mater. Sci. 2019, 169, 109118. [Google Scholar] [CrossRef]
- Gao, L.-K.; Tang, Y.-L.; Diao, X.-F. Theoretical study on photoelectric properties of FAPbI3 doped with Ge. Mater. Res. Express 2020, 7, 116201. [Google Scholar] [CrossRef]
- Eperon, G.E.; Leijtens, T.; Bush, K.A.; Prasanna, R.; Green, T.; Wang, J.T.-W.; McMeekin, D.P.; Volonakis, G.; Milot, R.L.; May, R. Perovskite-perovskite tandem photovoltaics with optimized band gaps. Science 2016, 354, 861–865. [Google Scholar] [CrossRef]
- Diao, X.-F.; Tang, Y.-L.; Xie, Q. First-principles study on optic-electronic properties of doped formamidinium lead iodide perovskite. Chin. Phys. B 2019, 28, 017802. [Google Scholar] [CrossRef]
- Ali, R.; Zhu, Z.-G.; Yan, Q.-B.; Zheng, Q.-R.; Su, G.; Laref, A.; Saraj, C.S.; Guo, C. Compositional engineering study of lead-free hybrid perovskites for solar cell applications. ACS Appl. Mater. Interfaces 2020, 12, 49636–49647. [Google Scholar] [CrossRef]
- Xue, J.; Wang, R.; Wang, K.-L.; Wang, Z.-K.; Yavuz, I.; Wang, Y.; Yang, Y.; Gao, X.; Huang, T.; Nuryyeva, S. Crystalline liquid-like behavior: Surface-induced secondary grain growth of photovoltaic perovskite thin film. J. Am. Chem. Soc. 2019, 141, 13948–13953. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, C.; Li, G.; Dai, P.; Yang, L.; Liu, R.; Pan, B. Effect of cation replacement on the phase stability of formamidinium lead iodide perovskite. J. Chem. Phys. 2019, 151, 134104. [Google Scholar] [CrossRef]
- Phung, N.; Félix, R.; Meggiolaro, D.; Al-Ashouri, A.; Sousa e Silva, G.; Hartmann, C.; Hidalgo, J.; Köbler, H.; Mosconi, E.; Lai, B. The doping mechanism of halide perovskite unveiled by alkaline earth metals. J. Am. Chem. Soc. 2020, 142, 2364–2374. [Google Scholar] [CrossRef]
- Yang, W.; Tang, Y.; Zhang, Q.; Wang, L.; Song, B.; Wong, C. Reducing Pb concentration in α-CsPbI3 based perovskite solar cell materials via alkaline-earth metal doping: A DFT computational study. Ceram. Int. 2017, 43, 13101–13112. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, J.; Bakr, O.M.; Sun, H.-T. Metal-doped lead halide perovskites: Synthesis, properties, and optoelectronic applications. Chem. Mater. 2018, 30, 6589–6613. [Google Scholar] [CrossRef]
- Goldschmidt, V.M. Die gesetze der krystallochemie. Naturwissenschaften 1926, 14, 477–485. [Google Scholar] [CrossRef]
- RaeisianAsl, M.; Panahi, S.F.K.S.; Jamaati, M.; Tafreshi, S.S. A review on theoretical studies of structural and optoelectronic properties of FA-based perovskite materials with a focus on FAPbI3. Int. J. Energy Res. 2022, 46, 13117–13151. [Google Scholar] [CrossRef]
- Kontos, A.G.; Manolis, G.K.; Kaltzoglou, A.; Palles, D.; Kamitsos, E.I.; Kanatzidis, M.G.; Falaras, P. Halogen–NH2+ Interaction, Temperature-Induced Phase Transition, and Ordering in (NH2CHNH2) PbX3 (X= Cl, Br, I) Hybrid Perovskites. J. Phys. Chem. C 2020, 124, 8479–8487. [Google Scholar] [CrossRef]
- Li, D.; Meng, J.; Niu, Y.; Zhao, H.; Liang, C. Understanding the low-loss mechanism of general organic–inorganic perovskites from first-principles calculation. Chem. Phys. Lett. 2015, 627, 13–19. [Google Scholar] [CrossRef]
- Zhao, X.-G.; Dalpian, G.M.; Wang, Z.; Zunger, A. Polymorphous nature of cubic halide perovskites. Phys. Rev. B 2020, 101, 155137. [Google Scholar] [CrossRef]
- Espinosa, N.; Serrano-Luján, L.; Urbina, A.; Krebs, F.C. Solution and vapour deposited lead perovskite solar cells: Ecotoxicity from a life cycle assessment perspective. Sol. Energy Mater. Sol. Cells 2015, 137, 303–310. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.; Kvasnicka, D.; Luitz, J. wien2k. An Augmented Plane Wave+ Local Orbitals Program for Calculating Crystal Properties; Vienna University of Technology: Vienna, Austria, 2001; Volume 60, ISBN 3-9501031-1-2. [Google Scholar]
- Lovell, R. Application of Kramers-Kronig relations to the interpretation of dielectric data. J. Phys. C: Solid State Phys. 1974, 7, 4378. [Google Scholar] [CrossRef]
- Kato, M.; Fujiseki, T.; Miyadera, T.; Sugita, T.; Fujimoto, S.; Tamakoshi, M.; Chikamatsu, M.; Fujiwara, H. Universal rules for visible-light absorption in hybrid perovskite materials. J. Appl. Phys. 2017, 121, 115501. [Google Scholar] [CrossRef]
- El-Ghtami, H.; Laref, A.; Laref, S. Electronic and optical behaviors of methylammonium and formamidinium lead trihalide perovskite materials. J. Mater. Sci. Mater. Electron. 2019, 30, 711–720. [Google Scholar] [CrossRef]
- Leguy, A.M.; Azarhoosh, P.; Alonso, M.I.; Campoy-Quiles, M.; Weber, O.J.; Yao, J.; Bryant, D.; Weller, M.T.; Nelson, J.; Walsh, A. Experimental and theoretical optical properties of methylammonium lead halide perovskites. Nanoscale 2016, 8, 6317–6327. [Google Scholar] [CrossRef]
- Lopper, P.; Stuckellger, M.; Niesen, B.; Werner, J.; Filpie, M.; Moon, S.; Yum, J.; Topic, M.; Wolf, D.; Ballif, C. Complex refractive index spectra of CH3NH3PbI3 perovskite thin films determined by spectroscopic ellipsometry and spectrophotometry. Phys. Chem. Lett. 2015, 6, 66–71. [Google Scholar] [CrossRef] [PubMed]
- Wetzelaer, G.J.A.; Scheepers, M.; Sempere, A.M.; Momblona, C.; Ávila, J.; Bolink, H.J. Trap-assisted non-radiative recombination in organic–inorganic perovskite solar cells. Adv. Mater. 2015, 27, 1837–1841. [Google Scholar] [CrossRef] [PubMed]
- Korshunova, K.; Winterfeld, L.; Beenken, W.J.; Runge, E. Thermodynamic stability of mixed Pb: Sn methyl-ammonium halide perovskites. Phys. Status Solidi (B) 2016, 253, 1907–1915. [Google Scholar] [CrossRef]
- Choi, Y.; Seol, M.; Kim, W.; Yong, K. Chemical bath deposition of stoichiometric CdSe quantum dots for efficient quantum-dot-sensitized solar cell application. J. Phys. Chem. C 2014, 118, 5664–5670. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Haruyama, J.; Sodeyama, K.; Han, L.; Tateyama, Y. Termination dependence of tetragonal CH3NH3PbI3 surfaces for perovskite solar cells. J. Phys. Chem. Lett. 2014, 5, 2903–2909. [Google Scholar] [CrossRef]

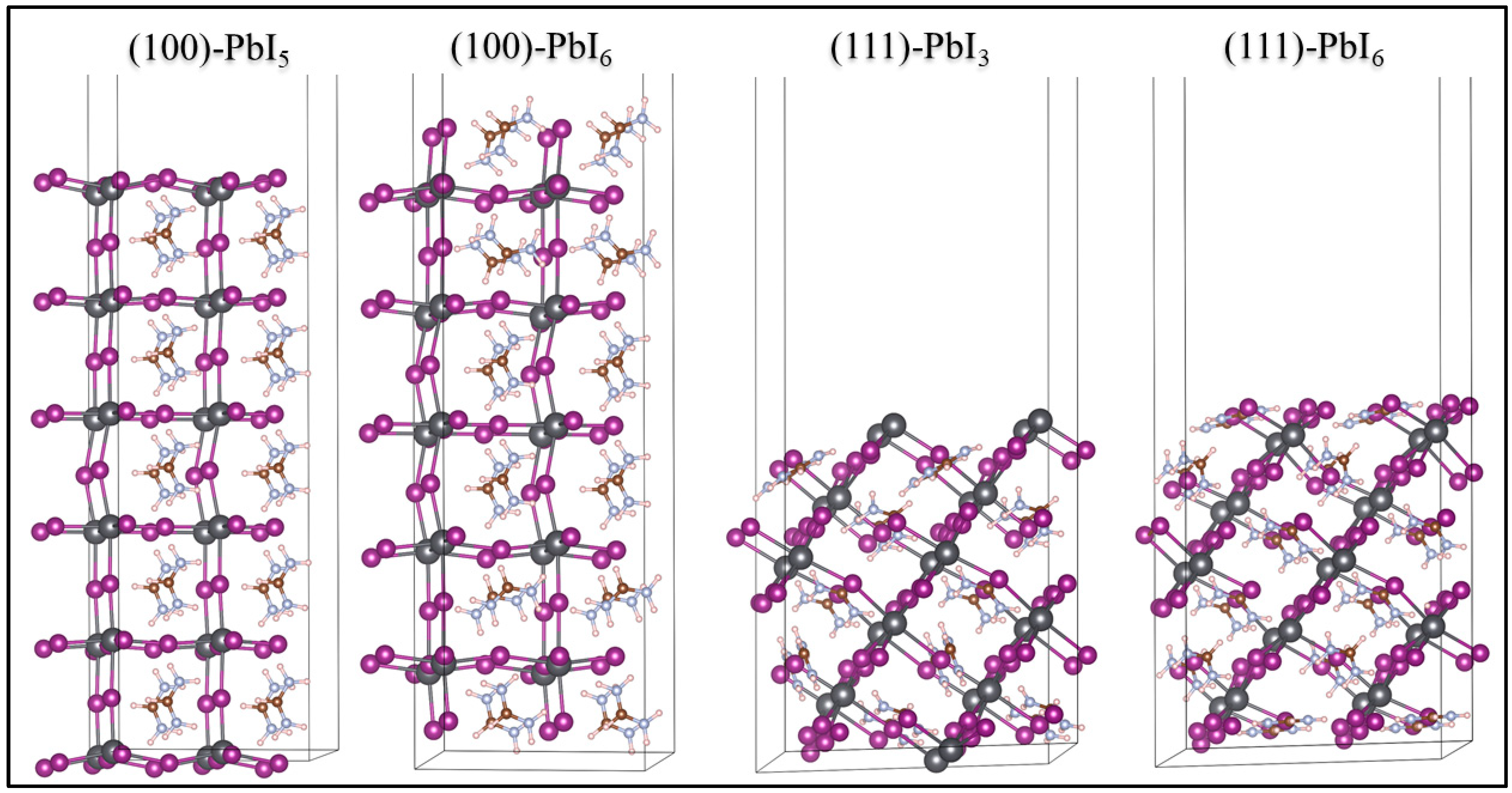
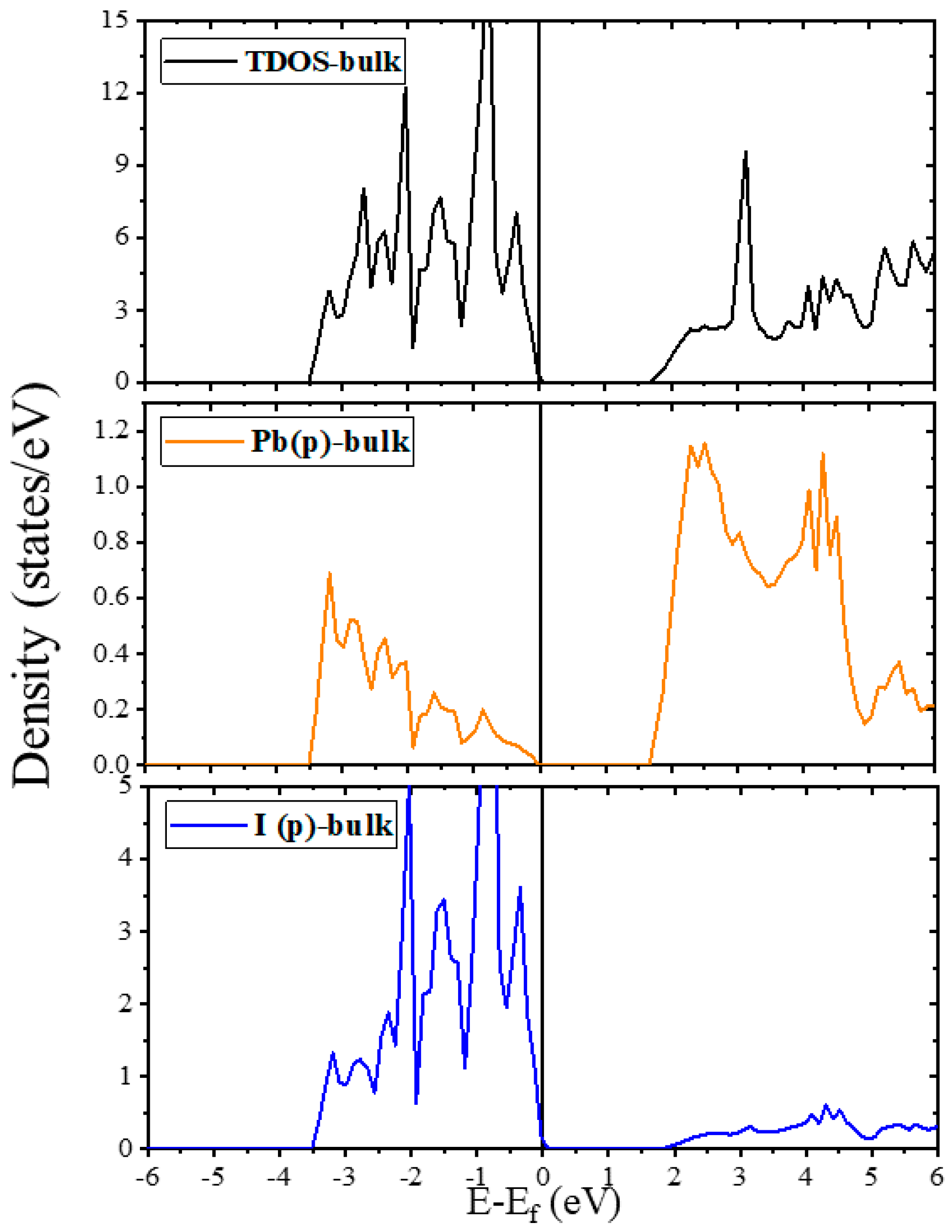
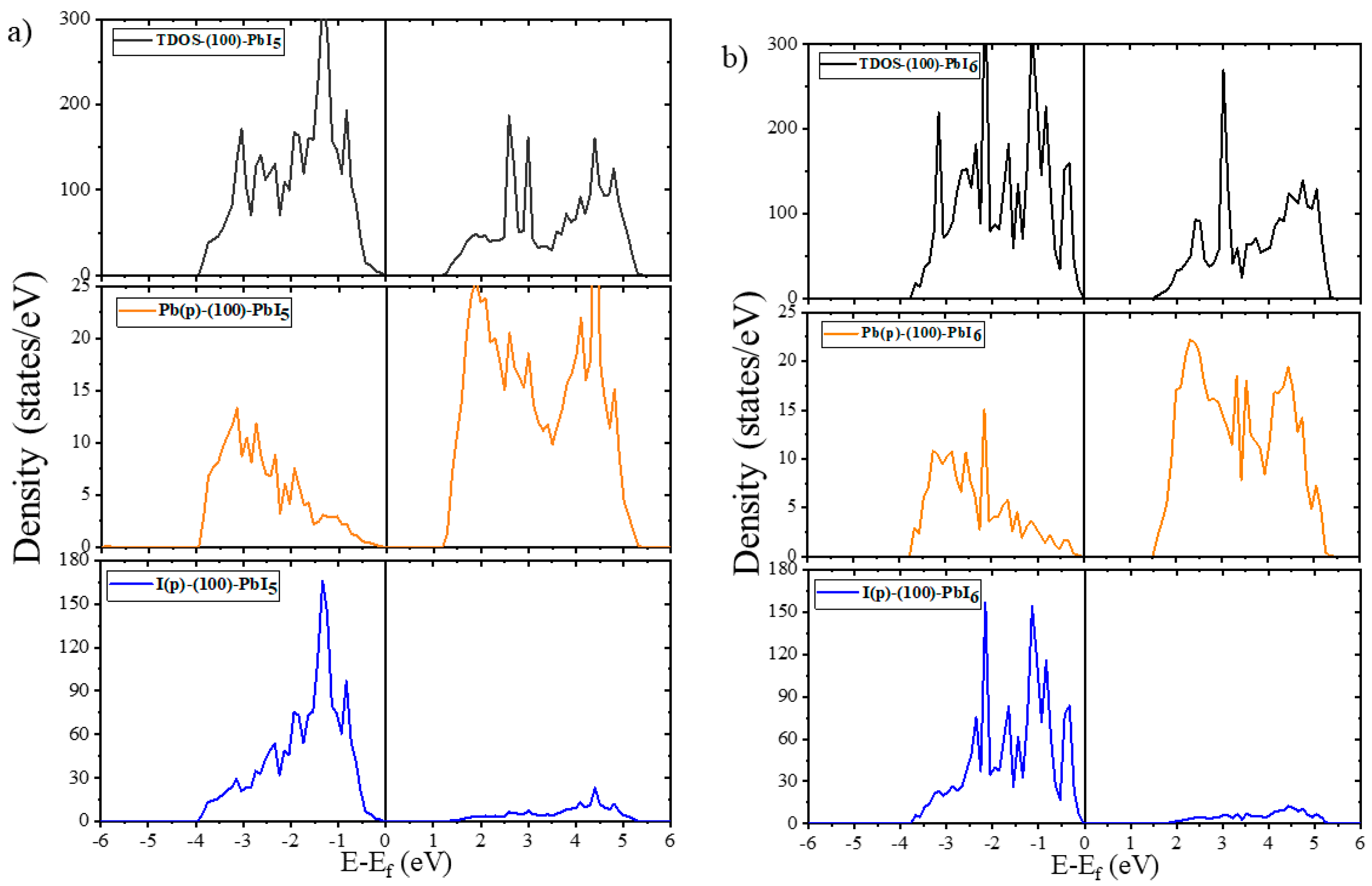
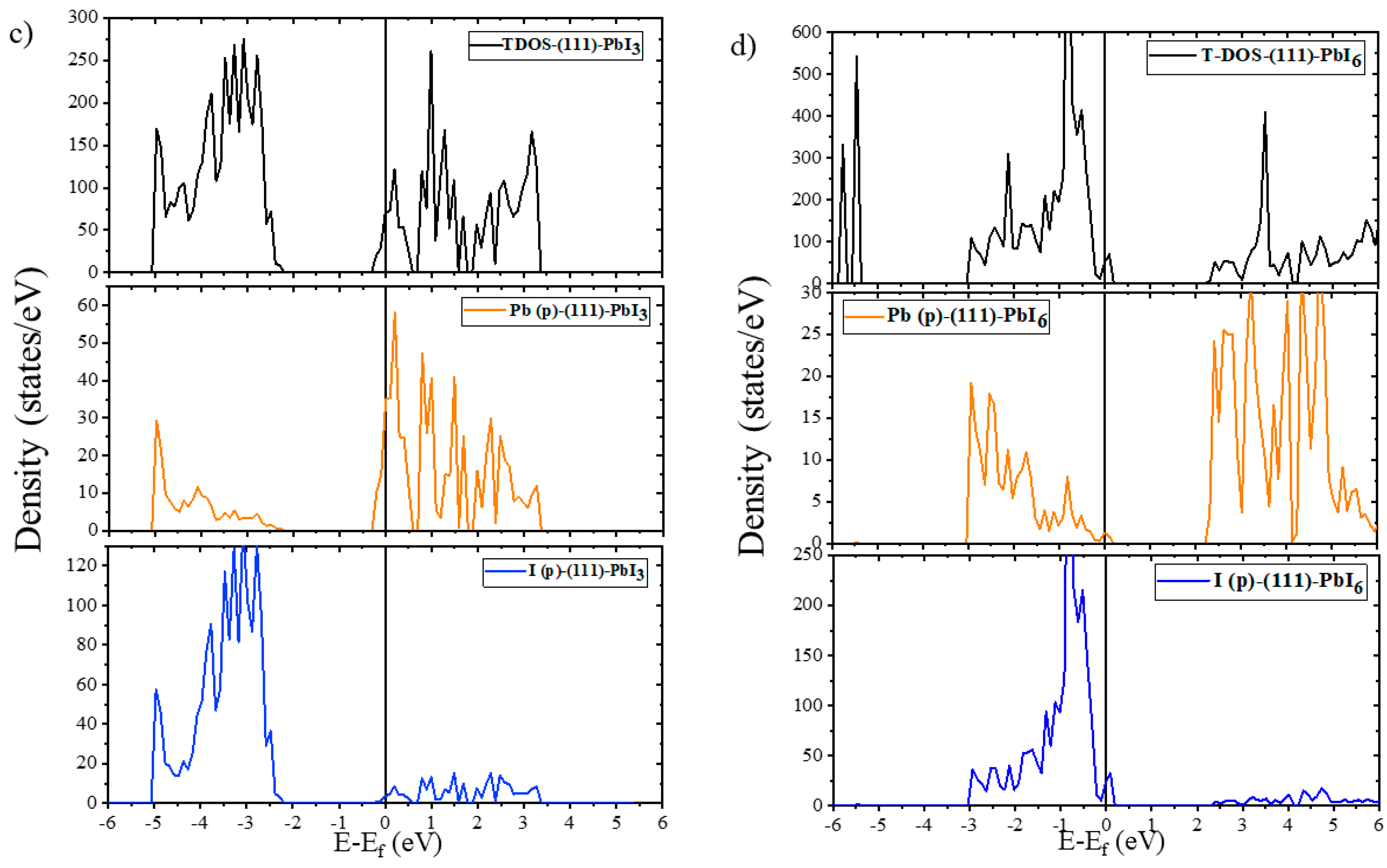
| Surfaces | (eV) | (eV) | (eV/A°2) | (eV/A°2) | (eV/A°2) |
|---|---|---|---|---|---|
| (1 0 0)-PbI5 | −1162.813 | −1165.512 | 0.059 | −0.009 | 0.051 |
| (1 0 0)-PbI6 | −1315.501 | −1318.417 | 0.059 | −0.009 | 0.050 |
| (1 1 1)-PbI3 | −1129.200 | −1136.183 | 0.048 | −0.011 | 0.037 |
| (1 1 1)-PbI6 | −1325.358 | −1331.876 | 0.048 | −0.010 | 0.038 |
| (100)-PbI5 and (111)-PbI3 | (100)-PbI6 and (111)-PbI6 | ||||
|---|---|---|---|---|---|
| Number-Percentage of the Doped Metals | Doped Surface | t | Number-Percentage of the Doped Metals | Doped Surface | t |
| 1 atom-0.04Be | FAPb0.96Be0.04I3 | 0.996 | 1 atom-0.05Be | FAPb0.95Be0.05I3 | 0.997 |
| 1 atom-0.04Mg | FAPb0.96Mg0.04I3 | 0.992 | 1 atom-0.05Mg | FAPb0.95Mg0.05I3 | 0.993 |
| 2 atoms-0.08Mg | FAPb0.92Mg0.08I3 | 0.998 | |||
| 1 atom-0.04Ca | FAPb0.96Ca0.04I3 | 0.989 | 1 atom-0.05Ca | FAPb0.95Ca0.05I3 | 0.989 |
| 2 atoms-0.08Ca | FAPb0.92Ca0.08I3 | 0.991 | 2 atoms-0.1Ca | FAPb0.9Ca0.1I3 | 0.992 |
| 3 atoms-0.12Ca | FAPb0.88Ca0.12I3 | 0.993 | 3 atoms-0.15Ca | FAPb0.85Ca0.15I3 | 0.995 |
| 4 atoms-0.16Ca | FAPb0.84Ca0.16I3 | 0.996 | 4 atoms-0.2Ca | FAPb0.8Ca0.2I3 | 0.998 |
| 5 atoms-0.2Ca | FAPb0.8Ca0.2I3 | 0.998 | |||
| Structure | Bandgap | Valence Band | Conduction Band |
|---|---|---|---|
| Bulk | 1.689, 1.7 [76], 1.72 [61], 1.75 [77], 1.58 [75], 1.53 [74] | −0.026 | 1.663 |
| (1 1 1)-PbI3 | 0 | –2.284 | −0.299 |
| FAPb0.96Be0.04I3 | 0 | −2.282 | −0.293 |
| FAPb0.96Mg0.04I3 | 0 | −2.208 | −0.318 |
| FAPb0.92Mg0.08I3 | 0 | −2.315 | −0.323 |
| FAPb0.96Ca0.04I3 | 0 | −2.201 | −0.305 |
| FAPb0.92Ca0.08I3 | 0 | −2.265 | −0.297 |
| FAPb0.88Ca0.12I3 | 0 | −2.204 | −0.334 |
| FAPb0.84Ca0.16I3 | 0 | −2.374 | −0.310 |
| FAPb0.8Ca0.2I3 | 0 | −2.275 | −0.319 |
| (1 1 1)-PbI6 | 0 | 0.088 | 2.208 |
| FAPb0.95Be0.05I3 | 0 | 0.093 | 2.210 |
| FAPb0.95Mg0.05I3 | 0 | 0.074 | 2.192 |
| FAPb0.95Ca0.05I3 | 0 | 0.023 | 2.187 |
| FAPb0.9Ca0.1I3 | 0 | 0.017 | 2.281 |
| FAPb0.85Ca0.15I3 | 0 | 0.052 | 2.214 |
| FAPb0.8Ca0.2I3 | 0 | 0.057 | 2.216 |
| (1 0 0)-PbI5 | 1.309 | −0.126 | 1.183 |
| FAPb0.96Be0.04I3 | 1.405 | −0.025 | 1.380 |
| FAPb0.96Mg0.04I3 | 1.409 | −0.126 | 1.283 |
| FAPb0.92Mg0.08I3 | 1.408 | −0.050 | 1.358 |
| FAPb0.96Ca0.04I3 | 1.459 | −0.130 | 1.329 |
| FAPb0.92Ca0.08I3 | 1.350 | −0.026 | 1.324 |
| FAPb0.88Ca0.12I3 | 1.365 | −0.053 | 1.312 |
| FAPb0.84Ca0.16I3 | 1.355 | −0.130 | 1.225 |
| FAPb0.8Ca0.2I3 | 1.468 | −0.052 | 1.416 |
| (1 0 0)-PbI6 | 1.623 | −0.127 | 1.496 |
| FAPb0.95Be0.05I3 | 1.308 | −0.126 | 1.182 |
| FAPb0.95Mg0.05I3 | 1.714 | −0.126 | 1.588 |
| FAPb0.95Ca0.05I3 | 1.659 | −0.052 | 1.607 |
| FAPb0.9Ca0.1I3 | 1.657 | −0.129 | 1.528 |
| FAPb0.85Ca0.15I3 | 1.662 | −0.130 | 1.532 |
| FAPb0.8Ca0.2I3 | 1.640 | −0.128 | 1.512 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
RaeisianAsl, M.; Sarabadani Tafreshi, S.; de Leeuw, N.H. A DFT Study of Alkaline Earth Metal-Doped FAPbI3 (111) and (100) Surfaces. Molecules 2023, 28, 372. https://doi.org/10.3390/molecules28010372
RaeisianAsl M, Sarabadani Tafreshi S, de Leeuw NH. A DFT Study of Alkaline Earth Metal-Doped FAPbI3 (111) and (100) Surfaces. Molecules. 2023; 28(1):372. https://doi.org/10.3390/molecules28010372
Chicago/Turabian StyleRaeisianAsl, Maryam, Saeedeh Sarabadani Tafreshi, and Nora H. de Leeuw. 2023. "A DFT Study of Alkaline Earth Metal-Doped FAPbI3 (111) and (100) Surfaces" Molecules 28, no. 1: 372. https://doi.org/10.3390/molecules28010372
APA StyleRaeisianAsl, M., Sarabadani Tafreshi, S., & de Leeuw, N. H. (2023). A DFT Study of Alkaline Earth Metal-Doped FAPbI3 (111) and (100) Surfaces. Molecules, 28(1), 372. https://doi.org/10.3390/molecules28010372







