Exploring Intra- and Intermolecular Interactions in Selected N-Oxides—The Role of Hydrogen Bonds
Abstract
:1. Introduction
- (i)
- a single dimer and
- (ii)
- a double acceptor bifurcated complex [50].
2. Computational Methodology
2.1. Density Functional Theory (DFT) in the Electronic Ground State
2.2. Symmetry-Adapted Perturbation Theory (SAPT) Protocol for Energy Decomposition in Dimers and Clusters
2.3. Time-Dependent Density Functional Theory (TD-DFT)
3. Results and Discussion
3.1. Structural, Energetic and Reactivity Properties of the N-Oxides
3.2. Self-Assembly and Microsolvation of the Studied N-Oxides
3.3. Impact of Microsolvation on Electron Excitations in the Studied N-Oxides
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| PES | Potential Energy Surface |
| PCM | Polarizable Continuum Model |
| TD-DFT | Time-Dependent Density Functional Theory |
| CCDC | Cambridge Crystallographic Data Centre |
| FT-IR | Fourier-Transform Infrared spectroscopy |
| NMR | Nuclear Magnetic Resonance |
| NBO | Natural Bond Orbital |
| SAPT | Symmetry-Adapted Perturbation Theory |
| BSSE | Basis Set Superposition Error |
References
- Zheng, N.; Xu, Y.; Zhao, Q.; Xie, T. Dynamic Covalent Polymer Networks: A Molecular Platform for Designing Functions beyond Chemical Recycling and Self-Healing. Chem. Rev. 2021, 121, 1716–1745. [Google Scholar] [CrossRef] [PubMed]
- Würthner, F. Dipole–Dipole Interaction Driven Self-Assembly of Merocyanine Dyes: From Dimers to Nanoscale Objects and Supramolecular Materials. Acc. Chem. Res. 2016, 49, 868–876. [Google Scholar] [CrossRef] [PubMed]
- Zeng, F.; Zimmerman, S.C. Dendrimers in Supramolecular Chemistry: From Molecular Recognition to Self-Assembly. Chem. Rev. 1997, 97, 1681–1712. [Google Scholar] [CrossRef] [PubMed]
- Elacqua, E.; Lye, D.S.; Weck, M. Engineering Orthogonality in Supramolecular Polymers: From Simple Scaffolds to Complex Materials. Acc. Chem. Res. 2014, 47, 2405–2416. [Google Scholar] [CrossRef]
- Terban, M.W.; Billinge, S.J.L. Structural Analysis of Molecular Materials Using the Pair Distribution Function. Chem. Rev. 2021, 122, 1208–1272. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, E.R. (Ed.) Intra- and Intermolecular Interactions between Non-Covalently Bonded Species; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Grabowski, S. New Type of Halogen Bond: Multivalent Halogen Interacting with π- and σ-Electrons. Molecules 2017, 22, 2150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grabowski, S. Tetrel Bonds with π-Electrons Acting as Lewis Bases—Theoretical Results and Experimental Evidences. Molecules 2018, 23, 1183. [Google Scholar] [CrossRef] [Green Version]
- Jabłoński, M. Hydride-Triel Bonds. J. Comput. Chem. 2018, 39, 1177–1191. [Google Scholar] [CrossRef] [PubMed]
- Jabłoński, M. Study of Beryllium, Magnesium, and Spodium Bonds to Carbenes and Carbodiphosphoranes. Molecules 2021, 26, 2275. [Google Scholar] [CrossRef] [PubMed]
- Hobza, P.; Zahradník, R.; Müller-Dethlefs, K. The World of Non-Covalent Interactions: 2006. Coll. Czechoslovak Chem. Commun. 2006, 71, 443–531. [Google Scholar] [CrossRef] [Green Version]
- Černý, J.; Hobza, P. Non-covalent interactions in biomacromolecules. Phys. Chem. Chem. Phys. 2007, 9, 5291. [Google Scholar] [CrossRef] [PubMed]
- Rest, C.; Kandanelli, R.; Fernández, G. Strategies to create hierarchical self-assembled structures via cooperative non-covalent interactions. Chem. Soc. Rev. 2015, 44, 2543–2572. [Google Scholar] [CrossRef] [PubMed]
- Müller-Dethlefs, K.; Hobza, P. Noncovalent Interactions: A Challenge for Experiment and Theory. Chem. Rev. 2000, 100, 143–167. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, S.E. Understanding Substituent Effects in Noncovalent Interactions Involving Aromatic Rings. Acc. Chem. Res. 2012, 46, 1029–1038. [Google Scholar] [CrossRef]
- Hobza, P.; Řezáč, J. Introduction: Noncovalent Interactions. Chem. Rev. 2016, 116, 4911–4912. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Li, Y.; Xu, F.J. Versatile Functionalization of Polysaccharides via Polymer Grafts: From Design to Biomedical Applications. Acc. Chem. Res. 2017, 50, 281–292. [Google Scholar] [CrossRef]
- Newberry, R.W.; Raines, R.T. The n→π* Interaction. Acc. Chem. Res. 2017, 50, 1838–1846. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, P.; Nag, A.; Chakraborty, A.; Pradeep, T. Approaching Materials with Atomic Precision Using Supramolecular Cluster Assemblies. Acc. Chem. Res. 2018, 52, 2–11. [Google Scholar] [CrossRef]
- Puzzarini, C.; Spada, L.; Alessandrini, S.; Barone, V. The challenge of non-covalent interactions: Theory meets experiment for reconciling accuracy and interpretation. J. Phys. Condens. Matter 2020, 32, 343002. [Google Scholar] [CrossRef]
- Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Competition between Intra and Intermolecular Triel Bonds. Complexes between Naphthalene Derivatives and Neutral or Anionic Lewis Bases. Molecules 2020, 25, 635. [Google Scholar] [CrossRef] [Green Version]
- Lodish, H.; Berk, A.; Zipursky, S.; Matsudaira, P.; Baltimore, D.; Darnell, J. Section 2.2, Noncovalent Bonds. In Molecular Cell Biology, 4th ed.; W. H. Freeman: New York, NY, USA, 2000. [Google Scholar]
- Anslyn, E.; Dougherty, D. Modern Physical Organic Chemistry; University Science Books: Sausalito, CA, USA, 2005. [Google Scholar]
- Sobczyk, L.; Grabowski, S.J.; Krygowski, T.M. Interrelation between H-Bond and Pi-Electron Delocalization. Chem. Rev. 2005, 105, 3513–3560. [Google Scholar] [CrossRef]
- Grabowski, S.J. Hydrogen and halogen bonds are ruled by the same mechanisms. Phys. Chem. Chem. Phys. 2013, 15, 7249. [Google Scholar] [CrossRef]
- Jeffrey, G.A. An Introduction to Hydrogen Bonding, 1st ed.; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Denisov, G.S.; Mavri, J.; Sobczyk, L. Potential Energy Shape for the Proton Motion in Hydrogen Bonds Reflected in Infrared and NMR Spectra. In Hydrogen Bonding—New Insights, (Challenges and Advances in Computational Chemistry and Physics, 3), 1st ed.; Grabowski, S.J., Ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 377–416. [Google Scholar]
- Grabowski, S.J. Chapter 3. Theoretical Approaches. In Theoretical and Computational Chemistry Series; Royal Society of Chemistry: London, UK, 2020; pp. 99–224. [Google Scholar] [CrossRef]
- Warshel, A. Computer Modelling of Chemical Reactions in Enzymes and Solutions, 1st ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Matsuura, H.; Yoshida, H.; Hieda, M.; ya Yamanaka, S.; Harada, T.; Shin-ya, K.; Ohno, K. Experimental Evidence for Intramolecular Blue-Shifting C-H···O Hydrogen Bonding by Matrix-Isolation Infrared Spectroscopy. J. Am. Chem. Soc. 2003, 125, 13910–13911. [Google Scholar] [CrossRef]
- Dhanishta, P.; Kumar, P.S.S.; Mishra, S.K.; Suryaprakash, N. Intramolecular hydrogen bond directed stable conformations of benzoyl phenyl oxalamides: Unambiguous evidence from extensive NMR studies and DFT-based computations. RSC Adv. 2018, 8, 11230–11240. [Google Scholar] [CrossRef] [Green Version]
- Straka, M.; Andris, E.; Vícha, J.; Růžička, A.; Roithová, J.; Rulíšek, L. Spectroscopic and Computational Evidence of Intramolecular AuI···H+-N Hydrogen Bonding. Angew. Chem. Int. Ed. 2019, 58, 2011–2016. [Google Scholar] [CrossRef] [Green Version]
- Król-Starzomska, I.; Filarowski, A.; Rospenk, M.; Koll, A.; Melikova, S. Proton Transfer Equilibria in Schiff Bases with Steric Repulsion. J. Phys. Chem. A 2004, 108, 2131–2138. [Google Scholar] [CrossRef]
- Filarowski, A.; Koll, A.; Karpfen, A.; Wolschann, P. Intramolecular hydrogen bond in molecular and proton-transfer forms of Schiff bases. Chem. Phys. 2004, 297, 323–332. [Google Scholar] [CrossRef]
- Panek, J.J.; Filarowski, A.; Jezierska-Mazzarello, A. Impact of proton transfer phenomena on the electronic structure of model Schiff bases: An AIM/NBO/ELF study. J. Chem. Phys. 2013, 139, 154312. [Google Scholar] [CrossRef]
- Ishikita, H.; Saito, K. Proton transfer reactions and hydrogen-bond networks in protein environments. J. R. Soc. Interface 2014, 11, 20130518. [Google Scholar] [CrossRef]
- Joshi, H.C.; Antonov, L. Excited-State Intramolecular Proton Transfer: A Short Introductory Review. Molecules 2021, 26, 1475. [Google Scholar] [CrossRef] [PubMed]
- Kułacz, K.; Pocheć, M.; Jezierska, A.; Panek, J.J. Naphthazarin Derivatives in the Light of Intra- and Intermolecular Forces. Molecules 2021, 26, 5642. [Google Scholar] [CrossRef] [PubMed]
- Jezierska, A.; Kizior, B.; Szyja, B.M.; Panek, J.J. On the nature of inter- and intramolecular interactions involving benzo[h]quinoline and 10-hydroxybenzo[h]quinoline: Electronic ground state vs excited state study. J. Mol. Struct. 2021, 1234, 130126. [Google Scholar] [CrossRef]
- Brela, M.Z.; Boczar, M.; Wójcik, M.J.; Sato, H.; Nakajima, T.; Ozaki, Y. The Born-Oppenheimer molecular simulations of infrared spectra of crystalline poly-(R)-3-hydroxybutyrate with analysis of weak C-H···O=C hydrogen bonds. Chem. Phys. Lett. 2017, 678, 112–118. [Google Scholar] [CrossRef]
- Künzle, M.; Lach, M.; Budiarta, M.; Beck, T. Higher-Order Structures Based on Molecular Interactions for the Formation of Natural and Artificial Biomaterials. ChemBioChem 2019, 20, 1637–1641. [Google Scholar] [CrossRef]
- Lugger, S.J.D.; Houben, S.J.A.; Foelen, Y.; Debije, M.G.; Schenning, A.P.H.J.; Mulder, D.J. Hydrogen-Bonded Supramolecular Liquid Crystal Polymers: Smart Materials with Stimuli-Responsive, Self-Healing, and Recyclable Properties. Chem. Rev. 2021. [Google Scholar] [CrossRef]
- Rospenk, M.; Koll, A.; Głowiak, T.; Sobczyk, L. The hydrogen bond in 2-(N,N-dimethylamino-N-oxymethyl)-4,6-dimethylophenol. J. Mol. Struct. 1989, 195, 33–41. [Google Scholar] [CrossRef]
- Wojciechowski, G.; Ratajczak-Sitarz, M.; Katrusiak, A.; Brzezinski, B. Shape of the proton potential in an intramolecular hydrogen-bonded system. Part II. J. Mol. Struct. 2002, 612, 59–64. [Google Scholar] [CrossRef]
- Jezierska, A.; Panek, J.J.; Koll, A. Spectroscopic Properties of a Strongly Anharmonic Mannich Base N-oxide. ChemPhysChem 2008, 9, 839–846. [Google Scholar] [CrossRef]
- Jezierska, A. N–H···O versus O–H···O: Density functional calculation and first principle molecular dynamics study on a quinoline-2-carboxamide N-oxide. J. Mol. Mod. 2015, 21, 47. [Google Scholar] [CrossRef] [Green Version]
- Balevicius, V.; Aidas, K.; Svoboda, I.; Fuess, H. Hydrogen Bonding in Pyridine N-Oxide/Acid Systems: Proton Transfer and Fine Details Revealed by FTIR, NMR, and X-ray Diffraction. J. Phys. Chem. A 2012, 116, 8753–8761. [Google Scholar] [CrossRef]
- Saraswatula, V.G.; Bhat, M.A.; Gurunathan, P.K.; Saha, B.K. Comparison of pyridyl and pyridyl N-oxide groups as acceptor in hydrogen bonding with carboxylic acid. CrystEngComm 2014, 16, 4715–4721. [Google Scholar] [CrossRef]
- Panek, J.J.; Błaziak, K.; Jezierska, A. Hydrogen bonds in quinoline N-oxide derivatives: First-principle molecular dynamics and metadynamics ground state study. Struct. Chem. 2015, 27, 65–75. [Google Scholar] [CrossRef] [Green Version]
- Rybarczyk-Pirek, A.J.; Łukomska-Rogala, M.; Wojtulewski, S.; Palusiak, M. N-Oxide as a Proton Accepting Group in Multicomponent Crystals: X-ray and Theoretical Studies on New p-Nitropyridine-N-oxide Co-Crystals. Cryst. Growth Des. 2015, 15, 5802–5815. [Google Scholar] [CrossRef]
- Love, I. Characteristics of Multiple N,O Bonds. J. Phys. Chem. A 2006, 110, 10507–10512. [Google Scholar] [CrossRef]
- Berski, S.; Latajka, Z.; Gordon, A.J. Quantum chemical topology study on the electronic structure of cis- and trans-FONO. J. Chem. Phys. 2010, 133, 034304. [Google Scholar] [CrossRef]
- Berski, S.; Gordon, A.J. Topological (ELF and ρ) study of the unusually long N–O bond in (CF3)2NO–NO. Chem. Phys. Lett. 2012, 525–526, 24–31. [Google Scholar] [CrossRef]
- CCDC Structural Database. Available online: https://www.ccdc.cam.ac.uk/ (accessed on 7 May 2021).
- Koll, A.; Rospenk, M.; Sobczyk, L.; Glowiak, T. Properties of a strong intramolecular OHO hydrogen bond in 2-(N,N-diethylamino-N-oxymethyl)-4,6-dichlorophenol. Can. J. Chem. 1986, 64, 1850–1854. [Google Scholar] [CrossRef]
- Ptasiewicz-Bąk, H.; Tellgren, R.; Olovsson, I.; Koll, A. Location of the proton in the very strong OHO hydrogen bonds in 2-(N,N-diethylamino-N-oxymethyl)-4,6-dichlorophenol. A single crystal neutron diffraction study. Z. Kristallogr. 1997, 212, 126–129. [Google Scholar] [CrossRef]
- Wojciechowski, G.; Brzeziński, B. Shape of the proton potential in an intramolecular hydrogen-bonded system. J. Mol. Struct. 2001, 595, 195–199. [Google Scholar] [CrossRef]
- Janoschek, R.; Weidemann, E.G.; Pfeiffer, H.; Zundel, G. Extremely high polarizability of hydrogen bonds. J. Am. Chem. Soc. 1972, 94, 2387–2396. [Google Scholar] [CrossRef]
- Janoschek, R.; Weidemann, E.G.; Zundel, G. Calculated frequencies and intensities associated with coupling of the proton motion with the hydrogen bond stretching vibration in a double minimum potential surface. J. Chem. Soc. Faraday Trans. 2 1973, 69, 505–520. [Google Scholar] [CrossRef]
- Schuster, P.; Zundel, G.; Sandorfy, C. (Eds.) Theory and Experiments, vol. II; North Holland: Amsterdam, The Netherland, 1976; Chapter 15; p. 687. [Google Scholar]
- Car, R.; Parrinello, M. Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [Green Version]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Panek, J.J.; Jezierska, A. N-oxide Derivatives: Car–Parrinello Molecular Dynamics and Electron Localization Function Study on Intramolecular Hydrogen Bonds. J. Phys. Chem. A 2018, 122, 6605–6614. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Truhlar, D.G. Exploring the Limit of Accuracy of the Global Hybrid Meta Density Functional for Main-Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2008, 4, 1849–1868. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision E.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision A.03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Parr, R.G.; Yang, W. Density functional approach to the frontier-electron theory of chemical reactivity. J. Am. Chem. Soc. 1984, 106, 4049–4050. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Boys, S.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Hohenstein, E.G.; Sherrill, C.D. Density fitting of intramonomer correlation effects in symmetry-adapted perturbation theory. J. Chem. Phys. 2010, 133, 014101. [Google Scholar] [CrossRef] [Green Version]
- Parker, T.M.; Burns, L.A.; Parrish, R.M.; Ryno, A.G.; Sherrill, C.D. Levels of symmetry adapted perturbation theory (SAPT). I. Efficiency and performance for interaction energies. J. Chem. Phys. 2014, 140, 094106. [Google Scholar] [CrossRef]
- Parrish, R.M.; Burns, L.A.; Smith, D.G.A.; Simmonett, A.C.; DePrince, A.E.; Hohenstein, E.G.; Bozkaya, U.; Sokolov, A.Y.; Remigio, R.D.; Richard, R.M.; et al. Psi4 1.1: An Open-Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability. J. Chem. Theory Comput. 2017, 13, 3185–3197. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
- Papajak, E.; Zheng, J.; Xu, X.; Leverentz, H.R.; Truhlar, D.G. Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions. J. Chem. Theory Comput. 2011, 7, 3027–3034. [Google Scholar] [CrossRef]
- Bauernschmitt, R.; Ahlrichs, R. Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory. Chem. Phys. Lett. 1996, 256, 454–464. [Google Scholar] [CrossRef]
- Jezierska, A.; Błaziak, K.; Klahm, S.; Lüchow, A.; Panek, J.J. Non-Covalent Forces in Naphthazarin—Cooperativity or Competition in the Light of Theoretical Approaches. Int. J. Mol. Sci. 2021, 22, 8033. [Google Scholar] [CrossRef]
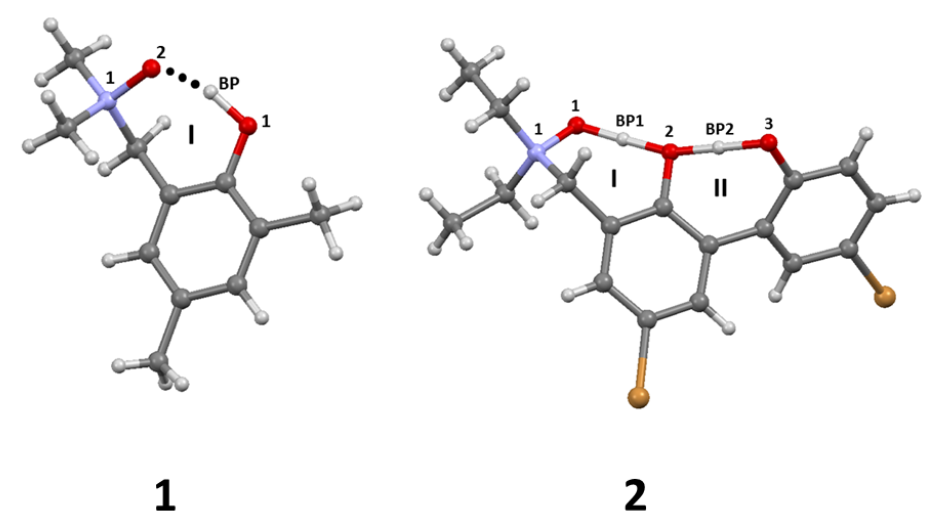
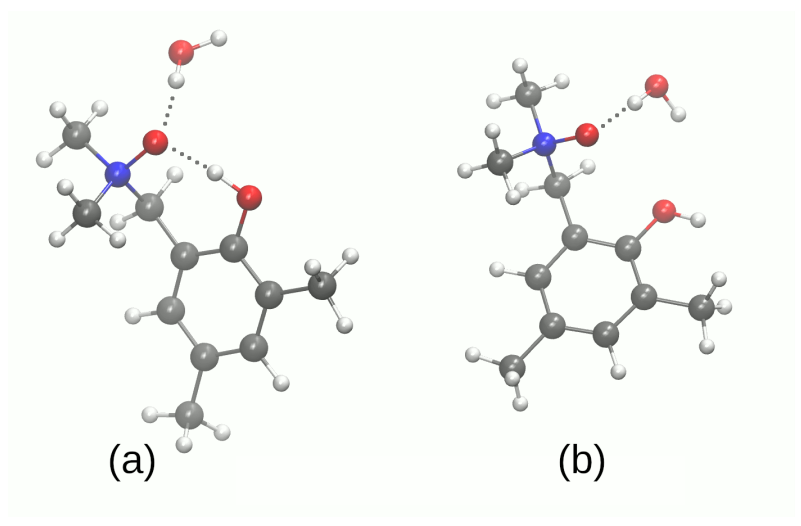
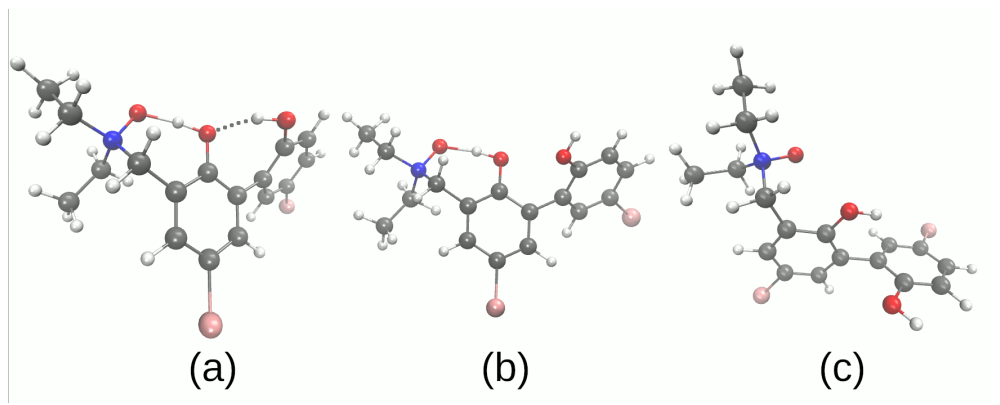
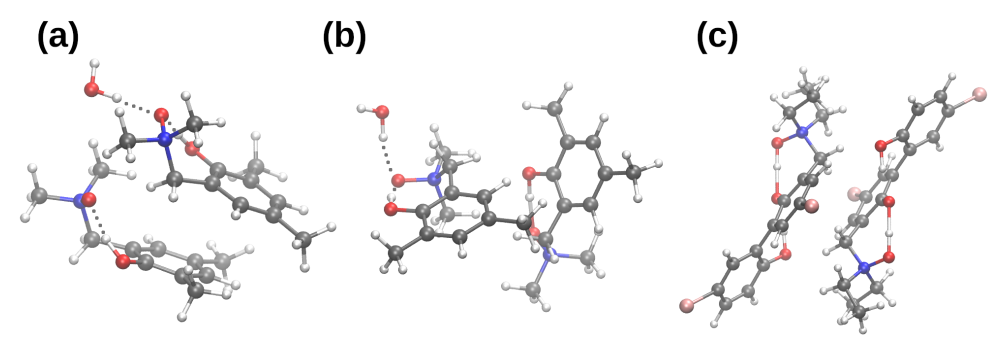
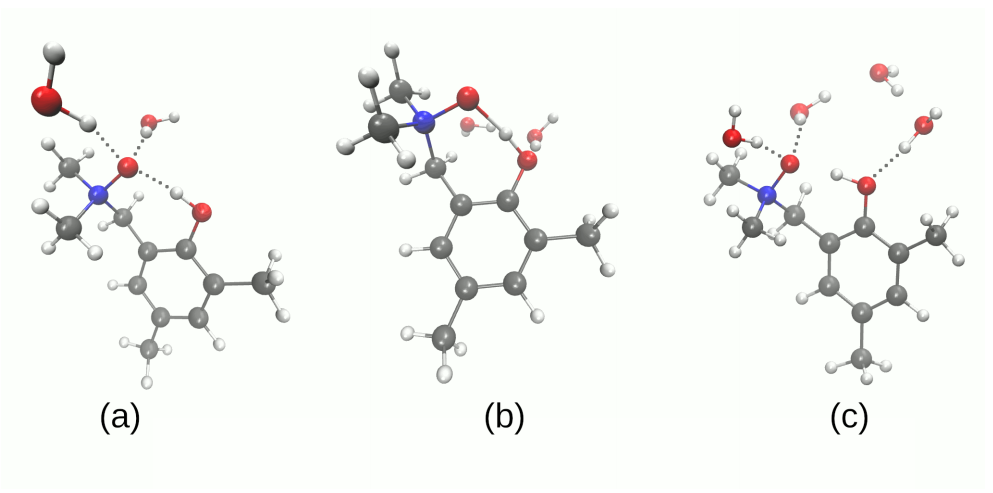

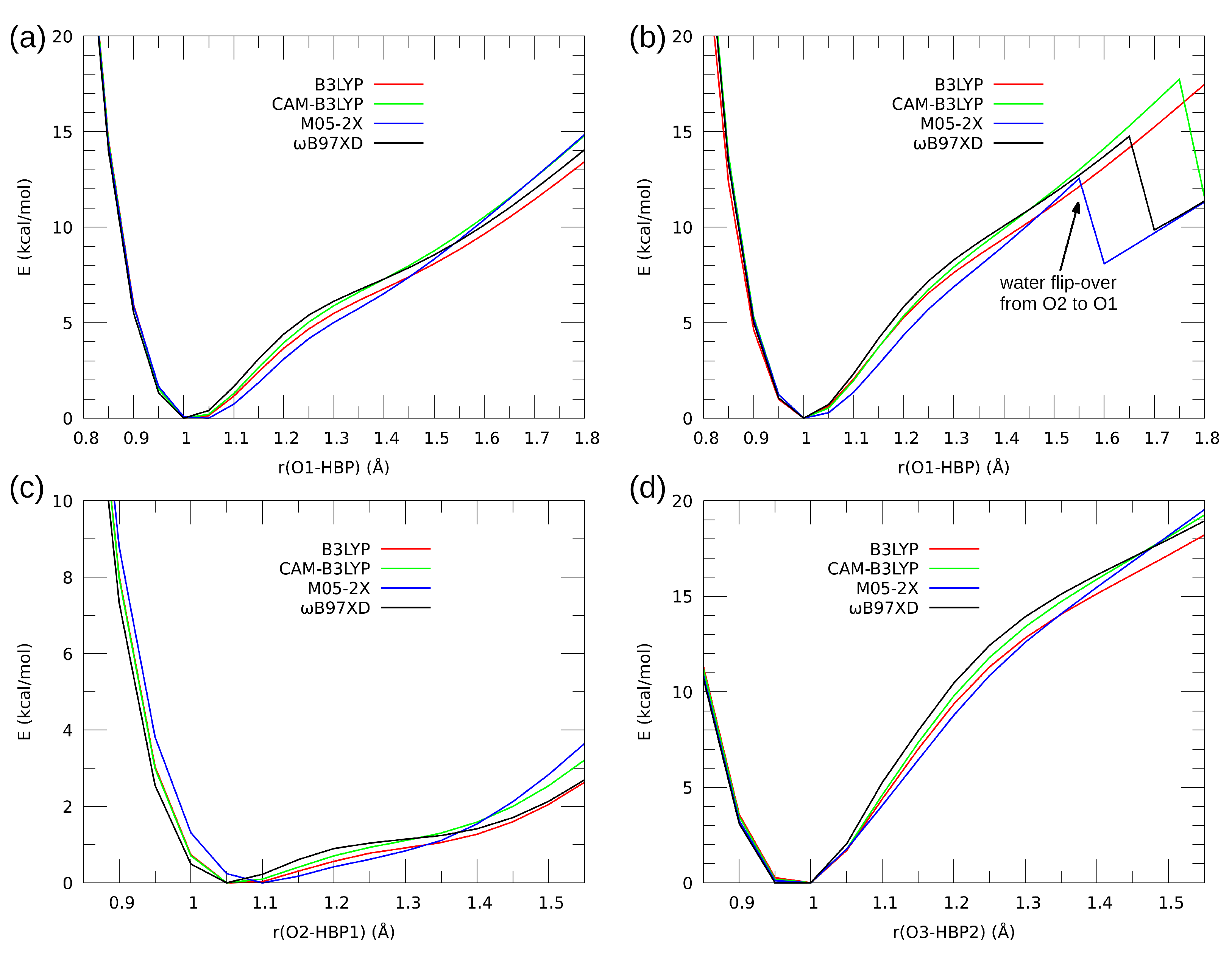
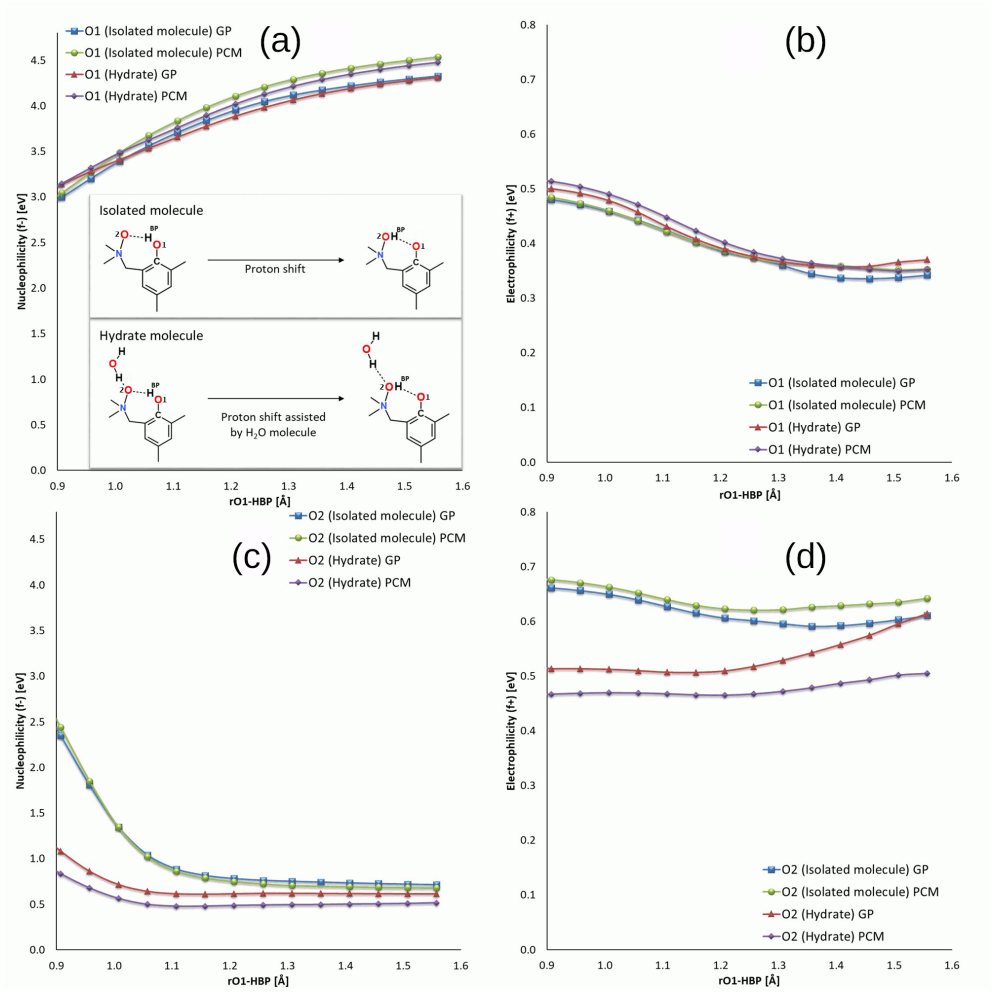
| System | Electrostatics | Exchange | Induction | Dispersion | SAPT0 | SAPT2 |
|---|---|---|---|---|---|---|
| Dimers based on X-ray coordinates, no water molecules | ||||||
| 1, dimer 1 | −4.23 | 7.47 | −1.65 | −9.22 | −8.28 | −7.63 |
| 1, dimer 2 | −3.71 | 3.91 | −1.12 | −4.99 | −6.49 | −5.91 |
| 2, dimer 1 | −20.29 | 13.06 | −6.62 | −18.54 | −32.40 | - |
| DFT−optimized dimers, with or without one water molecule for 1 | ||||||
| 1, dimer 1+HO | −24.27 | 35.21 | −6.92 | −22.87 | −21.34 | −18.86 |
| 1, dimer 1 | −19.65 | 30.54 | −5.61 | −21.51 | −18.34 | −16.23 |
| 1, dimer 2+HO | −13.60 | 19.25 | −3.72 | −13.62 | −13.28 | −11.69 |
| 1, dimer 2 | −13.59 | 19.37 | −3.70 | −13.62 | −13.16 | −11.53 |
| 2, dimer 1 | −26.93 | 30.55 | −9.24 | −28.79 | −34.41 | - |
| Microsolvation | ||||||
| 1-A2 | −39.21 | 41.75 | −12.66 | −8.34 | −22.70 | −18.46 |
| 1-AD | −27.14 | 30.41 | −8.50 | −7.87 | −16.74 | −13.10 |
| 1-A2D2 | −52.45 | 54.36 | −16.56 | −12.52 | −33.36 | −27.17 |
| 2-A2 | −35.39 | 39.12 | −11.22 | −8.71 | −20.34 | −16.21 |
| 2-A2D | −41.02 | 45.96 | −12.47 | −12.58 | −24.99 | −20.11 |
| 2−A2D | −45.47 | 50.41 | −14.26 | −11.30 | −26.11 | −20.62 |
| System | N-Oxide Moiety | Donor –OH 1 | Donor –OH 2 | |||
|---|---|---|---|---|---|---|
| N1 | O2 in 1, O1 in 2 | HBP1 | O1 in 1, O2 in 2 | HBP2 | O3 | |
| 1 | −0.036 | −0.737 | 0.507 | −0.722 | - | - |
| 1-A2 | −0.032 | −0.767 | 0.505 | −0.722 | - | - |
| 1-AD | −0.033 | −0.749 | 0.516 | −0.764 | - | - |
| 1-A2D2 | −0.030 | −0.759 | 0.514 | −0.788 | - | - |
| 2 | −0.042 | −0.713 | 0.508 | −0.754 | 0.503 | −0.711 |
| 2-A2 | −0.040 | −0.765 | 0.512 | −0.778 | 0.500 | −0.706 |
| 2-A2D | −0.042 | −0.747 | 0.505 | −0.794 | 0.502 | −0.704 |
| 2-A2D | −0.039 | −0.763 | 0.513 | −0.781 | 0.511 | −0.740 |
| System | S State | S State | S State | |||
|---|---|---|---|---|---|---|
| f | f | f | ||||
| isolated 1 | 261.12 | 0.0804 | 238.77 | 0.0016 | 224.75 | 0.0293 |
| 1-A2 | 257.03 | 0.0707 | 228.43 | 0.0015 | 221.66 | 0.0268 |
| 1-AD | 254.11 | 0.0617 | 219.77 | 0.0100 | 218.95 | 0.0060 |
| 1-A2D2 | 251.52 | 0.0570 | 218.92 | 0.0208 | 216.88 | 0.0018 |
| isolated 2 | 276.60 | 0.2321 | 266.75 | 0.0137 | 238.22 | 0.0018 |
| 2-A2 | 271.96 | 0.2174 | 264.75 | 0.0102 | 237.08 | 0.0018 |
| 2-A2D | 269.13 | 0.2043 | 263.34 | 0.0098 | 235.58 | 0.0041 |
| 2-A2D | 269.35 | 0.1992 | 261.93 | 0.0266 | 235.89 | 0.0121 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jezierska, A.; Panek, J.J.; Błaziak, K.; Raczyński, K.; Koll, A. Exploring Intra- and Intermolecular Interactions in Selected N-Oxides—The Role of Hydrogen Bonds. Molecules 2022, 27, 792. https://doi.org/10.3390/molecules27030792
Jezierska A, Panek JJ, Błaziak K, Raczyński K, Koll A. Exploring Intra- and Intermolecular Interactions in Selected N-Oxides—The Role of Hydrogen Bonds. Molecules. 2022; 27(3):792. https://doi.org/10.3390/molecules27030792
Chicago/Turabian StyleJezierska, Aneta, Jarosław J. Panek, Kacper Błaziak, Kamil Raczyński, and Aleksander Koll. 2022. "Exploring Intra- and Intermolecular Interactions in Selected N-Oxides—The Role of Hydrogen Bonds" Molecules 27, no. 3: 792. https://doi.org/10.3390/molecules27030792
APA StyleJezierska, A., Panek, J. J., Błaziak, K., Raczyński, K., & Koll, A. (2022). Exploring Intra- and Intermolecular Interactions in Selected N-Oxides—The Role of Hydrogen Bonds. Molecules, 27(3), 792. https://doi.org/10.3390/molecules27030792






