An Accurate Approach for Computational pKa Determination of Phenolic Compounds
Abstract
1. Introduction
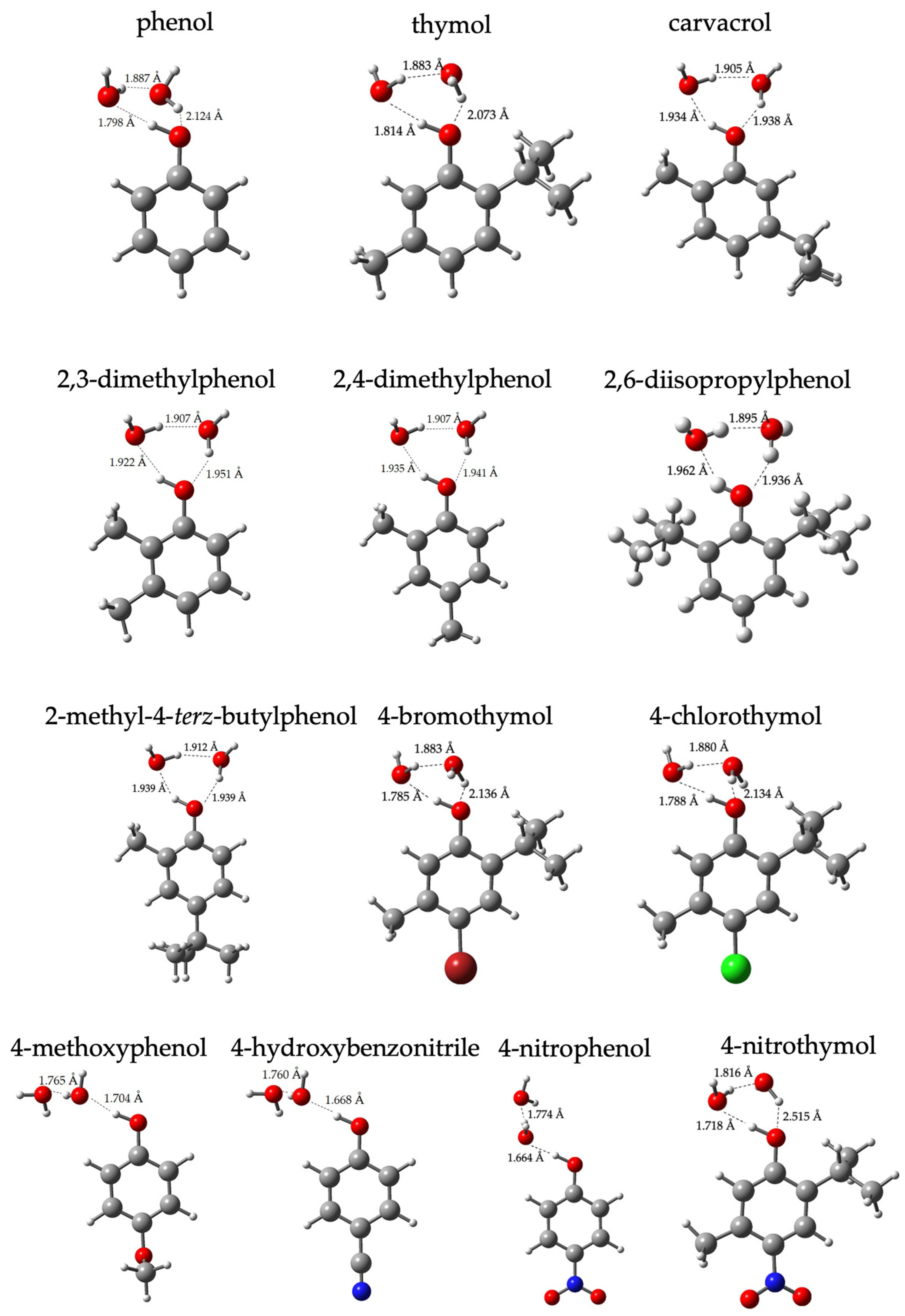
2. Results and Discussion
3. Materials and Methods
3.1. Chemicals and Synthesis
3.2. Computational Method and Data Analysis
3.3. Experimental pKa Determination
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Floris, B.; Galloni, P.; Conte, V.; Sabuzi, F. Tailored Functionalization of Natural Phenols to Improve Biological Activity. Biomolecules 2021, 11, 1325. [Google Scholar] [CrossRef]
- Le, M.D.; Matrat, M.; Amara, A.B.; Foucher, F.; Moreau, B.; Yu, Y.; Goussougli, M.; Fournet, R.; Sirjean, S.; Glaude, P.-A. Antioxidant effect of 2–4 xylenol on fuel oxidation in liquid and gas phase over a wide temperature range. Fuel Process. Technol. 2022, 236, 107414. [Google Scholar] [CrossRef]
- Stasiuk, M.; Kozubek, A. Biological activity of phenolic lipids. Cell. Mol. Life Sci. 2010, 67, 841–860. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, P.; Singh, M.; Kumari, H.; Kumari, A.; Mukhopadhyay, K. Bactericidal activity of curcumin I is Associated with damaging of bacterial membrane. PLoS ONE 2015, 10, e0121313. [Google Scholar] [CrossRef] [PubMed]
- Nazzaro, F.; Fratianni, F.; De Martino, L.; Coppola, R.; De Feo, V. Effect of essential oils on pathogenic bacteria. Pharmaceuticals 2013, 6, 1451–1474. [Google Scholar] [CrossRef]
- Antimicrobial Resistance Collaborators. Global burden of bacterial antimicrobial resistance in 2019: A systematic analysis. Lancet 2022, 399, 629–655. [Google Scholar] [CrossRef]
- Hehre, W. A Guide to Molecular Mechanics and Quantum Chemical Calculations; Wavefunction Inc.: Irvine, CA, USA, 2003. [Google Scholar]
- Guan, L.; Yang, H.; Cai, Y.; Sun, L.; Di, P.; Li, W.; Liu, G.; Tang, Y. ADMET-score a comprehensive scoring function for evaluation of chemical drug-likeness. MedChemComm 2019, 10, 148–157. [Google Scholar] [CrossRef]
- Wu, J.; Kang, Y.; Pan, P.; Hou, T. Machine learning methods for pKa prediction of small molecules: Advances and challenges. Drug Discov. 2022, 27, 103372. [Google Scholar] [CrossRef]
- Lian, P.; Johnston, R.C.; Parks, J.M.; Smith, J.C. Quantum chemical calculation of pKa of envirionmetally relevant functional groups: Carboxylic acis, amines, and thiols in aqueos solution. J. Phys. Chem. A 2018, 122, 4366–4374. [Google Scholar] [CrossRef]
- Banerjee, S.; Bhanja, S.K.; Chattopadhyay, P.K. Quantum chemical predictions of aqueous pKa values for OH groups of some a-hydroxycarboxylic acids based on ab initio and DFT calculations. Comput. Theor. Chem. 2018, 1125, 29–38. [Google Scholar] [CrossRef]
- Dutra, F.R.; de Souza Silva, C.; Custodio, R. On the Accuracy of the Direct Method to Calculate pKa from electronic Structure Calculations. J. Phys. Chem. A 2021, 125, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Busch, M.; Ahlberg, E.; Ahlberg, E.; Laasonen, K. How to Predict the pKa of Any Compound in Any Solvent. ACS Omega 2022, 7, 17369–17383. [Google Scholar] [CrossRef] [PubMed]
- Namazian, M.; Zakery, M.; Noorbala, M.R.; Coote, M.L. Accurate calculation of the pKa of trifluoroacetic acid using high-level ab initio calculations. Chem. Phys. Lett. 2008, 451, 163–168. [Google Scholar] [CrossRef]
- Morency, M.; Neron, S.; Iftime, R.; Wuest, J. Predicting pKa Values of quinols and related aromatic compounds with multiple OH groups. J. Org. Chem. 2021, 86, 14444–14460. [Google Scholar] [CrossRef] [PubMed]
- Ho, J.; Coote, M.L.A. Universal Approach for Continuum Solvent pKa Calculations: Are We There Yet? Theor. Chem. Acc. 2010, 125, 3. [Google Scholar] [CrossRef]
- Cunningham, I.D.; Bhaila, K.; Povey, D.C. Computational calculation of absolute aqueous pKa values for phenols. Comput. Theor. Chem. 2013, 1019, 55–60. [Google Scholar] [CrossRef]
- Sabuzi, F.; Lentini, S.; Sforza, F.; Pezzola, S.; Fratelli, S.; Bortolini, O.; Floris, B.; Conte, V.; Galloni, P. KuQuinones Equilibria Assessment for Biomedical Applications. J. Org. Chem. 2017, 82, 10129–10138. [Google Scholar] [CrossRef]
- Galasso, V.; Pichierri, F. Probing the molecular and electronic structure of norhipposudoric and hipposudoric acid from the red sweat of hippopotamus amphibius: A DFT investigation. J. Phys. Chem. A 2009, 113, 2534–2543. [Google Scholar] [CrossRef]
- Jia, Z.; Du, D.; Zhou, Z.; Zhang, A.; Hou, R. Accurate pKa determinations for some organic acids using an extended cluster method. Chem. Phys. Lett. 2007, 439, 374–380. [Google Scholar] [CrossRef]
- Pracht, P.; Grimme, S. Efficient Quantum-Chemical Calculations of Acid Dissociation Constants from Free. J. Phys. Chem. A 2021, 125, 5681–5692. [Google Scholar] [CrossRef]
- Ebrahimi, H.P.; Shaghaghi, H.; Tafazzoli, M. Gauge invariant atomic orbital-density functional theory prediction of accurate gas phase 1H and 13C NMR chemical shift. Concepts Magn. Reson. 2011, 38A, 269–279. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Foresman, J.B.; Frisch, Æ. Exploring Chemistry with Electronic Structure Methods, 3rd ed.; Gaussian, Inc.: Wallingford, CT, USA, 2015; ISBN 978-1-935522-03-4. [Google Scholar]
- Sabuzi, F.; Stefanelli, M.; Monti, D.; Conte, V.; Galloni, P. Amphiphilic porphyrin aggregates: A DFT Investigation. Molecules 2020, 25, 133. [Google Scholar] [CrossRef] [PubMed]
- Suarez, E.D.; Lima, F.C.D.A.; Dias, M.P.; Costantino, V.R.; Petrilli, H.M. Theoretical UV-Vis spectra of tetracationic porhyrin: Effects of environment on electronic spectral properties. J. Mol. Model. 2019, 25, 264. [Google Scholar] [CrossRef]
- Klamt, A.; Moya, C.; Palomar, J. A comprehensive comparison of the IEFPCM and SS(V)PE continuum solvation methods with the COSMO approach. J. Chem. Theory Compt. 2015, 11, 4220–4225. [Google Scholar] [CrossRef]
- Ghiami-Shomami, A.; Ashtari-Delivand, M.; Ghalami-Choobar, B.; Leito, I. Computational studies of acidities of some hydroxycoumarins. Comput. Theor. Chem. 2020, 1190, 113008. [Google Scholar] [CrossRef]
- Kazachenko, A.S.; Medimagh, M.; Issaoui, N.; Al-Dossary, O.; Wojcik, M.J.; Kazachenko, A.S.; Miroshnokova, A.V.; Malyar, Y.N. Sulfamic acid/water complexes (SH 2 O (1–8)) intermolecular hydrogen bond interactions: FTIR, X-ray, DFT and AIM analysis. J. Mol. Struct. 2022, 1265, 133394. [Google Scholar] [CrossRef]
- Kazachenko, A.S.; Issaoui, N.; Sagaama, A.; Malyar, Y.N.; Al-Dossary, O.; Bousiakou, L.G.; Kazachenko, A.S.; Miroshnokova, A.V.; Xiang, Z. Hydrogen bonds interactions in biuret-water clusters: FTIR, X-ray diffraction, AIM, DFT, RDG, ELF, NLO analysis. J. King Saud Univ. Sci. 2022, 34, 102350. [Google Scholar] [CrossRef]
- Pan, Y.; Zhu, W.; Xiao, H. DFT studies on trinitromethyl- or dinitromethyl-modified derivatives of RDX and b-HMX. Comput. Theor. Chem. 2013, 1019, 116–124. [Google Scholar] [CrossRef]
- Steel, W.H.; Foresman, J.B.; Burden, D.K.; Lau, Y.Y.; Walker, R.A. Solvation of Nitrophenol Isomers: Consequences for Solute Electronic Structure and Alkane/Water Partitioning. J. Phys. Chem. B 2009, 113, 759–766. [Google Scholar] [CrossRef]
- Liptak, M.D.; Gross, K.C.; Seybold, P.G.; Feldgus, S.; Shields, G.S. Absolute pKa Determinations for Substituted Phenols. J. Am. Chem. Soc. 2002, 124, 6421–6427. [Google Scholar] [CrossRef] [PubMed]
- Baldasare, C.A.; Seybold, P.G. Computational Estimation of the Gas-Phase and Aqueous Acidities of Carbon Acids. J. Phys. Chem. A 2020, 124, 2152–2159. [Google Scholar] [CrossRef] [PubMed]
- Baldasare, C.A.; Seybold, P.G. Computational Estimation of the Aqueous Acidities of Alcohols, Hydrates, and Enol. J. Phys. Chem. A 2021, 125, 3600–3605. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhang, S. A reliable and efficient first principle-based method for predicting pKa values. III. Adding explicit water molecules: Can the theoretical slope be reproduced and pKa values predicted more accurately? J. Compt. Chem. 2012, 33, 229–241. [Google Scholar] [CrossRef]
- Sabuzi, F.; Churakova, E.; Galloni, P.; Wever, R.; Hollmann, F.; Floris, B.; Conte, V. Thymol Bromination—A Comparison between Enzymatic and Chemical Catalysis. Eur. J. Inorg. Chem. 2015, 2015, 3519–3525. [Google Scholar] [CrossRef]
- Piombino, C.; Lange, H.; Sabuzi, F.; Galloni, P.; Conte, V.; Crestini, C. Lignosulfonate Microcapsules for Delivery and Controlled Release of Thymol and Derivatives. Molecules 2020, 25, 866. [Google Scholar] [CrossRef]
- Joshi, A.V.; Baidoosi, M.; Mukhopadhyay, S.; Sasson, Y. Nitration of Phenol and Substituted Phenols with Dilute Nitric Acid Using Phase-Transfer Catalysts. Org. Proc. Res. Dev. 2003, 7, 95–97. [Google Scholar] [CrossRef]
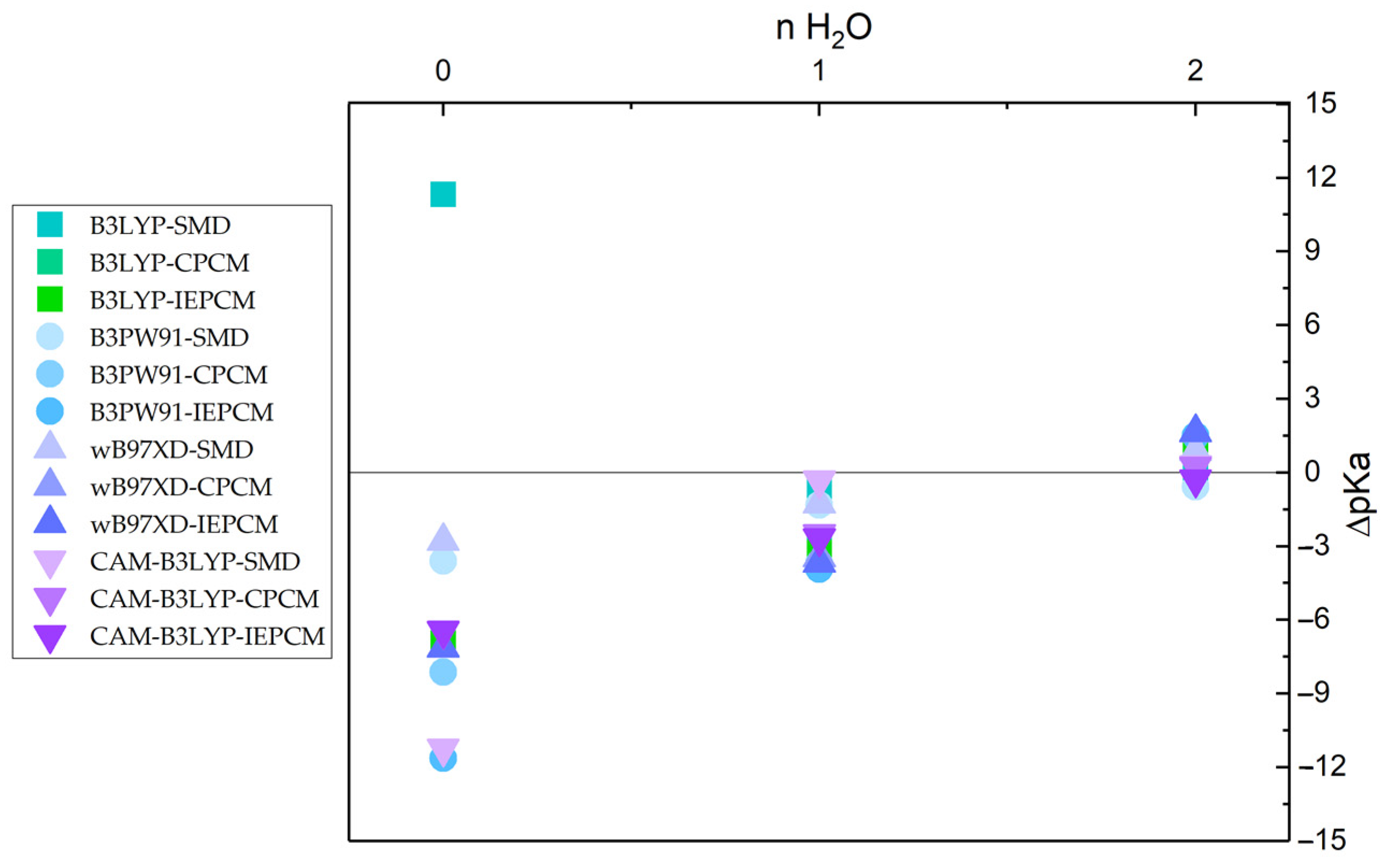
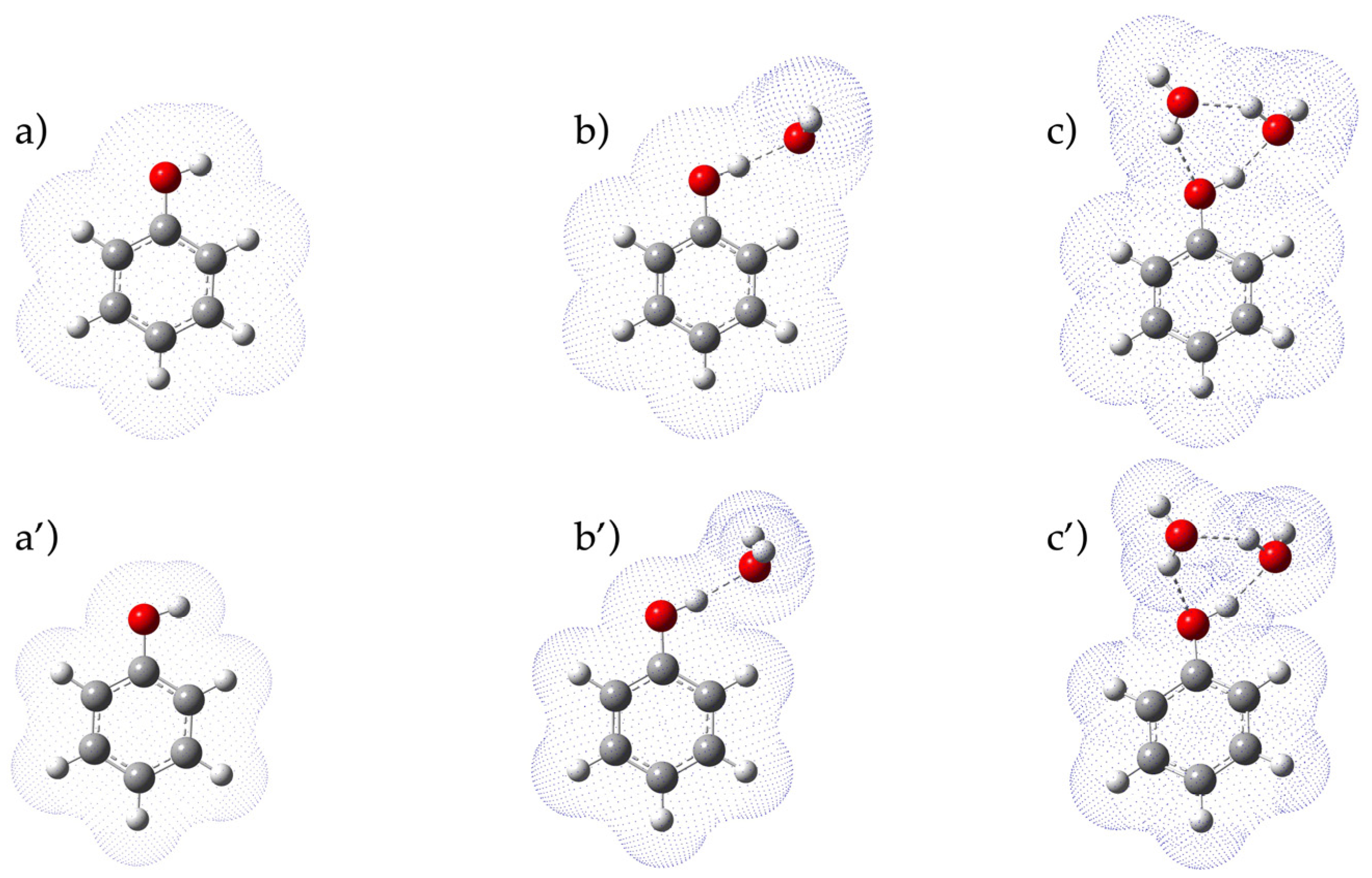
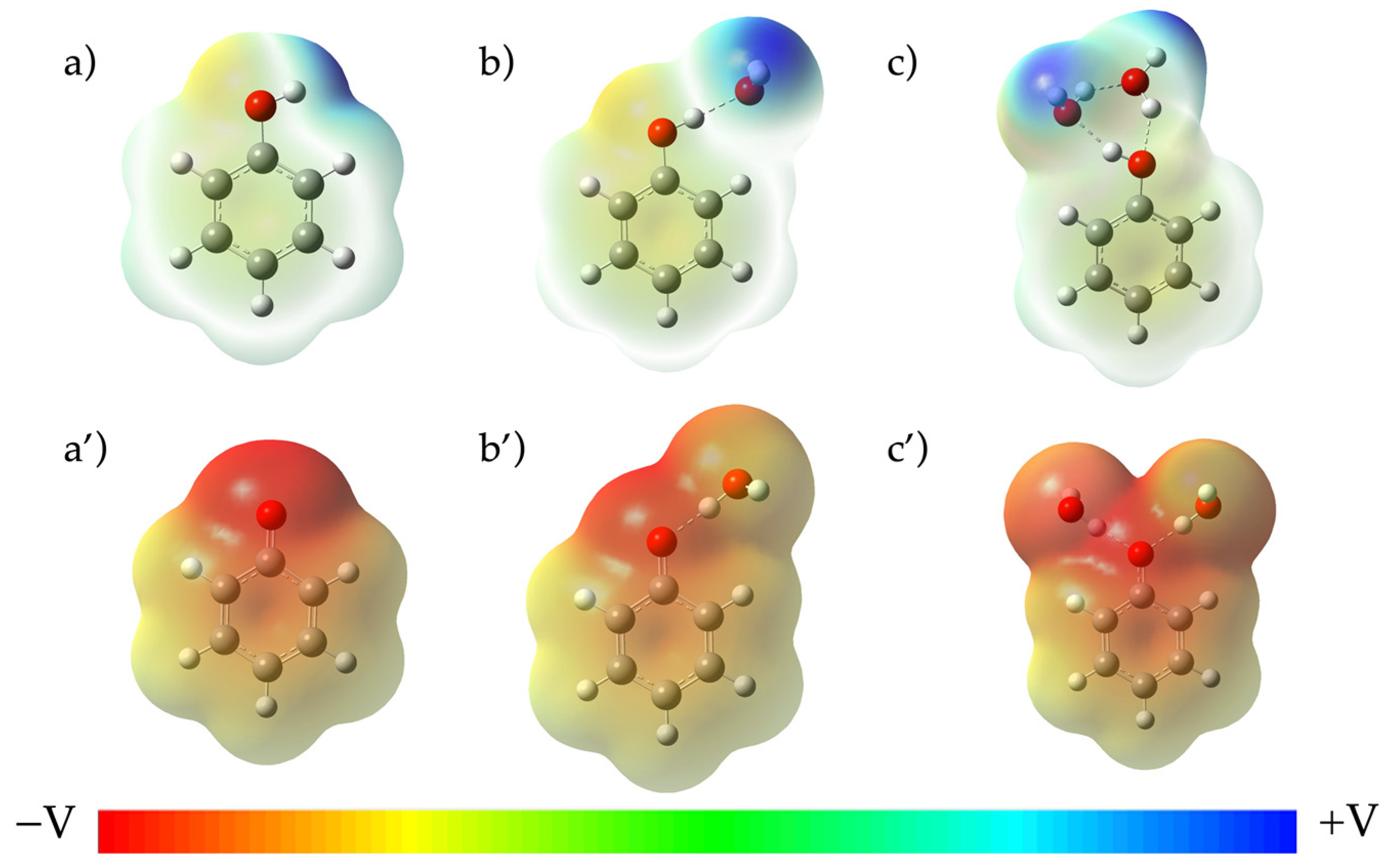
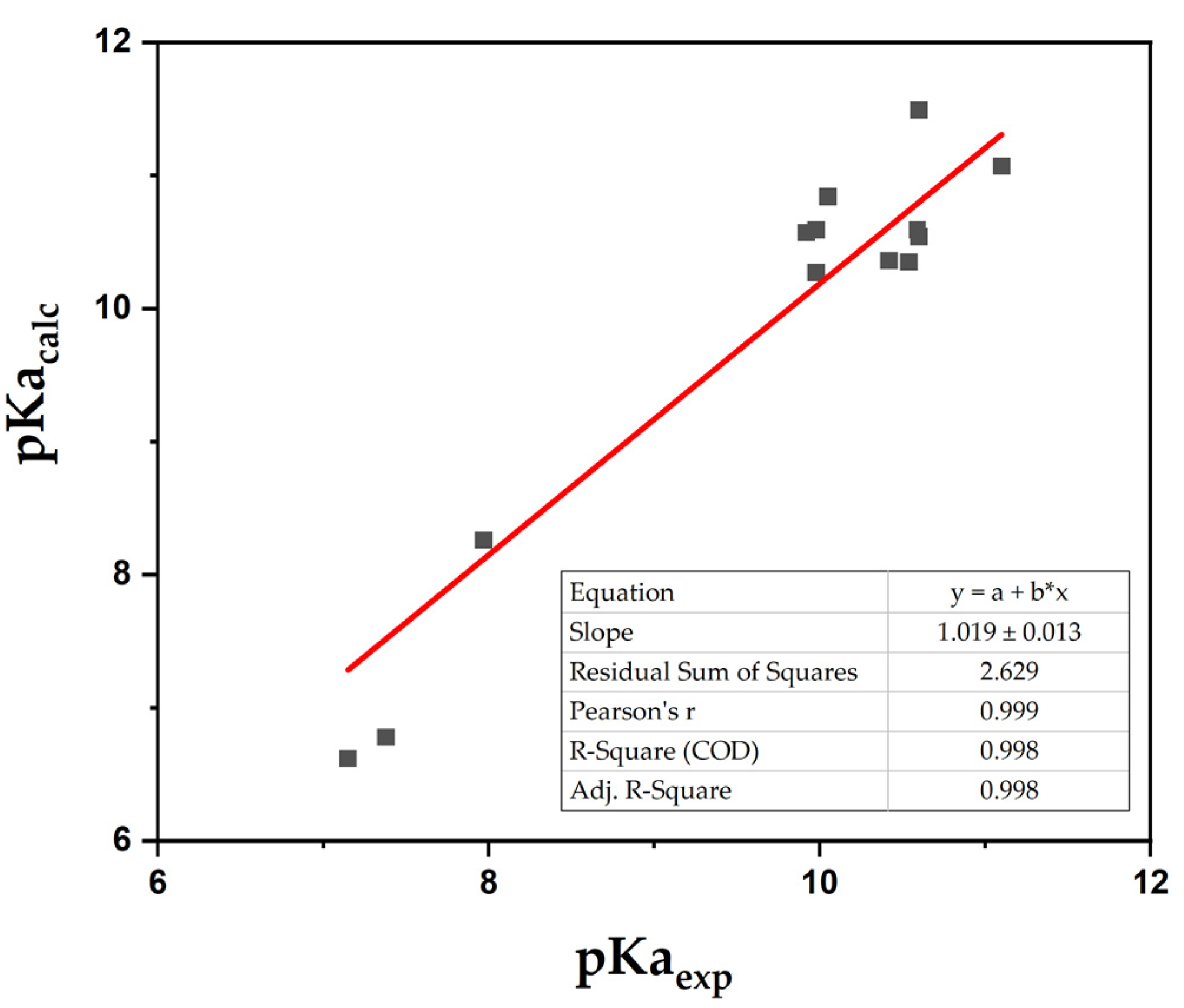
| Compound | pKa(ref) | B3LYP 6-311G+dp | B3PW91 6-311G+dp | WB97XD 6-311G+dp | CAM-B3LYP 6-311G+dp | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SMD | CPCM | PCM | SMD | CPCM | PCM | SMD | CPCM | PCM | SMD | CPCM | PCM | ||
| Phenol | 9.98 | −11.24 | −6.43 | −6.45 | 11.33 | −6.93 | −6.95 | −2.78 | −7.13 | −7.15 | −3.60 | −11.63 | −8.12 |
| Thymol | 10.60 | −10.16 | −4.79 | −4.84 | 12.43 | −5.36 | −5.40 | −1.77 | −5.55 | −5.60 | −2.63 | −6.69 | −6.71 |
| Compound | pKa(ref) | B3LYP | B3PW91 | WB97XD | CAM-B3LYP | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SMD | CPCM | PCM | SMD | CPCM | PCM | SMD | CPCM | PCM | SMD | CPCM | PCM | ||
| Phenol | 9.98 | −0.69 | −3.04 | −3.26 | −1.33 | −3.70 | −3.93 | −1.26 | −3.46 | −3.67 | −0.32 | −2.50 | −2.67 |
| Thymol | 10.60 | −0.07 | −1.97 | −2.11 | −1.17 | −3.28 | −3.49 | −1.06 | −2.96 | −3.16 | −0.06 | −1.96 | −1.97 |
| Compound | pKa(ref) | B3LYP | B3PW91 | WB97XD | CAM-B3LYP | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SMD | PCM | CPCM | SMD | PCM | CPCM | SMD | PCM | CPCM | SMD | CPCM | PCM | ||
| Phenol | 9,98 | 0.02 | 0.91 | 0.96 | 0.58 | 1.48 | 1.49 | 0.86 | 1.62 | 1.65 | 0.29 | 0.24 | 0.28 |
| Thymol | 10,60 | −0.72 | 0.13 | 0.16 | −0.27 | 1.08 | 1.10 | 0.44 | 1.14 | 1.17 | 0.89 | −0.37 | −0.18 |
| Compound | pKaref | CAM-B3LYP | B3LYP | |||
|---|---|---|---|---|---|---|
| 1H2O | 2H2O | 2H2O | 2H2O | 2H2O | ||
| SMD | SMD | PCM | CPCM | SMD | ||
| pKacalc | pKacalc | pKacalc | pKacalc | pKacalc | ||
| Phenol | 9.98 | 9.35 | 10.27 | 10.23 | 10.15 | 9.95 |
| 2-isopropyl-5-methylphenol (thymol) | 10.60 | 10.23 | 11.49 | 11.80 | 11.78 | 11.39 |
| 5-isopropyl-2-methylphenol (carvacrol) | 10.42 | 9.59 | 10.36 | 11.19 | 11.15 | 9.89 |
| 2,3-dimethylphenol | 10.54 | 9.45 | 10.35 | 11.04 | 11.01 | 9.87 |
| 2,4-dimethylphenol | 10.60 | 9.74 | 10.54 | 11.32 | 11.29 | 9.99 |
| 2,6-diisopropylphenol | 11.10 | 10.02 | 11.07 | 11.58 | 11.53 | 10.26 |
| 2-methyl-4-terz-butylphenol | 10.59 | 10.41 | 10.59 | 11.31 | 11.27 | 10.03 |
| 4-bromo-2-isopropyl-5-methylphenol | 9.92 | 9.31 | 10.57 | 10.42 | 10.38 | 9.90 |
| 4-chloro-2-isopropyl-5-methylphenol | 9.98 | 9.34 | 10.59 | 10.61 | 10.58 | 10.08 |
| 4-methoxyphenol | 10.05 | 10.84 | 10.84 | 11.02 | 10.97 | 11.14 |
| 4-hydroxybenzonitrile | 7.97 | 6.25 | 8.26 | 6.55 | 6.54 | 7.73 |
| 4-nitrophenol | 7.15 | 4.11 | 6.62 | 6.22 | 6.22 | 5.33 |
| 4-nitro-2-isopropyl-5-methylphenol | 7.38 | 4.85 | 6.78 | 5.98 | 5.97 | 6.39 |
| Compound | pKaref | CAM-B3LYP | B3LYP | |||
|---|---|---|---|---|---|---|
| 1H2O | 2H2O | 2H2O | 2H2O | 2H2O | ||
| SMD | SMD | PCM | CPCM | SMD | ||
| pKacalc | pKacalc | pKacalc | pKacalc | pKacalc | ||
| Phenol | 9.98 | −0.63 | 0.29 | 0.25 | 0.17 | −0.03 |
| 2-isopropyl-5-methylphenol (thymol) | 10.60 | −0.37 | 0.89 | 1.20 | 1.18 | 0.79 |
| 5-isopropyl-2-methylphenol (carvacrol) | 10.42 | −0.83 | 0.06 | 0.77 | 0.73 | −0.53 |
| 2,3-dimethylphenol | 10.54 | −1.09 | −0.19 | 0.50 | 0.47 | −0.67 |
| 2,4-dimethylphenol | 10.60 | −0.86 | −0.06 | 0.72 | 0.69 | −0.61 |
| 2,6-diisopropylphenol | 11.10 | −1.08 | −0,03 | 0.48 | 0.43 | −0.84 |
| 2-methyl-4-terz-butylphenol | 10.59 | −0.18 | 0.00 | 0.72 | 0.68 | −0.56 |
| 4-bromo-2-isopropyl-5-methylphenol | 9.92 | −0.61 | 0.65 | 0.50 | 0.46 | −0.02 |
| 4-chloro-2-isopropyl-5-methylphenol | 9.98 | −0.64 | 0.61 | 0.63 | 0.60 | −0.10 |
| 4-methoxyphenol | 10.05 | 0.79 | 0.79 | 0.97 | 0.92 | 1.09 |
| 4-hydroxybenzonitrile | 7.97 | −1.72 | 0.29 | −1.42 | −1.43 | −0.24 |
| 4-nitrophenol | 7.15 | −3.04 | −0.53 | −0.93 | −0.93 | −1.82 |
| 4-nitro-2-isopropyl-5-methylphenol | 7.38 | −2.53 | −0.60 | −1.40 | −1.41 | −0.99 |
| MAE | 1.25 | 0.39 | 0.88 | 0.85 | 0.70 | |
| Std. dev. | 0.97 | 0.30 | 0.45 | 0.47 | 0.53 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pezzola, S.; Tarallo, S.; Iannini, A.; Venanzi, M.; Galloni, P.; Conte, V.; Sabuzi, F. An Accurate Approach for Computational pKa Determination of Phenolic Compounds. Molecules 2022, 27, 8590. https://doi.org/10.3390/molecules27238590
Pezzola S, Tarallo S, Iannini A, Venanzi M, Galloni P, Conte V, Sabuzi F. An Accurate Approach for Computational pKa Determination of Phenolic Compounds. Molecules. 2022; 27(23):8590. https://doi.org/10.3390/molecules27238590
Chicago/Turabian StylePezzola, Silvia, Samuele Tarallo, Alessandro Iannini, Mariano Venanzi, Pierluca Galloni, Valeria Conte, and Federica Sabuzi. 2022. "An Accurate Approach for Computational pKa Determination of Phenolic Compounds" Molecules 27, no. 23: 8590. https://doi.org/10.3390/molecules27238590
APA StylePezzola, S., Tarallo, S., Iannini, A., Venanzi, M., Galloni, P., Conte, V., & Sabuzi, F. (2022). An Accurate Approach for Computational pKa Determination of Phenolic Compounds. Molecules, 27(23), 8590. https://doi.org/10.3390/molecules27238590








