Quasi-3D Hyperbolic Shear Deformation Theory for the Free Vibration Study of Honeycomb Microplates with Graphene Nanoplatelets-Reinforced Epoxy Skins
Abstract
1. Introduction
2. Theoretical Formulation
3. Governing Equations of the Problem
4. Analytical Solution Procedure
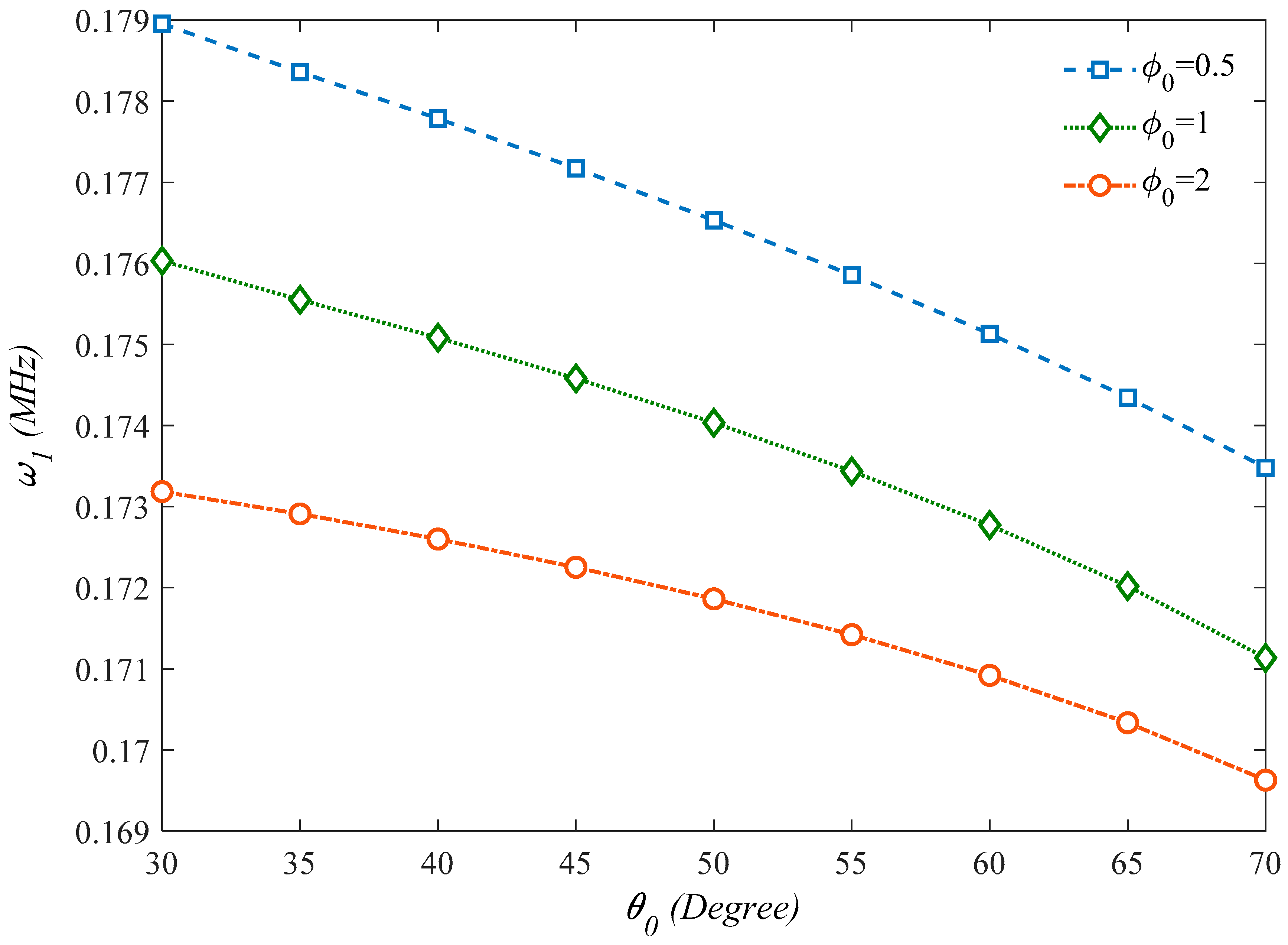
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Maheri, M.R.; Adams, R.D. Steady-state flexural vibration damping of honeycomb sandwich beams. Compos. Sci. Technol. 1994, 52, 333–347. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, J. Shock Absorbing Characteristics and Vibration Transmissibility of Honeycomb Paperboard. Shock Vib. 2004, 11, 521–531. [Google Scholar] [CrossRef]
- Li, Y.; Jin, Z. Free flexural vibration analysis of symmetric rectangular honeycomb panels with SCSC edge supports. Compos. Struct. 2008, 83, 154–158. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, Y.S.; Li, R.F.; Au, F.T.K. A semi-analytical method for bending, buckling, and free vibration analyses of sandwich panels with square-hoeycomb cores. Int. J. Struct. Stab. Dyn. 2010, 10, 127–151. [Google Scholar] [CrossRef]
- Burlayenko, V.N.; Sadowski, T. Influence of skin/core debonding on free vibration behavior of foam and honeycomb cored sandwich plates. Int. J. Non Linear Mech. 2010, 45, 959–968. [Google Scholar] [CrossRef]
- Katunin, A. Vibration-based spatial damage identification in honeycomb-core sandwich composite structures using wavelet analysis. Compos. Struct. 2014, 118, 385–391. [Google Scholar] [CrossRef]
- Mukhopadhyay, T.; Adhikari, S. Free-Vibration Analysis of Sandwich Panels with Randomly Irregular Honeycomb Core. J. Eng. Mech. 2016, 142, 06016008. [Google Scholar] [CrossRef]
- Duc, N.D.; Seung-Eock, K.; Tuan, N.D.; Tran, P.; Khoa, N.D. New approach to study nonlinear dynamic response and vibration of sandwich composite cylindrical panels with auxetic honeycomb core layer. Aerosp. Sci. Technol. 2017, 70, 396–404. [Google Scholar] [CrossRef]
- Piollet, E.; Fotsing, E.R.; Ross, A.; Michon, G. High damping and nonlinear vibration of sandwich beams with entangled cross-linked fibres as core material. Compos. Part B Eng. 2019, 168, 353–366. [Google Scholar] [CrossRef]
- Kumar, S.; Renji, K. Estimation of strains in composite honeycomb sandwich panels subjected to low frequency diffused acoustic field. J. Sound Vib. 2019, 449, 84–97. [Google Scholar] [CrossRef]
- Sobhy, M. Differential quadrature method for magneto-hygrothermal bending of functionally graded graphene/Al sandwich-curved beams with honeycomb core via a new higher-order theory. J. Sandw. Struct. Mater. 2020. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Xiao, D.; Wu, W.; Fang, D. The Dynamic response of shallow sandwich arch with auxetic metallic honeycomb core under localized impulsive loading. Int. J. Impact Eng. 2020, 137, 103442. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Nonlinear vibration and postbuckling of functionally graded graphene reinforced porous nanocomposite beams. Compos. Sci. Technol. 2017, 142, 235–245. [Google Scholar] [CrossRef]
- Karimiasl, M.; Ebrahimi, F.; Mahesh, V. On Nonlinear Vibration of Sandwiched Polymer- CNT/GPL-Fiber Nanocomposite Nanoshells. Thin-Walled Struct. 2020, 146, 106431. [Google Scholar] [CrossRef]
- Eyvazian, A.; Hamouda, A.M.; Tarlochan, F.; Mohsenizadeh, S.; Dastjerdi, A.A. Damping and vibration response of viscoelastic smart sandwich plate reinforced with non-uniform Graphene platelet with magnetorheological fluid core. Steel Compos. Struct. 2019, 33, 891–906. [Google Scholar]
- Torabi, J.; Ansari, R. Numerical Phase-Field Vibration Analysis of Cracked Functionally Graded GPL-RC Plates. Mech. Based Des. Struct. Mach. 2020, 1–20. [Google Scholar] [CrossRef]
- Khoa, N.D.; Anh, V.M.; Duc, N.D. Nonlinear dynamic response and vibration of functionally graded nanocomposite cylindrical panel reinforced by carbon nanotubes in thermal environment. J. Sandw. Struct. Mater. 2019. [Google Scholar] [CrossRef]
- Ibrahim, H.H.; Tawfik, M.; Al-Ajmi, M. Thermal buckling and nonlinear flutter behavior of functionally graded material panels. J. Aircr. 2007, 44, 1610–1618. [Google Scholar] [CrossRef]
- Li, Y.; Li, F.; He, Y. Geometrically nonlinear forced vibrations of the symmetric rectangular honeycomb sandwich panels with completed clamped supported boundaries. Compos. Struct. 2011, 93, 360–368. [Google Scholar] [CrossRef]
- Mehar, K.; Panda, S.K. Thermal Free Vibration Behavior of FG-CNT Reinforced Sandwich Curved Panel Using Finite Element Method. Polym. Compos. 2017. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Pham, C.H. Nonlinear dynamic response and vibration of sandwich composite plates with negative Poisson’s ratio in auxetic honeycombs. J. Sandw. Struct. Mater. 2017, 20, 692–717. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Reddy, J.N. An equivalent layer-wise approach for the free vibration analysis of thick and thin laminated and sandwich shells. Appl. Sci. 2017, 7, 17. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E.; Reddy, J.N. A numerical investigation on the natural frequencies of FGM sandwich shells with variable thickness by the local generalized differential quadrature method. Appl. Sci. 2017, 7, 131. [Google Scholar] [CrossRef]
- Jouneghani, F.Z.; Dimitri, R.; Tornabene, F. Structural response of porous FG nanobeams under hygro-thermo-mechanical loadings. Compos. Part B Eng. 2018, 152, 71–78. [Google Scholar] [CrossRef]
- Tornabene, F.; Brischetto, S. 3D capability of refined GDQ models for the bending analysis of composite and sandwich plates, spherical and doubly-curved shells. Thin Walled Struct. 2018, 129, 94–124. [Google Scholar] [CrossRef]
- Karimiasl, M.; Ebrahimi, F.; Mahesh, V. Nonlinear forced vibration of smart multiscale sandwich composite doubly curved porous shell. Thin Walled Struct. 2019, 143, 106152. [Google Scholar] [CrossRef]
- Nejati, M.; Ghasemi-Ghalebahman, A.; Soltanimaleki, A.; Dimitri, R.; Tornabene, F. Thermal vibration analysis of SMA hybrid composite double curved sandwich panels. Compos. Struct. 2019, 224, 111035. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Foam core composite sandwich plates and shells with variable stiffness: Effect of the curvilinear fiber path on the modal response. J. Sandw. Struct. Mater. 2019, 21, 320–365. [Google Scholar] [CrossRef]
- Hebali, H.; Tounsi, A.; Houari, A.M.S.; Bessaim, A.; Abbes, E. New Quasi-3D Hyperbolic Shear Deformation Theory for the Static and Free Vibration Analysis of Functionally Graded Plates. J. Eng. Mech. 2014, 140, 374–383. [Google Scholar] [CrossRef]
- Guerroudj, H.Z.; Yeghnem, R.; Kaci, A.; Zaoui, F.Z.; Benyoucef, S.; Tounsi, A. Eigenfrequencies of advanced composite plates using an efficient hybrid quasi-3D shear deformation theory. Smart Struct. Syst. 2018, 22, 121. [Google Scholar]
- Amir, S.; Arshid, E.; Rasti-alhosseini, S.M.A.; Loghman, A. Quasi-3D tangential shear deformation theory for size-dependent free vibration analysis of three-layered FG porous micro rectangular plate integrated by nano-composite faces in hygrothermal environment. J. Therm. Stresses 2019, 43, 133–156. [Google Scholar] [CrossRef]
- Benahmed, A.; Houari, A.M.S.; Benyoucef, S.; Belakhdar, K.; Tounsi, A. A novel quasi-3D hyperbolic shear deformation theory for functionally graded thick rectangular plates on elastic foundation. Geomech. Eng. 2017, 12, 9–34. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Karimiasl, M.; Mahesh, V. Vibration analysis of magneto-flexo-electrically actuated porous rotary nanobeams considering thermal effects via nonlocal strain gradient elasticity theory. Adv. Nano Res. 2019, 7, 223–231. [Google Scholar]
- Torabi, K.; Afshari, H.; Aboutalebi, F.H. Vibration and flutter analyses of cantilever trapezoidal honeycomb sandwich plates. J. Sandw. Struct. Mater. 2019, 21. [Google Scholar] [CrossRef]
- Arshid, E.; Amir, S.; Loghman, A. Static and Dynamic Analyses of FG-GNPs Reinforced Porous Nanocomposite Annular Micro-Plates Based on MSGT. Int. J. Mech. Sci. 2020, 180, 105656. [Google Scholar] [CrossRef]
- Mohammad-Rezaei Bidgoli, E.; Arefi, M. Free vibration analysis of micro plate reinforced with functionally graded graphene nanoplatelets based on modified strain-gradient formulation. J. Sandw. Struct. Mater. 2019. [Google Scholar] [CrossRef]
- Amir, S.; Arshid, E.; Ghorbanpour Arani, M.R. Size-Dependent Magneto-Electro-Elastic Vibration Analysis of FG Saturated Porous Annular/ Circular Micro Sandwich Plates Embedded with Nano-Composite Face sheets Subjected to Multi-Physical Pre Loads. Smart Struct. Syst. 2019, 23, 429–447. [Google Scholar]
- Arshid, E.; Khorshidvand, A.R. Thin-Walled Structures Free vibration analysis of saturated porous FG circular plates integrated with piezoelectric actuators via differential quadrature method. Thin Walled Struct. 2018, 125, 220–233. [Google Scholar] [CrossRef]
- Amir, S.; Soleymani-Javid, Z.; Arshid, E. Size-dependent free vibration of sandwich micro beam with porous core subjected to thermal load based on SSDBT. Appl. Math. Mech. 2019, 99, e201800334. [Google Scholar] [CrossRef]
- Arshid, E.; Khorshidvand, A.R.; Khorsandijou, S.M. The Effect of Porosity on Free Vibration of SPFG Circular Plates Resting on visco-Pasternak Elastic Foundation Based on CPT, FSDT and TSDT. Struct. Eng. Mech. 2019, 70, 97–112. [Google Scholar]
- Kiani, Y.; Dimitri, R.; Tornabene, F. Free vibration of FG-CNT reinforced composite skew cylindrical shells using the Chebyshev-Ritz formulation. Compos. Part B Eng. 2018, 147, 169–177. [Google Scholar] [CrossRef]
- Amir, S.; BabaAkbar-Zarei, H.; Khorasani, M. Flexoelectric vibration analysis of nanocomposite sandwich plates. Mech. Based Des. Struct. Mach. 2020, 48, 146–163. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, W.; Gao, W.; Zhang, L.; Zhang, E. Mechanical responses of a composite sandwich structure with Nomex honeycomb core. J. Reinf. Plast. Compos. 2019, 38, 601–615. [Google Scholar] [CrossRef]
- Lin, H.G.; Cao, D.Q.; Xu, Y.Q. Vibration, Buckling and Aeroelastic Analyses of Functionally Graded Multilayer Graphene-Nanoplatelets-Reinforced Composite Plates Embedded in Piezoelectric Layers. Int. J. Appl. Mech. 2018, 10, 1850023. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Tran, T.D.; Phung-Van, P. A size-dependent quasi-3D isogeometric model for functionally graded graphene platelet-reinforced composite microplates based on the modified couple stress theory. Compos. Struct. 2020, 234, 111695. [Google Scholar] [CrossRef]
- Dindarloo, M.H.; Li, L.; Dimitri, R.; Tornabene, F. Nonlocal Elasticity response of Doubly-Curved Nanoshells. Symmetry 2020, 12, 466. [Google Scholar] [CrossRef]
- Karimi, M.; Khorshidi, K.; Dimitri, R.; Tornabene, F. Size-dependent hydroelastic vibration of FG microplates partially in contact with a fluid. Compos. Struct. 2020, 244, 112320. [Google Scholar] [CrossRef]
- Khorasani, M.; Eyvazian, A.; Karbon, M.; Tounsi, A.; Lampani, L.; Sebaey, T.A. Magneto-electro-elastic vibration analysis of modified couple stress-based three-layered micro rectangular plates exposed to multi-physical fields considering the flexoelectricity effects. Smart Struct. Syst. 2020, 26, 331–343. [Google Scholar]
- Arshid, E.; Kiani, A.; Amir, S. Magneto-electro-elastic vibration of moderately thick FG annular plates subjected to multi physical loads in thermal environment using GDQ method by considering neutral surface. Mater. Des. Appl. 2019. [Google Scholar] [CrossRef]
- Amir, S.; Khorasani, M.; BabaAkbar-Zarei, H. Buckling analysis of nanocomposite sandwich plates with piezoelectric face sheets based on flexoelectricity and first-order shear deformation theory. J. Sandw. Struct. Mater. 2020, 22, 2186–2209. [Google Scholar] [CrossRef]


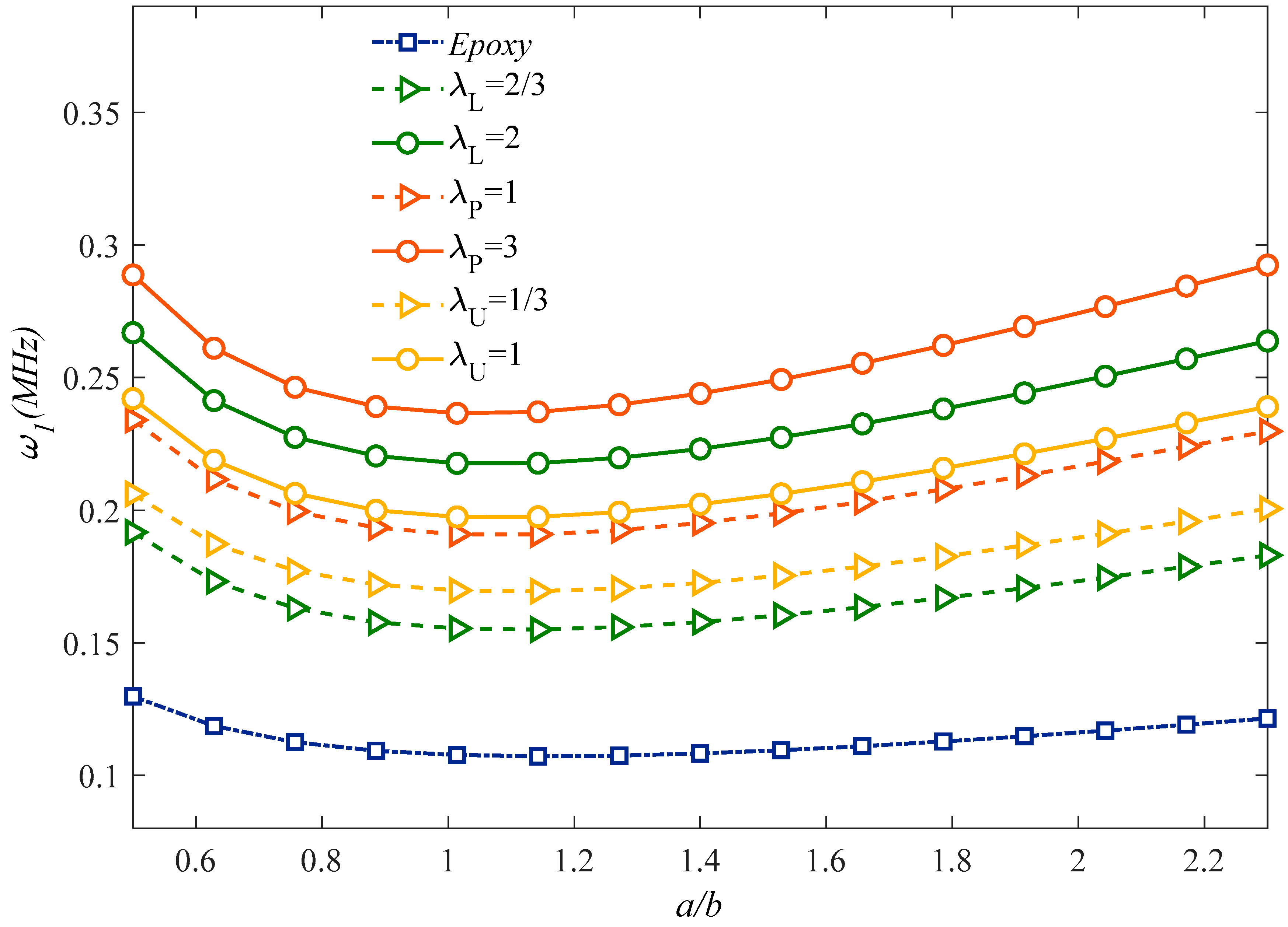
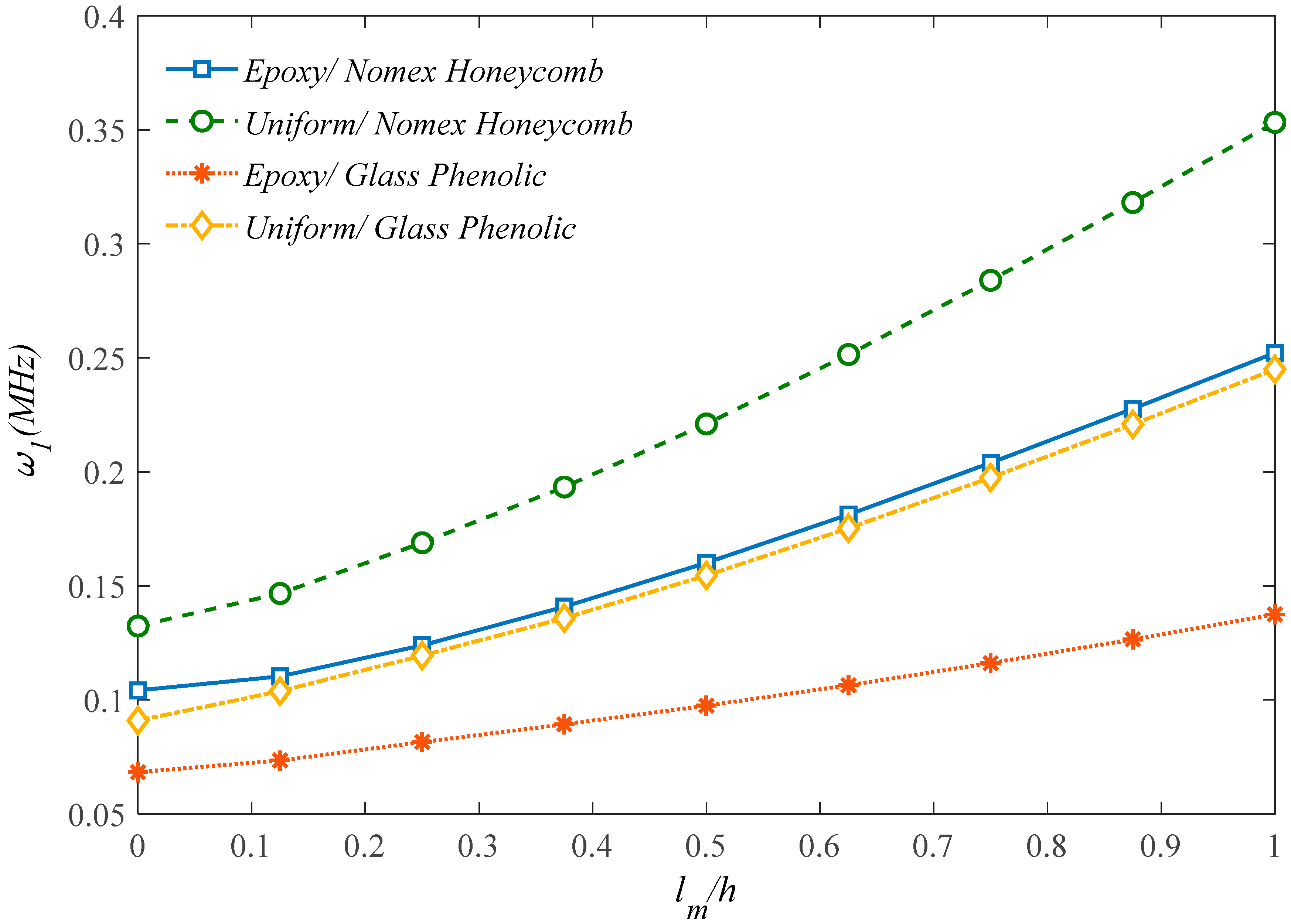
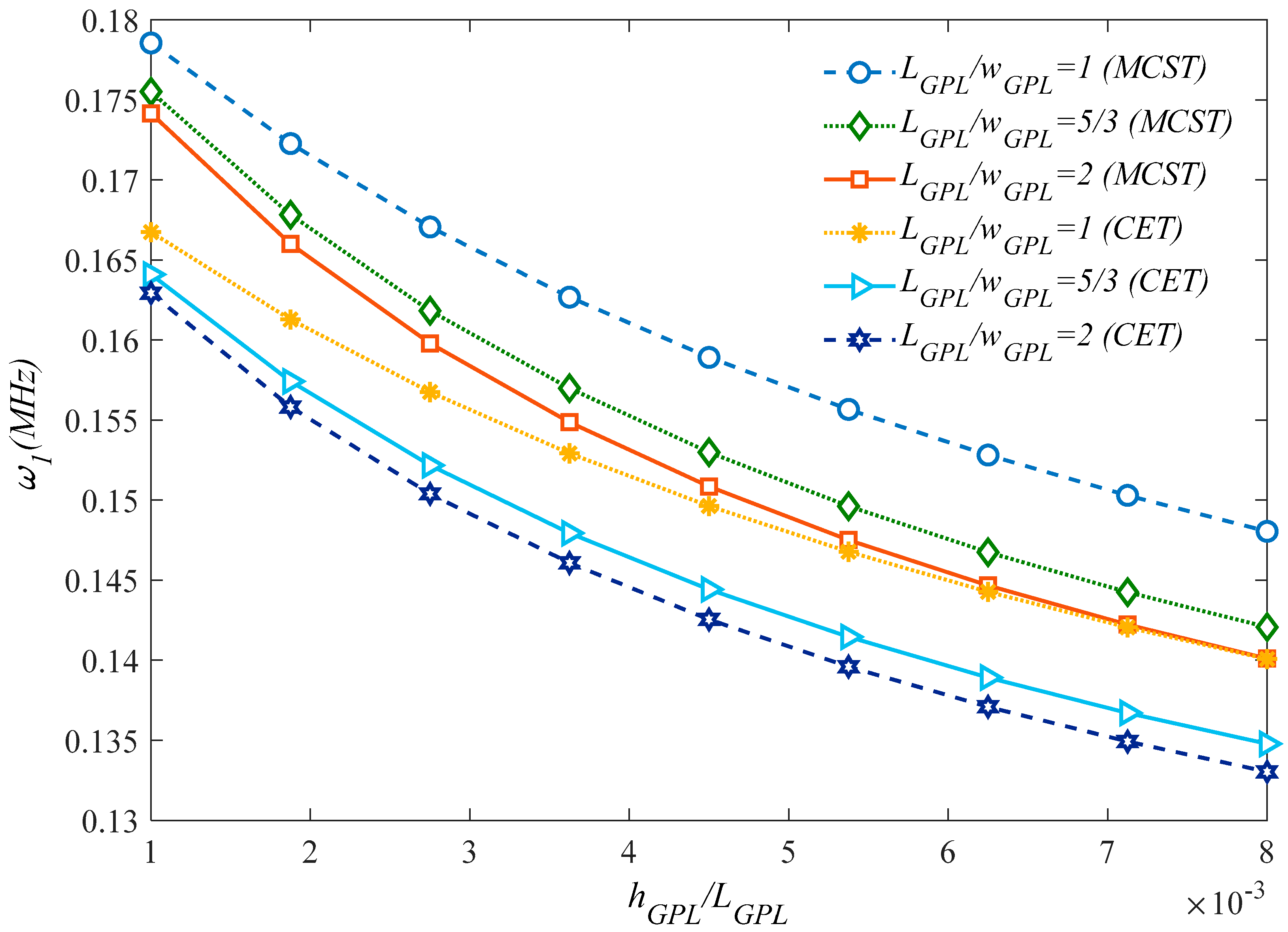
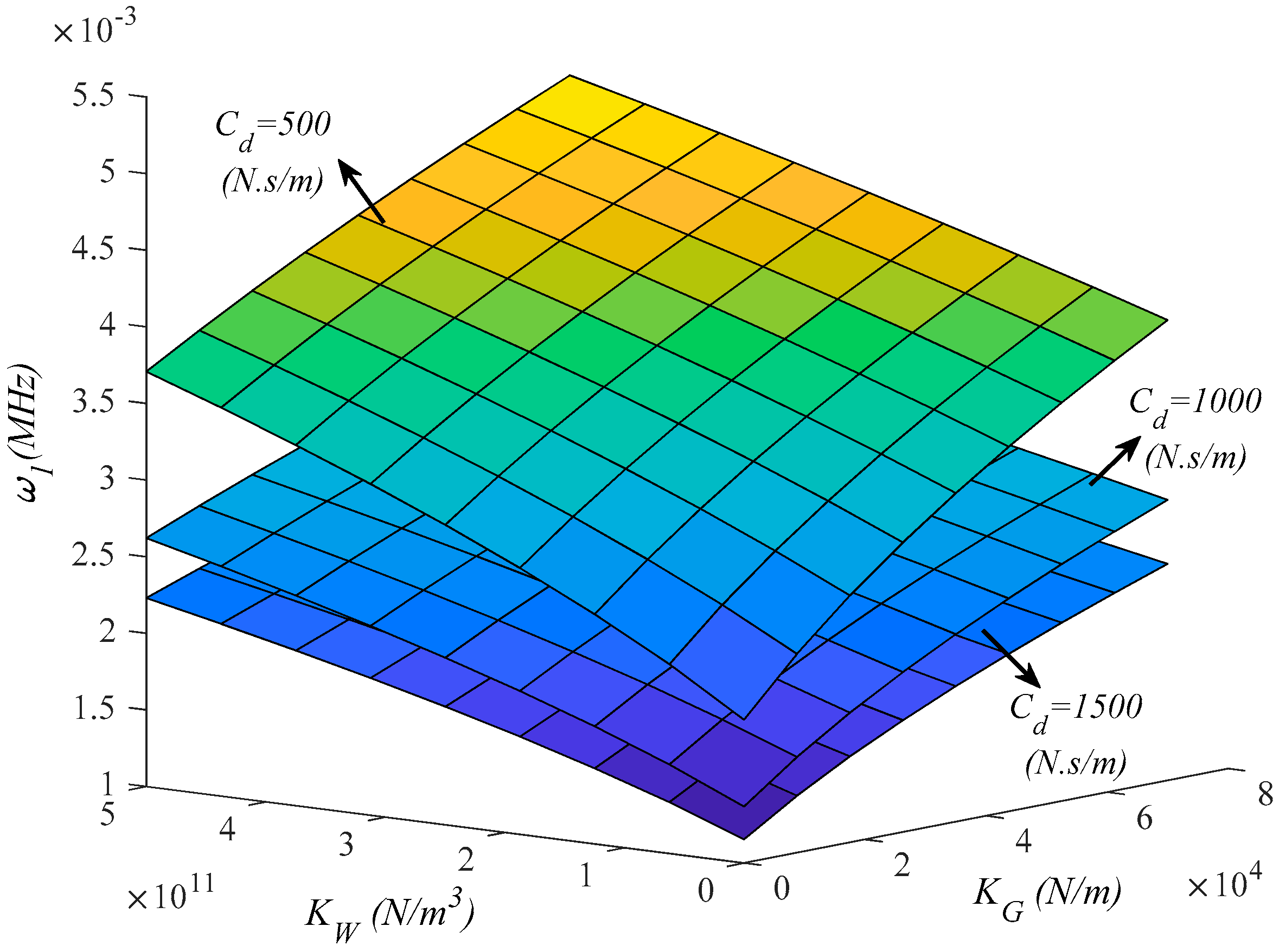
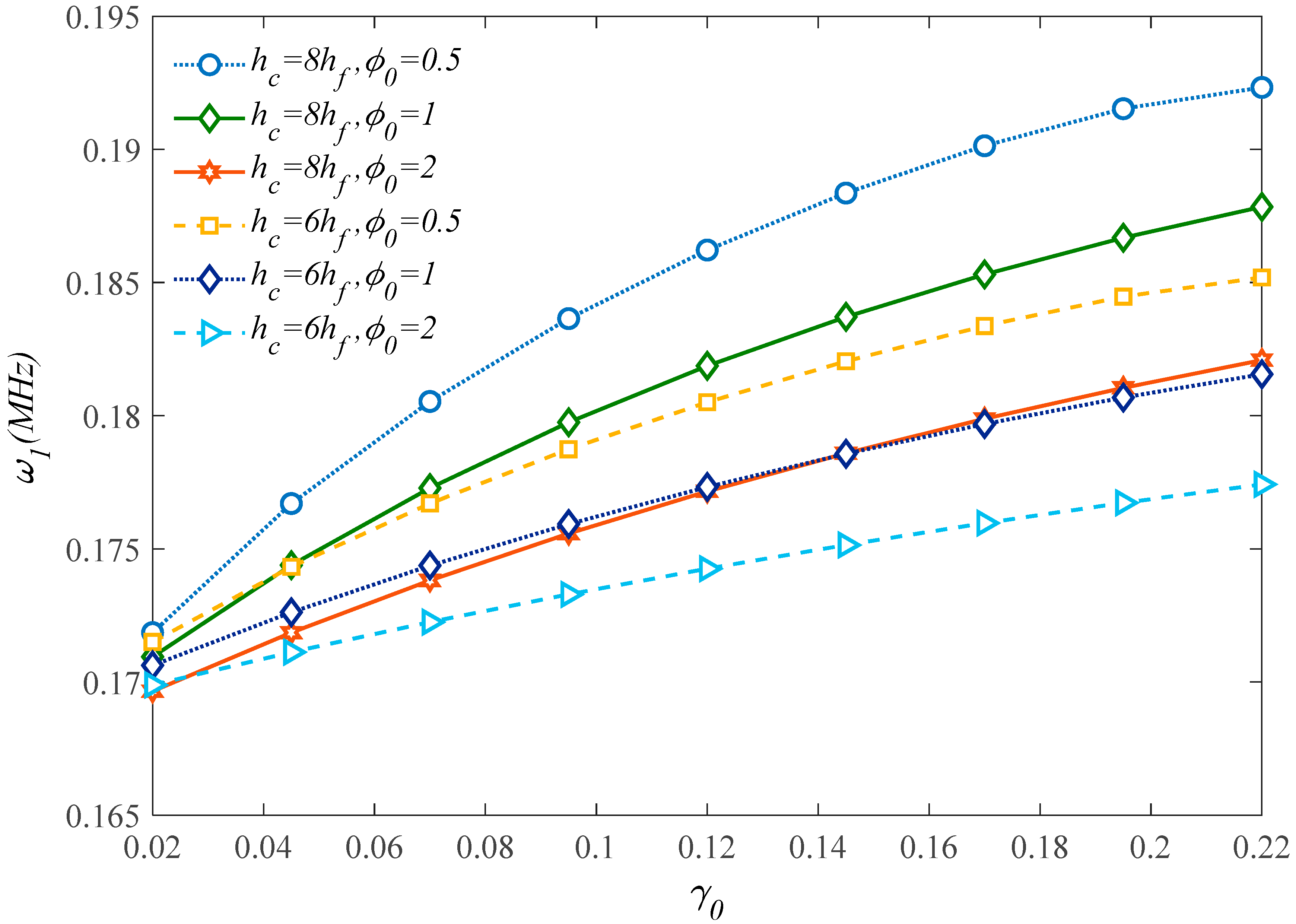

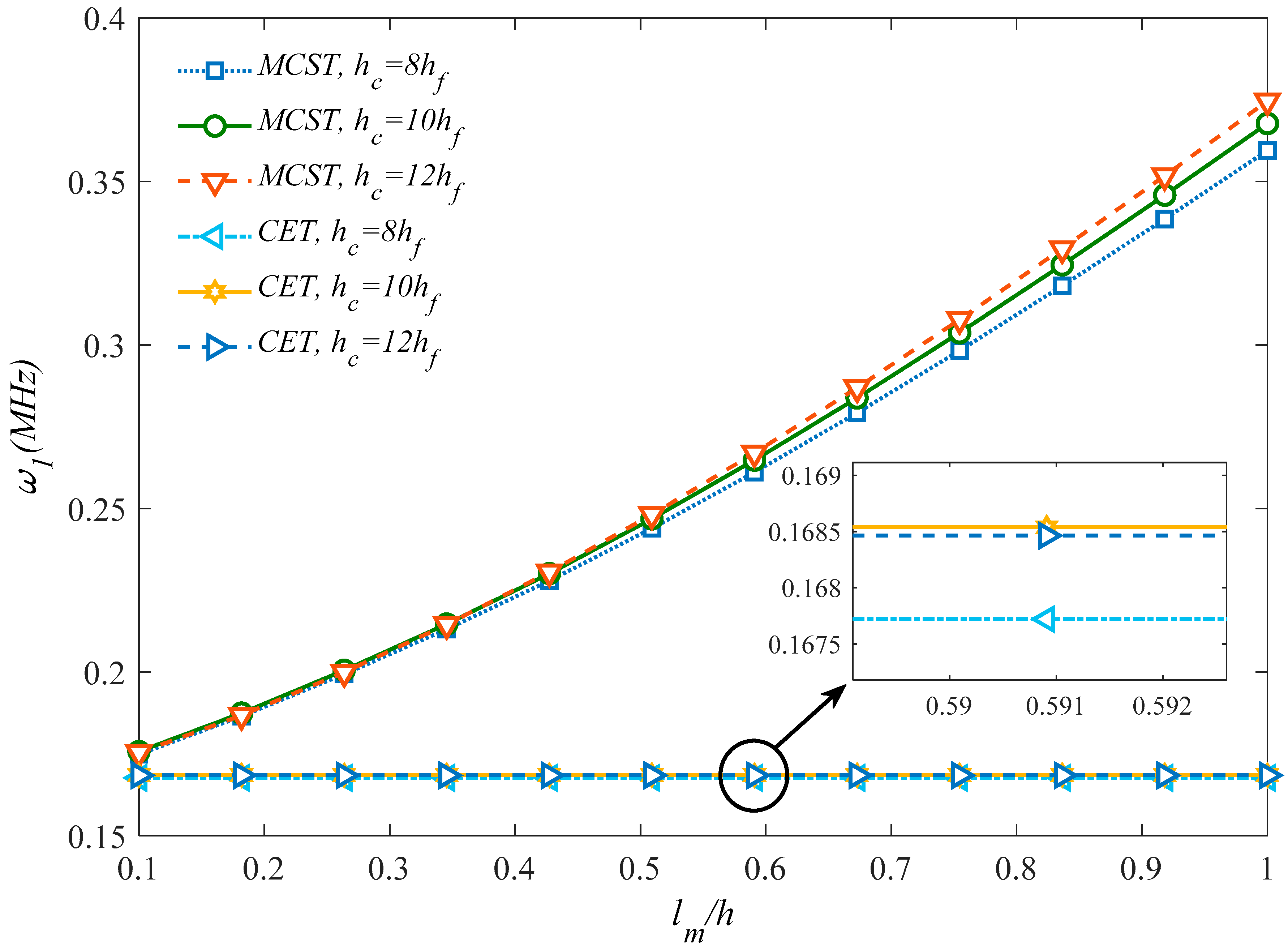
| Total GPLs Content (Percentage) | λU | λL | λP |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1/3 | 1/3 | 2/3 | 1 |
| 1 | 1 | 2 | 3 |
| a/h | lm/h | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | |||
| 5 | Epoxy | Present | 0.2145 | 0.2322 | 0.2786 | 0.3319 | 0.4143 | 0.4815 |
| Ref. [45] | 0.2148 | 0.2301 | 0.2708 | 0.3271 | 0.3920 | 0.4615 | ||
| Uniform | Present | 0.4460 | 0.4820 | 0.5794 | 0.7114 | 0.8622 | 1.0220 | |
| Ref. [45] | 0.4468 | 0.4789 | 0.5639 | 0.6813 | 0.8164 | 0.9613 | ||
| 10 | Epoxy | Present | 0.0586 | 0.0632 | 0.0752 | 0.0918 | 0.1109 | 0.1315 |
| Ref. [45] | 0.0586 | 0.0629 | 0.0745 | 0.0905 | 0.1091 | 0.1290 | ||
| Uniform | Present | 0.1219 | 0.1314 | 0.1564 | 0.1910 | 0.2308 | 0.2736 | |
| Ref. [45] | 0.1219 | 0.1310 | 0.1551 | 0.1885 | 0.2271 | 0.2686 | ||
| ω (MHz) | ||||
|---|---|---|---|---|
| (m, n) | ||||
| MCST | (1, 1) | 0.1789 | 0.1762 | 0.1728 |
| (2, 1) | 0.3821 | 0.3691 | 0.3542 | |
| (2, 2) | 0.5113 | 0.4940 | 0.4758 | |
| CET | (1, 1) | 0.1678 | 0.1633 | 0.1577 |
| (2, 1) | 0.3555 | 0.3376 | 0.3166 | |
| (2, 2) | 0.4545 | 0.4310 | 0.4064 | |
| ω (MHz) | ||||
|---|---|---|---|---|
| (m, n) | Uniform (λU = 1) | Parabolic (λP = 1) | Linear (λL = 2) | Epoxy |
| (1, 1) | 0.1745 | 0.1637 | 0.2115 | 0.1044 |
| (2, 1) | 0.3584 | 0.3368 | 0.4246 | 0.2192 |
| (2, 2) | 0.4832 | 0.4521 | 0.5670 | 0.2950 |
| (3, 1) | 0.5849 | 0.5505 | 0.6799 | 0.3656 |
| (3, 2) | 0.6794 | 0.6378 | 0.7860 | 0.4287 |
| (3, 3) | 0.8131 | 0.7606 | 0.9387 | 0.5016 |
Sample Availability: Samples of the compounds are not available from the authors. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arshid, H.; Khorasani, M.; Soleimani-Javid, Z.; Dimitri, R.; Tornabene, F. Quasi-3D Hyperbolic Shear Deformation Theory for the Free Vibration Study of Honeycomb Microplates with Graphene Nanoplatelets-Reinforced Epoxy Skins. Molecules 2020, 25, 5085. https://doi.org/10.3390/molecules25215085
Arshid H, Khorasani M, Soleimani-Javid Z, Dimitri R, Tornabene F. Quasi-3D Hyperbolic Shear Deformation Theory for the Free Vibration Study of Honeycomb Microplates with Graphene Nanoplatelets-Reinforced Epoxy Skins. Molecules. 2020; 25(21):5085. https://doi.org/10.3390/molecules25215085
Chicago/Turabian StyleArshid, Hossein, Mohammad Khorasani, Zeinab Soleimani-Javid, Rossana Dimitri, and Francesco Tornabene. 2020. "Quasi-3D Hyperbolic Shear Deformation Theory for the Free Vibration Study of Honeycomb Microplates with Graphene Nanoplatelets-Reinforced Epoxy Skins" Molecules 25, no. 21: 5085. https://doi.org/10.3390/molecules25215085
APA StyleArshid, H., Khorasani, M., Soleimani-Javid, Z., Dimitri, R., & Tornabene, F. (2020). Quasi-3D Hyperbolic Shear Deformation Theory for the Free Vibration Study of Honeycomb Microplates with Graphene Nanoplatelets-Reinforced Epoxy Skins. Molecules, 25(21), 5085. https://doi.org/10.3390/molecules25215085








