Charge Displacement Analysis—A Tool to Theoretically Characterize the Charge Transfer Contribution of Halogen Bonds
Abstract
1. Introduction
2. Methodological Aspects
3. Applications
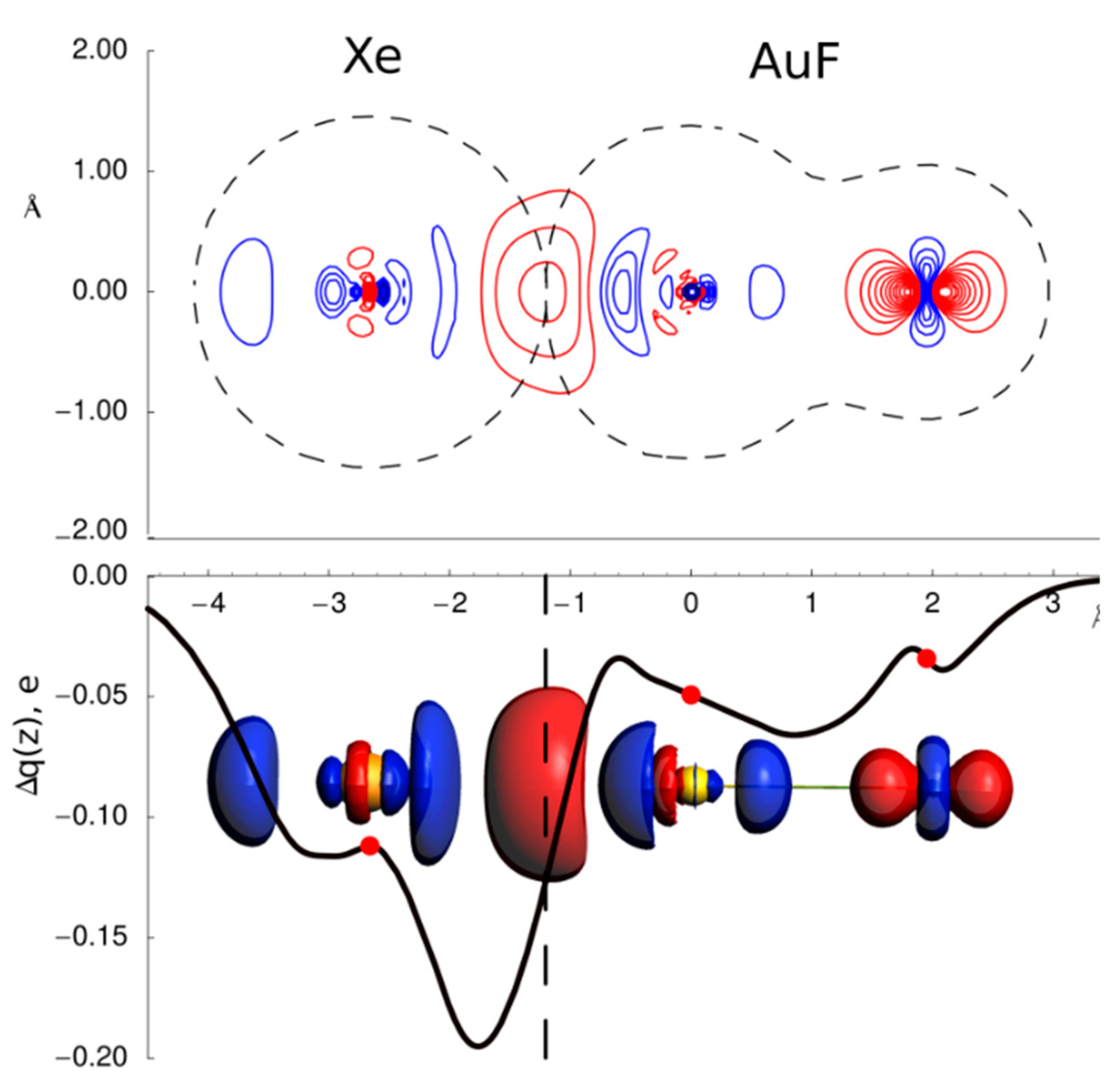
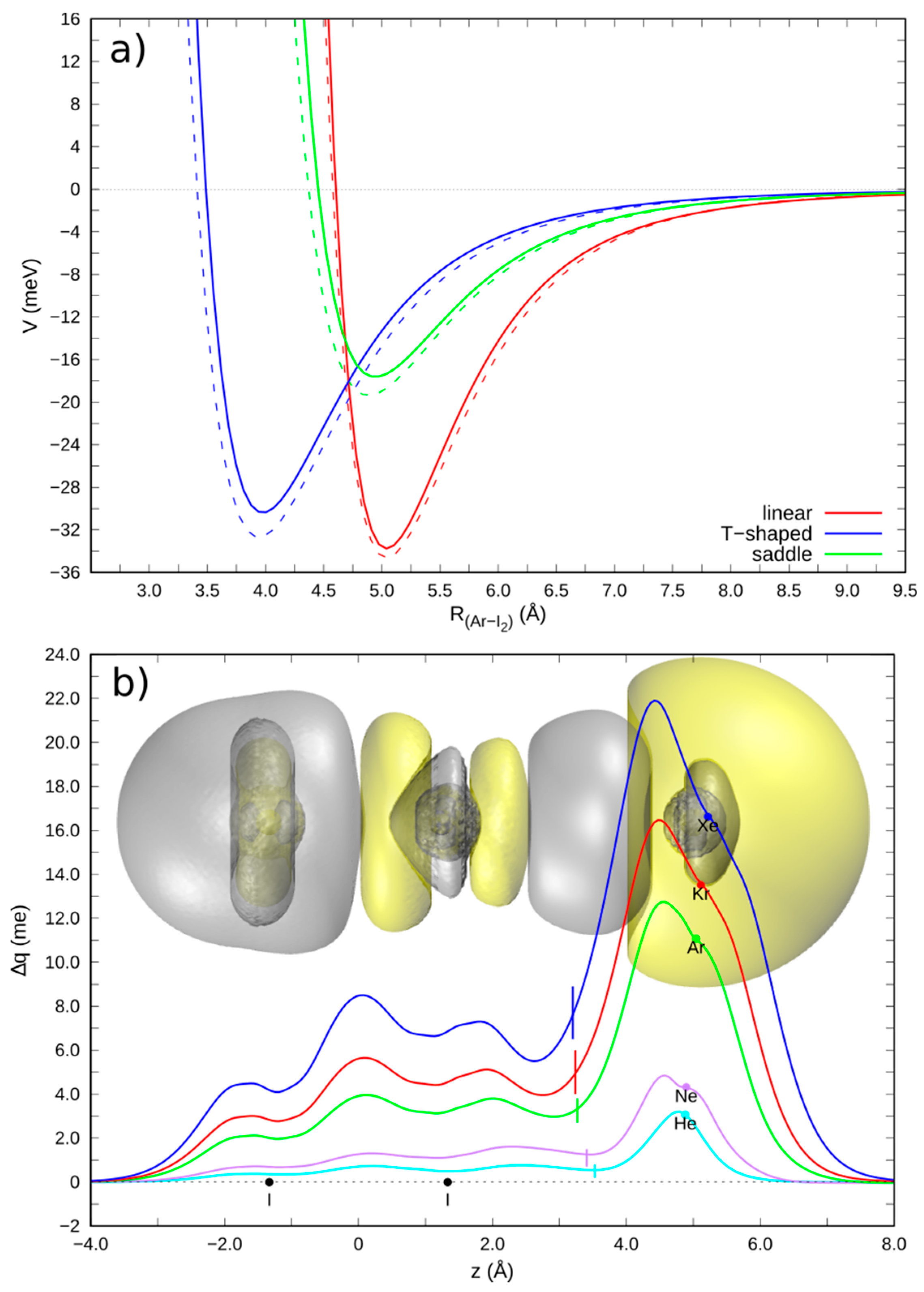
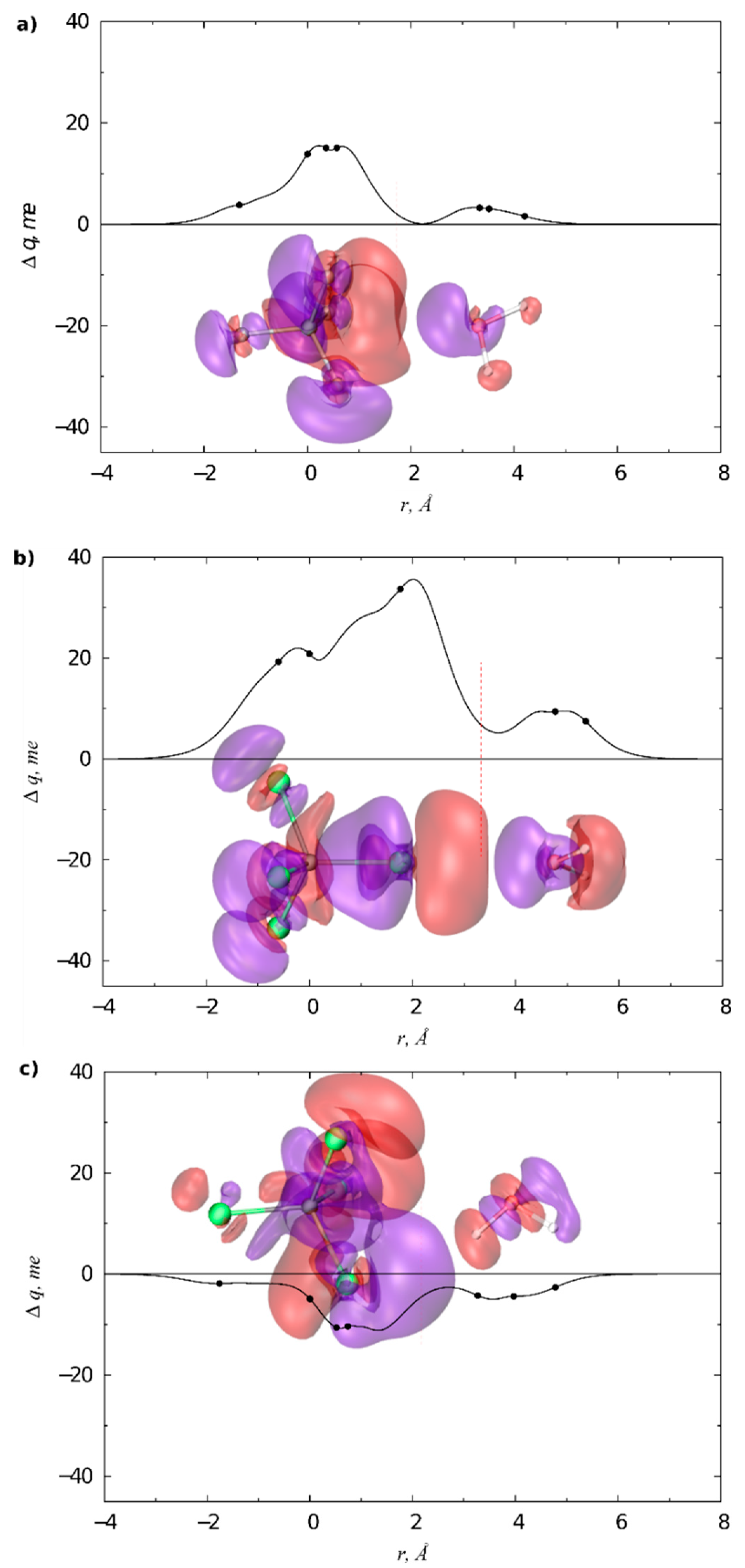
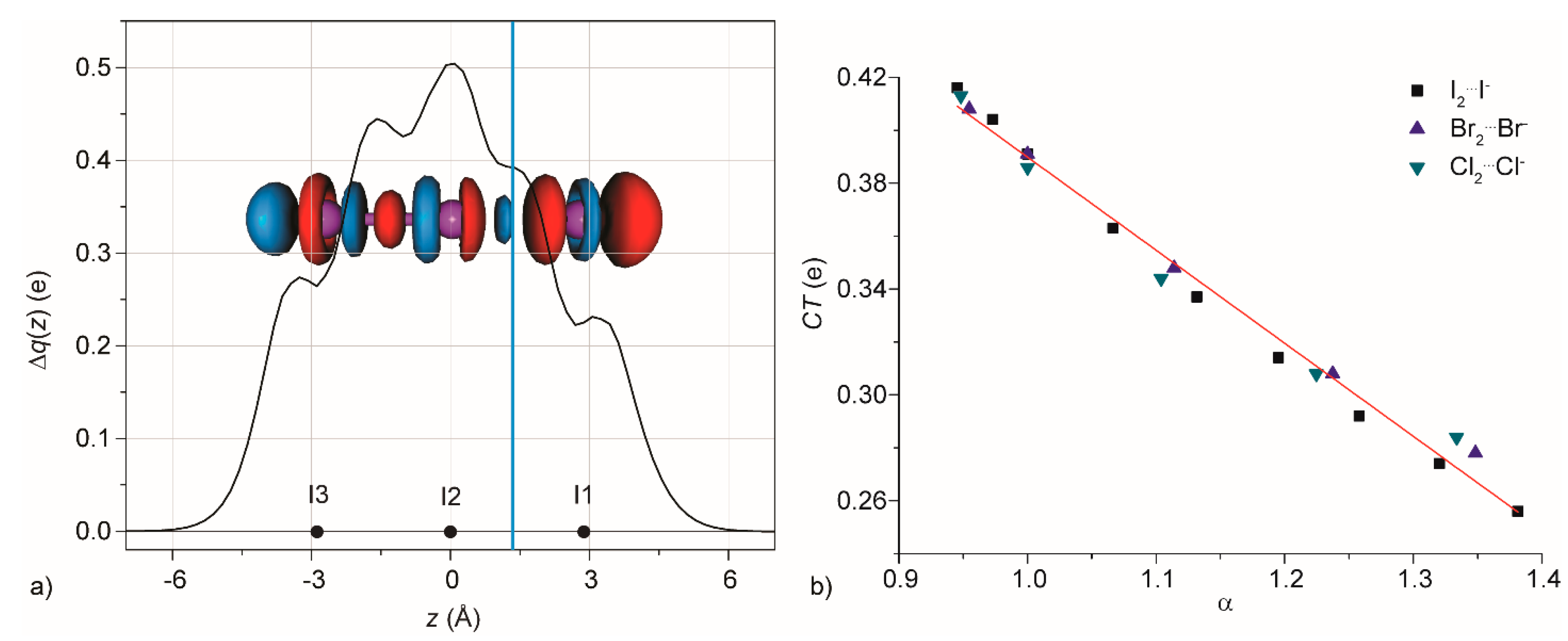
3.1. Gas Phase
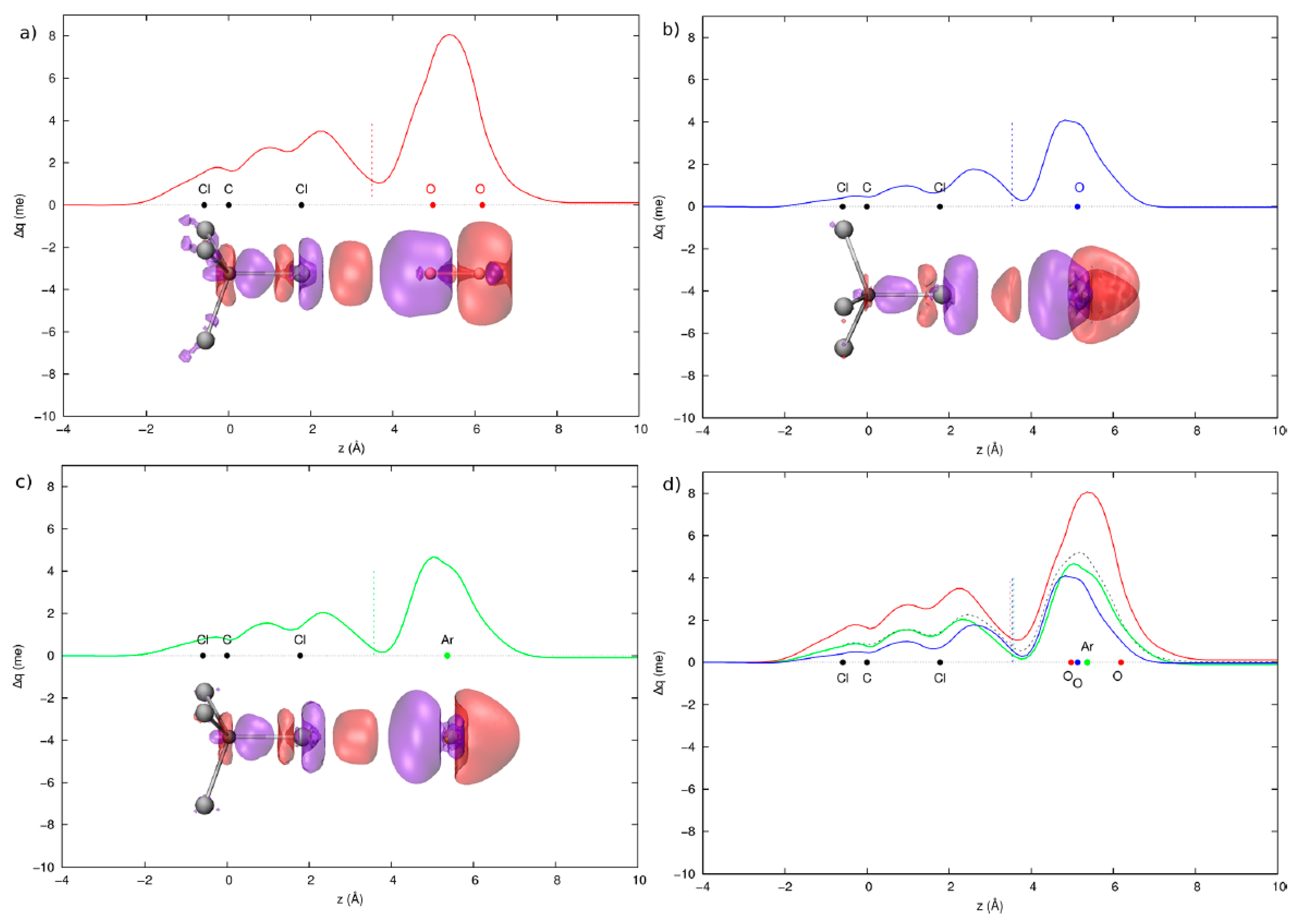
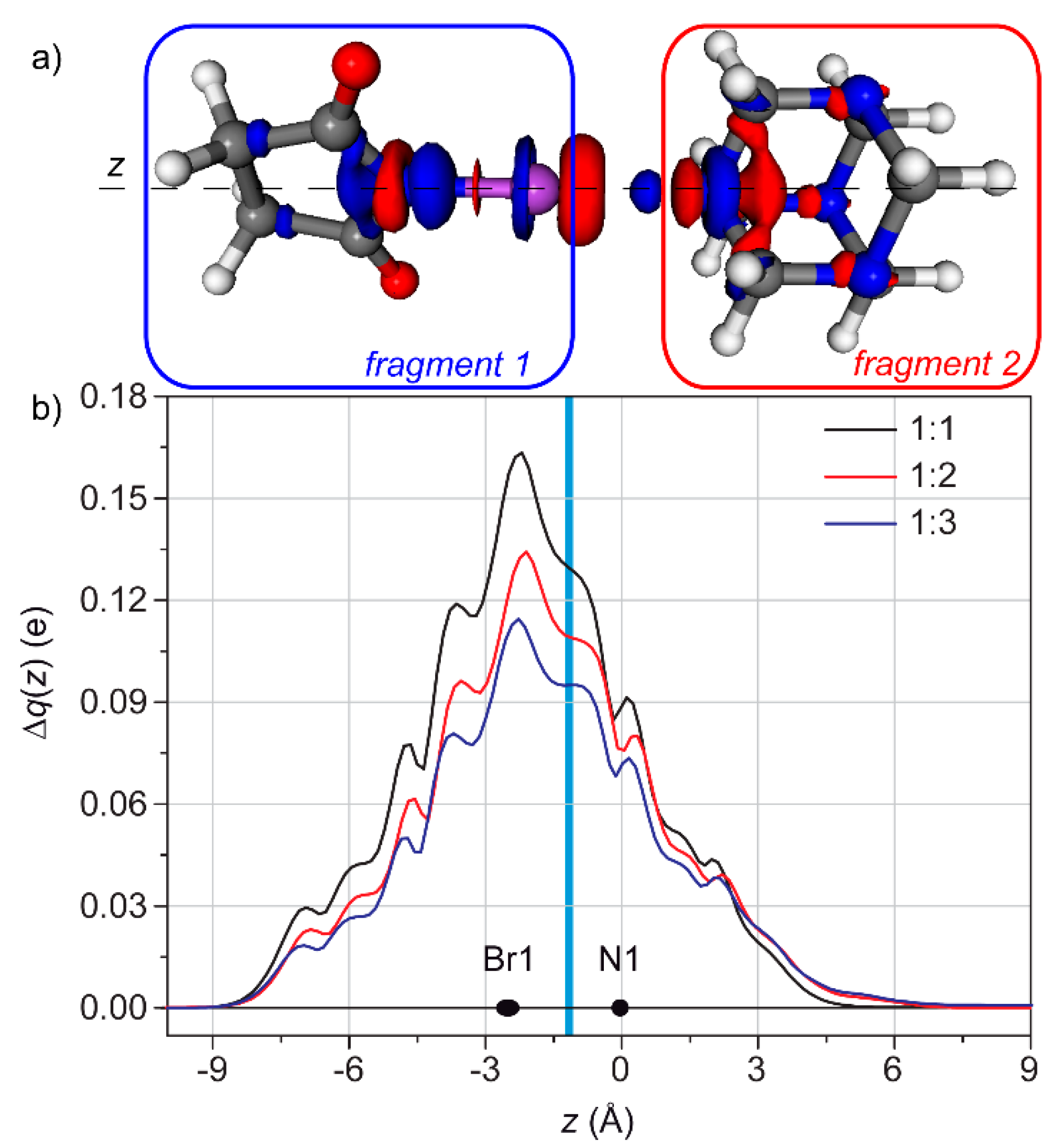
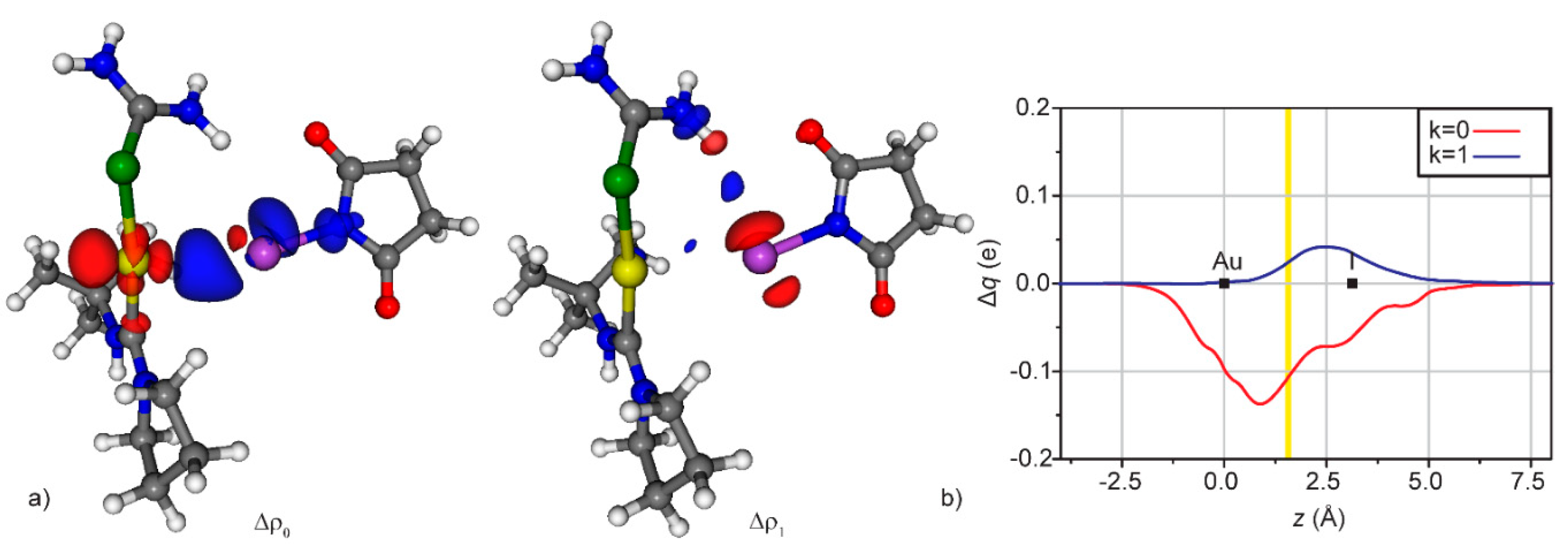
3.2. Condensed Phase
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Frenking, G.; Krapp, A. Unicorns in the World of Chemical Bonding Models. J. Comput. Chem. 2007, 28, 15–24. [Google Scholar] [CrossRef] [PubMed]
- Gross, L.; Schuler, B.; Pavliček, N.; Fatayer, S.; Majzik, Z.; Moll, N.; Peña, D.; Meyer, G. Atomic Force Microscopy for Molecular Structure Elucidation. Angew. Chem. Int. Ed. 2018, 57, 3888–3908. [Google Scholar] [CrossRef]
- Freund, S.; Pawlak, R.; Moser, L.; Hinaut, A.; Steiner, R.; Marinakis, N.; Constable, E.C.; Meyer, E.; Housecroft, C.E.; Glatzel, T. Transoid-to-Cisoid Conformation Changes of Single Molecules on Surfaces Triggered by Metal Coordination. ACS Omega 2018, 3, 12851–12856. [Google Scholar] [CrossRef] [PubMed]
- Ebeling, D.; Zhong, Q.; Ahles, S.; Chi, L.; Wegner, H.A.; Schirmeisen, A. Chemical Bond Imaging Using Higher Eigenmodes of Tuning Fork Sensors in Atomic Force Microscopy. Appl. Phys. Lett. 2017, 110, 183102. [Google Scholar] [CrossRef]
- Iwata, K.; Yamazaki, S.; Mutombo, P.; Hapala, P.; Ondráček, M.; Jelínek, P.; Sugimoto, Y. Chemical Structure Imaging of a Single Molecule by Atomic Force Microscopy at Room Temperature. Nat. Commun. 2015, 6, 7766. [Google Scholar] [CrossRef] [PubMed]
- Von Hopffgarten, M.; Frenking, G. Energy Decomposition Analysis. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 43–62. [Google Scholar] [CrossRef]
- Popelier, P.L.A. The QTAIM Perspective of Chemical Bonding. In The Chemical Bond: Fundamental Aspects of Chemical Bonding; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2014; Volume 9783527333, pp. 271–308. [Google Scholar]
- Stone, A.J.; Misquitta, A.J. Charge-Transfer in Symmetry-Adapted Perturbation Theory. Chem. Phys. Lett. 2009, 473, 201–205. [Google Scholar] [CrossRef]
- Mo, Y.; Bao, P.; Gao, J. Energy Decomposition Analysis Based on a Block-Localized Wavefunction and Multistate Density Functional Theory. Phys. Chem. Chem. Phys. 2011, 13, 6760–6775. [Google Scholar] [CrossRef]
- Mitoraj, M.; Michalak, A. Natural Orbitals for Chemical Valence as Descriptors of Chemical Bonding in Transition Metal Complexes. J. Mol. Model. 2007, 13, 347–355. [Google Scholar] [CrossRef]
- Radoń, M. On the Properties of Natural Orbitals for Chemical Valence. Theory Chem. Acc. 2008, 120, 337–339. [Google Scholar] [CrossRef]
- Schneider, W.B.; Bistoni, G.; Sparta, M.; Saitow, M.; Riplinger, C.; Auer, A.A.; Neese, F. Decomposition of Intermolecular Interaction Energies within the Local Pair Natural Orbital Coupled Cluster Framework. J. Chem. Theory Comput. 2016, 12, 4778–4792. [Google Scholar] [CrossRef] [PubMed]
- Belpassi, L.; Infante, I.; Tarantelli, F.; Visscher, L. The Chemical Bond between Au(I) and the Noble Gases. Comparative Study of NgAuF and NgAu+ (Ng = Ar, Kr, Xe) by Density Functional and Coupled Cluster Methods. J. Am. Chem. Soc. 2008, 130, 1048–1060. [Google Scholar] [CrossRef] [PubMed]
- Cappelletti, D.; Ronca, E.; Belpassi, L.; Tarantelli, F.; Pirani, F. Revealing Charge-Transfer Effects in Gas-Phase Water Chemistry. Acc. Chem. Res. 2012, 45, 1571–1580. [Google Scholar] [CrossRef] [PubMed]
- Belpassi, L.; Reca, M.L.; Tarantelli, F.; Roncaratti, L.F.; Pirani, F.; Cappelletti, D.; Faure, A.; Scribano, Y. Charge-Transfer Energy in the Water-Hydrogen Molecular Aggregate Revealed by Molecular-Beam Scattering Experiments, Charge Displacement Analysis, and Ab Initio Calculations. J. Am. Chem. Soc. 2010, 132, 13046–13058. [Google Scholar] [CrossRef]
- Ronca, E.; Belpassi, L.; Tarantelli, F. A Quantitative View of Charge Transfer in the Hydrogen Bond: The Water Dimer Case. ChemPhysChem 2014, 15, 2682–2687. [Google Scholar] [CrossRef]
- Nunzi, F.; Di Erasmo, B.; Tarantelli, F.; Cappelletti, D.; Pirani, F. The Halogen-Bond Nature in Noble Gas–Dihalogen Complexes from Scattering Experiments and Ab Initio Calculations. Molecules 2019, 24, 4274. [Google Scholar] [CrossRef]
- Pirani, F.; Cappelletti, D.; Falcinelli, S.; Cesario, D.; Nunzi, F.; Belpassi, L.; Tarantelli, F. Selective Emergence of the Halogen Bond in Ground and Excited States of Noble-Gas–Chlorine Systems. Angew. Chem. Int. Ed. 2019, 58, 4195–4199. [Google Scholar] [CrossRef]
- Ronca, E.; Pastore, M.; Belpassi, L.; Tarantelli, F.; De Angelis, F. Influence of the Dye Molecular Structure on the TiO2 Conduction Band in Dye-Sensitized Solar Cells: Disentangling Charge Transfer and Electrostatic Effects. Energy Environ. Sci. 2013, 6, 183–193. [Google Scholar] [CrossRef]
- Ronca, E.; Pastore, M.; Belpassi, L.; De Angelis, F.; Angeli, C.; Cimiraglia, R.; Tarantelli, F. Charge-Displacement Analysis for Excited States. J. Chem. Phys. 2014, 140, 054110. [Google Scholar] [CrossRef]
- Sorbelli, D.; Belpassi, L.; Tarantelli, F.; Belanzoni, P. Ligand Effect on Bonding in Gold(III) Carbonyl Complexes. Inorg. Chem. 2018, 57, 6161–6175. [Google Scholar] [CrossRef]
- Salvi, N.; Belpassi, L.; Tarantelli, F. On the Dewar-Chatt-Duncanson Model for Catalytic Gold(I) Complexes. Chem. A Eur. J. 2010, 16, 7231–7240. [Google Scholar] [CrossRef] [PubMed]
- Gaggioli, C.A.; Bistoni, G.; Ciancaleoni, G.; Tarantelli, F.; Belpassi, L.; Belanzoni, P. Modulating the Bonding Properties of N-Heterocyclic Carbenes (NHCs): A Systematic Charge-Displacement Analysis. Chem. A Eur. J. 2017, 23, 7558–7569. [Google Scholar] [CrossRef] [PubMed]
- Bartalucci, N.; Belpassi, L.; Marchetti, F.; Pampaloni, G.; Zacchini, S.; Ciancaleoni, G. Ubiquity of Cis-Halide → Isocyanide Direct Interligand Interaction in Organometallic Complexes. Inorg. Chem. 2018, 57, 14554–14563. [Google Scholar] [CrossRef] [PubMed]
- Ciancaleoni, G.; Belpassi, L.; Marchetti, F. Back-Donation in High-Valent D0 Metal Complexes: Does It Exist? The Case of NbV. Inorg. Chem. 2017, 56, 11266–11274. [Google Scholar] [CrossRef] [PubMed]
- Bistoni, G.; Rampino, S.; Scafuri, N.; Ciancaleoni, G.; Zuccaccia, D.; Belpassi, L.; Tarantelli, F. How π Back-Donation Quantitatively Controls the CO Stretching Response in Classical and Non-Classical Metal Carbonyl Complexes. Chem. Sci. 2016, 7, 1174–1184. [Google Scholar] [CrossRef]
- Ciancaleoni, G.; Biasiolo, L.; Bistoni, G.; Macchioni, A.; Tarantelli, F.; Zuccaccia, D.; Belpassi, L. Selectively Measuring Π Back-Donation in Gold(I) Complexes by NMR Spectroscopy. Chem. A Eur. J. 2015, 21, 2467–2473. [Google Scholar] [CrossRef]
- Marchione, D.; Izquierdo, M.A.; Bistoni, G.; Havenith, R.W.A.; Macchioni, A.; Zuccaccia, D.; Tarantelli, F.; Belpassi, L. 13C NMR Spectroscopy of N-Heterocyclic Carbenes Can Selectively Probe σ Donation in Gold(I) Complexes. Chem. A Eur. J. 2017, 23, 2722–2728. [Google Scholar] [CrossRef]
- Azzopardi, K.M.; Bistoni, G.; Ciancaleoni, G.; Tarantelli, F.; Zuccaccia, D.; Belpassi, L. Quantitative Assessment of the Carbocation/Carbene Character of the Gold–Carbene Bond. Dalton Trans. 2015, 44, 13999–14007. [Google Scholar] [CrossRef]
- Nunzi, F.; Cesario, D.; Pirani, F.; Belpassi, L.; Frenking, G.; Grandinetti, F.; Tarantelli, F. Helium Accepts Back-Donation in Highly Polar Complexes: New Insights into the Weak Chemical Bond. J. Phys. Chem. Lett. 2017, 8, 3334–3340. [Google Scholar] [CrossRef]
- Cesario, D.; Nunzi, F.; Belpassi, L.; Pirani, F.; Ronca, E.; Tarantelli, F. Chemical Bond Mechanism for Helium Revealed by Electronic Excitation. J. Phys. Chem. A 2019, 123, 6572–6577. [Google Scholar] [CrossRef]
- Ciancaleoni, G.; Santi, C.; Ragni, M.; Braga, A.L. Charge-Displacement Analysis as a Tool to Study Chalcogen Bonded Adducts and Predict Their Association Constants in Solution. Dalton Trans. 2015, 44, 20168–20175. [Google Scholar] [CrossRef] [PubMed]
- Ciancaleoni, G. Lewis Base Activation of Lewis Acid: A Detailed Bond Analysis. ACS Omega 2018, 3, 16292–16300. [Google Scholar] [CrossRef] [PubMed]
- Novák, M.; Foroutan-Nejad, C.; Marek, R. Asymmetric Bifurcated Halogen Bonds. Phys. Chem. Chem. Phys. 2015, 17, 6440–6450. [Google Scholar] [CrossRef] [PubMed]
- Bora, P.L.; Novák, M.; Novotný, J.; Foroutan-Nejad, C.; Marek, R. Supramolecular Covalence in Bifurcated Chalcogen Bonding. Chem. A Eur. J. 2017, 23, 7315–7323. [Google Scholar] [CrossRef] [PubMed]
- Mitoraj, M.P.; Michalak, A. Theoretical Description of Halogen Bonding—An Insight Based on the Natural Orbitals for Chemical Valence Combined with the Extended-Transition—State Method (ETS-NOCV). J. Mol. Model. 2013, 19, 4681–4688. [Google Scholar] [CrossRef] [PubMed]
- Buttarazzi, E.; Rosi, F.; Ciancaleoni, G. Influence of Halogen Bonding on Gold(i)—Ligand Bond Components and DFT Characterization of a Gold–Iodine Halogen Bond. Phys. Chem. Chem. Phys. 2019, 21, 20478–20485. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the Halogen Bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Halogen Bonding: An Interim Discussion. ChemPhysChem 2013, 14, 278–294. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen Bonding: An Electrostatically-Driven Highly Directional Noncovalent Interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef]
- Brinck, T.; Borrfors, A.N. Electrostatics and Polarization Determine the Strength of the Halogen Bond: A Red Card for Charge Transfer. J. Mol. Model. 2019, 25, 125. [Google Scholar] [CrossRef]
- Wolters, L.P.; Schyman, P.; Pavan, M.J.; Jorgensen, W.L.; Bickelhaupt, F.M.; Kozuch, S. The Many Faces of Halogen Bonding: A Review of Theoretical Models and Methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 523–540. [Google Scholar] [CrossRef]
- Robertson, C.C.; Perutz, R.N.; Brammer, L.; Hunter, C.A. A Solvent-Resistant Halogen Bond. Chem. Sci. 2014, 5, 4179–4183. [Google Scholar] [CrossRef]
- Weinberger, C.; Hines, R.; Zeller, M.; Rosokha, S.V. Continuum of Covalent to Intermolecular Bonding in the Halogen-Bonded Complexes of 1,4-Diazabicyclo [2.2.2] Octane with Bromine-Containing Electrophiles. Chem. Commun. 2018, 54, 8060–8063. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Halogen Bonding: A Halogen-Centered Noncovalent Interaction yet to Be Understood. Inorganics 2019, 7, 40. [Google Scholar] [CrossRef]
- Eraković, M.; Cinčić, D.; Molčanov, K.; Stilinović, V. A Crystallographic Charge Density Study of the Partial Covalent Nature of Strong N⋅⋅⋅Br Halogen Bonds. Angew. Chem. Int. Ed. 2019, 58, 15702–15706. [Google Scholar] [CrossRef]
- Altun, A.; Neese, F.; Bistoni, G. Effect of Electron Correlation on Intermolecular Interactions: A Pair Natural Orbitals Coupled Cluster Based Local Energy Decomposition Study. J. Chem. Theory Comput. 2019, 15, 215–228. [Google Scholar] [CrossRef]
- Nalewajski, R.F.; Köster, A.M.; Jug, K. Chemical Valence from the Two-Particle Density Matrix. Theory Chim. Acta 1993, 85, 463–484. [Google Scholar] [CrossRef]
- Nalewajski, R.F.; Ozek, J. Modified Valence Indices from the Two-particle Density Matrix. Int. J. Quantum Chem. 1994, 51, 187–200. [Google Scholar] [CrossRef]
- Nalewajski, R.F.; Mrozek, J.; Michalak, A. Two-Electron Valence Indices from the Kohn-Sham Orbitals. Int. J. Quantum Chem. 1997, 61, 589–601. [Google Scholar] [CrossRef]
- Bistoni, G.; Rampino, S.; Tarantelli, F.; Belpassi, L. Charge-Displacement Analysis via Natural Orbitals for Chemical Valence: Charge Transfer Effects in Coordination Chemistry. J. Chem. Phys. 2015, 142, 084112. [Google Scholar] [CrossRef]
- Cooke, S.A.; Gerry, M.C.L. XeAuF. J. Am. Chem. Soc. 2004, 126, 17000–17008. [Google Scholar] [CrossRef] [PubMed]
- Evans, C.J.; Lesarri, A.; Gerry, M.C.L. Noble Gas-Metal Chemical Bonds. Microwave Spectra, Geometries, and Nuclear Quadrupole Coupling Constants of Ar-AuCl and Kr-AuCl. J. Am. Chem. Soc. 2000, 122, 6100–6105. [Google Scholar] [CrossRef]
- Nunzi, F.; Cesario, D.; Belpassi, L.; Tarantelli, F.; Roncaratti, L.F.; Falcinelli, S.; Cappelletti, D.; Pirani, F. Insight into the Halogen-Bond Nature of Noble Gas-Chlorine Systems by Molecular Beam Scattering Experiments: Ab Initio Calculations and Charge Displacement Analysis. Phys. Chem. Chem. Phys. 2019, 21, 7330–7340. [Google Scholar] [CrossRef] [PubMed]
- Pirani, F.; Brizi, S.; Roncaratti, L.F.; Casavecchia, P.; Cappelletti, D.; Vecchiocattivi, F. Beyond the Lennard-Jones Model: A Simple and Accurate Potential Function Probed by High Resolution Scattering Data Useful for Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2008, 10, 5489–5503. [Google Scholar] [CrossRef] [PubMed]
- Cappelletti, D.; Aquilanti, V.; Bartocci, A.; Nunzi, F.; Tarantelli, F.; Belpassi, L.; Pirani, F. Interaction of O2 with CH4, CF4, and CCl4 by Molecular Beam Scattering Experiments and Theoretical Calculations. J. Phys. Chem. A 2016, 120, 5197–5207. [Google Scholar] [CrossRef]
- De Santis, M.; Nunzi, F.; Cesario, D.; Belpassi, L.; Tarantelli, F.; Cappelletti, D.; Pirani, F. Cooperative Role of Halogen and Hydrogen Bonding in the Stabilization of Water Adducts with Apolar Molecules. New J. Chem. 2018, 42, 10603–10614. [Google Scholar] [CrossRef]
- Aragoni, M.C.; Arca, M.; Devillanova, F.A.; Isaia, F.; Lippolis, V. Adducts of S/Se Donors with Dihalogens as a Source of Information for Categorizing the Halogen Bonding. Cryst. Growth Des. 2012, 12, 2769–2779. [Google Scholar] [CrossRef]
- Brown, I.D. Bond Valence Theory: Part I, a New Twist to an Old Description of Chemical Bonding. J. Chem. Educ. 1976, 53, 100–101. [Google Scholar] [CrossRef]
- Brown, I.D. Bond Valence Theory: Part II, Examples. J. Chem. Educ. 1976, 53, 231. [Google Scholar] [CrossRef]
- Ciancaleoni, G.; Arca, M.; Caramori, G.F.; Frenking, G.; Schneider, F.S.S.; Lippolis, V. Bonding Analysis in Homo- and Hetero-Trihalide Species: A Charge Displacement Study. Eur. J. Inorg. Chem. 2016, 2016, 3804–3812. [Google Scholar] [CrossRef]
- Schneider, F.S.S.; Caramori, G.F.; Parreira, R.L.T.; Lippolis, V.; Arca, M.; Ciancaleoni, G. Bond Analysis in Dihalogen—Halide and Dihalogen—Dimethylchalcogenide Systems. Eur. J. Inorg. Chem. 2018, 2018, 1007–1015. [Google Scholar] [CrossRef]
- Turney, J.M.; Simmonett, A.C.; Parrish, R.M.; Hohenstein, E.G.; Evangelista, F.A.; Fermann, J.T.; Mintz, B.J.; Burns, L.A.; Wilke, J.J.; Abrams, M.L.; et al. Psi4: An Open-Source Ab Initio Electronic Structure Program. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 556–565. [Google Scholar] [CrossRef]
- Ciancaleoni, G.; Macchioni, A.; Rocchigiani, L.; Zuccaccia, C. A PGSE NMR Approach to the Characterization of Single and Multi-Site Halogen-Bonded Adducts in Solution. RSC Adv. 2016, 6, 80604–80612. [Google Scholar] [CrossRef]
- McDowell, S.A.C.; Joseph, J.A. Cooperative Effects of Noncovalent Bonds to the Br Atom of Halogen-Bonded H3NBrZ and HCNBrZ (Z F, Br) Complexes. J. Chem. Phys. 2012, 137, 074310. [Google Scholar] [CrossRef] [PubMed]
- George, J.; Deringer, V.L.; Dronskowski, R. Cooperativity of Halogen, Chalcogen, and Pnictogen Bonds in Infinite Molecular Chains by Electronic Structure Theory. J. Phys. Chem. A 2014, 118, 3193–3200. [Google Scholar] [CrossRef]
- Ciancaleoni, G. Cooperativity between Hydrogen- and Halogen Bonds: The Case of Selenourea. Phys. Chem. Chem. Phys. 2018, 20, 8506–8514. [Google Scholar] [CrossRef]
- Esrafili, M.D.; Mousavian, P. Unusual Cooperativity Effects between Halogen Bond and Donor-Acceptor Interactions: The Role of Orbital Interaction. Chem. Phys. Lett. 2017, 678, 275–282. [Google Scholar] [CrossRef]
- Kelly, R.A.; Clavier, H.; Giudice, S.; Scott, N.M.; Stevens, E.D.; Bordner, J.; Samardjiev, I.; Hoff, C.D.; Cavallo, L.; Nolan, S.P. Determination of N-Heterocyclic Carbene (NHC) Steric and Electronic Parameters Using the [(NHC)Ir(CO)2Cl] System. Organometallics 2008, 27, 202–210. [Google Scholar] [CrossRef]
- Nelson, D.J.; Nolan, S.P. Quantifying and Understanding the Electronic Properties of N-Heterocyclic Carbenes. Chem. Soc. Rev. 2013, 42, 6723–6753. [Google Scholar] [CrossRef]
- Bistoni, G.; Belanzoni, P.; Belpassi, L.; Tarantelli, F. π Activation of Alkynes in Homogeneous and Heterogeneous Gold Catalysis. J. Phys. Chem. A 2016, 120, 5239–5247. [Google Scholar] [CrossRef]
- Rogachev, A.Y.; Hoffmann, R. Iodine (I2) as a Janus-Faced Ligand in Organometallics. J. Am. Chem. Soc. 2013, 135, 3262–3275. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.; Li, Q.; Li, H.B.; Li, W.; Cheng, J. How Do Organic Gold Compounds and Organic Halogen Molecules Interact? Comparison with Hydrogen Bonds. RSC Adv. 2015, 5, 12488–12497. [Google Scholar] [CrossRef]
- Ivanov, D.M.; Novikov, A.S.; Ananyev, I.V.; Kirina, Y.V.; Kukushkin, V.Y. Halogen Bonding between Metal Centers and Halocarbons. Chem. Commun. 2016, 52, 5565–5568. [Google Scholar] [CrossRef] [PubMed]
| Fragments | CT0 | CT1 | CT2 | CT3 | CTtot,back |
|---|---|---|---|---|---|
| [(SeU)Au]+…[NAC] | 0.359 | −0.049 | −0.030 | −0.013 | −0.092 |
| [SeU]…[Au(NAC)]+ | 0.346 | 0.024 | −0.021 | −0.016 | −0.037 |
| [(SeU)(ICF2CF3)Au]+…[NAC] | 0.372 | −0.040 | −0.030 | −0.010 | −0.080 |
| [(SeU)(ICF2CF3)]…[Au(NAC)]+ | 0.344 | 0.020 | −0.021 | −0.015 | −0.036 |
| [ICF2CF3]…[Au(SeU)(NAC)]+ | −0.039 | 0.005 | - | - | - |
| [(SeU)(NIS)Au]+…[NAC] | 0.375 | −0.044 | −0.027 | −0.010 | −0.081 |
| [SeU]…[Au(NIS)(NAC)]+ | 0.373 | 0.033 | −0.018 | −0.014 | −0.032 |
| [NIS]…[Au(SeU)(NAC)]+ | −0.106 | 0.024 | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciancaleoni, G.; Nunzi, F.; Belpassi, L. Charge Displacement Analysis—A Tool to Theoretically Characterize the Charge Transfer Contribution of Halogen Bonds. Molecules 2020, 25, 300. https://doi.org/10.3390/molecules25020300
Ciancaleoni G, Nunzi F, Belpassi L. Charge Displacement Analysis—A Tool to Theoretically Characterize the Charge Transfer Contribution of Halogen Bonds. Molecules. 2020; 25(2):300. https://doi.org/10.3390/molecules25020300
Chicago/Turabian StyleCiancaleoni, Gianluca, Francesca Nunzi, and Leonardo Belpassi. 2020. "Charge Displacement Analysis—A Tool to Theoretically Characterize the Charge Transfer Contribution of Halogen Bonds" Molecules 25, no. 2: 300. https://doi.org/10.3390/molecules25020300
APA StyleCiancaleoni, G., Nunzi, F., & Belpassi, L. (2020). Charge Displacement Analysis—A Tool to Theoretically Characterize the Charge Transfer Contribution of Halogen Bonds. Molecules, 25(2), 300. https://doi.org/10.3390/molecules25020300