Analysis of the Stochastic Quarter-Five Spot Problem Using Polynomial Chaos
Abstract
1. Introduction
2. Mathematical Statement of the Quarter-Five Spot Problem
2.1. The Deterministic Problem
2.2. The Stochastic Problem
3. Solution Implementation
3.1. The Deterministic Problem
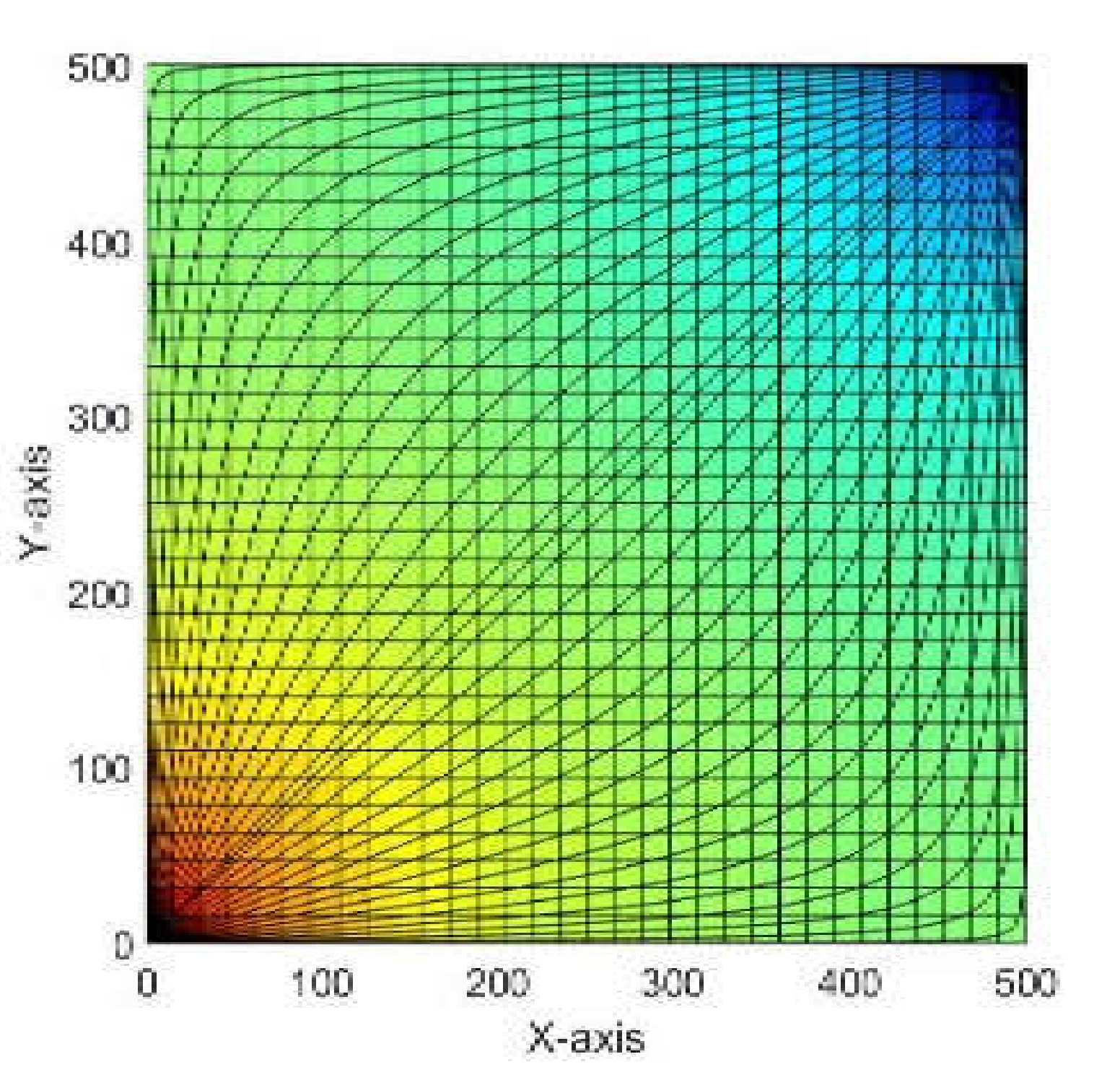
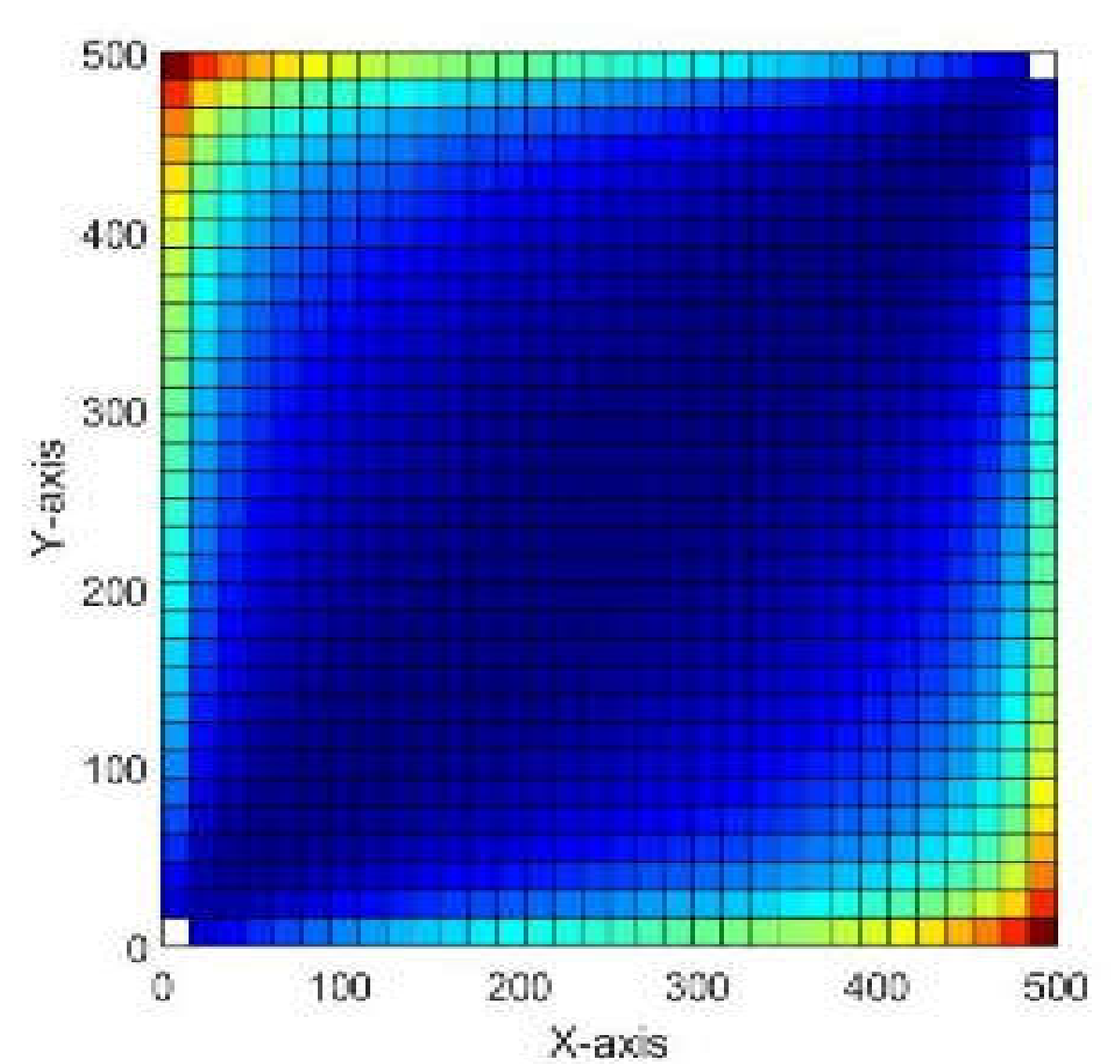
Numerical Example
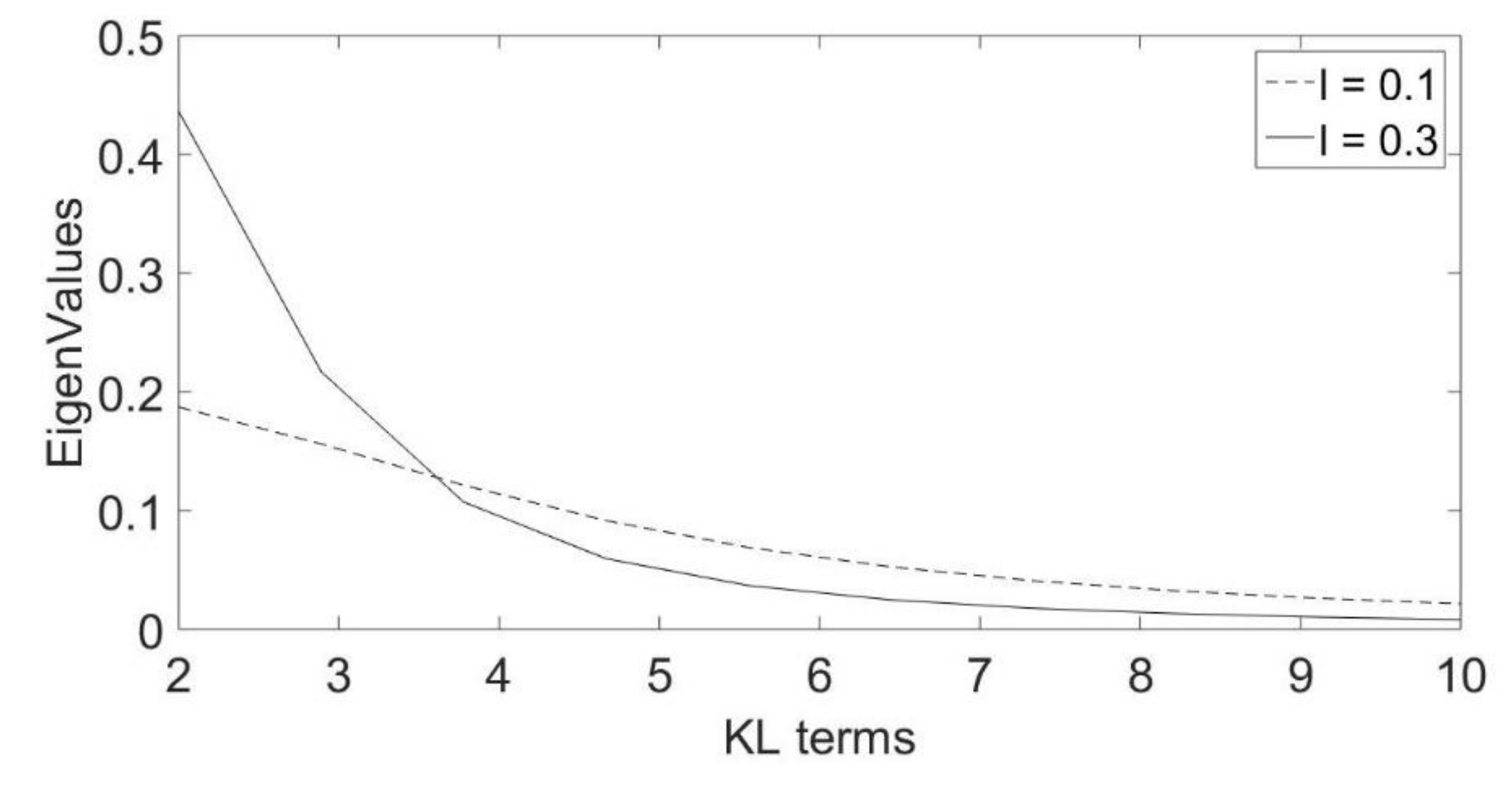
3.2. The Stochastic Quarter-Five Spot Problem
- First: Using PCE
- Second: Using KL expansion
4. Results
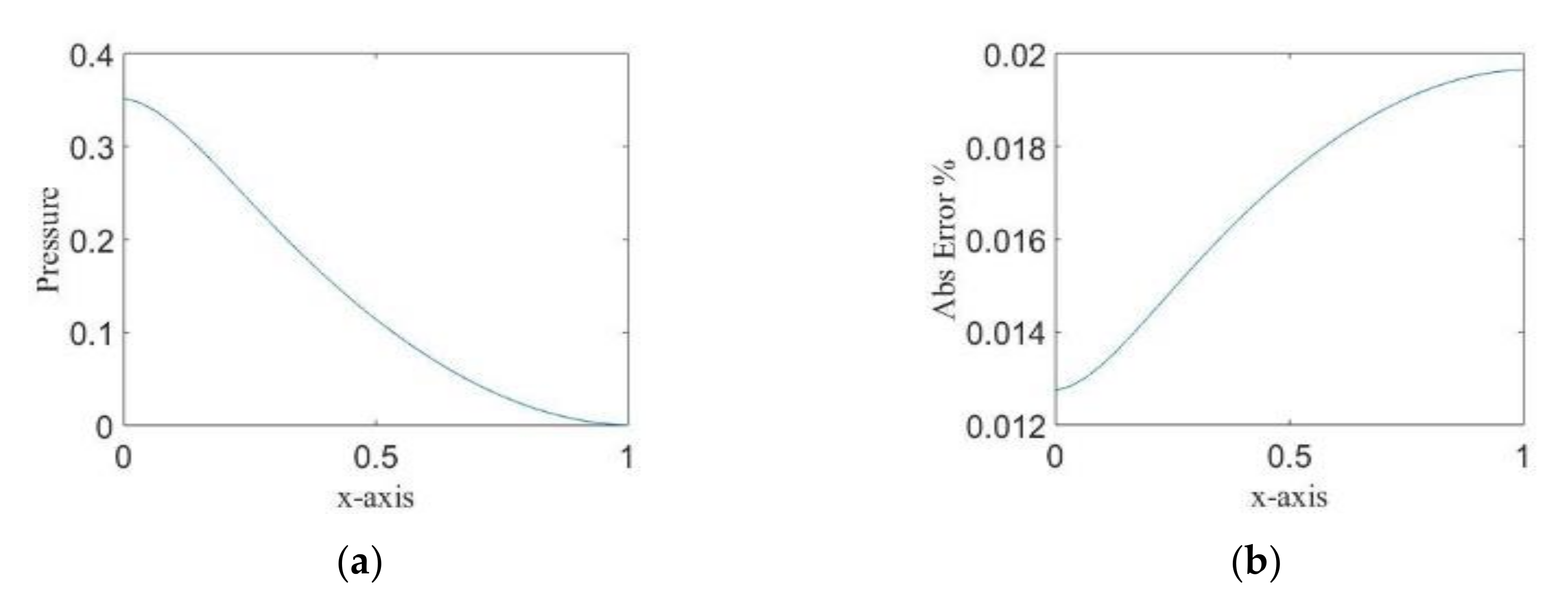
4.1. Case of PCE Only
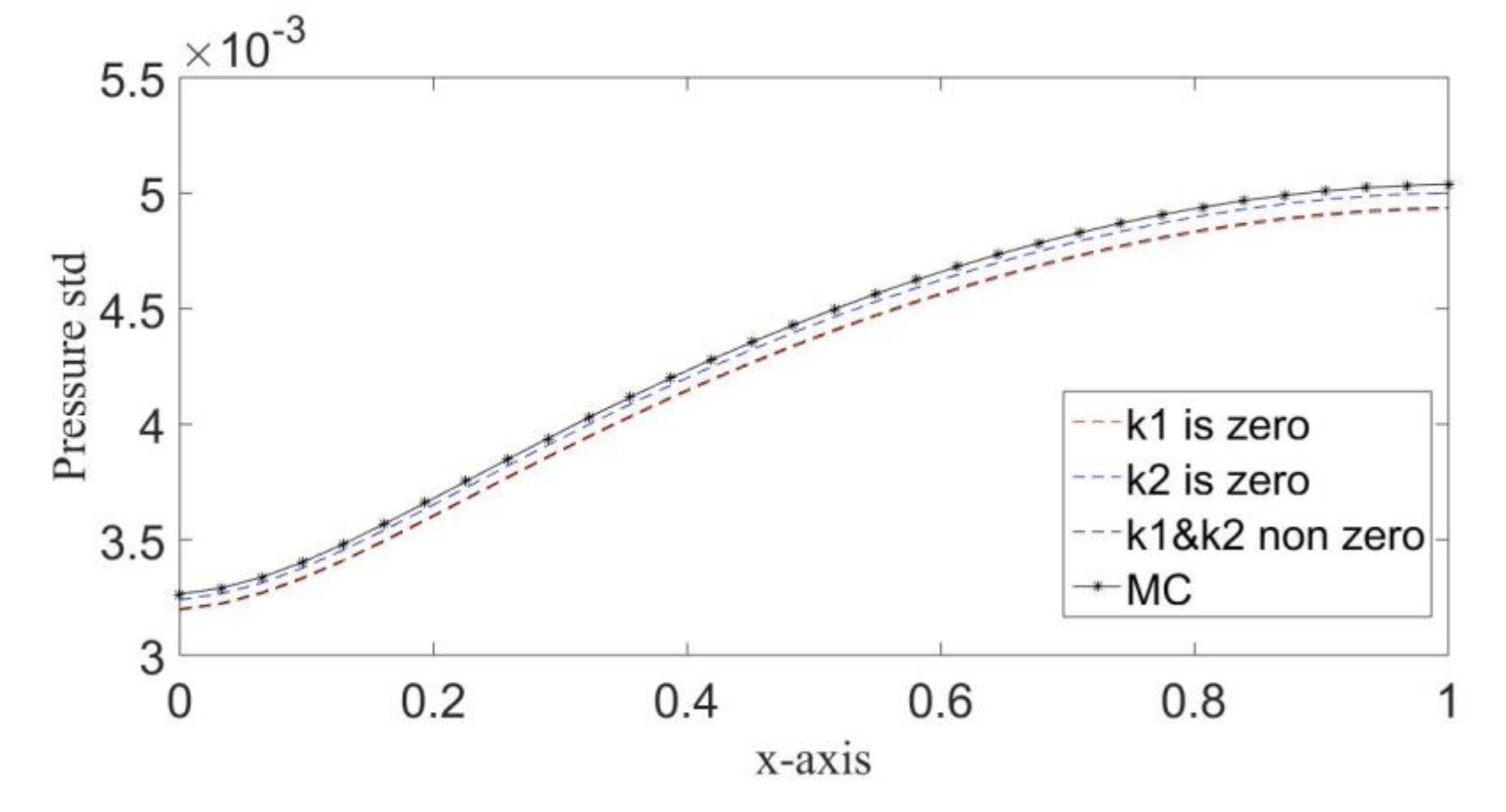
4.2. Case of KL with PCE
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shenoy, A.V. Non-Newtonian Fluid Heat Transfer in Porous Media. In Advances in Heat Transfer; Hartnett, J.P., Irvine, T.F., Cho, Y.I., Eds.; Elsevier: Amsterdam, The Netherlands, 1994; Volume 24, pp. 101–190. [Google Scholar]
- El-Beltagy, M.A. A practical comparison between the spectral techniques in solving the SDEs. Eng. Comput. 2019, 36, 2369–2402. [Google Scholar]
- Le Maître, O.; Knio, O. Spectral Methods for Uncertainty Quantification: With Applications to Computational Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Giles, M.B. Multilevel Monte Carlo Path Simulation. Op. Res. 2008, 56, 607–617. [Google Scholar] [CrossRef]
- Doucet, A.; de Freitas, N.; Gordon, N. An Introduction to Sequential Monte Carlo Methods. In Sequential Monte Carlo Methods in Practice; Doucet, A., de Freitas, N., Gordon, N., Eds.; Springer: New York, NY, USA, 2001; pp. 3–14. [Google Scholar]
- Caflisch, R.E. Monte Carlo and quasi-Monte Carlo methods. Acta Numer. 1998, 7, 1–49. [Google Scholar] [CrossRef]
- Gelhar, L.W. Stochastic subsurface hydrology from theory to applications. Water Resour. Res. 1986, 22, 135S–145S. [Google Scholar] [CrossRef]
- Ketabchi, H.; Ataie-Ashtiani, B. Review: Coastal groundwater optimization—advances, challenges, and practical solutions. Hydrogeol. J. 2015, 23, 1129–1154. [Google Scholar] [CrossRef]
- Razavi, S.; Tolson, B.A.; Burn, D.H. Review of surrogate modeling in water resources. Water Resour. Res. 2012, 48, W07401. [Google Scholar] [CrossRef]
- Frangos, M.; Marzouk, Y.; Willcox, K.; van Bloemen Waanders, B. Surrogate and Reduced-Order Modeling: A Comparison of Approaches for Large-Scale Statistical Inverse Problems. In Computational Methods for Large-Scale Inverse Problems and Quantification of Uncertainty; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 123–149. [Google Scholar]
- Ghanem, R. Ingredients for a general purpose stochastic finite elements implementation. Comput. Methods Appl. Mech. Eng. 1999, 168, 19–34. [Google Scholar] [CrossRef]
- Xiu, D.; Em Karniadakis, G. Modeling uncertainty in steady state diffusion problems via generalized polynomial chaos. Comput. Methods Appl. Mech. Eng. 2002, 191, 4927–4948. [Google Scholar] [CrossRef]
- Cameron, R.H.; Martin, W.T. The Orthogonal Development of Non-Linear Functionals in Series of Fourier-Hermite Functionals. Ann. Math. 1947, 48, 385–392. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener-Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Askey, R.; Wilson, J. Some basic hypergeometric orthogonal polynomials that generalize Jacobi polynomials. Mem. Am. Math. Soc. 1985, 54, 1–63. [Google Scholar] [CrossRef]
- Paulson, J.; Buehler, E.; Mesbah, A. Arbitrary Polynomial Chaos for Uncertainty Propagation of Correlated Random Variables in Dynamic Systems. IFAC PapersOnLine 2017, 50, 3548–3553. [Google Scholar] [CrossRef]
- Oladyshkin, S.; Nowak, W. Data-driven uncertainty quantification using the arbitrary polynomial chaos expansion. Reliab. Eng. Syst. Saf. 2012, 106, 179–190. [Google Scholar] [CrossRef]
- Loève, M. Probability Theory I; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Sapsis, T.P.; Lermusiaux, P.F.J. Dynamically orthogonal field equations for continuous stochastic dynamical systems. Phys. D Nonlinear Phenom. 2009, 238, 2347–2360. [Google Scholar] [CrossRef]
- Cheng, M.; Hou, T.Y.; Zhang, Z. A dynamically bi-orthogonal method for time-dependent stochastic partial differential equations I: Derivation and algorithms. J. Comput. Phys. 2013, 242, 843–868. [Google Scholar] [CrossRef]
- Chavent, G.; Jaffre, J. Mathematical Models and Finite Elements in Reservoir Simulation; Elsevier: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Hasle, G.; Lie, K.; Quak, E. Geometric Modelling, Numerical Simulation, and Optimization: Applied Mathematics at SINTEF; Springer: Heidelberg, Germany, 2007. [Google Scholar]
- Zhang, D. Stochastic Methods for Flow in Porous Media: Coping with Uncertainties; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- El-Beltagy, M.A.; Wafa, M.I. Stochastic 2D incompressible Navier-Stokes solver using the vorticity-stream function formulation. J. Appl. Math. 2013, 2013, 14. [Google Scholar] [CrossRef]
- Augustin, F.; Gilg, A.; Paffrath, M.; Rentrop, P.; Wever, U. Polynomial chaos for the approximation of uncertainties: Chances and limits. Eur. J. Appl. Math. 2008, 19, 149–190. [Google Scholar] [CrossRef]
- Gentle, J.E. Numerical Linear Algebra for Applications in Statistics; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Lie, K.-A. An Introduction to Reservoir Simulation Using MATLAB; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Pollock, D.W. Semianalytical Computation of Path Lines for Finite-Difference Models. Groundwater 1988, 26, 743–750. [Google Scholar] [CrossRef]
- Noor, A.; Barnawi, A.; Nour, R.; Assiri, A.; El-Beltagy, M. Analysis of the Stochastic Population Model with Random Parameters. Entropy 2020, 22, 562. [Google Scholar] [CrossRef]
- Paleologos, E.K.; Avanidou, T.; Mylopoulos, N. Stochastic analysis and prioritization of the influence of parameter uncertainty on the predicted pressure profile in heterogeneous, unsaturated soils. J. Hazard. Mater. 2006, 136, 137–143. [Google Scholar] [CrossRef]
- Kourakos, G.; Harter, T. Parallel simulation of groundwater non-point source pollution using algebraic multigrid preconditioners. Comput. Geosci. 2014, 18, 851–867. [Google Scholar] [CrossRef]
- Crevillén-García, D.; Leung, P.K.; Rodchanarowan, A.; Shah, A.A. Uncertainty Quantification for Flow and Transport in Highly Heterogeneous Porous Media Based on Simultaneous Stochastic Model Dimensionality Reduction. Transp. Porous Media 2019, 126, 79–95. [Google Scholar] [CrossRef] [PubMed]
| Mean difference percentage | 0.0035 | 0.0039 | 0.0031 |
| Variance difference percentage | 2.56 | 2.61 | 2.52 |
| Number of terms for convergence | 12 | 8 | 5 |
| Method | |||
|---|---|---|---|
| PCE | 0.4 | 1 | |
| KL-PCE | 0.01 | 0.5 | 0.1 |
| KL-PCE | 0.02 | 0.3 | 0.9 |
| KL-PCE | 0.1 | 0.8 | 4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
AbdelFattah, H.; Al-Johani, A.; El-Beltagy, M. Analysis of the Stochastic Quarter-Five Spot Problem Using Polynomial Chaos. Molecules 2020, 25, 3370. https://doi.org/10.3390/molecules25153370
AbdelFattah H, Al-Johani A, El-Beltagy M. Analysis of the Stochastic Quarter-Five Spot Problem Using Polynomial Chaos. Molecules. 2020; 25(15):3370. https://doi.org/10.3390/molecules25153370
Chicago/Turabian StyleAbdelFattah, Hesham, Amnah Al-Johani, and Mohamed El-Beltagy. 2020. "Analysis of the Stochastic Quarter-Five Spot Problem Using Polynomial Chaos" Molecules 25, no. 15: 3370. https://doi.org/10.3390/molecules25153370
APA StyleAbdelFattah, H., Al-Johani, A., & El-Beltagy, M. (2020). Analysis of the Stochastic Quarter-Five Spot Problem Using Polynomial Chaos. Molecules, 25(15), 3370. https://doi.org/10.3390/molecules25153370








