Effects of Foam Microbubbles on Electrical Resistivity and Capillary Pressure of Partially Saturated Porous Media
Abstract
1. Introduction
2. Results and Discussions
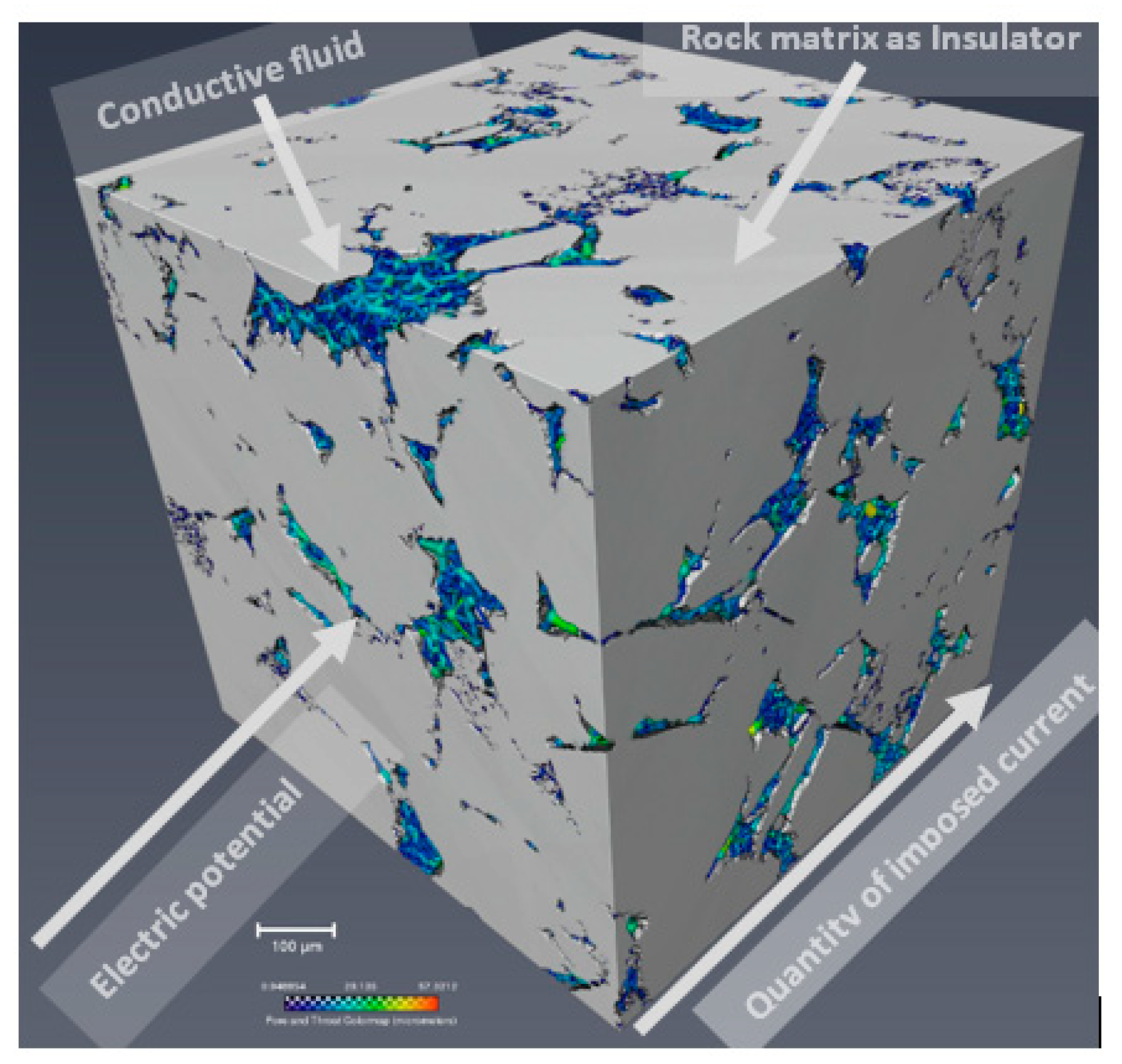
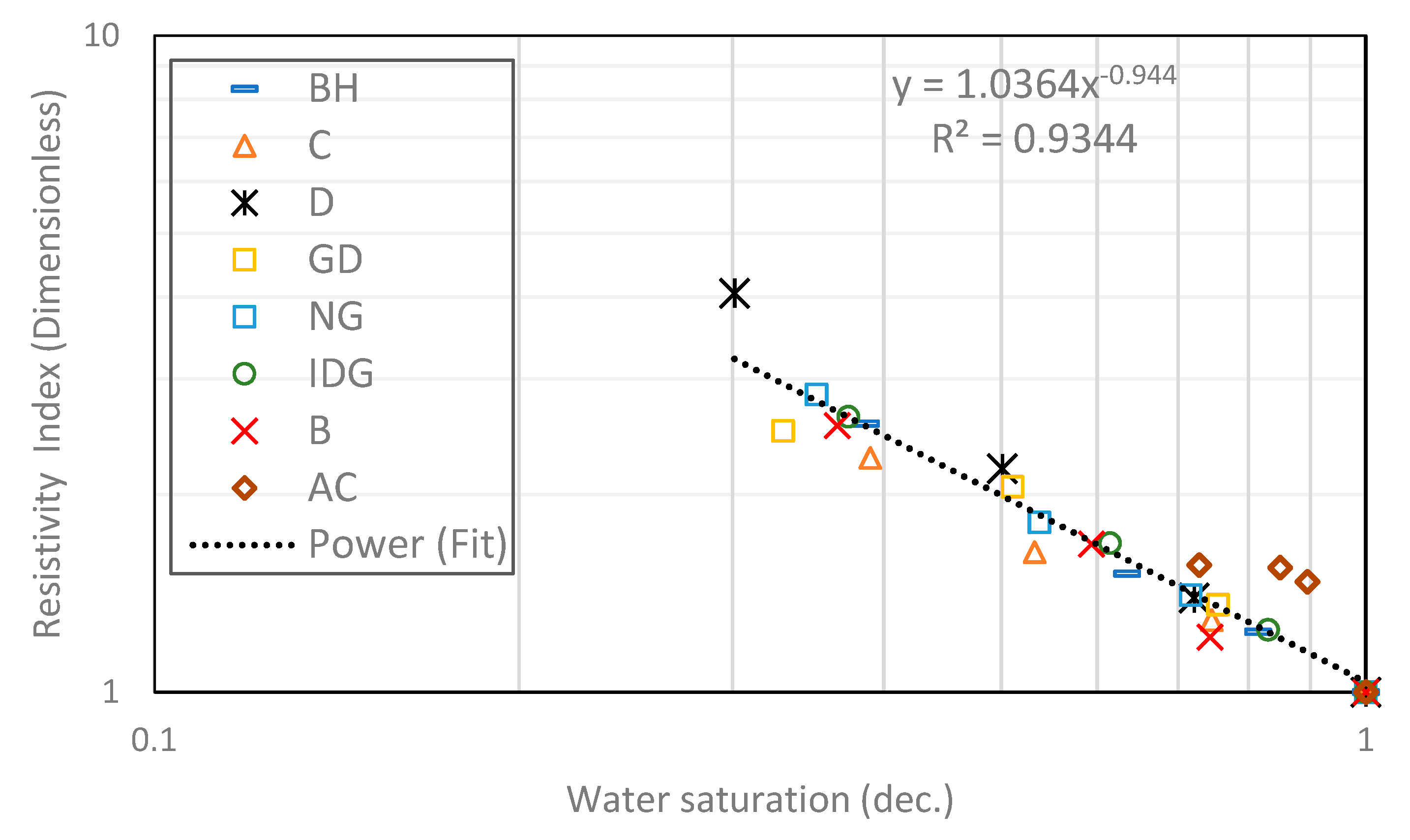
2.1. Heterogeneous Composite Rock
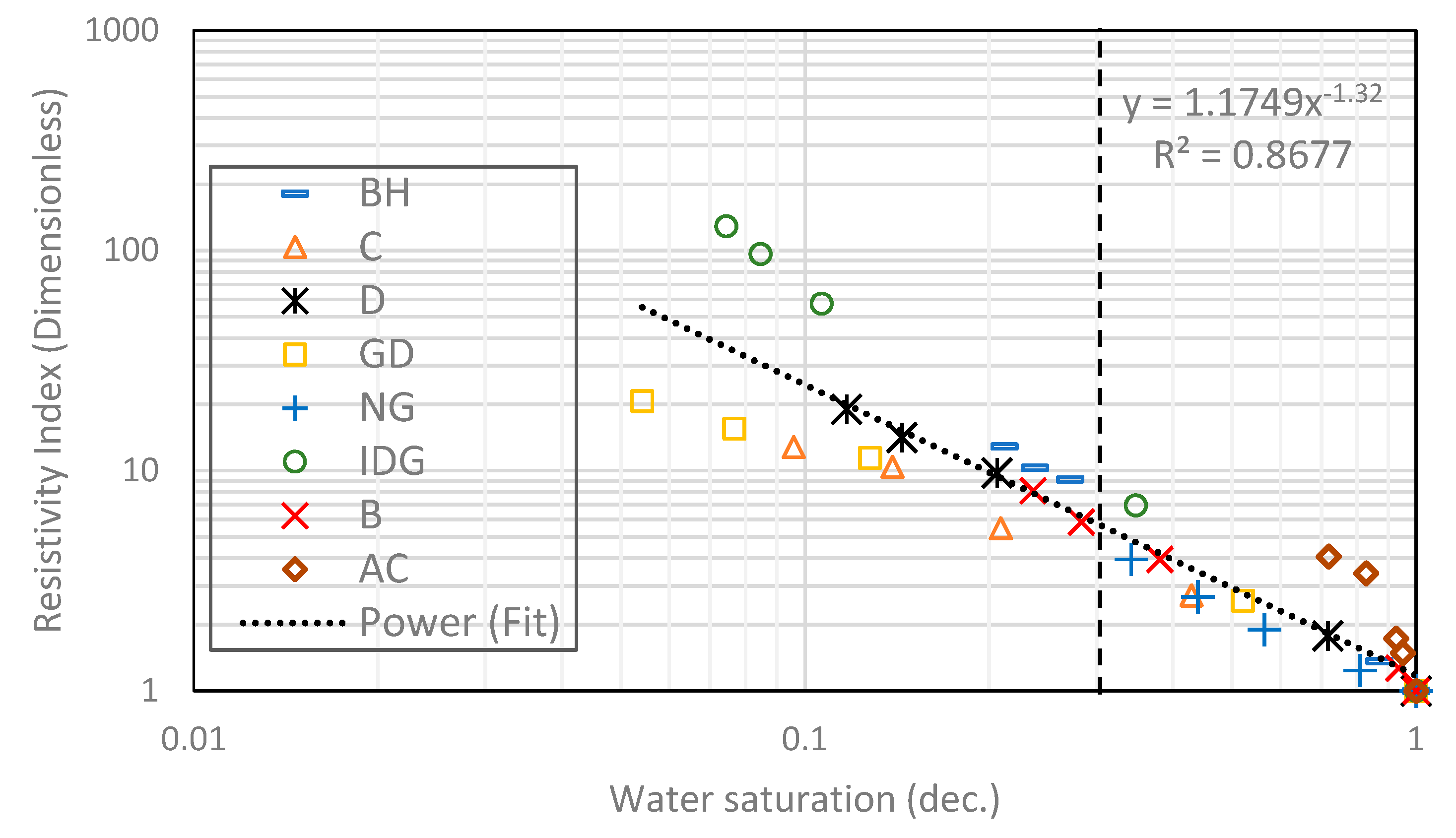
2.2. Homogenous Rocks
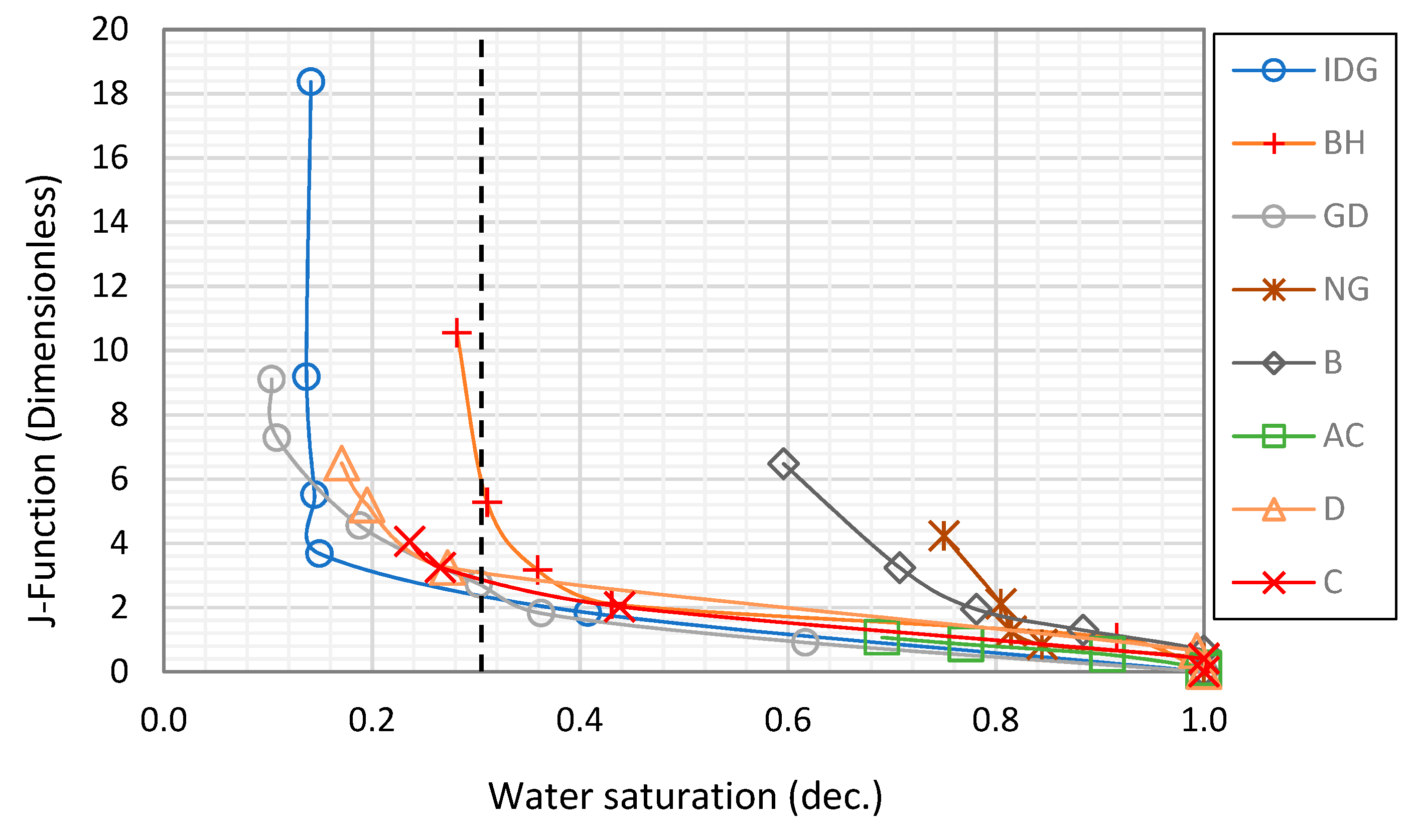
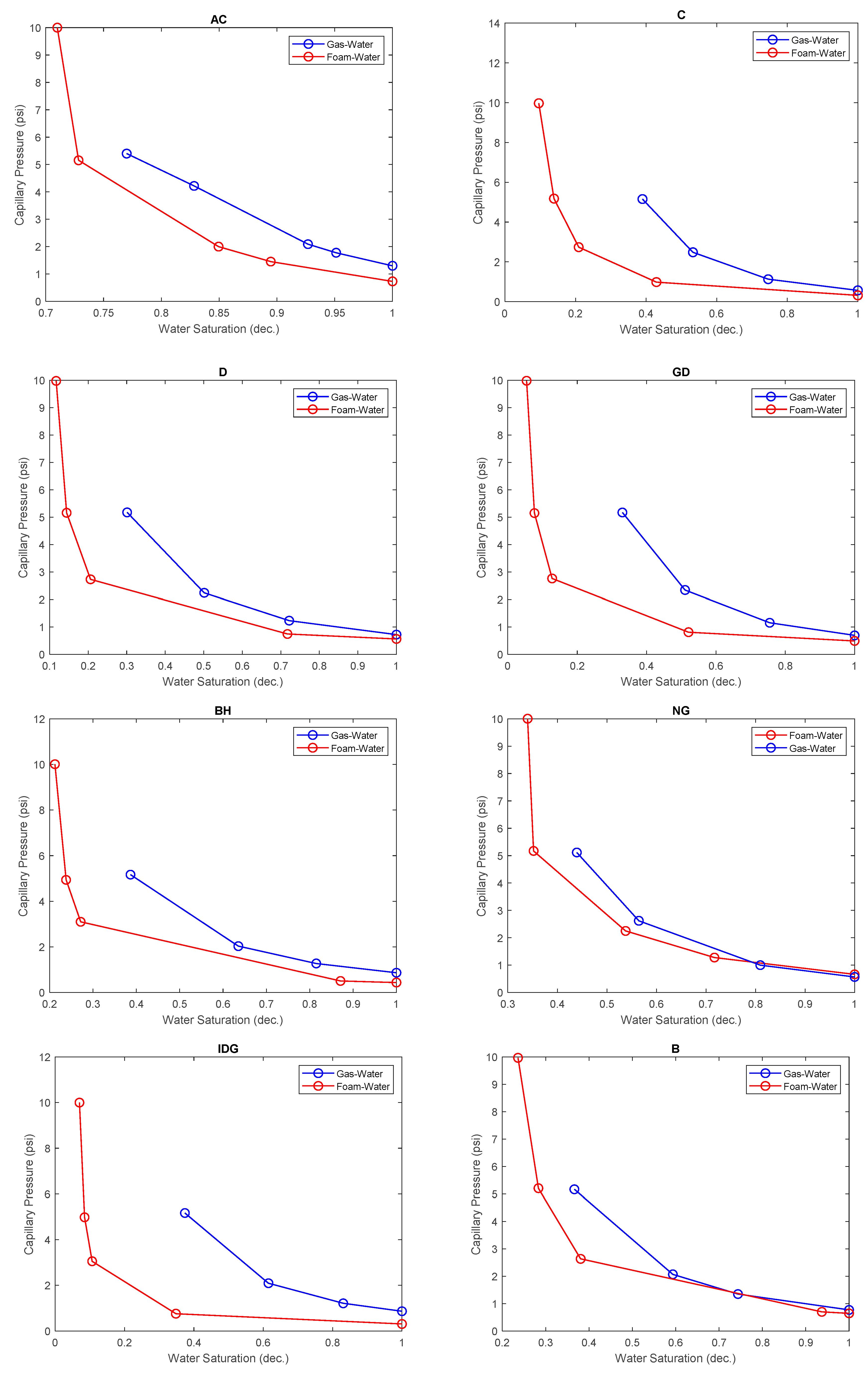
2.3. Effect of Foam on Capillary Pressure Curve
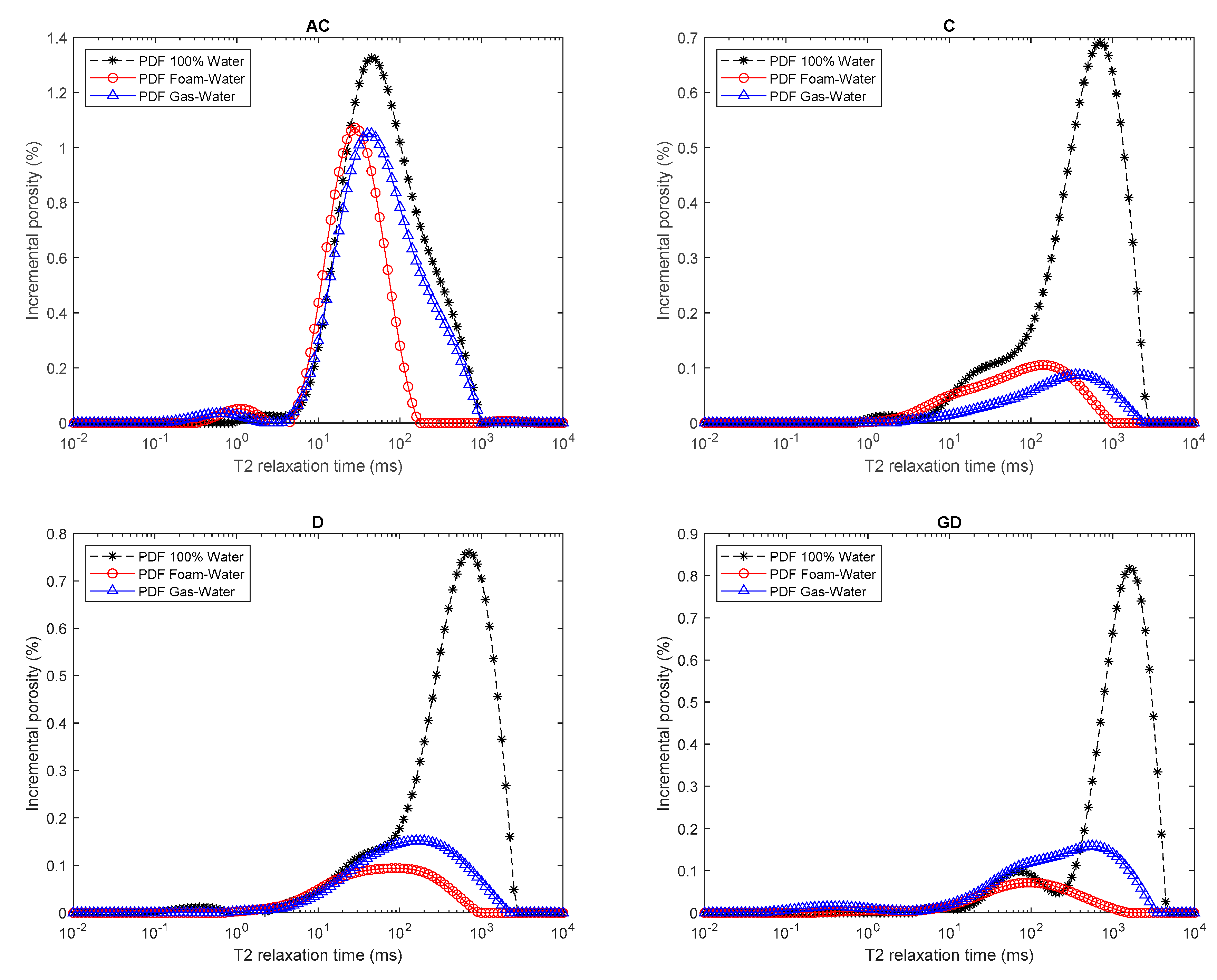
2.4. NMR Measurements of Water Distribution
3. Materials and Methods
3.1. Sample Preparation
3.2. Experimental Apparatus
3.3. Experimental Procedures
4. Conclusions
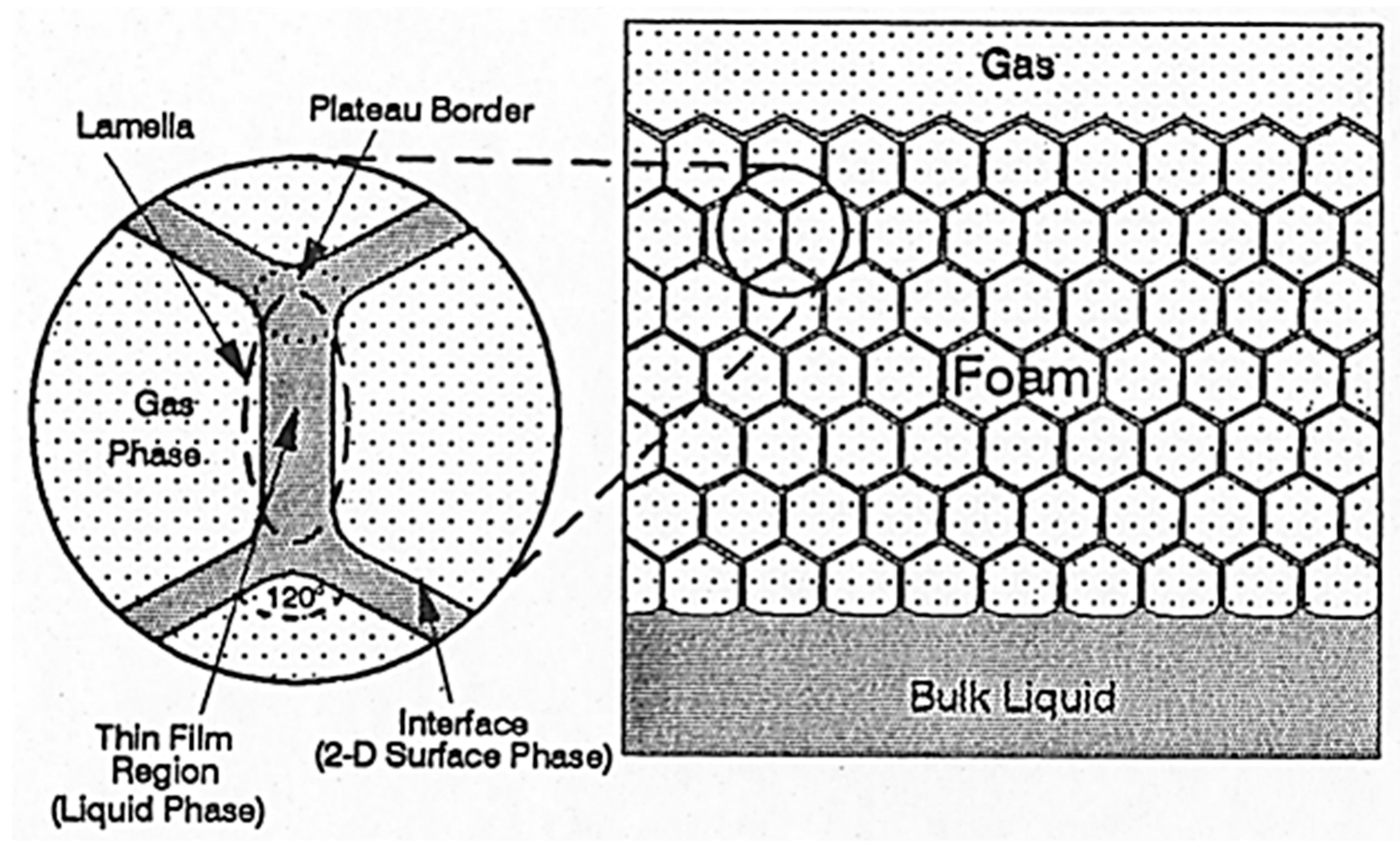
- Foam bubbles use some of the rock pore water to form thin water films called lamellae. As a result, the volume of the straight and continuous (with large surface area) water phase is reduced while the water phase in the lamellae makes the electric current path more tortuous. Hence, at the same water saturation and for the same rock, the electrical resistivity is higher for a foam–water than for a gas–water system.
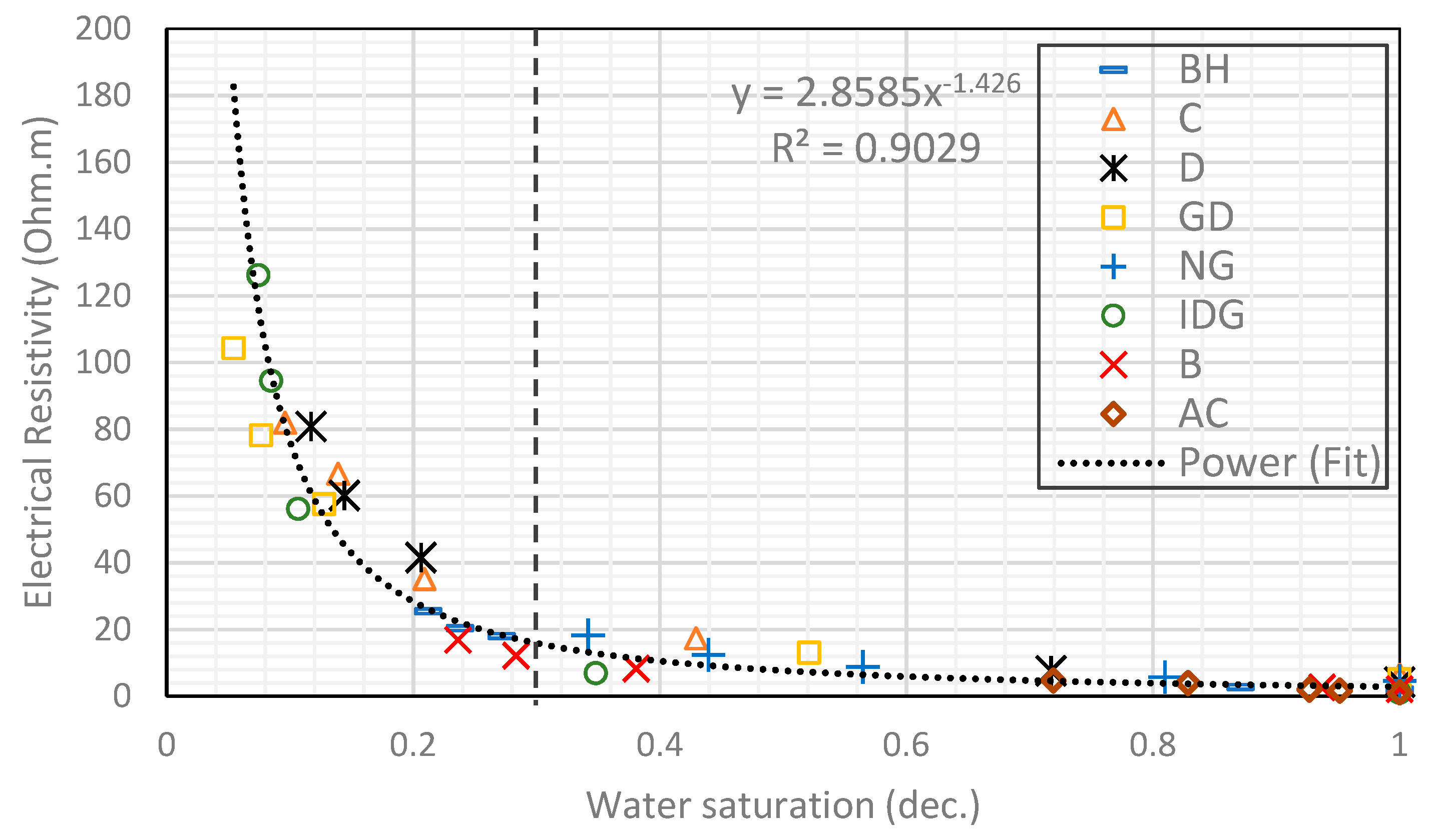
- The electrical tortuosity (caused by foam bubbles) increases as the total water saturation of the rock decreases. Below a critical water saturation, the tortuosity increases exponentially. Hence, the relationship between electrical resistivity and water saturation exhibits a power-law behavior in a foam-water system.
- Archie’s model can fit the experimental data from foam. However, the saturation exponent for a foamed gas–water system is consistently higher than that of a pure gas–water system.
- Generally, foam affects the saturation exponent like an oil-wet pore surface would, in the sense that it increases the value of n at lower water saturation. There is a competing and opposite effect on the saturation exponent by the presence of foam and the presence of clay, micropores, and conductive minerals in a porous medium. Foam tends to increase the saturation exponent while clay, micropores, and conductive minerals tend to decrease it.
- The presence of a surface-active agent such as surfactant reduces the surface tension between gas and water. This causes the capillary pressure curve at a given water saturation to be lower in a foam–gas system than in a gas–water system. The presence of foam also allows smaller pores to be drained, resulting in lower irreducible water saturation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mohammadmoradi, P.; Behrang, A.; Kantzas, A. Effective thermal and electrical conductivity of two-phase saturated porous media. In Proceedings of the SPE Canada Heavy Oil Technical Conference, Calgary, AL, Canada, 7–9 June 2016. [Google Scholar]
- Worthington, P.F.; Pallatt, N. Effect of variable saturation exponent on the evaluation of hydrocarbon saturation. SPE Form. Eval. 1990, 7, 331–333. [Google Scholar] [CrossRef]
- Rasmus, J.C. A summary of the effects of various pore geometries and their wettabilities on measured and in-situ values of cementation and saturation exponents. In Proceedings of the SPWLA 27th Annual Logging Symposium, Houstan, TX, USA, 9–13 June 1986. [Google Scholar]
- Dicker, A.I.M.; Bemelmans, W.A. Models for Simulating the Electrical Resistance of Porous Media. Proceedings of SPWLA 25th Annual Logging Symposium, New Orleans, LA, USA, 10–13 June 1984. [Google Scholar]
- Swanson, B.F. Microporosity in reservoir rocks: Its measurement and influence on electrical resistivity. Proceedings of SPLWA 26th Annual Logging Syposium, Dallas, TX, USA, 17–20 June 1985. [Google Scholar]
- Tiab, D.; Donaldson, C. Petrophysics Second Edition–Theory and Practice of Measuring Reservoir Rock and Fluid Transport Properties; Gulf professional Publishing: Houston, TX, USA, 2004. [Google Scholar]
- Olusola, B.K.; Yu, G.; Aguilera, R. The use of electromagnetic mixing rules for petrophysical evaluation of dual-and triple-porosity reservoirs. SPE Reserv. Eval. Eng. 2013, 16, 378–389. [Google Scholar] [CrossRef]
- Longeron, D.G.; Argaud, M.J.; Feraud, J.P. Effect of overburden pressure and the nature and microscopic distribution of fluids on electrical properties of rock samples. SPE Form. Eval. 1989, 4, 194–202. [Google Scholar] [CrossRef]
- Adebayo, A.R.; Al-Yousef, H.Y.; Mahmoud, M. An investigation of the effect of CO2–brine–rock interaction on determination of Archie’s saturation exponent for carbon dioxide evaluation in carbonate reservoirs. J. Pet. Sci. Eng. 2015, 133, 665–676. [Google Scholar] [CrossRef]
- Nemes, I. Revisiting the applications of drainage capillary pressure curves in water-wet hydrocarbon systems. Open Geosci. 2016, 22. [Google Scholar] [CrossRef]
- Dos Santos Lucas, C.R.; Aum, Y.K.P.G.; De Andrade Araújo, E.; de Castro Dantas, T.N.; Araújo, E.A.; Sousa, T.N.; Aum, P.T.P. Investigating the fluid–solid interaction of acid nonionic nanoemulsion with carbonate porous media. Molecules 2020, 25, 1475. [Google Scholar] [CrossRef] [PubMed]
- Cortés, F.B.; Lozano, M.; Santamaria, O.; Betancur Marquez, S.; Zapata, K.; Ospina, N.; Franco, C.A. Development and evaluation of surfactant nanocapsules for chemical enhanced oil recovery (EOR) applications. Molecules 2018, 23, 1523. [Google Scholar]
- Bernard, G.G.; Holm, L.W. Method for the Subterranean Storage of Gas. U.S. Patent No. 3,330,352, 11 July 1967. [Google Scholar]
- Smith, D.H.; Jikich, S.A. Foams and surfactants for improved underground storage of natural gas by blockage of water coning. In Proceedings of the SPE Eastern Regional Meeting, Pittsburgh, PA, USA, 2–4 November 1993. [Google Scholar]
- Hirasaki, G.J.; Miller, C.A.; Szafranski, R.; Lawson, L.B.; Tanzil, D.; Jackson, R.E.; Londergan, J.; Meinardus, H. Field demonstration of the surfactant/foam process for aquifer remediation. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 5–8 October 1997. [Google Scholar]
- Al Sofi, A.M.; Vitoonkijvanich, S.; Blunt, M.J. Design of foam-assisted carbon dioxide storage in a North Sea aquifer using streamline-based simulation. In Proceedings of the 17th European Symposium on Improved Oil Recovery, St. Petersburg, Russia, 16 April 2013. [Google Scholar]
- Adebayo, A.R. Viability of foam to enhance capillary trapping of CO2 in saline aquifers—An experimental investigation. Int. J. Greenh. Gas Control 2018, 78, 117–124. [Google Scholar] [CrossRef]
- Adebayo, A.R. Sequential storage and in-situ tracking of gas in geological formations by a systematic and cyclic foam injection-A useful application for mitigating leakage risk during gas injection. J. Nat. Gas Sci. Eng. 2019, 62, 1–12. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Freedman, V.L.; Zhong, L. Foam Transport in Porous Media–A Review. A Report Prepared for the U.S. Department of Energy under Contract DE-AC05-76RL01830. 2009. Available online: https://pdfs.semanticscholar.org/cf07/990b2d319b2a89afda1eab6cd3b85c22a464.pdf (accessed on 10 March 2020).
- Kovscek, A.R.; Patzek, T.W.; Radke, C.J. Simulation of foam displacement in porous media. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1993. [Google Scholar]
- Farajzadeh, R.; Andrianov, A.; Krastev, R.; Hirasaki, G.J.; Rossen, W.R. Foam–oil interaction in porous media: Implications for foam assisted enhanced oil recovery. Adv. Coll. Interface Sci. 2012, 183, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Falls, A.H.; Hirasaki, G.J.; Patzek, T.E.A.; Gauglitz, D.A.; Miller, D.D.; Ratulowski, T. Development of a mechanistic foam simulator: The population balance and generation by snap-off. SPE Reserv. Eng. 1988, 3, 884–892. [Google Scholar] [CrossRef]
- Hirasaki, G.J. A review of steam-foam process mechanisms. J. Pet. Technol. 1989, 41, 19518. [Google Scholar]
- Permatasari, K.A.; Reekhi, G.S.; Irawan, S.; Lubis, L.A. Resistivity wave for monitoring foam flood propagation. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Jakarta, Indonesia, 17–19 October 2017. [Google Scholar]
- Schramm, L.L.; Wassmuth, F. Foams: Basic principles in foams. In Fundamentals and Application in the Petroleum Industry; Schramm, L.L., Ed.; American Chemical Society: Washington, DC, USA, 1994. [Google Scholar]
- Haroun, M.; Mohammed, A.M.; Somra, B.; Punjabi, S.; Temitope, A.; Yim, Y.; Corova, F. Real-time resistivity monitoring tool for in-situ foam front tracking. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, 13–16 November 2017. [Google Scholar]
- Berge, C. An Experimental Study of Foam Flow in Water Saturated Porous Media. Master’s Thesis, Department of Physics and Technology, University of Bergen, Bergen, Norway, 2017. [Google Scholar]
- Adebayo, A.R.; Kanj, M.Y. Exploring a mechanistic approach for characterizing transient and steady state foam flow in porous media. J. Nat. Gas Sci. Eng. 2018, 60, 214–227. [Google Scholar] [CrossRef]
- Liu, F.; Darjani, S.; Akhmetkhanova, N.; Maldarelli, C.; Banerjee, S.; Pauchard, V. Mixture effect on the dilatation rheology of asphaltenes-laden interfaces. Langmuir 2017, 33, 1927–1942. [Google Scholar] [CrossRef] [PubMed]
- Darjani, S.; Koplik, J.; Pauchard, V. Extracting the equation of state of lattice gases from random sequential adsorption simulations by means of the Gibbs adsorption isotherm. Phys. Rev. E 2017, 96, 052803. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; McClure, J.E.; Armstrong, R.T. Influence of wettability on phase connectivity and electrical resistivity. Phys. Rev. E 2018, 98, 43102. [Google Scholar] [CrossRef]
- Mozaffari, S.; Tchoukov, P.; Mozaffari, A.; Atias, J.; Czarnecki, J.; Nazemifard, N. Capillary driven flow in nanochannels–Application to heavy oil rheology studies. Colloids Surf. A Physicochem. Eng. Asp. 2017, 513, 178–187. [Google Scholar] [CrossRef]
Sample Availability: Not available. |

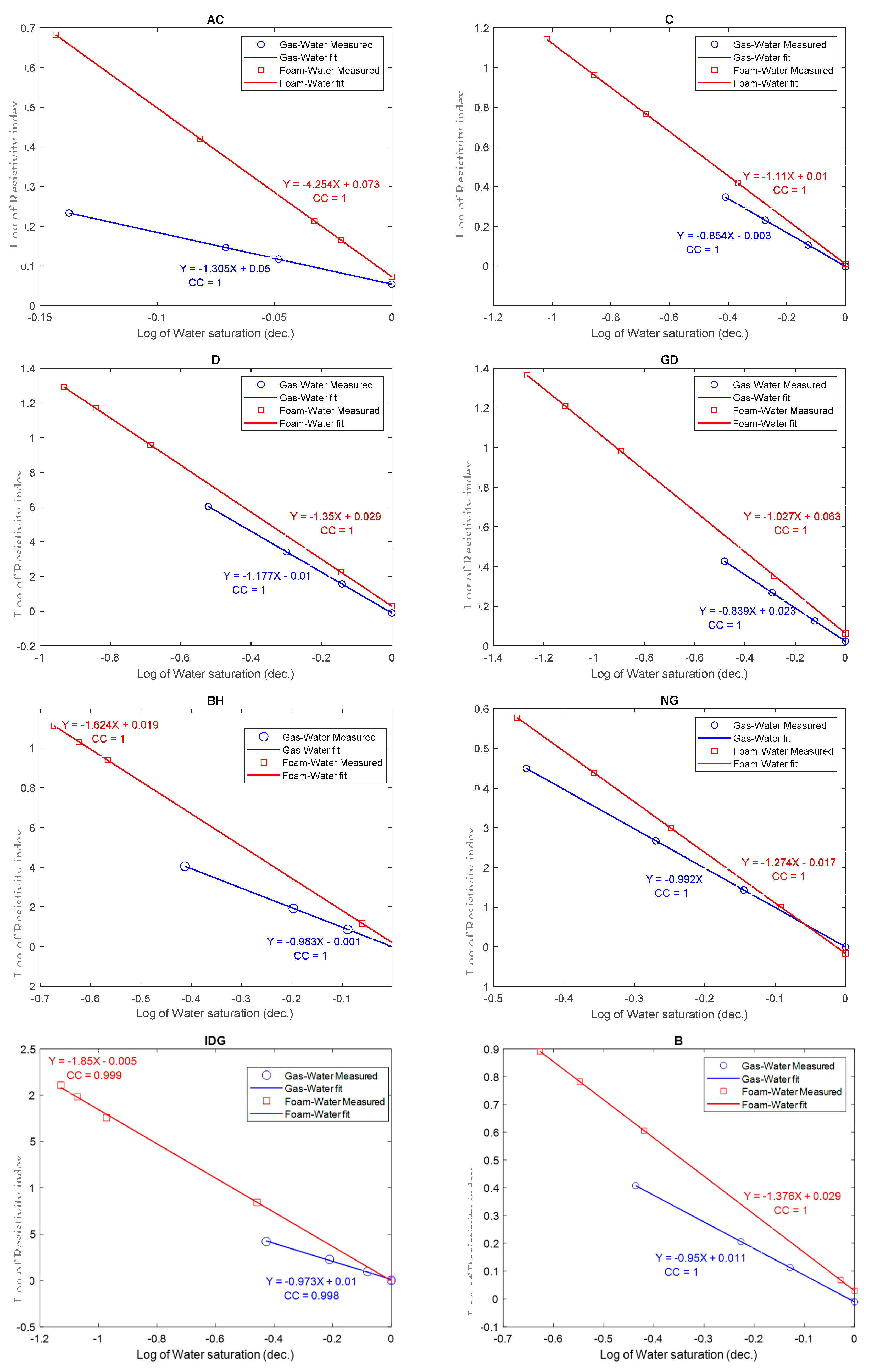



| Sample | Lithology | k | φ | Saturation Exponent ‘n’ | |
|---|---|---|---|---|---|
| (mD) | (%) | Gas–Water | Foam–Water | ||
| AC | Austin Chalk | 26 | 26.89 | 1.305 | 4.254 |
| C | Silurian Dolomites | 136.61 | 12.81 | 0.854 | 1.110 |
| D | Dolomite | 327.83 | 15.29 | 1.177 | 1.351 |
| GD | Guelph Dolomite | 637.26 | 20.85 | 0.839 | 1.027 |
| BH | Brill Hill Sand | 1100 | 18.92 | 0.983 | 1.624 |
| NG | Nugget sand | 111.32 | 12.3 | 0.992 | 1.274 |
| IDG | Idaho Grey sand | 5000 | 29.2 | 0.973 | 1.850 |
| B | Berea sand | 270 | 20 | 0.960 | 1.376 |
| Composite | Heterogenous | - | - | 0.944 | 1.32 |
| Sample | Lithology | L (cm) | D (cm) | k (mD) | φ (%) |
|---|---|---|---|---|---|
| AC | Austin Chalk | 3.559 | 3.787 | 26 | 26.89 |
| C | Silurian Dolomites | 8.643 | 3.748 | 136.61 | 12.81 |
| D | Dolomite | 9.337 | 3.744 | 327.83 | 15.29 |
| GD | Guelph Dolomite | 9.771 | 3.801 | 637.26 | 20.85 |
| BH | Briarhill Sand | 9.907 | 3.760 | 1100 | 18.92 |
| NG | Nugget sand | 9.776 | 3.791 | 111.32 | 12.3 |
| IDG | Idaho Grey sand | 10.09 | 3.780 | 5000 | 29.2 |
| B | Berea sand | 9.267 | 3.795 | 270 | 20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
R. Adebayo, A.; Isah, A.; Mahmoud, M.; Al-Shehri, D. Effects of Foam Microbubbles on Electrical Resistivity and Capillary Pressure of Partially Saturated Porous Media. Molecules 2020, 25, 3385. https://doi.org/10.3390/molecules25153385
R. Adebayo A, Isah A, Mahmoud M, Al-Shehri D. Effects of Foam Microbubbles on Electrical Resistivity and Capillary Pressure of Partially Saturated Porous Media. Molecules. 2020; 25(15):3385. https://doi.org/10.3390/molecules25153385
Chicago/Turabian StyleR. Adebayo, Abdulrauf, Abubakar Isah, Mohamed Mahmoud, and Dhafer Al-Shehri. 2020. "Effects of Foam Microbubbles on Electrical Resistivity and Capillary Pressure of Partially Saturated Porous Media" Molecules 25, no. 15: 3385. https://doi.org/10.3390/molecules25153385
APA StyleR. Adebayo, A., Isah, A., Mahmoud, M., & Al-Shehri, D. (2020). Effects of Foam Microbubbles on Electrical Resistivity and Capillary Pressure of Partially Saturated Porous Media. Molecules, 25(15), 3385. https://doi.org/10.3390/molecules25153385








