Investigating the Formation of Structural Elements in Proteins Using Local Sequence-Dependent Information and a Heuristic Search Algorithm
Abstract
1. Introduction and Related Work
2. Results and Discussion
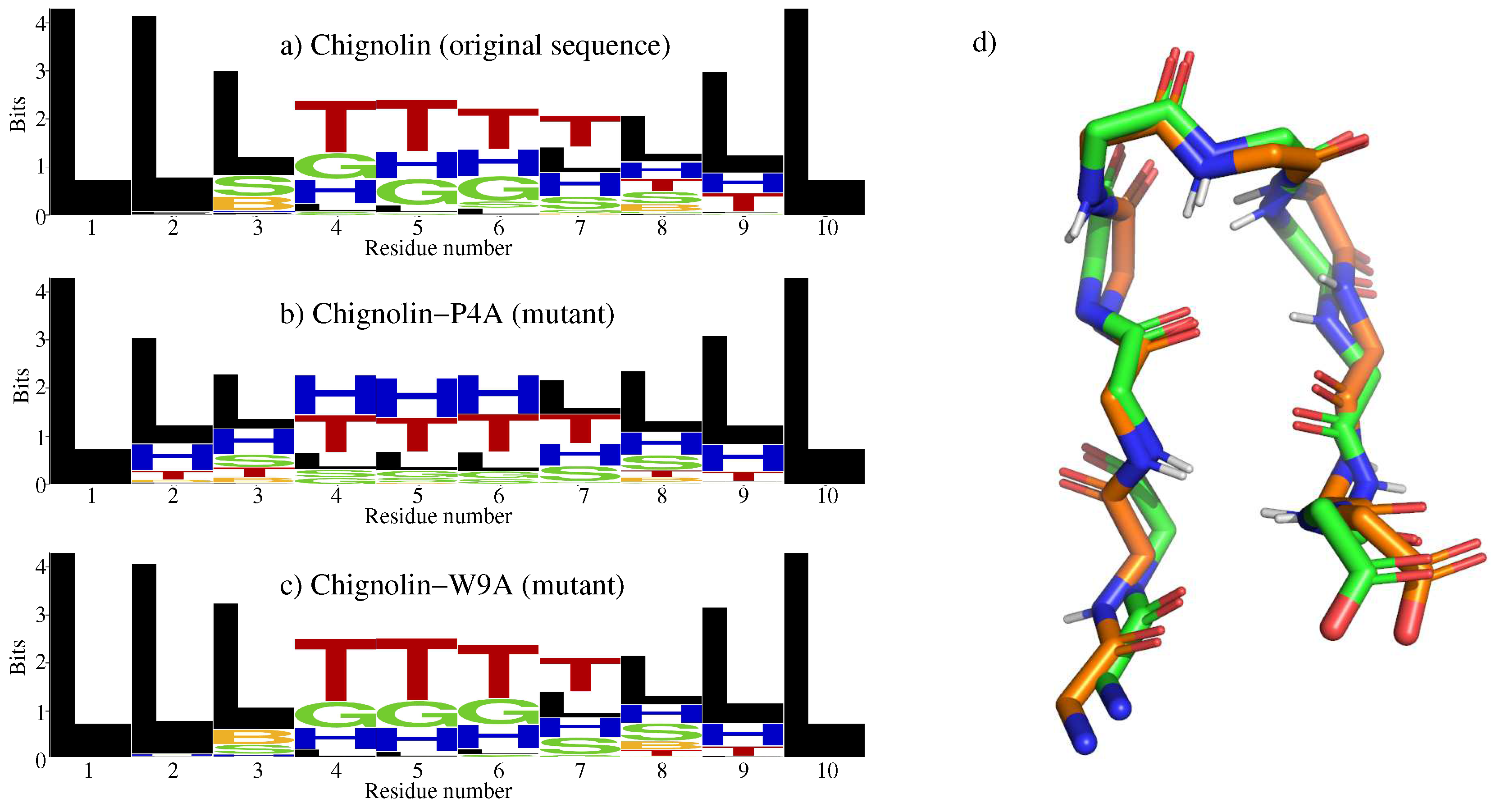
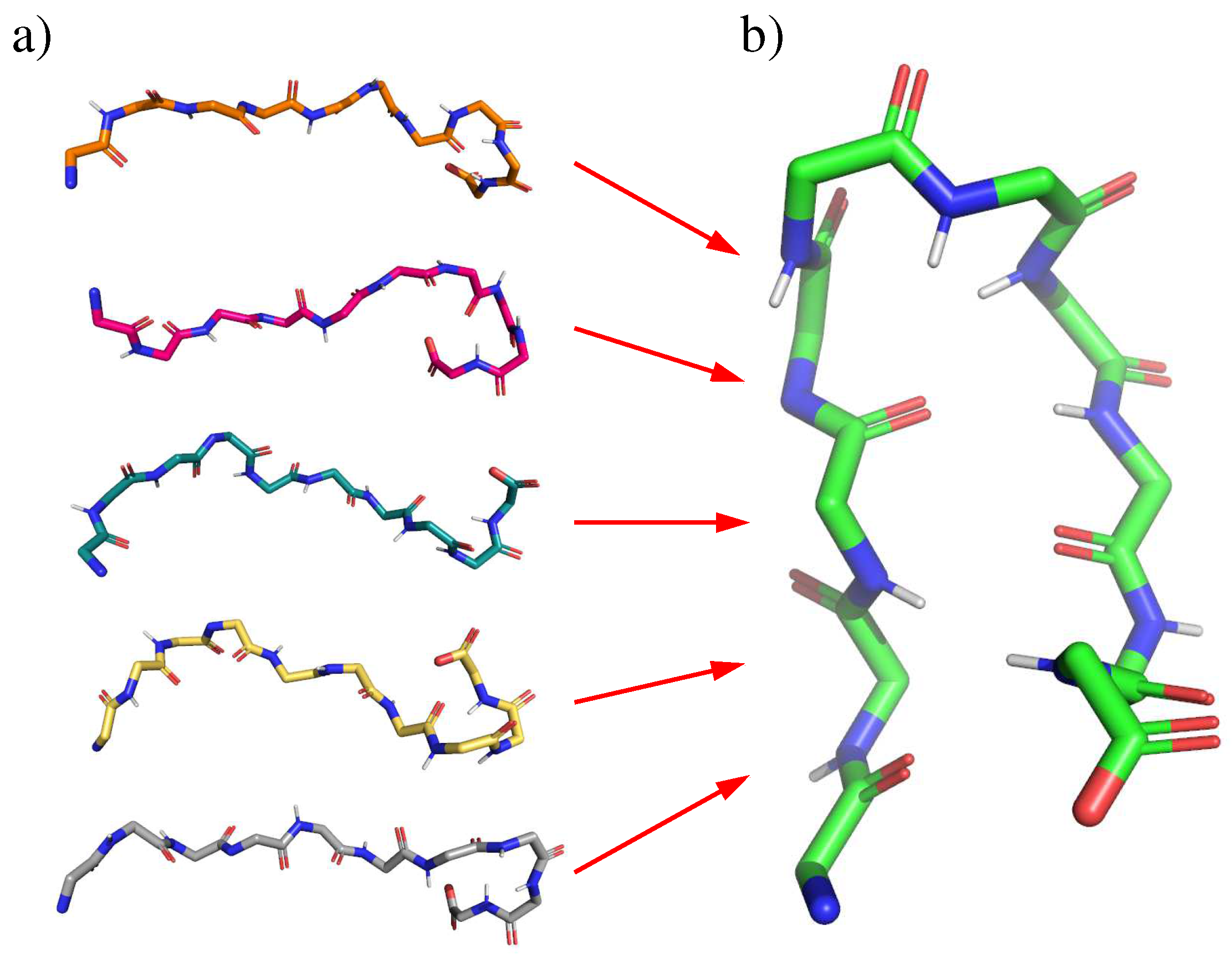
2.1. Chignolin
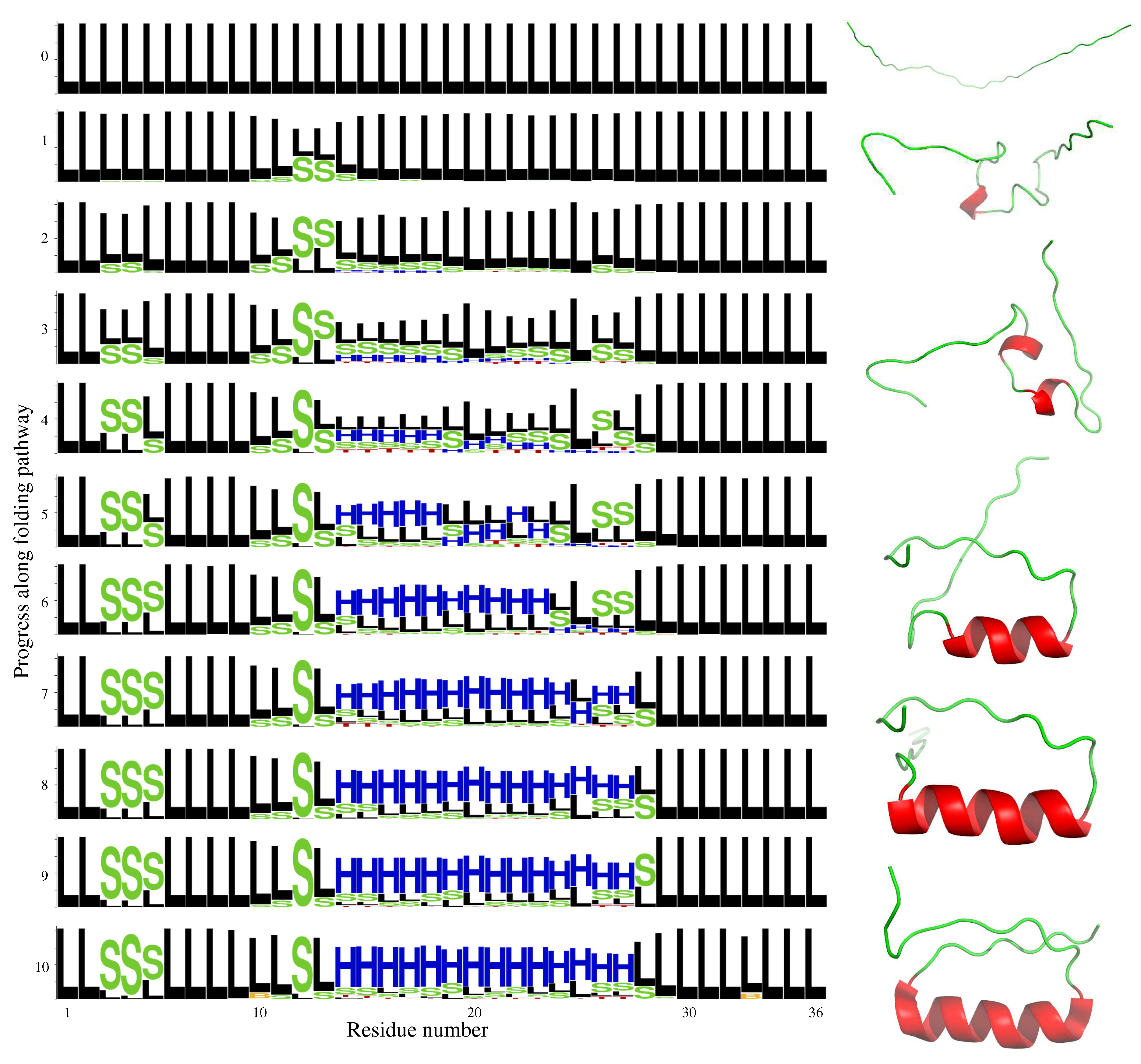
2.2. DS119
3. Materials and Methods
3.1. Structural Database
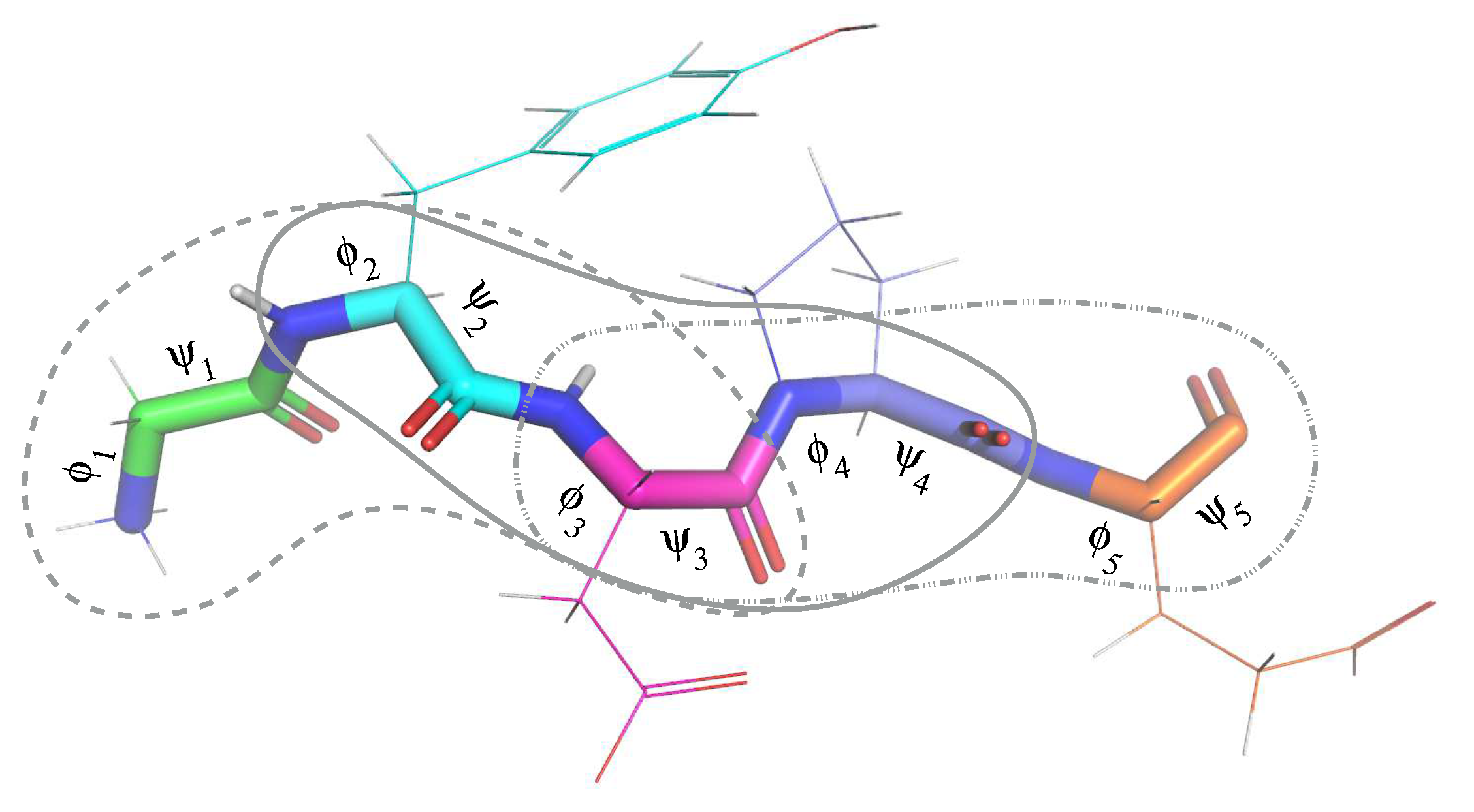
3.2. Formal Statement of the Conformation Path Finding Problem
- (i)
- the values and meet the constraints of Equation (2), and
- (ii)
- there are no collisions between the atoms of the protein in the state .
3.3. Search Algorithm
3.3.1. Heuristic Guidance Function
3.3.2. Properties of HDFS
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Vendruscolo, M.; Zurdo, J.; Macphee, C.; M Dobson, C. Protein folding and misfolding: A paradigm of self-assembly and regulation in complex biological systems. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2003, 361, 1205–1222. [Google Scholar] [CrossRef]
- Valastyan, J.S.; Lindquist, S. Mechanisms of protein-folding diseases at a glance. Dis. Models Mech. 2014, 7, 9–14. [Google Scholar] [CrossRef]
- Knowles, T.; Vendruscolo, M.; Dobson, C. The amyloid state and its association with protein misfolding diseases. Structure 2014, 15, 384–396. [Google Scholar] [CrossRef]
- Baldwin, R.L. Protein folding: Matching speed and stability. Nature 1994, 369, 183–184. [Google Scholar] [CrossRef]
- Wolynes, P.; Onuchic, J.; Thirumalai, D. Navigating the folding routes. Science 1995, 267, 1619–1620. [Google Scholar] [CrossRef]
- Dobson, C.M. Protein folding and misfolding. Nature 2003, 426, 884–890. [Google Scholar] [CrossRef]
- Rose, G.D.; Fleming, P.J.; Banavar, J.R.; Maritan, A. A backbone-based theory of protein folding. Proc. Natl. Acad. Sci. USA 2006, 103, 16623–16633. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Shaw, D.E. How fast-folding proteins fold. Science 2011, 334, 517–520. [Google Scholar] [CrossRef]
- Best, R.B. Atomistic molecular simulations of protein folding. Curr. Opin. Struct. Biol. 2012, 22, 52–61. [Google Scholar] [CrossRef] [PubMed]
- Pancsa, R.; Fuxreiter, M. Interactions via intrinsically disordered regions: What kind of motifs? IUBMB Life 2012, 64, 513–520. [Google Scholar] [CrossRef]
- Tompa, P.; Davey, N.E.; Gibson, T.J.; Babu, M.M. A Million Peptide Motifs for the Molecular Biologist. Mol. Cell 2014, 55, 161–169. [Google Scholar] [CrossRef] [PubMed]
- Tompa, P.; Schad, E.; Tantos, A.; Kalmar, L. Intrinsically disordered proteins: Emerging interaction specialists. Curr. Opin. Struct. Biol. 2015, 35, 49–59. [Google Scholar] [CrossRef]
- Dunbrack, R. Rotamer libraries in the 21st century. Curr. Opin. Struct. Biol. 2002, 12, 431–440. [Google Scholar] [CrossRef]
- Smith, L.J.; Bolin, K.A.; Schwalbe, H.; MacArthur, M.W.; Thornton, J.M.; Dobson, C.M. Analysis of main chain torsion angles in proteins: Prediction of NMR coupling constants for native and random coil conformations. J. Mol. Biol. 1996, 255, 494–506. [Google Scholar] [CrossRef] [PubMed]
- Jha, A.K.; Colubri, A.; Freed, K.F.; Sosnick, T.R. Statistical coil model of the unfolded state: Resolving the reconciliation problem. Proc. Natl. Acad. Sci. USA 2005, 102, 13099–13104. [Google Scholar] [CrossRef]
- Bernadó, P.; Blanchard, L.; Timmins, P.; Marion, D.; Ruigrok, R.W.H.; Blackledge, M. A structural model for unfolded proteins from residual dipolar couplings and small-angle X-ray scattering. Proc. Natl. Acad. Sci. USA 2005, 102, 17002–17007. [Google Scholar] [CrossRef]
- Kolodny, R.; Koehl, P.; Guibas, L.; Levitt, M. Small libraries of protein fragments model native protein structures accurately. J. Mol. Biol. 2002, 323, 297–307. [Google Scholar] [CrossRef]
- Rohl, C.A.; Strauss, C.E.; Misura, K.M.; Baker, D. Protein structure prediction using Rosetta. In Numerical Computer Methods, Part D; Academic Press: Cambridge, UK, 2004; Volume 383, pp. 66–93. [Google Scholar]
- Baeten, L.; Reumers, J.; Tur, V.; Stricher, F.; Lenaerts, T.; Serrano, L.; Rousseau, F.; Schymkowitz, J. Reconstruction of protein backbones from the BriX collection of canonical protein fragments. PLOS Comput. Biol. 2008, 4, e1000083. [Google Scholar] [CrossRef]
- Maupetit, J.; Derreumaux, P.; Tufféry, P. A fast method for large-scale De Novo peptide and miniprotein structure prediction. J. Comput. Chem. 2010, 31, 726–738. [Google Scholar]
- Molloy, K.; Shehu, A. A general, adaptive, roadmap-based algorithm for protein motion computation. IEEE Trans. Nano Biosci. 2016, 15, 158–165. [Google Scholar] [CrossRef]
- Huang, J.R.; Ozenne, V.; Jensen, M.R.; Blackledge, M. Direct prediction of NMR residual dipolar couplings from the primary sequence of unfolded proteins. Angew. Chem. Int. Ed. 2013, 52, 687–690. [Google Scholar] [CrossRef] [PubMed]
- Estaña, A.; Sibille, N.; Delaforge, E.; Vaisset, M.; Cortés, J.; Bernadó, P. Realistic ensemble models of intrinsically disordered proteins using a structure-encoding coil database. Structure 2019, 27, 381–391. [Google Scholar] [CrossRef] [PubMed]
- Levinthal, C. How to fold graciously. Mössbauer Spectroscopy in Biological Systems Proceedings. In Proceedings of a meeting held at Allerton House, Chicago, IL, USA, 17–18 March 1969; pp. 22–24. [Google Scholar]
- Rooman, M.; Dehouck, Y.; Kwasigroch, J.; Biot, C.; Gilis, D. What is paradoxical about Levinthal paradox? J. Biomol. Struct. Dyn. 2003, 20, 327–329. [Google Scholar] [CrossRef]
- Al-Bluwi, I.; Siméon, T.; Cortés, J. Motion planning algorithms for molecular simulations: A survey. Comput. Sci. Rev. 2012, 6, 125–143. [Google Scholar] [CrossRef]
- Gipson, B.; Hsu, D.; Kavraki, L.; Latombe, J.C. Computational models of protein kinematics and dynamics: Beyond simulation. Ann. Rev. Anal. Chem. 2012, 5, 273–291. [Google Scholar] [CrossRef] [PubMed]
- Shehu, A.; Plaku, E. A survey of computational treatments of biomolecules by robotics-inspired methods modeling equilibrium structure and dynamic. J. Artif. Intell. Res. 2016, 57, 509–572. [Google Scholar] [CrossRef]
- Ghallab, M.; Nau, D.; Traverso, P. Automated Planning: Theory and Practice; The Morgan Kaufmann Series in Artificial Intelligence; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Richter, S.; Westphal, M. The LAMA planner: Guiding cost-based anytime planning with landmarks. J. Artif. Intell. Res. 2010, 39, 127–177. [Google Scholar] [CrossRef]
- Wales, D. Energy Landscapes: Applications to Clusters, Biomolecules and Glasses; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Honda, S.; Yamasaki, K.; Sawada, Y.; Morii, H. 10 residue folded peptide designed by segment statistics. Structure 2004, 12, 1507–1518. [Google Scholar] [CrossRef]
- Liang, H.; Chen, H.; Fan, K.; Wei, P.; Guo, X.; Jin, C.; Zeng, C.; Tang, C.; Lai, L. De novo design of a βαβ Motif. Angew. Chem. Int. Ed. 2009, 48, 3301–3303. [Google Scholar] [CrossRef]
- Enemark, S.; Kurniawan, N.A.; Rajagopalan, R. β-Hairpin forms by rolling up from C-terminal: Topological guidance of early folding dynamics. Sci. Rep. 2012, 2, 649. [Google Scholar] [CrossRef]
- Qi, Y.; Huang, Y.; Liang, H.; Liu, Z.; Lai, L. Folding simulations of a de novo designed protein with a βαβ fold. Biophys. J. 2010, 98, 321–329. [Google Scholar] [CrossRef] [PubMed]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Snow, C.; Zagrovic, B.; Pande, V. The Trp-cage: Folding kinetics and unfolded state topology via molecular dynamics simulations. J. Am. Chem. Soc. 2003, 124, 14548–14549. [Google Scholar] [CrossRef]
- Satoh, D.; Shimizu, K.; Nakamura, S.; Terada, T. Folding free-energy landscape of a 10-residue mini-protein, chignolin. FEBS Lett. 2006, 580, 3422–3426. [Google Scholar] [CrossRef]
- The PyMOL Molecular Graphics System, Version 2.0; Schrödinger, LLC: New York, NY, USA, 2018.
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef]
- Crooks, G.E.; Hon, G.; Chandonia, J.M.; Brenner, S.E. WebLogo: a sequence logo generator. Genome Res. 2004, 14, 1188–1190. [Google Scholar] [CrossRef] [PubMed]
- Kührová, P.; De Simone, A.; Otyepka, M.; Best, R.B. Force-field dependence of Chignolin folding and misfolding: Comparison with experiment and redesign. Biophys. J. 2012, 102, 1897–1906. [Google Scholar] [CrossRef]
- Fox, N.K.; Brenner, S.E.; Chandonia, J.M. SCOPe: Structural classification of proteins–extended, integrating SCOP and ASTRAL data and classification of new structures. Nucleic Acids Res. 2014, 42, D304–D309. [Google Scholar] [CrossRef]
- Scott, R.A.; Scheraga, H.A. Conformational analysis of macromolecules. III. Helical structures of polyglycine and poly-l-alanine. J. Chem. Phys. 1966, 45, 2091–2101. [Google Scholar] [CrossRef]
- Levitt, M. A simplified representation of protein conformations for rapid simulation of protein folding. J. Mol. Biol. 1976, 104, 59–107. [Google Scholar] [CrossRef]
- Ruiz de Angulo, V.; Cortés, J.; Porta, J.M. Rigid-CLL: Avoiding constant-distance computations in cell linked-lists algorithms. J. Comput. Chem. 2012, 33, 294–300. [Google Scholar] [CrossRef]
- Bondi, A. Van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Devaurs, D.; Molloy, K.; Vaisset, M.; Shehu, A.; Siméon, T.; Cortés, J. Characterizing energy landscapes of peptides using a combination of stochastic algorithms. IEEE Trans. NanoBiosci. 2015, 14, 545–552. [Google Scholar] [CrossRef] [PubMed]



| Tripeptide Sequence | No. of Conformations |
|---|---|
| Gly-Tyr-Asp | 994 |
| Tyr-Asp-Pro | 710 |
| Asp-Pro-Glu | 1541 |
| Pro-Glu-Thr | 1030 |
| Glu-Thr-Gly | 1446 |
| Thr-Gly-Thr | 1779 |
| Gly-Thr-Trp | 545 |
| Thr-Trp-Gly | 240 |
| Chignolin (Original Sequence) | ||||
|---|---|---|---|---|
| C-ter T→folded | C-ter T→misfolded | extended→folded | extended→misfolded | |
| CPU time (s) | 11.1 | 8.7 | 5.2 | 3.5 |
| # states | 5416.4 | 2587.7 | 2800.1 | 849.5 |
| # backtracks | 234.6 | 136.6 | 124.6 | 39.2 |
| Path length (# steps) | 133.8 | 54.5 | 106.3 | 48.7 |
| Path distance (rad) | 8.8 | 5.1 | 6.0 | 7.0 |
| Path density | 31.9 | 5.5 | 23.3 | 4.5 |
| Chignolin-W9A (Mutant) | ||||
| C-ter T→folded | C-ter T→misfolded | extended→folded | extended→misfolded | |
| CPU time (s) | 12.2 | 8.8 | 5.6 | 5.1 |
| # states | 4943.6 | 2567.8 | 2317.0 | 2946.0 |
| # backtracks | 219.6 | 139.0 | 101.3 | 126.3 |
| Path length (# steps) | 140.3 | 51.3 | 103.0 | 125.7 |
| Path distance (rad) | 8.2 | 9.0 | 5.8 | 8.2 |
| Path density | 31.2 | 4.6 | 23.4 | 23.8 |
| DS119: Extended→Folded | |
|---|---|
| CPU time (s) | 25.2 |
| # states | 70558.2 |
| # backtracks | 8210.4 |
| Path length (# steps) | 158.2 |
| Path distance (rad) | 11.3 |
| Path density | 124.4 |
| Tripeptide Sequence | No. Conformations | Tripeptide Sequence | No. Conformations |
|---|---|---|---|
| Gly-Ser-Gly | 3727 | Lys-Lys-Leu | 2286 |
| Ser-Gly-Gln | 1118 | Lys-Leu-Lys | 1996 |
| Gly-Gln-Val | 1294 | Leu-Lys-Glu | 3100 |
| Gln-Val-Arg | 607 | Leu-Glu-Glu | 1631 |
| Val-Arg-Thr | 970 | Glu-Glu-Ala | 2591 |
| Arg-Thr-Ile | 757 | Glu-Ala-Lys | 1514 |
| Thr-Ile-Trp | 181 | Ala-Lys-Lys | 1714 |
| Ile-Trp-Val | 180 | Lys-Lys-Ala | 1629 |
| Trp-Val-Gly | 279 | Lys-Ala-Asn | 1009 |
| Val-Gly-Gly | 2443 | Ala-Asn-Ile | 1010 |
| Gly-Gly-Thr | 2510 | Asn-Ile-Arg | 647 |
| Gly-Thr-Pro | 1428 | Ile-Arg-Val | 998 |
| Thr-Pro-Glu | 1738 | Arg-Val-Thr | 1351 |
| Pro-Glu-Glu | 1752 | Val-Thr-Phe | 888 |
| Glu-Glu-Leu | 3433 | Thr-Phe-Trp | 151 |
| Glu-Leu-Lys | 2378 | Phe-Trp-Gly | 192 |
| Leu-Lys-Lys | 2528 | Trp-Gly-Asp | 257 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estaña, A.; Ghallab, M.; Bernadó, P.; Cortés, J. Investigating the Formation of Structural Elements in Proteins Using Local Sequence-Dependent Information and a Heuristic Search Algorithm. Molecules 2019, 24, 1150. https://doi.org/10.3390/molecules24061150
Estaña A, Ghallab M, Bernadó P, Cortés J. Investigating the Formation of Structural Elements in Proteins Using Local Sequence-Dependent Information and a Heuristic Search Algorithm. Molecules. 2019; 24(6):1150. https://doi.org/10.3390/molecules24061150
Chicago/Turabian StyleEstaña, Alejandro, Malik Ghallab, Pau Bernadó, and Juan Cortés. 2019. "Investigating the Formation of Structural Elements in Proteins Using Local Sequence-Dependent Information and a Heuristic Search Algorithm" Molecules 24, no. 6: 1150. https://doi.org/10.3390/molecules24061150
APA StyleEstaña, A., Ghallab, M., Bernadó, P., & Cortés, J. (2019). Investigating the Formation of Structural Elements in Proteins Using Local Sequence-Dependent Information and a Heuristic Search Algorithm. Molecules, 24(6), 1150. https://doi.org/10.3390/molecules24061150






