The Effects of Reactant Concentration and Air Flow Rate in the Consumption of Dissolved O2 during the Photochemistry of Aqueous Pyruvic Acid
Abstract
:1. Introduction
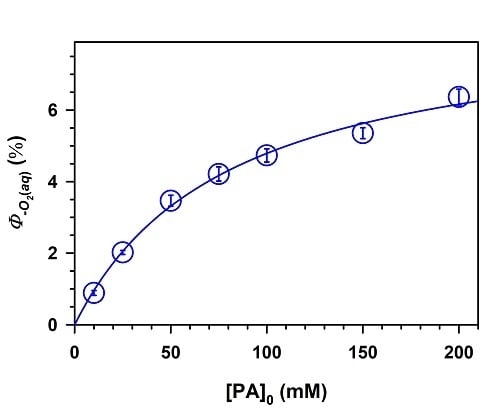
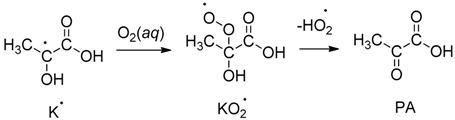
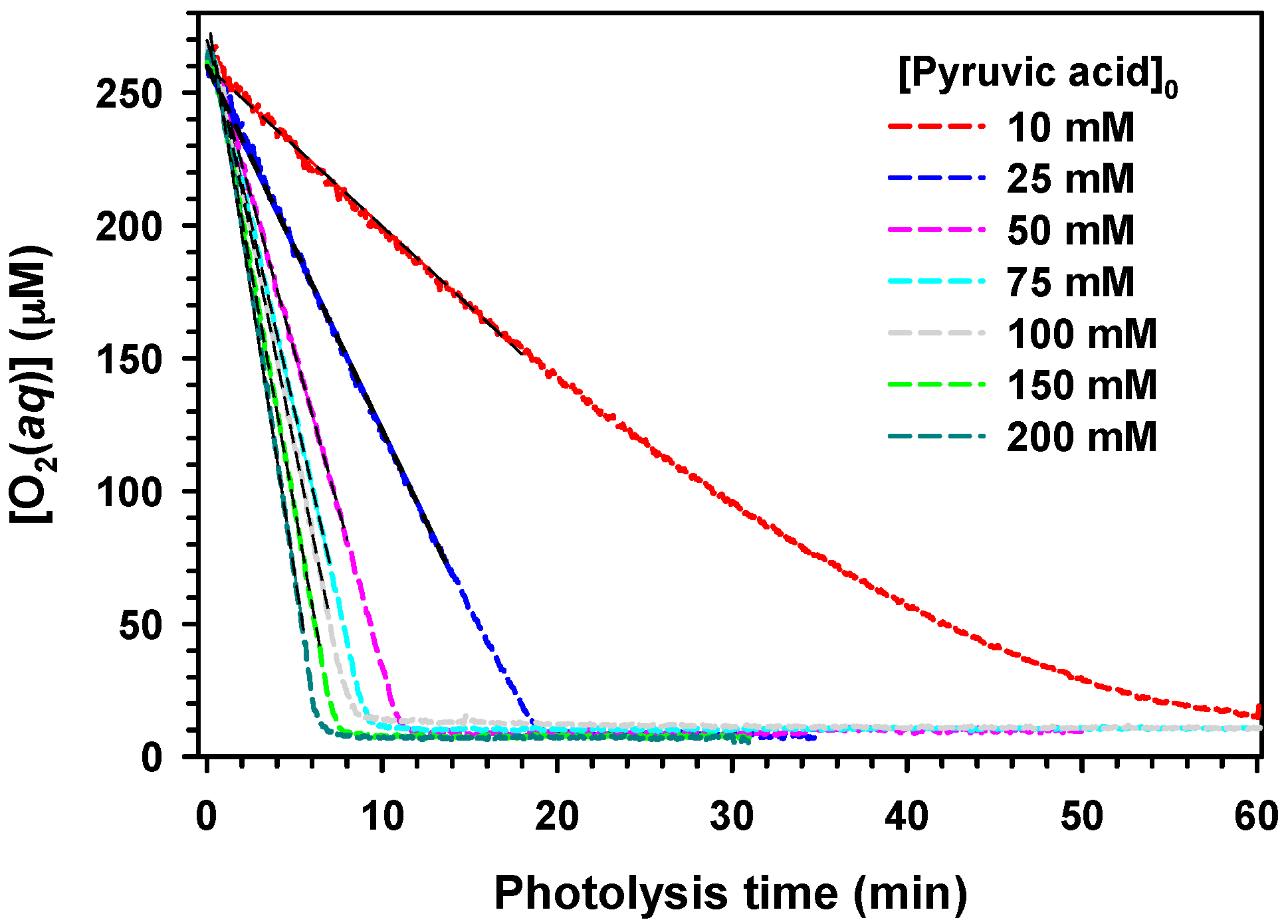
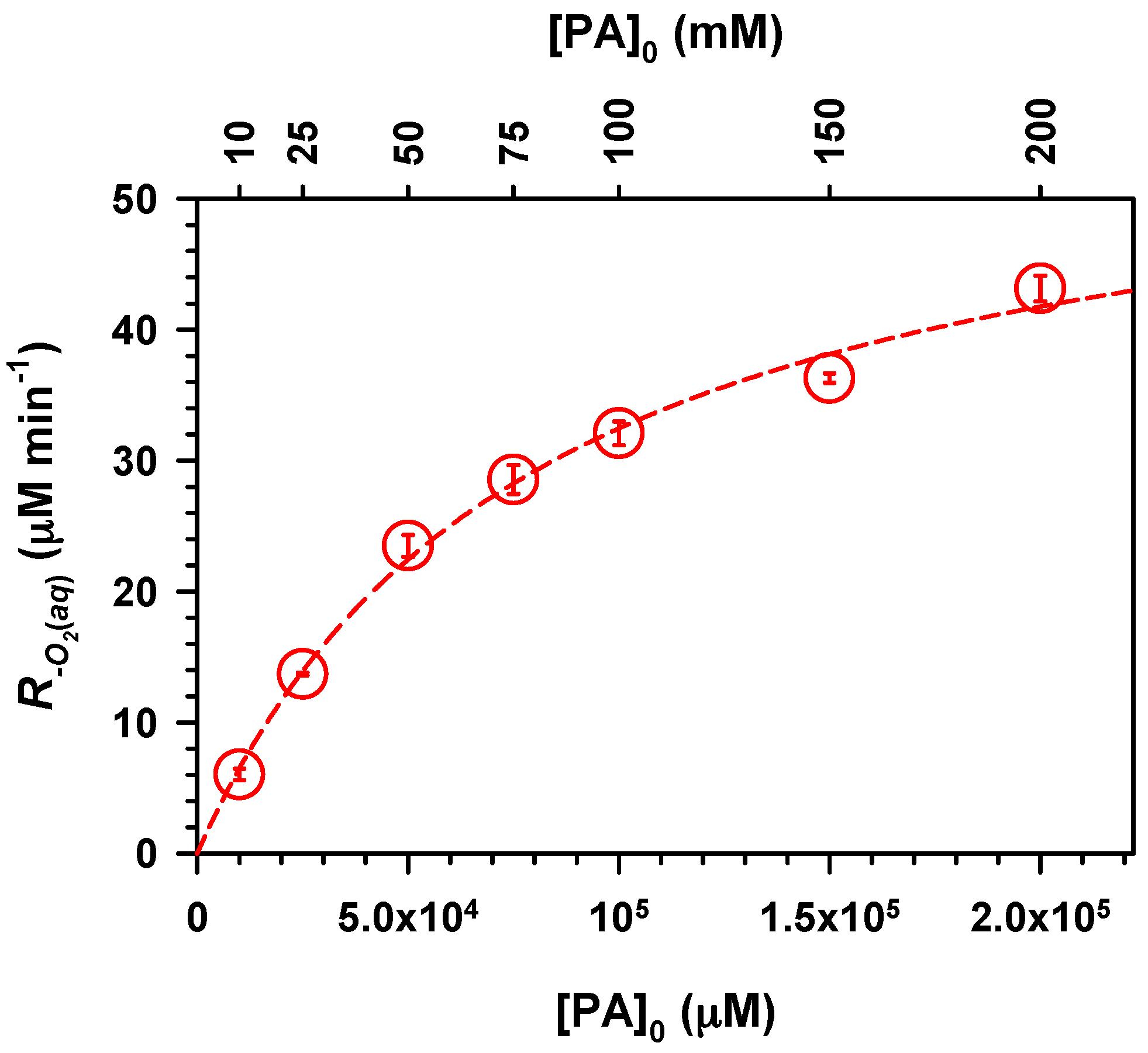
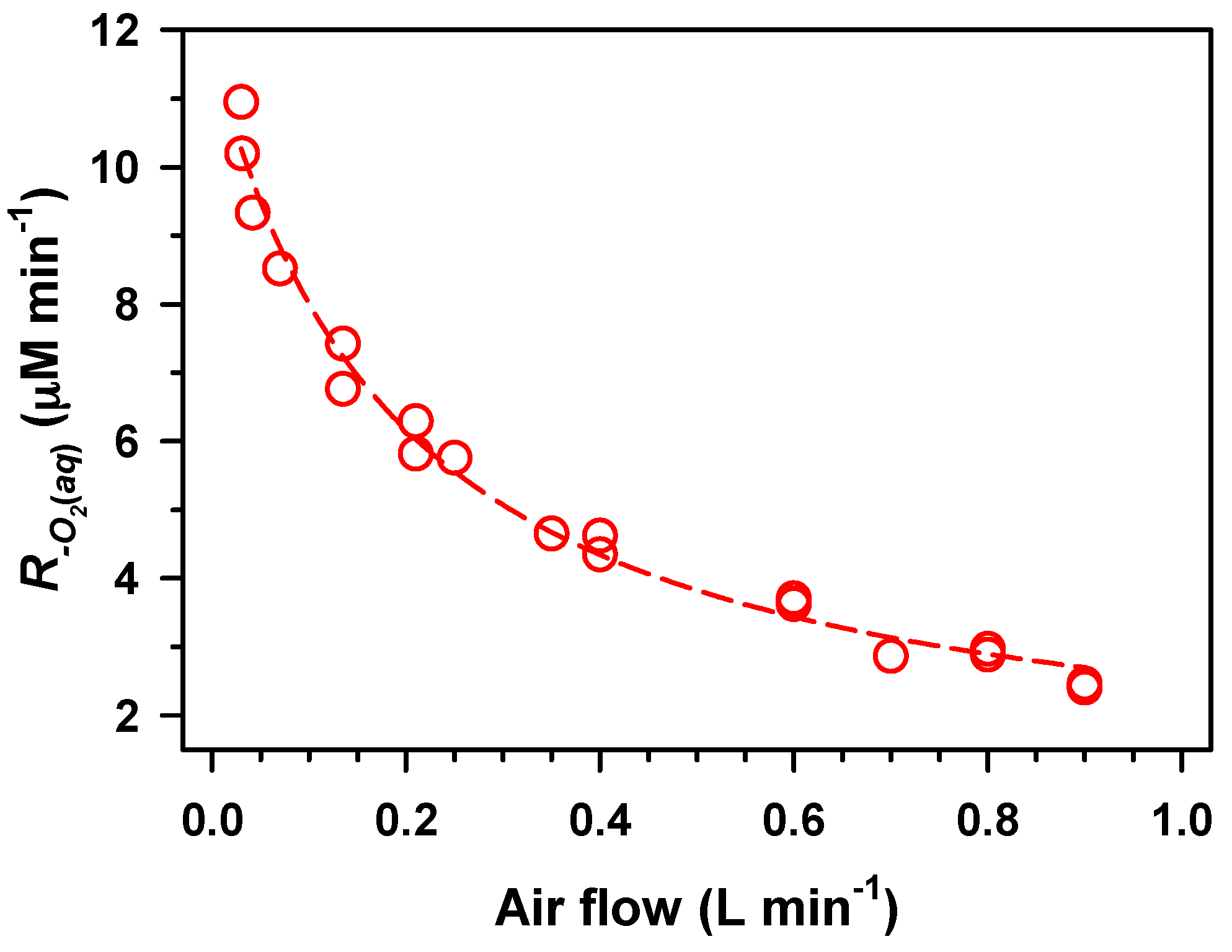
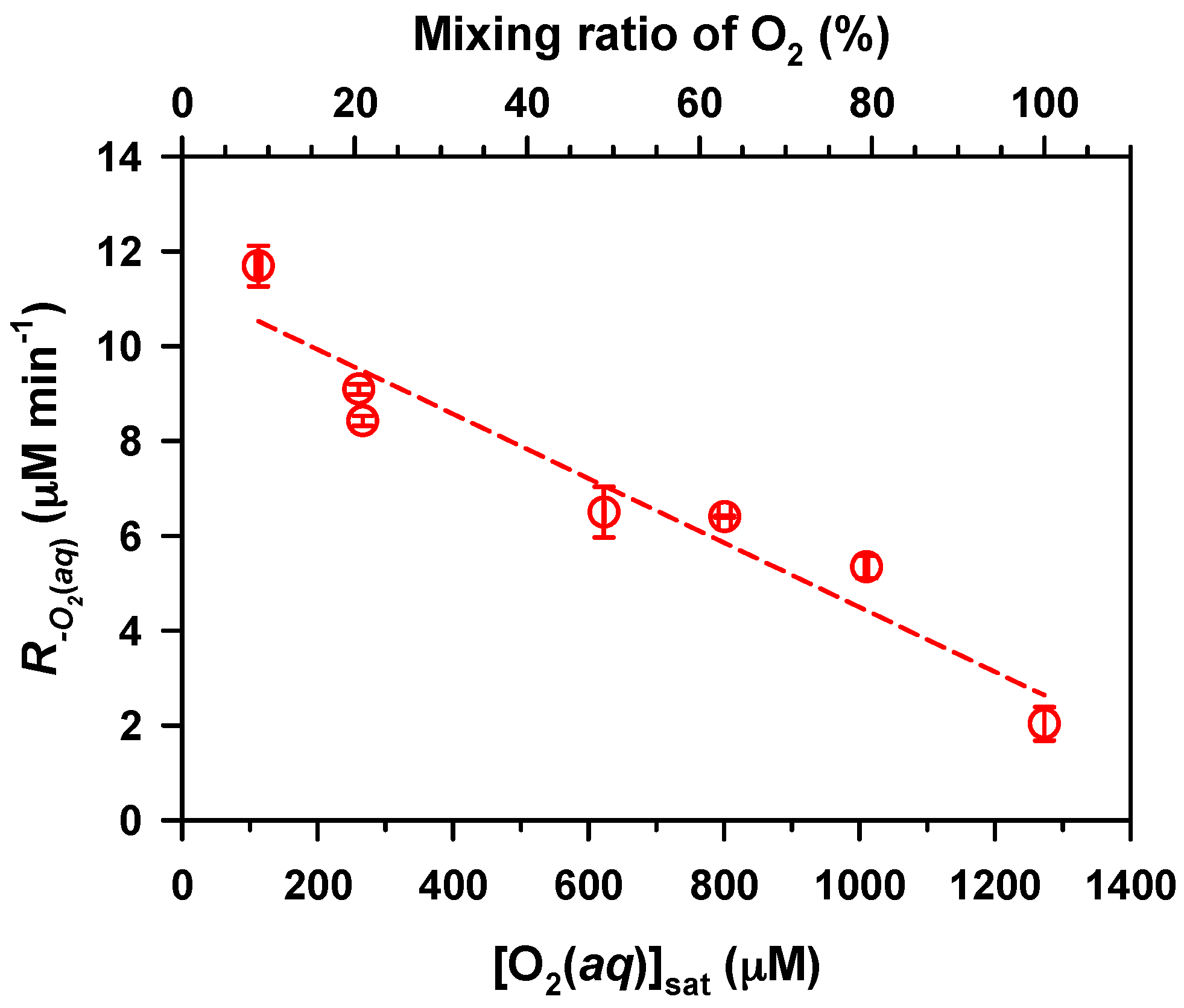
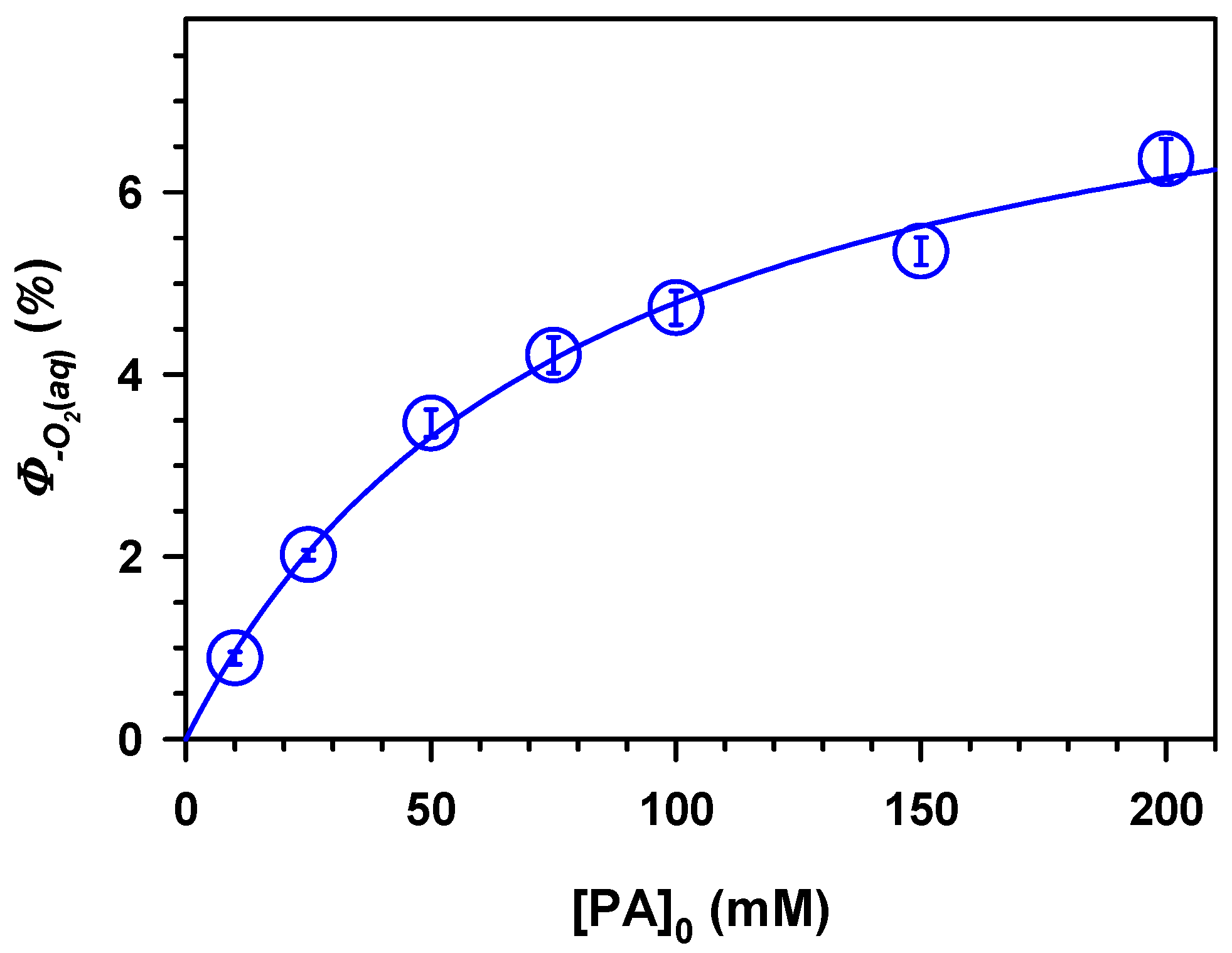
2. Results and Discussion
 ,
,
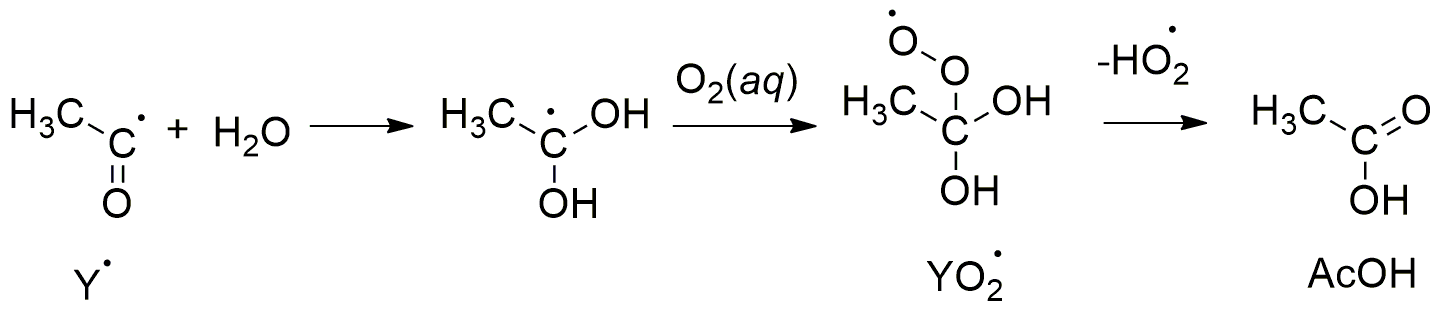 .
.
3. Materials and Methods
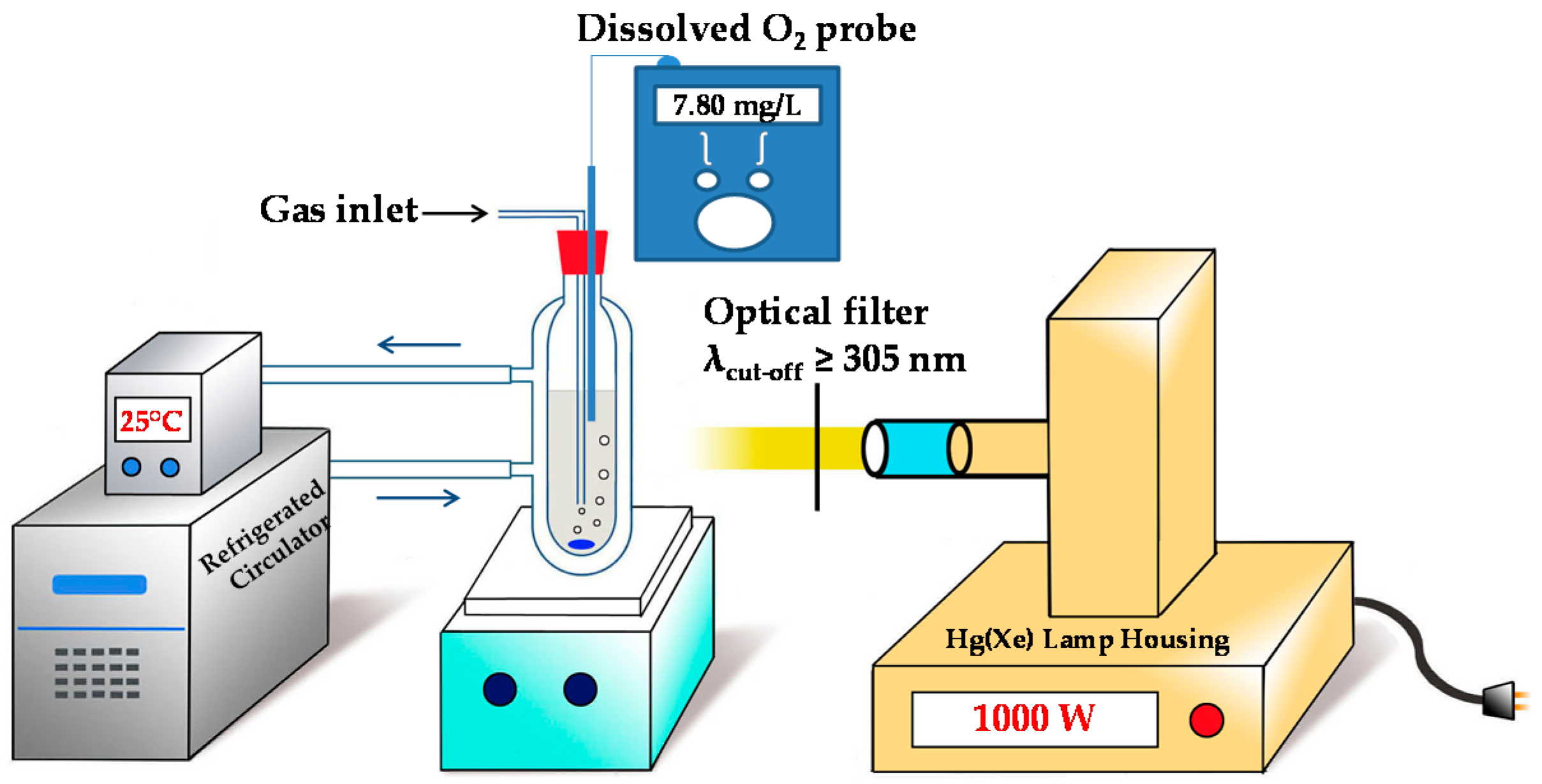
3.1. Preparation of Experiments
3.2. Photochemical Conditions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haynes, W.M. (Ed.) Physical Constants of Organic Compunds. In CRC Handbook of Chemistry and Physics, 97th ed.; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2017. [Google Scholar]
- Fu, P.; Kawamura, K.; Usukura, K.; Miura, K. Dicarboxylic acids, ketocarboxylic acids and glyoxal in the marine aerosols collected during a round-the-world cruise. Mar. Chem. 2013, 148, 22–32. [Google Scholar] [CrossRef]
- Kawamura, K.; Tachibana, E.; Okuzawa, K.; Aggarwal, S.G.; Kanaya, Y.; Wang, Z.F. High abundances of water-soluble dicarboxylic acids, ketocarboxylic acids and α-dicarbonyls in the mountaintop aerosols over the North China Plain during wheat burning season. Atmos. Chem. Phys. 2013, 13, 8285–8302. [Google Scholar] [CrossRef]
- Mkoma, S.L.; Kawamura, K. Molecular composition of dicarboxylic acids, ketocarboxylic acids, α-dicarbonyls and fatty acids in atmospheric aerosols from Tanzania, East Africa during wet and dry seasons. Atmos. Chem. Phys. 2013, 13, 2235–2251. [Google Scholar] [CrossRef]
- Guzman, M.I.; Colussi, A.J.; Hoffmann, M.R. Photogeneration of distant radical pairs in aqueous pyruvic acid glasses. J. Phys. Chem. A 2006, 110, 931–935. [Google Scholar] [CrossRef] [PubMed]
- Guzman, M.I.; Hoffmann, M.R.; Colussi, A.J. Photolysis of pyruvic acid in ice: Possible relevance to CO and CO2 ice core record anomalies. J. Geophys. Res. Atmos. 2007, 112, D10123. [Google Scholar] [CrossRef]
- Eugene, A.J.; Guzman, M.I. Reactivity of ketyl and acetyl radicals from direct solar actinic photolysis of aqueous pyruvic acid. J. Phys. Chem. A 2017, 121, 2924–2935. [Google Scholar] [CrossRef]
- Eugene, A.J.; Guzman, M.I. Reply to “Comment on ‘Reactivity of Ketyl and Acetyl Radicals from Direct Solar Actinic Photolysis of Aqueous Pyruvic Acid’”. J. Phys. Chem. A 2017, 121, 8741–8744. [Google Scholar] [CrossRef]
- Eugene, A.J.; Xia, S.-S.; Guzman, M.I. Negative production of acetoin in the photochemistry of aqueous pyruvic acid. Proc. Nat. Acad. Sci. USA 2013, 110, E4274–E4275. [Google Scholar] [CrossRef]
- Rapf, R.J.; Perkins, R.J.; Dooley, M.R.; Kroll, J.A.; Carpenter, B.K.; Vaida, V. Environmental processing of lipids driven by aqueous photochemistry of α-keto acids. ACS Cent. Sci. 2018. [Google Scholar] [CrossRef]
- Carlton, A.G.; Turpin, B.J.; Lim, H.J.; Altieri, K.E.; Seitzinger, S. Link between isoprene and secondary organic aerosol (SOA): Pyruvic acid oxidation yields low volatility organic acids in clouds. Geophys. Res. Lett. 2006, 33, L06822. [Google Scholar] [CrossRef]
- Pillar, E.A.; Guzman, M.I. Oxidation of substituted catechols at the air–water interface: Production of carboxylic acids, quinones, and polyphenols. Environ. Sci. Technol. 2017, 51, 4951–4959. [Google Scholar] [CrossRef]
- Saxena, P.; Hildemann, L.M. Water-soluble organics in atmospheric particles: A critical review of the literature and application of thermodynamics to identify candidate compounds. J. Atmos. Chem. 1996, 24, 57–109. [Google Scholar] [CrossRef]
- Eugene, A.J.; Pillar, E.A.; Colussi, A.J.; Guzman, M.I. Enhanced acidity of acetic and pyruvic acids on the surface of water. Langmuir 2018, 34, 9307–9312. [Google Scholar] [CrossRef] [PubMed]
- Parashar, S.; Lesnicki, D.; Sulpizi, M. Increased acid dissociation at the quartz/water interface. J. Phys. Chem. Lett. 2018, 9, 2186–2189. [Google Scholar] [CrossRef] [PubMed]
- Guzmán, M.I.; Hildebrandt, L.; Colussi, A.J.; Hoffmann, M.R. Cooperative hydration of pyruvic acid in ice. J. Am. Chem. Soc. 2006, 128, 10621–10624. [Google Scholar] [CrossRef] [PubMed]
- Buschmann, H.J.; Dutkiewicz, E.; Knoche, W. The reversible hydration of carbonyl-compounds in aqueous-solution. 2. The kinetics of the keto gem-diol transition. Ber. Bunsen. Phys. Chem. 1982, 86, 129–134. [Google Scholar] [CrossRef]
- Buschmann, H.J.; Fuldner, H.H.; Knoche, W. Reversible hydration of carbonyl-compounds in aqueous-solution. 1. Keto-gem-diol equilibrium. Ber. Bunsen. Phys. Chem. 1980, 84, 41–44. [Google Scholar] [CrossRef]
- Knoche, W.; Lopezquintela, M.A.; Weiffen, J. The hydration of aliphatic-aldehydes and pyruvic-acid in mixed-solvents. Ber. Bunsen. Phys. Chem. 1985, 89, 1047–1050. [Google Scholar] [CrossRef]
- Pocker, Y.; Meany, J.E.; Nist, B.J.; Zadorojny, C. Reversible hydration of pyruvic acid. I. Equilibrium studies. J. Phys. Chem. 1969, 73, 2879. [Google Scholar] [CrossRef]
- Leermakers, P.A.; Vesley, G.F. The photochemistry of α-keto acids and α-keto esters. I. Photolysis of pyruvic acid and benzoylformic acid. J. Am. Chem. Soc. 1963, 85, 3776–3779. [Google Scholar] [CrossRef]
- Rapf, R.J.; Dooley, M.R.; Kappes, K.; Perkins, R.J.; Vaida, V. pH Dependence of the Aqueous Photochemistry of α-Keto Acids. J. Phys. Chem. A 2017, 121, 8368–8379. [Google Scholar] [CrossRef] [PubMed]
- Guzman, M.I.; Colussi, A.J.; Hoffmann, M.R. Photoinduced oligomerization of aqueous pyruvic acid. J. Phys. Chem. A 2006, 110, 3619–3626. [Google Scholar] [CrossRef] [PubMed]
- Rincón, A.G.; Guzmán, M.I.; Hoffmann, M.R.; Colussi, A.J. Optical absorptivity versus molecular composition of model organic aerosol matter. J. Phys. Chem. A 2009, 113, 10512–10520. [Google Scholar] [CrossRef]
- Rincón, A.G.; Guzmán, M.I.; Hoffmann, M.R.; Colussi, A.J. Thermochromism of model organic aerosol matter. J. Phys. Chem. Lett. 2010, 1, 368–373. [Google Scholar] [CrossRef]
- Xia, S.-S.; Eugene, A.J.; Guzman, M.I. Cross photoreaction of glyoxylic and pyruvic acids in model aqueous aerosol. J. Phys. Chem. A 2018, 122, 6457–6466. [Google Scholar] [CrossRef] [PubMed]
- Guzman, M.I. Photochemistry of Pyruvic Acid in Water and Ice. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2007. [Google Scholar]
- Renard, P.; Reed Harris, A.E.; Rapf, R.J.; Ravier, S.; Demelas, C.; Coulomb, B.; Quivet, E.; Vaida, V.; Monod, A. Aqueous phase oligomerization of methyl vinyl ketone by atmospheric radical reactions. J. Phys. Chem. C 2014, 118, 29421–29430. [Google Scholar] [CrossRef]
- Lee, W.; Baasandorj, M.; Stevens, P.S.; Hites, R.A. Monitoring OH-initiated oxidation kinetics of isoprene and its products using online mass spectrometry. Environ. Sci. Technol. 2005, 39, 1030–1036. [Google Scholar] [CrossRef] [PubMed]
- Von Sonntag, C.; Schuchmann, H.P. The elucidation of peroxyl radical reactions in aqueous solution with the help of radiation-chemical methods. Angew. Chem. Int. Edit. 1991, 30, 1229–1253. [Google Scholar] [CrossRef]
- Ferrell, R.T.; Himmelblau, D.M. Diffusion coefficients of nitrogen and oxygen in water. J. Chem. Eng. Data 1967, 12, 111–115. [Google Scholar] [CrossRef]
- Pillar-Little, E.A.; Guzman, M.I. An overview of dynamic heterogeneous oxidations in the troposphere. Environments 2018, 5, 104. [Google Scholar] [CrossRef]
- Eugene, A.J.; Xia, S.-S.; Guzman, M.I. Aqueous photochemistry of glyoxylic acid. J. Phys. Chem. A 2016, 120, 3817–3826. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Guzman, M.I. CO2 reduction under periodic illumination of ZnS. J. Phys. Chem. C 2014, 118, 11649–11656. [Google Scholar] [CrossRef]
- Blanchard, D.C.; Syzdek, L.D. Production of air bubbles of a specified size. Chem. Eng. Sci. 1977, 32, 1109–1112. [Google Scholar] [CrossRef]
- Zhou, R.; Guzman, M.I. Photocatalytic Reduction of Fumarate to Succinate on ZnS Mineral Surfaces. J. Phys. Chem. C 2016, 120, 7349–7357. [Google Scholar] [CrossRef]
- Aguirre, M.E.; Zhou, R.; Eugene, A.J.; Guzman, M.I.; Grela, M.A. Cu2O/TiO2 Heterostructures for CO2 Reduction Through a Direct Z-scheme: Protecting Cu2O from Photocorrosion. Appl. Catal. B 2017, 217, 485–493. [Google Scholar] [CrossRef]
- Görner, H.; Kuhn, H.J. Photodecarboxylation of phenylglyoxylic acid: Influence of para-substituents on the triplet state properties. J. Chem. Soc. Perkin Trans. 1999, 2, 2671–2680. [Google Scholar] [CrossRef]
- Kuhn, H.J.; Goerner, H. Triplet state and photodecarboxylation of phenylglyoxylic acid in the presence of water. J. Phys. Chem. 1988, 92, 6208–6219. [Google Scholar] [CrossRef]
- Ervens, B. Modeling the processing of aerosol and trace gases in clouds and fogs. Chem. Rev. 2015, 115, 4157–4198. [Google Scholar] [CrossRef]
- McNeill, V.F. Aqueous organic chemistry in the atmosphere: Sources and chemical processing of organic aerosols. Environ. Sci. Technol. 2015, 49, 1237–1244. [Google Scholar] [CrossRef]
- Finlayson-Pitts, B.J.; Pitts, J. Chemistry of the Upper and Lower Atmosphere; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eugene, A.J.; Guzman, M.I. The Effects of Reactant Concentration and Air Flow Rate in the Consumption of Dissolved O2 during the Photochemistry of Aqueous Pyruvic Acid. Molecules 2019, 24, 1124. https://doi.org/10.3390/molecules24061124
Eugene AJ, Guzman MI. The Effects of Reactant Concentration and Air Flow Rate in the Consumption of Dissolved O2 during the Photochemistry of Aqueous Pyruvic Acid. Molecules. 2019; 24(6):1124. https://doi.org/10.3390/molecules24061124
Chicago/Turabian StyleEugene, Alexis J., and Marcelo I. Guzman. 2019. "The Effects of Reactant Concentration and Air Flow Rate in the Consumption of Dissolved O2 during the Photochemistry of Aqueous Pyruvic Acid" Molecules 24, no. 6: 1124. https://doi.org/10.3390/molecules24061124
APA StyleEugene, A. J., & Guzman, M. I. (2019). The Effects of Reactant Concentration and Air Flow Rate in the Consumption of Dissolved O2 during the Photochemistry of Aqueous Pyruvic Acid. Molecules, 24(6), 1124. https://doi.org/10.3390/molecules24061124