Construction of Quantitative Structure Activity Relationship (QSAR) Models to Predict Potency of Structurally Diversed Janus Kinase 2 Inhibitors
Abstract
1. Introduction
2. Results
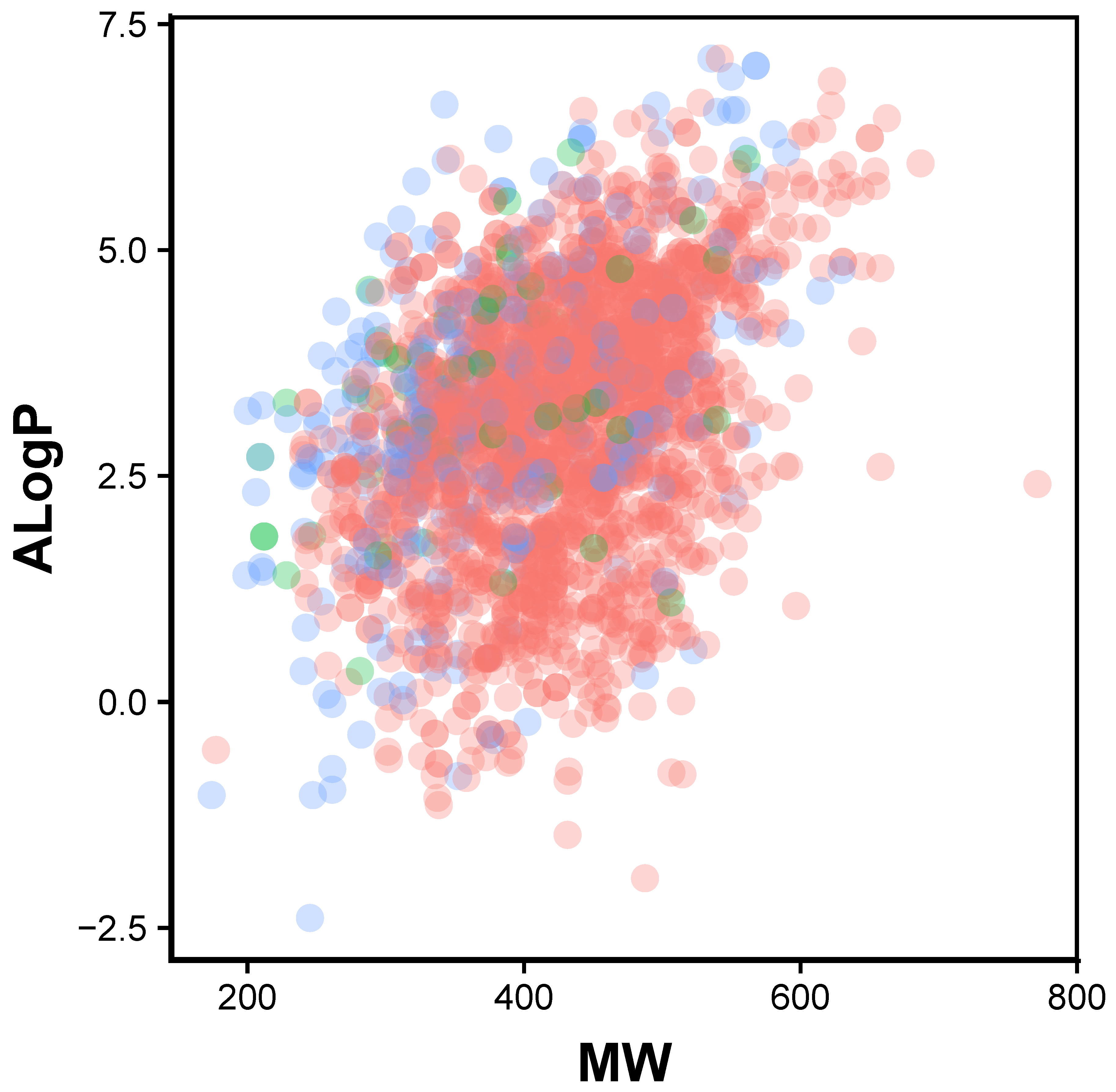
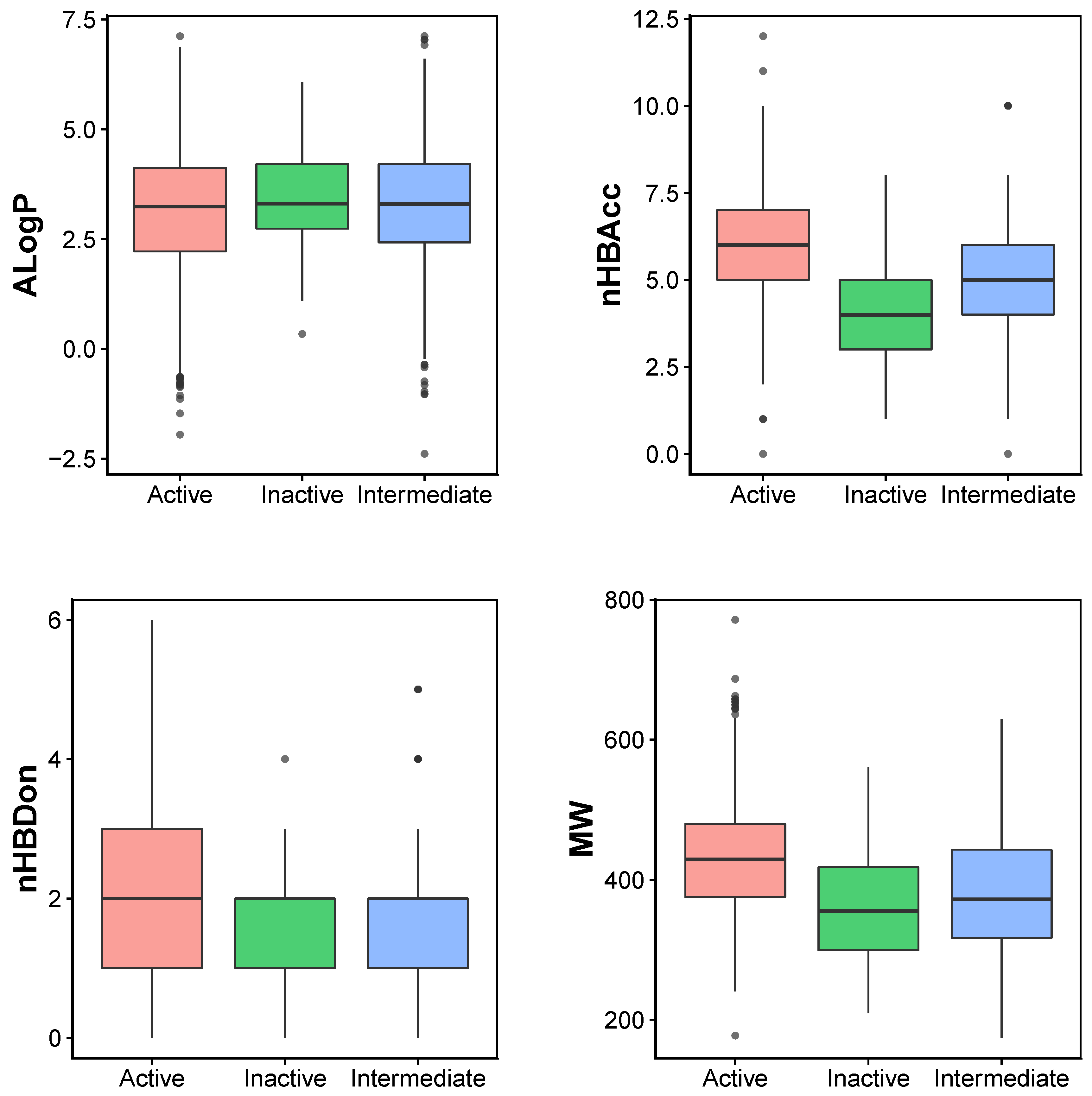
2.1. Chemical Space of JAK2 Inhibitors
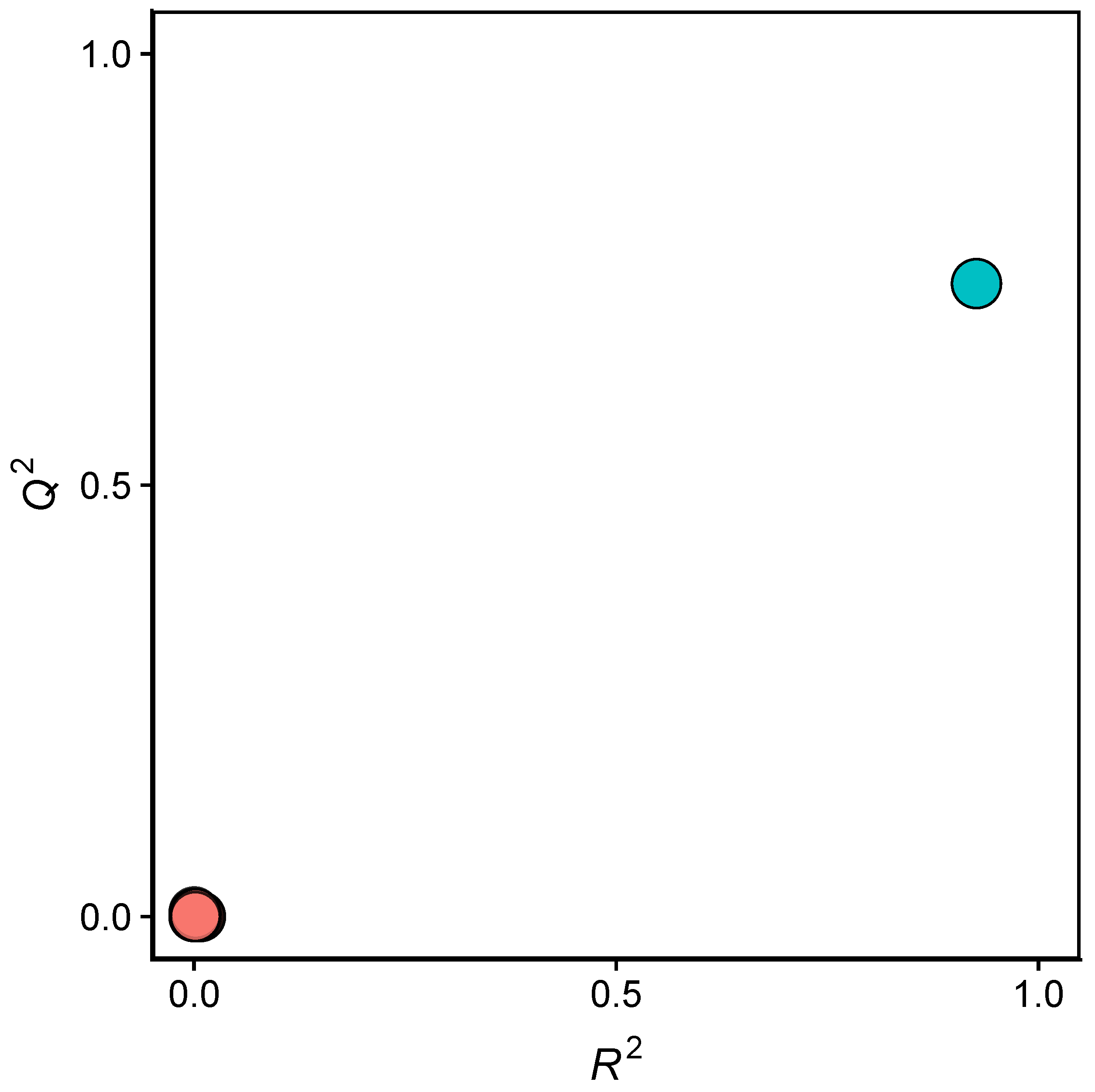
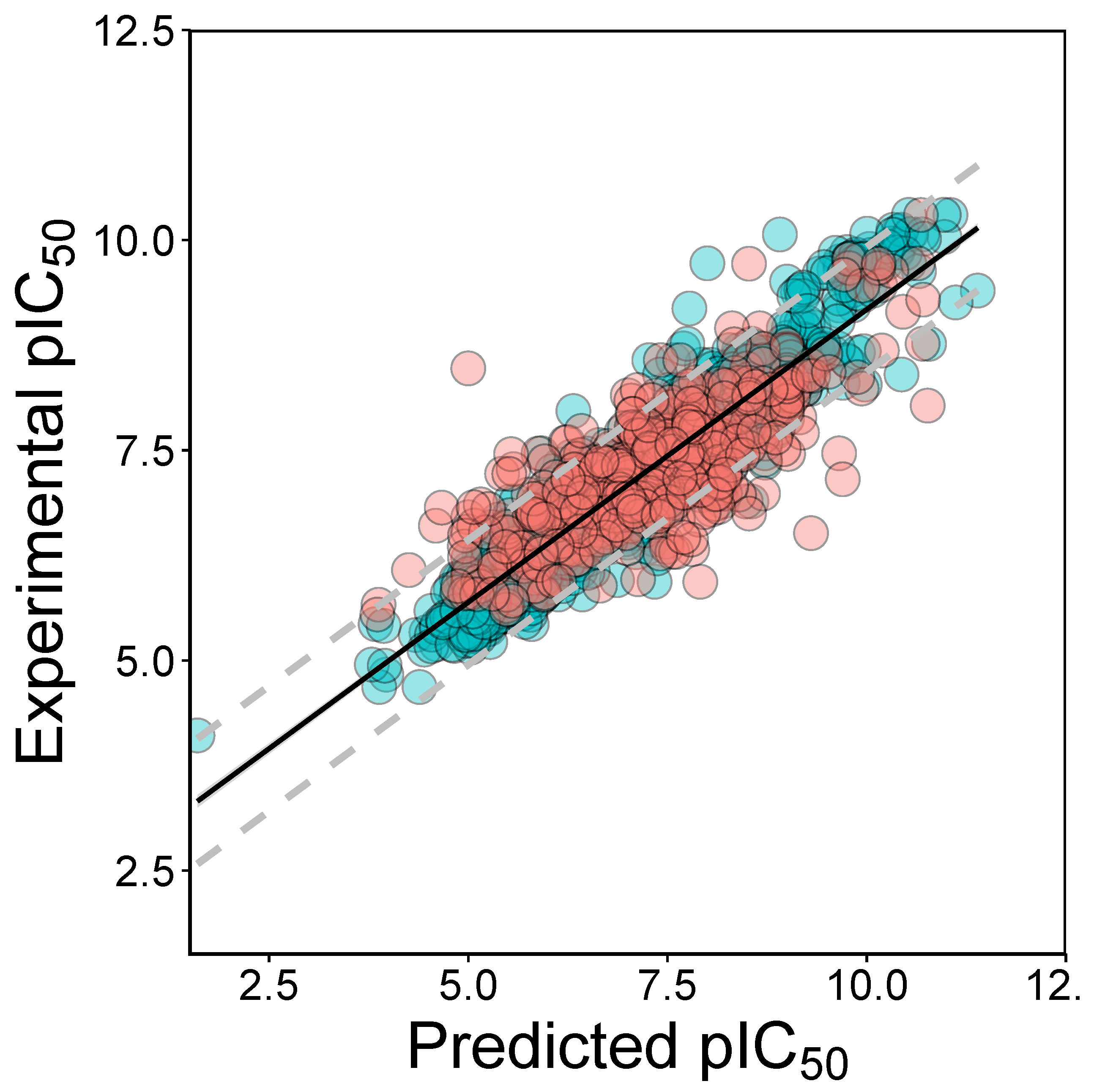
2.2. QSAR Modeling
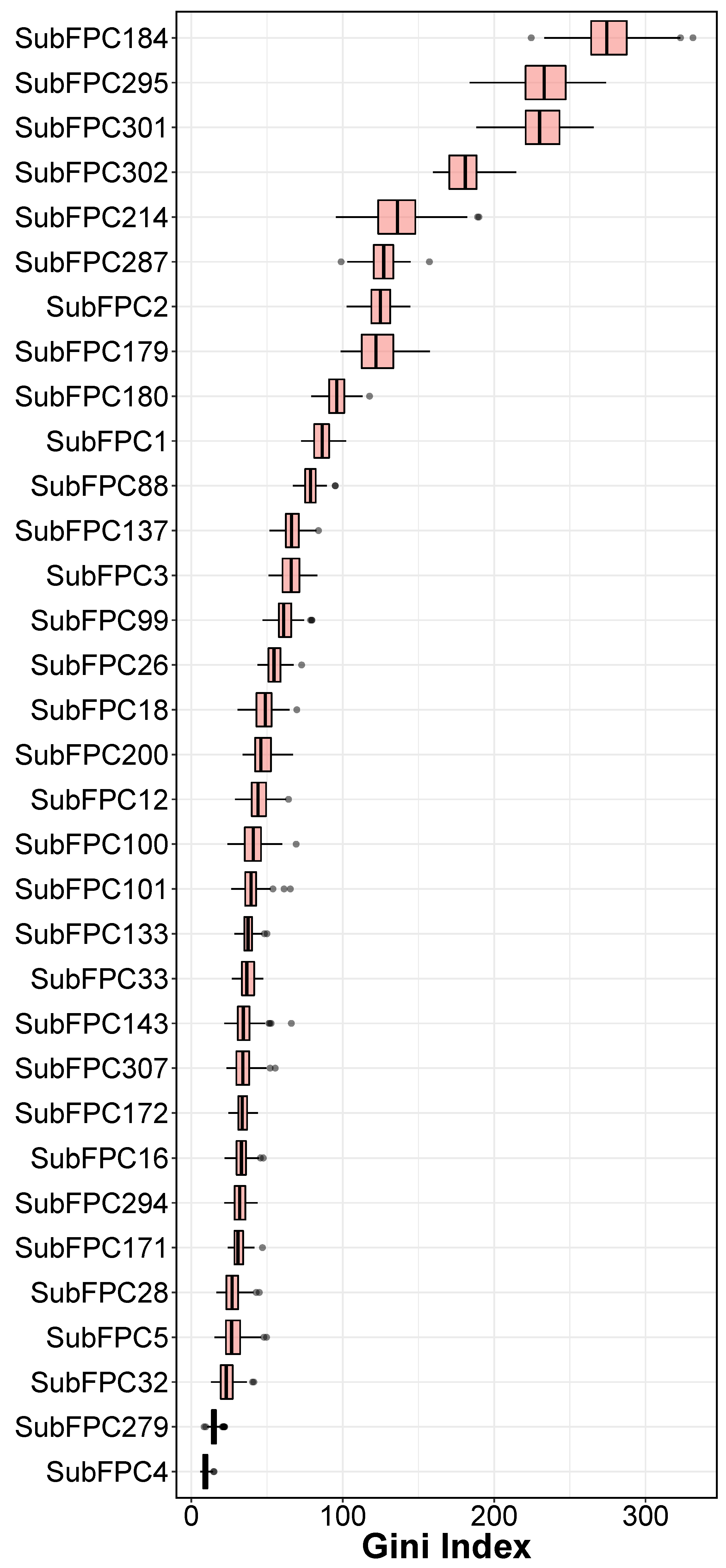
2.3. Interpretation of QSAR Models
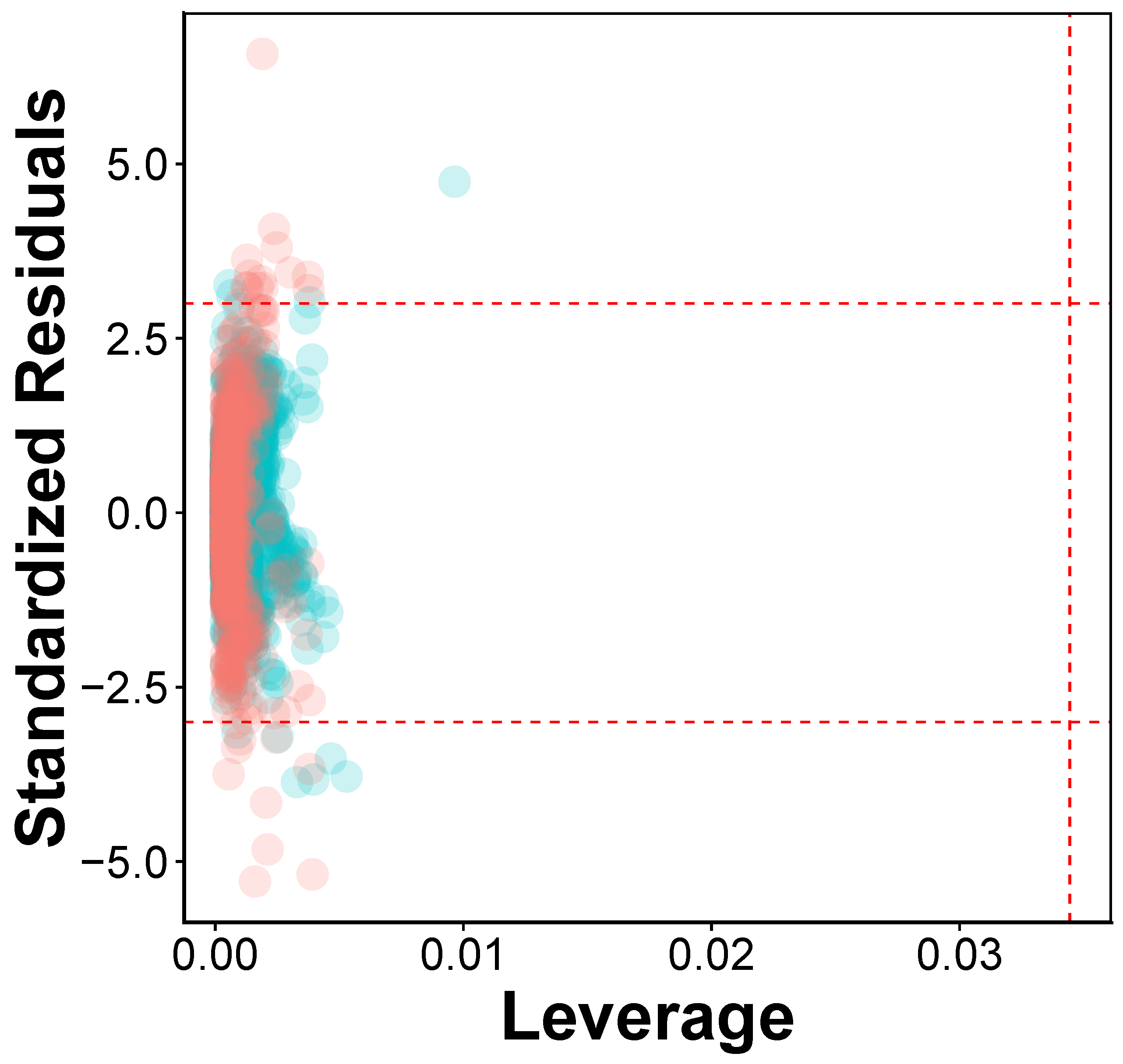
2.4. Applicability Domain
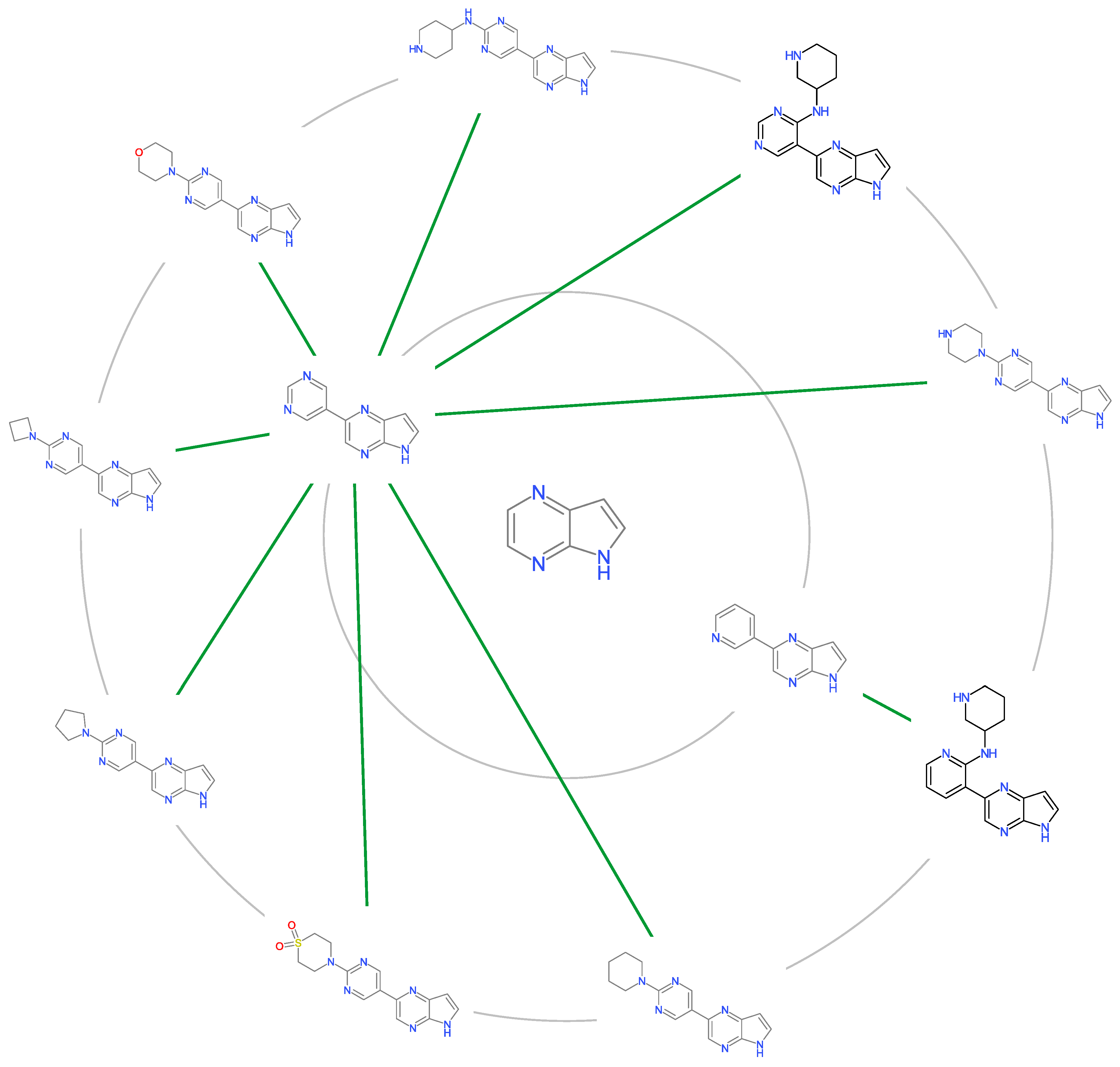
2.5. Molecular Cluster Analysis of JAK2 Inhibitors
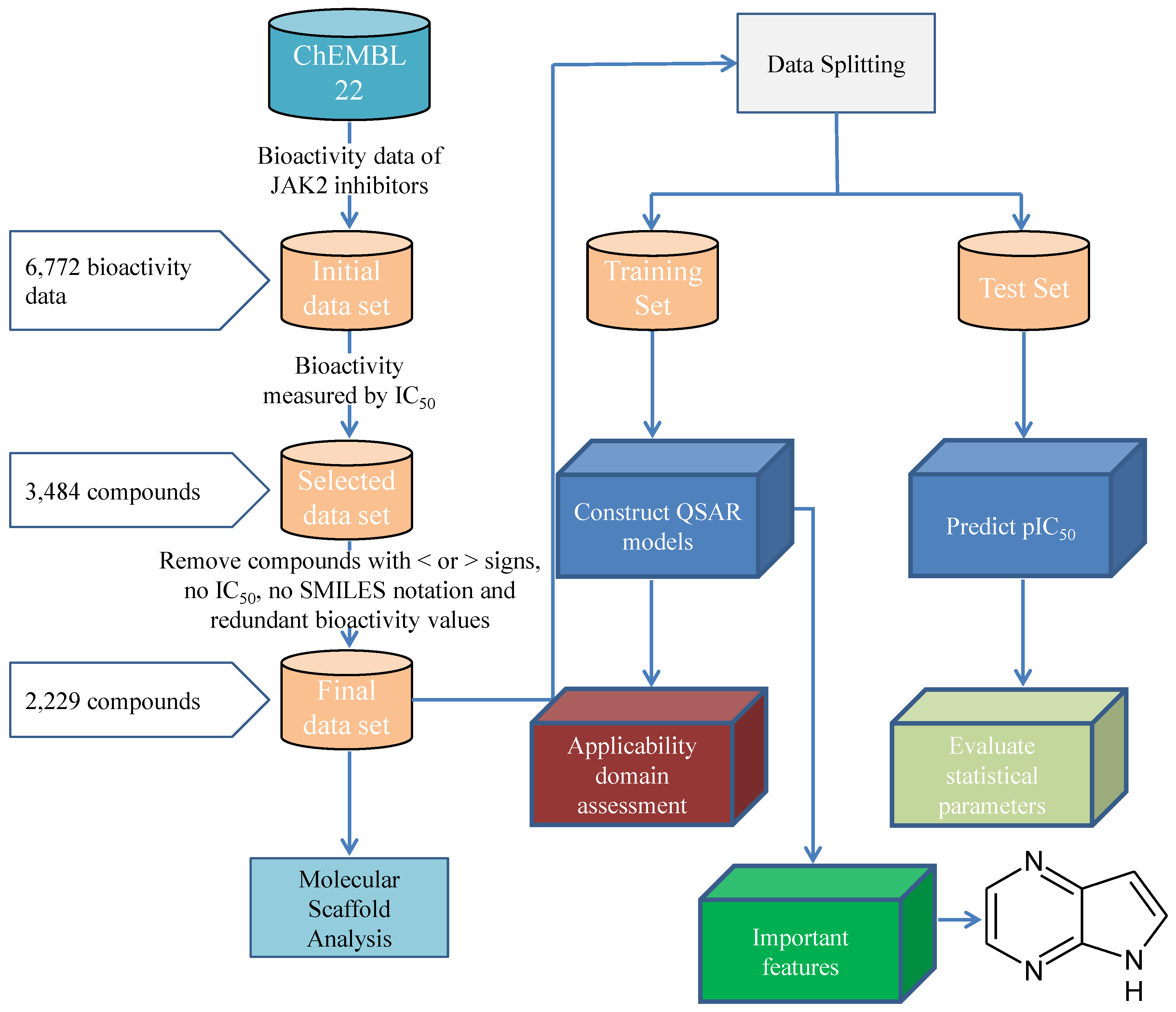
3. Materials and Methods
3.1. Data Set
3.1.1. Description of Compounds
3.1.2. Feature Selection
3.1.3. Data Splitting
3.1.4. Multivariate Analysis
3.2. Validation of QSAR Models
3.3. Applicability Domain Analysis
3.4. Molecular Cluster Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| JAK2 | Janus Kinase 2 |
| QSAR | Quantitative Structure-Activity Relationship |
| DT | Decision Tree |
| SVM | Support Vector Machine |
| DNN | Deep Neural Network |
| RF | Random Forest |
| RMSE | Root Mean Square Error |
| CV | Cross Validation |
| OECD | Organisation for Economic Cooperation and Development |
| MW | Molecular Weight |
| ALogP | Octanol-Water Partition Coefficient |
| nHBDon | Number of Hydrogen Bond Donors |
| nHBAcc | Number of Hydrogen Bond Acceptors |
References
- Miao, Q.; Ma, K.; Chen, D.; Wu, X.; Jiang, S. Targeting tropomyosin receptor kinase for cancer therapy. Eur. J. Med. Chem. 2019. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Jove, R. The STATs of cancer—New molecular targets come of age. Nat. Rev. Cancer 2004, 4, 97–105. [Google Scholar] [CrossRef] [PubMed]
- Meyer, S.C. Mechanisms of resistance to JAK2 inhibitors in myeloproliferative neoplasms. Hematol. Clin. 2017, 31, 627–642. [Google Scholar] [CrossRef] [PubMed]
- Quintás-Cardama, A. The role of Janus kinase 2 (JAK2) in myeloproliferative neoplasms: Therapeutic implications. Leuk. Res. 2013, 37, 465–472. [Google Scholar] [CrossRef]
- Ghoreschi, K.; Laurence, A.; O’Shea, J.J. Selectivity and therapeutic inhibition of kinases: To be or not to be? Nat. Immunol. 2009, 10, 356–360. [Google Scholar] [CrossRef]
- Britschgi, A.; Radimerski, T.; Bentires-Alj, M. Targeting PI3K, HER2 and the IL-8/JAK2 axis in metastatic breast cancer: Which combination makes the whole greater than the sum of its parts? Drug Resist. Updat. 2013, 16, 68–72. [Google Scholar] [CrossRef]
- Verma, A.; Kambhampati, S.; Parmar, S.; Platanias, L.C. Jak family of kinases in cancer. Cancer Metastasis Rev. 2003, 22, 423–434. [Google Scholar] [CrossRef]
- Chen, Q.; Luo, H.; Zhang, C.; Chen, Y.P.P. Bioinformatics in protein kinases regulatory network and drug discovery. Math. Biosci. 2015, 262, 147–156. [Google Scholar] [CrossRef]
- Singh, P.K.; Singh, H.; Silakari, O. Kinases inhibitors in lung cancer: From benchside to bedside. Biochim. Et Biophys. Acta (BBA)-Rev. Cancer 2016, 1866, 128–140. [Google Scholar] [CrossRef]
- Santos, F.P.; Verstovsek, S. Therapy with JAK2 inhibitors for myeloproliferative neoplasms. Hematol. Clin. 2012, 26, 1083–1099. [Google Scholar] [CrossRef][Green Version]
- Santos, F.P.; Verstovsek, S. JAK2 inhibitors: Are they the solution? Clin. Lymphoma Myeloma Leuk. 2011, 11, S28–S36. [Google Scholar] [CrossRef] [PubMed]
- Harrison, C.; Kiladjian, J.J.; Al-Ali, H.K.; Gisslinger, H.; Waltzman, R.; Stalbovskaya, V.; McQuitty, M.; Hunter, D.S.; Levy, R.; Knoops, L.; et al. JAK inhibition with ruxolitinib versus best available therapy for myelofibrosis. N. Engl. J. Med. 2012, 366, 787–798. [Google Scholar] [CrossRef] [PubMed]
- Hatzimichael, E.; Georgiou, G.; Benetatos, L.; Briasoulis, E. Gene mutations and molecularly targeted therapies in acute myeloid leukemia. Am. J. Blood Res. 2013, 3, 29–51. [Google Scholar] [PubMed]
- Simeon, S.; Möller, R.; Almgren, D.; Li, H.; Phanus-umporn, C.; Prachayasittikul, V.; Bülow, L.; Nantasenamat, C. Unraveling the origin of splice switching activity of hemoglobin β-globin gene modulators via QSAR modeling. Chemom. Intell. Lab. Syst. 2016, 151, 51–60. [Google Scholar] [CrossRef]
- Hao, C.-Z.; Xia, S.-W.; Wang, H.; Xue, J.; Yu, L. Using 3D-QSAR and molecular docking insight into inhibitors binding with complex-associated kinases CDK8. J. Mol. Struct. 2018, 1173, 498–511. [Google Scholar] [CrossRef]
- Aouidate, A.; Ghaleb, A.; Ghamali, M.; Ousaa, A.; Choukrad, M.; Sbai, A.; Bouachrine, M.; Lakhlifi, T. 3D QSAR studies, molecular docking and ADMET evaluation, using thiazolidine derivatives as template to obtain new inhibitors of PIM1 kinase. Comput. Biol. Chem. 2018, 74, 201–211. [Google Scholar] [CrossRef]
- Divya, V.; Pushpa, V.; Sarithamol, S.; Manoj, K. Computational approach for generating robust models for discovering novel molecules as Cyclin Dependent Kinase 4 inhibitors. J. Mol. Graph. Model. 2018, 82, 48–58. [Google Scholar] [CrossRef]
- Shahin, R.; Mansi, I.; Swellmeen, L.; Alwidyan, T.; Al-Hashimi, N.; Al-Qarar’h, Y.; Shaheen, O. Ligand-based computer aided drug design reveals new tropomycin receptor kinase a (TrkA) inhibitors. J. Mol. Graph. Model. 2018, 80, 327–352. [Google Scholar] [CrossRef]
- Schöning, V.; Krähenbühl, S.; Drewe, J. The hepatotoxic potential of protein kinase inhibitors predicted with Random Forest and Artificial Neural Networks. Toxicol. Lett. 2018, 299, 145–148. [Google Scholar] [CrossRef]
- Rampogu, S.; Son, M.; Baek, A.; Park, C.; Rana, R.M.; Zeb, A.; Parameswaran, S.; Lee, K.W. Targeting natural compounds against HER2 kinase domain as potential anticancer drugs applying pharmacophore based molecular modelling approaches. Comput. Biol. Chem. 2018, 74, 327–338. [Google Scholar] [CrossRef]
- Li, D.D.; Meng, X.F.; Wang, Q.; Yu, P.; Zhao, L.G.; Zhang, Z.P.; Wang, Z.Z.; Xiao, W. Consensus scoring model for the molecular docking study of mTOR kinase inhibitor. J. Mol. Graph. Model. 2018, 79, 81–87. [Google Scholar] [CrossRef] [PubMed]
- Jasuja, H.; Chadha, N.; Singh, P.K.; Kaur, M.; Bahia, M.S.; Silakari, O. Putative dual inhibitors of Janus kinase 1 and 3 (JAK1/3): Pharmacophore based hierarchical virtual screening. Comput. Biol. Chem. 2018, 76, 109–117. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.D.; Karthikeyan, M.; Kirubakaran, P.; Nagamani, S. Pharmacophore filtering and 3D-QSAR in the discovery of new JAK2 inhibitors. J. Mol. Graph. Model. 2011, 30, 186–197. [Google Scholar] [CrossRef] [PubMed]
- Jasuja, H.; Chadha, N.; Kaur, M.; Silakari, O. Dual inhibitors of Janus kinase 2 and 3 (JAK2/3): Designing by pharmacophore-and docking-based virtual screening approach. Mol. Divers. 2014, 18, 253–267. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.D.; Naveena, Q.; Karthikeyan, M. Jak2 inhibitor–a jackpot for pharmaceutical industries: A comprehensive computational method in the discovery of new potent Jak2 inhibitors. Mol. BioSystems 2014, 10, 2146–2159. [Google Scholar] [CrossRef]
- Gade, D.R.; Kunala, P.; Raavi, D.; Reddy, P.K.; Prasad, R.V. Structural insights of JAK2 inhibitors: Pharmacophore modeling and ligand-based 3D-QSAR studies of pyrido-indole derivatives. J. Recept. Signal Transduct. 2015, 35, 189–201. [Google Scholar] [CrossRef]
- Wu, X.; Wan, S.; Zhang, J. Three Dimensional Quantitative Structure-Activity Relationship of 5H-Pyrido [4, 3-b] indol-4-carboxamide JAK2 Inhibitors. Int. J. Mol. Sci. 2013, 14, 12037–12053. [Google Scholar] [CrossRef]
- Chekkara, R.; Susithra, E.; Kandakatla, N.; Gorla, V.R.; Tenkayala, S.R. Pharmacophore generation and atom-based 3D-QSAR analysis of substituted aromatic bicyclic compounds containing pyrimidine and pyridine rings as Janus kinase 2 (JAK2) inhibitors. J. Chem. Pharm. Res. 2014, 6, 1146–1152. [Google Scholar]
- Chekkara, R.; Gorla, V.R.; Tenkayala, S.R.; Susithra, E. 2, 4-Diamino-1, 3, 5-Triazine Derivatives as Janus Kinase 2 (JAK2) inhibitors: Pharmacophore modeling, atom-based 3d-qsar and molecular docking study. Indo Am. J. Pharm. Res. 2015, 5, 2127–2135. [Google Scholar]
- Yao, T.T.; Xie, J.F.; Liu, X.G.; Cheng, J.L.; Zhu, C.Y.; Zhao, J.H.; Dong, X.W. Integration of pharmacophore mapping and molecular docking in sequential virtual screening: Towards the discovery of novel JAK2 inhibitors. RSC Adv. 2017, 7, 10353–10360. [Google Scholar] [CrossRef]
- Sathe, R.Y.; Kulkarni, S.A.; Sella, R.N.; Madhavan, T. Computational identification of JAK2 inhibitors: A combined pharmacophore mapping and molecular docking approach. Med. Chem. Res. 2015, 24, 1449–1467. [Google Scholar] [CrossRef]
- Itteboina, R.; Ballu, S.; Sivan, S.K.; Manga, V. Molecular docking, 3D QSAR and dynamics simulation studies of imidazo-pyrrolopyridines as janus kinase 1 (JAK 1) inhibitors. Comput. Biol. Chem. 2016, 64, 33–46. [Google Scholar] [CrossRef] [PubMed]
- Rajeswari, M.; Santhi, N.; Bhuvaneswari, V. Pharmacophore and Virtual Screening of JAK3 inhibitors. Bioinformation 2014, 10, 157. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.L.; Cheng, L.P.; Wang, T.C.; Deng, W.; Wu, F.H. Molecular modeling study of CP-690550 derivatives as JAK3 kinase inhibitors through combined 3D-QSAR, molecular docking, and dynamics simulation techniques. J. Mol. Graph. Model. 2017, 72, 178–186. [Google Scholar] [CrossRef] [PubMed]
- Sang, Y.L.; Duan, Y.T.; Qiu, H.Y.; Wang, P.F.; Makawana, J.A.; Wang, Z.C.; Zhu, H.L.; He, Z.X. Design, synthesis, biological evaluation and molecular docking of novel metronidazole derivatives as selective and potent JAK3 inhibitors. RSC Adv. 2014, 4, 16694–16704. [Google Scholar] [CrossRef]
- Marzaro, G.; Chilin, A.; Guiotto, A.; Uriarte, E.; Brun, P.; Castagliuolo, I.; Tonus, F.; González-Díaz, H. Using the TOPS-MODE approach to fit multi-target QSAR models for tyrosine kinases inhibitors. Eur. J. Med. Chem. 2011, 46, 2185–2192. [Google Scholar] [CrossRef]
- Speck-Planche, A.; Cordeiro, M.N.D. Fragment-based in silico modeling of multi-target inhibitors against breast cancer-related proteins. Mol. Divers. 2017, 21, 511–523. [Google Scholar] [CrossRef]
- Ambure, P.; Halder, A.K.; González-Díaz, H.; Dias Soeiro Cordeiro, M.N.D. QSAR-Co: An Open Source Software for Developing Robust Multi-tasking or Multi-target Classification-Based QSAR Models. J. Chem. Inf. Model. 2019. [Google Scholar] [CrossRef]
- Kuseva, C.; Schultz, T.W.; Yordanova, D.; Tankova, K.; Kutsarova, S.; Pavlov, T.; Chapkanov, A.; Georgiev, M.; Gissi, A.; Sobanski, T.; et al. The implementation of RAAF in the OECD QSAR Toolbox. Regul. Toxicol. Pharmacol. 2019, 105, 51–61. [Google Scholar] [CrossRef]
- Eriksson, L.; Jaworska, J.; Worth, A.P.; Cronin, M.T.; McDowell, R.M.; Gramatica, P. Methods for reliability and uncertainty assessment and for applicability evaluations of classification-and regression-based QSARs. Environ. Health Perspect. 2003, 111, 1361. [Google Scholar] [CrossRef]
- Tropsha, A.; Gramatica, P.; Gombar, V.K. The importance of being earnest: Validation is the absolute essential for successful application and interpretation of QSPR models. QSAR Comb. Sci. 2003, 22, 69–77. [Google Scholar] [CrossRef]
- Eriksson, L.; Johansson, E. Multivariate design and modeling in QSAR. Chemom. Intell. Lab. Syst. 1996, 34, 1–19. [Google Scholar] [CrossRef]
- Mesa, R.A.; Yasothan, U.; Kirkpatrick, P. Ruxolitinib. Nat. Rev. Drug Discov. 2012, 11, 103–104. [Google Scholar] [CrossRef] [PubMed]
- Kaur, K.; Kalra, S.; Kaushal, S. Systematic review of tofacitinib: A new drug for the management of rheumatoid arthritis. Clin. Ther. 2014, 36, 1074–1086. [Google Scholar] [CrossRef] [PubMed]
- Markham, A. Baricitinib: First global approval. Drugs 2017, 77, 697–704. [Google Scholar] [CrossRef]
- Williams, R. Discontinued in 2013: Oncology drugs. Expert Opin. Investig. Drugs 2015, 24, 95–110. [Google Scholar] [CrossRef]
- Leroy, E.; Constantinescu, S.N. Rethinking JAK2 inhibition: Towards novel strategies of more specific and versatile janus kinase inhibition. Leukemia 2017, 31, 1023. [Google Scholar] [CrossRef]
- Jismy, B.; Allouchi, H.; Guillaumet, G.; Akssira, M.; Abarbri, M. An Efficient Synthesis of New 7-Trifluoromethyl-2, 5-disubstituted Pyrazolo [1, 5-a] pyrimidines. Synthesis 2018, 50, 1675–1686. [Google Scholar]
- Apsel, B.; Blair, J.A.; Gonzalez, B.; Nazif, T.M.; Feldman, M.E.; Aizenstein, B.; Hoffman, R.; Williams, R.L.; Shokat, K.M.; Knight, Z.A. Targeted polypharmacology: Discovery of dual inhibitors of tyrosine and phosphoinositide kinases. Nat. Chem. Biol. 2008, 4, 691. [Google Scholar] [CrossRef]
- Schnur, D.M.; Hermsmeier, M.A.; Tebben, A.J. Are target-family-privileged substructures truly privileged? J. Med. Chem. 2006, 49, 2000–2009. [Google Scholar] [CrossRef]
- Gaulton, A.; Bellis, L.J.; Bento, A.P.; Chambers, J.; Davies, M.; Hersey, A.; Light, Y.; McGlinchey, S.; Michalovich, D.; Al-Lazikani, B.; et al. ChEMBL: A large-scale bioactivity database for drug discovery. Nucleic Acids Res. 2012, 40, D1100–D1107. [Google Scholar] [CrossRef] [PubMed]
- Fourches, D.; Muratov, E.; Tropsha, A. Trust, but verify: On the importance of chemical structure curation in cheminformatics and QSAR modeling research. J. Chem. Inf. Model. 2010, 50, 1189–1204. [Google Scholar] [CrossRef] [PubMed]
- Standardizer. Version 15.9.14.0 Software; ChemAxon: Budapest, Hungary, 2010. [Google Scholar]
- Khan, A.U. Descriptors and their selection methods in QSAR analysis: Paradigm for drug design. Drug Discov. Today 2016, 21, 1291–1302. [Google Scholar]
- Tuppurainen, K. Frontier orbital energies, hydrophobicity and steric factors as physical QSAR descriptors of molecular mutagenicity. A review with a case study: MX compounds. Chemosphere 1999, 38, 3015–3030. [Google Scholar] [CrossRef]
- Abraham, M.H.; Acree, W.E., Jr. Descriptors for ions and ion-pairs for use in linear free energy relationships. J. Chromatogr. A 2016, 1430, 2–14. [Google Scholar] [CrossRef]
- Caron, G.; Reymond, F.; Carrupt, P.A.; Girault, H.H.; Testa, B. Combined molecular lipophilicity descriptors and their role in understanding intramolecular effects. Pharm. Sci. Technol. Today 1999, 2, 327–335. [Google Scholar] [CrossRef]
- Fey, N.; Orpen, A.G.; Harvey, J.N. Building ligand knowledge bases for organometallic chemistry: Computational description of phosphorus (III)-donor ligands and the metal–phosphorus bond. Coord. Chem. Rev. 2009, 253, 704–722. [Google Scholar] [CrossRef]
- Laggner, C. SMARTS Patterns for Functional Group Classification; Inte: Ligand Software-Entwicklungs und Consulting GmbH: Maria Enzersdorf, Austria, 2005. [Google Scholar]
- Yap, C.W. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. [Google Scholar] [CrossRef]
- Cronin, M.T.; Schultz, T.W. Pitfalls in QSAR. J. Mol. Struct. 2003, 622, 39–51. [Google Scholar] [CrossRef]
- Tomaschek, F.; Hendrix, P.; Baayen, R.H. Strategies for addressing collinearity in multivariate linguistic data. J. Phon. 2018, 71, 249–267. [Google Scholar] [CrossRef]
- Tušar, T.; Gantar, K.; Koblar, V.; Ženko, B.; Filipič, B. A study of overfitting in optimization of a manufacturing quality control procedure. Appl. Soft Comput. 2017, 59, 77–87. [Google Scholar] [CrossRef]
- Booth, G.D.; Niccolucci, M.J.; Schuster, E.G. Identifying Proxy Sets in Multiple Linear Regression: An Aid to Better Coefficient Interpretation; Research Paper INT-470; United States Department of Agriculture, Forest Service: Ogden, UT, USA, 1994.
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Puzyn, T.; Mostrag-Szlichtyng, A.; Gajewicz, A.; Skrzyński, M.; Worth, A.P. Investigating the influence of data splitting on the predictive ability of QSAR/QSPR models. Struct. Chem. 2011, 22, 795–804. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Therneau, T.; Atkinson, B.; Ripley, B.; Ripley, M.B. Package ‘rpart’. Available online: https://cran.r-project.org/web/packages/rpart/rpart.pdf (accessed on 20 April 2019).
- Dimitriadou, E.; Hornik, K.; Leisch, F.; Meyer, D.; Weingessel, A. Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. Available online: https://cran.r-project.org/web/packages/e1071/e1071.pdf (accessed on 13 August 2019).
- Falbel, D.; Allaire, J.; Chollet, F.; Tang, Y.; Van Der Bijl, W.; Studer, M.; Keydana, S. Keras: R Interface to ‘Keras’. Available online: https://cran.r-project.org/web/packages/keras/keras.pdf (accessed on 15 August 2019).
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News, 3 December 2002; 18–22. [Google Scholar]
- Alexander, D.L.; Tropsha, A.; Winkler, D.A. Beware of R2: Simple, unambiguous assessment of the prediction accuracy of QSAR and QSPR models. J. Chem. Inf. Model. 2015, 55, 1316–1322. [Google Scholar] [CrossRef] [PubMed]
- Gramatica, P.; Sangion, A. A historical excursus on the statistical validation parameters for QSAR models: A clarification concerning metrics and terminology. J. Chem. Inf. Model. 2016, 56, 1127–1131. [Google Scholar] [CrossRef]
- Roy, K.; Chakraborty, P.; Mitra, I.; Ojha, P.K.; Kar, S.; Das, R.N. Some case studies on application of “rm2” metrics for judging quality of quantitative structure–activity relationship predictions: Emphasis on scaling of response data. J. Comput. Chem. 2013, 34, 1071–1082. [Google Scholar] [CrossRef]
- Roy, K.; Das, R.N.; Ambure, P.; Aher, R.B. Be aware of error measures. Further studies on validation of predictive QSAR models. Chemom. Intell. Lab. Syst. 2016, 152, 18–33. [Google Scholar] [CrossRef]
- Todeschini, R.; Ballabio, D.; Grisoni, F. Beware of unreliable Q 2! A comparative study of regression metrics for predictivity assessment of QSAR models. J. Chem. Inf. Model. 2016, 56, 1905–1913. [Google Scholar] [CrossRef]
- Shacham, M.; Brauner, N.; Cholakov, G.S.; Stateva, R.P. Identifying applicability domains for quantitative structure property relationships. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2007; Volume 24, pp. 327–332. [Google Scholar]
- Simeon, S.; Anuwongcharoen, N.; Shoombuatong, W.; Malik, A.A.; Prachayasittikul, V.; Wikberg, J.E.; Nantasenamat, C. Probing the origins of human acetylcholinesterase inhibition via QSAR modeling and molecular docking. PeerJ 2016, 4, e2322. [Google Scholar] [CrossRef]
- Cao, Y.; Charisi, A.; Cheng, L.C.; Jiang, T.; Girke, T. ChemmineR: A compound mining framework for R. Bioinformatics 2008, 24, 1733–1734. [Google Scholar] [CrossRef]
- Schäfer, T.; Kriege, N.; Humbeck, L.; Klein, K.; Koch, O.; Mutzel, P. Scaffold Hunter: A comprehensive visual analytics framework for drug discovery. J. Cheminf. 2017, 9, 28. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the compounds are not available from the authors. |
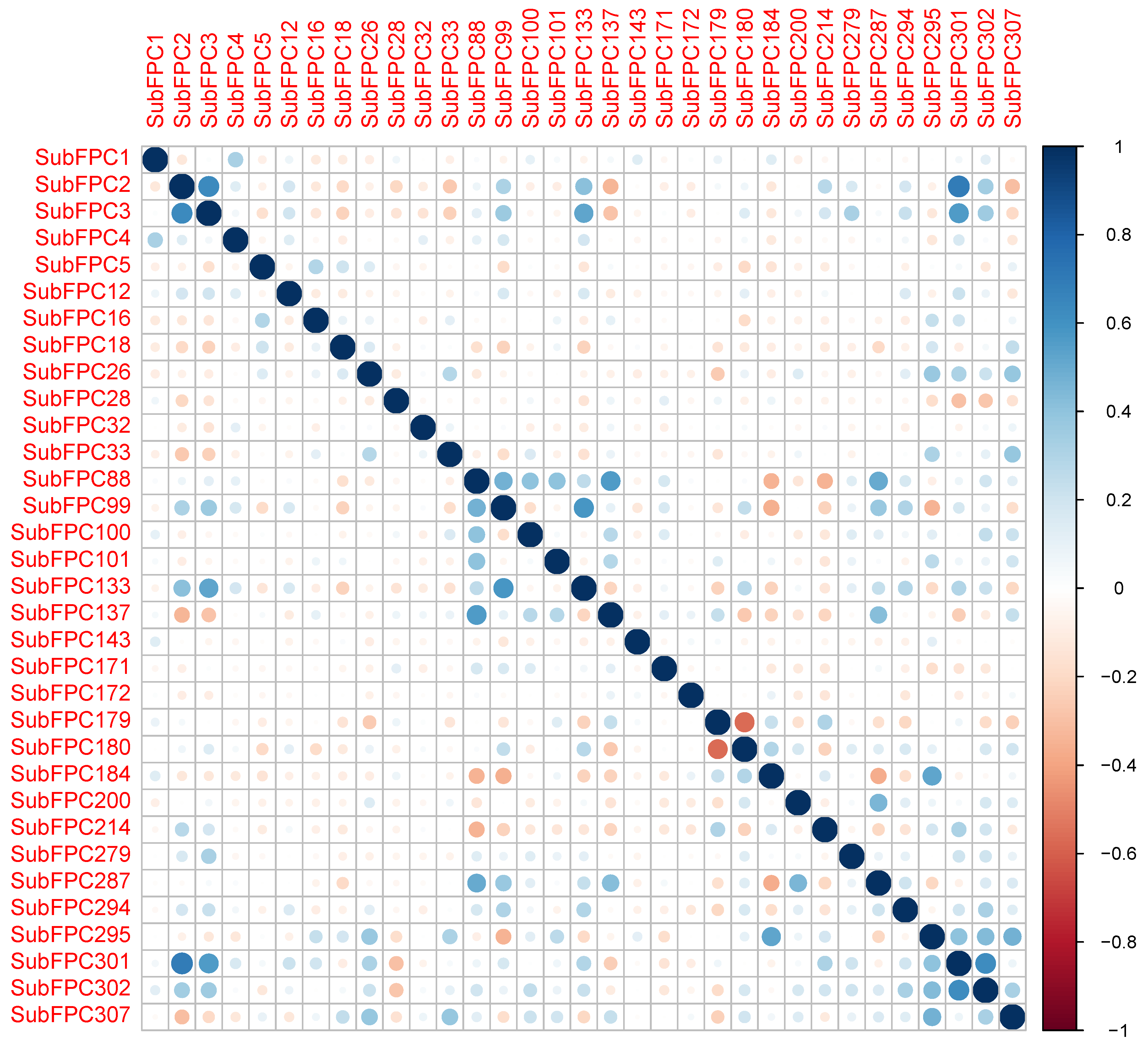
| Models | Training Set | 10-Fold CV | Test Set | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | RMSE | RMSE | ||||||||||||
| DT | 0.65 ± 0.02 | 0.72 ± 0.02 | 0.65 ± 0.02 | 0.28 ± 0.01 | 0.45 ± 0.07 | 0.91 ± 0.06 | 0.40 ± 0.09 | 0.20 ± 0.06 | 0.29 ± 0.05 | 1.02 ± 0.04 | 0.28 ± 0.05 | 0.31 ± 0.05 | ||
| SVM | 0.72 ± 0.01 | 0.65 ± 0.02 | 0.66 ± 0.02 | 0.26 ± 0.01 | 0.57 ± 0.05 | 0.80 ± 0.06 | 0.54 ± 0.04 | 0.33 ± 0.03 | 0.58 ± 0.05 | 0.79 ± 0.05 | 0.56 ± 0.03 | 0.33 ± 0.02 | ||
| DNN | 0.59 ± 0.04 | 0.82 ± 0.07 | 0.57 ± 0.04 | 0.32 ± 0.03 | 0.47 ± 0.07 | 0.93 ± 0.08 | 0.43 ± 0.07 | 0.29 ± 0.08 | 0.49 ± 0.04 | 0.90 ± 0.06 | 0.47 ± 0.04 | 0.31 ± 0.05 | ||
| RF | 0.75 ± 0.02 | 0.62 ± 0.02 | 0.69 ± 0.01 | 0.24 ± 0.01 | 0.74 ± 0.05 | 0.63 ± 0.05 | 0.67 ± 0.04 | 0.25 ± 0.03 | 0.75 ± 0.03 | 0.62 ± 0.04 | 0.68 ± 0.03 | 0.25 ± 0.02 | ||
| Models | Training Set | 10-Fold CV | Test Set | |||
|---|---|---|---|---|---|---|
| MAE | MAE | MAE | ||||
| DT | 0.53 ± 0.02 | 0.65 ± 0.05 | 0.76 ± 0.03 | |||
| SVM | 0.42 ± 0.02 | 0.55 ± 0.04 | 0.54 ± 0.03 | |||
| DNN | 0.64 ± 0.06 | 0.71 ± 0.07 | 0.70 ± 0.05 | |||
| RF | 0.42 ± 0.01 | 0.43 ± 0.04 | 0.42 ± 0.02 |
| Fingerprints | Description |
|---|---|
| SubFPC1 | Primary Carbon |
| SubFPC2 | Secondary Carbon |
| SubFPC3 | Tertiary Carbon |
| SubFPC4 | Quaternary Carbon |
| SubFPC5 | Alkene |
| SubFPC12 | Alcohol |
| SubFPC16 | Dialkylether |
| SubFPC18 | Alkylarylether |
| SubFPC26 | Tertiary Aliphalitic Amine |
| SubFPC28 | Primary Aromatic Amine |
| SubFPC32 | Secondary Mixed Amine |
| SubFPC33 | Tertiary Mixed Amine |
| SubFPC88 | Carboxylic Acid derivative |
| SubFPC99 | Primary Amide |
| SubFPC100 | Secondary Amide |
| SubFPC101 | Tertiary Amide |
| SubFPC133 | Nitrile |
| SubFPC137 | Vinylogous Ester |
| SubFPC143 | Carbonic Acid Derivatives |
| SubFPC171 | Arylchloride |
| SubFPC172 | Arylfluoride |
| SubFPC179 | Hetero N basic H |
| SubFPC180 | Hetero N basic no H |
| SubFPC184 | Heteroaromatic |
| SubFPC200 | Sulfon |
| SubFPC214 | Sulfonic Derivative |
| SubFPC279 | Annelated Rings |
| SubFPC287 | Spiro |
| SubFPC294 | Trifluoromethyl |
| SubFPC295 | C ONS Bond |
| SubFPC301 | 1,5-Tautomerizable |
| SubFPC302 | Rotatable Bond |
| SubFPC307 | Chiral Center Specified |
| Cluster No. | pIC | N | MW | AlogP |
|---|---|---|---|---|
| 1 | 7.30 ± 1.12 | 876 | 456.11 ± 75.65 | 3.87 ± 1.16 |
| 2 | 7.57 ± 0.68 | 491 | 432.38 ± 58.91 | 3.59 ± 0.95 |
| 3 | 7.70 ± 0.81 | 137 | 455.01 ± 43.35 | 1.68 ± 0.99 |
| 4 | 6.98 ± 0.52 | 23 | 333.59 ± 55.50 | 2.01 ± 1.01 |
| 5 | 9.76 ± 0.75 | 58 | 385.45 ± 33.55 | 1.11 ± 0.69 |
| 6 | 10.04 ± 0.32 | 38 | 461.42 ± 44.55 | 0.74 ± 0.98 |
| 7 | 6.48 ± 0.41 | 25 | 436.48 ± 34.56 | 2.33 ± 0.95 |
| 8 | 8.12 ± 1.09 | 25 | 441.67 ± 24.85 | 3.78 ± 0.50 |
| 9 | 6.06 ± 0.85 | 20 | 287.99 ± 30.95 | 1.30 ± 1.59 |
| 10 | 6.97 ± 0.44 | 24 | 283.09 ± 15.28 | 1.68 ± 0.48 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simeon, S.; Jongkon, N. Construction of Quantitative Structure Activity Relationship (QSAR) Models to Predict Potency of Structurally Diversed Janus Kinase 2 Inhibitors. Molecules 2019, 24, 4393. https://doi.org/10.3390/molecules24234393
Simeon S, Jongkon N. Construction of Quantitative Structure Activity Relationship (QSAR) Models to Predict Potency of Structurally Diversed Janus Kinase 2 Inhibitors. Molecules. 2019; 24(23):4393. https://doi.org/10.3390/molecules24234393
Chicago/Turabian StyleSimeon, Saw, and Nathjanan Jongkon. 2019. "Construction of Quantitative Structure Activity Relationship (QSAR) Models to Predict Potency of Structurally Diversed Janus Kinase 2 Inhibitors" Molecules 24, no. 23: 4393. https://doi.org/10.3390/molecules24234393
APA StyleSimeon, S., & Jongkon, N. (2019). Construction of Quantitative Structure Activity Relationship (QSAR) Models to Predict Potency of Structurally Diversed Janus Kinase 2 Inhibitors. Molecules, 24(23), 4393. https://doi.org/10.3390/molecules24234393





