Advances in the Interpretation of Frequency-Dependent Nuclear Magnetic Resonance Measurements from Porous Material
Abstract
1. Introduction
2. The Model
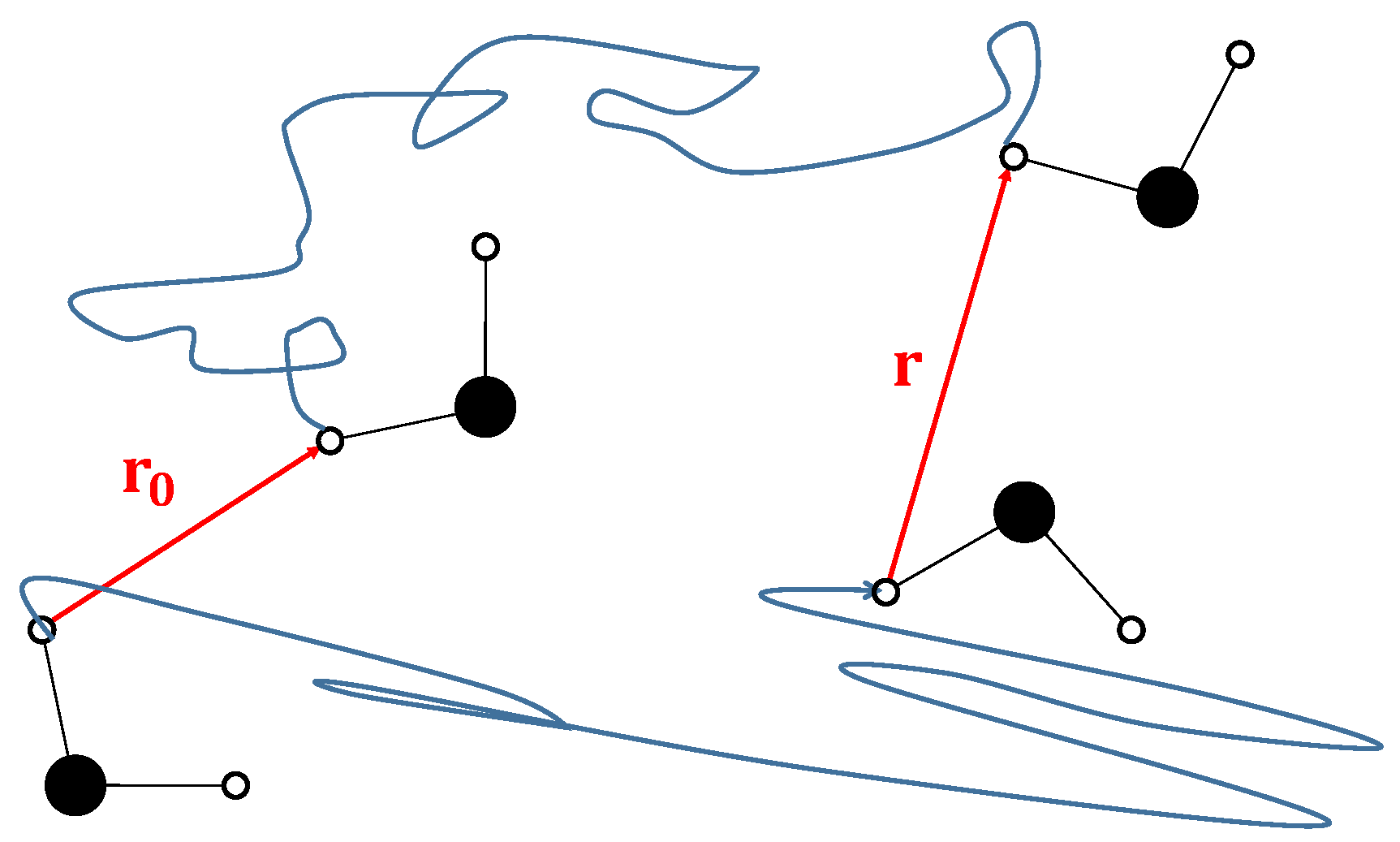
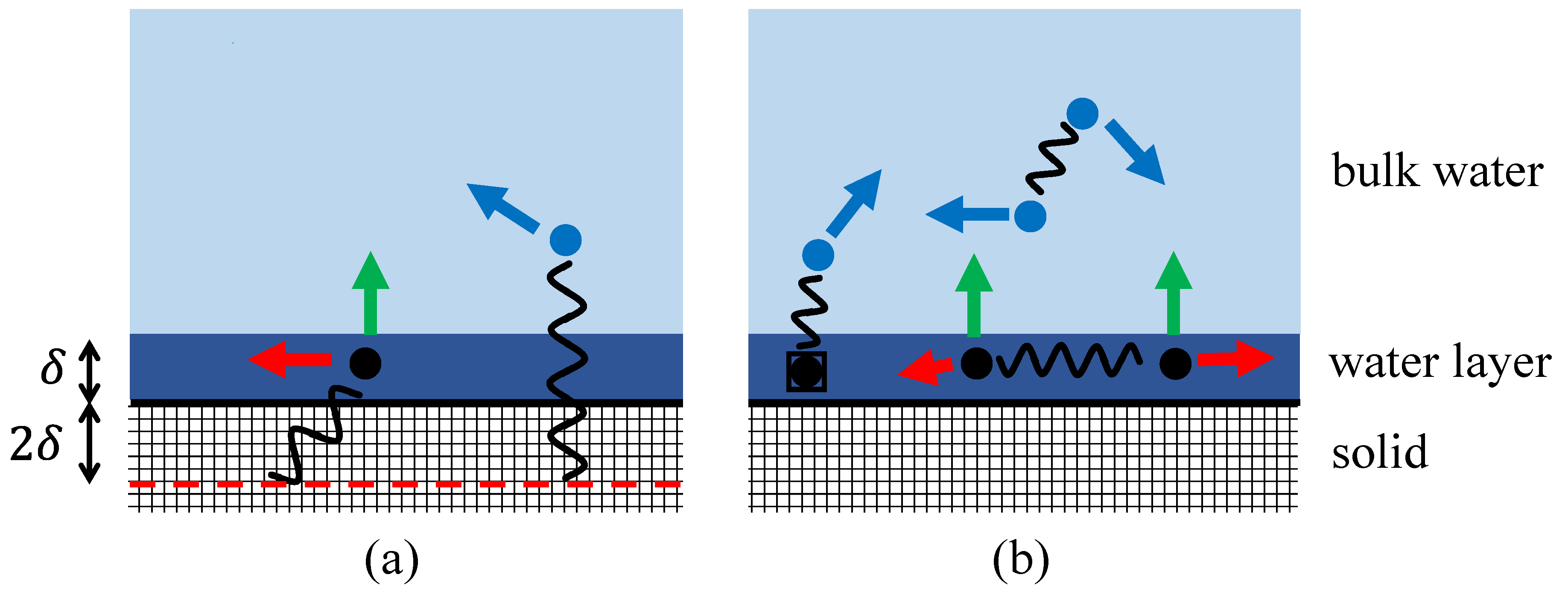
2.1. The Physics behind the Model
2.2. Calculating the Spin–Lattice Relaxation Rate Dispersion
2.3. Comparison of Models
3. Results
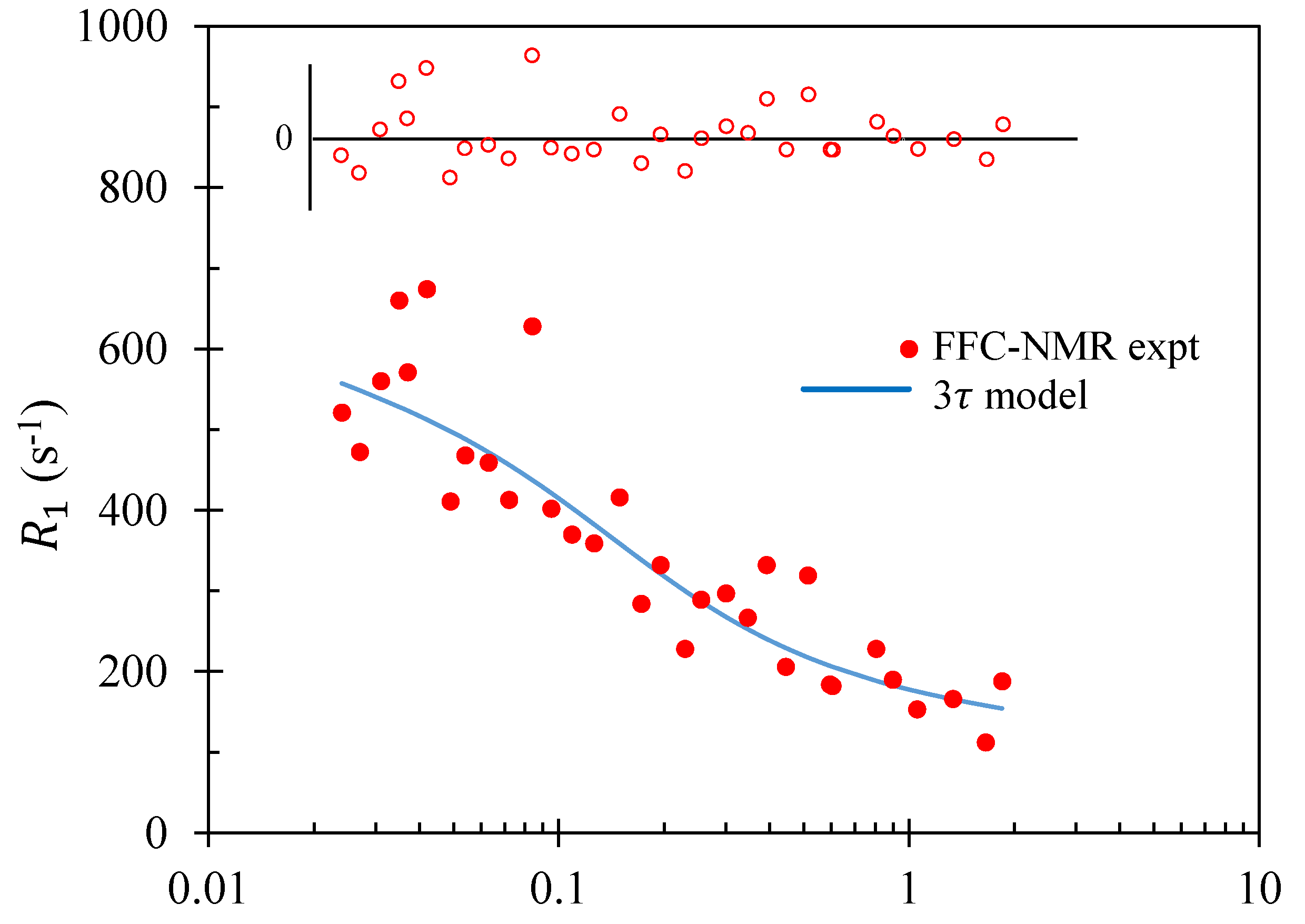
3.1. Mortar
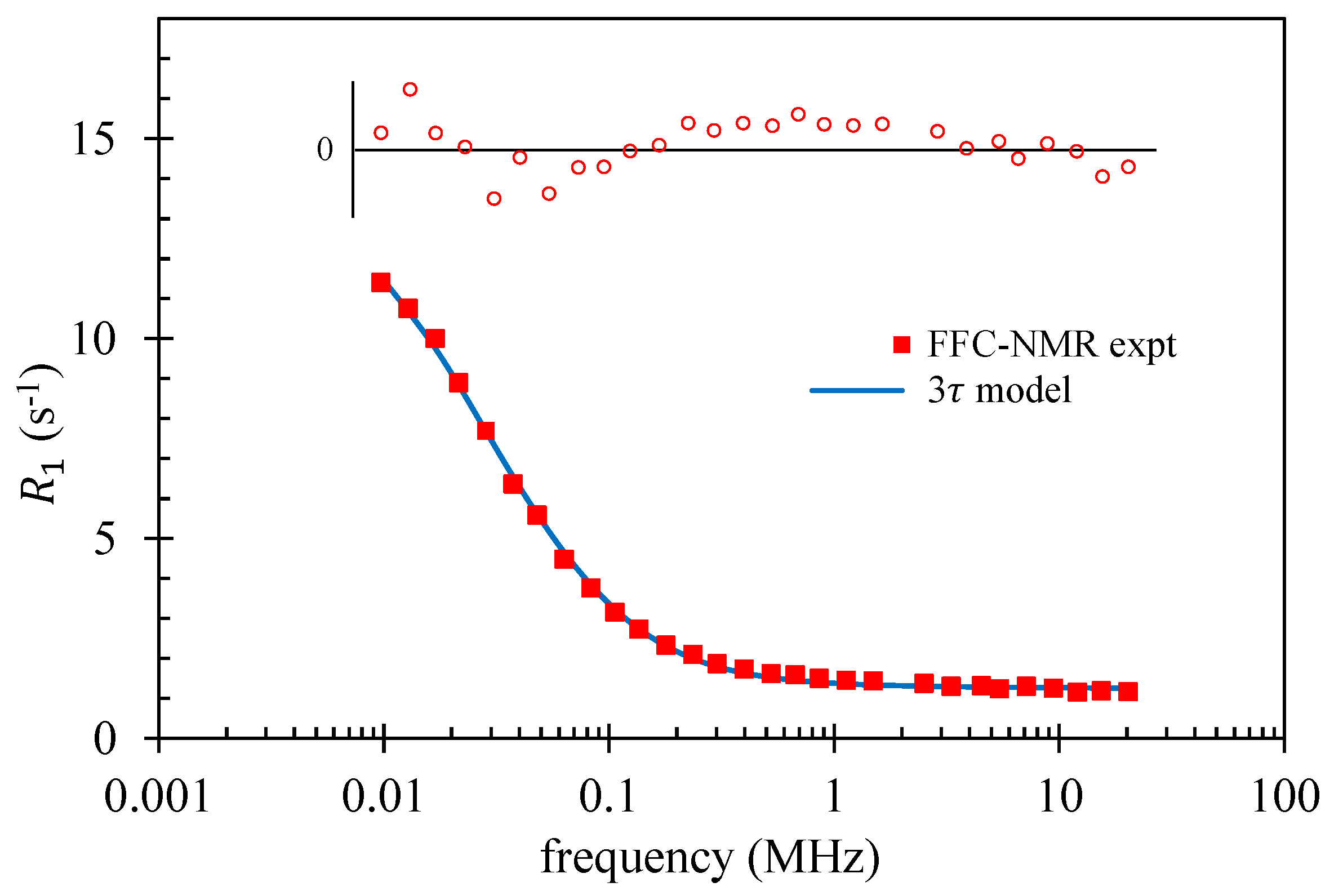
3.2. Plaster
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NMR | nuclear magnetic resonance |
| FFC-NMR | fast-field-cycling NMR |
| BMSD | bulk-mediated surface diffusion |
References
- Callaghan, P.T. Principles of Nuclear Magnetic Resonance Microscopy; Oxford University Press on Demand: Oxford, England, 1991. [Google Scholar]
- Steele, R.M.; Korb, J.P.; Ferrante, G.; Bubici, S. New applications and perspectives of fast field cycling NMR relaxometry. Magn. Reson. Chem. 2016, 54, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Godefroy, S.; Korb, J.P.; Fleury, M.; Bryant, R.G. Surface nuclear magnetic relaxation and dynamics of water and oil in macroporous media. Phys. Rev. E 2001, 64, 021605. [Google Scholar] [CrossRef] [PubMed]
- Godefroy, S.; Korb, J.P.; Fleury, M.; Bryant, R. New ways of probing surface nuclear relaxation and microdynamics of water and oil in porous media. Magn. Reson. Imaging 2001, 19, 517–519. [Google Scholar] [CrossRef]
- Korb, J.P. Nuclear magnetic relaxation of liquids in porous media. New J. Phys. 2011, 13, 035016. [Google Scholar] [CrossRef]
- Korb, J.P.; Nicot, B.; Jolivet, I. Dynamics and wettability of petroleum fluids in shale oil probed by 2D T1-T2 and fast field cycling NMR relaxation. Microporous Mesoporous Mater. 2018, 269, 7–11. [Google Scholar] [CrossRef]
- Korb, J.P.; Nicot, B.; Louis-Joseph, A.; Bubici, S.; Ferrante, G. Dynamics and wettability of oil and water in oil shales. J. Phys. Chem. C 2014, 118, 23212. [Google Scholar] [CrossRef]
- Fleury, M.; Romero-Sarmiento, M. Characterization of shales using T1–T2 NMR maps. J. Pet. Sci. Technol. 2016, 137, 55–62. [Google Scholar] [CrossRef]
- Monteilhet, L.; Korb, J.P.; Mitchell, J.; McDonald, P.J. Observation of exchange of micropore water in cement pastes by two-dimensional T2–T2 nuclear magnetic resonance relaxometry. Phys. Rev. E 2006, 74, 061404. [Google Scholar] [CrossRef]
- Barberon, F.; Korb, J.P.; Petit, D.; Morin, V.; Bermejo, E. Probing the surface area of a cement-based material by nuclear magnetic relaxation dispersion. Phys. Rev. Lett. 2003, 90, 116103. [Google Scholar] [CrossRef]
- Philippot, S.; Korb, J.; Petit, D.; Zanni, H. Analysis of microporosity and setting of reactive powder concrete by proton nuclear relaxation. Magn. Reson. Imaging 1998, 16, 515–519. [Google Scholar] [CrossRef]
- Korb, J.P.; McDonald, P.J.; Monteilhet, L.; Kalinichev, A.G.; Kirkpatrick, R.J. Comparison of proton field-cycling relaxometry and molecular dynamics simulations for proton–water surface dynamics in cement-based materials. Cem. Concr. Res. 2007, 37, 348. [Google Scholar] [CrossRef]
- Holly, R.; Reardon, E.J.; Hansson, C.M.; Peemoeller, H. Proton spin-spin relaxation study of the effect of temperature on white cement hydration. J. Am. Ceram. Soc. 2007, 90, 570–577. [Google Scholar] [CrossRef]
- Plassais, A.; Pomiés, M.P.; Lequeux, N.; Korb, J.P.; Petit, D.; Barberon, F.; Bresson, B. Microstructure evolution of hydrated cement pastes. Phys. Rev. E 2005, 72, 041401. [Google Scholar] [CrossRef] [PubMed]
- McDonald, P.J.; Korb, J.P.; Mitchell, J.; Monteilhet, L. Surface relaxation and chemical exchange in hydrating cement pastes: A two-dimensional NMR relaxation study. Phys. Rev. E 2005, 72, 011409. [Google Scholar] [CrossRef] [PubMed]
- Halperin, W.P.; Jehng, J.Y.; Song, Y.Q. Application of spin-spin relaxation to measurement of surface area and pore size distributions in a hydrating cement paste. Magn. Reson. Imaging 1994, 12, 169–173. [Google Scholar] [CrossRef]
- Jehng, J.Y.; Sprague, D.T.; Halperin, W.P. Pore structure of hydrating cement paste by magnetic resonance relaxation analysis and freezing. Magn. Reson. Imaging 1996, 14, 785–791. [Google Scholar] [CrossRef]
- Korb, J.P. NMR and nuclear spin relaxation of cement and concrete materials. Curr. Opin. Colloid Interface Sci. 2009, 14, 192–202. [Google Scholar] [CrossRef]
- Gladden, L.F.; Mitchell, J. Measuring adsorption, diffusion and flow in chemical engineering: Applications of magnetic resonance to porous media. New J. Phys. 2011, 13, 035001. [Google Scholar] [CrossRef]
- Sur, S.K.; Heinsbergen, J.F.; Listinsky, J.J.; Bryant, R.G. Electron spin resonance and nuclear magnetic relaxation dispersion studies of commercial clay minerals and zeolites. J. Colloid Interface Sci. 1993, 157, 141–146. [Google Scholar] [CrossRef]
- Sur, S.; Heinsbergen, J.; Bryant, R. Nuclear magnetic relaxation dispersion studies on bentonite clay suspensions. J. Magn. Reson. Ser. A 1993, 103, 8–12. [Google Scholar] [CrossRef]
- Telkki, V.V.; Yliniemi, M.; Jokisaari, J. Moisture in softwoods: Fiber saturation point, hydroxyl site content, and the amount of micropores as determined from NMR relaxation time distributions. Holzforschung 2013, 67, 291–300. [Google Scholar] [CrossRef]
- Korb, J.P.; Delville, A.; Xu, S.; Demeulenaere, G.; Costa, P.; Jonas, J. Relative role of surface interactions and topological effects in nuclear magnetic resonance of confined liquids. J. Chem. Phys. 1994, 101, 7074–7081. [Google Scholar] [CrossRef]
- Stapf, S.; Kimmich, R.; Seitter, R.O. Proton and deuteron field-cycling NMR relaxometry of liquids in porous glasses: Evidence for Lévy-walk statistics. Phys. Rev. Lett. 1995, 75, 2855. [Google Scholar] [CrossRef] [PubMed]
- Zavada, T.; Kimmich, R.; Grandjean, J.; Kobelkov, A. Field-cycling NMR relaxometry of water in synthetic saponites: Lévy walks on finite planar surfaces. J. Chem. Phys. 1999, 110, 6977. [Google Scholar] [CrossRef]
- Korb, J.P.; Whaley-Hodges, M.; Gobron, T.; Bryant, R.G. Anomalous surface diffusion of water compared to aprotic liquids in nanopores. Phys. Rev. E 1999, 60, 3097. [Google Scholar] [CrossRef] [PubMed]
- Sitnitsky, A.E.; Pimenov, G.G.; Anisimov, A.V. Spin-lattice NMR relaxation by anomalous translational diffusion. J. Magn. Reson. 2005, 172, 48. [Google Scholar] [CrossRef] [PubMed]
- Fries, P. Dipolar nuclear spin relaxation in liquids and plane fluids undergoing chemical reactions. Mol. Phys. 1983, 48, 503–526. [Google Scholar] [CrossRef]
- Helm, L. Relaxivity in paramagnetic systems: Theory and mechanisms. Prog. Nucl. Magn. Reson. Spectrosc. 2006, 49, 45–64. [Google Scholar] [CrossRef]
- Faux, D.A.; McDonald, P.J.; Howlett, N.C. Nuclear-magnetic-resonance relaxation due to the translational diffusion of fluid confined to quasi-two-dimensional pores. Phys. Rev. E 2017, 95, 033116. [Google Scholar] [CrossRef]
- Faux, D.A.; McDonald, P.J. Explicit calculation of nuclear-magnetic-resonance relaxation rates in small pores to elucidate molecular-scale fluid dynamics. Phys. Rev. E 2017, 95, 033117. [Google Scholar] [CrossRef]
- Faux, D.A.; McDonald, P.J. A model for the interpretation of nuclear magnetic resonance spin-lattice dispersion measurements on mortar, plaster paste, synthetic clay and oil-bearing shale. Phys. Rev. E 2018, 96, 063110. [Google Scholar] [CrossRef]
- Faux, D.A.; McDonald, P.J.; Howlett, N.C.; Bhatt, J.S.; Churakov, S.V. Nuclear magnetic resonance relaxometry of water in two and quasi-two dimensions. Phys. Rev. E 2013, 87, 062309. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, J.S.; McDonald, P.J.; Faux, D.A.; Howlett, N.C.; Churakov, S.V. NMR relaxation parameters from molecular simulations of hydrated inorganic nanopores. Int. J. Quant. Chem. 2014, 114, 1220. [Google Scholar] [CrossRef]
- Faux, D.A.; Cachia, S.H.P.; McDonald, P.J.; Bhatt, J.S.; Howlett, N.C.; Churakov, S.V. Model for the interpretation of nuclear magnetic resonance relaxometry of hydrated porous silicate materials. Phys. Rev. E 2015, 91, 032311. [Google Scholar] [CrossRef] [PubMed]
- Calero, C.; Martí, J.; Guàrdia, E. 1H nuclear spin relaxation of liquid water from molecular dynamics simulations. J. Phys. Chem. B 2015, 119, 1966–1973. [Google Scholar] [CrossRef] [PubMed]
- Fries, P.H. Two-particle random walk simulation of outer-sphere nuclear relaxation. J. Chem. Phys. 2010, 132, 224103. [Google Scholar] [CrossRef] [PubMed]
- Abragam, A. Principles of Nuclear Magnetism; Clarendon Press: Oxford, UK, 1961. [Google Scholar]
- Korb, J.P.; Xu, S.; Jonas, J. Confinement effects on dipolar relaxation by translational dynamics of liquids in porous silica glasses. J. Chem. Phys. 1993, 98, 2411. [Google Scholar] [CrossRef]
- Korb, J.P.; Whaley-Hodges, M.; Bryant, R.G. Translational diffusion of liquids at surfaces of microporous materials: Theoretical analysis of field-cycling magnetic relaxation measurements. Phys. Rev. E 1997, 56, 1934. [Google Scholar] [CrossRef]
- Kimmich, R. Strange kinetics, porous media, and NMR. Chem. Phys. 2002, 284, 253. [Google Scholar] [CrossRef]
- Levitz, P. Random flights in confining interfacial systems. J. Phys. Condens. Matter 2005, 17, S4059. [Google Scholar] [CrossRef]
- Levitz, P.; Korb, J.P. Probing glass transition of clay colloids by NMR relaxometry: Interplay between fluid Brownian dynamics and particle jamming. EPL Europhys. Lett. 2005, 70, 684. [Google Scholar] [CrossRef]
- Levitz, P.; Zinsmeister, M.; Davidson, P.; Constantin, D.; Poncelet, O. Intermittent Brownian dynamics over a rigid strand: Heavily tailed relocation statistics in a simple geometry. Phys. Rev. E 2008, 78, 030102. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C.; Lévy, S.V.; Souza, A.M.; Maynard, R. Determination of the Electron’s Atomic Mass and the Proton/Electron Mass Ratio via Penning Trap Mass Spectroscopy. Phys. Rev. Lett. 1995, 75, 3598. [Google Scholar]
- Zolotarev, V.M. One-Dimensional Stable Distributions; American Mathematical Soc.: Providence, RI, USA, 1986; Volume 65. [Google Scholar]
- Mall, K. Molecular Dynamic Simulations of Porous Material. Master’s Thesis, University of Surrey, Guildford, UK, 2018. [Google Scholar]
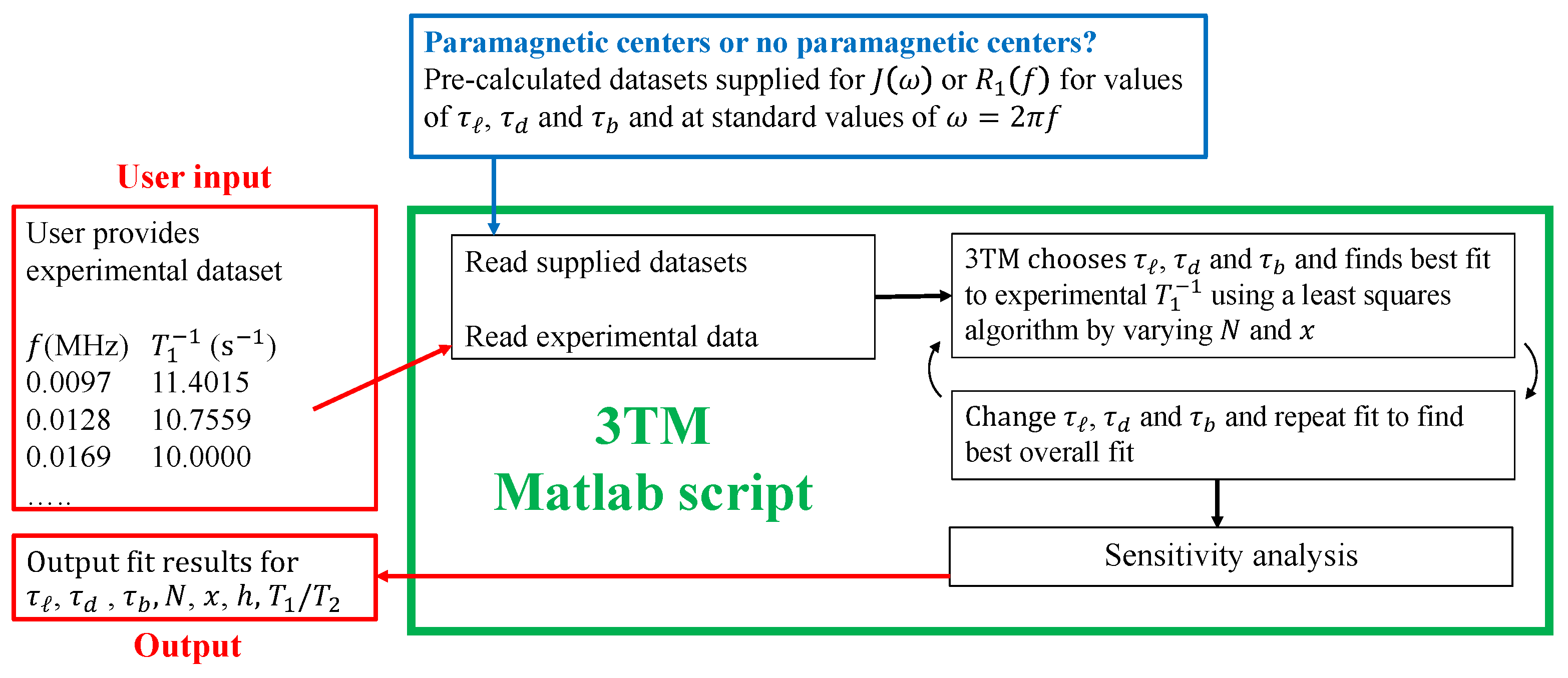
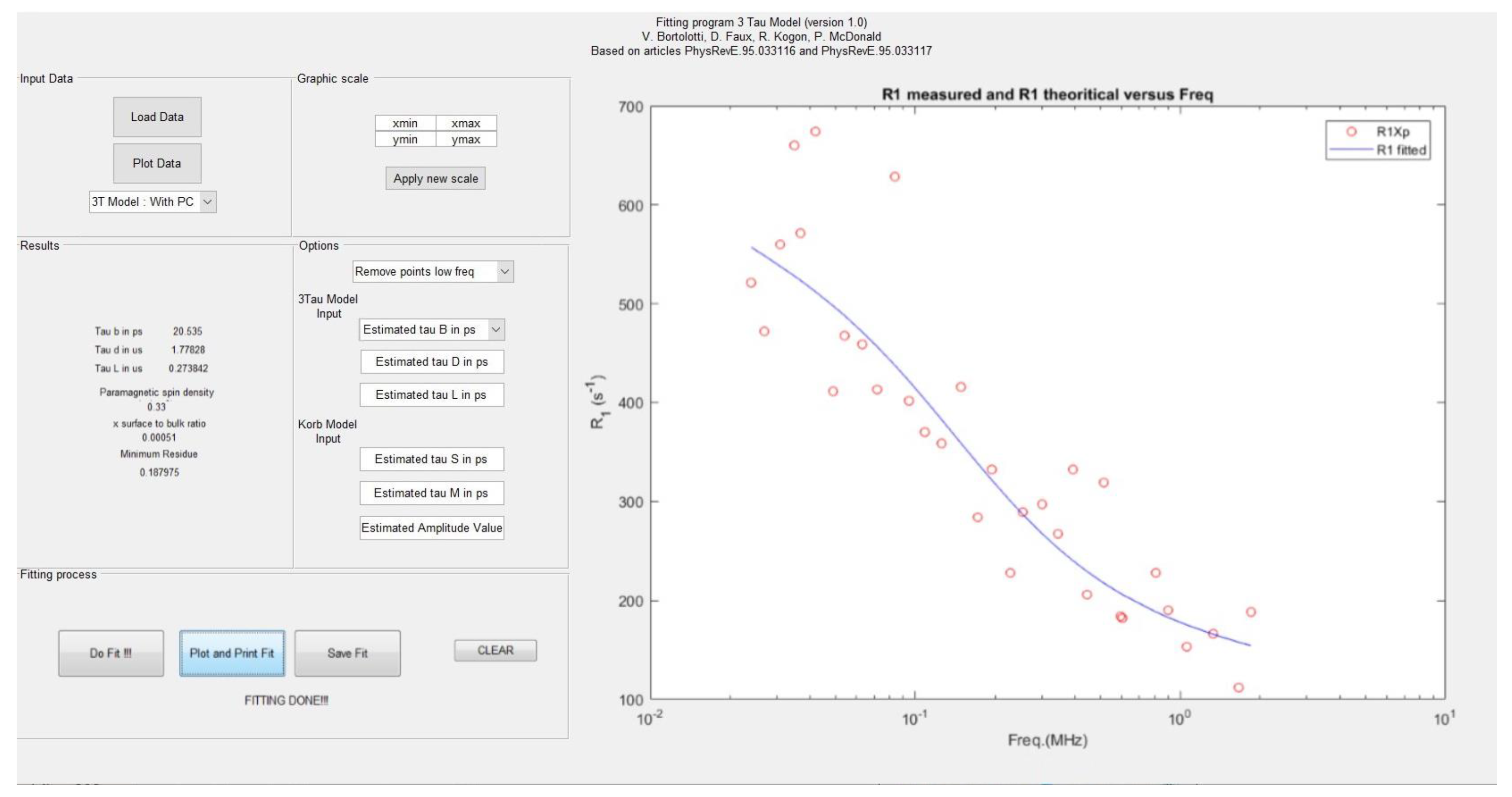
- Kogon, R.; Bortolotti, V.; Faux, D.; McDonald, P. Versions of the 3TM Fitting Software. Available online: github.com (accessed on 13 October 2019).
| Quantity | Korb | BMSD | Comments | |
|---|---|---|---|---|
| ✓ | ✓ | ✓ | Diffusion correlation time for fluid at the pore surface. | |
| ✓ | ✓ | Desorption time constant for the surface fluid. | ||
| ✓ | Bulk fluid diffusion time constant related to the diffusion coefficient. | |||
| ✓ | Each model employs a scaling factor proportional to the number of paramagnetic ions per unit volume in the solid. 3 provides the equivalent spin density for the effective paramagnetic layer. | |||
| ✓ | For water, the surface spin density is normally set to 66.6 spins/nm as for the bulk. can act as an additional fit parameter within the model. | |||
| ✓ | The dimensionless ratio of the volume of the pore surface (thickness assumed to be 0.27 nm) to the pore volume. | |||
| h | ✓ | The “planar-pore-equivalent" pore thickness is equal to in units of m. Useful characteristic pore dimension. | ||
| ✓ | ✓ | The Lévy parameter is a measure of the departure from Fickian dynamics. in most BMSD models. Lévy dynamics is trivially introduced into but is not necessary to secure good fits to FFC-NMR data. | ||
| ✓ | ✓ | The ratio of time constants is approximately equal to the number of hops a spin makes at a surface before desorption. It is linked to surface affinity (see text). | ||
| ✓ | ✓ | ✓ | The ratio of spin–lattice relaxation time to the spin–spin relaxation time is sometimes available at a spot frequency from separate – correlation measurements. Easily estimated by any model for comparison. |
| Quantity | Value | Comments |
|---|---|---|
| 0.27 s | Best fit result for the surface water diffusion correlation time. | |
| 1.8 s | Best fit desorption time constant. | |
| 21 ps | Best fit bulk water diffusion time constant equivalent to a diffusion coefficient of 0.6 × 10 ms | |
| 0.028 ions/nm | The best fit paramagnetic ion number density is close to the measured value of 0.03 [10]. | |
| x | 0.00073 | The best fit surface-to-volume ratio. |
| h | 0.74 m | The planar-pore-equivalent pore thickness. |
| 6.5 | The number of surface hops of water before desorption. | |
| 0.15–0.42 s | Range of values obtained from good fits (see text). | |
| 1.2–2.1 s | Range of values obtained from good fits (see text). | |
| 21 ps | All good fits yielded the same value of the bulk diffusion time constant. | |
| 0.24 s | Mean value of from the spread of good fits. | |
| 1.5 s | Mean value of from the spread of good fits. | |
| 2.9–3.3 | Range of values obtained from the set of good fits. The experimental value is typically 4 for cement paste at 20 MHz [15]. |
| Quantity | Value | Comments |
|---|---|---|
| 2.4 s | Best fit result for the surface water diffusion correlation time. | |
| 6.5 s | Best fit desorption time constant. | |
| 13 ps | Best fit bulk water diffusion time constant equivalent to a diffusion coefficient of 0.9 × 10 ms | |
| 73 spins/nm | The best fit H spin density for the surface layer is similar to the 66.6 spins/nm for bulk water. | |
| x | 0.00144 | The best fit surface-to-volume ratio. |
| h | 0.38 m | The planar-pore-equivalent pore thickness. |
| 2.7 | The number of surface hops of water before desorption. | |
| 3.9 | The experimental value is typically 4 20 MHz for cement paste [15]. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faux, D.; Kogon, R.; Bortolotti, V.; McDonald, P. Advances in the Interpretation of Frequency-Dependent Nuclear Magnetic Resonance Measurements from Porous Material. Molecules 2019, 24, 3688. https://doi.org/10.3390/molecules24203688
Faux D, Kogon R, Bortolotti V, McDonald P. Advances in the Interpretation of Frequency-Dependent Nuclear Magnetic Resonance Measurements from Porous Material. Molecules. 2019; 24(20):3688. https://doi.org/10.3390/molecules24203688
Chicago/Turabian StyleFaux, David, Rémi Kogon, Villiam Bortolotti, and Peter McDonald. 2019. "Advances in the Interpretation of Frequency-Dependent Nuclear Magnetic Resonance Measurements from Porous Material" Molecules 24, no. 20: 3688. https://doi.org/10.3390/molecules24203688
APA StyleFaux, D., Kogon, R., Bortolotti, V., & McDonald, P. (2019). Advances in the Interpretation of Frequency-Dependent Nuclear Magnetic Resonance Measurements from Porous Material. Molecules, 24(20), 3688. https://doi.org/10.3390/molecules24203688





