Development and Validation of a Virtual Gelatin Model Using Molecular Modeling Computational Tools
Abstract
1. Introduction
2. Results
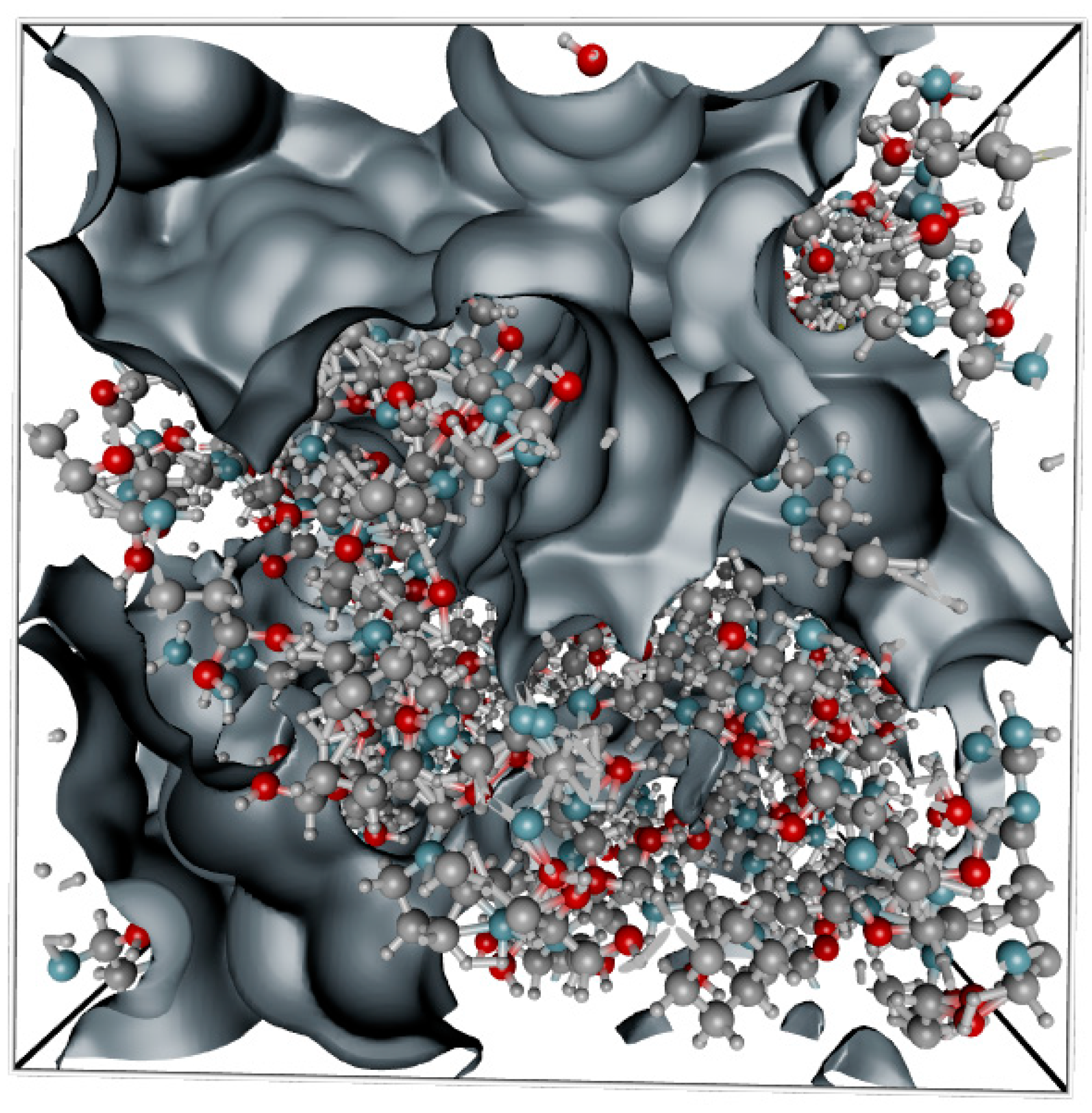
2.1. Structural Model of Gelatin
2.2. Veryfication of the Model
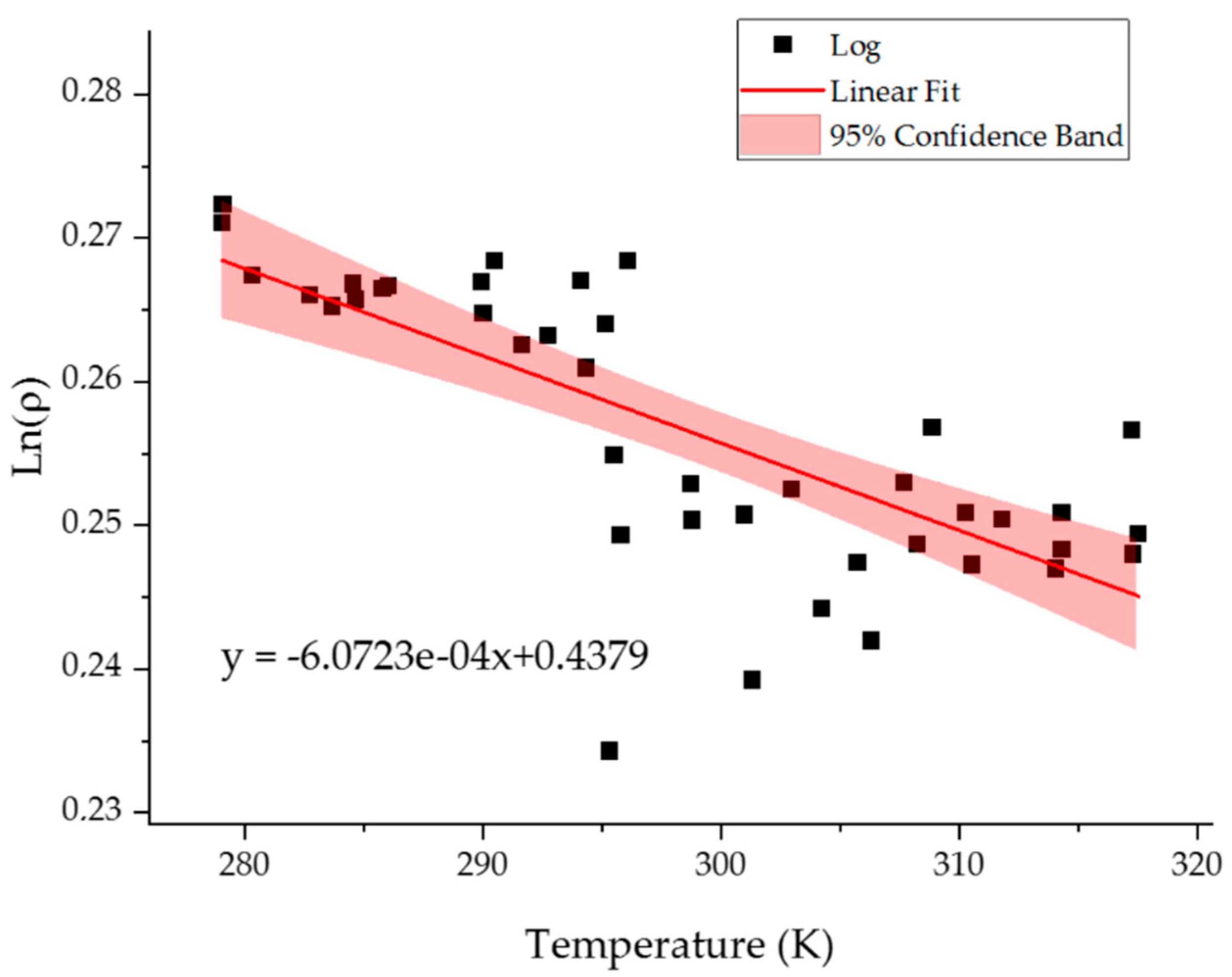
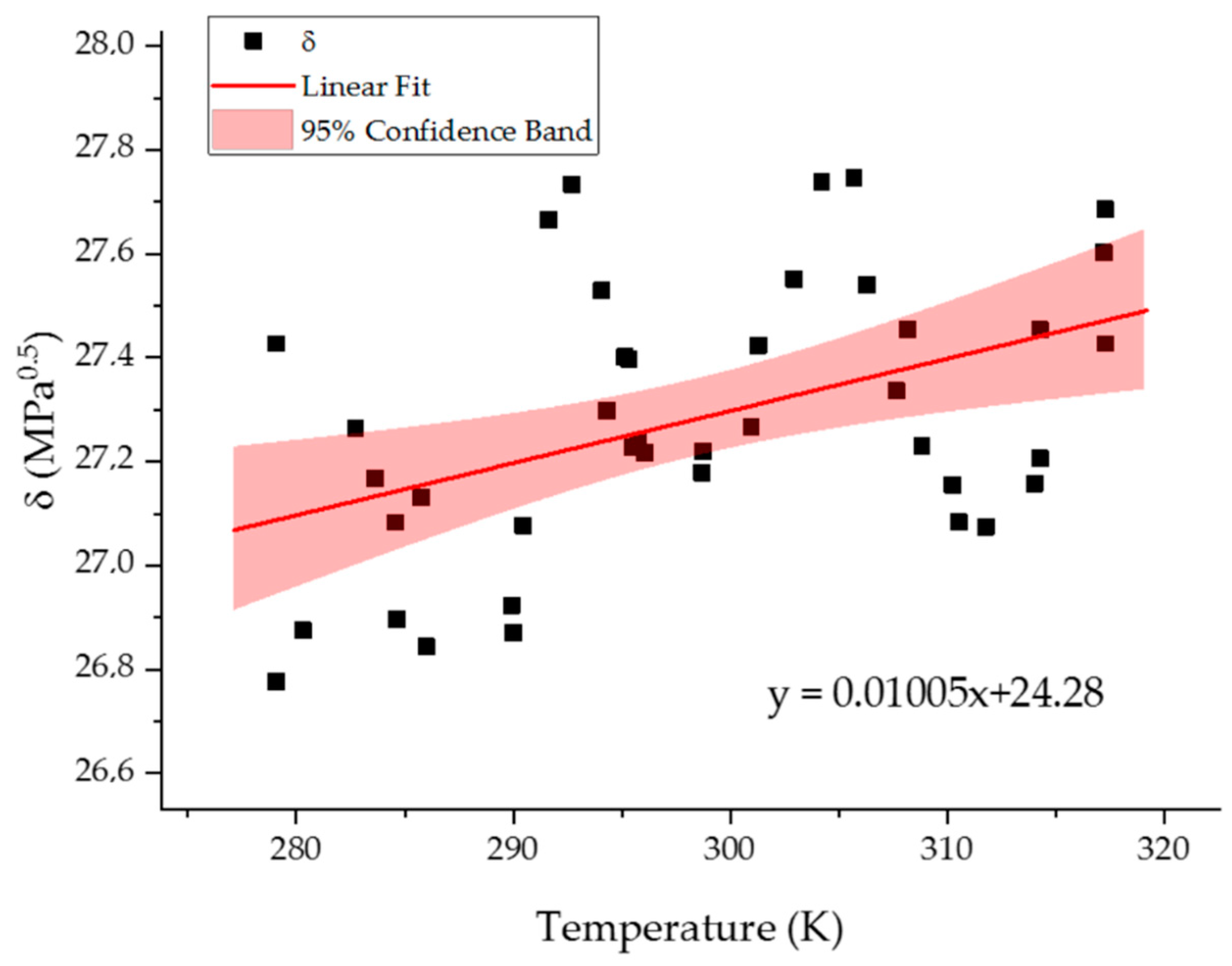
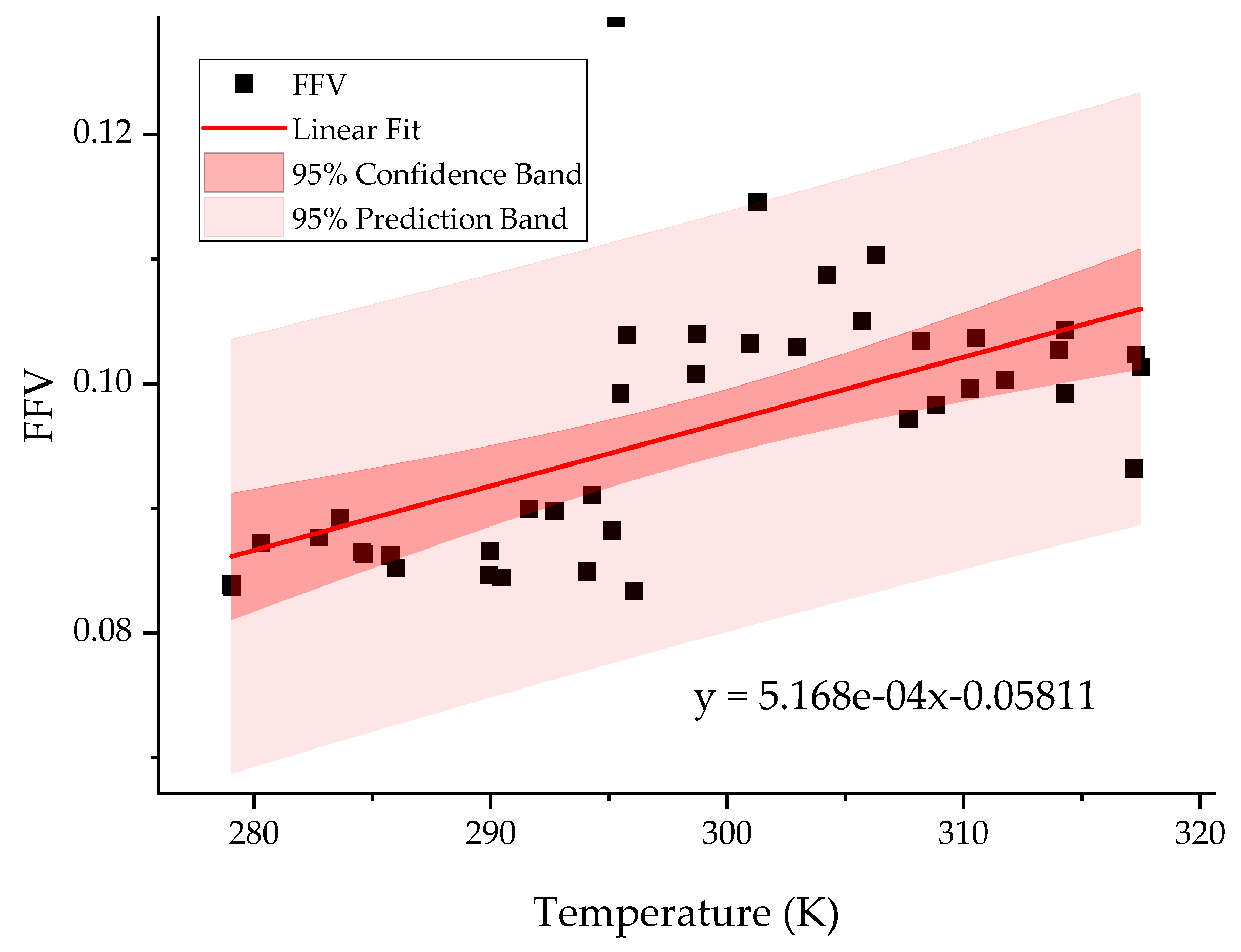
2.3. Temperature Resolution of the Model
3. Discussion
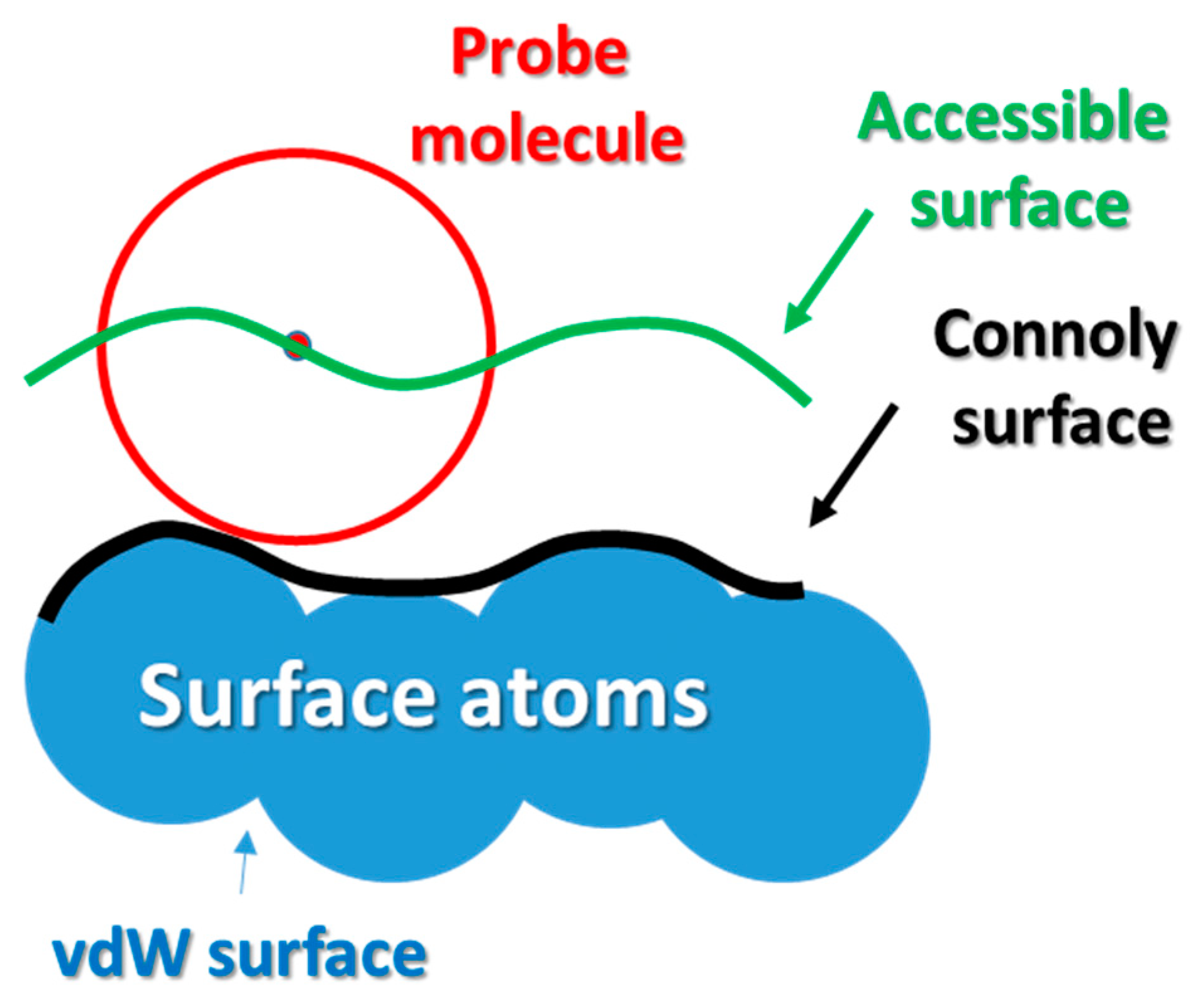
4. Materials and Methods
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kalia, S.; Avérous, L. Biopolymers. Biomedical and Environmental Applications, 1st ed.; Kalia, S., Avérous, L., Eds.; Wiley-Scrivener: Salem, MA, USA, 2011. [Google Scholar]
- Ha, T.L.B.; Quan, T.M.; Vu, D.N.; Si, D.M. Chapter 11: Naturally Derived Biomaterials: Preparation and Application. In Regenerative Medicine and Tissue Engineering; InTech: London, UK, 2013; pp. 247–272. [Google Scholar]
- Bilal, M.; Iqbal, H.M.N. Naturally-derived biopolymers: Potential platforms for enzyme immobilization. Int. J. Biol. Macromol. 2019, 130, 462–482. [Google Scholar] [CrossRef] [PubMed]
- Gironi, F.; Piemonte, V. Bioplastics and petroleum-based plastics: Strengths and weaknesses. Energy Sources Part A Recover. Util. Environ. Eff. 2011, 33, 1949–1959. [Google Scholar] [CrossRef]
- Hottle, T.A.; Bilec, M.M.; Landis, A.E. Sustainability assessments of bio-based polymers. Polym. Degrad. Stab. 2013, 98, 1898–1907. [Google Scholar] [CrossRef]
- Höök, M.; Davidsson, S.; Johansson, S.; Tang, X. Decline and depletion rates of oil production: A comprehensive investigation Decline and depletion rates of oil production: A comprehensive investigation. Phil. Trans. R. Soc. A 2013, 372, 1–21. [Google Scholar]
- Abas, N.; Kalair, A.; Khan, N. Review of fossil fuels and future energy technologies. Futures 2015, 69, 31–49. [Google Scholar] [CrossRef]
- Park, S.B.; Lih, E.; Park, K.S.; Joung, Y.K.; Han, D.K. Biopolymer-based functional composites for medical applications. Prog. Polym. Sci. 2017, 68, 77–105. [Google Scholar] [CrossRef]
- Reddy, N.; Reddy, R.; Jiang, Q. Crosslinking biopolymers for biomedical applications. Trends Biotechnol. 2015, 33, 362–369. [Google Scholar] [CrossRef] [PubMed]
- Xie, A.W.; Murphy, W.L. Engineered biomaterials to mitigate growth factor cost in cell biomanufacturing. Curr. Opin. Biomed. Eng. 2019, 10, 1–10. [Google Scholar] [CrossRef]
- Santos, L.F.; Correia, I.J.; Silva, A.S.; Mano, J.F. Biomaterials for drug delivery patches. Eur. J. Pharm. Sci. 2018, 118, 49–66. [Google Scholar] [CrossRef]
- Jacob, J.; Haponiuk, J.T.; Thomas, S.; Gopi, S. Biopolymer based nanomaterials in drug delivery systems: A review. Mater. Today Chem. 2018, 9, 43–55. [Google Scholar] [CrossRef]
- Labus, K.; Trusek-Holownia, A.; Semba, D.; Ostrowska, J.; Tynski, P.; Bogusz, J. Biodegradable polylactide and thermoplastic starch blends as drug release device - Mass transfer study. Pol. J. Chem. Technol. 2018, 20, 75–80. [Google Scholar] [CrossRef]
- Tavassoli-Kafrani, E.; Shekarchizadeh, H.; Masoudpour-Behabadi, M. Development of edible films and coatings from alginates and carrageenans. Carbohydr. Polym. 2016, 137, 360–374. [Google Scholar] [CrossRef] [PubMed]
- Batista, R.A.; Espitia, P.J.P.; Quintans, J.D.S.S.; Freitas, M.M.; Cerqueira, M.Â.; Teixeira, J.A.; Cardoso, J.C. Hydrogel as an alternative structure for food packaging systems. Carbohydr. Polym. 2019, 205, 106–116. [Google Scholar] [CrossRef] [PubMed]
- Joye, I.J. Cereal biopolymers for nano- and microtechnology: A myriad of opportunities for novel (functional) food applications. Trends Food Sci. Technol. 2019, 83, 1–11. [Google Scholar] [CrossRef]
- Czyzewska, K.; Trusek, A. Encapsulated catalase from Serratia genus for H2O2 decomposition in food applications. Pol. J. Chem. Technol. 2018, 20, 39–43. [Google Scholar] [CrossRef]
- Lin, Y.H.; Wang, S.H.; Wu, M.H.; Pan, T.M.; Lai, C.S.; Luo, J.D.; Chiou, C.C. Integrating solid-state sensor and microfluidic devices for glucose, Urea and creatinine detection based on enzyme-carrying alginate microbeads. Biosens. Bioelectron. 2013, 43, 328–335. [Google Scholar] [CrossRef] [PubMed]
- Shipovskaya, A.B.; Shmakov, S.L.; Gegel, N.O. Optical activity anisotropy of chitosan-based films. Carbohydr. Polym. 2019, 206, 476–486. [Google Scholar] [CrossRef] [PubMed]
- Hamouche, H.; Makhlouf, S.; Chaouchi, A.; Laghrouche, M. Humidity Sensor Based on Keratin bio Polymer Film. Sens. Actuat. A Phys. 2018, 282, 132–141. [Google Scholar] [CrossRef]
- D’Souza, S.F. Immobilization and stabilization of biomaterials for biosensor applications. Appl. Biochem. Biotechnol. Part A Enzym. Eng. Biotechnol. 2001, 96, 225–238. [Google Scholar] [CrossRef]
- Majeed, Z.; Ramli, N.K.; Mansor, N.; Man, Z. A comprehensive review on biodegradable polymers and their blends used in controlled-release fertilizer processes. Rev. Chem. Eng. 2015, 31, 69–95. [Google Scholar] [CrossRef]
- Lubkowski, K. Coating fertilizer granules with biodegradable materials for controlled fertilizer release. Environ. Eng. Manag. J. 2014, 13, 2573–2581. [Google Scholar] [CrossRef]
- Gross, R.A.; Kalra, B. Biodegradable Polymers for the. Source Sci. New Ser. 2002, 297, 803–807. [Google Scholar]
- Pan, L.; Wang, Z.; Zhao, X.; He, H. Efficient removal of lead and copper ions from water by enhanced strength-toughness alginate composite fibers. Int. J. Biol. Macromol. 2019, 134, 223–229. [Google Scholar] [CrossRef]
- Miretzky, P.; Cirelli, A.F. Hg(II) removal from water by chitosan and chitosan derivatives: A review. J. Hazard. Mater. 2009, 167, 10–23. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, G.T. Evaluation of Selected Natural Hydrogels As Entrapping Materials for Enzyme. J. Chronother. Drug Deliv. 2011, 2, 107–112. [Google Scholar]
- Zucca, P.; Fernandez-Lafuente, R.; Sanjust, E. Agarose and its derivatives as supports for enzyme immobilization. Molecules 2016, 21, 1577. [Google Scholar] [CrossRef]
- Elnashar, M.M.M. The Art of Immobilization Using Biopolymers, Biomaterials and Nanobiotechnology. In Biotechnology of Biopolymers; InTech: London, UK, 2011; pp. 3–32. ISBN 978-953-307-179-4. [Google Scholar]
- Chapman, J.; Ismail, A.; Dinu, C. Industrial Applications of Enzymes: Recent Advances, Techniques, and Outlooks. Catalysts 2018, 8, 238. [Google Scholar] [CrossRef]
- Labus, K.; Drozd, A.; Trusek-Holownia, A. Preparation and characterisation of gelatine hydrogels predisposed to use as matrices for effective immobilisation of biocatalysts. Chem. Pap. 2016, 70, 523–530. [Google Scholar] [CrossRef]
- Trusek-Holownia, A.; Noworyta, A. Efficient utilisation of hydrogel preparations with encapsulated enzymes—A case study on catalase and hydrogen peroxide degradation. Biotechnol. Rep. 2015, 6, 13–19. [Google Scholar] [CrossRef]
- Ahmed, E.M. Hydrogel: Preparation, characterization, and applications: A review. J. Adv. Res. 2015, 6, 105–121. [Google Scholar] [CrossRef]
- Mohammadinejad, R.; Maleki, H.; Larrañeta, E.; Fajardo, A.R.; Nik, A.B.; Shavandi, A.; Sheikhi, A.; Ghorbanpour, M.; Farokhi, M.; Govindh, P.; et al. Status and future scope of plant-based green hydrogels in biomedical engineering. Appl. Mater. Today 2019, 16, 213–246. [Google Scholar] [CrossRef]
- Mahinroosta, M.; Jomeh Farsangi, Z.; Allahverdi, A.; Shakoori, Z. Hydrogels as intelligent materials: A brief review of synthesis, properties and applications. Mater. Today Chem. 2018, 8, 42–55. [Google Scholar] [CrossRef]
- Joly-Duhamel, C.; Hellio, D.; Djabourov, M. All gelatin networks: 1. Biodiversity and physical chemistry. Langmuir 2002, 18, 7208–7217. [Google Scholar] [CrossRef]
- Lin, L.; Regenstein, J.M.; Lv, S.; Lu, J.; Jiang, S. An overview of gelatin derived from aquatic animals: Properties and modification. Trends Food Sci. Technol. 2017, 68, 102–112. [Google Scholar] [CrossRef]
- Gomez-Guillen, M.C.; Gimenez, B.; Lopez-Caballero, M.E.; Montero, M.P. Functional and bioactive properties of collagen and gelatin from alternative sources: A review. Food Hydrocoll. 2011, 25, 1813–1827. [Google Scholar] [CrossRef]
- Huang, T.; Tu, Z.C.; Shangguan, X.; Sha, X.; Wang, H.; Zhang, L.; Bansal, N. Fish gelatin modifications: A comprehensive review. Trends Food Sci. Technol. 2019, 86, 260–269. [Google Scholar] [CrossRef]
- Elzoghby, A.O. Gelatin-based nanoparticles as drug and gene delivery systems: Reviewing three decades of research. J. Control. Release 2013, 172, 1075–1091. [Google Scholar] [CrossRef]
- Santoro, M.; Tatara, A.M.; Mikos, A.G. Gelatin carriers for drug and cell delivery in tissue engineering. J. Control. Release 2014, 190, 210–218. [Google Scholar] [CrossRef]
- Laffleur, F.; Strasdat, B. Gelatin-based formulations for dermal application. Eur. Polym. J. 2019, 118, 542–550. [Google Scholar] [CrossRef]
- Abdullah, M.S.P.; Noordin, M.I.; Mohd Ismail, S.I.; Mustapha, N.M.; Jasamai, M.; Danik, M.F.; Wan Ismail, W.A.; Shamsuddin, A.F. Recent advances in the use of animal-sourced gelatine as natural polymers for food, cosmetics and pharmaceutical applications. Sains Malays. 2018, 47, 323–336. [Google Scholar]
- Zaupa, A. Physical Crosslinking of Gelatin: A Supramolecular Approach to Biomaterials. Ph.D. Thesis, Universitätsbibliothek der Universität Potsdam, Potsdam, Germany, 2011. [Google Scholar]
- Neffe, A.T.; Zaupa, A.; Pierce, B.F.; Hofmann, D.; Lendlein, A. Knowledge-based tailoring of gelatin-based materials by functionalization with tyrosine-derived groups. Macromol. Rapid Commun. 2010, 31, 1534–1539. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zaupa, A.; Neffe, A.T.; Pierce, B.F.; Lendlein, A.; Hofmann, D. A molecular dynamic analysis of gelatin as an amorphous material: Prediction of mechanical properties of gelatin systems. Int. J. Artif. Organs 2011, 34, 139–151. [Google Scholar] [CrossRef] [PubMed]
- Knani, D.; Barkay, H.; Alperstein, D.; Zilberman, M. Simulation of novel soy protein-based systems for tissue regeneration applications. Polym. Adv. Technol. 2017, 28, 496–505. [Google Scholar] [CrossRef]
- Radosinski, L.; Labus, K. Molecular modeling studies of structural properties of polyvinyl alcohol: A comparative study using INTERFACE force field. J. Mol. Model. 2017, 23, 305. [Google Scholar] [CrossRef] [PubMed]
- Elliott, J.A. Novel approaches to multiscale modelling in materials science. Int. Mater. Rev. 2011, 56, 207–225. [Google Scholar] [CrossRef]
- Abbott, L.J.; Hart, K.E.; Colina, C.M. Polymatic: A generalized simulated polymerization algorithm for amorphous polymers. Theor. Chem. Acc. 2013, 132, 1–19. [Google Scholar] [CrossRef]
- Mark, J.E. Polymer Data Handbook; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Subramanian, K. Evaluation of isophorone diisocyanate crosslinked gelatin as a carrier for controlled delivery of drugs. Polym. Bull. 2013, 70, 733–753. [Google Scholar] [CrossRef]
- Zhao, B. Gelatin. In Polymer Data Handbook; Mark, J.E., Ed.; Oxford University Press: New York, NY, USA, 1999; pp. 121–129. ISBN 978-0195107890. [Google Scholar]
- Taffel, A. CCXXXVI.—Thermal Expansion of Gelatin Gels. J. Chem. Soc. Trans. 1922, 121, 1971–1984. [Google Scholar] [CrossRef]
- Milliman, H.W.; Boris, D.; Schiraldi, D.A. Experimental determination of Hansen solubility parameters for select POSS and polymer compounds as a guide to POSS-polymer interaction potentials. Macromolecules 2012, 45, 1931–1936. [Google Scholar] [CrossRef]
- Connolly, M.L. Analytical molecular surface calculation. J. Appl. Crystallogr. 1983, 16, 548–558. [Google Scholar] [CrossRef]

| DF | SSE | MSE | F Value | p-Value | ||
|---|---|---|---|---|---|---|
| Model | 1 | 0.00211 | 0.00211 | 47.56219 | 2.61381 × 10−8 | |
| Error | 40 | 0.00177 | 4.42581 × 10−5 | |||
| Total | 41 | 0.00388 | ||||
| DF | SSE | MSE | F Value | p-Value | ||
|---|---|---|---|---|---|---|
| Model | 1 | 0.54061 | 0.54061 | 9.68304 | 0.00347 | |
| Error | 39 | 2.17741 | 0.05583 | |||
| Total | 40 | 2.71802 | ||||
| DF | SSE | MSE | F Value | p-Value | ||
|---|---|---|---|---|---|---|
| FFV | Model | 1 | 0.00153 | 0.00153 | 22.45198 | 2.71 × 10−5 |
| Error | 40 | 0.00272 | 6.79 × 10−5 | |||
| Total | 41 | 0.00424 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radosinski, L.; Labus, K.; Zemojtel, P.; Wojciechowski, J.W. Development and Validation of a Virtual Gelatin Model Using Molecular Modeling Computational Tools. Molecules 2019, 24, 3365. https://doi.org/10.3390/molecules24183365
Radosinski L, Labus K, Zemojtel P, Wojciechowski JW. Development and Validation of a Virtual Gelatin Model Using Molecular Modeling Computational Tools. Molecules. 2019; 24(18):3365. https://doi.org/10.3390/molecules24183365
Chicago/Turabian StyleRadosinski, Lukasz, Karolina Labus, Piotr Zemojtel, and Jakub W. Wojciechowski. 2019. "Development and Validation of a Virtual Gelatin Model Using Molecular Modeling Computational Tools" Molecules 24, no. 18: 3365. https://doi.org/10.3390/molecules24183365
APA StyleRadosinski, L., Labus, K., Zemojtel, P., & Wojciechowski, J. W. (2019). Development and Validation of a Virtual Gelatin Model Using Molecular Modeling Computational Tools. Molecules, 24(18), 3365. https://doi.org/10.3390/molecules24183365







