How Far Can One Push the Noble Gases Towards Bonding?: A Personal Account
Abstract
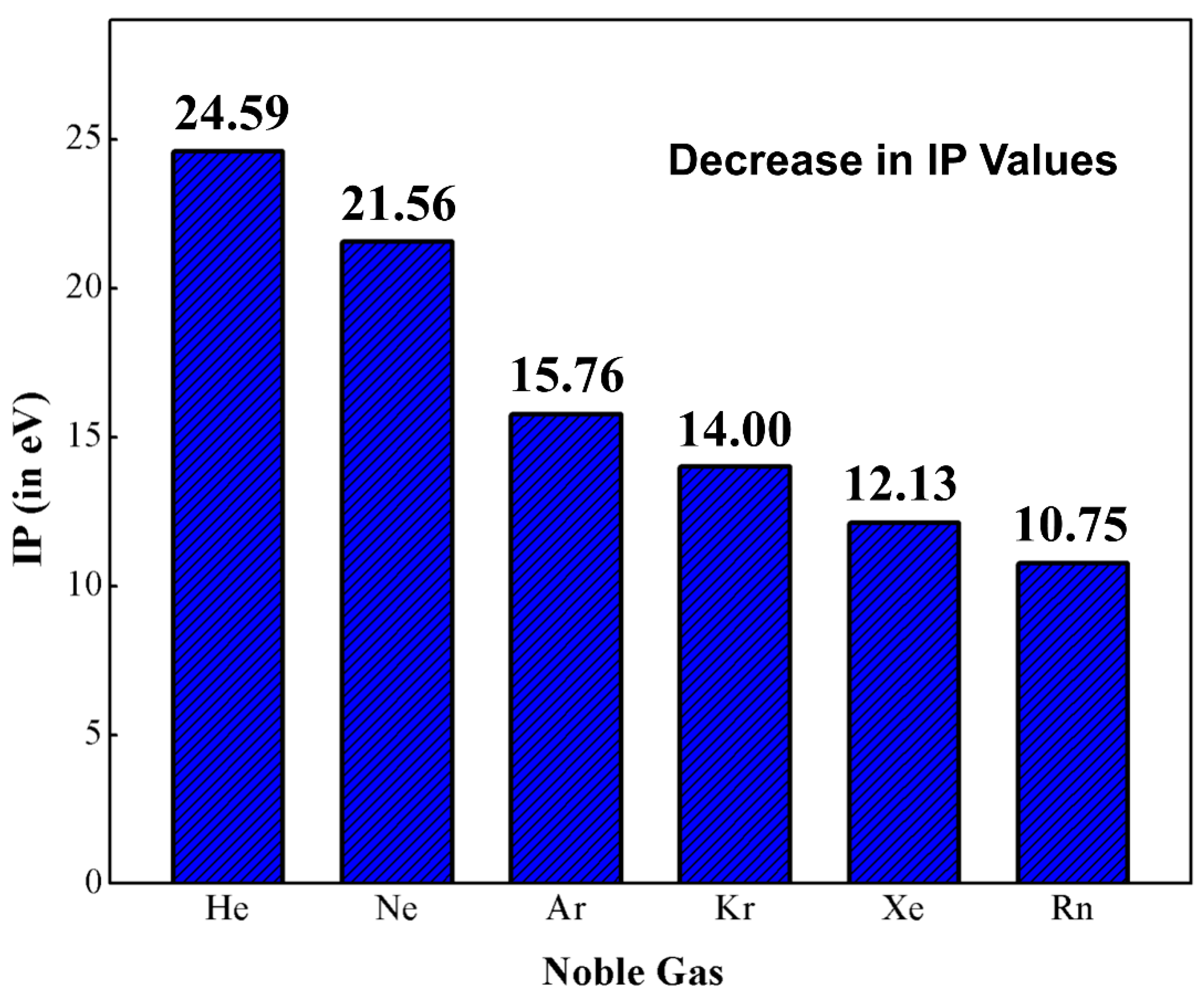
1. Introduction
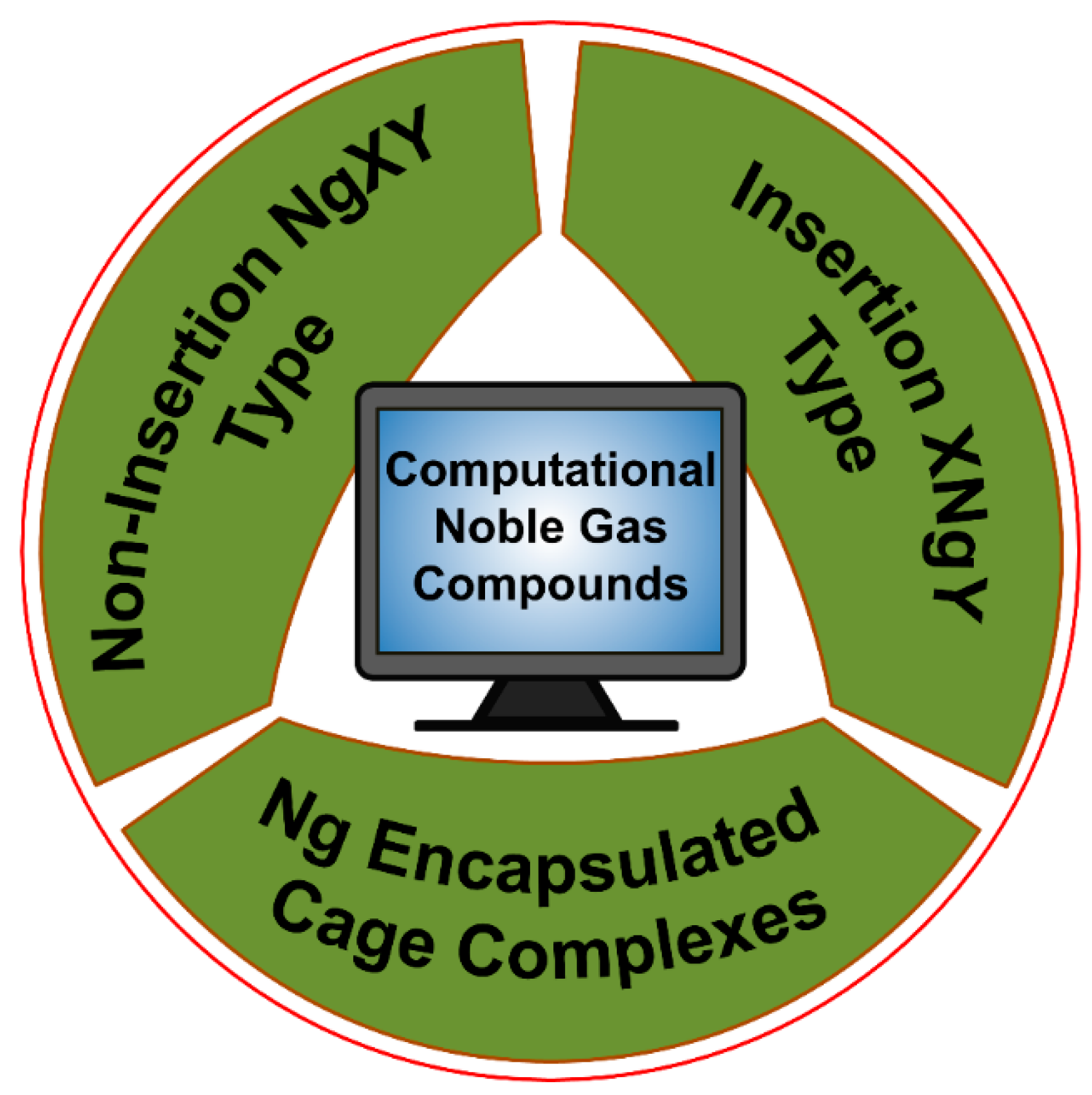
2. Ng Compounds under the Light of Theoretical Chemistry
3. Discussion
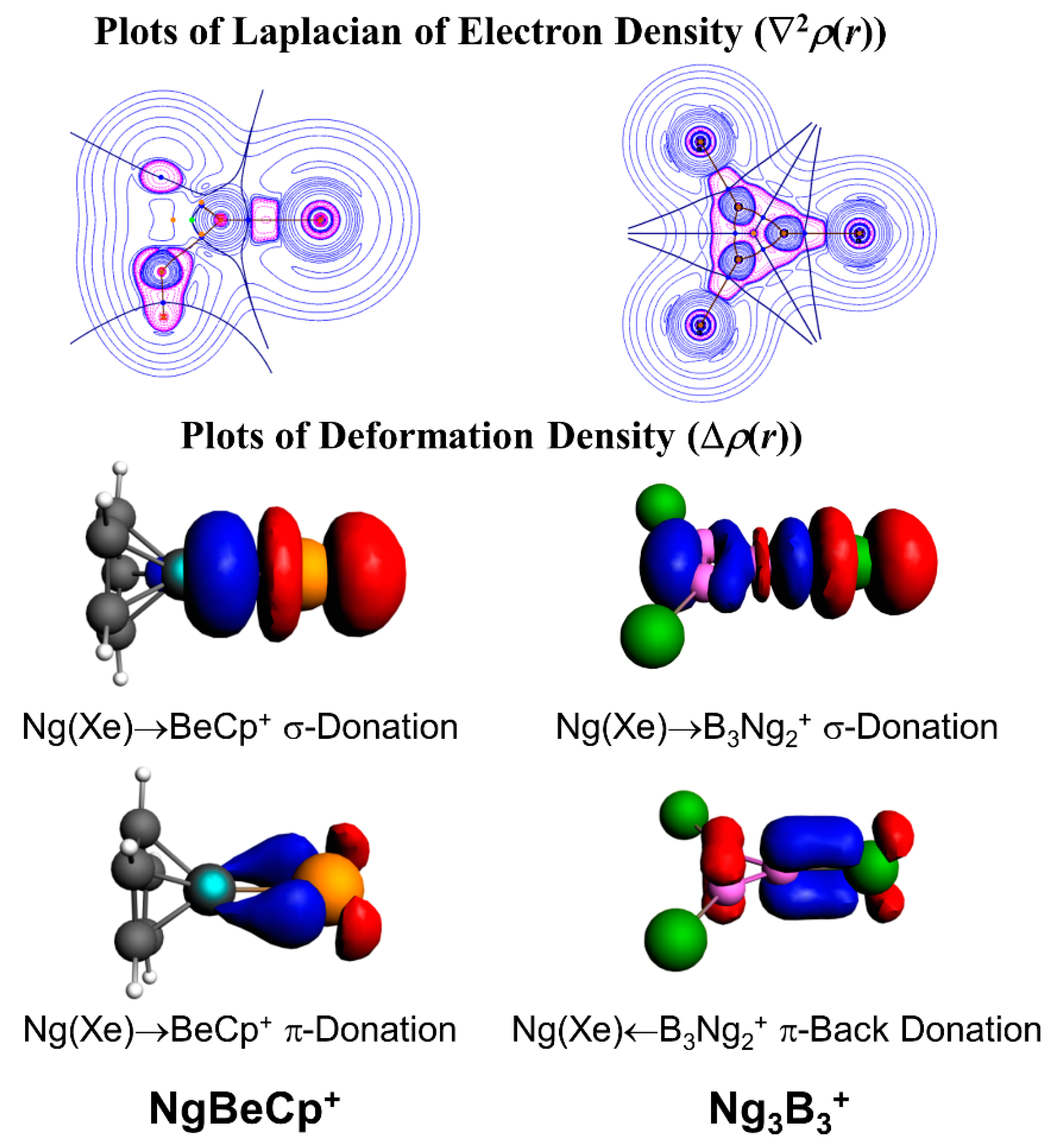
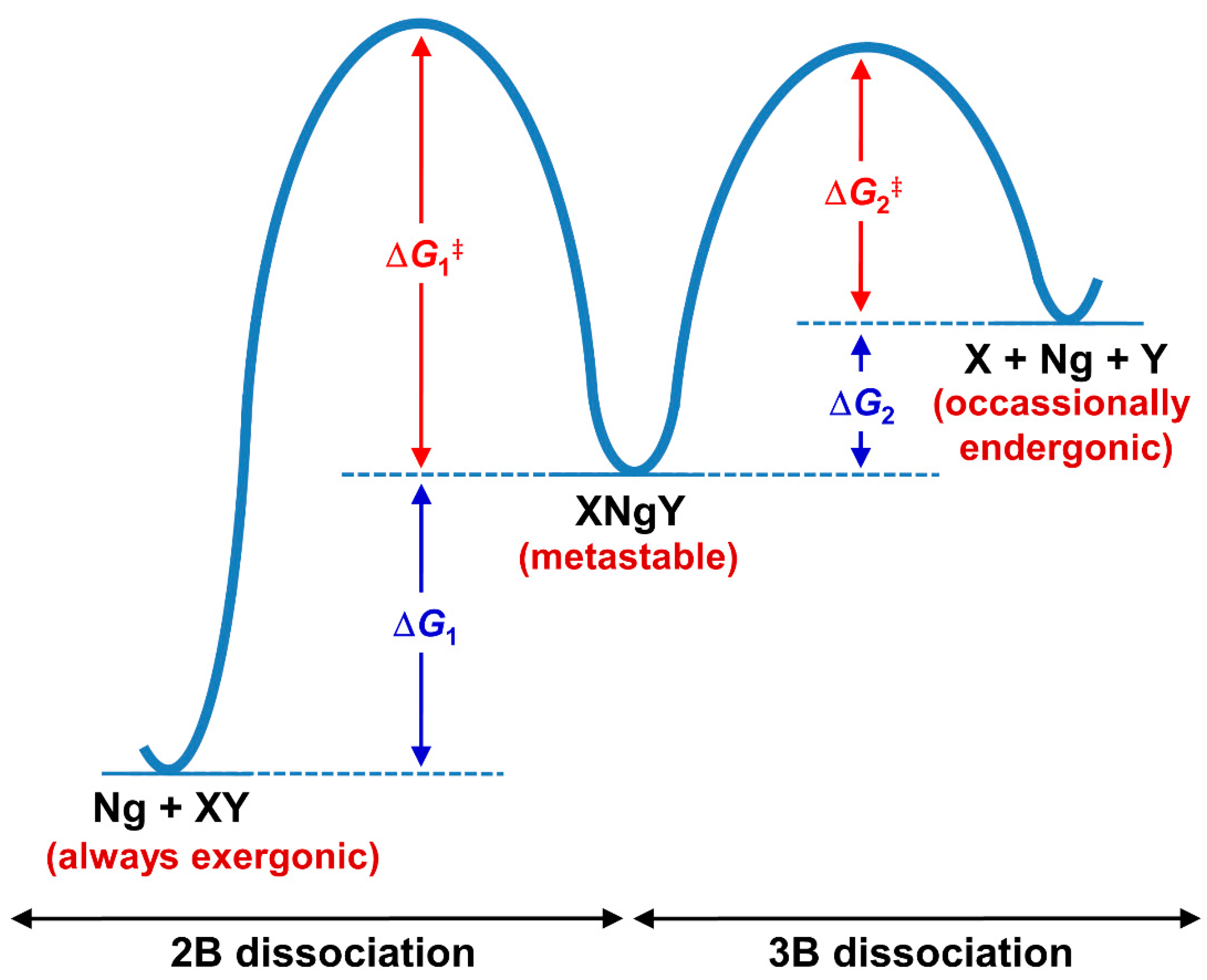
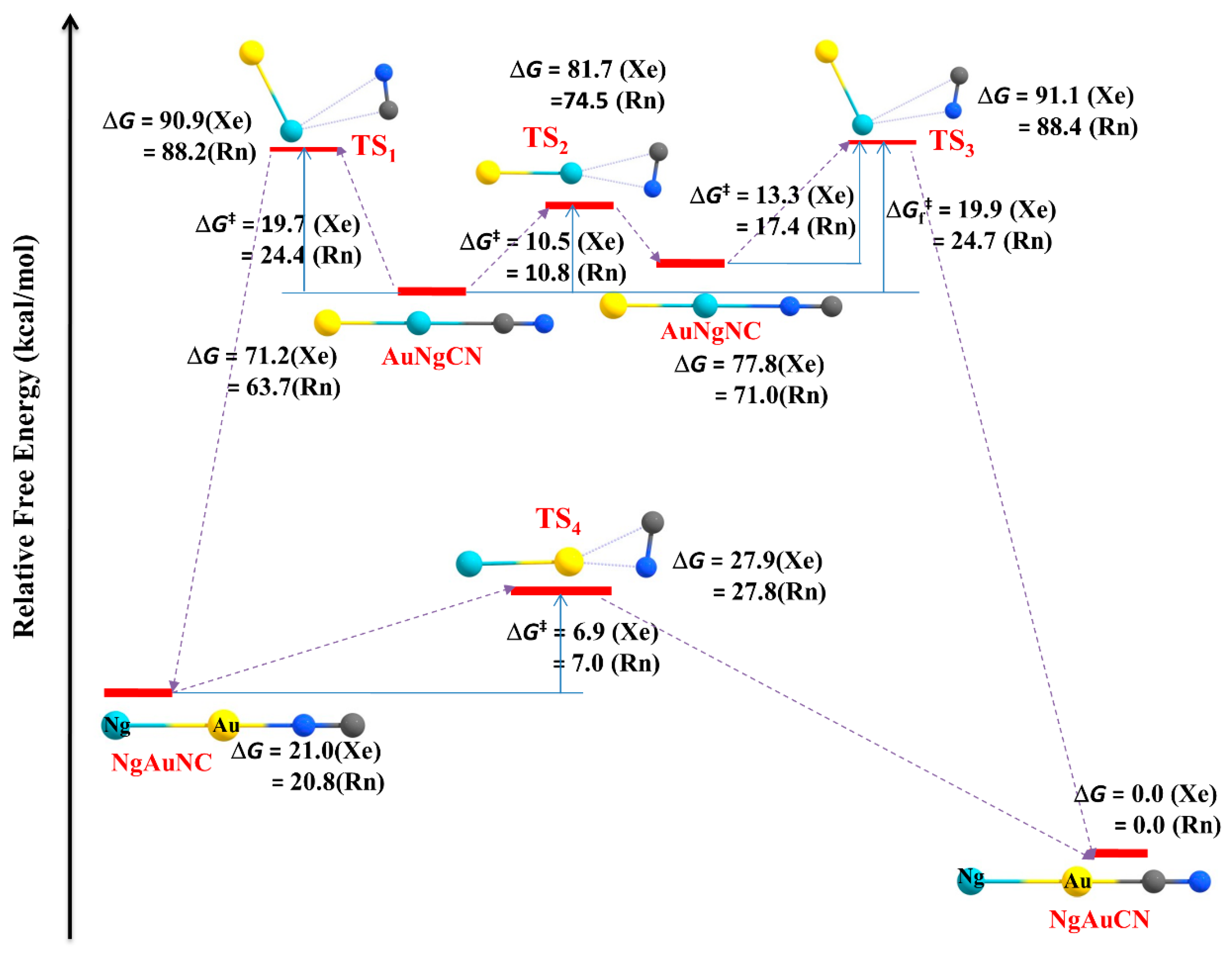
3.1. Non-Insertion Complexes of NgXY Type
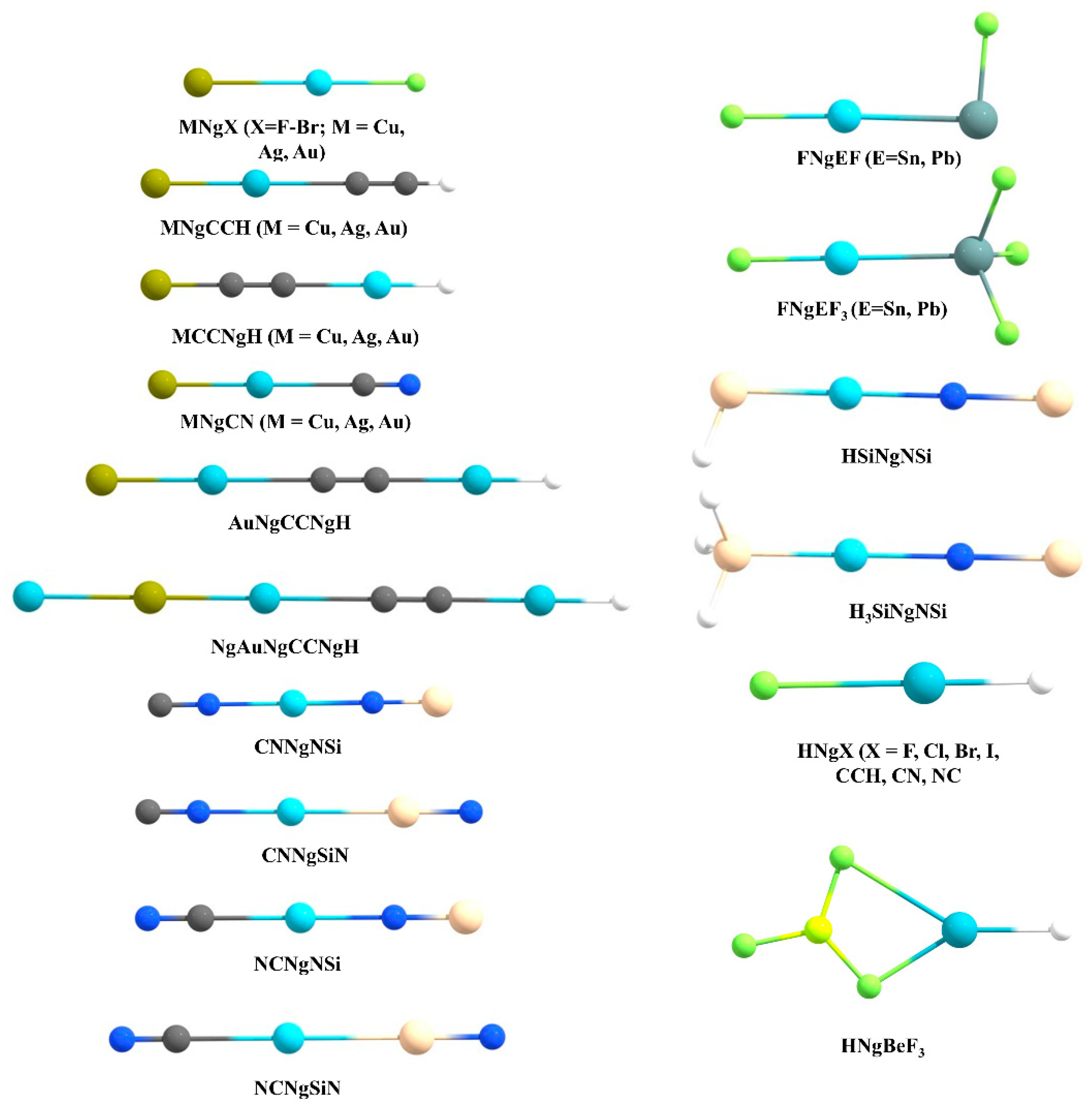
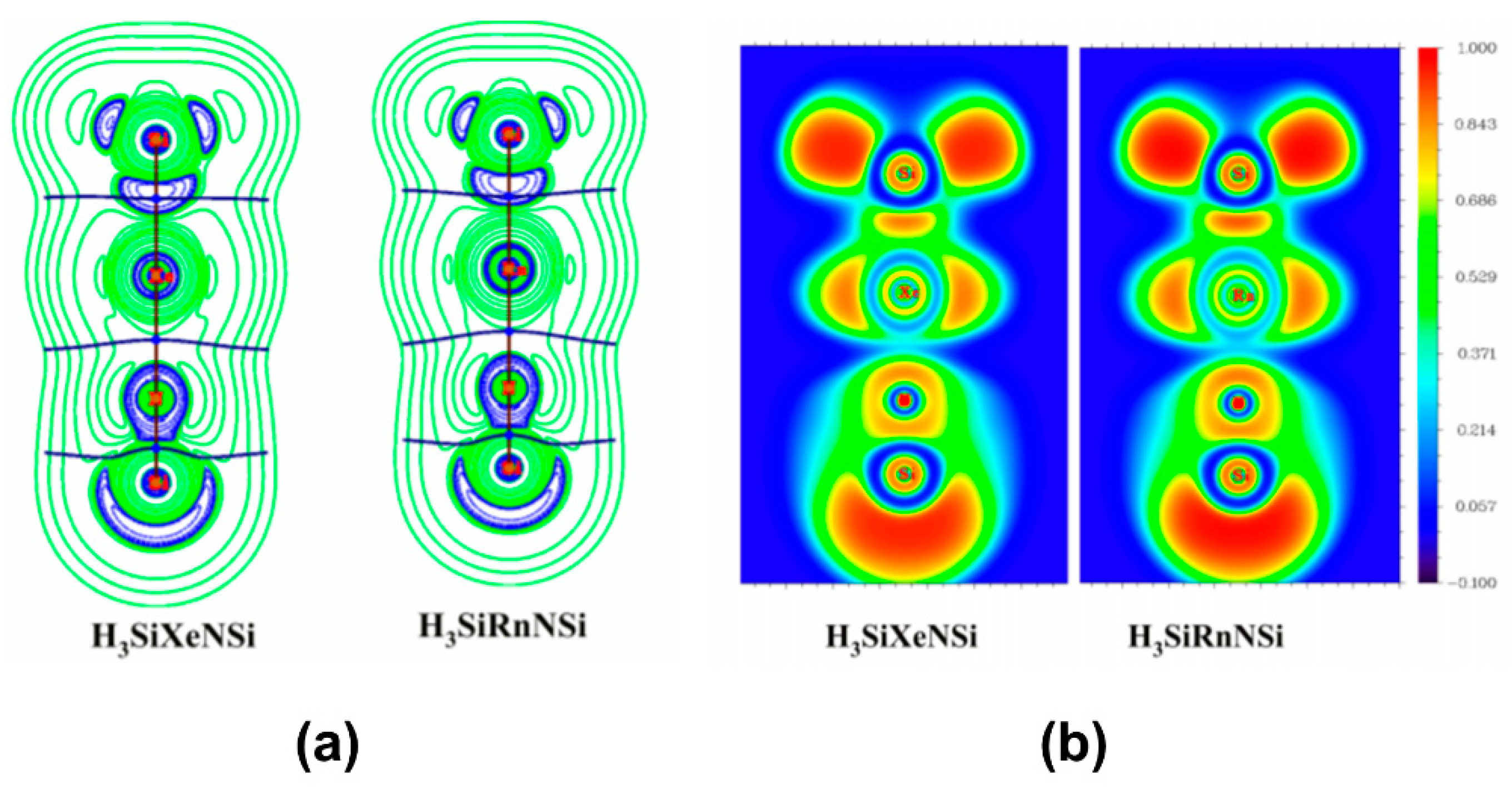
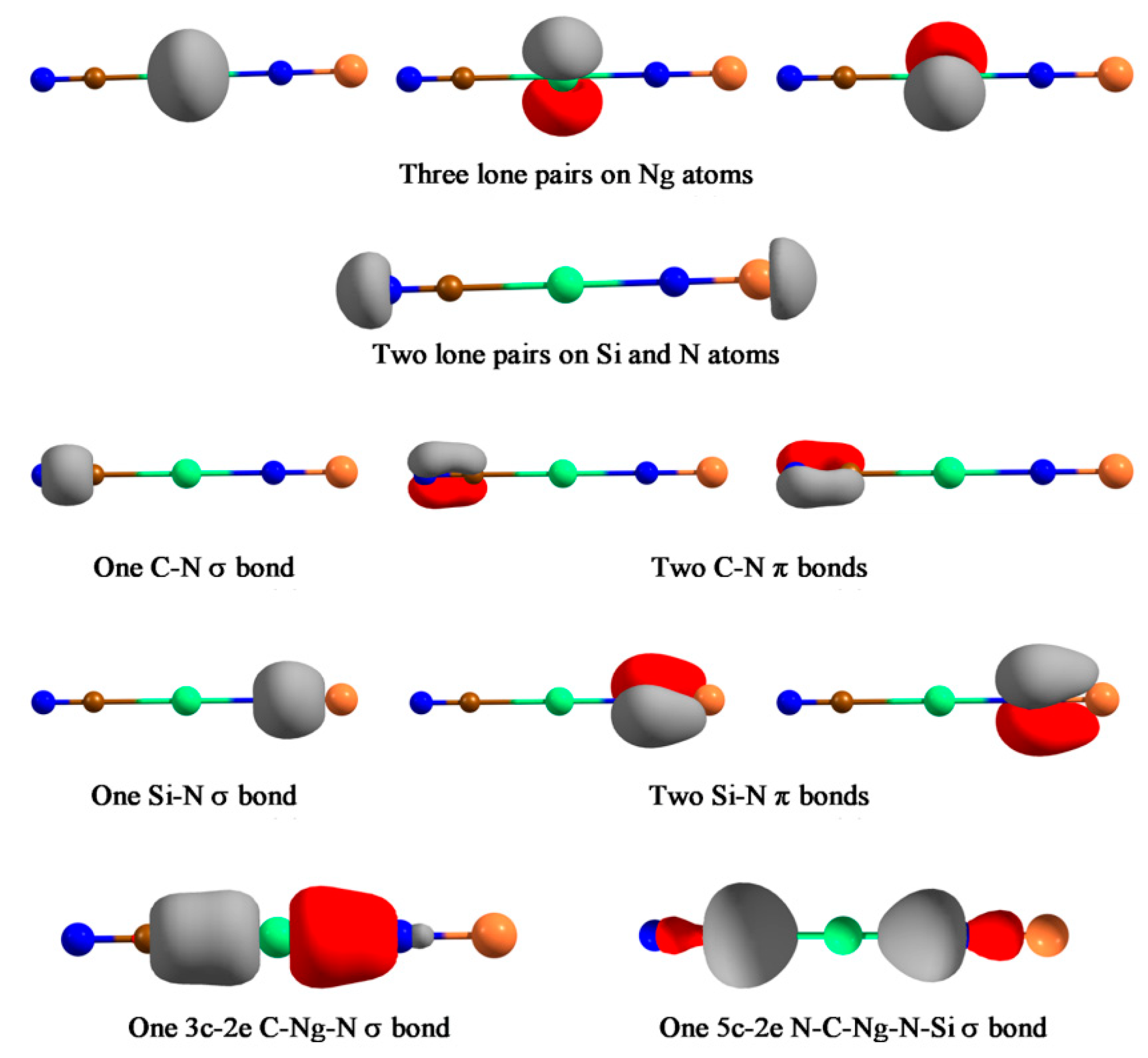
3.2. Insertion Complexes of XNgY Type
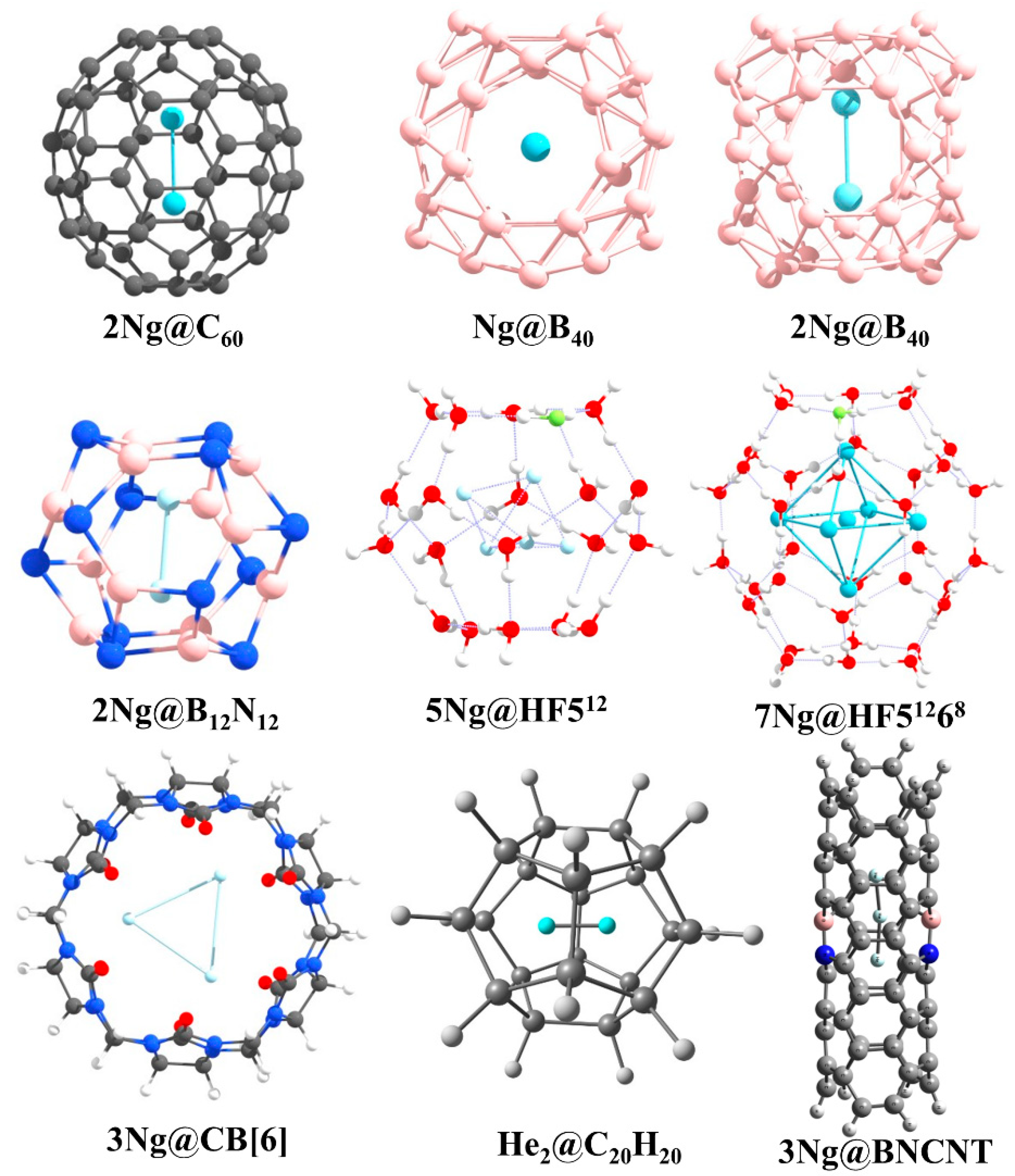
3.3. Ng-Encapsulated Cage Complexes
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mendeleev, D. Osnovy Khimii [The Principles of Chemistry]. Ch. 10. 1902, Volume 15, pp. 448–472, S.-Peterburg, M.P. Frolova. Available online: https://www.bookvica.com/pages/books/233/d-i-mendeleev/osnovy-khimii-i-e-the-principles-of-chemistry/?soldItem=true (accessed on 11 July 2019).
- Mewes, J.-M.; Smits, O.R.; Jerabek, P.; Schwerdtfeger, P. Oganesson is a Semiconductor: On the Relativistic Band-Gap Narrowing in the Heaviest Noble-Gas Solids. Angew. Chem. Int. Ed. 2019. [Google Scholar] [CrossRef] [PubMed]
- Arny, L.R. The Search for Data in the Physical and Chemical Sciences; Special Libraries Association: Alexandria, VA, USA, 1984. [Google Scholar]
- Kossel, W. Über Molekülbildung als Frage des Atombaus. Annalen der Physik 1916, 354, 229–362. [Google Scholar] [CrossRef]
- Von Antropoff, A. Die Wertigkeit der Edelgase und ihre Stellung im periodischen System. II. Angew. Chem. Int. Ed. 1924, 37, 695–696. [Google Scholar] [CrossRef]
- Laszlo, P.; Schrobilgen, G.J. One or Several Pioneers? The Discovery of Noble-Gas Compounds. Angew. Chem. Int. Ed. 1988, 27, 479–489. [Google Scholar] [CrossRef]
- Pauling, L. The formulas of antimonic acid and the antimonates. J. Am. Chem. Soc. 1933, 55, 1895–1900. [Google Scholar] [CrossRef]
- Bartlett, N.; Lohmann, D. 1005. Fluorides of the noble metals. Part II. Dioxygenyl hexafluoroplatinate (V), O2+[PtF6]−. J. Am. Chem. Soc. 1962, 5253–5261. [Google Scholar] [CrossRef]
- Bartlett, N. Xenon hexafluoroplatinate (V) Xe+[PtF6]-. Proc. Chem. Soc. Lond. 1962, 1962, 218. [Google Scholar]
- Hargittai, I. Neil Bartlett and the First Noble-Gas Compound; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Graham, L.; Graudejus, O.; Jha, N.K.; Bartlett, N. Concerning the nature of XePtF6. Coord. Chem. Rev. 2000, 197, 321–334. [Google Scholar] [CrossRef]
- Craciun, R.; Picone, D.; Long, R.T.; Li, S.; Dixon, D.A.; Peterson, K.A.; Christe, K.O. Third row transition metal hexafluorides, extraordinary oxidizers, and Lewis acids: Electron affinities, fluoride affinities, and heats of formation of WF6, ReF6, OsF6, IrF6, PtF6, and AuF6. Inorg. Chem. 2010, 49, 1056–1070. [Google Scholar] [CrossRef]
- Christe, K.O. Bartlett’s discovery of noble gas fluorides, a milestone in chemical history. Chem. Commun. 2013, 49, 4588–4590. [Google Scholar] [CrossRef]
- Streng, A.; Kirshenbaum, A.; Streng, L.; Grosse, A. Preparation of Rare-Gas Fluorides and Oxyfluorides by the Electric Discharge Method and their Properties. In Noble Gas Compounds; Hyman, H.H., Ed.; The University of Chicago Press: Chicago, IL, USA, 1963; pp. 73–80. [Google Scholar]
- Lehmann, J.F.; Mercier, H.P.; Schrobilgen, G.J. The chemistry of krypton. Coord. Chem. Rev. 2002, 233, 1–39. [Google Scholar] [CrossRef]
- Claassen, H.H.; Selig, H.; Malm, J.G. Xenon tetrafluoride. J. Am. Chem. Soc. 1962, 84, 3593. [Google Scholar] [CrossRef]
- Slivnik, J.; Brcic, B.; Volavsek, B.; Marsel, J.; Vrscaj, V.; Smalc, A.; Frlec, B.; Zemljic, Z. Über die Synthese von XeF6. Croat. Chem. Acta 1962, 34, 253. [Google Scholar]
- Turner, J.; Pimentel, G.C. Krypton fluoride: Preparation by the matrix isolation technique. Science 1963, 140, 974–975. [Google Scholar] [CrossRef] [PubMed]
- Nelson, L.Y.; Pimentel, G.C. Infrared detection of xenon dichloride. Inorg. Chem. 1967, 6, 1758–1759. [Google Scholar] [CrossRef]
- Bartlett, N.; Wechsberg, M. The Xenon Difluoride Complexes XeF2 · XeOF4; XeF2 · XeF6 · AsF5 and XeF2 · 2 XeF6 · 2 AsF5 and Their Relevance to Bond Polarity and Fluoride Ion Donor Ability of XeF2 and XeF6. Z. Anorg. Allg. Chem. 1951, 455, 5–17. [Google Scholar] [CrossRef]
- Holloway, J.H.; Hope, E.G. Recent advances in noble-gas chemistry. Adv. Inorg. Chem. 1998, 46, 51–100. [Google Scholar]
- Stein, L. Ionic radon solutions. Science 1970, 168, 362–364. [Google Scholar] [CrossRef]
- Khriachtchev, L.; Pettersson, M.; Runeberg, N.; Lundell, J.; Räsänen, M. A stable argon compound. Nature 2000, 406, 874. [Google Scholar] [CrossRef]
- Frenking, G. Another noble gas conquered. Nature 2000, 406, 836. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, X. Infrared Spectra of NgBeS (Ng = Ne, Ar, Kr, Xe) and BeS2 in Noble-Gas Matrices. J. Phys. Chem. A 2013, 117, 1508–1513. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Chen, M.; Zhou, M.; Andrada, D.M.; Frenking, G. Experimental and Theoretical Studies of the Infrared Spectra and Bonding Properties of NgBeCO3 and a Comparison with NgBeO (Ng = He, Ne, Ar, Kr, Xe). J. Phys. Chem. A 2014, 119, 2543–2552. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Liu, X.; Xu, B.; Xing, X.; Wang, X. Infrared Spectra of Novel NgBeSO2 Complexes (Ng = Ne, Ar, Kr, Xe) in Low Temperature Matrixes. J. Phys. Chem. A 2016, 120, 8590–8598. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Li, W.L.; Zhao, L.; Chen, M.; Zhou, M.; Li, J.; Frenking, G. A Very Short Be-Be Distance but No Bond: Synthesis and Bonding Analysis of Ng-Be2O2-Ng′ (Ng, Ng′= Ne, Ar, Kr, Xe). Chem. Eur. J. 2017, 23, 2035–2039. [Google Scholar] [CrossRef] [PubMed]
- Hogness, T.R.; Lunn, E.G. The ionization of hydrogen by electron impact as interpreted by positive ray analysis. Phys. Rev. 1925, 26, 44–55. [Google Scholar] [CrossRef]
- Dong, X.; Oganov, A.R.; Goncharov, A.F.; Stavrou, E.; Lobanov, S.; Saleh, G.; Qian, G.-R.; Zhu, Q.; Gatti, C.; Deringer, V.L.; et al. A stable compound of helium and sodium at high pressure. Nat. Chem. 2017, 9, 440–445. [Google Scholar] [CrossRef]
- Bellert, D.; Breckenridge, W. Bonding in Ground-State and Excited-State A+·Rg van der Waals Ions (A = Atom, Rg = Rare-Gas Atom): A Model-Potential Analysis. Chem. Rev. 2002, 102, 1595–1622. [Google Scholar] [CrossRef]
- Liebman, J.F.; Deakyne, C.A. Noble gas compounds and chemistry: A brief review of interrelations and interactions with fluorine-containing species. J. Fluor. Chem. 2003, 121, 1–8. [Google Scholar] [CrossRef]
- Schrobilgen, G.J.; Moran, M.D. Noble-gas compounds. In Kirk-Othmer Encyclopedia of Chemical Technology, 5th ed.; Wiley and Sons, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Gerber, R. Formation of novel rare-gas molecules in low-temperature matrices. Annu. Rev. Phys. Chem. 2004, 55, 55–78. [Google Scholar] [CrossRef]
- Tavčar, G.; Tramšek, M.; Bunič, T.; Benkič, P.; Žemva, B. New class of coordination compounds with noble gas fluorides as ligands to metal ions. J. Fluor. Chem. 2004, 125, 1579–1584. [Google Scholar] [CrossRef]
- Pettersson, M.; Khriachtchev, L.; Lundell, J.; Räsänen, M. Noble gas hydride compounds. In Inorganic Chemistry in Focus II; Meyer, G., Naumann, D., Wesemann, L., Eds.; Wiley-VCH: Weinheim, Germany, 2005; pp. 15–34. [Google Scholar]
- Gerber, R. New Chemistry of the Noble Gas Elements: Novel Molecules, Polymers and Clusters. ChemInform 2006, 37, 1–8. [Google Scholar] [CrossRef]
- Schrobilgen, G.J.; Gerken, M. Noble gas elements. In The Encyclopedia of Magnetic Resonance, Harris, R.K.; Wasylishen, R.E., Ed.; John Wiley and Sons: New York, NY, USA, 2011. [Google Scholar]
- Grochala, W. Atypical compounds of gases, which have been called ‘noble’. Chem. Soc. Rev. 2007, 36, 1632–1655. [Google Scholar] [CrossRef] [PubMed]
- Khriachtchev, L.; Räsänen, M.; Gerber, R.B. Noble-gas hydrides: New chemistry at low temperatures. Acc. Chem. Res. 2008, 42, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Calladine, J.A.; Vuong, K.Q.; Sun, X.Z.; George, M.W. Recent advances in organometallic alkane and noble gas complexes. Pure Appl. Chem. 2009, 81, 1667–1675. [Google Scholar] [CrossRef]
- Grandinetti, F. Noble Gas Chemistry: Structure, Bonding, and Gas-Phase Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Balta, B.; Gianturco, F.; Paesani, F. Structural properties and quantum effects in protonated helium clusters. II. Quantum Monte Carlo calculations for the smaller aggregates. Chem. Phys. 2000, 254, 215–229. [Google Scholar] [CrossRef]
- Ward, T.; Carnegie, P.; Duncan, M. Infrared spectroscopy of the Ti (H2O) Ar+ ion–molecule complex: Electronic state switching induced by argon. Chem. Phys. Lett. 2016, 654, 1–5. [Google Scholar] [CrossRef]
- Wagner, J.P.; McDonald, D.C.; Duncan, M.A. An Argon–Oxygen Covalent Bond in the ArOH+ Molecular Ion. Angew. Chem. Int. Ed. 2018, 57, 5081–5085. [Google Scholar] [CrossRef]
- Čurík, R.; Gianturco, F. Indirect dissociative recombination of LiHe+ ions driven by vibrational Feshbach resonances. Phys. Rev. A 2013, 87, 012705. [Google Scholar] [CrossRef]
- Rodríguez-Cantano, R.; de Tudela, R.P.; López-Durán, D.; González-Lezana, T.; Gianturco, F.A.; Delgado-Barrio, G.; Villarreal, P. Quantum rotation of Rb2 (3Σu+) attached to HeN droplets: A path-integral Monte Carlo study. Eur. Phys. J. D 2013, 67, 119. [Google Scholar] [CrossRef]
- González-Sánchez, L.; Wester, R.; Gianturco, F. Collisional cooling of internal rotation in MgH+ ions trapped with He atoms: Quantum modeling meets experiments in Coulomb crystals. Phys. Rev. A 2018, 98, 053423. [Google Scholar] [CrossRef]
- Zou, W.; Nori-Shargh, D.; Boggs, J.E. On the covalent character of rare gas bonding interactions: A new kind of weak interaction. J. Phys. Chem. A 2012, 117, 207–212. [Google Scholar] [CrossRef] [PubMed]
- Schlenker, C.; Dumas, J.; Greenblatt, M.; van Smaalen, S. Physics and Chemistry of Low-Dimensional Inorganic Conductors; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 354. [Google Scholar]
- Grandinetti, F. Gas-phase ion chemistry of the noble gases: Recent advances and future perspectives. Eur. J. Mass Spectrom. 2011, 17, 423–463. [Google Scholar] [CrossRef] [PubMed]
- Schrobilgen, G.J.; Brock, D.S. Noble Gases. Annu. Rep. Prog. Chem., Sect. A 2011, 107, 135–141. [Google Scholar] [CrossRef]
- Hope, E.G. Coordination chemistry of the noble gases and noble gas fluorides. Coord. Chem. Rev. 2013, 257, 902–909. [Google Scholar] [CrossRef]
- Brock, D.S.; Schrobilgen, G.J. Noble-Gas Chemistry. In Comprehensive Inorganic Chemistry II; Reedijk, J., Poepplemeier, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 1, pp. 755–822. [Google Scholar]
- Haner, J.; Schrobilgen, G.J. The chemistry of Xenon (IV). Chem. Rev. 2015, 115, 1255–1295. [Google Scholar] [CrossRef] [PubMed]
- Lai, T.-Y.; Yang, C.-Y.; Lin, H.-J.; Yang, C.-Y.; Hu, W.-P. Benchmark of density functional theory methods on the prediction of bond energies and bond distances of noble-gas containing molecules. J. Chem. Phys. 2011, 134, 244110. [Google Scholar] [CrossRef] [PubMed]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 6.0: Natural bond orbital analysis program. J. Comput. Chem. 2013, 34, 1429–1437. [Google Scholar] [CrossRef]
- Bader, R.F. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Michalak, A.; Mitoraj, M.; Ziegler, T. Bond orbitals from chemical valence theory. J. Phys. Chem. A 2008, 112, 1933–1939. [Google Scholar] [CrossRef]
- Mitoraj, M.P.; Michalak, A.; Ziegler, T. A combined charge and energy decomposition scheme for bond analysis. J. Chem. Theory. Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef]
- Saha, R.; Pan, S.; Merino, G.; Chattaraj, P.K. Unprecedented Bonding Situation in Viable E2(NHBMe)2 (E = Be, Mg; NHBMe = (HCNMe)2B) Complexes: Neutral E2 Forms a Single E-E Covalent Bond. Angew. Chem. Int. Ed. 2019, 58, 8372–8377. [Google Scholar] [CrossRef] [PubMed]
- Saha, R.; Pan, S.; Chattaraj, P.K. Stabilization of Boron-Boron Triple Bonds by Mesoionic Carbenes. ACS Omega 2018, 3, 13720–13730. [Google Scholar] [CrossRef]
- Saha, R.; Pan, S.; Frenking, G.; Chattaraj, P.K.; Merino, G. The Strongest CO Binding and the Largest C-O Stretching Frequency. Phys. Chem. Chem. Phys. 2017, 19, 2286–2293. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Saha, R.; Osorio, E.; Chattaraj, P.K.; Frenking, G.; Merino, G. Ligand Supported E3 Clusters (E = Si - Sn). Chem. Eur. J. 2017, 23, 7463–7473. [Google Scholar] [CrossRef] [PubMed]
- Barroso, J.; Cabellos, J.L.; Pan, S.; Murillo, F.; Zarate, X.; Fernandez-Herrera, M.A.; Merino, G. Revisiting the Racemization Mechanism of Helicenes. Chem. Commun. 2018, 54, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Pecher, L.; Pan, S.; Frenking, G. Chemical bonding in the hexamethylbenzene–SO2+ dication. Theor. Chem. Acc. 2019, 138, 47. [Google Scholar] [CrossRef]
- Jin, J.; Pan, S.; Jin, X.; Lei, S.; Zhao, L.; Frenking, G.; Zhou, M. Octacarbonyl Anion Complexes of the Late Lanthanides Ln(CO)8− (Ln = Tm, Yb, Lu) and the 32-Electron Rule. Chem. Eur. J. 2019, 25, 3229–3234. [Google Scholar] [CrossRef] [PubMed]
- Chi, C.; Pan, S.; Meng, L.; Luo, M.; Zhao, L.; Zhou, M.; Frenking, G. Alkali Metal Covalent Bonding in Nickel Carbonyl Complexes ENi(CO)3−. Angew. Chem. Int. Ed. 2019, 58, 1732–1738. [Google Scholar] [CrossRef]
- Su, W.; Pan, S.; Sun, X.; Wang, S.; Zhao, L.; Frenking, G.; Zhu, C. Double dative bond between divalent carbon(0) and uranium. Nat. Commun. 2018, 9, 4997. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, L.; Jin, J.; Pan, S.; Li, W.; Jin, X.; Wang, G.; Zhou, M.; Frenking, G. Observation of alkaline earth complexes M(CO)8 (M = Ca, Sr, or Ba) that mimic transition metals. Science 2018, 361, 912–916. [Google Scholar] [CrossRef]
- Zhao, L.; Pan, S.; Holzmann, N.; Schwerdtfeger, P.; Frenking, G. Chemical Bonding and Bonding Models of Main-Group Compounds. Chem. Rev. 2019, 119, 8781–8845. [Google Scholar] [CrossRef] [PubMed]
- Pauzat, F.; Ellinger, Y. H3+ as a trap for noble gases: 1—The case of Argon. Planet. Space Sci. 2005, 53, 1389–1399. [Google Scholar] [CrossRef]
- Pauzat, F.; Ellinger, Y. H3+ as a trap for noble gases-2: structure and energetics of XH3+ complexes from X= neon to xenon. J. Chem. Phys. 2007, 127, 014308. [Google Scholar] [CrossRef] [PubMed]
- Pauzat, F.; Ellinger, Y.; Pilmé, J.; Mousis, O. H3+ as a trap for noble gases-3: Multiple trapping of neon, argon, and krypton in XnH3+(n= 1–3). J. Chem. Phys. 2009, 130, 174313. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, A.; Giri, S.; Chattaraj, P.K. Trapping of noble gases (He–Kr) by the aromatic H3+ and Li3+ species: a conceptual DFT approach. New J. Chem. 2010, 34, 1936–1945. [Google Scholar] [CrossRef]
- Jana, G.; Pan, S.; Rodríguez-Kessler, P.L.; Merino, G.; Chattaraj, P.K. Adsorption of Molecular Hydrogen on Lithium-Phosphorus Double-Helices. J. Phys. Chem. C 2018, 122, 27941–27946. [Google Scholar] [CrossRef]
- Pan, S.; Giri, S.; Chattaraj, P.K. A Computational study on the hydrogen adsorption capacity of various lithium-doped boron hydrides. J. Comp. Chem. 2012, 33, 425–434. [Google Scholar] [CrossRef]
- Pan, S.; Banerjee, S.; Chattaraj, P.K. Role of Lithium Decoration on Hydrogen Storage. J. Mex. Chem. Soc. 2012, 56, 229–240. [Google Scholar] [CrossRef]
- Pan, S.; Merino, G.; Chattaraj, P.K. Hydrogen Trapping Potential of Some Li-doped Star-like Clusters and Super-alkali Systems. Phys. Chem. Chem. Phys. 2012, 14, 10345–10350. [Google Scholar] [CrossRef]
- Saha, R.; Pan, S.; Chattaraj, P.K. Hydrogen storage in all-metal and non-metal aromatic clusters. In Emerging Materials for Energy Conversion and Storage; Cheong, K.Y., Impellizzeri, G., Fraga, M.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 329–362. [Google Scholar]
- Perez-Peralta, N.; Contreras, M.; Tiznado, W.; Stewart, J.; Donald, K.J.; Merino, G. Stabilizing carbon-lithium stars. Phys. Chem. Chem. Phys. 2011, 13, 12975–12980. [Google Scholar] [CrossRef]
- Tong, J.; Li, Y.; Wu, D.; Li, Z.-R.; Huang, X.-R. Ab Initio Investigation on a New Class of Binuclear Superalkali Cations M2Li2k+1+ (F2Li3+, O2Li5+, N2Li7+, and C2Li9+). J. Phys. Chem. A 2011, 115, 2041–2046. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Contreras, M.; Romero, J.; Reyes, A.; Chattaraj, P.K.; Merino, G. C5Li7+ and O2Li5+ as Noble-Gas-Trapping Agents. Chem. Eur. J. 2013, 19, 2322–2329. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Jalife, S.; Romero, J.; Reyes, A.; Merino, G.; Chattaraj, P.K. Attractive Xe-Li Interaction in Li-Decorated Clusters. Comput. Theor. Chem. 2013, 1021, 62–69. [Google Scholar] [CrossRef]
- Pan, S.; Saha, R.; Gupta, A.; Chattaraj, P.K. Modeling of 1-D Nanowires and analyzing their Hydrogen and Noble Gas Binding Ability. J. Chem. Sci. 2017, 129, 849–858. [Google Scholar] [CrossRef]
- Frenking, G.; Koch, W.; Gauss, J.; Cremer, D. Stabilities and nature of the attractive interactions in HeBeO, NeBeO, and ArBeO and a comparison with analogs NgLiF, NgBN, and NgLiH (Ng = He, Ar). A theoretical investigation. J. Am. Chem. Soc. 1988, 110, 8007–8016. [Google Scholar] [CrossRef]
- Thompson, C.A.; Andrews, L. Noble gas complexes with BeO: infrared spectra of NG-BeO (NG = Ar, Kr, Xe). J. Am. Chem. Soc. 1994, 116, 423–424. [Google Scholar] [CrossRef]
- Linguerri, R.; Komiha, N.; Hochlaf, M. Solvation effects and stabilization of multicharged ions: a case study of ArmBeOq+ complexes. Phys. Chem. Chem. Phys. 2012, 14, 4236–4243. [Google Scholar] [CrossRef]
- Pan, S.; Jalife, S.; Kumar, R.M.; Subramanian, V.; Merino, G.; Chattaraj, P.K. Structure and Stability of (NG)nCN3Be3+ Clusters and Comparison with (NG)BeY0/+. Chem. Phys. Chem. 2013, 14, 2511–2517. [Google Scholar] [CrossRef]
- Pan, S.; Moreno, D.; Cabellos, J.L.; Merino, G.; Chattaraj, P.K. Ab initio study on the stability of NgnBe2N2, NgnBe3N2 and NgBeSiN2 Clusters. Chem. Phys. Chem. 2014, 15, 2618–2625. [Google Scholar] [CrossRef]
- Borocci, S.; Bronzolino, N.; Grandinetti, F. From OBeHe to H3BOBeHe: Enhancing the stability of a neutral helium compound. Chem. Phys. Lett. 2005, 406, 179–183. [Google Scholar] [CrossRef]
- Pan, S.; Moreno, D.; Cabellos, J.L.; Romero, J.; Reyes, A.; Merino, G.; Chattaraj, P.K. In quest of strong Be–Ng bonds among the neutral Ng–Be complexes. J. Phys. Chem. A 2013, 118, 487–494. [Google Scholar] [CrossRef] [PubMed]
- Saha, R.; Pan, S.; Merino, G.; Chattaraj, P.K. Comparative Study on the Noble-Gas Binding Ability of BeX Clusters (X = SO4, CO3, O). J. Phys. Chem. A 2015, 119, 6746–6752. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Ghara, M.; Ghosh, S.; Chattaraj, P.K. Noble gas bound beryllium chromate and beryllium hydrogen phosphate: a comparison with noble gas bound beryllium oxide. RSC Adv. 2016, 6, 92786–92794. [Google Scholar] [CrossRef]
- Pan, S.; Saha, R.; Chattaraj, P.K. On the stability of noble gas bound 1-tris (pyrazolyl) borate beryllium and magnesium complexes. New J. Chem. 2015, 39, 6778–6786. [Google Scholar] [CrossRef]
- Saha, R.; Pan, S.; Chattaraj, P.K. NgMCp+: Noble Gas Bound Half-Sandwich Complexes (Ng= He–Rn, M= Be–Ba, and Cp = η5-C5H5). J. Phys. Chem. A 2017, 121, 3526–3539. [Google Scholar] [CrossRef] [PubMed]
- Saha, R.; Pan, S.; Mandal, S.; Orozco, M.; Merino, G.; Chattaraj, P.K. Noble gas supported B3+ cluster: formation of strong covalent noble gas–boron bonds. RSC Adv. 2016, 6, 78611–78620. [Google Scholar] [CrossRef]
- Li, Z.Z.; Li, A.Y. (Rg= He∼Rn, n= 1–4): In quest of the potential trapping ability of the aromatic ring. Int. J. Quantum Chem. 2018, 118, e25530. [Google Scholar] [CrossRef]
- Li, Z.Z.; Li, A.Y. Monocyclic aromatic compounds BnRgn(n−2)+ of boron and rare gases. Phys. Chem. Chem. Phys. 2017, 19, 19109–19119. [Google Scholar] [CrossRef]
- Huang, Y.H.; Li, Z.Z.; Li, A.Y. Hexagonal boron-noble gas compounds B6Ngn4+: Structures and bonding. Chem. Phys. Lett. 2017, 689, 82–91. [Google Scholar] [CrossRef]
- Pan, S.; Moreno, D.; Merino, G.; Chattaraj, P.K. Stability of Noble-Gas-Bound SiH3+ Clusters. Chem. Phys. Chem. 2014, 15, 3554–3564. [Google Scholar] [CrossRef]
- Pan, S.; Moreno, D.; Ghosh, S.; Chattaraj, P.K.; Merino, G. Structure and stability of noble gas bound compounds (E = C, Ge, Sn, Pb; X= H, F, Cl, Br). J. Comput. Chem. 2016, 37, 226–236. [Google Scholar] [CrossRef] [PubMed]
- Ghara, M.; Pan, S.; Kumar, A.; Merino, G.; Chattaraj, P.K. Structure, Stability, and Nature of Bonding in Carbon Monoxide bound EX3+ Complexes (E = Group 14 element; X = H, F, Cl, Br, I). J. Comp. Chem. 2016, 37, 2202–2211. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, D.; Chattaraj, P.K. In quest of a superhalogen supported covalent bond involving a noble gas atom. J. Phys. Chem. A 2015, 119, 3064–3074. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Saha, R.; Mandal, S.; Chattaraj, P.K. σ-Aromatic cyclic M3+ (M = Cu, Ag, Au) clusters and their complexation with dimethyl imidazol-2-ylidene, pyridine, isoxazole, furan, noble gases and carbon monoxide. Phys. Chem. Chem. Phys. 2016, 18, 11661–11676. [Google Scholar] [CrossRef] [PubMed]
- Ghara, M.; Pan, S.; Deb, J.; Kumar, A.; Sarkar, U.; Chattaraj, P.K. A computational study on structure, stability and bonding in Noble Gas bound metal Nitrates, Sulfates and Carbonates (Metal = Cu, Ag, Au). J. Chem. Sci. 2016, 128, 1537–1548. [Google Scholar] [CrossRef]
- Pan, S.; Gupta, A.; Saha, R.; Merino, G.; Chattaraj, P.K. A coupled-cluster study on the noble gas binding ability of metal cyanides versus metal halides (metal = Cu, Ag, Au). J. Comput. Chem. 2015, 36, 2168–2176. [Google Scholar] [CrossRef]
- Pan, S.; Saha, R.; Kumar, A.; Gupta, A.; Merino, G.; Chattaraj, P.K. A noble interaction: An assessment of noble gas binding ability of metal oxides (metal = Cu, Ag, Au). Int. J. Quantum Chem. 2016, 116, 1016–1024. [Google Scholar] [CrossRef]
- Jana, G.; Pan, S.; Chattaraj, P.K. Binding of Small Gas Molecules by Metal–Bipyridyl Monocationic Complexes (Metal = Cu, Ag, Au) and Possible Bond Activations Therein. J. Phys. Chem. A 2017, 121, 3803–3817. [Google Scholar] [CrossRef] [PubMed]
- Jana, G.; Saha, R.; Pan, S.; Kumar, A.; Merino, G.; Chattaraj, P.K. Noble Gas Binding Ability of Metal-Bipyridine Monocationic Complexes (Metal = Cu, Ag, Au): A Computational Study. ChemistrySelect 2016, 1, 5842–5849. [Google Scholar] [CrossRef]
- Pan, S.; Jana, G.; Merino, G.; Chattaraj, P.K. Noble-Noble Strong Union: Gold at Its Best to Make a Bond with a Noble Gas Atom. ChemistryOpen 2019, 8, 173–187. [Google Scholar] [CrossRef]
- Li, T.-H.; Liu, Y.-L.; Lin, R.-J.; Yeh, T.-Y.; Hu, W.-P. On the stability of noble gas molecules. Chem. Phys. Lett. 2007, 434, 38–41. [Google Scholar] [CrossRef]
- Perez-Peralta, N.; Juarez, R.; Cerpa, E.; Bickelhaupt, F.M.; Merino, G. Bonding of Xenon Hydrides. J. Phys. Chem. A 2009, 113, 9700–9706. [Google Scholar] [CrossRef] [PubMed]
- Juarez, R.; Zavala-Oseguera, C.; Jimenez-Halla, J.O.C.; Bickelhaupt, F.M.; Merino, G. Radon hydrides: structure and bonding. Phys. Chem. Chem. Phys. 2011, 13, 2222–2227. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Saha, R.; Chattaraj, P. Exploring the nature of silicon-noble gas bonds in H3SiNgNSi and HSiNgNSi compounds (Ng = Xe, Rn). Int. J. Mol. Sci. 2015, 16, 6402–6418. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Gupta, A.; Mandal, S.; Moreno, D.; Merino, G.; Chattaraj, P.K. Metastable behavior of noble gas inserted tin and lead fluorides. Phys. Chem. Chem. Phys. 2015, 17, 972–982. [Google Scholar] [CrossRef] [PubMed]
- Samanta, D. Prediction of superhalogen-stabilized noble gas compounds. J. Phys. Chem. Lett. 2014, 5, 3151–3156. [Google Scholar] [CrossRef]
- Saha, R.; Mandal, B.; Chattaraj, P.K. HNgBeF3 (Ng= Ar-Rn): Superhalogen-supported noble gas insertion compounds. Int. J. Quantum Chem. 2018, 118, e25499. [Google Scholar] [CrossRef]
- Pan, S.; Jana, G.; Ravell, E.; Zarate, X.; Osorio, E.; Merino, G.; Chattaraj, P.K. Stable NCNgNSi (Ng=Kr, Xe, Rn) Compounds with Covalently Bound C-Ng-N Unit: Possible Isomerization of NCNSi through the Release of the Noble Gas Atom. Chem. Eur. J. 2018, 24, 2879–2887. [Google Scholar] [CrossRef]
- Mondal, S.; Cabellos, J.L.; Pan, S.; Osorio, E.; Torres-Vega, J.J.; Tiznado, W.; Restrepo, A.; Merino, G. 10-π-Electron arenes à la carte: structure and bonding of the [E–(CnHn)–E]n−6 (E = Ca, Sr, Ba; n = 6–8) complexes. Phys. Chem. Chem. Phys. 2016, 18, 11909–11918. [Google Scholar] [CrossRef]
- Wang, Q.; Pan, S.; Lei, S.; Jin, J.; Deng, G.; Wang, G.; Zhao, L.; Zhou, M.; Frenking, G. Octa-coordinated alkaline earth metal–dinitrogen complexes M(N2)8 (M = Ca, Sr, Ba). Nat. Commun. 2019, 10, 3375. [Google Scholar] [CrossRef]
- Jana, G.; Pan, S.; Merino, G.; Chattaraj, P.K. Noble Gas Inserted Metal Acetylides (Metal= Cu, Ag, Au). J. Phys. Chem. A 2018, 122, 7391–7401. [Google Scholar] [CrossRef] [PubMed]
- Jana, G.; Pan, S.; Merino, G.; Chattaraj, P.K. MNgCCH (M= Cu, Ag, Au; Ng= Xe, Rn): The First Set of Compounds with M–Ng–C Bonding Motif. J. Phys. Chem. A 2017, 121, 6491–6499. [Google Scholar] [CrossRef] [PubMed]
- Jana, G.; Pan, S.; Osorio, E.; Zhao, L.; Merino, G.; Chattaraj, P.K. Cyanide–isocyanide isomerization: stability and bonding in noble gas inserted metal cyanides (metal= Cu, Ag, Au). Phys. Chem. Chem. Phys. 2018, 20, 18491–18502. [Google Scholar] [CrossRef] [PubMed]
- Yoshizawa, M.; Tamura, M.; Fujita, M. Diels-Alder in Aqueous Molecular Hosts: Unusual regioselectivity and Efficient Catalysis. Science 2006, 312, 251–254. [Google Scholar]
- Krapp, A.; Frenking, G. Is this a chemical bond? a theoretical study of Ng2@C60 (Ng= He, Ne, Ar, Kr, Xe). Chem. Eur. J. 2007, 13, 8256–8270. [Google Scholar] [CrossRef] [PubMed]
- Khatua, M.; Pan, S.; Chattaraj, P.K. Movement of Ng2 molecules confined in a C60 cage: an ab initio molecular dynamics study. Chem. Phys. Lett. 2014, 610, 351–356. [Google Scholar] [CrossRef]
- Kroto, H.W. The Stability of the Fullerenes Cn, with n = 24, 28, 32, 25, 36, 50, 60 and 70. Nature 1987, 329, 529–531. [Google Scholar] [CrossRef]
- Jalife, S.; Mondal, S.; Cabellos, J.L.; Pan, S.; Méndez-Rojas, M.A.; Fernández, I.; Frenking, G.; Merino, G. Breaking the isolated pentagon rule by encapsulating Xe2 in C60: The guest defines the shape of the host. ChemistrySelect 2016, 1, 2405–2408. [Google Scholar] [CrossRef]
- Cerpa, E.; Krapp, A.; Flores-Moreno, R.; Donald, K.J.; Merino, G. Influence of endohedral confinement on the electronic interaction between He atoms: A He2@C20H20 case study. Chem. Eur. J. 2009, 15, 1985–1990. [Google Scholar] [CrossRef]
- Cerpa, E.; Krapp, A.; Vela, A.; Merino, G. The implications of symmetry of the external potential on bond paths. Chem. Eur. J. 2008, 14, 10232–10234. [Google Scholar] [CrossRef]
- Khatua, M.; Pan, S.; Chattaraj, P.K. Confinement induced binding of noble gas atoms. J. Chem. Phys. 2014, 140, 164306. [Google Scholar] [CrossRef]
- Mondal, S.; Chattaraj, P.K. Noble gas encapsulation: clathrate hydrates and their HF doped analogues. Phys. Chem. Chem. Phys. 2014, 16, 17943–17954. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Jana, G.; Gupta, A.; Merino, G.; Chattaraj, P.K. Endohedral Gas Adsorption by Cucurbit[7]uril: A Theoretical Study. Phys. Chem. Chem. Phys 2017, 19, 24448–24452. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Saha, R.; Mandal, S.; Mondal, S.; Gupta, A.; Fernández, H.M.; Merino, G.; Chattaraj, P.K. Selectivity in Gas Adsorption by Molecular Cucurbit[6]uril. J. Phys. Chem. C 2016, 120, 13911–13921. [Google Scholar] [CrossRef]
- Pan, S.; Mondal, S.; Chattaraj, P.K. Cucurbiturils as Promising Hydrogen Storage Materials: A Case Study of Cucurbit[7]uril. New J. Chem. 2013, 37, 2492–2499. [Google Scholar] [CrossRef]
- Pan, S.; Mandal, S.; Chattaraj, P.K. Cucurbit [6] uril: a possible host for noble gas atoms. J. Phys. Chem. B 2015, 119, 10962–10974. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, D.; Pan, S.; Chattaraj, P.K. Encapsulation of small gas molecules and rare gas atoms inside the octa acid cavitand. Theor. Chem. Acc. 2016, 135, 119. [Google Scholar] [CrossRef]
- Chakraborty, D.; Chattaraj, P.K. Confinement induced binding in noble gas atoms within a BN-doped carbon nanotube. Chem. Phys. Lett. 2015, 621, 29–34. [Google Scholar] [CrossRef]
- Pan, S.; Ghara, M.; Kar, S.; Zarate, X.; Merino, G.; Chattaraj, P.K. Noble gas encapsulated B40 cage. Phys. Chem. Chem. Phys. 2018, 20, 1953–1963. [Google Scholar] [CrossRef]
- Hua-Jin, Z.; Jin-Chang, G.; Lin-Yan, F.; Ying-Jin, W.; Jalife, S.; Vásquez-Espinal, A.; Cabellos, J.L.; Pan, S.; Merino, G. Triple Coaxial- layered versus helical Be6B11− cluster: dual structural fluxionality and multifold aromaticity. Angew. Chem. Int. Ed. 2017, 129, 10308–10311. [Google Scholar]
- Saha, R.; Kar, S.; Pan, S.; Martínez-Guajardo, G.; Merino, G.; Chattaraj, P.K. A spinning umbrella: carbon monoxide and dinitrogen bound MB12− clusters (M = Co, Rh, Ir). J. Phys. Chem. A 2017, 121, 2971–2979. [Google Scholar] [CrossRef]
- Jalife, S.; Liu, L.; Pan, S.; Cabellos, J.L.; Osorio, E.; Lu, C.; Heine, T.; Donald, K.J.; Merino, G. Dynamical behavior of boron clusters. Nanoscale 2016, 8, 17639–17644. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Moreno, D.; Osorio, E.; Castro, A.C.; Pan, S.; Chattaraj, P.K.; Heine, T.; Merino, G. Structure and bonding of IrB12−: Converting a rigid boron B12 platelet to a Wankel motor. RSC Adv. 2016, 6, 27177–27182. [Google Scholar] [CrossRef]
- Moreno, D.; Pan, S.; Martínez-Guajardo, G.; Lei-Zeonjuk, L.; Islas, R.; Osorio, E.; Chattaraj, P.K.; Heine, T.; Merino, G. B182−: A quasi-planar bowl member of the Wankel motor family. Chem. Commun. 2014, 50, 8140–8143. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Guajardo, G.; Cabellos, J.L.; Diaz-Celaya, A.; Pan, S.; Islas, R.; Chattaraj, P.K.; Heine, T.; Merino, G. Dynamical behavior of borospherene: A nanobubble. Sci. Rep. 2015, 5, 11287. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, D.; Chattaraj, P.K. Bonding, Reactivity and Dynamics in Confined Systems. J. Phys. Chem. A 2019, 123, 4513–4531. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, R.; Jana, G.; Pan, S.; Merino, G.; Chattaraj, P.K. How Far Can One Push the Noble Gases Towards Bonding?: A Personal Account. Molecules 2019, 24, 2933. https://doi.org/10.3390/molecules24162933
Saha R, Jana G, Pan S, Merino G, Chattaraj PK. How Far Can One Push the Noble Gases Towards Bonding?: A Personal Account. Molecules. 2019; 24(16):2933. https://doi.org/10.3390/molecules24162933
Chicago/Turabian StyleSaha, Ranajit, Gourhari Jana, Sudip Pan, Gabriel Merino, and Pratim Kumar Chattaraj. 2019. "How Far Can One Push the Noble Gases Towards Bonding?: A Personal Account" Molecules 24, no. 16: 2933. https://doi.org/10.3390/molecules24162933
APA StyleSaha, R., Jana, G., Pan, S., Merino, G., & Chattaraj, P. K. (2019). How Far Can One Push the Noble Gases Towards Bonding?: A Personal Account. Molecules, 24(16), 2933. https://doi.org/10.3390/molecules24162933






