The High Efficiency of Anionic Dye Removal Using Ce-Al13/Pillared Clay from Darbandikhan Natural Clay
Abstract
1. Introduction
2. Materials and Methods
2.1. Adsorbate
2.2. Adsorbents
2.2.1. Acid-Activated Clay
2.2.2. Ce-Al13/Pillared Clay
2.3. Adsorbent Characterization
2.4. Adsorption Studies
3. Results and Discussion
3.1. Characterization of the Adsorbent
3.2. Adsorption Studies
3.2.1. Operational Condition Effects
3.2.2. Adsorption Kinetics
3.2.3. Adsorption Isotherms
3.2.4. Adsorption Thermodynamics
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- He, X.Y.; Male, K.B.; Nesterenko, P.N.; Brabazon, D.; Paull, B.; Luong, J.H.T. Adsorption and Desorption of Methylene Blue on Porous Carbon Monoliths and Nanocrystalline Cellulose Adsorption and Desorption of Methylene Blue on Porous Carbon Monoliths and Nanocrystalline Cellulose. ACS Appl. Mater. Interfaces 2013, 5, 8796–8804. [Google Scholar] [CrossRef] [PubMed]
- Piccin, J.S.; Feris, L.A.; Cooper, M.; Gutterres, M. Dye adsorption by leather waste: Mechanism diffusion, nature studies, and thermodynamic data. J. Chem. Eng. Data 2013, 58, 873–882. [Google Scholar] [CrossRef]
- Demey, H.; Melkior, T.; Chatroux, A.; Attar, K.; Thiery, S.; Miller, H.; Grateau, M.; Sastre, A.M.; Marchand, M. Evaluation of torre fi ed poplar-biomass as a low-cost sorbent for lead and terbium removal from aqueous solutions and energy co-generation. Chem. Eng. J. 2019, 361, 839–852. [Google Scholar] [CrossRef]
- Demey, H.; Tria, S.A.; Soleri, R.; Guiseppi-elie, A.; Bazin, I. Sorption of his-tagged Protein G and Protein G onto chitosan/divalent metal ion sorbent used for detection of microcystin-LR. Environ. Sci. Pollut. Res. 2017, 24, 15–24. [Google Scholar] [CrossRef] [PubMed]
- Ge, M.; Xi, Z.; Zhu, C.; Liang, G.; Hu, G. Preparation and Characterization of Magadiite—Magnetite Nanocomposite with Its Sorption Performance Analyses on Removal of Methylene Blue from Aqueous Solutions. Polymers 2019, 11, 607. [Google Scholar] [CrossRef] [PubMed]
- Attar, K.; Bouazza, D.; Miloudi, H.; Tayeb, A.; Boos, A.; Sastre, A.M.; Demey, H.P.T. Cadmium Removal by A Low-Cost Magadiite-Based Material: Characterization and Sorption Applications. J. Environ. Chem. Eng. 2018, 6, 5351–5360. [Google Scholar] [CrossRef]
- Kamal, B.; Ahmed, B.; Amin, H. Suitabilty of the Twelve-Emam natural clay for the synthesis of Al 13, and (Fe, Li)/Al Pillared-clay nanoparticles Abstract. In Proceedings of the 4th International Conference on Nanostructures, Bandar Lengeh, Iran, 12–14 March 2012. [Google Scholar]
- Mokaya, R.; Jones, W. Pillared Acid-activated Clay Catalysts. J. Chem. Soc. Chem. Commun. 1994, 8, 929–930. [Google Scholar] [CrossRef]
- Yildiz, N.; Çalimli, A. Alteration of Three Turkish Bentonites by Treatment with Na2CO3 and H2SO4. Turk. J. Chem. 2002, 26, 393–401. [Google Scholar]
- Yurdakoc, M.K. Nonyl-and Dodecylamines Intercalated Bentonite and Illite from Turkey. Turk. J. Chem. 1999, 23, 105–113. [Google Scholar]
- Duong, L.V.; Kloprogge, J.T.; Frost, R.L.; Van Veen, J.A.R. An improved route for the synthesis of Al13-pillared montmorillonite catalysts. J. Porous Mater. 2007, 14, 71–79. [Google Scholar] [CrossRef]
- Kaufhold, S.; Decher, A. Natural Acidic Bentonites from the Island of Milos, Greece. Z. Angew. Geol 2003, 49, 7–12. [Google Scholar]
- De León, M.A.; De Los Santos, C.; Latrónica, L.; Cesio, A.M.; Volzone, C.; Castiglioni, J.; Sergio, M. High catalytic activity at low temperature in oxidative dehydrogenation of propane with Cr-Al pillared clay. Chem. Eng. J. 2014, 241, 336–343. [Google Scholar] [CrossRef]
- González, F.; Pesquera, C.; Blanco, C.; Benito, I.; Mendioroz, S. Synthesis and Characterization of Al-Ga Pillared Clays with High Thermal and Hydrothermal Stability. Inorg. Chem. 1992, 31, 727–731. [Google Scholar] [CrossRef]
- Timofeeva, M.N.; Khankhasaeva, S.T.; Chesalov, Y.A.; Tsybulya, S.V.; Panchenko, V.N.; Dashinamzhilova, E.T. Synthesis of Fe, Al-pillared clays starting from the Al, Fe-polymeric precursor: Effect of synthesis parameters on textural and catalytic properties. Appl. Catal. B Environ. 2009, 88, 127–134. [Google Scholar] [CrossRef]
- Ajibola, A.; Idowu, A.; Adeoye, O.; Solomon, O. Adsorption of dyes using different types of clay: A review. Appl. Water Sci. 2017, 7, 543–568. [Google Scholar]
- Elmoubarki, R.; Mahjoubi, F.Z.; Tounsadi, H.; Moustadraf, J.; Abdennouri, M.; Zouhri, A.; El Albani, A.; Barka, N. Adsorption of textile dyes on raw and decanted Moroccan clays: Kinetics, equilibrium and thermodynamics. Water Resour. Ind. 2015, 9, 16–29. [Google Scholar] [CrossRef]
- Chen, H.; Zhong, A.; Wu, J.; Zhao, J.; Yan, H. Adsorption behaviors and mechanisms of methyl orange on heat-treated palygorskite clays. Ind. Eng. Chem. Res. 2012, 51, 14026–14036. [Google Scholar] [CrossRef]
- Tang, J.; Yang, Z.F.; Yi, Y.J. Enhanced Adsorption of Methyl Orange by Vermiculite Modified by Cetyltrimethylammonium Bromide (CTMAB). Procedia Environ. Sci. 2012, 13, 2179–2187. [Google Scholar] [CrossRef]
- Huang, R.; Liu, Q.; Huo, J.; Yang, B. Adsorption of methyl orange onto protonated cross-linked chitosan. Arab. J. Chem. 2017, 10, 24–32. [Google Scholar] [CrossRef]
- Tawarah, K.M.; Abu-Shamleh, H.M. A spectrophotometric study of the tautomeric and acid- base equilibria of methyl orange and methyl yellow in aqueous acidic solutions. Dye. Pigment. 1991, 16, 241–251. [Google Scholar] [CrossRef]
- Boolj, E.; Kloprogge, J.T.; Van Veen, J.A.R. Preparation, structural characteristics and catalytic properties of large-pore rare earth element (Ce, La)/A1-pillared smectites. Clays Clay Miner. 1996, 44, 774–782. [Google Scholar]
- Valverde, J.L.; Ca, P.; Sun, M.R.K.; Molina, C.B. Enhanced thermal stability of Al-pillared smectites modified with Ce and La. Clays Clay Miner. 2000, 48, 424–432. [Google Scholar] [CrossRef]
- Thommes, M.; Cychosz, K.A. Advanced Physical Adsorption Characterization of Nanoporous Carbons. In Novel Carbon Adsorbents; Elsevier: Amsterdam, The Netherlands, 2012; ISBN 9780080977447. [Google Scholar]
- Bertier, P.; Schweinar, K.; Stanjek, H.; Ghanizadeh, A.; Clarkson, C.R.; Busch, A.; Kampman, N.; Prinz, D.; Amann, A.; Krooss, B.M.; et al. On the use and abuse of N2 physisorption for the characterization of the pore structure of shales. Clay Miner. Soc. Workshop Lect. Ser. 2016, 21, 151–161. [Google Scholar]
- Meier, L.P. Determination of the Cation Exchange Capacity (CEC) of Clay Minerals Using the Complexes of Copper(II) Ion with Triethylenetetramine and Tetraethylenepentamine. Clays Clay Miner. 2006, 47, 386–388. [Google Scholar] [CrossRef]
- Asgari, M.; Anisi, H.; Mohammadi, H.; Sadighi, S. Designing a commercial scale pressure swing adsorber for hydrogen purification. Pet. Coal 2014, 56, 552–561. [Google Scholar]
- Piccolo, A.; Celano, G.; Pietramellara, G. Adsorption of the herbicide glyphosate on a metal-humic acid complex. Sci. Environ. 1992, 124, 77–82. [Google Scholar] [CrossRef]
- Kannan, N.; Sundaram, M.M. Kinetics and mechanism of removal of methylene blue by adsorption on various carbons—A comparative study. Dye. Pigment. 2001, 51, 25–40. [Google Scholar] [CrossRef]
- Fil, B.A.; Özmetin, C.; Korkmaz, M. Characterization and electrokinetic properties of montmorillonite. Bulg. Chem. Commun. 2014, 46, 258–263. [Google Scholar]
- Kooli, F.; Khimyak, Y.Z.; Alshahateet, S.F.; Chen, F. Effect of the acid activation levels of montmorillonite clay on the cetyltrimethylammonium cations adsorption. Langmuir 2005, 21, 8717–8723. [Google Scholar] [CrossRef]
- Pesquera, C.; Gonzalez, F.; Blanc, C.; Benito, I.; Mendioroz, S. A1-The effect of pre-heating of pillared clays on the evolution of the acidity. Methods 1993, 219, 179–189. [Google Scholar]
- Yuan, P.; Annabi-bergaya, F.; Tao, Q.; Fan, M.; Liu, Z.; Zhu, J.; He, H. A combined study by XRD, FTIR, TG and HRTEM on the structure of delaminated Fe-intercalated/pillared clay. J. Colloid Interface Sci. 2008, 324, 142–149. [Google Scholar] [CrossRef] [PubMed]
- Plante, A.F.; Fernández, J.M.; Leifeld, J. Application of thermal analysis techniques in soil science. Geoderma 2009, 153, 1–10. [Google Scholar] [CrossRef]
- Kaufhold, S.; Dohrmann, R.; Klinkenberg, M.; Siegesmund, S.; Ufer, K. N2-BET specific surface area of bentonites. J. Colloid Interface Sci. 2010, 349, 275–282. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, H.; Blanco, C.; Gil, A.; Vicente, M.; Galeano, L. Preparation of Al/Fe-Pillared Clays: Effect of the Starting Mineral. Materials 2017, 10, 1364. [Google Scholar] [CrossRef] [PubMed]
- Amari, A.; Gannouni, H.; Khan, M.I.; Almesfer, M.K. Effect of Structure and Chemical Activation on the Adsorption Properties of Green Clay Minerals for the Removal of Cationic Dye. Appl. Sci. 2018, 8, 2302. [Google Scholar] [CrossRef]
- Ai, L.; Zhang, C.; Meng, L. Adsorption of Methyl Orange from Aqueous Solution on Hydrothermal Synthesized Mg À Al Layered Double Hydroxide. J. Chem. Eng. Data 2011, 56, 4217–4225. [Google Scholar] [CrossRef]
- Arshadi, M.; Salimivahid, F.; Salvacion, J.W.L.; Soleymanzadeh, M. Adsorption studies of methyl orange on an immobilized Mn-nanoparticle: Kinetic and thermodynamic. RSC Adv. 2014, 4, 16005–16017. [Google Scholar] [CrossRef]
- Mnasri-Ghnimi, S.; Frini-Srasra, N. Promoting effect of cerium on the characteristic and catalytic activity of Al, Zr, and Al-Zr pillared clay. Appl. Clay Sci. 2014, 88–89, 214–220. [Google Scholar] [CrossRef]
- Attallah, O.A.; Al-Ghobashy, M.A.; Nebsen, M.; Salem, M.Y. Removal of cationic and anionic dyes from aqueous solution with magnetite/pectin and magnetite/silica/pectin hybrid nanocomposites: Kinetic, isotherm and mechanism analysis. RSC Adv. 2016, 6, 11461–11480. [Google Scholar] [CrossRef]
- Nassar, M.Y.; Abdallah, S. Facile controllable hydrothermal route for a porous CoMn2O4 nanostructure: Synthesis, characterization, and textile dye removal from aqueous media. RSC Adv. 2016, 6, 84050–84067. [Google Scholar] [CrossRef]
- Meziti, C.; Boukerroui, A. Removal of a basic textile dye from aqueous solution by adsorption on regenerated clay. Procedia Eng. 2012, 33, 303–312. [Google Scholar] [CrossRef]
- Aksu, Z. Determination of the equilibrium, kinetic and thermodynamic parameters of the batch biosorption of nickel (II) ions onto Chlorella v ulgaris. Process Biochem. 2002, 38, 89–99. [Google Scholar] [CrossRef]
- EL Miz, M.; Salhi, S.; Chraibi, I.; Bachiri, A.E.; Fauconnier, M.; Tahani, A. Characterization and Adsorption Study of Thymol on Pillared Bentonite. Open J. Phys. Chem. 2013, 4, 98–116. [Google Scholar] [CrossRef]
- Khan, A.A.; Singh, R.P. Adsorption Thermodynamics of Carbofuran on Sn (IV) Arsenosilicate in H+ Na+ and Ca2+ Forms. Colloids Surf. 1987, 24, 33–42. [Google Scholar] [CrossRef]
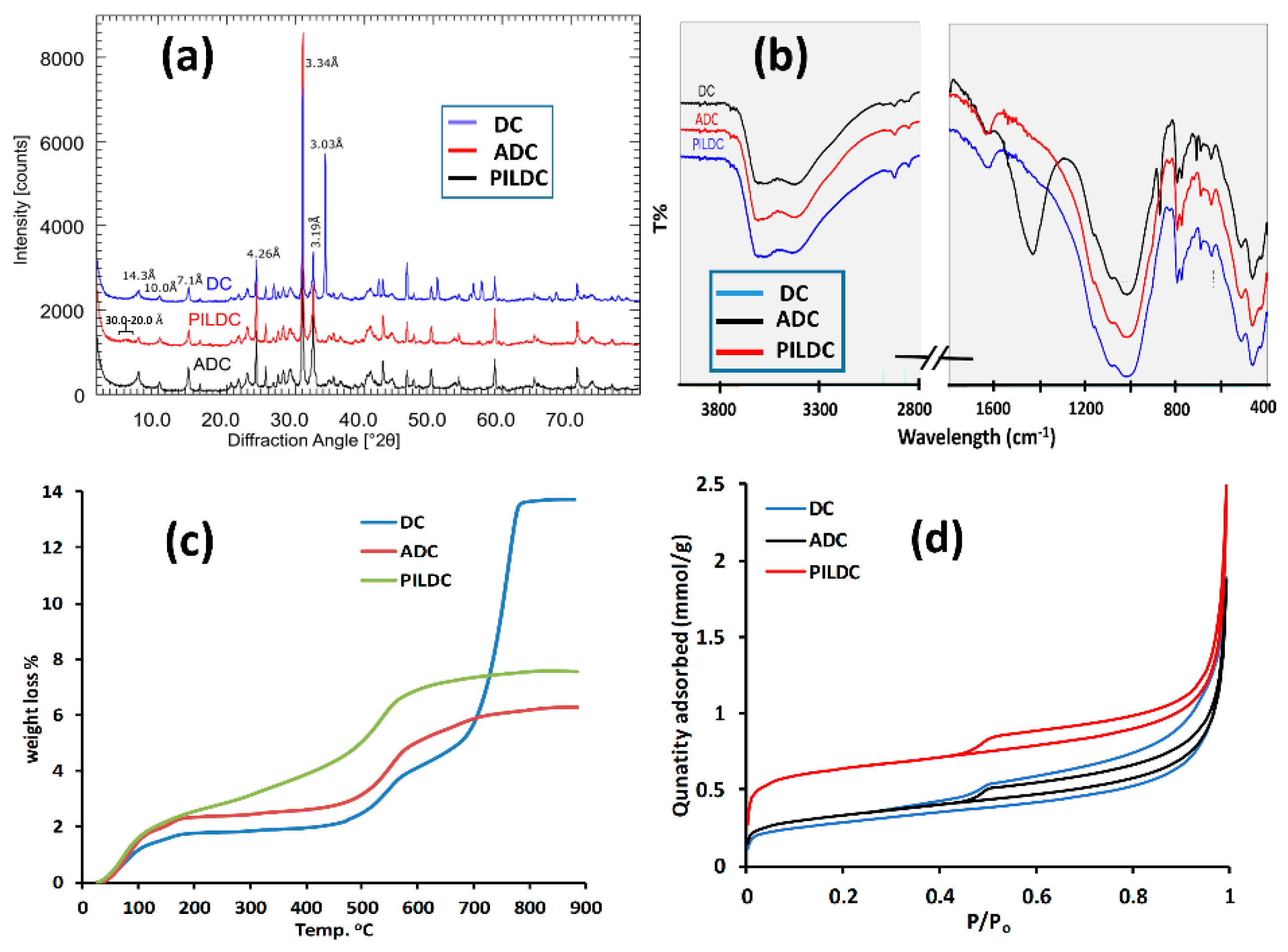
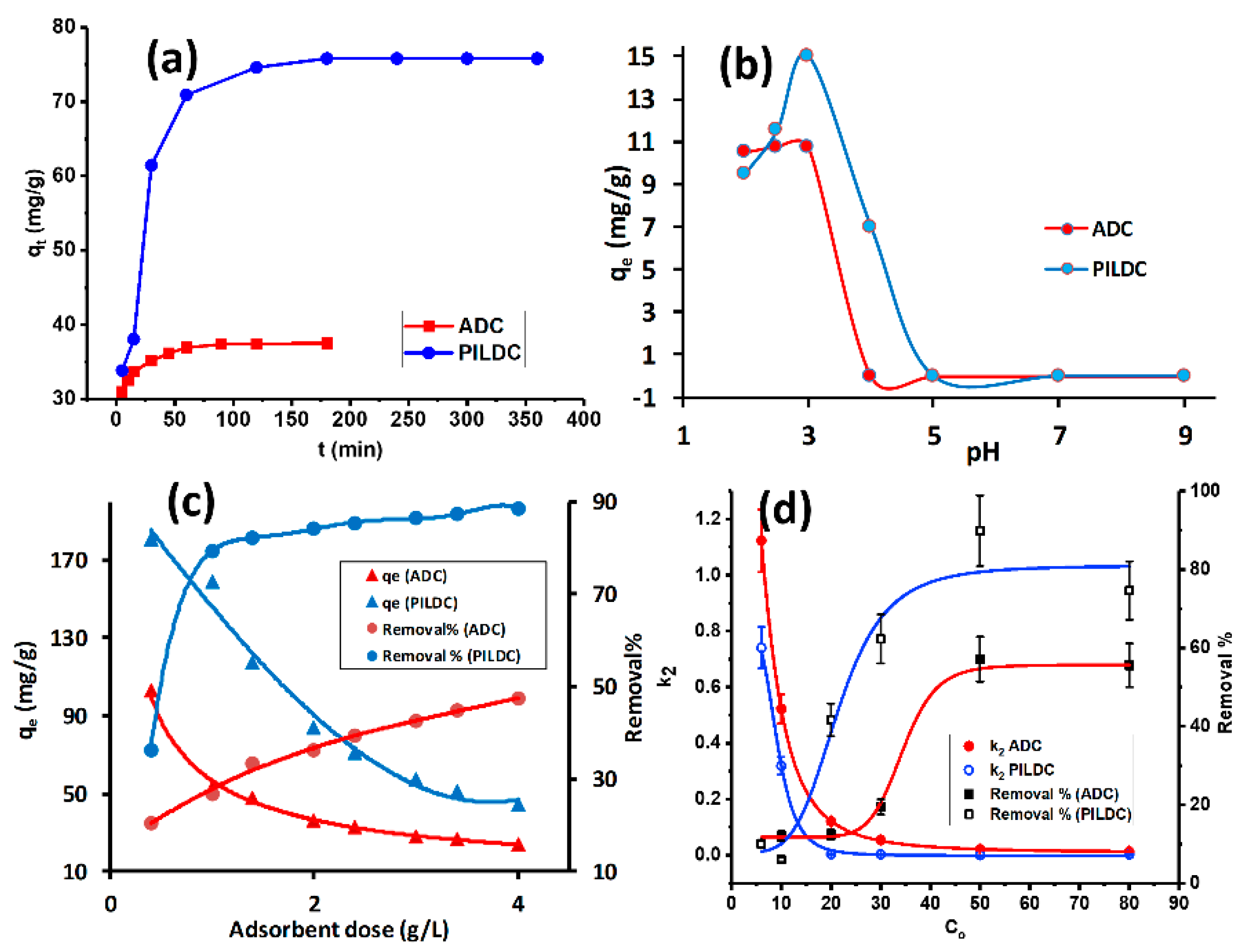

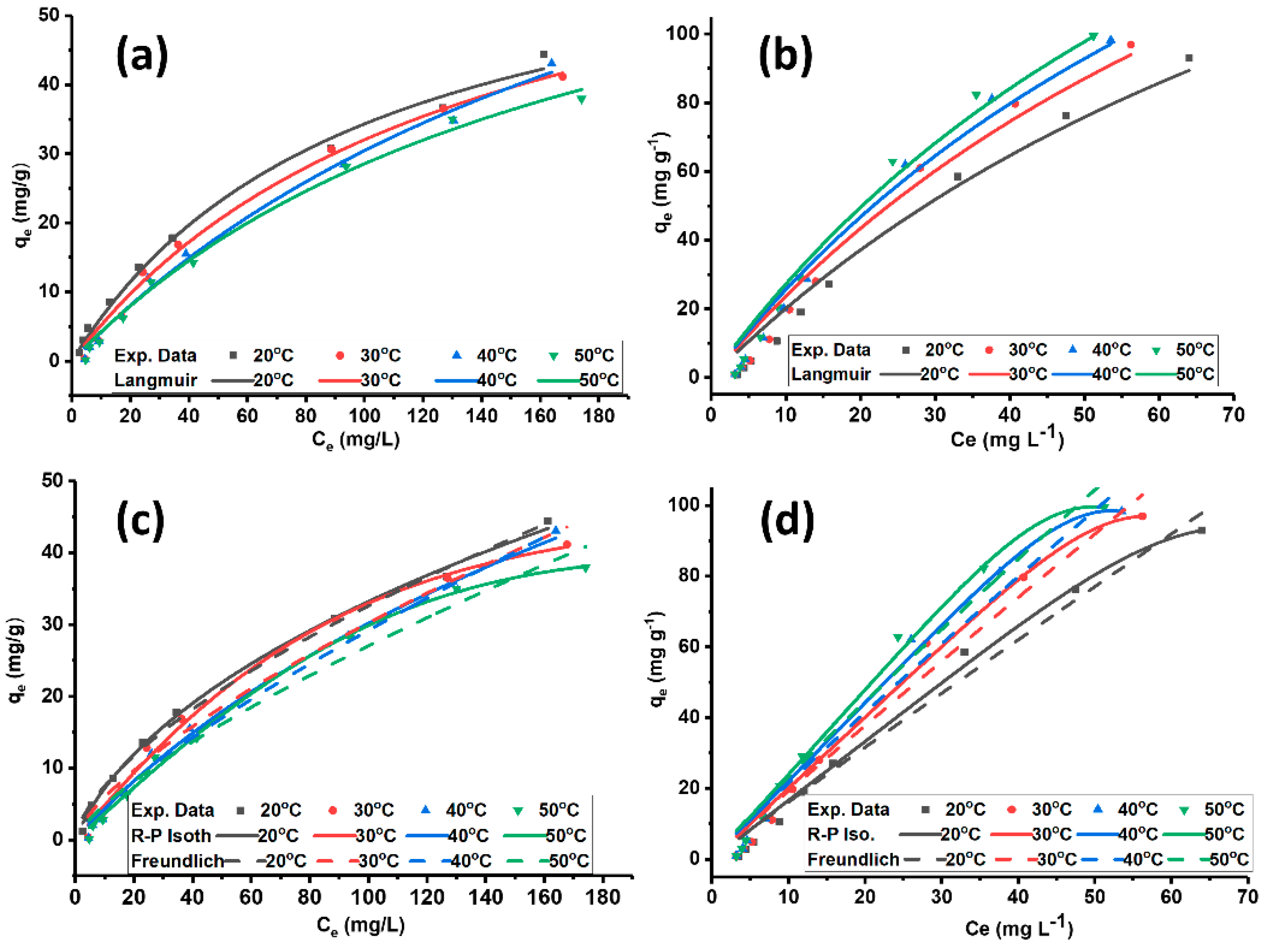
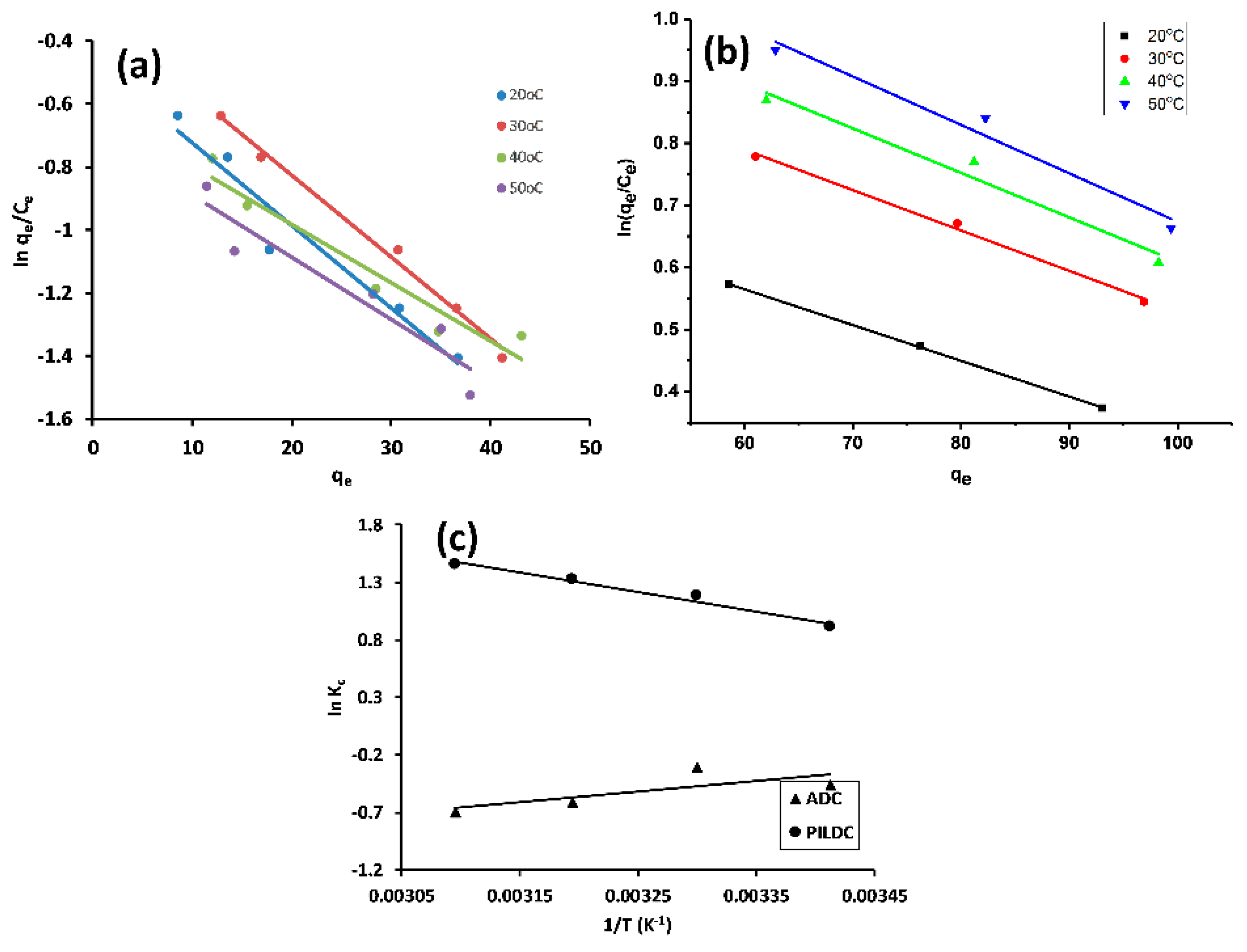
| SiO2% | TiO2% | Al2O3% | Fe2O3% | MnO% | MgO% | CaO% | Na2O% | K2O% | P2O5% | SO3% | LOI | Sum | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DC | 45.4 | 0.8 | 12.5 | 6.2 | 0.1 | 4.3 | 12.0 | 1.5 | 1.9 | 0.1 | 0.04 | 14.9 | 99.7 |
| ADC | 57.4 | 0.9 | 15.6 | 7.5 | 0.1 | 5.0 | 1.3 | 1.9 | 2.4 | 0.1 | <0.01 | 7.5 | 99.7 |
| PILDC | 54.9 | 0.9 | 19.1 | 7.2 | 0.1 | 4.7 | 0.4 | 1.7 | 2.2 | 0.1 | <0.01 | 8.6 | 99.01 |
| Material | SBET (m2·g−1) | t-Plot | Pore Volume | BJH Pore Diameter (nm) | ||
|---|---|---|---|---|---|---|
| S micropore (m2·g−1) | Sext (m2·g−1) | VT (cm3·g−1) | t- Micro Volume (cm3·g−1) | |||
| DC | 22.39 | 9.72 | 12.68 | 0.0652 | 0.00503 | 13.91 |
| ADC | 26.33 | 6.53 | 19.80 | 0.0646 | 0.00290 | 15.78 |
| PILDC | 53.20 | 29.95 | 23.25 | 0.0877 | 0.01210 | 17.46 |
| Kinetics Model | Kinetic Parameters | Temperature (K) | ||||
|---|---|---|---|---|---|---|
| 293 | 303 | 313 | 323 | |||
| ADC | Experimental | qexp (mg/g) | 36.5 | 37.0 | 37.5 | 38.0 |
| Pseudo-first-order | k1(min−1) | 0.3312 | 0.3347 | 0.3631 | 0.3640 | |
| qcalc (mg/g) | 34.26 | 34.99 | 35.89 | 36.92 | ||
| Dev. % of qcalc | 6.1 | 5.4 | 4.3 | 2.8 | ||
| SSE | 27.0 | 23.2 | 17.3 | 12.5 | ||
| R2 | 0.506 | 0.558 | 0.574 | 0.665 | ||
| Pseudo-second-order | k2 | 0.0191 | 0.0196 | 0.0226 | 0.0234 | |
| qcalc | 35.83 | 36.5 | 37.3 | 38.2 | ||
| Dev. % of q | 1.8 | 1.4 | 0.5 | 0.5 | ||
| SSE | 7.9 | 6.5 | 3.4 | 1.5 | ||
| R2 | 0.855 | 0.876 | 0.915 | 0.960 | ||
| PILDC | Experimental | qexp. (mg/g) | 74.5 | 78.6 | 77.0 | 77.0 |
| Pseudo-first-order | k2 | 0.0268 | 0.0528 | 0.0610 | 0.0968 | |
| qcalc (mg/g) | 74.3 | 79.4 | 75.0 | 73.3 | ||
| Dev. % of qcalc | 0.3 | 1.0 | 2.6 | 4.8 | ||
| SSE | 198.9 | 140.5 | 257.9 | 404.9 | ||
| R2 | 0.953 | 0.958 | 0.893 | 0.728 | ||
| Pseudo-second-order | k2 | 4.5 × 10−4 | 9.6 × 10−4 | 13.1 × 10−4 | 24.1 × 10−4 | |
| qm | 82.1 | 84.5 | 78.9 | 76.0 | ||
| Dev. % of qcalc | 10.2 | 7.5 | 2.5 | 1.3 | ||
| SSE | 7.9 | 6.5 | 3.4 | 1.4 | ||
| R2 | 0.987 | 0.991 | 0.931 | 0.843 | ||
| Material | Isotherm | Temp. (K) | 293 | 303 | 313 | 323 |
|---|---|---|---|---|---|---|
| ADC | Langmuir | KL (L/mg) | 0.0102 | 0.0075 | 0.0044 | 0.0056 |
| qm (mg/g) | 68.1 | 75.0 | 100.0 | 79.8 | ||
| SSE | 12.4 | 14.6 | 12.4 | 12.1 | ||
| R2 | 0.994 | 0.993 | 0.994 | 0.993 | ||
| Redlich-Peterson | KRP (L/mg) | 1.23 | 0.49 | 0.48 | 0.37 | |
| αrp (L/mg) | 0.19 | 7.17 | 0.02 | 3 × 10−5 | ||
| β | 0.58 | 1.42 | 0.79 | 1.93 | ||
| SSE | 4.7 | 11.2 | 11.9 | 6.4 | ||
| R2 | 0.998 | 0.994 | 0.994 | 0.996 | ||
| Freundlich | KF (mg/g)(L/mg)1/n | 1.747 | 1.167 | 0.795 | 0.877 | |
| n | 1.57 | 1.42 | 1.28 | 1.34 | ||
| SSE | 9.1 | 44.4 | 17.6 | 33.6 | ||
| R2 | 0.995 | 0.977 | 0.991 | 0.981 | ||
| PILDC | Langmuir | KL (L/mg) | 0.0088 | 0.0098 | 0.0104 | 0.0107 |
| qm (mg/g) | 248.7 | 264.2 | 271.9 | 279.5 | ||
| SSE | 241.2 | 308.7 | 298.5 | 308.4 | ||
| R2 | 0.975 | 0.970 | 0.972 | 0.972 | ||
| Redlich-Peterson | KRP (L/mg) | 1.66 | 2.01 | 2.21 | 2.40 | |
| αrp × 1012 (L/mg) | 5.2 | 0.27 | 0.35 | 9.5 | ||
| Β | 5.8 | 6.7 | 6.8 | 6.1 | ||
| SSE | 96 | 135 | 136 | 154 | ||
| R2 | 0.990 | 0.987 | 0.987 | 0.986 | ||
| Freundlich | KF (mg/g)(L/mg)1/n | 1.844 | 2.193 | 2.628 | 2.979 | |
| n | 1.05 | 1.05 | 1.08 | 1.10 | ||
| SSE | 134.8 | 202.2 | 238.5 | 277.4 | ||
| R2 | 0.984 | 0.978 | 0.975 | 0.971 |
| Acid-Activated Clay (ADC) | Pillared Clay (PILDC) | |||||||
|---|---|---|---|---|---|---|---|---|
| Temp. (K) | Ln Kc | Ln Kc | ||||||
| 293 | −0.458 | 7.86 | 29.86 | −10.54 | 0.911 | 14.03 | 55.74 | −2.30 |
| 303 | −0.307 | −11.17 | 1.180 | −2.86 | ||||
| 313 | −0.695 | −11.79 | 1.325 | −3.42 | ||||
| 323 | −12.42 | 1.454 | −3.97 | |||||
| Adsorbent | qm·(mg·g−1) | Reference |
|---|---|---|
| H-δ-MnO2 nanoparticles | 427.0 | MO 5 |
| PANF-g-HPEI0.6 | 194.0 | MO 7 |
| PED-MIL-101 | 194.0 | MO 8 |
| BFSAP | 167.0 | MO 2 |
| Activated porous carbon | 97.1 | MO 4 |
| Protonated Chitosan | 89.3 | MO 1 |
| surfactant modified silkworm exuvia | 87.0 | MO 6 |
| Fe2O3-BC nanocomposite | 20.5 | MO 3 |
| ADC | 68.1 | This work |
| PILDC | 248.7 | This work |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
K. Aziz, B.; M. Salh, D.; Kaufhold, S.; Bertier, P. The High Efficiency of Anionic Dye Removal Using Ce-Al13/Pillared Clay from Darbandikhan Natural Clay. Molecules 2019, 24, 2720. https://doi.org/10.3390/molecules24152720
K. Aziz B, M. Salh D, Kaufhold S, Bertier P. The High Efficiency of Anionic Dye Removal Using Ce-Al13/Pillared Clay from Darbandikhan Natural Clay. Molecules. 2019; 24(15):2720. https://doi.org/10.3390/molecules24152720
Chicago/Turabian StyleK. Aziz, Bakhtyar, Dler M. Salh, Stephan Kaufhold, and Pieter Bertier. 2019. "The High Efficiency of Anionic Dye Removal Using Ce-Al13/Pillared Clay from Darbandikhan Natural Clay" Molecules 24, no. 15: 2720. https://doi.org/10.3390/molecules24152720
APA StyleK. Aziz, B., M. Salh, D., Kaufhold, S., & Bertier, P. (2019). The High Efficiency of Anionic Dye Removal Using Ce-Al13/Pillared Clay from Darbandikhan Natural Clay. Molecules, 24(15), 2720. https://doi.org/10.3390/molecules24152720





