Thermal Decomposition of Maya Blue: Extraction of Indigo Thermal Decomposition Steps from a Multistep Heterogeneous Reaction Using a Kinetic Deconvolution Analysis
Abstract
1. Introduction
2. Results and Discussion
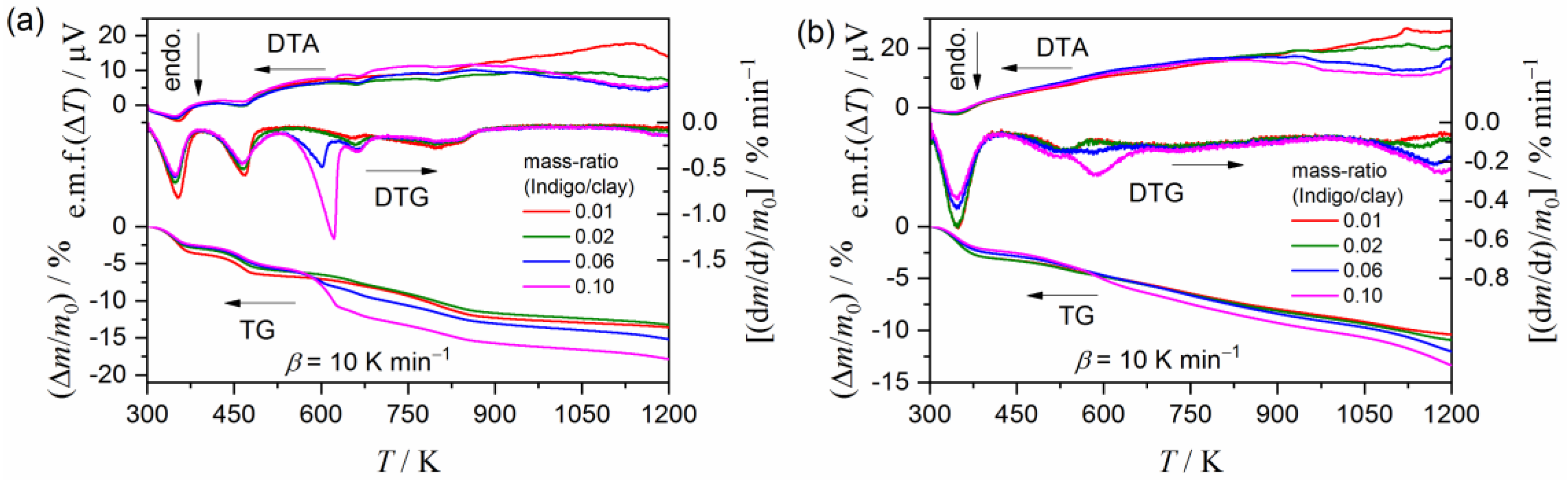
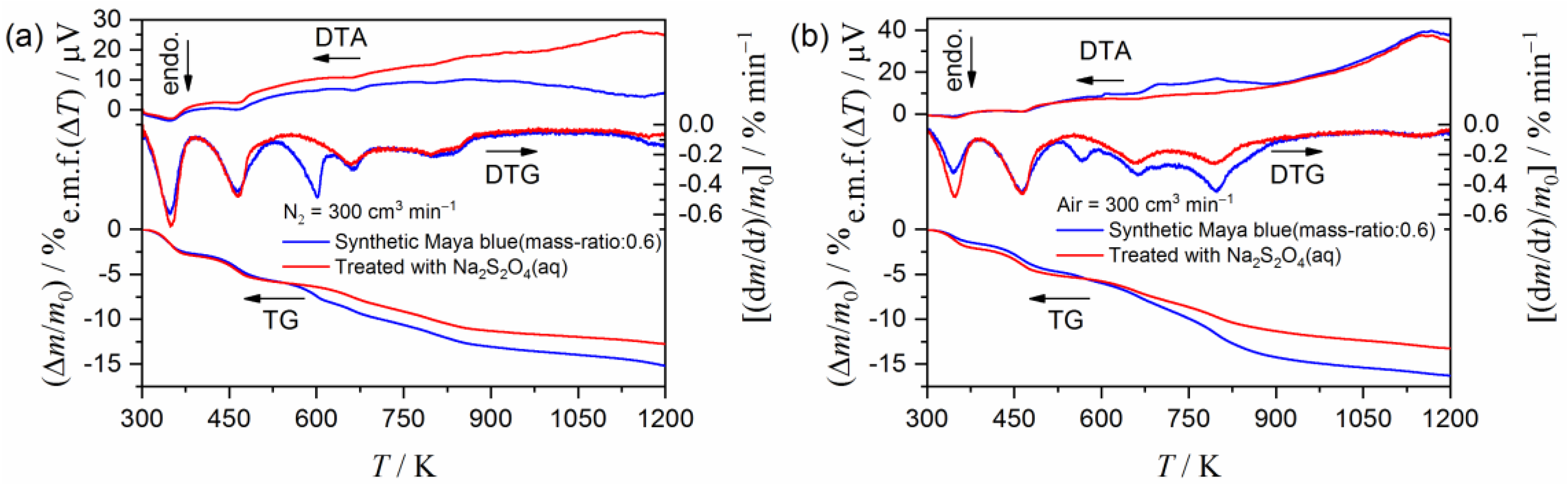
2.1. Sample Preparation and Characterization
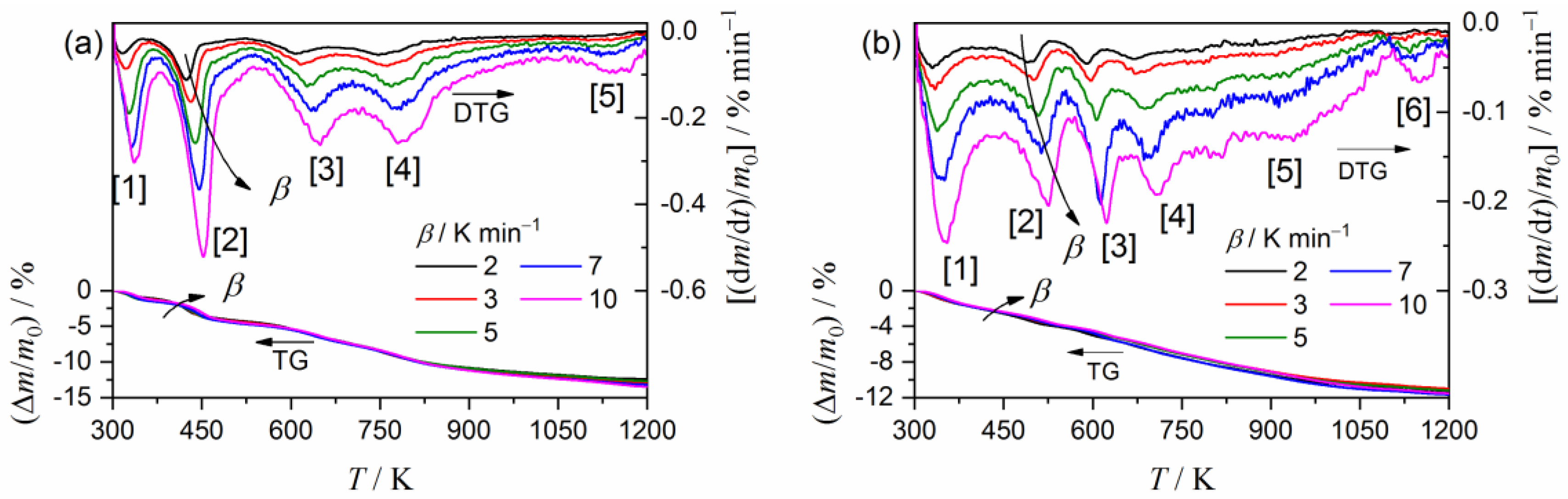
2.2. Kinetic Analysis of the Thermal Decomposition of Clay Minerals
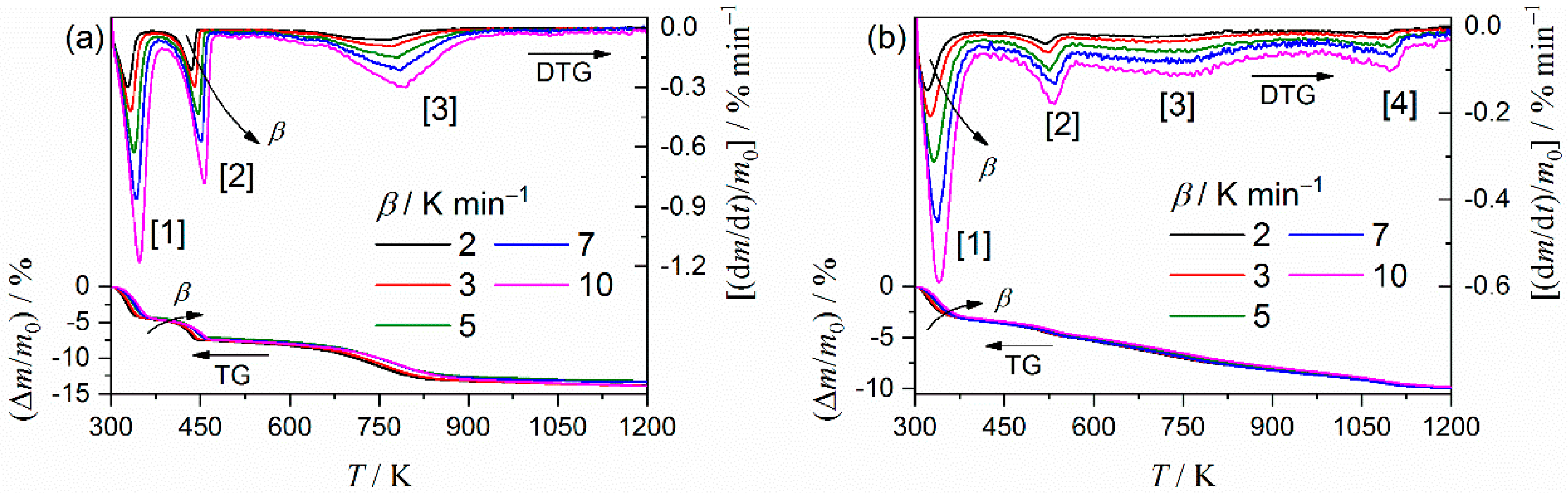
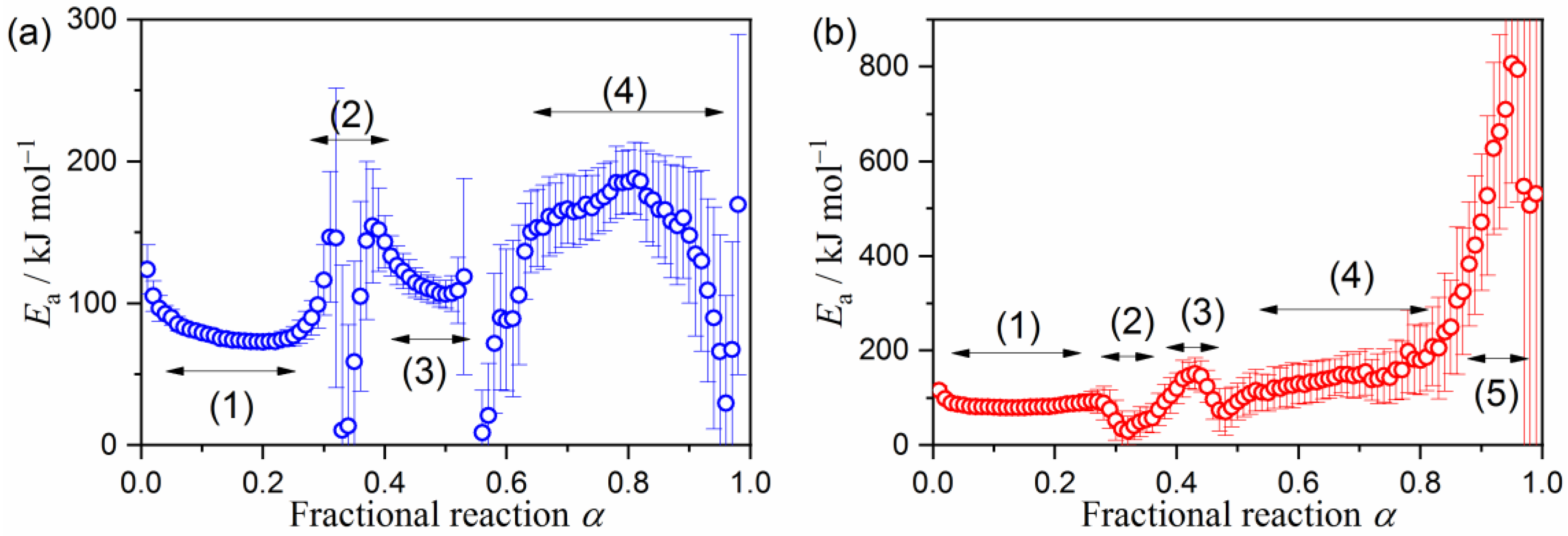
2.3. Kinetic Deconvolution Analysis for the Thermal Decomposition of MB
3. Materials and Methods
3.1. Sample Preparation
3.2. Sample Characterization
3.3. Tracking of the Thermal Decomposition Process
3.4. Measurement of the Kinetic Data for the Thermal Decomposition
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Galwey, A.K.; Brown, M.E. Thermal Decomposition of Ionic Solids; Elsevier: Amsterdam, The Netherlands, 1999; ISBN 9780444824370. [Google Scholar]
- Galwey, A.K. Structure and order in thermal dehydrations of crystalline solids. Thermochim. Acta 2000, 355, 181–238. [Google Scholar] [CrossRef]
- Koga, N.; Tanaka, H. A physico-geometric approach to the kinetics of solid-state reactions as exemplified by the thermal dehydration and decomposition of inorganic solids. Thermochim. Acta 2002, 388, 41–61. [Google Scholar] [CrossRef]
- Kitabayashi, S.; Koga, N. Thermal decomposition of tin(II) oxyhydroxide and subsequent oxidation in air: Kinetic deconvolution of overlapping heterogeneous processes. J. Phys. Chem. C 2015, 119, 16188–16199. [Google Scholar] [CrossRef]
- Nakano, M.; Wada, T.; Koga, N. Exothermic behavior of thermal decomposition of sodium percarbonate: Kinetic deconvolution of successive endothermic and exothermic processes. J. Phys. Chem. A 2015, 119, 9761–9769. [Google Scholar] [CrossRef]
- Muravyev, N.V.; Koga, N.; Meerov, D.B.; Pivkina, A.N. Kinetic analysis of overlapping multistep thermal decomposition comprising exothermic and endothermic processes: Thermolysis of ammonium dinitramide. Phys. Chem. Chem. Phys. 2017, 19, 3254–3264. [Google Scholar] [CrossRef] [PubMed]
- Koga, N.; Kameno, N.; Tsuboi, Y.; Fujiwara, T.; Nakano, M.; Nishikawa, K.; Iwasaki-Murata, A. Multistep thermal decomposition of granular sodium perborate tetrahydrate: A kinetic approach to complex reactions in solid-gas systems. Phys. Chem. Chem. Phys. 2018, 20, 12557–12573. [Google Scholar] [CrossRef] [PubMed]
- Koga, N.; Kodani, S. Thermally induced carbonation of Ca(OH)2 in a CO2 atmosphere: Kinetic simulation of overlapping mass-loss and mass-gain processes in a solid-gas system. Phys. Chem. Chem. Phys. 2018, 20, 26173–26189. [Google Scholar] [CrossRef]
- Noda, Y.; Koga, N. Phenomenological kinetics of the carbonation reaction of lithium hydroxide monohydrate: Role of surface product layer and possible existence of a liquid phase. J. Phys. Chem. C 2014, 118, 5424–5436. [Google Scholar] [CrossRef]
- Koga, N.; Suzuki, Y.; Tatsuoka, T. Thermal dehydration of magnesium acetate tetrahydrate: Formation and in situ crystallization of anhydrous glass. J. Phys. Chem. B 2012, 116, 14477–14486. [Google Scholar] [CrossRef]
- Koga, N.; Yamada, S.; Kimura, T. Thermal decomposition of silver carbonate: Phenomenology and physicogeometrical kinetics. J. Phys. Chem. C 2013, 117, 326–336. [Google Scholar] [CrossRef]
- Wada, T.; Koga, N. Kinetics and mechanism of the thermal decomposition of sodium percarbonate: Role of the surface product layer. J. Phys. Chem. A 2013, 117, 1880–1889. [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, M.; Yamada, S.; Koga, N. Phenomenological interpretation of the multistep thermal decomposition of silver carbonate to form silver metal. J. Phys. Chem. C 2014, 118, 8059–8070. [Google Scholar] [CrossRef]
- Wada, T.; Nakano, M.; Koga, N. Multistep kinetic behavior of the thermal decomposition of granular sodium percarbonate: Hindrance effect of the outer surface layer. J. Phys. Chem. A 2015, 119, 9749–9760. [Google Scholar] [CrossRef] [PubMed]
- Tsuboi, Y.; Koga, N. Thermal decomposition of biomineralized calcium carbonate: Correlation between the thermal behavior and structural characteristics of avian eggshell. ACS Sustainable Chem. Eng. 2018, 6, 5283–5295. [Google Scholar] [CrossRef]
- Kameno, N.; Koga, N. Heterogeneous kinetic features of the overlapping thermal dehydration and melting of thermal energy storage material: Sodium thiosulfate pentahydrate. J. Phys. Chem. C 2018, 122, 8480–8490. [Google Scholar] [CrossRef]
- Koga, N. Physico-Geometric Approach to the Kinetics of Overlapping Solid-State Reactions. In Handbook of Thermal Analysis and Calorimetry, 2nd ed.; Vyazovkin, S., Koga, N., Schick, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 6, pp. 213–251. [Google Scholar] [CrossRef]
- Koga, N.; Goshi, Y.; Yamada, S.; Pérez-Maqueda, L.A. Kinetic approach to partially overlapped thermal decomposition processes. J. Therm. Anal. Calorim. 2013, 111, 1463–1474. [Google Scholar] [CrossRef]
- Sánchez-Jiménez, P.E.; Perejón, A.; Criado, J.M.; Diánez, M.J.; Pérez-Maqueda, L.A. Kinetic model for thermal dehydrochlorination of poly(vinyl chloride). Polymer 2010, 51, 3998–4007. [Google Scholar] [CrossRef]
- Kitabayashi, S.; Koga, N. Physico-geometrical mechanism and overall kinetics of thermally induced oxidative decomposition of tin(II) oxalate in air: Formation process of microstructural tin(IV) oxide. J. Phys. Chem. C 2014, 118, 17847–17861. [Google Scholar] [CrossRef]
- Ogasawara, H.; Koga, N. Kinetic modeling for thermal dehydration of ferrous oxalate dihydrate polymorphs: A combined model for induction period-surface reaction-phase boundary reaction. J. Phys. Chem. A 2014, 118, 2401–2412. [Google Scholar] [CrossRef]
- Fukuda, M.; Koga, N. Kinetics and mechanisms of the thermal decomposition of copper(II) hydroxide: A consecutive process comprising induction period, surface reaction, and phase boundary-controlled reaction. J Phys Chem C 2018, 122, 12869–12879. [Google Scholar] [CrossRef]
- Nishikawa, K.; Ueta, Y.; Hara, D.; Yamada, S.; Koga, N. Kinetic characterization of multistep thermal oxidation of carbon/carbon composite in flowing air. J. Therm. Anal. Calorim. 2017, 128, 891–906. [Google Scholar] [CrossRef]
- Hara, D.; Nishikawa, K.; Koga, N. Characterization of carbon/carbon composites by kinetic deconvolution analysis for a thermal oxidation process: An examination using a series of mechanical pencil leads. Ind. Eng. Chem. Res. 2018, 57, 14460–14469. [Google Scholar] [CrossRef]
- Kikuchi, S.; Koga, N.; Yamazaki, A. Comparative study on the thermal behavior of structural concretes of sodium-cooled fast reactor. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Koga, N.; Kikuchi, S. Thermal behavior of perlite concrete used in a sodium-cooled fast reactor: Multistep reaction kinetics and melting for safety assessment. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Nakano, M.; Fujiwara, T.; Koga, N. Thermal decomposition of silver acetate: Physico-geometrical kinetic features and formation of silver nanoparticles. J. Phys. Chem. C 2016, 120, 8841–8854. [Google Scholar] [CrossRef]
- Fujiwara, T.; Yoshikawa, M.; Koga, N. Kinetic approach to multistep thermal behavior of Ag2CO3–graphite mixtures: Possible formation of intermediate solids with Ag2O–Ag and Ag2CO3–Ag core–shell structures. Thermochim. Acta 2016, 644, 50–60. [Google Scholar] [CrossRef]
- Koga, N.; Kasahara, D.; Kimura, T. Aragonite crystal growth and solid-state aragonite–calcite transformation: A physico–geometrical relationship via thermal dehydration of included water. Cryst. Growth Des. 2013, 13, 2238–2246. [Google Scholar] [CrossRef]
- Koga, N.; Nishikawa, K. Mutual Relationship between solid-state aragonite–calcite transformation and thermal dehydration of included water in coral aragonite. Cryst. Growth Des. 2014, 14, 879–887. [Google Scholar] [CrossRef]
- Polette-Niewold, L.A.; Manciu, F.S.; Torres, B.; Alvarado, M., Jr.; Chianelli, R.R. Organic/inorganic complex pigments: Ancient colors Maya blue. J. Inorg. Biochem. 2007, 101, 1958–1973. [Google Scholar] [CrossRef]
- Giustetto, R.; Seenivasan, K.; Bordiga, S. Spectroscopic characterization of a sepiolite-based Maya blue pigment. Period. Mineral. 2010, 79, 21–37. [Google Scholar] [CrossRef]
- Chiari, G.; Giustetto, R.; Druzik, J.; Doehne, E.; Ricchiardi, G. Pre-columbian nanotechnology: Reconciling the mysteries of the maya blue pigment. Appl. Phys. A 2007, 90, 3–7. [Google Scholar] [CrossRef]
- Ovarlez, S.; Giulieri, F.; Delamare, F.; Sbirrazzuoli, N.; Chaze, A.-M. Indigo–sepiolite nanohybrids: Temperature-dependent synthesis of two complexes and comparison with indigo–palygorskite systems. Microporous Mesoporous Mater. 2011, 142, 371–380. [Google Scholar] [CrossRef]
- Giustetto, R.; Seenivasan, K.; Bonino, F.; Ricchiardi, G.; Bordiga, S.; Chierotti, M.R.; Gobetto, R. Host/guest interactions in a sepiolite-based Maya blue pigment: A Spectroscopic Study. J. Phys. Chem. C 2011, 115, 16764–16776. [Google Scholar] [CrossRef]
- Hubbard, B.; Kuang, W.; Moser, A.; Facey, G.A.; Detellier, C. Structural study of Maya blue: Textural, thermal and solidstate multinuclear magnetic resonance characterization of the palygorskite-indigo and sepiolite-indigo adducts. Clays Clay Miner. 2003, 51, 318–326. [Google Scholar] [CrossRef]
- Sánchez-Ochoa, F.; Cocoletzi, G.H.; Canto, G. Trapping and diffusion of organic dyes inside of palygorskite clay: The ancient Maya blue pigment. Microporous Mesoporous Mater. 2017, 249, 111–117. [Google Scholar] [CrossRef]
- Giustetto, R.; Wahyudi, O. Sorption of red dyes on palygorskite: Synthesis and stability of red/purple Mayan nanocomposites. Microporous Mesoporous Mater. 2011, 142, 221–235. [Google Scholar] [CrossRef]
- Tartaglione, G.; Tabuani, D.; Camino, G. Thermal and morphological characterisation of organically modified sepiolite. Microporous Mesoporous Mater. 2008, 107, 161–168. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, H.; Xu, T.; Jin, Y.; Ding, S.; Chen, J. Insertion of isatin molecules into the nanostructure of palygorskite. RSC Adv. 2014, 4, 51978–51983. [Google Scholar] [CrossRef]
- Giustetto, R.; Llabres, I.X.F.X.; Ricchiardi, G.; Bordiga, S.; Damin, A.; Gobetto, R.; Chierotti, M.R. Maya blue: A computational and spectroscopic study. J. Phys. Chem. B 2005, 109, 19360–19368. [Google Scholar] [CrossRef]
- Ovarlez, S.; Giulieri, F.; Chaze, A.M.; Delamare, F.; Raya, J.; Hirschinger, J. The incorporation of indigo molecules in sepiolite tunnels. Chem. Eur. J. 2009, 15, 11326–11332. [Google Scholar] [CrossRef]
- Manciu, F.S.; Reza, L.; Polette, L.A.; Torres, B.; Chianelli, R.R. Raman and infrared studies of synthetic Maya pigments as a function of heating time and dye concentration. J. Raman Spectrosc. 2007, 38, 1193–1198. [Google Scholar] [CrossRef]
- Ovarlez, S.; Chaze, A.-M.; Giulieri, F.; Delamare, F. Indigo chemisorption in sepiolite. Application to Maya blue formation. C. R. Chim. 2006, 9, 1243–1248. [Google Scholar] [CrossRef]
- Tilocca, A.; Fois, E. The color and stability of Maya blue: TDDFT Calculations. J. Phys. Chem. C 2009, 113, 8683–8687. [Google Scholar] [CrossRef]
- Post, J.E.; Heaney, P.J. Synchrotron powder X-ray diffraction study of the structure and dehydration behavior of palygorskite. Am. Mineral. 2008, 93, 667–675. [Google Scholar] [CrossRef]
- Nagata, H. On dehydration of bound water of sepiolite. Clays Clay Miner. 1974, 22, 285–293. [Google Scholar] [CrossRef]
- Koga, N.; Šesták, J.; Simon, P. Some Fundamental and Historical Aspects of Phenomenological Kinetics in the Solid State Studied by Thermal Analysis. In Thermal Analysis of Micro, Nano- and Non-Crystalline Materials; Šesták, J., Simon, P., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 1–28. [Google Scholar]
- Friedman, H.L. Kinetics of thermal degradation of cha-forming plastics from thermogravimetry, application to a phenolic plastic. J. Polym. Sci., Part C 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Perejón, A.; Sánchez-Jiménez, P.E.; Criado, J.M.; Pérez-Maqueda, L.A. Kinetic analysis of complex solid-state reactions. A new deconvolution procedure. J. Phys. Chem. B 2011, 115, 1780–1791. [Google Scholar] [CrossRef] [PubMed]
- Svoboda, R.; Málek, J. Applicability of Fraser–Suzuki function in kinetic analysis of complex crystallization processes. J. Therm. Anal. Calorim. 2013, 111, 1045–1056. [Google Scholar] [CrossRef]
- Šesták, J.; Berggren, G. Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures. Thermochim. Acta 1971, 3, 1–12. [Google Scholar] [CrossRef]
- Šesták, J. Diagnostic limits of phenomenological kinetic models introducing the accommodation function. J. Therm. Anal. 1990, 36, 1997–2007. [Google Scholar] [CrossRef]
- Šesták, J. Rationale and fallacy of thermoanalytical kinetic patterns. J. Therm. Anal. Calorim. 2011, 110, 5–16. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. I. General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. II. Transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–223. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. III. Granulation, phase change, and microstructure. J. Chem. Phys. 1941, 9, 177–184. [Google Scholar] [CrossRef]
- Johnson, W.A.; Mehl, K.F. Reaction kinetics in processes of nucleation and growth. Trans. Am. Inst. Mining. Metall. Eng. 1939, 135, 416–458. [Google Scholar]
- Jander, W. Reaktionen im festen zustande bei höheren temperaturen. Reaktionsgeschwindigkeiten endotherm verlaufender umsetzungen. Z. Anorg. Allg. Chem. 1927, 163, 1–30. [Google Scholar] [CrossRef]
- Cui, W.; Zhang, H.; Xia, Y.; Zou, Y.; Xiang, C.; Chu, H.; Qiu, S.; Xu, F.; Sun, L. Preparation and thermophysical properties of a novel form-stable CaCl2·6H2O/sepiolite composite phase change material for latent heat storage. J. Therm. Anal. Calorim. 2017, 131, 57–63. [Google Scholar] [CrossRef]
- Leitão, I.M.V.; Seixas de Melo, J.S. Maya blue, an ancient guest–host pigment: Synthesis and models. J. Chem. Educ. 2013, 90, 1493–1497. [Google Scholar] [CrossRef]
- Boykin, D.W. A convenient apparatus for small-scale dyeing with indigo. J. Chem. Educ. 1998, 75, 769. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are available from the authors. |

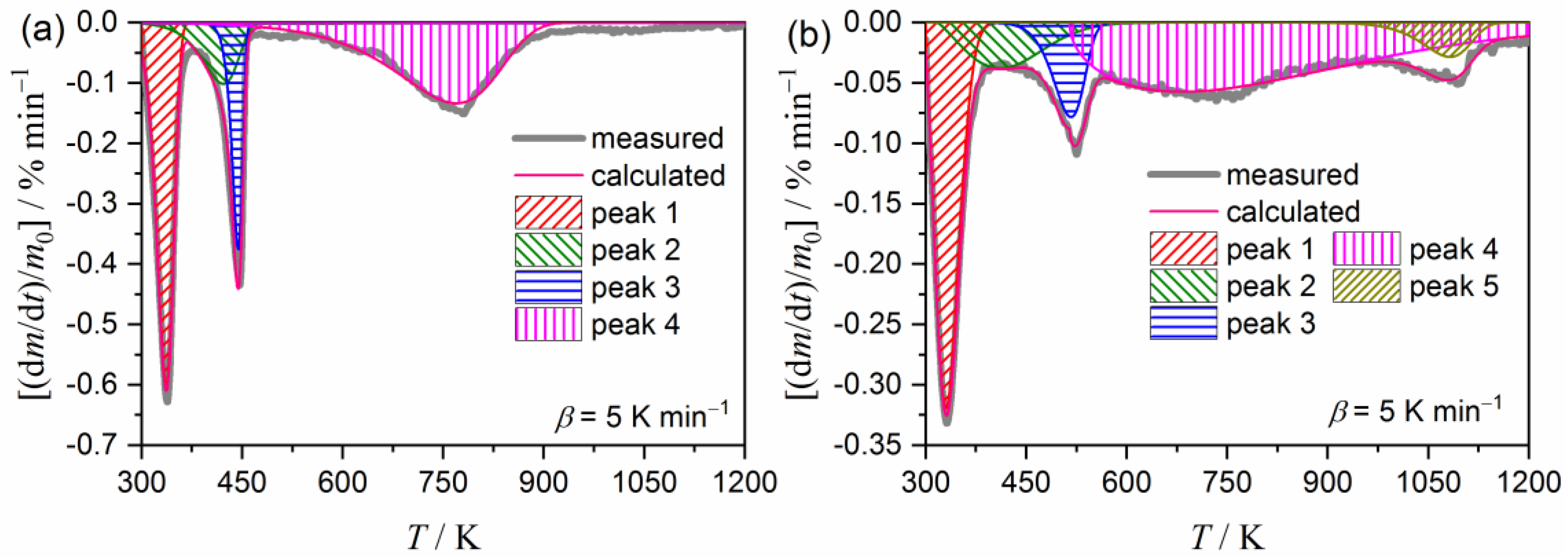
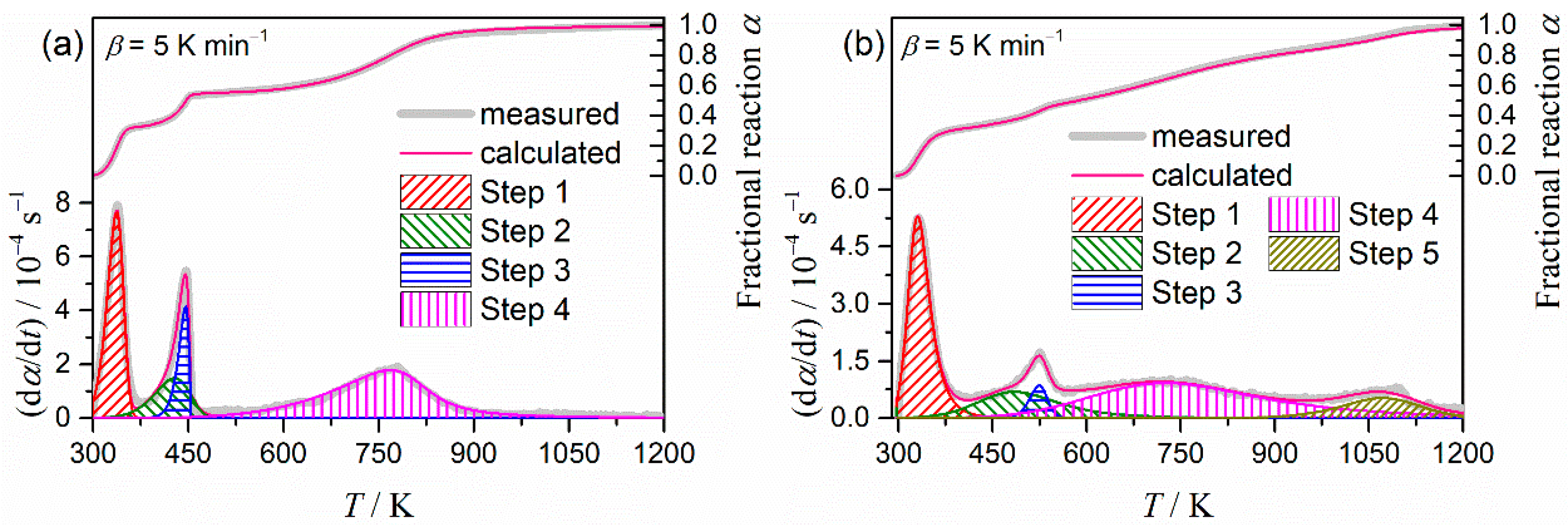
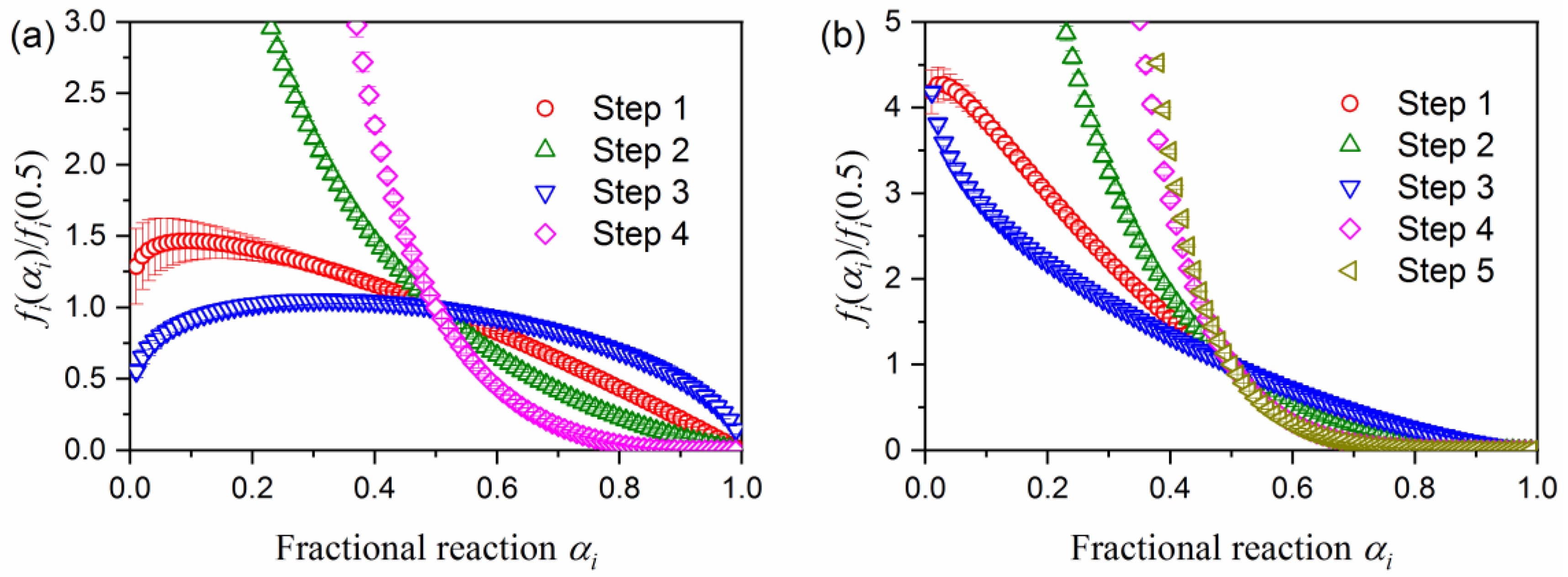


| Sample | i | ci | Ea,i/kJ mol−1 | Ai/s−1 | fi(αi)=αim(1−αi)n[−ln(1−αi)]p | R2 | ||
|---|---|---|---|---|---|---|---|---|
| m | n | p | ||||||
| Palygorskite | 1 | 0.32 ± 0.01 | 63.7 ± 0.2 | (4.35 ± 0.07) × 107 | −0.63 ± 0.04 | 1.26 ± 0.03 | 0.73 ± 0.03 | 0.99 ± 0.01 |
| 2 | 0.12 ± 0.02 | 90.5 ± 1.7 | (2.94 ± 0.01) × 108 | −0.33 ± 0.02 | 1.13 ± 0.09 | –0.35 ± 0.02 | ||
| 3 | 0.11 ± 0.01 | 114.4 ± 0.2 | (2.00 ± 0.02) × 1011 | 0.03 ± 0.01 | 0.61 ± 0.07 | 0.21 ± 0.01 | ||
| 4 | 0.45 ± 0.01 | 190.0 ± 1.5 | (4.79 ± 0.05) × 108 | –32.8 ± 3.8 | 13.8 ± 1.7 | 29.5 ± 3.7 | ||
| Sepiolite | 1 | 0.31 ± 0.01 | 80.4 ± 0.1 | (3.25 ± 0.02) × 1010 | 0.33 ± 0.02 | 2.34 ± 0.04 | –0.27 ± 0.01 | 0.99 ± 0.01 |
| 2 | 0.14 ± 0.01 | 64.6 ± 0.9 | (1.28 ± 0.01) × 104 | −0.01 ± 0.01 | 2.30 ± 0.05 | –0.59 ± 0.01 | ||
| 3 | 0.04 ± 0.01 | 213.0 ± 1.0 | (1.01 ± 0.01) × 1019 | –0.02 ± 0.01 | 1.41 ± 0.02 | –0.09 ± 0.01 | ||
| 4 | 0.41 ± 0.01 | 124.3 ± 1.4 | (2.37 ± 0.01) × 105 | –0.46 ± 0.01 | 2.93 ± 0.05 | –1.43 ± 0.02 | ||
| 5 | 0.10 ± 0.01 | 738.4 ± 1.6 | (9.50 ± 0.01) × 1032 | –1.29 ± 0.01 | 2.30 ± 0.01 | –1.78 ± 0.02 | ||
| Sample | i | ci | Ea,i/kJ mol−1 | Ai/s−1 | fi(αi)=αim(1 − αi)n[−ln(1 − αi)]p | R2 | ||
|---|---|---|---|---|---|---|---|---|
| m | n | p | ||||||
| P-MB | 1 | 0.08 ± 0.01 | 61.7 ± 0.5 | (4.33 ± 0.02) × 107 | –0.57 ± 0.10 | 1.69 ± 0.09 | 0.73 ± 0.05 | 0.99 ± 0.01 |
| 2 | 0.10 ± 0.01 | 46.4 ± 0.3 | (1.95 ± 0.01) × 103 | −0.04 ± 0.01 | 2.68 ± 0.22 | –0.18 ± 0.01 | ||
| 3 | 0.10 ± 0.01 | 113.0 ± 0.6 | (1.70 ± 0.01) × 1011 | 0.02 ± 0.01 | 0.85 ± 0.01 | –0.07 ± 0.01 | ||
| 4 | 0.09 ± 0.01 | 43.7 ± 2.0 | (1.96 ± 0.02) × 102 | 1.19 ± 0.06 | 1.05 ± 0.03 | –1.10 ± 0.05 | ||
| 5 | 0.15 ± 0.03 | 143.2 ± 0.3 | (1.99 ± 0.02) × 109 | –0.11 ± 0.01 | 1.64 ± 0.17 | –0.35 ± 0.03 | ||
| 6 | 0.31 ± 0.03 | 183.2 ± 2.5 | (4.99 ± 0.03) × 108 | –26.61 ± 3.69 | 11.94 ± 2.27 | 24.50 ± 4.38 | ||
| 7 | 0.13 ± 0.01 | 634.3 ± 3.6 | (1.70 ± 0.01) × 1032 | –2.44 ± 0.19 | 3.79 ± 0.57 | –3.82 ± 0.43 | ||
| 8 | 0.05 ± 0.01 | 448.3 ± 2.8 | (8.84 ± 0.08) × 1017 | –0.39 ± 0.03 | 1.21 ± 0.12 | –0.48 ± 0.06 | ||
| S-MB | 1 | 0.22 ± 0.01 | 82.4 ± 0.5 | (2.16 ± 0.01) × 1010 | 0.25 ± 0.01 | 5.57 ± 0.09 | –0.35 ± 0.01 | 0.98 ± 0.02 |
| 2 | 0.15 ± 0.01 | 64.5 ± 0.8 | (1.29 ± 0.01) × 104 | −0.01 ± 0.01 | 2.45 ± 0.08 | –0.40 ± 0.01 | ||
| 3 | 0.02 ± 0.01 | 206.2 ± 1.9 | (9.68 ± 0.01) × 1018 | –0.02 ± 0.01 | 1.26 ± 0.01 | –0.11 ± 0.01 | ||
| 4 | 0.05 ± 0.01 | 160.3 ± 0.4 | (4.48 ± 0.02) × 1011 | 0.06 ± 0.01 | 1.35 ± 0.08 | 0.24 ± 0.01 | ||
| 5 | 0.34 ± 0.01 | 127.9 ± 2.4 | (2.33 ± 6.98) × 105 | –0.46 ± 0.01 | 1.17 ± 0.02 | –1.39 ± 0.05 | ||
| 6 | 0.04 ± 0.01 | 180.6 ± 0.7 | (1.36 ± 0.01) × 1011 | –0.20 ± 0.01 | 0.78 ± 0.01 | –0.20 ± 0.01 | ||
| 7 | 0.08 ± 0.01 | 120.8 ± 3.3 | (9.94 ± 0.02) × 103 | 0.06 ± 0.01 | 1.07 ± 0.01 | 0.12 ± 0.01 | ||
| 8 | 0.06 ± 0.01 | 314.0 ± 5.5 | (1.51 ± 0.01) × 1013 | –0.40 ± 0.01 | 1.09 ± 0.01 | –0.33 ± 0.01 | ||
| 9 | 0.05 ± 0.01 | 780.9 ± 9.1 | (9.65 ± 0.01) × 1032 | –0.73 ± 0.01 | 2.14 ± 0.03 | –0.66 ± 0.01 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamamoto, Y.; Koga, N. Thermal Decomposition of Maya Blue: Extraction of Indigo Thermal Decomposition Steps from a Multistep Heterogeneous Reaction Using a Kinetic Deconvolution Analysis. Molecules 2019, 24, 2515. https://doi.org/10.3390/molecules24132515
Yamamoto Y, Koga N. Thermal Decomposition of Maya Blue: Extraction of Indigo Thermal Decomposition Steps from a Multistep Heterogeneous Reaction Using a Kinetic Deconvolution Analysis. Molecules. 2019; 24(13):2515. https://doi.org/10.3390/molecules24132515
Chicago/Turabian StyleYamamoto, Yui, and Nobuyoshi Koga. 2019. "Thermal Decomposition of Maya Blue: Extraction of Indigo Thermal Decomposition Steps from a Multistep Heterogeneous Reaction Using a Kinetic Deconvolution Analysis" Molecules 24, no. 13: 2515. https://doi.org/10.3390/molecules24132515
APA StyleYamamoto, Y., & Koga, N. (2019). Thermal Decomposition of Maya Blue: Extraction of Indigo Thermal Decomposition Steps from a Multistep Heterogeneous Reaction Using a Kinetic Deconvolution Analysis. Molecules, 24(13), 2515. https://doi.org/10.3390/molecules24132515








