Quantification of Total Phenolic and Carotenoid Content in Blackberries (Rubus Fructicosus L.) Using Near Infrared Spectroscopy (NIRS) and Multivariate Analysis
Abstract
1. Introduction
2. Results and Discussion
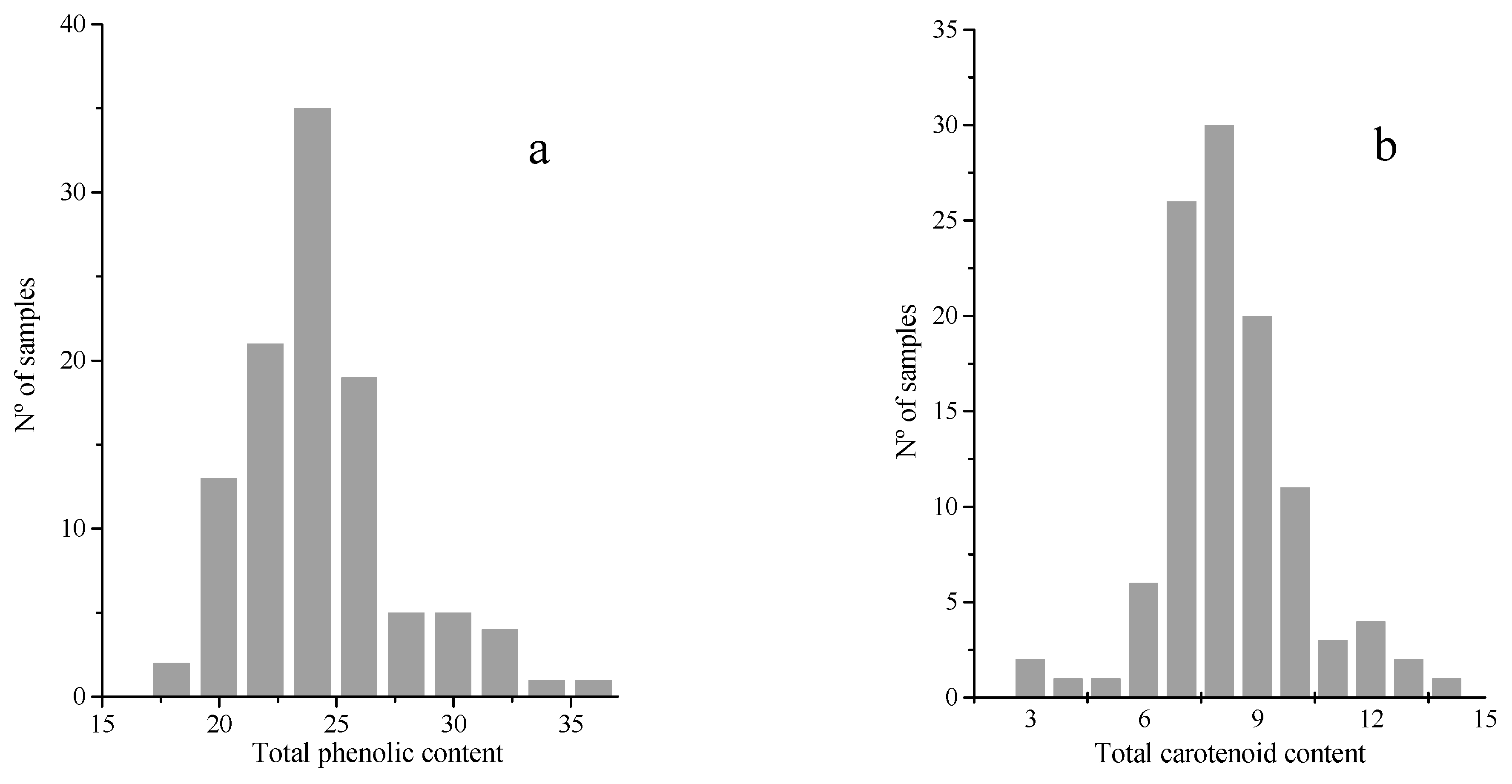
2.1. Reference Analysis of Total Phenolic and Carotenoid Contents in the Samples
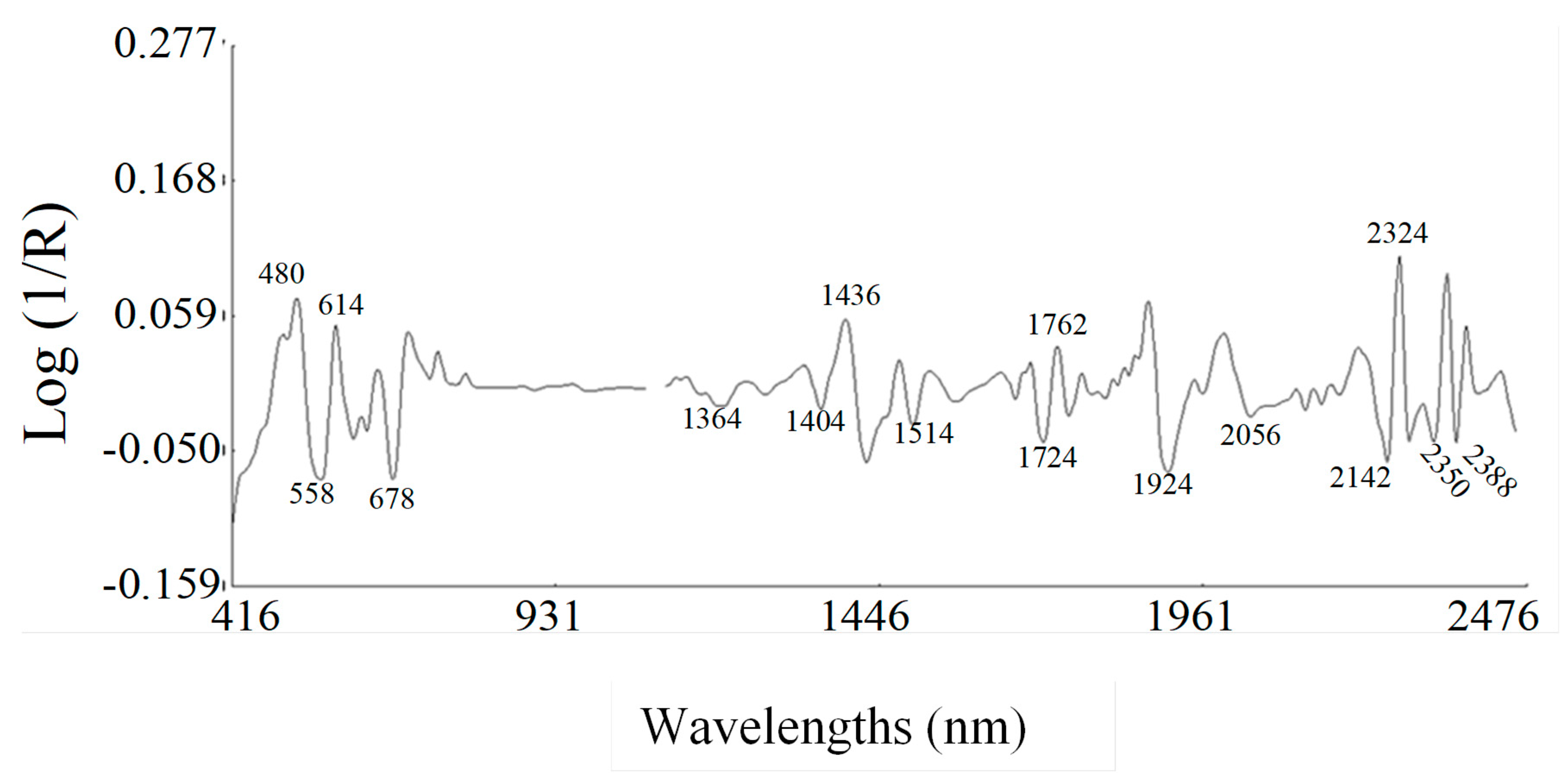
2.2. Spectral Data Pre-Treatments and Equation Performances. Second Derivative Spectra of Blueberry Fruit
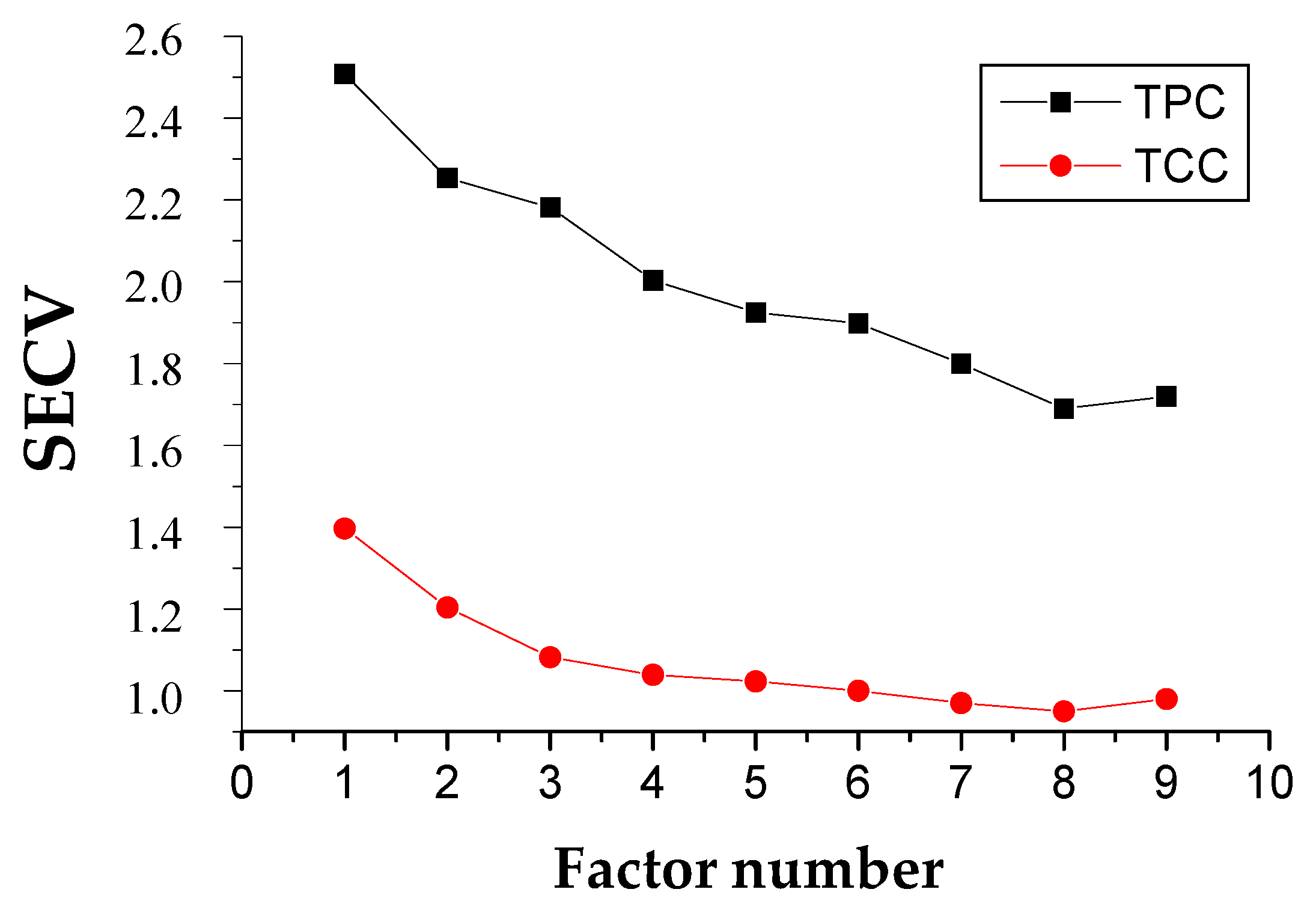
2.3. Calibration Development for TPC and TCC
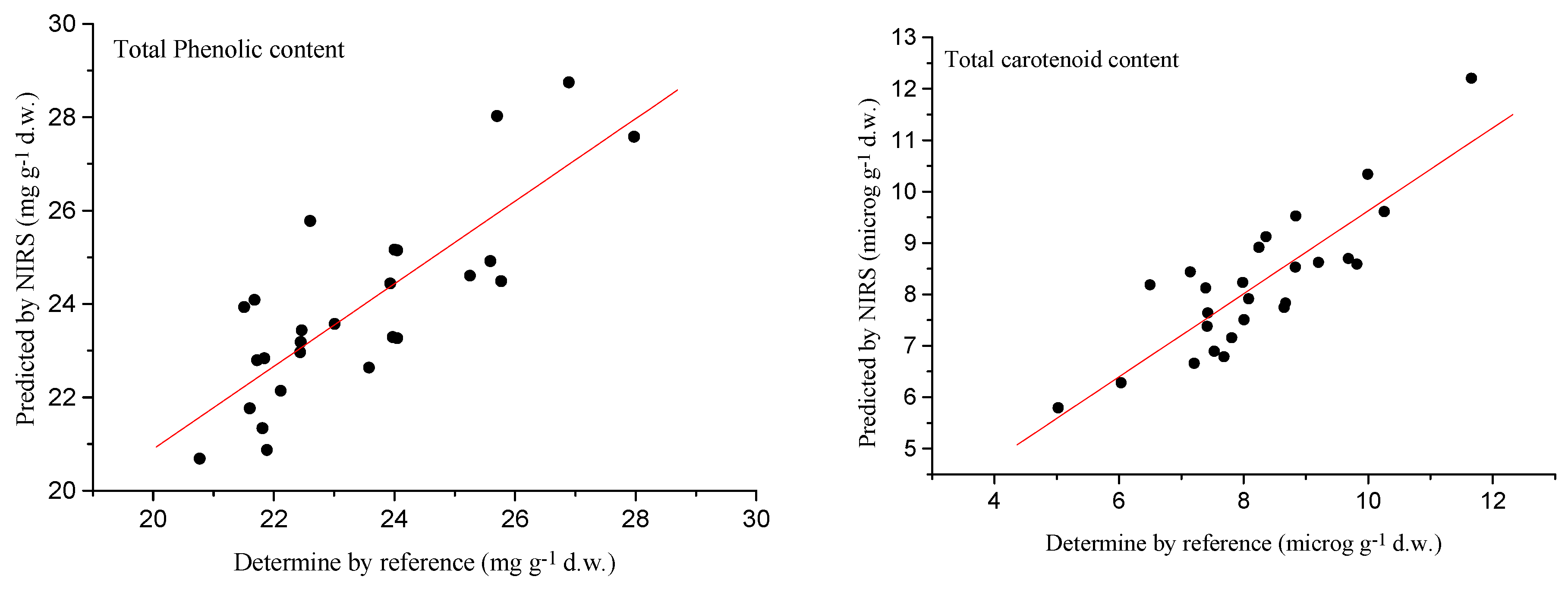
2.4. External Validation
2.5. Modified Partial Least Square Loadings for Total Phenolic Content
2.6. Modified Partial Least Square Loadings for Total Carotenoid Content
3. Materials and Methods
3.1. Plant Material and Greenhouse Experiments
3.2. Determination of the Total Phenolic Fraction
3.3. Determination of the Total Carotenoid Content
3.4. NIRS Analysis Calibration and Validation Development
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Joshipura, K.J.; Hu, F.B.; Manson, J.E.; Stampfer, M.J.; Rimm, E.B.; Speizer, F.E.; Colditz, G.; Ascherio, A.; Rosner, B.; Spiegelman, D.; et al. The effect of fruit and vegetable intake on risk for coronary heart disease. Ann. Intern. Med. 2001, 134, 1106–1114. [Google Scholar] [CrossRef] [PubMed]
- Maynard, M.; Gunnell, D.; Emmett, P.; Frankel, S.; Davey Smith, G. Fruit, vegetables, and antioxidants in childhood and risk of adult cancer: The Boyd Orrcohort. J. Epidemiol. Commun. Health 2003, 57, 218–225. [Google Scholar] [CrossRef]
- Ames, B.N.; Shigenaga, M.K.; Hagen, T.M. Oxidants, antioxidants, and the degenerative diseases of aging. Proc. Natl. Acad. Sci. USA 1993, 90, 7915–7922. [Google Scholar] [CrossRef] [PubMed]
- Freshfruitportal. 2018. Available online: http://www.freshfruitportal.com/news/2018/02/01/spain-sees-strong-growth-berry-plantings/ (accessed on 20 July 2017).
- Prior, R.; Cão, G.H.; Martin, A.; Sofic, E.; Mcewen, J.; O’brien, C.; Lischner, N.; Ehlenfeldt, M.; Kalt, W.; Krewer, G.; et al. Antioxidant capacity as influenced by Total phenolic and anthocyanin content, maturity, and variety of Vaccinium species. J. Agric. Food Chem. 1998, 46, 2686–2693. [Google Scholar] [CrossRef]
- Castrejón, A.; Eichholz, I.; Rohn, S.; Kroh, L.W.; Huyskens-Keil, S. Phenolic profile and antioxidant activity of highbush blueberry (Vaccinium corymbosum L.) during fruit maturation and ripening. Food Chem. 2008, 109, 564–572. [Google Scholar] [CrossRef]
- Cardeñosa, V.; Medrano, E.; Lorenzo, P.; Sánchez-Guerrero, M.C.; Cuevas, F.; Pradas, I.; Moreno-Rojas, J.M. Effects of salinity and nitrogen supply on the quality and health-related compounds of strawberry fruits (Fragaria × ananassa cv. Primoris). J. Sci. Food Agric. 2015, 95, 2924–2930. [Google Scholar] [CrossRef]
- Cardeñosa, V.; Girones-Vilaplana, A.; Muriel, J.L.; Moreno, D.A.; Moreno-Rojas, J.M. Influence of genotype, cultivation system and irrigation regime on antioxidant capacity and selected phenolics of blueberries (Vaccinium corymbosum L.). Food Chem. 2016, 202, 276–283. [Google Scholar] [CrossRef]
- Ruiz, D.; Egea, J.; Gil, M.I.; Tomas-Barberan, F.A. Characterization and quantitation of phenolic compounds in new apricot (Prunus armeniaca L.) varieties. J. Agric. Food Chem. 2005, 53, 9544–9552. [Google Scholar] [CrossRef]
- Contessa, C.; Mellano, M.G.; Beccaro, G.L.; Giusiano, A. Total antioxidant capacity and total phenolic and anthocyanin contents in fruit species grown in Northwest Italy. Sci. Hortic. 2013, 160, 351–357. [Google Scholar] [CrossRef]
- Souza, D.; Vera de Rosso, V.; Zerlotti, A. Compostos bioactivos presentes en amora-preta (Rubus spp.). Rev. Bras. Frutic. 2010, 32, 664–674. [Google Scholar]
- Lashmanova, K.; Kuzivanova, O.; Dymova, O. Northern berries as a source of carotenoids. ABP 2012, 59, 133–134. [Google Scholar]
- Rutz, J.K.; Voss, G.B.; Zambiazi, R.C. Influence of the degree of maturation on the bioactive compounds in blackberry (Rubus spp.) cv. Tupy. Food Nutr. Sci. 2012, 3, 1453–1460. [Google Scholar]
- Perkins-Veazie, P.; Fernández, G.E. Screening of Raspberry Fruit for Carotenoids: Impact on Flavor and Color. Available online: http://www.raspberryblackberry.com/wp-content/uploads/2011-Screening-of-Raspberry-Fruit-for-Carotenoids-Impact-on-Flavor-and-Color.pdf (accessed on 10 December 2012).
- Reyes, J.; Yousef, G.; Martínez, R.; Lila, M. Antioxidant capacity of fruit extracts of blackberry (Rubus sp.) produced in different climatic regions. J. Food Sci. 2005, 70, 497–503. [Google Scholar] [CrossRef]
- Heinonen, M.; Lehtonen, P.J.; Hopia, A.I. Antioxidant activity of berry and fruit wines and liquors. J. Agric. Food Chem. 1998, 46, 25–31. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Zhang, H.; Liu, W.; Li, C. Survey of antioxidant capacity and phenolic composition of blueberry, blackberry, and strawberry in Nanjing. J. Zhejiang Univ. Sci. B 2012, 13, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Berté, K.A.S.; Beurx, M.R.; Spada, P.K.D.S.; Slavador, M.; Hoffmann-Ribani, R. Chemical composition and antioxidant activity of yerba-mate (Ilex paraguariensis A.St.-Hil., Aquifoliaceae) extract as obtained by spray drying. J. Agric. Food Chem. 2011, 59, 5523–5527. [Google Scholar] [CrossRef] [PubMed]
- Cardozo, J.R.; Ferrarese-Filho, O.; Filho, L.C.; LucioFerrarese, M.D.; Donaduzzi, C.M.; Sturion, J.A. Methylxanthines and phenolic compounds in mate (Ilex paraguariensis St. Hil.) progenies grown in Brazil. J. Food Compos. Anal. 2007, 20, 553–558. [Google Scholar] [CrossRef]
- Jacques, R.A.; Santos, J.G.; Dariva, C.; Oliveira, J.V.; Caramarao, E.B. GC/MS ~ characterization of mate tea leaves extracts obtained from high-pressure CO2 extraction. J. Supercrit. Fluids 2007, 40, 354–359. [Google Scholar] [CrossRef]
- Nicolaï, B.M.; Beullens, K.; Bobelyn, E.; Peirs, A.; Saeys, W.; Theron, K.I. Nondestructive measurement of fruit and vegetable quality by means of NIR spectroscopy: A review. Postharvest Biol. Technol. 2007, 46, 99–118. [Google Scholar] [CrossRef]
- Pasquini, C. Near Infrared Spectroscopy: Fundamentals, practical aspects and analytical applications. J. Braz. Chem. Soc. 2003, 14, 198–219. [Google Scholar] [CrossRef]
- Gajdoš Kljusurić, J.; Mihalev, K.; Bečić, I.; Polović, I.; Georgieva, M.; Djaković, S.; Kurtanjek, Z. Near-infrared spectroscopic analysis of total phenolic content and antioxidant activity of berry fruits. Food Technol. Biotechnol. 2016, 54, 236–242. [Google Scholar] [CrossRef] [PubMed]
- Georgieva, M.; Nebojan, I.; Mihalev, K.; Yoncheva, N.; Gajdoš Kljusurić, J.; Kurtanjek, Ž. Application of NIR spectroscopy and chemometrics in quality control of wild berry fruit extracts during storage. Croat. J. Food Technol. Biotechnol. Nutr. 2013, 8, 67–73. [Google Scholar]
- Sinelli, N.; Spinardi, A.; Di Egidio, V.; Mignani, I.; Casiraghi, E. Evaluation of quality and nutraceutical content of blueberries (Vaccinium corymbosum L.) by near and mid-infrared spectroscopy. Postharvest Biol. Technol. 2008, 50, 1–36. [Google Scholar] [CrossRef]
- Meneses, E.; Arango, G.; Correa, G.; Ruíz, O.; Vargas, L.; Pérez, J. Detection of Eurhizococcus colombianus (Hemiptera: Margarodidae) in blackberry plants by near-infrared spectroscopy. Acta Agron. 2015, 64, 280–288. [Google Scholar] [CrossRef]
- Ali, L.; Svensson, B.; Alsanius, B.W.; Olsson, M.E. Late season harvest and storage of Rubus berries—Major antioxidant and sugar levels. Sci. Hortic. 2011, 129, 376–381. [Google Scholar] [CrossRef]
- Aaby, K.; Ekeberg, D.; Skrede, G. Characterization of phenolic compounds in strawberry (Fragaria × ananassa) fruits by different HPLC detectors and contribution of individual compounds to total antioxidant capacity. J. Agric. Food Chem. 2007, 55, 4395–4406. [Google Scholar] [CrossRef]
- Naes, T.; Isaksson, T.; Fearn, T.; Davies, T.A. 2 User-Friendly Guide to Multivariate Calibration and Classification; NIR: Chichester, UK, 2002. [Google Scholar]
- Miller, C.E. Chemical principles of near-infrared technology. In Near-Infrared Technology in the Agricultural and Food Industries, 2nd ed.; Williams, P.C., Norris, K.H., Eds.; American Association of Cereal Chemists: St. Paul, MN, USA, 2001. [Google Scholar]
- Tamburini, E.; Costa, S.; Rugiero, I.; Pedrini, P.; Marchetti, M.G. Quantification of lycopene, β-carotene, and Total soluble solids in intact red-flesh watermelon (Citrullus lanatus) using on-line Near-Infrared Spectroscopy. Sensors 2017, 17, 746. [Google Scholar] [CrossRef]
- Osborne, B.G.; Fearn, T.; Hindle, P. Practical NIR Spectroscopy with Applications in Food and Beverage Analysis; Longman Scientific and Technical: London, UK, 1993. [Google Scholar]
- Murray, I.; Williams, P.C. Chemical principles of near-infrared technology. In Near-Infrared Technology in the Agricultural and Food Industries; Williams, P., Norris, K., Eds.; American Association of Cereal Chemists, Inc.: St. Paul, MN, USA, 1987; pp. 17–34. [Google Scholar]
- Shenk, J.S.; Westerhaus, M.O. The application of near infrared reflectance spectroscopy (NIRS) to forage analysis. In Forage Quality, Evaluation and Utilization; Fahey, G.C., Jr., Collins, M., Mertens, D.R., Moser, L.E., Madison, W.I., Eds.; Crop Science Society of America, Soil Science Society of America: Madison, WI, USA, 1994; pp. 406–450. [Google Scholar]
- Williams, P.; Norris, K. Near-Infrared Technology in the Agricultural and Food Industries; Minnesota American Association: St. Paul, MN, USA, 2001. [Google Scholar]
- Williams, P.C.; Sobering, D.C. How do we do it: A brief summary of the methods we use in developing near infrared calibrations. In Near Infrared Spectroscopy: The Future Waves; Davies, A.M.C., Williams, P.C., Eds.; NIR Publications: Chichester, UK, 1996; pp. 185–188. [Google Scholar]
- Xie, L.; Ye, X.; Liu, D.; Ying, Y. Quantification of glucose, fructose and sucrose in bayberry juice by NIR and PLS. Food Chem. 2009, 114, 1135–1140. [Google Scholar] [CrossRef]
- Budić-Leto, I.; Gajdos Kljusurić, J.; Zdunić, G.; Tomić-Potrebuješ, I.; Banović, M.; Kurtanjek, Ž.; Lovrić, T. Usefulness of near infrared spectroscopy and chemometrics in screening of the quality of dessert wine Prošek. Croat. J. Food Sci. Technol. 2011, 3, 9–15. [Google Scholar]
- Tkachuk, R.; Kuzina, F.D. Chlorophyll analysis of whole rape-seed kernels by near infrared reflectance. Can. J. Plant Sci. 1982, 62, 875–884. [Google Scholar] [CrossRef]
- Venyaminov, S.Y.; Prendergast, F.G. Water (H2O and D2O) molar absorptivity in the 1000–4000 cm−1 range and quantitative infrared spectroscopy of aqueous solutions. Anal. Biochem. 1997, 248, 234–245. [Google Scholar] [CrossRef] [PubMed]
- Dewanto, V.; Wu, X.; Liu, R.H. Processed sweet corn has higher antioxidant activity. J. Agric. Food Chem. 2002, 50, 4959–4964. [Google Scholar] [CrossRef] [PubMed]
- Shenk, J.S.; Westerhaus, M.O. Population structuring of near infrared spectra and modified partial least squares regression. Crop Sci. 1991, 31, 1548–1555. [Google Scholar] [CrossRef]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard normal variate transformation and de-trending of near infrared diffuse reflectance spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Shenk, J.S.; Workman, J.; Westerhaus, M.O. Application of NIR spectroscopy to agricultural products. In Marcel Dekker Handbook of Near Infrared Analysis; Burns, D.A., Ciurczac, E.W., Eds.; Taylor Francis Group: New York, NY, USA, 2001; pp. 419–474. [Google Scholar]
Sample Availability: Samples of the compounds are not available from the authors. |


| Trait | Range | SD a | R2 b | SEC c | R2CV d | SECV e | RPDcv f | Treatment | Factor g |
|---|---|---|---|---|---|---|---|---|---|
| TPC | 17.36–35.67 | 3.06 | 0.86 | 1.14 | 0.69 | 1.69 | 1.81 | 2,5,5,2 | 8 |
| 17.36–35.67 | 3.06 | 0.71 | 1.66 | 0.59 | 1.95 | 1.58 | 1,4,4,1 | 8 | |
| 17.36–35.67 | 3.06 | 0.70 | 1.68 | 0.59 | 1.97 | 1.57 | 1,10,10,1 | 8 | |
| 17.36–35.67 | 3.06 | 0.76 | 1.49 | 0.67 | 1.75 | 1.75 | 2,20,20,2 | 8 | |
| TCC | 2.84–13.73 | 1.82 | 0.92 | 0.52 | 0.76 | 0.95 | 1.91 | 2,5,5,2 | 8 |
| 2.84–13.73 | 1.82 | 0.85 | 0.72 | 0.71 | 1.03 | 1.83 | 1,4,4,1 | 8 | |
| 2.84–13.73 | 1.82 | 0.83 | 0.75 | 0.71 | 0.99 | 1.82 | 1,10,10,1 | 8 | |
| 2.84–13.73 | 1.82 | 0.84 | 0.75 | 0.70 | 1.05 | 1.80 | 2,20,20,2 | 8 |
| Reference Values (n = 30) | External Validation | ||||||
|---|---|---|---|---|---|---|---|
| Parameters | Range | Mean | SD a | Q2 b | SEP c | RDPp d | RER e |
| TPC | 20.77–27.97 | 23.41 | 1.85 | 0.65 | 1.22 | 1.52 | 5.92 |
| TCC | 5.02–11.66 | 8.21 | 1.40 | 0.71 | 0.77 | 1.82 | 8.63 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toledo-Martín, E.M.; García-García, M.d.C.; Font, R.; Moreno-Rojas, J.M.; Salinas-Navarro, M.; Gómez, P.; Del Río-Celestino, M. Quantification of Total Phenolic and Carotenoid Content in Blackberries (Rubus Fructicosus L.) Using Near Infrared Spectroscopy (NIRS) and Multivariate Analysis. Molecules 2018, 23, 3191. https://doi.org/10.3390/molecules23123191
Toledo-Martín EM, García-García MdC, Font R, Moreno-Rojas JM, Salinas-Navarro M, Gómez P, Del Río-Celestino M. Quantification of Total Phenolic and Carotenoid Content in Blackberries (Rubus Fructicosus L.) Using Near Infrared Spectroscopy (NIRS) and Multivariate Analysis. Molecules. 2018; 23(12):3191. https://doi.org/10.3390/molecules23123191
Chicago/Turabian StyleToledo-Martín, Eva María, María del Carmen García-García, Rafael Font, José Manuel Moreno-Rojas, María Salinas-Navarro, Pedro Gómez, and Mercedes Del Río-Celestino. 2018. "Quantification of Total Phenolic and Carotenoid Content in Blackberries (Rubus Fructicosus L.) Using Near Infrared Spectroscopy (NIRS) and Multivariate Analysis" Molecules 23, no. 12: 3191. https://doi.org/10.3390/molecules23123191
APA StyleToledo-Martín, E. M., García-García, M. d. C., Font, R., Moreno-Rojas, J. M., Salinas-Navarro, M., Gómez, P., & Del Río-Celestino, M. (2018). Quantification of Total Phenolic and Carotenoid Content in Blackberries (Rubus Fructicosus L.) Using Near Infrared Spectroscopy (NIRS) and Multivariate Analysis. Molecules, 23(12), 3191. https://doi.org/10.3390/molecules23123191








