Skin Permeation of Solutes from Metalworking Fluids to Build Prediction Models and Test A Partition Theory
Abstract
1. Introduction
2. Results and Discussion
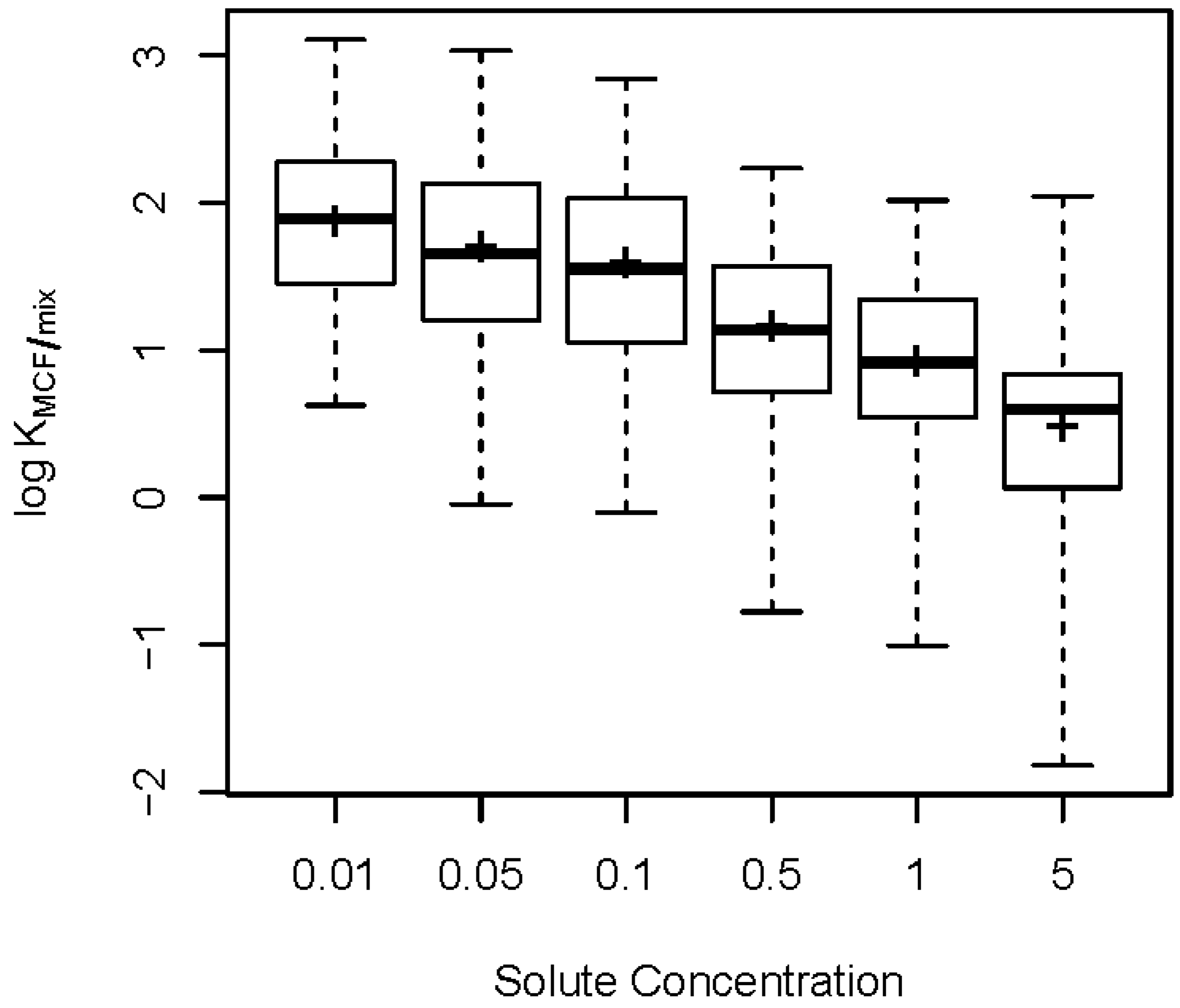
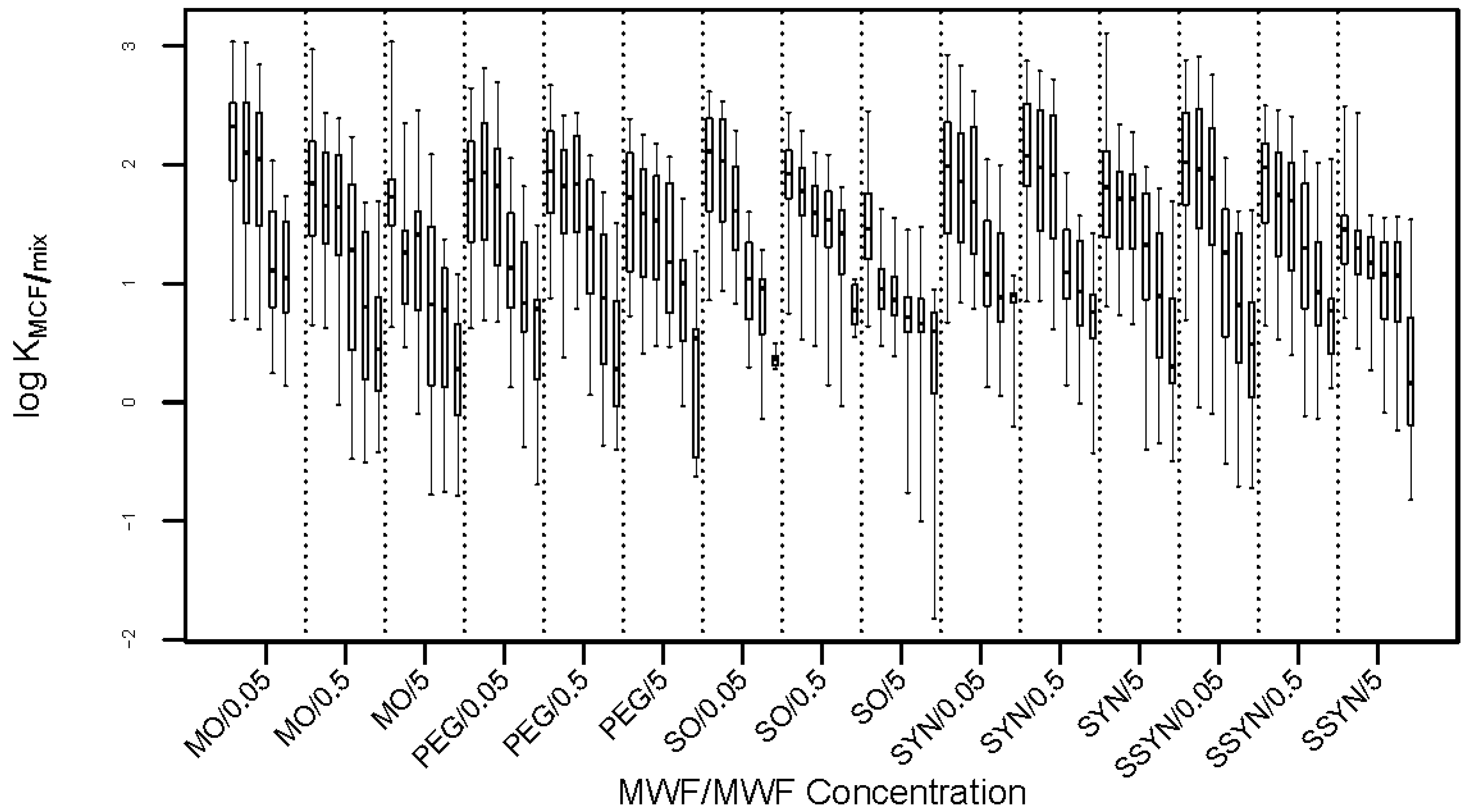
2.1. Data Summaries
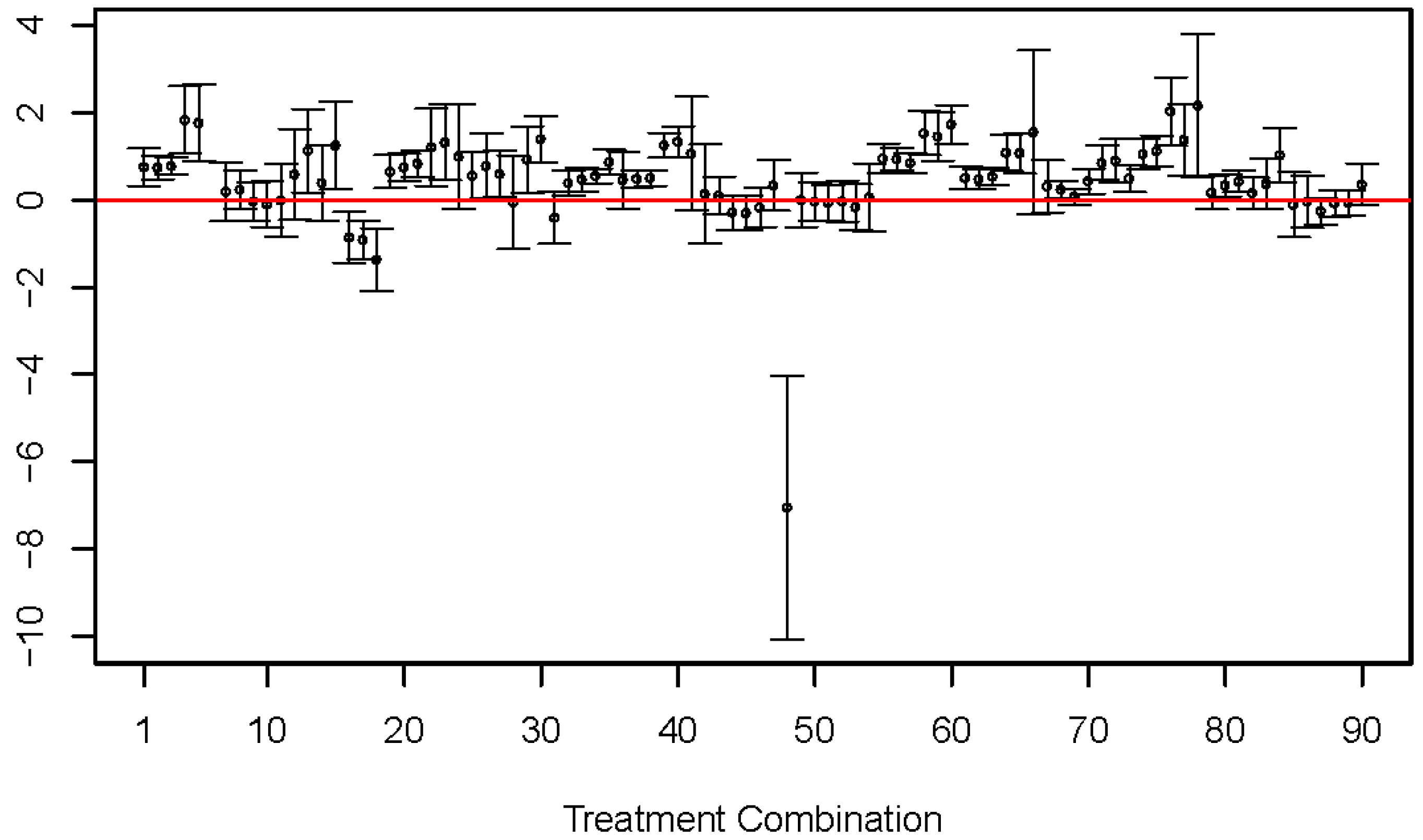
2.2. Insufficiency of the LFER Model
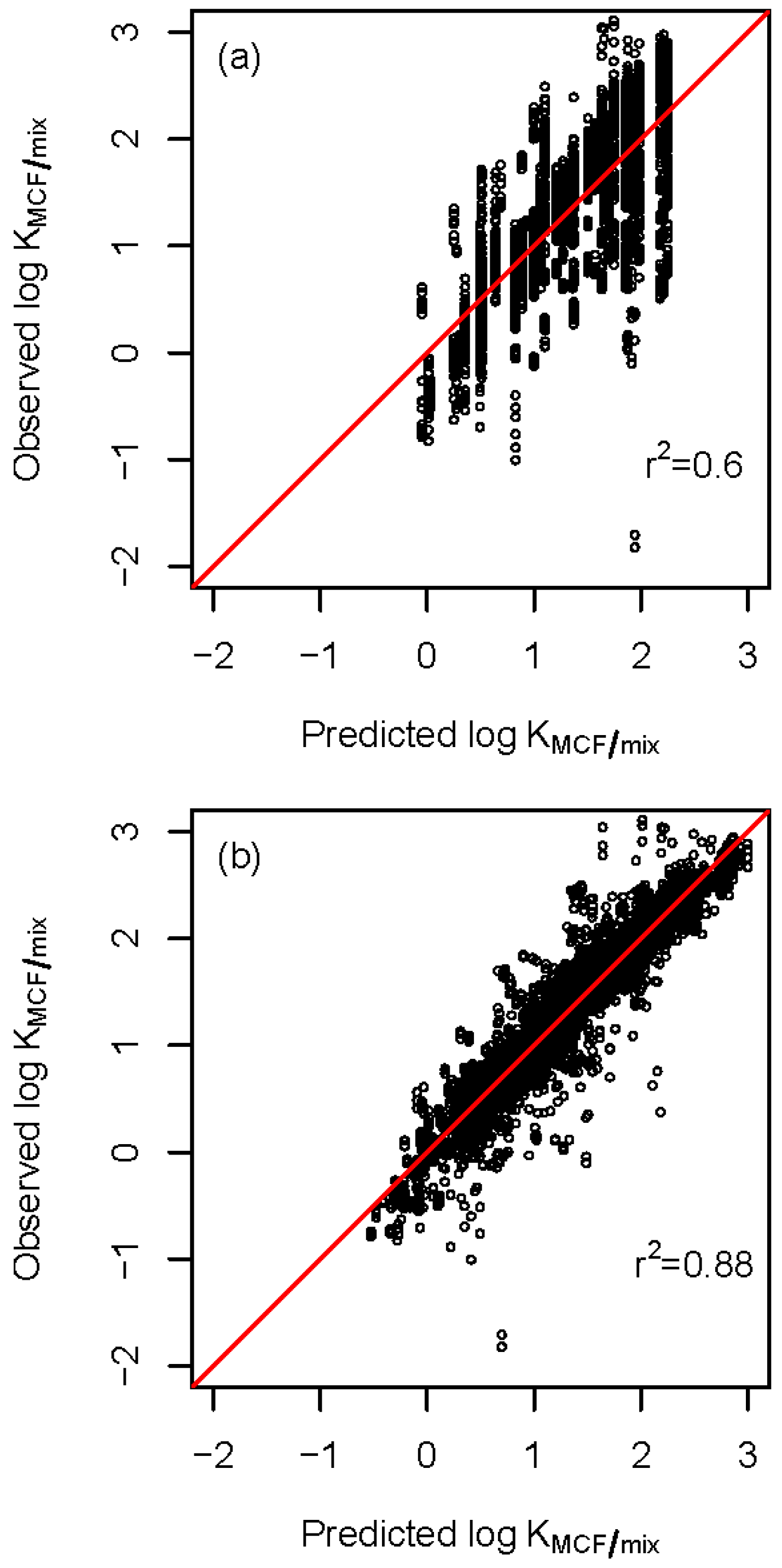
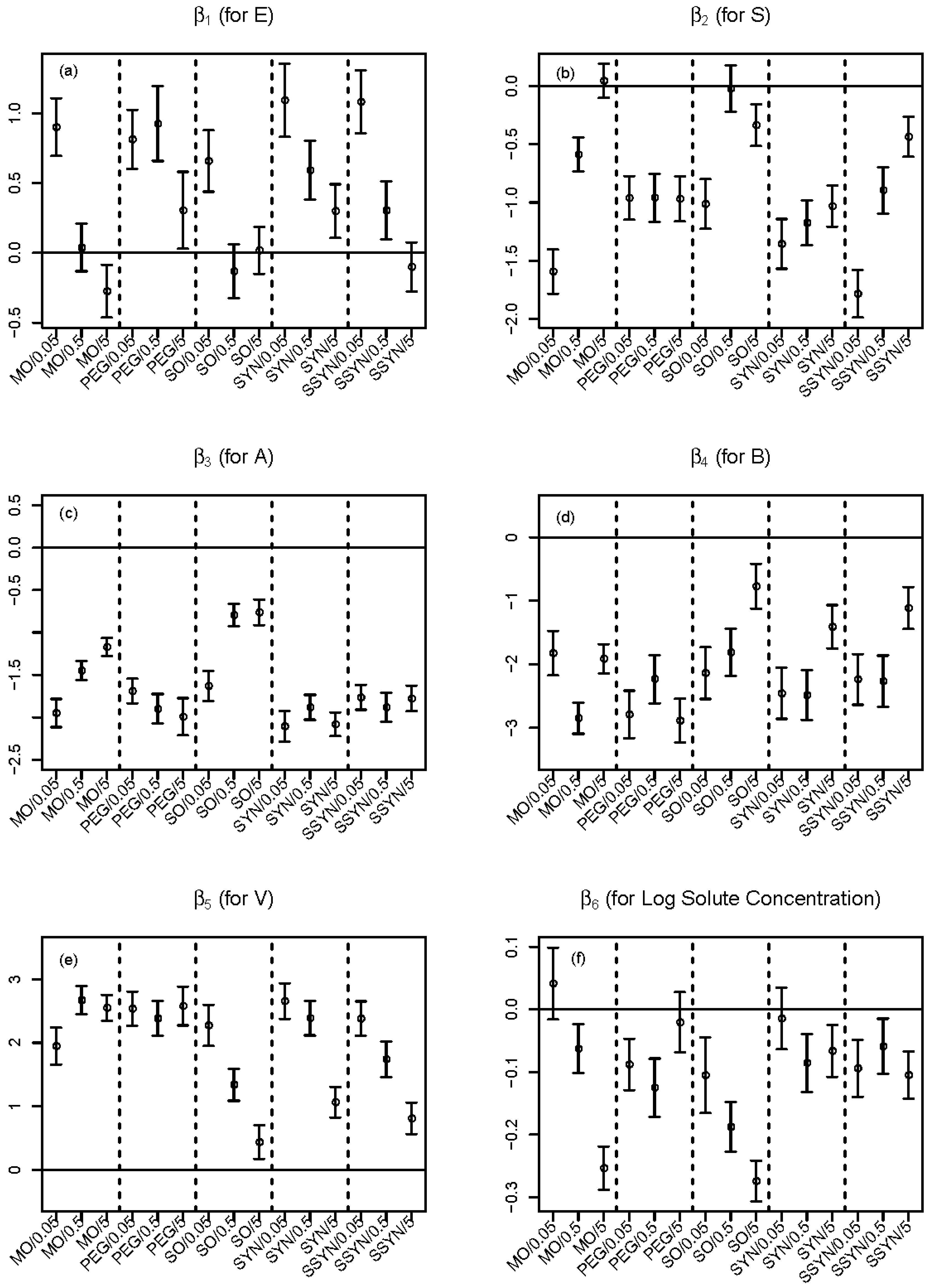
2.3. Improvement by Expanded LFER Models
2.4. Model Interpretation
2.5. Validation of Partition Theory
2.5.1. Implication of Partition Theory
2.5.2. Violation from Experimental Data
3. Materials and Methods
3.1. Solvent/Solute Preparation
3.2. SPME/GC-MS Analysis
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Treatment Combination | MWF | MWF Conc. (%) | Solute Conc. (ppm) | N |
|---|---|---|---|---|
| 1 | MO | 0.05 | 0.01 | 53 |
| 2 | MO | 0.05 | 0.05 | 65 |
| 3 | MO | 0.05 | 0.1 | 65 |
| 4 | MO | 0.05 | 0.5 | 43 |
| 5 | MO | 0.05 | 1 | 39 |
| 6 | MO | 0.05 | 5 | 0 |
| 7 | MO | 0.5 | 0.01 | 62 |
| 8 | MO | 0.5 | 0.05 | 67 |
| 9 | MO | 0.5 | 0.1 | 76 |
| 10 | MO | 0.5 | 0.5 | 80 |
| 11 | MO | 0.5 | 1 | 60 |
| 12 | MO | 0.5 | 5 | 34 |
| 13 | MO | 5 | 0.01 | 53 |
| 14 | MO | 5 | 0.05 | 57 |
| 15 | MO | 5 | 0.1 | 66 |
| 16 | MO | 5 | 0.5 | 85 |
| 17 | MO | 5 | 1 | 86 |
| 18 | MO | 5 | 5 | 50 |
| 19 | PEG | 0.05 | 0.01 | 52 |
| 20 | PEG | 0.05 | 0.05 | 65 |
| 21 | PEG | 0.05 | 0.1 | 68 |
| 22 | PEG | 0.05 | 0.5 | 51 |
| 23 | PEG | 0.05 | 1 | 43 |
| 24 | PEG | 0.05 | 5 | 34 |
| 25 | PEG | 0.5 | 0.01 | 50 |
| 26 | PEG | 0.5 | 0.05 | 56 |
| 27 | PEG | 0.5 | 0.1 | 59 |
| 28 | PEG | 0.5 | 0.5 | 40 |
| 29 | PEG | 0.5 | 1 | 34 |
| 30 | PEG | 0.5 | 5 | 22 |
| 31 | PEG | 5 | 0.01 | 35 |
| 32 | PEG | 5 | 0.05 | 50 |
| 33 | PEG | 5 | 0.1 | 50 |
| 34 | PEG | 5 | 0.5 | 47 |
| 35 | PEG | 5 | 1 | 36 |
| 36 | PEG | 5 | 5 | 28 |
| 37 | SO | 0.05 | 0.01 | 59 |
| 38 | SO | 0.05 | 0.05 | 68 |
| 39 | SO | 0.05 | 0.1 | 47 |
| 40 | SO | 0.05 | 0.5 | 38 |
| 41 | SO | 0.05 | 1 | 30 |
| 42 | SO | 0.05 | 5 | 5 |
| 43 | SO | 0.5 | 0.01 | 51 |
| 44 | SO | 0.5 | 0.05 | 71 |
| 45 | SO | 0.5 | 0.1 | 70 |
| 46 | SO | 0.5 | 0.5 | 79 |
| 47 | SO | 0.5 | 1 | 56 |
| 48 | SO | 0.5 | 5 | 14 |
| 49 | SO | 5 | 0.01 | 43 |
| 50 | SO | 5 | 0.05 | 48 |
| 51 | SO | 5 | 0.1 | 54 |
| 52 | SO | 5 | 0.5 | 74 |
| 53 | SO | 5 | 1 | 73 |
| 54 | SO | 5 | 5 | 76 |
| 55 | SYN | 0.05 | 0.01 | 43 |
| 56 | SYN | 0.05 | 0.05 | 55 |
| 57 | SYN | 0.05 | 0.1 | 59 |
| 58 | SYN | 0.05 | 0.5 | 42 |
| 59 | SYN | 0.05 | 1 | 41 |
| 60 | SYN | 0.05 | 5 | 16 |
| 61 | SYN | 0.5 | 0.01 | 57 |
| 62 | SYN | 0.5 | 0.05 | 67 |
| 63 | SYN | 0.5 | 0.1 | 73 |
| 64 | SYN | 0.5 | 0.5 | 46 |
| 65 | SYN | 0.5 | 1 | 40 |
| 66 | SYN | 0.5 | 5 | 17 |
| 67 | SYN | 5 | 0.01 | 47 |
| 68 | SYN | 5 | 0.05 | 63 |
| 69 | SYN | 5 | 0.1 | 62 |
| 70 | SYN | 5 | 0.5 | 62 |
| 71 | SYN | 5 | 1 | 53 |
| 72 | SYN | 5 | 5 | 34 |
| 73 | SSYN | 0.05 | 0.01 | 58 |
| 74 | SSYN | 0.05 | 0.05 | 65 |
| 75 | SSYN | 0.05 | 0.1 | 68 |
| 76 | SSYN | 0.05 | 0.5 | 47 |
| 77 | SSYN | 0.05 | 1 | 40 |
| 78 | SSYN | 0.05 | 5 | 20 |
| 79 | SSYN | 0.5 | 0.01 | 50 |
| 80 | SSYN | 0.5 | 0.05 | 65 |
| 81 | SSYN | 0.5 | 0.1 | 68 |
| 82 | SSYN | 0.5 | 0.5 | 63 |
| 83 | SSYN | 0.5 | 1 | 32 |
| 84 | SSYN | 0.5 | 5 | 19 |
| 85 | SSYN | 5 | 0.01 | 42 |
| 86 | SSYN | 5 | 0.05 | 57 |
| 87 | SSYN | 5 | 0.1 | 60 |
| 88 | SSYN | 5 | 0.5 | 70 |
| 89 | SSYN | 5 | 1 | 74 |
| 90 | SSYN | 5 | 5 | 54 |
(Intercept) | (for E) | (for S) | (for A) | (for B) | (for V) | (for t) | |
|---|---|---|---|---|---|---|---|
| MO/0.05 | 1.15(0.15) | 0.9(0.11) | −1.59(0.10) | −1.95(0.08) | −1.83(0.18) | 1.95(0.15) | 0.04(0.03) |
| MO/0.5 | 0.10(0.11) | 0.04(0.09) | −0.59(0.07) | −1.45(0.06) | −2.85(0.13) | 2.67(0.11) | −0.06(0.02) |
| MO/5 | −0.86(0.10) | −0.27(0.1) | 0.04(0.07) | −1.17(0.05) | −1.91(0.12) | 2.55(0.10) | −0.25(0.02) |
| PEG/0.05 | −0.12(0.11) | 0.81(0.11) | −0.96(0.10) | −1.69(0.07) | −2.79(0.19) | 2.54(0.14) | −0.09(0.02) |
| PEG/0.5 | −0.10(0.11) | 0.93(0.14) | −0.96(0.11) | −1.90(0.09) | −2.23(0.19) | 2.39(0.14) | −0.13(0.02) |
| PEG/5 | 0.15(0.15) | 0.3(0.14) | −0.97(0.10) | −1.99(0.11) | −2.88(0.18) | 2.58(0.16) | −0.02(0.02) |
| SO/0.05 | 0.30(0.13) | 0.66(0.11) | −1.01(0.11) | −1.63(0.09) | −2.14(0.21) | 2.27(0.17) | −0.11(0.03) |
| SO/0.5 | 0.69(0.11) | −0.13(0.10) | −0.02(0.10) | −0.79(0.07) | −1.82(0.19) | 1.34(0.13) | −0.19(0.02) |
| SO/5 | 0.74(0.12) | 0.02(0.09) | −0.34(0.09) | −0.76(0.08) | −0.77(0.18) | 0.44(0.14) | −0.27(0.02) |
| SYN/0.05 | 0.03(0.12) | 1.09(0.13) | −1.36(0.11) | −2.11(0.09) | −2.46(0.20) | 2.66(0.14) | −0.01(0.03) |
| SYN/0.5 | 0.53(0.11) | 0.59(0.11) | −1.17(0.10) | −1.88(0.07) | −2.48(0.20) | 2.39(0.14) | −0.09(0.02) |
| SYN/5 | 1.55(0.11) | 0.30(0.10) | −1.03(0.09) | −2.08(0.07) | −1.41(0.17) | 1.06(0.12) | −0.07(0.02) |
| SSYN/0.05 | 0.53(0.11) | 1.08(0.11) | −1.78(0.10) | −1.77(0.07) | −2.24(0.20) | 2.38(0.14) | −0.09(0.02) |
| SSYN/0.5 | 0.90(0.12) | 0.30(0.11) | −0.90(0.10) | −1.88(0.09) | −2.27(0.20) | 1.74(0.14) | −0.06(0.02) |
| SSYN/5 | 1.03(0.11) | −0.10(0.09) | −0.44(0.09) | −1.78(0.08) | −1.11(0.17) | 0.81(0.13) | −0.10(0.02) |
References
- McDougal, J.N.; Boeniger, M.F. Methods for assessing risks of dermal exposures in the workplace. Crit. Rev. Toxicol. 2002, 32, 291–327. [Google Scholar] [CrossRef] [PubMed]
- Semple, S. Dermal Exposure to Chemicals in the Workplace: Just How Important Is Skin Absorption? Occup. Environ. Med. 2004, 61, 376–382. [Google Scholar] [CrossRef] [PubMed]
- U.S. EPA Risk Assessment: Guidance for Superfund Volume I: Human Heatlh Evaluation Manual (Part E, Supplemental Guidance for Dermal Risk Assessment). Available online: https://www.google.com.tw/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=2ahUKEwjm5Len6uneAhUIV7wKHXKLCX0QFjAAegQICRAC&url=https%3A%2F%2Fwww.epa.gov%2Fsites%2Fproduction%2Ffiles%2F2015-09%2Fdocuments%2Fpart_e_final_revision_10-03-07.pdf&usg=AOvVaw0icHqYHCaEqHYIwkv7WVCg (accessed on 23 November 2018).
- Eisen, E.A.; Tolbert, P.E.; Monson, R.R.; Smith, T.J. Mortality Studies of Machining Fluid Exposure in the Automobile Industry I: A Standardized Mortality Ratio Analysis. Am. J. Ind. Med. 1992, 22, 809–824. [Google Scholar] [CrossRef] [PubMed]
- Gordon, T. Metalworking Fluid-The Toxicity of a Complex Mixture. J. Toxicol. Environ. Heal. Part A 2004, 67, 209–219. [Google Scholar] [CrossRef] [PubMed]
- Mehta, A.J.; Malloy, E.J.; Applebaum, K.M.; Schwartz, J.; Christiani, D.C.; Eisen, E.A. Reduced lung cancer mortality and exposure to synthetic fluids and biocide in the auto manufacturing industry. Scand. J. Work. Environ. Health 2010, 36, 499–508. [Google Scholar] [CrossRef] [PubMed]
- Monteiro-Riviere, N.A.; Inman, A.O.; Barlow, B.M.; Baynes, R.E. Dermatotoxicity of Cutting Fluid Mixtures: In Vitro and In Vivo Studies. Cutan. Ocul. Toxicol. 2006, 25, 235–247. [Google Scholar] [CrossRef] [PubMed]
- Feldstein, M.M.; Raigorodskii, I.M.; Iordanskii, A.L.; Hadgraft, J. Modeling of percutaneous drug transport in vitro using skin-imitating Carbosil membrane. J. Control. Release 1998, 52, 25–40. [Google Scholar] [CrossRef]
- Moeckly, D.M.; Matheson, L.E. The development of a predictive method for the estimation of flux through polydimethylsiloxane membranes: I. Identification of critical variables for a series of substituted benzenes. Int. J. Pharm. 1991, 77, 151–162. [Google Scholar] [CrossRef]
- Matheson, L.E.; Vayumhasuwan, P.; Moeckly, D.M. The development of a predictive method for the estimation of flux through polydimethylsiloxane membranes. II. Derivation of a diffusion parameter and its application to multisubstituted benzenes. Int. J. Pharm. 1991, 77, 163–168. [Google Scholar] [CrossRef]
- Baynes, R.E.; Xia, X.-R.; Barlow, B.M.; Riviere, J.E. Partitioning Behavior of Aromatic Components in Jet Fuel into Diverse Membrane-coated Fibers. J. Toxicol. Environ. Heal. Part A 2007, 70, 1879–1887. [Google Scholar] [CrossRef] [PubMed]
- Baynes, R.E.; Xia, X.R.; Imran, M.; Riviere, J.E. Quantification of Chemical Mixture Interactions Modulating Dermal Absorption Using a Multiple Membrane Fiber Array. Chem. Res. Toxicol. 2008, 21, 591–599. [Google Scholar] [CrossRef] [PubMed]
- Xia, X.-R.; Baynes, R.E.; Monteiro-Riviere, N.A.; Riviere, J.E. An experimentally based approach for predicting skin permeability of chemicals and drugs using a membrane-coated fiber array. Toxicol. Appl. Pharmacol. 2007, 221, 320–328. [Google Scholar] [CrossRef] [PubMed]
- Xia, X.; Baynes, R.E.; Monteiro-Riviere, N.A.; Leidy, R.B.; Shea, D.; Riviere, J.E. A Novel in-Vitro Technique for Studying Percutaneous Permeation with a Membrane-Coated Fiber and Gas Chromatography/Mass Spectrometry: Part I. Performances of the Technique and Determination of the Permeation Rates and Partition Coefficients of Chemical M. Pharm. Res. 2003, 20, 275–282. [Google Scholar] [CrossRef] [PubMed]
- Potts, R.O.; Guy, R.H. Predicting Skin Permeability. Pharm. Res. 1992, 9, 663–669. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.H. Scales of solute hydrogen-bonding: Their construction and application to physicochemical and biochemical processes. Chem. Soc. Rev. 1993, 22, 73–83. [Google Scholar] [CrossRef]
- Vijay, V.; White, E.M.; Kaminski, M.D.; Riviere, J.E.; Baynes, R.E. Dermal Permeation of Biocides and Aromatic Chemicals in Three Generic Formulations of Metalworking Fluids. J. Toxicol. Environ. Heal. Part A 2009, 72, 832–841. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Hughes-Oliver, J.M.; Brooks, J.D.; Yeatts, J.L.; Baynes, R.E. Selection of appropriate training and validation set chemicals for modelling dermal permeability by U-optimal design. SAR QSAR Environ. Res. 2013, 24, 135–156. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Hughes-Oliver, J.M.; Brooks, J.D.; Baynes, R.E. Predicting skin permeability from complex chemical mixtures: Incorporation of an expanded QSAR model. SAR QSAR Environ. Res. 2013, 24, 711–731. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.H.; Martins, F. Human Skin Permeation and Partition: General Linear Free-Energy Relationship Analyses. J. Pharm. Sci. 2004, 93, 1508–1523. [Google Scholar] [CrossRef] [PubMed]
- Advanced Chemistry Development Inc. ACD/ADME BOXES, Version 4.95. Available online: www.acdlabs.com (accessed on 23 November 2018).
Sample Availability: Samples of the compounds are not available from the authors. |
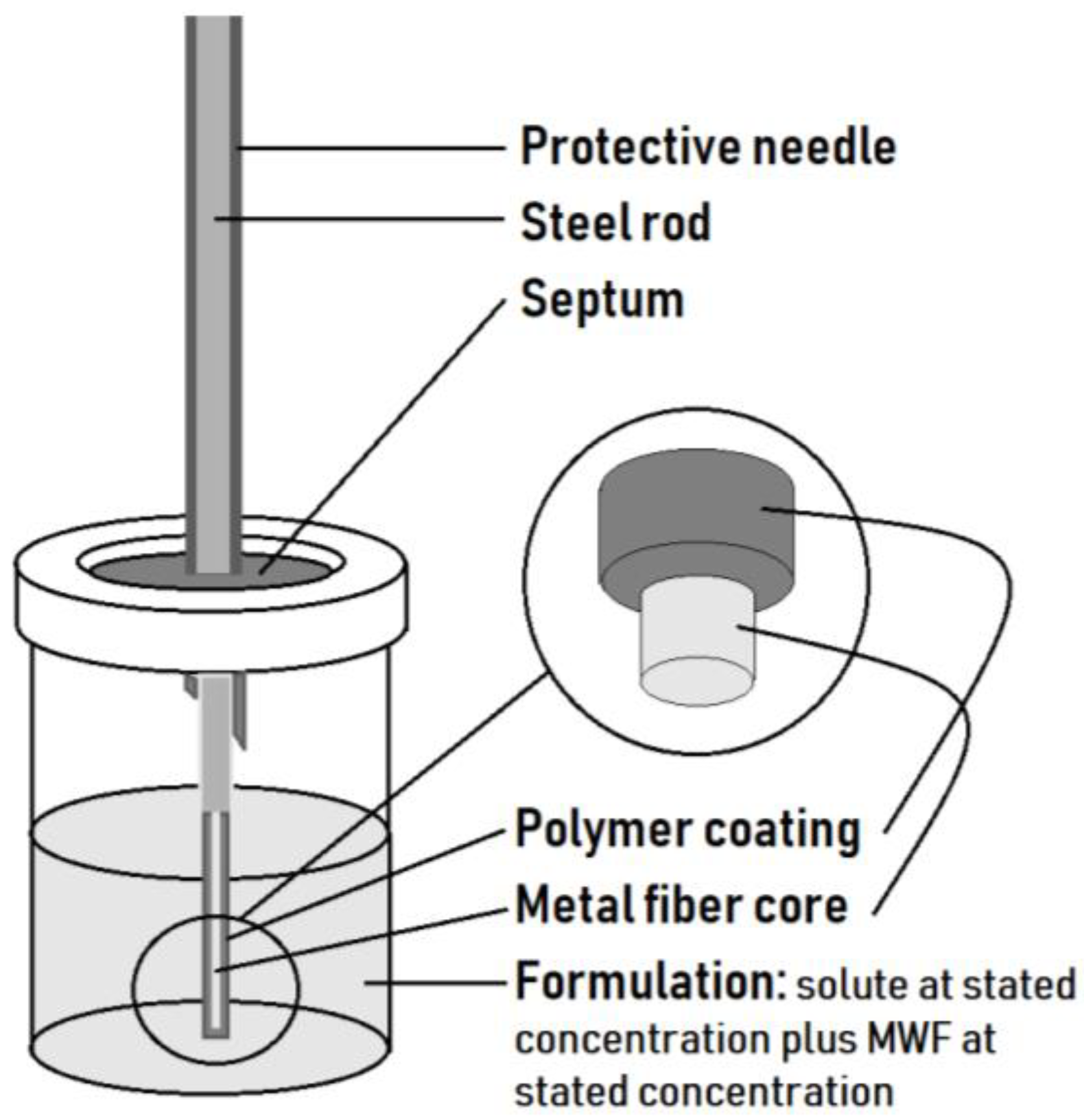
| Solute | Solute Name | E | S | A | B | V |
|---|---|---|---|---|---|---|
| 1 | Toluene | 0.60 | 0.52 | 0 | 0.14 | 0.8573 |
| 2 | Chloro-benzene | 0.72 | 0.65 | 0 | 0.07 | 0.8388 |
| 3 | Ethylbenzene | 0.61 | 0.51 | 0 | 0.15 | 0.9982 |
| 4 | p-Xylene | 0.61 | 0.52 | 0 | 0.16 | 0.9982 |
| 5 | Bromo-benzene | 0.88 | 0.73 | 0 | 0.09 | 0.8914 |
| 6 | Propyl-benzene | 0.60 | 0.50 | 0 | 0.15 | 1.1391 |
| 7 | 1-Chloro-4-methyl-benzene | 0.71 | 0.74 | 0 | 0.05 | 0.9797 |
| 8 | Phenol | 0.81 | 0.89 | 0.60 | 0.30 | 0.7751 |
| 9 | Benzonitrile | 0.74 | 1.11 | 0 | 0.33 | 0.8711 |
| 10 | 4-Fluoro-phenol | 0.67 | 0.97 | 0.63 | 0.23 | 0.7927 |
| 11 | Benzyl alcohol | 0.80 | 0.87 | 0.39 | 0.56 | 0.9160 |
| 12 | Iodo-benzene | 1.19 | 0.82 | 0 | 0.12 | 0.9746 |
| 13 | Phenyl ester acetic acid | 0.66 | 1.13 | 0 | 0.54 | 1.0726 |
| 14 | 2-Chloro-acetophenone | 1.02 | 1.59 | 0 | 0.41 | 1.1363 |
| 15 | Phenol, 4-methyl- | 0.82 | 0.87 | 0.57 | 0.31 | 0.9160 |
| 16 | Nitro-Benzene | 0.87 | 1.11 | 0 | 0.28 | 0.8906 |
| 17 | Methyl ester benzoic acid | 0.73 | 0.85 | 0 | 0.46 | 1.0726 |
| 18 | 1-chloro-4-methoxy-benzene | 0.84 | 0.86 | 0 | 0.24 | 1.0384 |
| 19 | Phenylethyl alcohol | 0.81 | 0.86 | 0.31 | 0.65 | 1.0569 |
| 20 | 3-Methylbenzyl alcohol | 0.82 | 0.90 | 0.39 | 0.59 | 1.0569 |
| 21 | 4-Ethyl-phenol | 0.80 | 0.90 | 0.55 | 0.36 | 1.0569 |
| 22 | 3,5-Dimethyl-phenol | 0.82 | 0.84 | 0.57 | 0.36 | 1.0569 |
| 23 | Ethyl ester benzoic acid | 0.69 | 0.85 | 0 | 0.46 | 1.2135 |
| 24 | 2-Methyl-methyl ester benzoic acid | 0.77 | 0.87 | 0 | 0.43 | 1.2135 |
| 25 | Naphthalene | 1.34 | 0.92 | 0 | 0.20 | 1.0854 |
| 26 | 3-Chloro-phenol | 0.91 | 1.06 | 0.69 | 0.15 | 0.8975 |
| 27 | p-Chloroaniline | 1.06 | 1.13 | 0.30 | 0.31 | 0.9386 |
| 28 | 1-methyl-4-nitro-benzene | 0.87 | 1.11 | 0 | 0.28 | 1.0315 |
| 29 | 1-(4-Chlorophenyl)-ethanone | 0.96 | 1.09 | 0 | 0.44 | 1.1363 |
| 30 | 3-Bromo-phenol | 1.06 | 1.13 | 0.70 | 0.16 | 0.9501 |
| 31 | 4-Chloro-3-methyl-phenol | 0.92 | 1.02 | 0.67 | 0.22 | 1.0384 |
| 32 | 1-Methyl-naphthalene | 1.34 | 0.92 | 0 | 0.20 | 1.2263 |
| 33 | Biphenyl | 1.36 | 0.99 | 0 | 0.26 | 1.3242 |
| 34 | Chloroxylenol | 0.93 | 0.96 | 0.64 | 0.21 | 1.1793 |
| 35 | 4-(1,1-Dimethylpropyl)-phenol | 0.79 | 0.80 | 0.50 | 0.44 | 1.4796 |
| 36 | o-Hydroxybiphenyl | 1.55 | 1.40 | 0.56 | 0.49 | 1.3829 |
| 37 | Clorophene | 1.53 | 1.42 | 0.67 | 0.47 | 1.6462 |
| Variable | Minimum | Lower Quartile | Mean | Median | Upper Quartile | Maximum | Std Dev |
|---|---|---|---|---|---|---|---|
| −1.820 | 0.841 | 1.329 | 1.380 | 1.879 | 3.107 | 0.719 | |
| E | 0.600 | 0.710 | 0.862 | 0.800 | 0.960 | 1.550 | 0.225 |
| S | 0.500 | 0.800 | 0.928 | 0.900 | 1.110 | 1.590 | 0.266 |
| A | 0.000 | 0.000 | 0.120 | 0.000 | 0.000 | 0.700 | 0.232 |
| B | 0.050 | 0.150 | 0.293 | 0.280 | 0.440 | 0.650 | 0.146 |
| V | 0.775 | 0.939 | 1.058 | 1.038 | 1.136 | 1.646 | 0.170 |
| T | (Intercept) | (for E) | (for S) | (for A) | (for B) | (for V) | |
|---|---|---|---|---|---|---|---|
| 5 | est(se) | 0.21(0.45) | 1.77(0.43) | −1.59(0.27) | −1.87(0.18) | −0.50(0.42) | 1.61(0.32) |
| ci | (−0.71, 1.12) | (0.89, 2.65) | (−2.14, −1.03) | (−2.23, −1.51) | (−1.36, 0.36) | (0.97, 2.25) | |
| 17 | est(se) | −0.61(0.27) | −0.91(0.22) | 0.42(0.18) | −1.14(0.12) | −2.00(0.24) | 2.47(0.25) |
| ci | (−1.15, −0.07) | (−1.35, −0.48) | (0.07, 0.77) | (−1.37, −0.91) | (−2.48, −1.53) | (1.97, 2.97) | |
| 52 | est(se) | 1.50(0.31) | −0.03(0.23) | −0.36(0.25) | −0.42(0.20) | −0.98(0.48) | −0.14(0.34) |
| ci | (0.89, 2.11) | (−0.50, 0.44) | (−0.87, 0.15) | (−0.83, −0.02) | (−1.94, −0.02) | (−0.81, 0.53) |
| Regression Statistics | LFER Model (1) | Expanded Crossed-Factors LFER Model (2) | Expanded Nested-Solute-Concentration LFER Model (5) |
|---|---|---|---|
| r2 | 0.60 | 0.90 | 0.88 |
| Adj-r2 | 0.60 | 0.89 | 0.87 |
| 0.60 | 0.87 | 0.87 | |
| 0.57 | 0.68 | 0.80 |
| Solute Concentrations | p-Value for H0 | Insignificant Conditions | Significant Conditions |
|---|---|---|---|
| All | < 0.0001 | MO/0.05(265), PEG/5(246), SYN/0.05(256), SSYN/0.5(297) | MO/0.5(379), MO/5(397), PEG/0.05(313), PEG/0.5(261), SO/0.05(247), SO/0.5(341), SO/5(368), SYN/0.5(300), SYN/5(321), SYN/0.05(298), SSYN/5(357) |
| 0.01, 0.05, 0.1, 0.5, 1 | < 0.0001 | MO/0.05(265), MO/0.5(345), PEG/0.05(279), PEG/5(218), SYN/0.05(240), SYN/5(287), SSYN/0.5(278) | MO/5(347), PEG/0.5(239), SO/0.05(242), SO/0.5(327), SO/5(292), SYN/0.5(283), SSYN/0.05(278), SSYN/5(303) |
| 0.01, 0.05, 0.1, 0.5 | < 0.0001 | MO/0.05(226), MO/0.5(285), PEG/0.05(236), PEG/0.5(205), PEG/5(182), SO/0.05(212), SYN/0.05(199), SYN/0.5(243), SYN/5(234), SSYN/0.05(238), SSYN/0.5(246) | MO/5(261), SO/0.5(271), SO/5(219), SSYN/5(229) |
| 0.01, 0.05, 0.1 | < 0.0001 | MO/0.05(183), PEG/0.05(185), PEG/0.5(165), PEG/5(135), SO/0.05 (174), SYN/0.05(157), SYN/0.5(197), SYN/5(172), SSYN/0.05(191), SSYN/0.5(183) | MO/0.5(205), MO/5(176), SO/0.5(192), SO/5(145), SSYN/5(159) |
| 0.05, 0.1, 0.5 | < 0.0001 | MO/0.05(173), MO/0.5(223),MO/5(208), PEG/0.05(184), PEG/0.5(155), PEG/5(147), SO/0.05(153), SYN/0.05(156), SYN/0.5(186), SYN/5(187), SSYN/0.05(180), SSYN/0.5(196), SSYN/5(187) | SO/0.5(141), SO/5(102) |
| 0.01, 0.05 | < 0.0001 | MO/0.05(118), PEG/0.05(117), PEG/5(85), SO/0.05(127), SO/0.5(122), SYN/0.05(98), SYN/0.5(124), SYN/5(110), SSYN/0.05(123), SSYN/0.5(115), SSYN/5(99) | MO/0.5(129), MO/5(110), PEG/0.5(106), SO/5(91) |
| 0.05, 0.1 | < 0.0001 | MO/0.05(130), MO/0.5(143), MO/5(123), PEG/0.5(115), PEG/5(100), SO/0.05(115), SO/5(102), SYN/0.05(114), SYN/0.5(140), SYN/5(125), SSYN/0.05(133), SSYN/0.5(133), SSYN/5(117) | PEG/0.05(133), SO/0.5(141) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hughes-Oliver, J.M.; Xu, G.; Baynes, R.E. Skin Permeation of Solutes from Metalworking Fluids to Build Prediction Models and Test A Partition Theory. Molecules 2018, 23, 3076. https://doi.org/10.3390/molecules23123076
Hughes-Oliver JM, Xu G, Baynes RE. Skin Permeation of Solutes from Metalworking Fluids to Build Prediction Models and Test A Partition Theory. Molecules. 2018; 23(12):3076. https://doi.org/10.3390/molecules23123076
Chicago/Turabian StyleHughes-Oliver, Jacqueline M., Guangning Xu, and Ronald E. Baynes. 2018. "Skin Permeation of Solutes from Metalworking Fluids to Build Prediction Models and Test A Partition Theory" Molecules 23, no. 12: 3076. https://doi.org/10.3390/molecules23123076
APA StyleHughes-Oliver, J. M., Xu, G., & Baynes, R. E. (2018). Skin Permeation of Solutes from Metalworking Fluids to Build Prediction Models and Test A Partition Theory. Molecules, 23(12), 3076. https://doi.org/10.3390/molecules23123076






