Next Article in Journal
Synthesis and Biological Evaluation of Hydrazone Derivatives as Antifungal Agents
Next Article in Special Issue
Interplay between Beryllium Bonds and Anion-π Interactions in BeR2:C6X6:Y− Complexes (R = H, F and Cl, X = H and F, and Y = Cl and Br)
Previous Article in Journal
Curcumin, Inflammation, and Chronic Diseases: How Are They Linked?
Previous Article in Special Issue
Pi-pi Stacking Mediated Cooperative Mechanism for Human Cytochrome P450 3A4
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 20
Issue 5
10.3390/molecules20059214
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

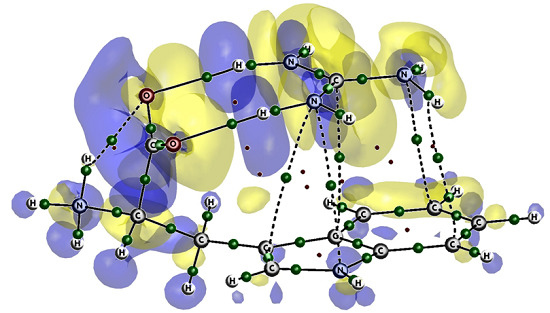
Aromatic Amino Acids-Guanidinium Complexes through Cation-π Interactions

by
Cristina Trujillo
1,
Ana A. Rodriguez-Sanz
2 and
Isabel Rozas
1,*
1
Trinity Biomedical Sciences Institute, School of Chemistry, Trinity College Dublin, 152-160 Pearse Street, Dublin 2, Ireland
2
Departamento de Química Física, Facultade de Ciencias, Universidade de Santiago de Compostela, Campus de Lugo, Avda. Alfonso X El Sabio s/n, 27002 Lugo, Spain
*
Author to whom correspondence should be addressed.
Molecules 2015, 20(5), 9214-9228; https://doi.org/10.3390/molecules20059214
Submission received: 23 April 2015 / Revised: 11 May 2015 / Accepted: 12 May 2015 / Published: 20 May 2015
(This article belongs to the Special Issue Noncovalent pi-Interactions)
Browse Figures
Versions Notes

Abstract

:
Continuing with our interest in the guanidinium group and the different interactions than can establish, we have carried out a theoretical study of the complexes formed by this cation and the aromatic amino acids (phenylalanine, histidine, tryptophan and tyrosine) using DFT methods and PCM-water solvation. Both hydrogen bonds and cation-π interactions have been found upon complexation. These interactions have been characterized by means of the analysis of the molecular electron density using the Atoms-in-Molecules approach as well as the orbital interactions using the Natural Bond Orbital methodology. Finally, the effect that the cation-π and hydrogen bond interactions exert on the aromaticity of the corresponding amino acids has been evaluated by calculating the theoretical NICS values, finding that the aromatic character was not heavily modified upon complexation.

Graphical Abstract

1. Introduction

Cation-π interactions have been the objective of a vast number of experimental and computational studies since Kerbarle’s seminal publication in 1981 [1]. A very important contribution to this topic has been made by Dougherty and co-workers who showed, for example, that even in water phenyl hosts bind to cationic guests stronger than to neutral or charged molecules [2]. Moreover, they carried out a protein database assessment showing that cation-stabilization is fundamental in protein structure and function and that arginine (Arg) in particular is the residue that most often [3] binds. In addition, they also reported the importance of these interactions for protein engineering [4,5]. During the 1990s, Thornton and Singh [6] analyzed a large number of crystal structures and found that aromatic amino acids prefer stacking interactions to hydrogen bonding [7].
In 2011, Frontera et al. published a review on cation-π interactions analyzing the forces involved in these contacts and found that some physical properties of the aromatic systems and interacting ions are directly related to the strength of the interaction [8]. Furthermore, in 2011, this same group published that π-π interactions are influenced by the presence or absence of hydrogen bonds (HBs) that are formed in a third aromatic system far from the stacking interaction analyzed [9]. In a recent article, this group have revisited the controversial proposal that substituent effects in cation-π interactions can be attributed mainly to electrostatic effects by analyzing 171 aromatic systems interacting with Na+; they found that both electrostatic and π-polarization effects describe cation-π interactions [10].
Gromiha and co-workers lleagues carried out several studies on cation-π interactions responsible of protein stability. They established that the roles of cation-π interactions are different from those of other non-covalent contacts in the stability of protein structures and that Arg is more likely to form cation-π interactions than lysine (Lys) [11]. Already in 1986, Burley and Patsko demonstrated that side-chain amino groups interact with aromatic side chains by analyzing 33 protein crystal structures; they found that positively charged amino groups of Lys or Arg are preferentially located over the ring centroids of aromatic amino acids [12]. Another similar study is that published by Karlin et al. where they found that this type of interactions could have implications in protein folding [13].
During the last 10 years, we have worked on the design, synthesis and biological evaluation of guanidinium derivatives some of which aim to target DNA; for that reason, we previously studied the complexes established by this cation and the four DNA heteroaromatic bases [14]. We proved that all of these interactions are deeply affected by the environment and, hence, to consider aqueous solvation of guanidinium is essential for a good description of its experimental/biological properties. Considering that different families of our guanidine derivatives are aimed to interact with proteins such as receptors (α2-adrenoceptors) [15] or enzymes (kinases) [16] and to continue with our interest [17,18,19,20] in the interactions and properties of the guanidinium cation, we have now carried out the theoretical study of the complexes formed by this particular cation and aromatic amino acids (phenylalanine –Phe-, tyrosine –Tyr-, tryptophan –Trp- and histidine –His-).
In this particular area, the recent work of Cabaleiro-Lago and Rodriguez-Otero deserves special attention. On the one hand, they have studied the interaction of microhydrated guanidinium with the aromatic systems existing in the aromatic amino acids and found that the presence of a small number of water molecules significantly affects the characteristics of the complexes. Hydrogen bonds formed by water with the cation, another water molecule, or the aromatic units lead to a large number of minima similar in energy but very different structurally. They found that the differences in stability were mainly a consequence of the different strength of the cation···π contact [21]. On the other hand, they have recently published the study of the interaction of guanidinium with Phe, Tyr and Trp in the gas phase as neutral systems finding that the most stable minima correspond to folded amino acids, with the cation interacting simultaneously with the carboxyl oxygen, the amino nitrogen and the aromatic ring, whereas zwitterionic amino acids are as stable as neutral ones [22].
In the present study, we have chosen to use bulk solvent instead of microhydration for coherence with our previous studies. In addition to the study of the corresponding complexes, we have carried out an evaluation of the aromaticity changes induced in the aromatic rings upon complexation by calculating the corresponding nucleus-independent chemical shift NICS indexes [23]. This study has allowed us to better understand the potential interactions that guanidinium derivatives can establish when targeting proteins, which can determined their biological activity and influence their molecular design.

2. Results and Discussion

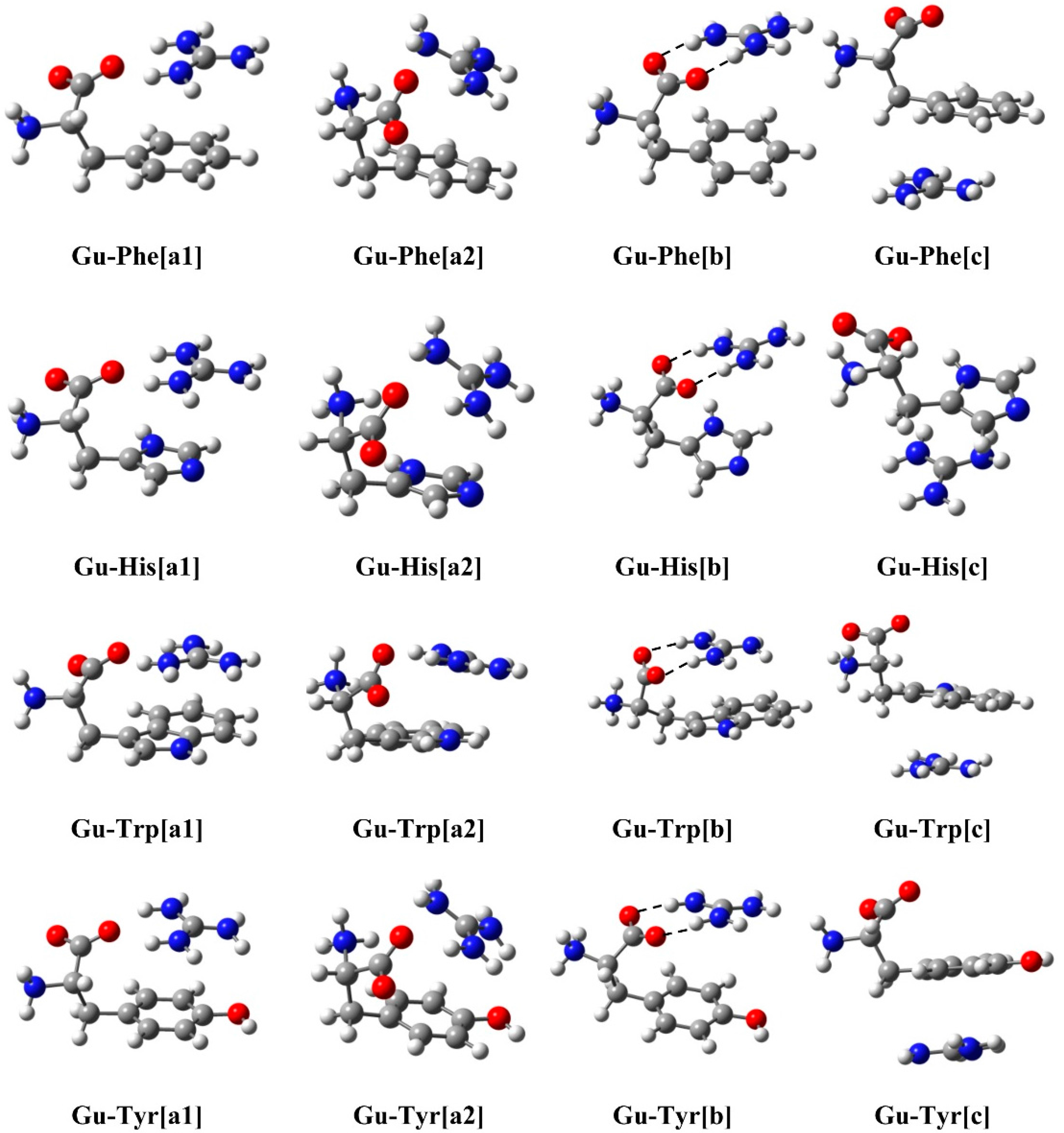
2.1. Structure and Energy

We have studied all the complexes formed by the interaction between the guanidium cation and four aromatic amino acids: Phe, His, Trp and Tyr, using the M06-2X [24] DFT method at the 6-311++G(d,p) [25] computational level including water solvation by means of the SCFR-PCM approach [26]. The optimized structures are presented in Figure 1.
Molecules 20 09214 g001 550
Figure 1. Optimized geometry of the complexes studied at the M06-2X/6-311++G(d,p) level.
Figure 1. Optimized geometry of the complexes studied at the M06-2X/6-311++G(d,p) level.
Molecules 20 09214 g001
In all the complexes both HBs and cation-π interactions have been found. Three types of complexes have been established depending on the interactions encountered within. Complexes type [a] which are formed by a bifurcated HB (between two guanidinium H atoms and one O atom of the carboxylic group belonging to the amino acid) plus an additional cation-π interaction. Two different orientations can be distinguished in this type of [a] complexes: in the [a1] conformation the NH2 group of the amino acid is oriented backward with respect to the guanidinium, while in the [a2] complexes the NH2 group is oriented towards the cation. Type [b] complexes are formed by a parallel HB interaction of two guanidinium H atoms with two O atoms of the amino acid carboxylic group and also a cation-π interaction (see Figure 1 complexes [b]). Finally, type [c] complexes are formed only by cation-π interactions between the guanidinium moiety and the π cloud of the aromatic ring of the respective amino acid.
Interaction energies (Ei, kJ·mol−1) are gathered in Table 1. For all amino acids, complexes of type [a] and [b], with both HBs and cation-π interactions, are quite more stable than complexes type [c], which are formed only by cation-π interactions. In all cases complexes [a1] with bifurcated HBs are the most stable, followed by complexes type [b] which present double HBs. Both kind of complexes, [a1] and [b] possess very close Ei values with only 2–3 kJ·mol−1 of difference. The only exception appears in the case of Trp, in which complex type [a2] is slightly more stable than complex [b].
Table
Table 1. Interaction energies (Ei, kJ·mol−1) for all the complexes studied at the M06-2X/6-311++G(d,p) computational level.
Table 1. Interaction energies (Ei, kJ·mol−1) for all the complexes studied at the M06-2X/6-311++G(d,p) computational level.
M06-2xGu-PheGu-HisGu-TrpGu-Tyr
[a1]−68.2−50.3−65.2−69.5
[a2]−60.8−41.1−60.1−64.3
[b]−65.6−48.1−55.7−66.8
[c]−21.4−21.4−15.9−19.8
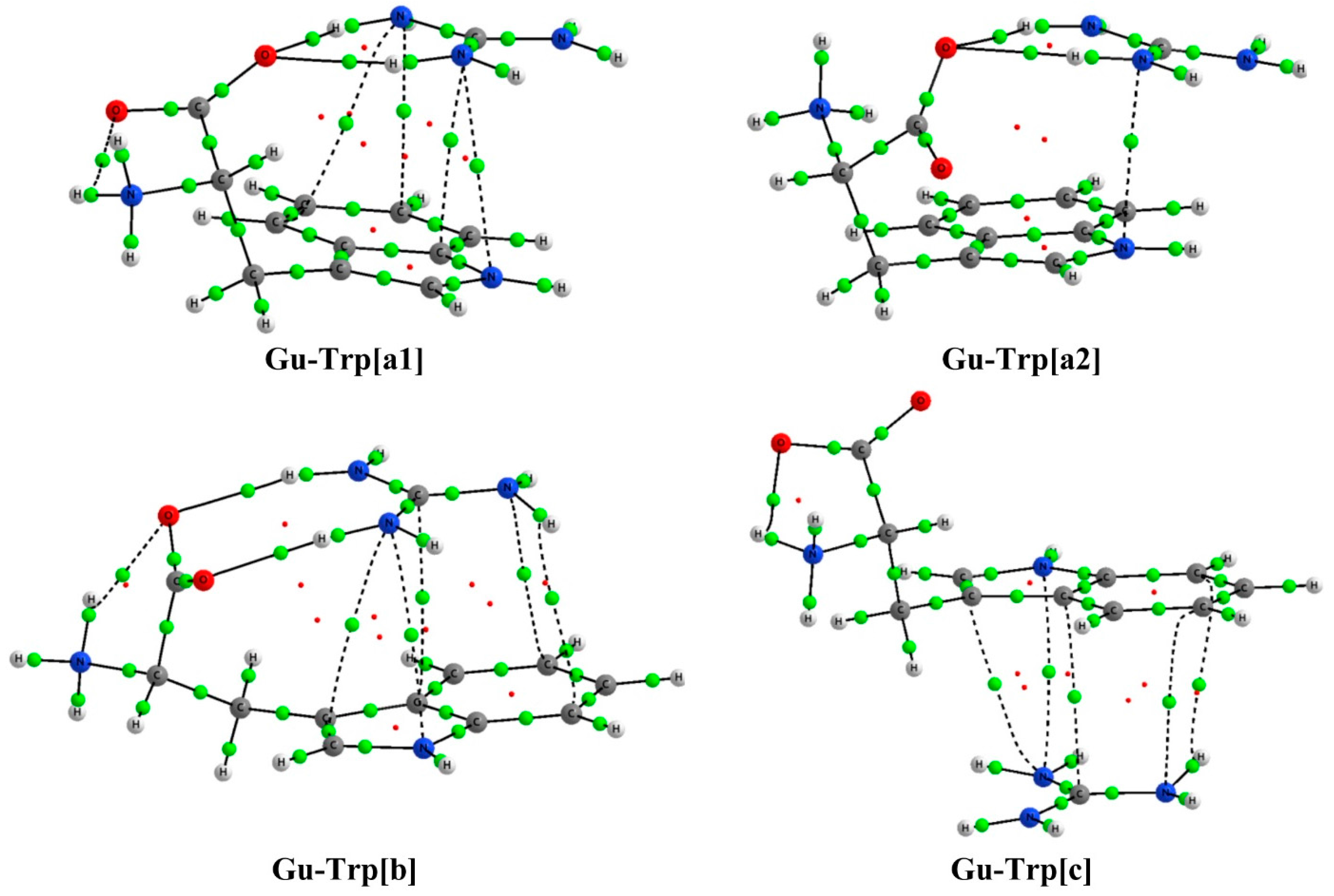
It is important to note that, looking at the interaction energy values for the different complexes, those with the larger Ei values (most stable) correspond to the complexes formed with Tyr and Phe, while the least stable complexes correspond to the guanidinium-His complexes. Even though the main contribution to the stability of these complexes should arise from the HBs established, His is considered to be the least aromatic of the four amino acids here considered and this could be the reason of the weaker interaction observed with guanidinium.

2.2. Analysis of the Electron Density: AIM Analysis

The topological analysis of the electron density of the guanidinium complexes obtained, using the AIM approach [27], indicates that a number of interactions are established with the four amino acids as shown by the bond critical points (BCP) detected in the graphical analysis [28]; some examples of these graphs are exhibited in Figure 2 and the rest are presented in the Supporting Information (Figure S1). The BCPs, both for HBs and cation-π interactions, present small values of the electron density (ρBCP) and positive Laplacian values (∇2ρBCP), as shown in Table 2, indicating the closed shell characteristics of the weak interactions established among the guanidinium and the amino acids. In general, HBs (N···H or O···H) show larger ρBCP values (10−2 a.u. order of magnitude) than those found in the cation-π interactions (10−3 a.u. order of magnitude) corresponding to the relative strength of these type of contacts.
Molecules 20 09214 g002 550
Figure 2. AIM-Molecular graphs of the Gu-Trp complexes calculated at the M06-2X/6-311++G(d,p) computational level in PCM−water. Green and red balls indicate bond and ring critical points, respectively.
Figure 2. AIM-Molecular graphs of the Gu-Trp complexes calculated at the M06-2X/6-311++G(d,p) computational level in PCM−water. Green and red balls indicate bond and ring critical points, respectively.
Molecules 20 09214 g002
As shown in Table 2, the largest values of the ρBCP correspond to parallel HBs, which are those present in complexes type [b]. This is in agreement with the fact that in the case of multiple HB systems, where parallel and bifurcated complexes can be compared, parallel HB interactions are more stable and preferred over the bifurcated ones [29]. Moreover, in the present study, the largest number of cation-π contributions is found for the complexes established with Trp, which is the only amino acid with a bicyclic structure (indole functional group). In contrast, when the complexation occurs with His, BCPs associated to cation-π interactions are not found for the complexes type [a2] and [c].
Amongst the different interactions established within these complexes (O…H, C…C, C…N, N…N) we have found an exponential relationship between the interatomic distances (in Å) and the density in the BCP for the HBs (ρBCP = 1.608 e−2.144(d), see Supporting Information Figure S2) with a good R2 correlation coefficient of 0.972. Moreover, an exponential relationship between the Laplacian of the electron density at the BCPs for cation-π interactions and the interatomic distances (Å) has been found (∇2 ρBCP = 4.698 e−1.616(d), see Supporting Information Figure S3), with a R2 coefficient of 0.804. These types of correlations have been found in previous studies with different HBs [30,31,32,33,34].
Table
Table 2. AIM analysis (interaction type, ρBCP and (∇2ρBCP, a.u.) of all the complexes studied at the M06-2X/6-311++G(d,p) computational level in PCM-water.
Table 2. AIM analysis (interaction type, ρBCP and (∇2ρBCP, a.u.) of all the complexes studied at the M06-2X/6-311++G(d,p) computational level in PCM-water.
ComplexTypeρBCP∇2ρBCPComplexTypeρBCP∇2ρBCP
Gu-Phe[a1]cation-π0.00720.0212Gu-Phe[a2]cation-π0.00530.0152
0.00720.02140.00830.0254
O1…H10.03030.1204O1…H10.02830.1119
O1…H20.02700.1130O1…H20.02200.0913
Gu-Phe[b]cation-π0.00530.0140Gu-Phe[c]cation-π0.00640.0193
0.00590.01730.00710.0229
O1…H10.03720.1292N…H0.00470.0144
O2…H20.03220.1149
Gu-His[a1]cation-π0.00620.0215Gu-His[a2]O1…H10.02700.1063
0.00880.0286O1…H20.02240.0940
O…N0.00910.0295N…H0.00900.0296
O1…H10.02990.11730.01250.0420
O1…H20.02660.1141
Gu-His[b]cation-π0.00410.0119Gu-His[c]N…H0.00510.0148
N…H0.00860.02640.01000.0337
O1…H10.03740.1280
O2…H20.03500.1228
Gu-Trp[a1]cation-π0.00640.0197Gu-Trp[a2]cation-π0.008410.02968
0.00690.0204O1…H10.026280.09790
0.00740.0223O1…H20.026000.10560
0.00780.0280
O1…H10.03050.1181
O1…H20.02560.1075
Gu-Trp[b]cation-π0.006220.01993Gu-Trp[c]cation-π0.006890.01947
0.006350.018430.007040.02092
0.006610.019010.007250.02356
0.007020.024660.007250.02218
0.007150.02102
O1…H10.030380.11460
O2…H20.028660.10782
Gu-Tyr[a1]cation-π0.008470.02842Gu-Tyr[a2]cation-π0.007400.02233
O…H0.007860.026640.008580.02565
O1…H10.028140.11408O…H0.011730.04084
O1…H20.029530.11944O1…H10.029580.07545
O1…H20.018370.11510
Gu-Tyr[b]cation-π0.005810.01535Gu-Tyr[c]cation-π0.006750.02034
N…H0.006060.018050.006950.02257
O1…H10.037930.13075
O2…H20.031640.11321
To achieve a visual description of the electron density changes that result from the complexation process, electron density shift maps (EDS) [35] have been calculated for the complexes Gu-Trp[a1], Gu-Trp[a2], Gu-Trp[b], and Gu-Trp[c] (Figure 3).
Molecules 20 09214 g003 550
Figure 3. Electron Density Shifts at 0.00045 a.u. of Gu-Tyr complexes at the M06-2X/6-311++G(d,p) computational level in PCM–water. Yellow and blue areas represent positive (increase) and negative (decrease) electron density regions respectively.
Figure 3. Electron Density Shifts at 0.00045 a.u. of Gu-Tyr complexes at the M06-2X/6-311++G(d,p) computational level in PCM–water. Yellow and blue areas represent positive (increase) and negative (decrease) electron density regions respectively.
Molecules 20 09214 g003
As observed for [a] and [b] complexes, a distinctive picture for the electronic density shift is obtained for HBs, i.e., a yellow area (positive) appears between the H and O atoms, which accounts for an increment of the electron density between those two atoms. Besides, the maps corresponding to the cation-π interaction show a charge-gaining region (yellow) between both moieties while a charge-depleting area (light blue) is obtained on top of the amino acids aromatic rings (complexes [a] and [b]) or the guanidinium cation (complex [c]), which evidences the cation-π interaction.

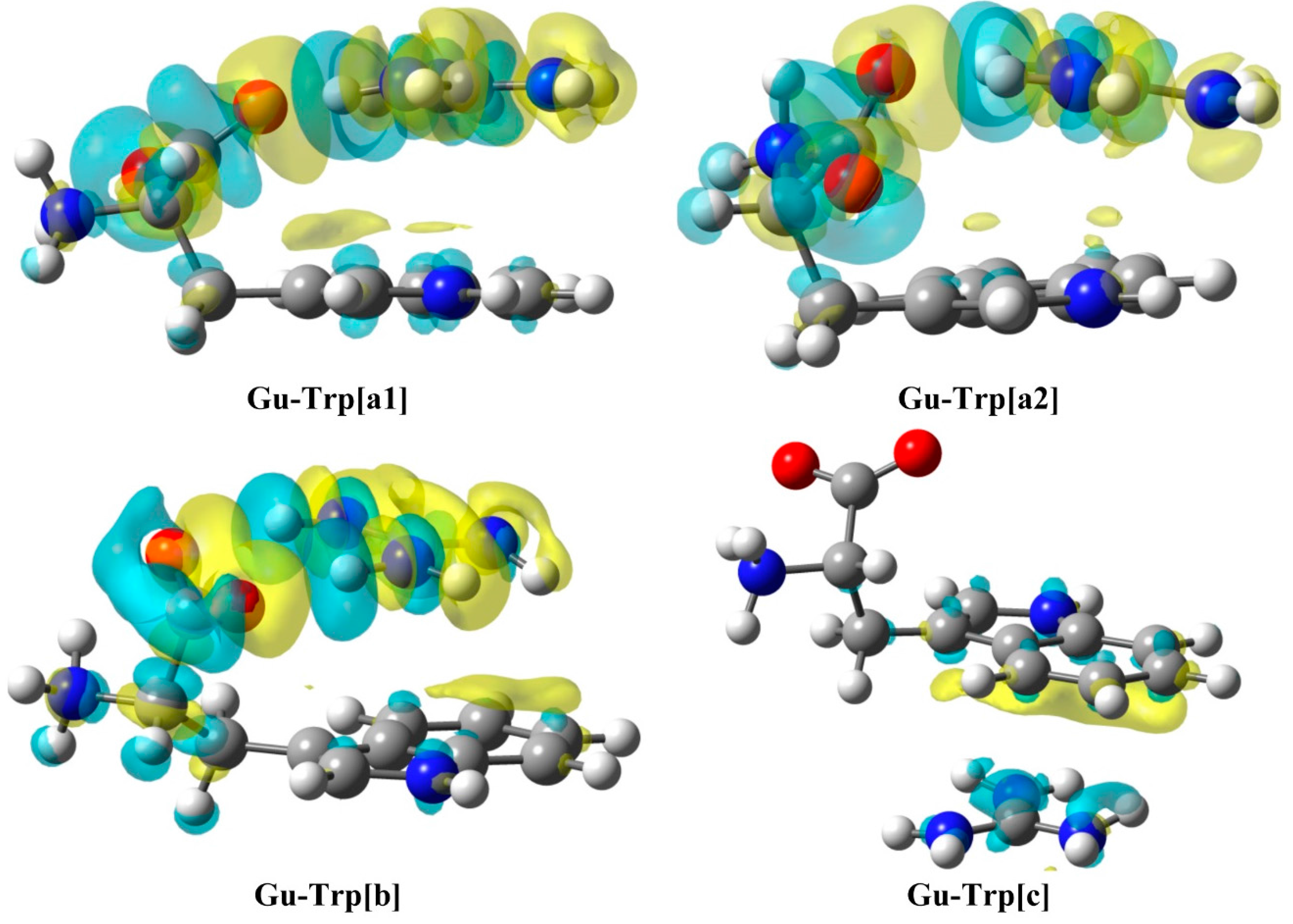
2.3. Natural Bond Orbital (NBO) Analysis

The NBO analysis [36] of all the complexes studied has been carried out to assess the orbital interactions established among the monomers and the corresponding second order orbital energies [E(2), kJ·mol−1] are presented in Table 3.
For the HB interactions within all the complexes, those of type [b] showed the largest E(2) values. These complexes involve two HBs between two heteroatoms interacting with the guanidinium as opposed to the bifurcated HBs interacting with one heteroatom observed in complexes of type [a]. The strongest E(2) values are observed in type [b] complexes and correspond to a donation from the carbonyl O lone-pairs to the N-H antibonding orbitals of guanidinium (between 56.7–116.9 kJ·mol−1). Comparing the E(2) values obtained for the different types of HBs within each complex it can be seen that, in general, the difference between both values is bigger for complexes with bifurcated HBs, finding the biggest difference for type [a2] complexes.
Table
Table 3. Orbital energy [E(2), kJ·mol−1] of the complexes studied at the M06-2X/6-311++G(d,p) computational level in PCM–water.
Table 3. Orbital energy [E(2), kJ·mol−1] of the complexes studied at the M06-2X/6-311++G(d,p) computational level in PCM–water.
ComplexOrbital InteractionE(2)ComplexOrbital InteractionE(2)
Gu-Phe[a1]BD CC → LP* CG7.2Gu-Phe[a2]LP CG → BD* CC4.4
BD CC → BD* NGH1.6LP O → BD* NH70.4
LP O → BD* NH63.3LP O → BD* NHʹ19.4
LP O → BD* NHʹ49.5
Gu-Phe[b]BD CC → LP* CG3.9Gu-Phe[c]LP CG → BD* CC2.4
LP O → BD* NH83.7
LP Oʹ → BD* NHʹ74.8
Gu-His[a1]BD NCG → BD* NC1.3Gu-His[a2]LP CG → BD* CC1.0
LP O → BD* NH64.8LP O → BD* NH64.6
LP O → BD* NHʹ43.8LP O → BD* NHʹ15.0
Gu-His[b]LP NG → BD* NH6.0Gu-His[c]BD CNG → BD* NH2.3
LP O → BD* NH104.2
LP Oʹ → BD* NHʹ89.4
Gu-Trp[a1]LP N → LP* CG4.7Gu-Trp[a2]LP NG → BD* CC5.6
BD CC→ BD* NCG4.7LP CG → BD* CC4.3
LP O → BD* NH41.2LP O → BD* NH45.1
LP O → BD* NHʹ34.3LP O → BD* NHʹ33.8
Gu-Trp[b]LP NG → BD* CC4.6Gu-Trp[c]LP NG → BD* NH2.9
LP CG → BD* CC1.1LP CG → BD* NH1.4
LP O → BD* NH57.4
LP Oʹ → BD* NHʹ56.7
Gu-Tyr[a1]LP CG → BD* CC3.7Gu-Tyr[a2]LP CG → BD* CC1.6
LP O → BD* NHG5.6LP NG → BD* CC1.5
LP O → BD* NH58.0LP O → BD* NHG9.9
LP O → BD* NHʹ52.8LP NG → BD* NH6.1
LP O → BD* NH89.6
LP O → BD* NHʹ3.3
Gu-Tyr[b]LP CG → BD* NH3.0Gu-Tyr[c]LP NG → BD* NH1.0
LP NG → BD* NH2.2LP CG → BD* NH0.7
LP O → BD* NH116.9
LP Oʹ → BD* NHʹ68.6
In the cation-π interactions the most important orbital exchanges are those from the C-C bonding orbitals of the aromatic systems to an “empty” lone pair of the guanidinium central C atom (BD CC → LP* CG) indicating a donation from the aromatic system to the guanidinium. However, also, when an acceptor orbital is appropriately positioned, donation from a guanidinium N or C lone pair to antibonding orbitals on the amino acids occurs. It is important to highlight that the magnitudes of the second order perturbation energies are smaller in cation-π interactions than in HB interactions.
In spite of the slight differences obtained between E(2) and Ei values for the different complexes, if a comparison between both is to be made, a good exponential correlation can be found [E(2) = 0.848 e−0.08(Ei), R2 = 0.823, see Supporting Information, Figure S4).

2.4. Effect on the Aromaticity

In order to study the effect that guanidinium complexation has on the aromaticity of the amino acids in all the systems considered, we have calculated the NICS values at 0, 1 and 2 Å over the ring center of each aromatic system. Some authors prefer the use of NICS(zz) [also called NICS(out-of-plane), zz denomination corresponds to the out-of-plane component in a planar ring system in which the molecular plane is contained into the XY plane] component to describe aromaticity or antiaromaticity. It is known that in some cases, NICS can diagnose delocalization and NICS(zz) predicts the opposite behavior or vice versa; also it has been shown that this occurs mainly because NICS values are contaminated by the in-plane contributions [37,38]. However, and following our previous experience [39,40], the average NICS values have been used for the discussion instead of the NICS(zz) component. Since we want to assess how the aromaticity on the amino acids is affected upon complexation, we have calculated the NICS values of all amino acids as well as of those of the complexes with the same level of theory. All calculated NICS values obtained at 0, 1, and 2 Å have been gathered in Table 4. For comparison purposes, the benzene NICS values calculated at the same level of theory have been included. As it was observed previously[41], the NICS(0) may lead to a non-reliable interpretation of the aromatic properties, since the proximity of the atom nuclei could distort the NICS values.
Table
Table 4. NICS values (ppm) for all cation-π interactions complexes studied at the M06-2X/6-311++G(d,p) computational level in PCM-water. In parenthesis are the values for five member ring for Trp and its complexes.
Table 4. NICS values (ppm) for all cation-π interactions complexes studied at the M06-2X/6-311++G(d,p) computational level in PCM-water. In parenthesis are the values for five member ring for Trp and its complexes.
ComplexNICS(0)NICS(1)NICS(2)
Benzene−7.5−10.5−5.2
Phe−7.5−10.4−5.1
Gu-Phe[a1]−7.4−10.3−5.2
Gu-Phe[a2]−8.5−10.9−5.1
Gu-Phe[b]−7.6−10.1−5.1
Gu-Phe[c]−7.9−10.8−5.2
His−11.5−10.1−4.1
Gu-His[a1]−12.5−10.9−4.4
Gu-His[a2]−12.2−10.9−4.6
Gu-His[b]−12.3−10.7−1.4
Gu-His[c]−12.0−10.4−4.2
Trp−9.0 (−12.3)−10.9 (−10.6)−5.3 (−4.3)
Gu-Trp[a1]−9.6 (−12.9)−11.0 (−10.5)−5.6 (−4.6)
Gu-Trp[a2]−9.0 (−12.7)−11.0 (−10.3)−5.5 (−4.6)
Gu-Trp[b]−9.4 (−13.1)−10.9 (−10.8)−5.4 (−4.8)
Gu-Trp[c]−9.3 (−13.0)−10.8 (−10.9)−5.3 (−4.9)
Tyr−8.7−10.0−4.8
Gu-Tyr[a1]−8.5−10.0−4.8
Gu-Tyr[a2]−8.8−9.8−4.9
Gu-Tyr[b]−9.8−10.4−4.6
Gu-Tyr[c]−9.2−10.4−5.0
The results indicate that, as expected, all amino acids under study are aromatic, with NICS values very close to those of benzene. When the complexes are formed no significant variance in the aromaticity has been found. However, some slight increase of the NICS values for type [b] complexes for all amino acids is observed, with the exception of Trp; actually, the NICS values for complexes formed with this amino acid remain practically constant. In contrast, it is important to note that for His all complexes formed show an increase slightly larger in absolute value than for the other amino acids.
In order to obtain additional information on the aromaticity of these systems, we have calculated and plotted the NICS values on the 0.001 a.u. electron density isosurface (resembling the van der Waals surface) for the amino acids selected and all the complexes studied in this work (Figure 4). Comparing the isosurfaces of the isolated amino acids with those of aromatic systems previously studied by us (benzene or pyridine) [41] it can be observed that their aromatic characterizations are similar to those of systems such as benzene or pyridine.
Molecules 20 09214 g004 550
Figure 4. 3D-Representation of the NICS values (ppm) on the 0.001 a.u. electron density isosurfaces of Phe, His and Tyr and of the cation-π guanidinium complexes studied at M06-2X/6-311+G(d,p) computational level. Color code: blue < −4.0, Green > −4.0, Yellow > −2.0, Red > 0.0. NICS minima values in the aromatic ring are marked with cyan dots.
Figure 4. 3D-Representation of the NICS values (ppm) on the 0.001 a.u. electron density isosurfaces of Phe, His and Tyr and of the cation-π guanidinium complexes studied at M06-2X/6-311+G(d,p) computational level. Color code: blue < −4.0, Green > −4.0, Yellow > −2.0, Red > 0.0. NICS minima values in the aromatic ring are marked with cyan dots.
Molecules 20 09214 g004
Minima NICS values on the 0.001 a.u. electron density isosurface for the complexes (Figure 4), localized in the center of the rings, reveal that upon complexation, the NICS distribution in the surfaces remains very similar to that in the isolated monomers. However, in the case of Phe minor changes are observed; thus, a minor decrease in the aromaticity is detected for the Gu-Phe[b] complex, while for complexes Gu-His[a1], Gu-His[a2] and Gu-Tyr[c] an slight increase is observed upon complexation.

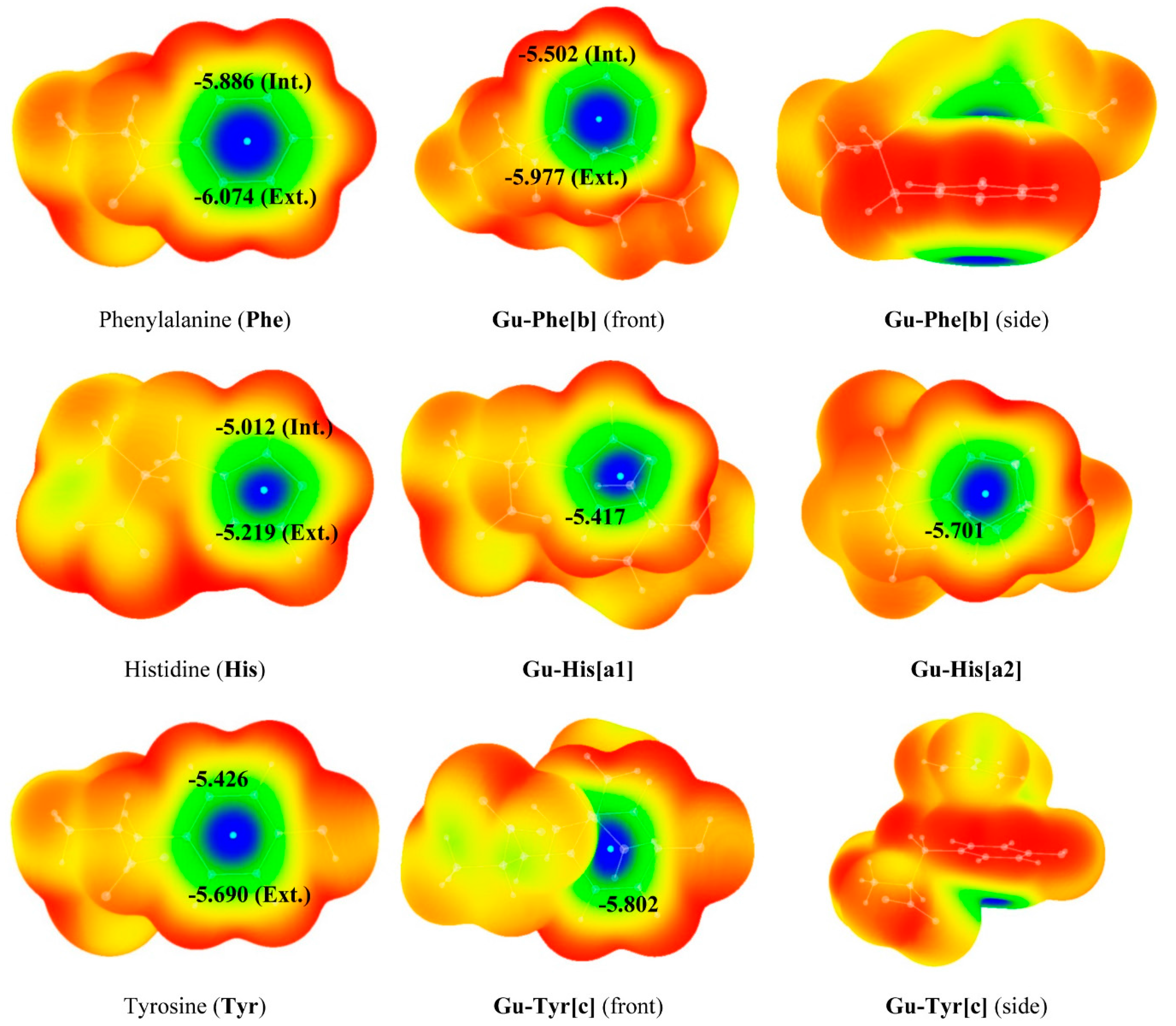
3. Experimental Section

All systems (monomers and complexes) have been optimized using the M06-2X [24] computational level with the 6-311++G(d,p) [25] basis sets. The M06-2X functional has been shown to properly describe weak interactions taking into account dispersion forces where other traditional functionals fail.
Effects of water solvation have been included by means of the SCFR-PCM approaches implemented in the Gaussian09 package [26] including dispersing, repulsing, and cavitating energy terms of the solvent starting from the gas-phase geometries and re-optimizing.
The interaction energy of the complexes has been calculated as the difference between the energy of the supermolecule (complex) and the sum of the energies of the isolated monomers in their minimum energy configuration.
The electron density of the complexes has been analyzed within the Atoms in Molecules (AIM) [27] theory using AIMAll software [28]. The Natural Bond Orbital (NBO) [36] method has been used to analyze the interaction of the occupied and unoccupied orbitals with the NBO-3 program [42], since this kind of interaction is of utmost importance in the formation of hydrogen bonds and other charge transfer complexes.
The theoretical NICS values were calculated using the GIAO method on the optimized geometries. To calculate the spatial distribution of the NICS, its values have been calculated on a three-dimensional (3D) cubic grid of 12 Å side following the procedure described by Sánchez-Sanz et al. [41]. The points in the grid are located at 0.2 Å from each other in the three spatial directions. The result is a cube with 226,981 NICS values that, in the next step, were represented within the electron density isosurface of 0.001 a.u. using the WFA program [43].
The intramolecular electron density shift (EDS) has been obtained using the fragmentation scheme proposed in ref 33. This method proposes the calculation of the EDS of the intramolecular interaction by comparing the electron density of the interacting moieties. The EDS is calculated using Equation (1):
EDS = ρ(complex) − ρ(amino acid) − ρ(guanidinium)

4. Conclusions

The complexes established by the guanidinium cation and the aromatic amino acids, Phe, His, Trp and Tyr by means of cation-π and hydrogen bonding interactions have been computationally studied using PCM–water at the M06-2X/6-311++G(d,p) level.
All the minima found correspond to complexes of three different types: complexes type [a] formed by a bifurcated HB between two guanidinium H atoms and one O atom of the carboxylic group belonging to the amino acid and a cation-π interaction between both monomers; complexes type [b] formed by a double parallel HB interaction of two guanidinium H atoms with two O of the carboxylic group of the amino acid plus a cation-π interaction; and complexes type [c] formed only by cation-π interactions between the aromatic moiety of the amino acids and guanidinium.
The computed interaction energies show that the most stable complexes found for all the aromatic amino acids were the complexes type [a] and [b], which exhibit both HB and cation-π interactions.
The AIM analysis of these guanidinium-amino acids complexes showed a number of interactions (HBs and cation-π) established between both moieties as shown by the bond critical points found. The electron density at the BCPs and its Laplacian are in agreement with weak interactions, being the parallel HBs of the complexes type [b] stronger than the bifurcated ones found in type [a] complexes. Different correlations have been found between the interatomic distances and the value of the electron density at the BCP for the HB interactions.
Natural Bond Orbital analysis has been performed allowing a better understanding of the nature of the interactions. Based on the perturbation energy E(2), the most important bonding interactions were the HBs found in complexes [a] and [b] from the lone pair of the oxygen in an amino acid to an antibonding N-H orbital of guanidinium (LP O → BD* NH). Further, cation-π interactions have been found in almost all complexes being the most important bonding contribution that corresponding to the interaction between a bonding C-C or C-N orbitals and the empty ‘lone pair’ of the guanidinium central C. In all these complexes, an exponential correlation was found between the E(2) and the interaction energy Ei.
Finally, to understand the effect that the complexation with a guanidinium cation has on the aromaticity of the amino acid studied, the NICS values were calculated and the 3D NICS surfaces were produced, finding that the aromatic character was not heavily modified upon complexation. All this information indicates that guanidinium containing compounds would positively interact with protein binding sites rich in aromatic amino acids without modifying the properties of those residues.

Supplementary Materials

Supplementary materials can be accessed at: https://www.mdpi.com/1420-3049/20/05/9214/s1.

Acknowledgments

Thanks are given to Irish Centre for High-End Computing (ICHEC) and the Trinity Centre for High-Performance Computing (TCHPC) for the provision of computational facilities. We are indebted to Goar Sánchez from the School of Physics at the University College Dublin, for the AIM analysis and for helpful discussions. A.A.R.S. thanks the financial support from the Ministerio de Ciencia e Innovación and the ERDF 2007–2013 (Grant No. CTQ2009-12524), to the Centro de Supercomputación de Galicia (CESGA) for the use of their computers and to the Spanish Ministerio de Ciencia e Innovación for a FPI grant.

Author Contributions

I.R. conceived the idea for this study. C.T. and A.A.R.-S. performed the calculations. C.T. and I.R. wrote the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Sunner, J.; Nishizawa, K.; Kebarle, P. Ion-solvent molecule interactions in the gas phase. The potassium ion and benzene. J. Phys. Chem. 1981, 85, 1814–1820. [Google Scholar] [CrossRef]
  2. Ma, J.C.; Dougherty, D.A. The Cation-π Interaction. Chem. Rev. 1997, 97, 1303–1324. [Google Scholar] [CrossRef] [PubMed]
  3. Gallivan, J.P.; Dougherty, D.A. Cation-π interactions in structural biology. Proc. Natl. Acad. Sci. USA 1999, 96, 9459–9464. [Google Scholar] [CrossRef] [PubMed]
  4. Dougherty, D.A. Cation-π Interactions Involving Aromatic Amino Acids. J. Nutr. 2007, 137, 1504S–1508S. [Google Scholar] [PubMed]
  5. Gallivan, J.P.; Dougherty, D.A. A Computational Study of Cation-π Interactions vs. Salt Bridges in Aqueous Media: Implications for Protein Engineering. J. Am. Chem. Soc. 2000, 122, 870–874. [Google Scholar] [CrossRef]
  6. Singh, J.; Thornton, J.M. SIRIUS: An automated method for the analysis of the preferred packing arrangements between protein groups. J. Mol. Biol. 1990, 211, 595–615. [Google Scholar] [CrossRef] [PubMed]
  7. Mitchell, J.B.O.; Nandi, C.L.; McDonald, I.K.; Thornton, J.M.; Price, S.L. Amino/Aromatic Interactions in Proteins: Is the Evidence Stacked Against Hydrogen Bonding? J. Mol. Biol. 1994, 239, 315–331. [Google Scholar] [CrossRef] [PubMed]
  8. Frontera, A.; Quiñonero, D.; Deyà, P.M. Cation-π and anion-π interactions. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 440–459. [Google Scholar] [CrossRef]
  9. Estarellas, C.; Frontera, A.; Quiñonero, D.; Deyà, P.M. Theoretical ab initio study of substituted benzene trimer: Interplay between hydrogen bonding and π-π interactions. Comput. Theor. Chem. 2011, 975, 106–110. [Google Scholar] [CrossRef]
  10. Bauza, A.; Deya, P.M.; Frontera, A.; Quinonero, D. Substituent effects in cation-[small pi] interactions revisited: A general approach based on intrinsic properties of the arenes. Phys. Chem. Chem. Phys. 2014, 16, 1322–1326. [Google Scholar] [CrossRef] [PubMed]
  11. Gromiha, M.M.; Santhosh, C.; Ahmad, S. Structural analysis of cation-π interactions in DNA binding proteins. Int. J. Biol. Macromol. 2004, 34, 203–211. [Google Scholar] [CrossRef] [PubMed]
  12. Burley, S.K.; Petsko, G.A. Amino-aromatic interactions in proteins. FEBS Lett. 1986, 203, 139–143. [Google Scholar] [CrossRef] [PubMed]
  13. Karlin, S.; Zuker, M.; Brocchieri, L. Measuring Residue Association in Protein Structures Possible Implications for Protein Folding. J. Mol. Biol. 1994, 239, 227–248. [Google Scholar] [CrossRef] [PubMed]
  14. Blanco, F.; Kelly, B.; Sánchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J.; Rozas, I. Non-Covalent Interactions: Complexes of Guanidinium with DNA and RNA Nucleobases. J. Phys. Chem. B 2013, 117, 11608–11616. [Google Scholar] [CrossRef] [PubMed]
  15. Kelly, B.; McMullan, M.; Muguruza, C.; Ortega, J.E.; Meana, J.J.; Callado, L.F.; Rozas, I. α2-Adrenoceptor Antagonists: Synthesis, Pharmacological Evaluation, and Molecular Modeling Investigation of Pyridinoguanidine, Pyridino-2-aminoimidazoline and Their Derivatives. J. Med. Chem. 2015, 58, 963–977. [Google Scholar] [CrossRef] [PubMed]
  16. Diez-Cecilia, E.; Kelly, B.; Perez, C.; Zisterer, D.M.; Nevin, D.K.; Lloyd, D.G.; Rozas, I. Guanidinium-based derivatives: Searching for new kinase inhibitors. Eur. J. Med. Chem. 2014, 81, 427–441. [Google Scholar] [CrossRef] [PubMed]
  17. Rozas, I.; Kruger, P.E. Theoretical Study of the Interaction between the Guanidinium Cation and Chloride and Sulfate Anions. J. Chem. Theor. Comput. 2005, 1, 1055–1062. [Google Scholar] [CrossRef]
  18. Rozas, I.; Alkorta, I.; Elguero, J. Hydrogen bonds and ionic interactions in Guanidine/Guanidinium complexes: A computational case study. Struct. Chem. 2008, 19, 923–933. [Google Scholar] [CrossRef]
  19. Blanco, F.; Kelly, B.; Alkorta, I.; Rozas, I.; Elguero, J. Cation-π interactions: Complexes of guanidinium and simple aromatic systems. Chem. Phys. Lett. 2011, 511, 129–134. [Google Scholar] [CrossRef]
  20. Kelly, B.; O'Donovan, D.H.; O'Brien, J.; McCabe, T.; Blanco, F.; Rozas, I. Pyridin-2-yl Guanidine Derivatives: Conformational Control Induced by Intramolecular Hydrogen-Bonding Interactions. J. Org. Chem. 2011, 76, 9216–9227. [Google Scholar] [CrossRef] [PubMed]
  21. Rodríguez-Sanz, A.; Cabaleiro-Lago, E.; Rodríguez-Otero, J. Effect of stepwise microhydration on the guanidinium···π interaction. J. Mol. Model. 2014, 20, 1–10. [Google Scholar] [CrossRef]
  22. Rodriguez-Sanz, A.A.; Cabaleiro-Lago, E.M.; Rodriguez-Otero, J. Interaction between the guanidinium cation and aromatic amino acids. Phys. Chem. Chem. Phys. 2014, 16, 22499–22512. [Google Scholar] [CrossRef] [PubMed]
  23. Schleyer, P.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; Hommes, N.J.R.E. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
  24. Zhao, Y.; Truhlar, D. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
  25. Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-Consistent Molecular-Orbital Methods 25. Supplementary Functions for Gaussian-Basis Sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
  26. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  27. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
  28. Keith, T.A. AIMAll (Version 14.11.23). TK Gristmill Software: Overland Park, KS, USA, 2014; Available online: aim.tkgristmill.com (accessed on 19 May 2015).
  29. Rozas, I. On the nature of hydrogen bonds: An overview on computational studies and a word about patterns. Phys. Chem. Chem. Phys. 2007, 9, 2782–2790. [Google Scholar] [CrossRef] [PubMed]
  30. Sanchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Weak interactions between hypohalous acids and dimethylchalcogens. Phys. Chem. Chem. Phys. 2012, 14, 9880–9889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  31. Rozas, I.; Sánchez-Sanz, G.; Alkorta, I.; Elguero, J. Solvent effects on guanidinium-anion interactions and the problem of guanidinium Y-aromaticity. J. Phys. Org. Chem. 2013, 26, 378–385. [Google Scholar] [CrossRef]
  32. Trujillo, C.; Sánchez-Sanz, G.; Alkorta, I.; Elguero, J.; Mó, O.; Yáñez, M. Resonance assisted hydrogen bonds in open-chain and cyclic structures of malonaldehyde enol: A theoretical study. J. Mol. Struct. 2013, 1048, 138–151. [Google Scholar] [CrossRef]
  33. Picazo, O.; Alkorta, I.; Elguero, J. Large Chiral Recognition in Hydrogen-Bonded Complexes and Proton Transfer in Pyrrolo[2,3-b]pyrrole Dimers as Model Compounds. J. Org. Chem. 2003, 68, 7485–7489. [Google Scholar] [CrossRef] [PubMed]
  34. Mata, I.; Alkorta, I.; Molins, E.; Espinosa, E. Universal Features of the Electron Density Distribution in Hydrogen-Bonding Regions: A Comprehensive Study Involving H···X (X = H, C, N, O, F, S, Cl, π) Interactions. Chem. Eur. J. 2010, 16, 2442–2452. [Google Scholar] [CrossRef] [PubMed]
  35. Sánchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Electron density shift description of non-bonding intramolecular interactions. Comput. Theor. Chem. 2012, 991, 124–133. [Google Scholar] [CrossRef]
  36. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  37. Islas, R.; Martínez-Guajardo, G.; Jiménez-Halla, J.O.C.; Solà, M.; Merino, G. Not All That Has a Negative NICS Is Aromatic: The Case of the H-Bonded Cyclic Trimer of HF. J. Chem. Theor. Comput. 2010, 6, 1131–1135. [Google Scholar] [CrossRef]
  38. Torres, J.J.; Islas, R.; Osorio, E.; Harrison, J.G.; Tiznado, W.; Merino, G. Is Al2Cl6 Aromatic? Cautions in Superficial NICS Interpretation. J. Phys. Chem. A 2013, 117, 5529–5533. [Google Scholar] [CrossRef] [PubMed]
  39. Sánchez-Sanz, G. Aromatic behaviour of benzene and naphthalene upon pnictogen substitution. Tetrahedron 2015, 71, 826–839. [Google Scholar] [CrossRef]
  40. Sánchez-Sanz, G.; Trujillo, C.; Rozas, I.; Elguero, J. A theoretical study on the aromaticity of benzene and related derivatives incorporating a C–CC–C fragment. Tetrahedron 2013, 69, 7333–7344. [Google Scholar] [CrossRef]
  41. Sánchez-Sanz, G.; Alkorta, I.; Trujillo, C.; Elguero, J. A theoretical NMR study of the structure of benzynes and some of their carbocyclic and heterocyclic analogs. Tetrahedron 2012, 68, 6548–6556. [Google Scholar] [CrossRef]
  42. Glendening, E.D.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO, Version 3.1. Available online: http://www.gaussian.com/g_tech/g_ur/m_citation.htm (accessed on 20 May 2015).
  43. Bulat, F.; Toro-Labbé, A.; Brinck, T.; Murray, J.; Politzer, P. Quantitative analysis of molecular surfaces: Areas, volumes, electrostatic potentials and average local ionization energies. J. Mol. Model. 2010, 16, 1679–1691. [Google Scholar] [CrossRef] [PubMed]
  • Samples Availability: Not available.

Share and Cite

MDPI and ACS Style

Trujillo, C.; Rodriguez-Sanz, A.A.; Rozas, I. Aromatic Amino Acids-Guanidinium Complexes through Cation-π Interactions. Molecules 2015, 20, 9214-9228. https://doi.org/10.3390/molecules20059214

AMA Style

Trujillo C, Rodriguez-Sanz AA, Rozas I. Aromatic Amino Acids-Guanidinium Complexes through Cation-π Interactions. Molecules. 2015; 20(5):9214-9228. https://doi.org/10.3390/molecules20059214

Chicago/Turabian Style

Trujillo, Cristina, Ana A. Rodriguez-Sanz, and Isabel Rozas. 2015. "Aromatic Amino Acids-Guanidinium Complexes through Cation-π Interactions" Molecules 20, no. 5: 9214-9228. https://doi.org/10.3390/molecules20059214

APA Style

Trujillo, C., Rodriguez-Sanz, A. A., & Rozas, I. (2015). Aromatic Amino Acids-Guanidinium Complexes through Cation-π Interactions. Molecules, 20(5), 9214-9228. https://doi.org/10.3390/molecules20059214

Article Metrics

Back to TopTop