This is a short discussion of my views on the so-called Gibbs paradox (
GP) . The fact is that Gibbs himself never mentioned this paradox [
1], and whatever is referred to as Gibbs paradox is not really a paradox at all.
There are several versions of the so-called Gibbs paradox. We shall discuss here two versions of the GP and show that one arises from treating the particle classically, not recognizing the indistinguishability (ID) of the particles, the other involves the fallacious idea that the ID of the particles is a property that can be changed continuously.
The first paradox arises when we use the (purely) classical partition function. As is well known, the classical
PF gives the correct equation of state, the correct heat capacity and some other properties of an ideal gas [
2]. It fails to give the correct entropy or the chemical potential. More specifically the entropy (or better the missing information) of a system, derived from the classical partition function, does not have the additive property, or more generally, S
Class is not an extensive function of the variables
E,
V,
N [
3].
It is also well known that by correcting the classical
PF for the
ID of the particles, the resulting entropy becomes an extensive function (see for example [
3]).
Clearly, the fact that a wrong result is obtained from the classical
PF does not consist of a paradox. In the history of science, there are abundant examples of incorrect results obtained from an inappropriate theory. For instance, lattice models of the liquid state yielded some correct results for mixtures, but
Figure 1.
Mixing and assimilation processes.
Figure 1.
Mixing and assimilation processes.
failed to predict the entropy of liquids. This discrepancy was never considered to be a paradox, it was, fixed in an ad-hoc manner by adding the so-called
communal entropy (see for example [
4]). However, this remedy was abandoned later when it was recognized that a lattice model is inherently inappropriate to describe the liquid state.
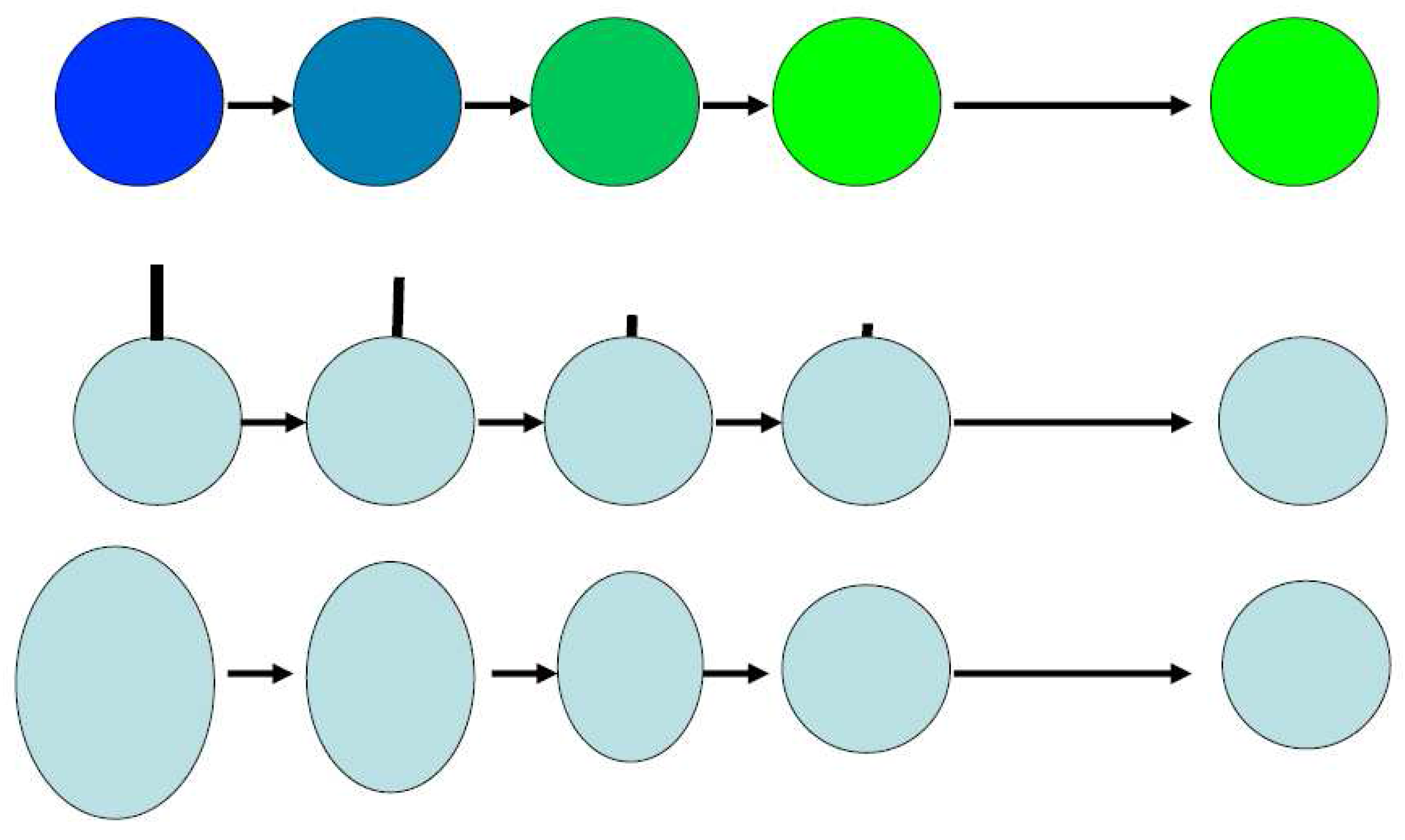
The second version of the paradox is associated with the so-called entropy of mixing. Consider the two processes depicted in
Figure 1. These two processes were analyzed by Gibbs [
1]. As is well known the entropy change in processes I and II in
Figure 1 are
We choose here the Boltzmann constant
k = 1. The paradox in this case is often stated as follows [
5]. Suppose we could have changed the extent of
ID of the particle continuously, say linearly from the distinguishable particles to
ID, Similar to the processes depicted in
Figure 2. If we do that, we should have expected that the value of ∆
S should also change continuously from ∆
SI, when the two components
A and
B are distinguishable, to ∆
SII when they become
ID. The fact is that one never observes any intermediary value between ∆
SI and ∆
SII. The fact that ∆
S changes
discontinuously as one changes the
ID continuously, is viewed as a paradox. However, there is no paradox here, and there was no allusion to any paradox in Gibbs writings. There are many examples that a discontinuous transition follows a continuous change of a parameter. For instance the fact that the density of water changes discontinuously when the temperature changes continuously, say between 90C to 110C is not viewed as a paradox. Furthermore, the presumed continuous change in the extent of
ID of the particles is now recognized as, in principle, invalid. Particles are either distinguishable or
ID-there are no intermediate values of indistinguishability [
6].
Figure 2.
Continuous change of colors, labels or shapes; The objects change from different to identical. However they remain distinguishable.
Figure 2.
Continuous change of colors, labels or shapes; The objects change from different to identical. However they remain distinguishable.
It should be noted that in Process I, the two components A and B are different, whereas in Process II, the particles are all identical. In the initial state, the particles in each compartment are ID among themselves, but the particles in one compartment are distinguishable from the particles that are in the second compartment. Upon removal of the partition in Process I, the particles A and B remain distin-guishable. On the other hand, removal of the partition in process II makes all the particles in the system indistinguishable.
Gibbs did notice the remarkable fact that the entropy of mixing is independent of the degree of similarity between the particles. This fact seems to him to be more puzzling than the fact that ∆
S collapses discontinuously to zero when the particles become identical. On this matter, Gibbs writes [
7]:
But if such considerations explain why the mixture of gas-masses of the same kind stands on different footing from mixtures of gas-masses of different kinds, the fact is not less significant that the increase of entropy due to mixture of gases of different kinds in such a case as we have supposed, is independent of the nature of the gases.
Indeed, if one conceives of the
mixing itself as the cause of entropy of mixing then it is quite puzzling to find that the entropy of mixing is independent of the
kind of the mixing molecule. It should be noted here that in mixing of two
liquids, the change in the entropy will, in general, depend on the type of molecules that are mixed. The reason is that in mixing liquids, the interactions between AA, AB and BB are different, and strongly dependent of the type of molecules. Similarly the entropy change in a chemical reaction between A and B will most likely depend on the type of molecules A and B. However, for ideal gases, the
mixing, in itself, does not play any role in determining the value of the so-called entropy of mixing. Once we recognize that it is the
expansion, not the
mixing, which causes a change in the entropy, then the puzzling fact that the change in entropy is independent of the kind of molecules evaporates (more on that in [
2]).
The real paradox that arises from Gibbs writings and that seemed to elude the attention of scientists is the following. In analyzing the two processes I and II, Gibbs correctly obtained the results (1) and (2). Today, we would say that process I, for which ∆
S > 0, is irreversible in the sense that it is not be reversed spontaneously. On the other hand, process II for which ∆
S = 0 is said to be reversible. At this juncture, let us turn to Gibbs himself [
1]:
If we should bring into contact two masses of the same kind of gas, they would also mix but there would be no increase in entropy.
When we say that when two different gases mix by diffusion, and the entropy receives a certain increase, we mean that the gases could be separated and brought to the same volumeby means of certain changes in external bodies, for example, by the passage of a certain amount of heat from a warmer to a colder body. But when we say that when two gas masses of the same kind are mixed under similar circumstances, there is no change of energy or entropy, we do not mean that the gases which have been mixed can be separated without change to external bodies. On the contrary, the separation of the gases is entirely impossible.
In plain words, Gibbs concluded that process I
can be
reversed in the sense that the system can be brought to its initial state. This reversal of process I would require investing energy. However, for process II, Gibbs concluded that its reversal is
entirely impossible. Here is a paradox: How can a process, which is deemed to be
reversible (process II), be at the same time
entirely impossible to reverse? As I have discussed in my book [
2], this apparent paradox is only an illusion. It is an illusion arising from our mental imaging of process II, in which particles are assigned mental coordinates, and mental trajectories. In this view, we can mentally reverse the process, simply by imagining that we can bring each particle back to its original compartment. However, Gibbs understood that if the particles are
ID, then we cannot reverse the process. Today, we say that,
in principle, we cannot follow their trajectories, and the assignment of mental coordinates to the particles is only a delusion. Therefore, it is impossible to reverse this process! It is impossible to bring each particle to its original compartment (while the same is possible for process I). Howeve, if we think of the particles as
ID from the
outset, then the question of whether or not one can bring each particle to its original compartment becomes meaningless. The only meaningful question is whether or not one can bring the system into its original
thermodynamic state. This is not
entirely impossible, as claimed by Gibbs, but is trivially possible; one has simply to place the partition back to its original place, and process II is reversed.
In conclusion I would like to add one point which in my view has caused a great deal of confusion in the literature. Consider the following chain of arguments:
Mixing two different gases causes increase in disorder.
Increase in disorder is conceived as an increase in entropy.
Therefore from 1 and 2 it follows that:
Mixing causes an increase in entropy.
But alas, it was proven that mixing of ideal gases has no effect on the entropy [
8]. So, where did we go wrong? Intuitively and qualitatively, mixing is viewed as an increase in disorder. This is correct. The fatal error is in the association of disorder with entropy (for an elementary discussion of this aspect of entropy, see [
9]).