Analyses
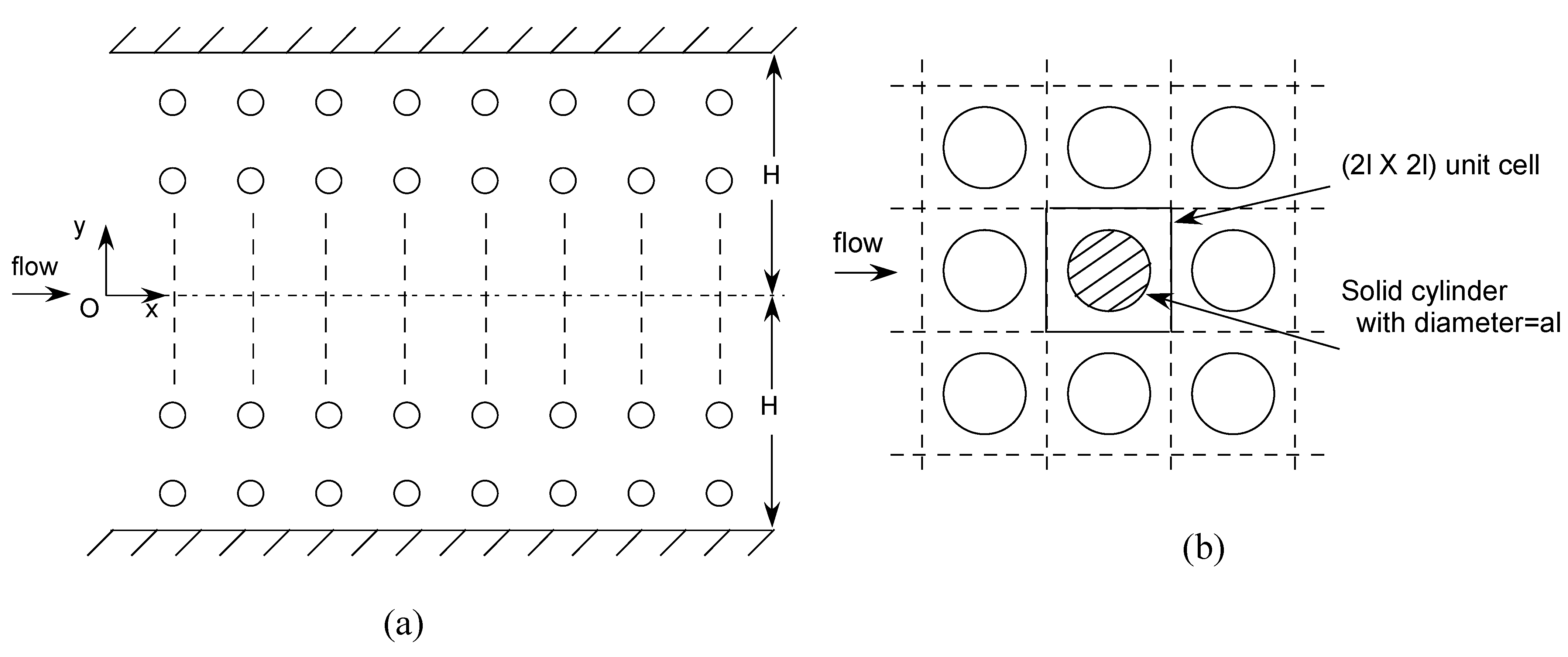
As shown in
Figure 1, we consider a steady, incompressible, fully-developed, very slow (
) flow across regular square arrays of circular cylinders, bounded by parallel plates. Governing equations based on the Darcy-Brinkman equation for porous media and the boundary conditions are,
where
= pressure,
= superficial velocity,
= permeability of porous medium. In terms of non-dimensional variables defined as,
,
(
= mean velocity =
,
= volume flow rate per channel width), the formulation and its solution become,
where (viscosity ratio), .
Figure 1.
(a) Flow between two parallel plates filled with regular square arrays of circular cylinders, (b) Regular square arrays of circular cylinders.
Figure 1.
(a) Flow between two parallel plates filled with regular square arrays of circular cylinders, (b) Regular square arrays of circular cylinders.
Upon an integration of the governing equation, Eq.(2a), over the channel half-depth,
,
we obtain the following equation for the pressure gradient;
Since
, the viscous flow limit is reached as
,
,
The viscous flow limit corresponds to the case of in the equation above.
The Darcian limit of flow through a porous medium is recovered as
, (
)
For the case of our interest, the porous medium consisting of regular square arrays of cylinders, the permeability,
, may be expressed as,
where
(solid fraction) =
(
= porosity),
= side length of a single square unit. (See
Figure 1.) The function,
, is given in an explicit form for high porosity arrays and in a graphical form for low porosity arrays in [
15].
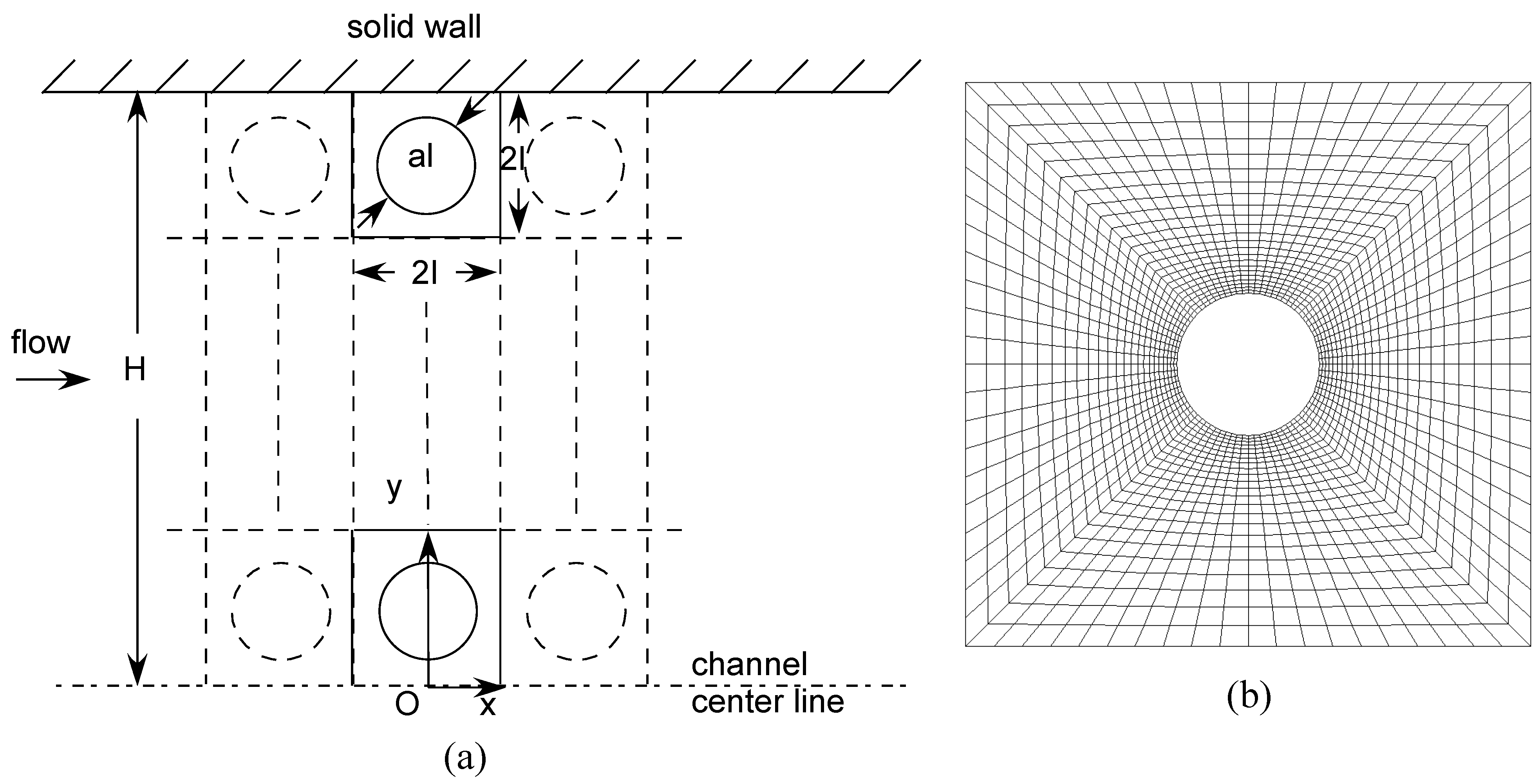
Figure 2.
(a) Coordinates for formulation, Eq.(8). (b) Typical computational grid for a unit cell.
Figure 2.
(a) Coordinates for formulation, Eq.(8). (b) Typical computational grid for a unit cell.
Flow, conditions of which lie between the two limits of Eqs.(5,6), is investigated numerically. Referring to
Figure 2, governing equations and boundary conditions are,
Two commercially-available computational programs for hydrodynamic analyses are used in our numerical experiments, FLUENT (by Fluent Inc.) and FEMLAB (by COMSOL Group). The former is used as the main program; while, the latter is employed to confirm results from the former. Eq.(8) is solved computationally as the porosity,
, and the length ratio,
, are varied systematically. The porosity represents a fraction of the flow field in the cross sectional area of a (
) unit cell; while, the ratio,
(integer), indicates a number of cell layers over the channel depth.
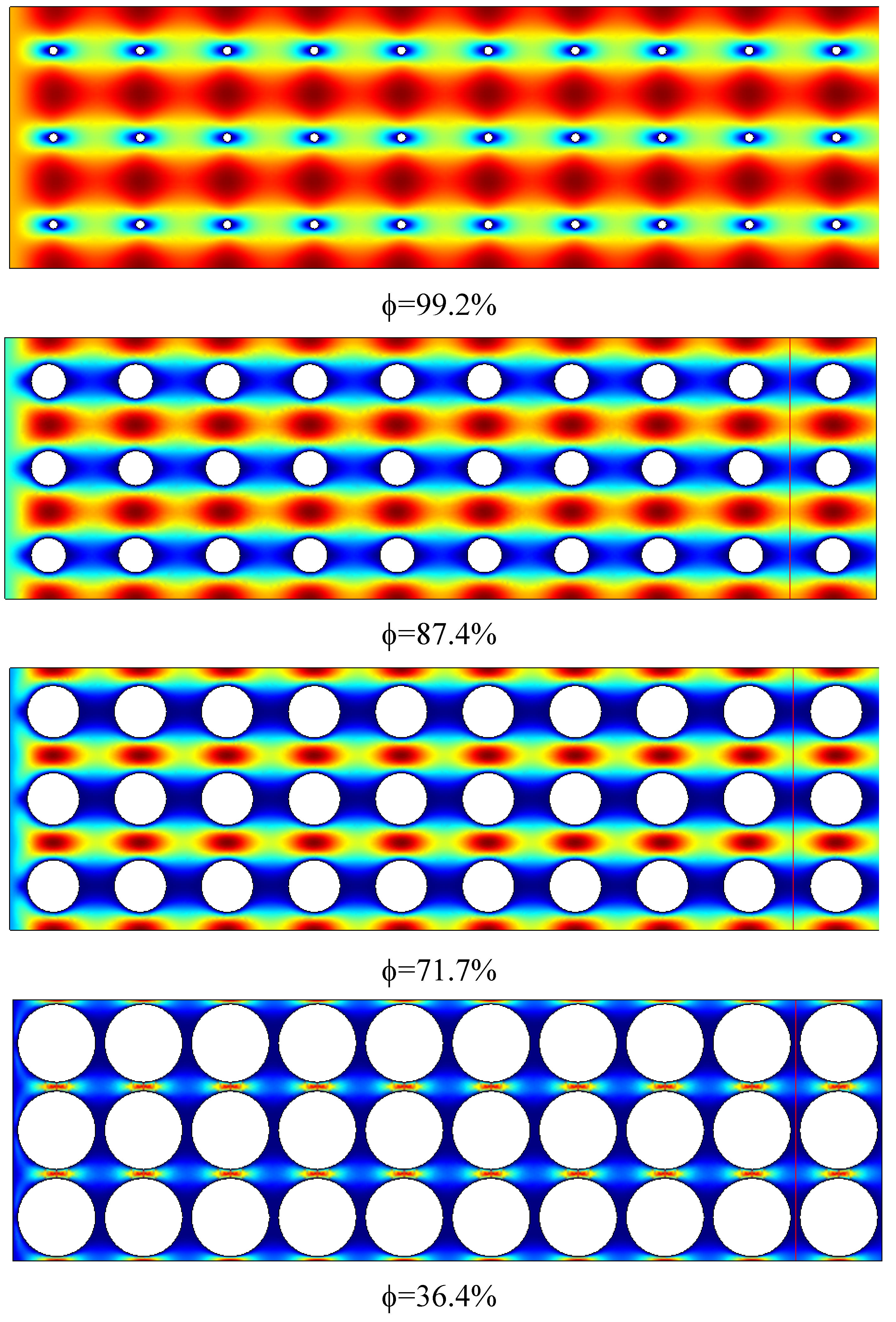
Figure 3 is presented to depict the range of the porosity of our investigation for the case of
. For the high porosity channel flow of
, the parabolic velocity profile of the viscous flow limit over the channel depth is disturbed by regularly placed arrays of small cylinders; while, at low porosity the flow may be approximated by the lubrication type flow through a narrow slot with the uniform Darcian flow velocity being modified by local geometric variations. Computations are performed in dimensional form under the following conditions:
Figure 3.
Examples of flow field over a channel half-depth.
Figure 3.
Examples of flow field over a channel half-depth.
The computational procedure is outlined below:
Solve Eq.(8) and find the x-direction pressure gradient,
), for a specified value of the porosity at the length ratio,
(that is, the case of a single unit cell over the channel). (Actual computations are performed over multiple longitudinal cell columns (5 - 10) to ensure that the periodic conditions at the cross-sectional cell boundaries are satisfied accurately.)
Increase the value of
by one, and repeat the computation.
In the case of
, the solid wall affects the entire flow field. As the magnitude of
increases, cells near the center of the channel (y = 0 in
Figure 1) become less sensitive to the presence of the solid walls. Computation for a fixed value of porosity is terminated when the size of the wall-affected region becomes independent of
.
Sangani and Acrivos [
15] reports solutions of the velocity field in a single unit cell (i.e. flow through square arrays of cylinders without solid bounding plates) by applying the least square collocation method [
4] to a series solution, which satisfies a part of the required boundary conditions exactly. We used this solution for confirmation of the validity of our computational results as well as for determination of the required numerical conditions (number and size of the computational mesh as well as the conversion criteria). The validity of the computational results is confirmed by recovering the permeability,
, (Eq.(7)) reported in [
15] over the range of 0
.215 (
(cylinders in contact with each other)
. When a unit cell becomes completely unaffected by the presence of the bounding walls, the velocity field should be identical to that of the solution in [
15] everywhere in the cell. However, it is not easy to find the identity for the two-dimensional velocity field we are analyzing. Instead, the identity of the rate of entropy generation over a unit cell is used to find a degree of the wall effects on the flow field in the respective unit cell. The local volumetric rate of entropy generation over a unit width of the channel,
, is related to the dissipation function
[
1]. The rate of entropy generation per unit cell per width,
, is evaluated for each cell located over the channel half-depth by numerically integrating the following equation for volumetric rate of entropy generation due to the viscous dissipation,
Results and Discussion
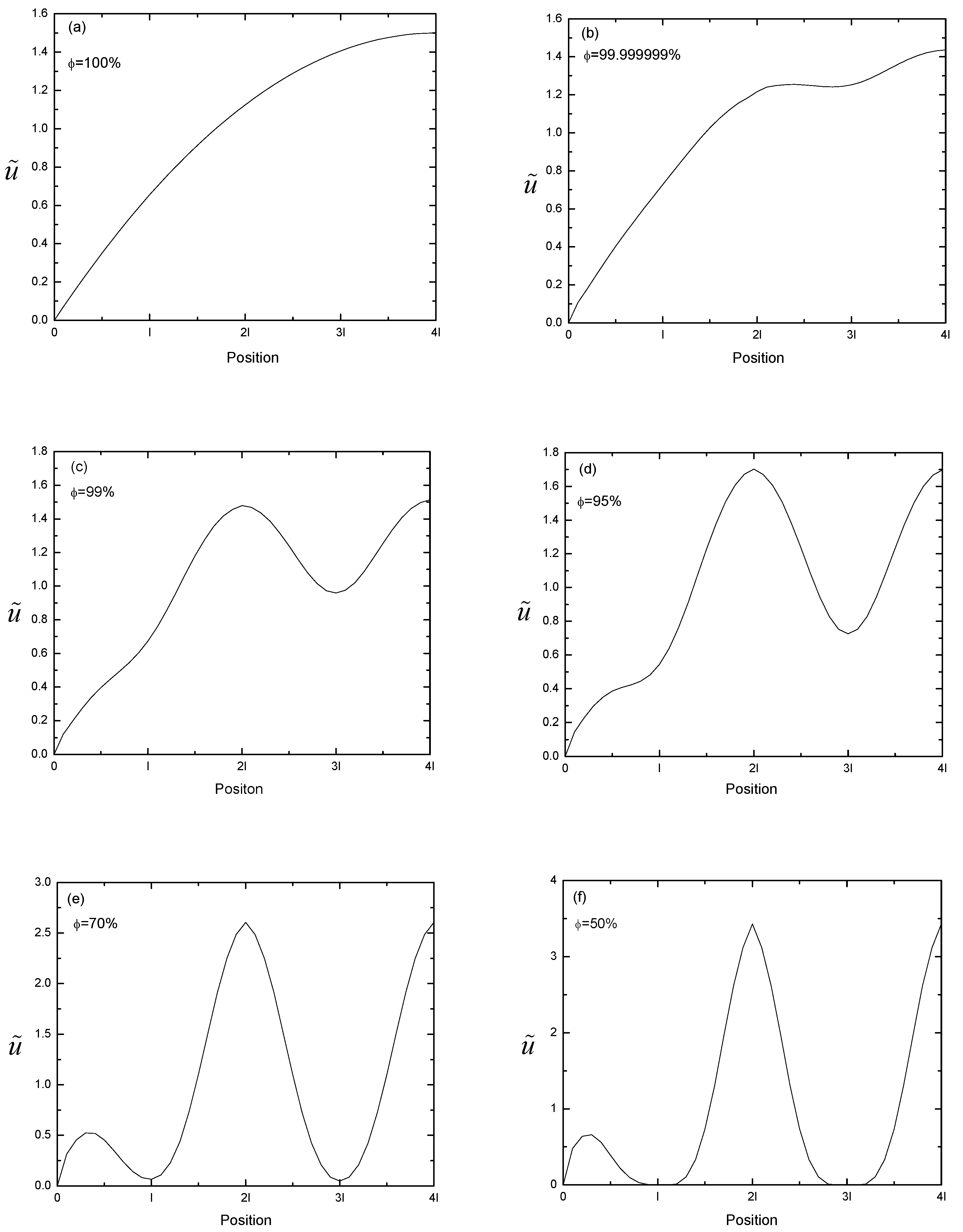
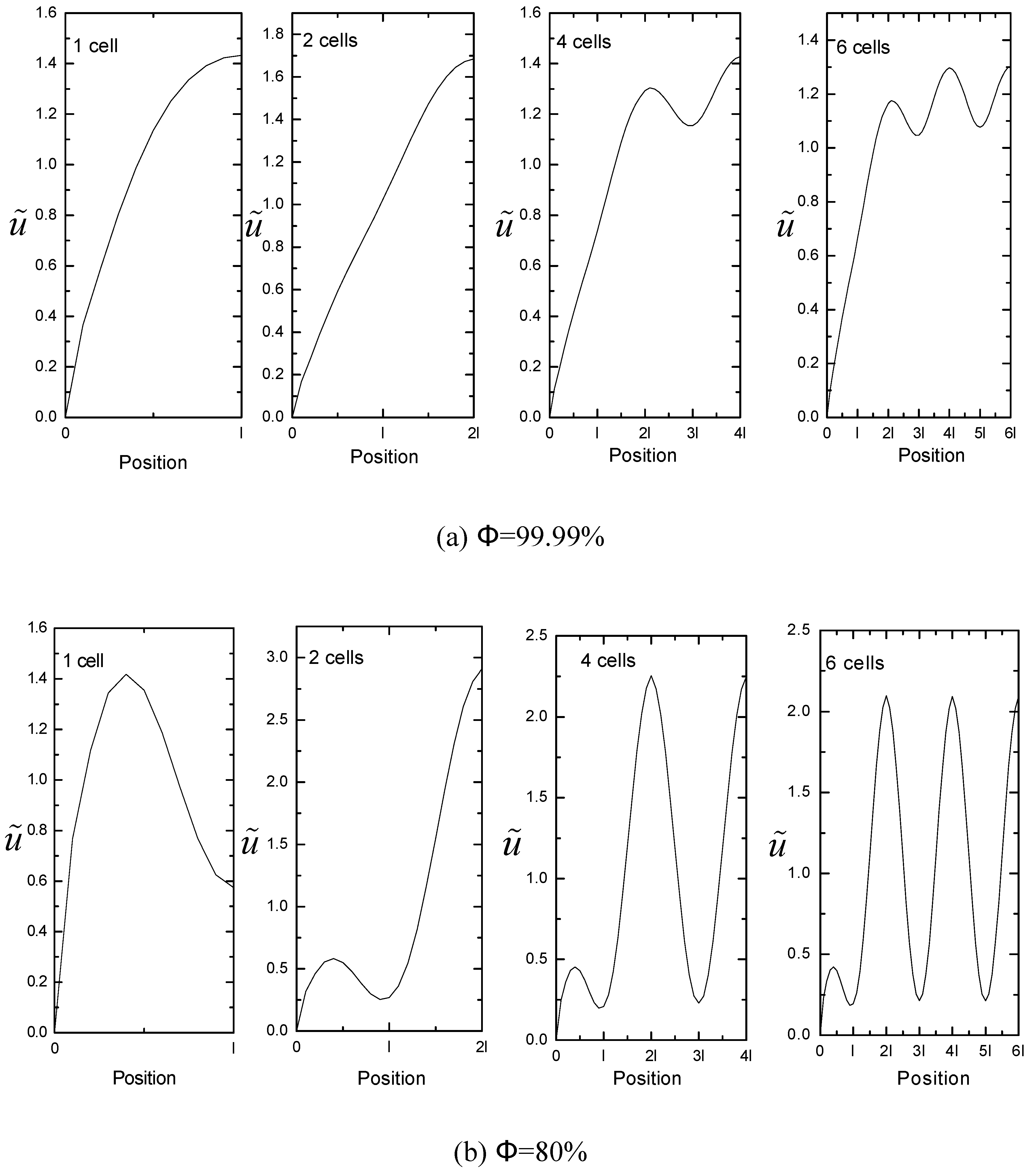
Figure 4 shows the axial velocity (
) profile over the channel half-depth at a cross sectional boundary between two lateral cell columns (with the number of cylinders per lateral column = four), as the porosity is varied. The centers of circular cylinders are located at x =
,
,
and
. The parabolic profile is computationally recovered for
(
Figure 4(a)) as viscous flow between two parallel plates. Even at a very low solid fraction (
) (
Figure 4 (b)), the presence of cylinders is seen to affect the velocity profile substantially near the middle region of the channel; while, the velocity profile retains parabolic characteristics near the plate. It should also be noted that the effects of the cylinder adjacent to the wall (with its center at
) are more significant for the low porosity cases.
Figure 4.
() Axial velocity profile at the boundary normal to flow and between two neighboring cells: Effects of porosity. Number of cells = 4, Volume flow rate , Wall at x = 0. Profiles over channel half-depth.
Figure 4.
() Axial velocity profile at the boundary normal to flow and between two neighboring cells: Effects of porosity. Number of cells = 4, Volume flow rate , Wall at x = 0. Profiles over channel half-depth.
Figure 5.
() Axial velocity profile at the boundary normal to flow and between two neighboring cells: Effects of number of cells. (a) , (b) . Volume flow rate = Number of cells
, Wall at x = 0. Profiles over channel half-depth
Figure 5.
() Axial velocity profile at the boundary normal to flow and between two neighboring cells: Effects of number of cells. (a) , (b) . Volume flow rate = Number of cells
, Wall at x = 0. Profiles over channel half-depth
In
Figure 5, similar to
Figure 4, the velocity profiles over the half-depth are presented to show the effects of the number of cells across the channel. Two cases are shown for
(
Figure 5(a)), and
(
Figure 5(b)). Large velocity changes around the cylinders compared to the corresponding changes near the plate (located at
) result in a smaller rate of entropy generation in the cell adjacent to the plate.
Table 1 lists computational results of the rate of entropy generation of each cell for the case of ten cells across the entire channel depth. Even at a very high porosity of
, the plate effects are limited to the region within three cells from the plate wall with the affected region becoming even smaller as the porosity is decreased.
Table 1.
Variation of over Channel Half-Width.(Cell I in contact with the bounding plate at y=H in Fig 2(a))
Table 1.
Variation of over Channel Half-Width.(Cell I in contact with the bounding plate at y=H in Fig 2(a))
| (Cell i)/(Cell 5) (i = 1-5) |
| = 85% | 95 % | 99 % | 99.99 % |
| Cell 1 | 0.639 | 0.647 | 0.656 | 0.692 |
| Cell 2 | 0.999 | 0.995 | 0.981 | 0.927 |
| Cell 3 | 1.0 | 0.999 | 0.999 | 0.997 |
| Cell 4 | 1.0 | 1.0 | 1.0 | 1.0 |
| Cell 5 | 1.0 | 1.0 | 1.0 | 1.0 |
Figure 6.
vs
.
Figure 6.
vs
.
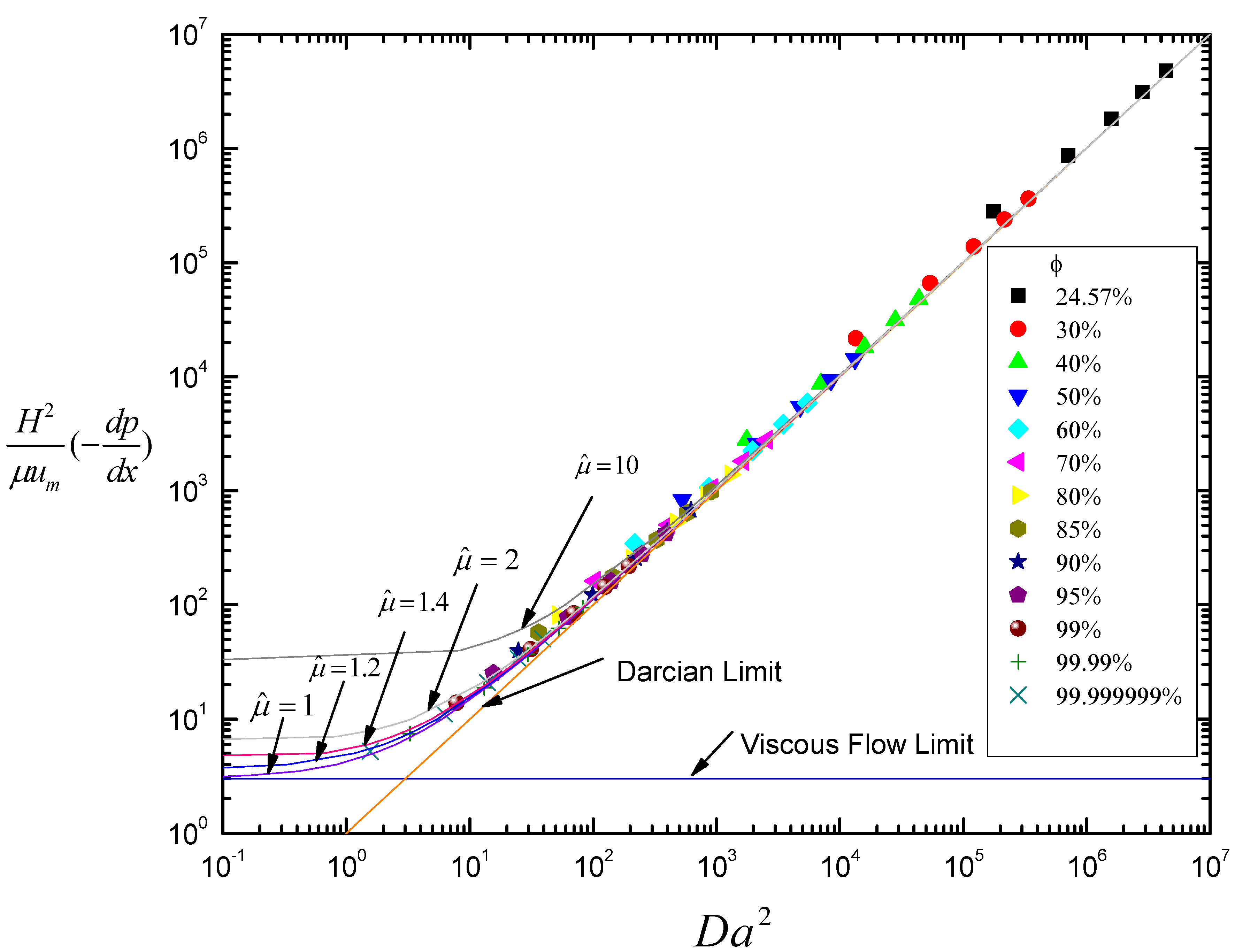
Figure 6 summarizes the computational results of the (non-dimensional) axial pressure gradient vs
, Eq.(4), covering the porosity range up to
. As was shown in
Table 1 the bounding wall affects the flow up to
unit cells away from the wall. The convergence of the non-dimensional pressure gradient to the Darcian limit is computationally confirmed, indicating that a critical value of
for convergence depends on the porosity. Computations are terminated for a specified value of
upon reaching a condition sufficiently close to the Darcian limit. On the other hand, even at the solid fraction of
, the viscous effect of the flow around the cylinder remains important with the minimum value of
being limited to
. (The computational lower limit is due to difficulties of the computational grid generation that is small in size and large in numbers sufficiently for accurate resolution of the velocity field near the cylinder.) The lowest value of
corresponds to the case of
(a single cylinder over the channel width) for each set of numerical results with a fixed value of
. Also, results may not be presented in a continuous curve as an incremental change in the number of cylinders in the lateral direction leads to a step change in
. Figure 6 indicates that, between the Darcian and the viscous flow limit, all numerical results may be recovered by setting
in Eq.(4). Our numerical range is limited to
. Classical Darcy’s law is valid under the assumption of very slow (
) flow through a layer of a porous medium in which the local (microscopic) length scale (
in the present analysis) is sufficiently small compared to the overall (macroscopic) length scale (
). For the two cases of (a)
and (b)
,
Figure 6 yields the following results:
A corresponding thermal problem had been analyzed [
2,
6,
16] for stability of a fluid saturated porous medium between two horizontal plates heated from below. Results, obtained under an assumption of
(
)
, indicate that the Darcian limit is reached in terms of the critical Rayleigh number for the onset of convection if
, and that the viscous flow limit is valid if
.Our computational results along with
Figure 6 indicate that the Darcy- Brinkman equation with the viscosity ratio substantially different from unity fails to satisfy the non-slip condition at bounding walls, particularly under the high porosity condition of
, and that the effect of the bounding walls on the flow structure, which is confined to a narrow region near the walls, may be approximated by a porous medium with
.
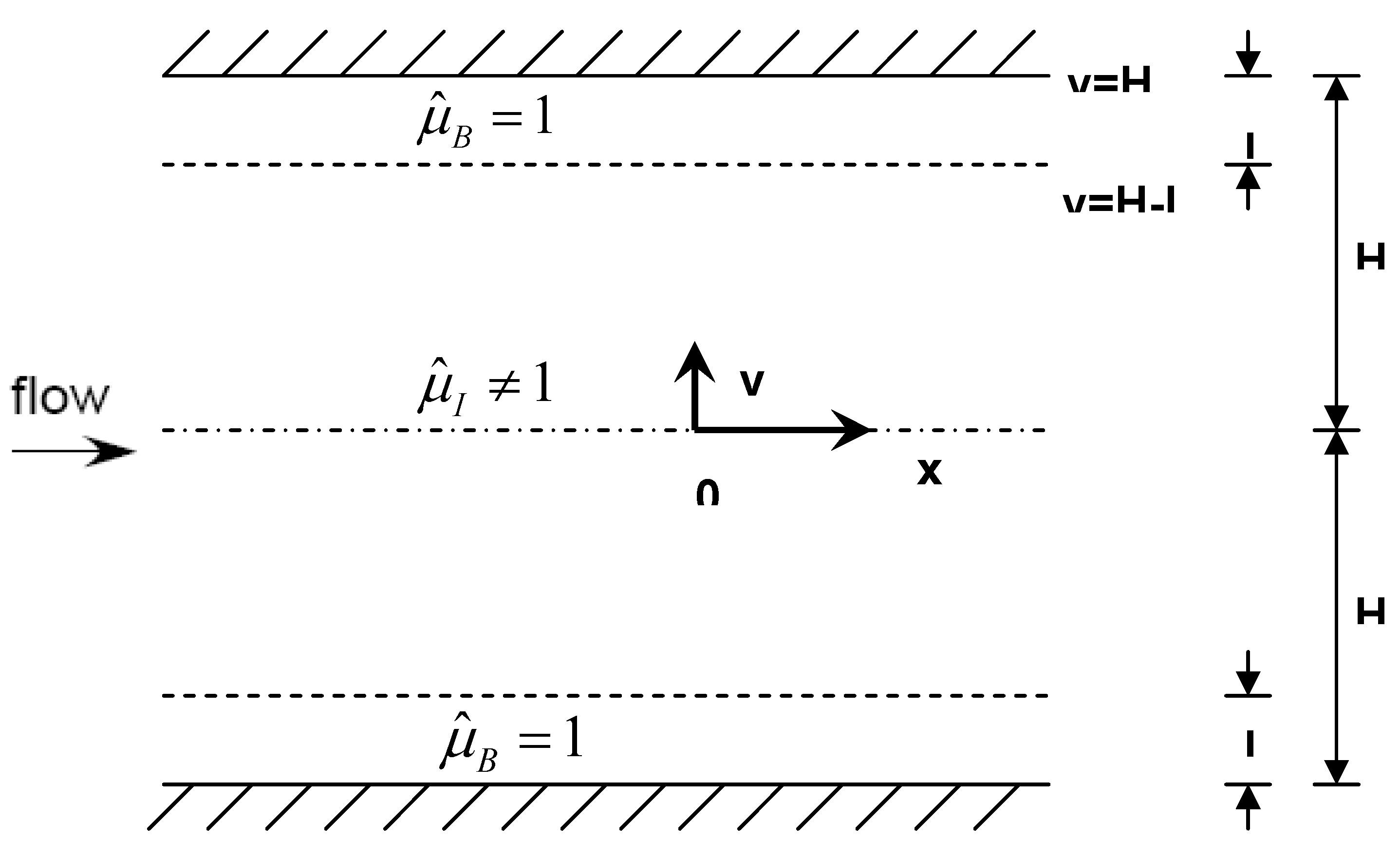
Figure 7 is a sketch of a three layer model, proposed to accommodate the wall effects in the analyses of a Brinkman porous medium with
. It consists of two layers near the bounding walls with
(viscosity ratio of the top and the bottom layer)
, and a middle (interior) layer with
(viscosity ratio of the middle layer)
. A solution for a parallel flow through the three layers may be sought from the Darcy-Brinkman equation for the top (
) as well as for the middle layer (
) under the conditions of the symmetry at
, the non-slip condition at
, and the velocity- and the shear stress-continuity at
. By setting
and 1 in Eq.(10), Eq.(4) is recovered for a porous layer with
and with
, respectively. The left hand side of Eq.(10) is the ratio of the non-dimensional pressure gradient of the three layer model to that of a single layer (= the Darcian limit of
). For a common pressure gradient, therefore, the mean velocity,
, of the three layer model is higher than that of the single layer. Greater the effective viscosity of the middle layer is relative to the fluid viscosity, more flow is channeled through the top (bottom) layer. The length scale of the top layer depth,
, is of the order of
in
Figure 2, implying that the depth ratio,
, depends on the characteristic length scale of the porous structure (such as
l in
Figure 2) as well as on the macroscopic scale of the channel depth,
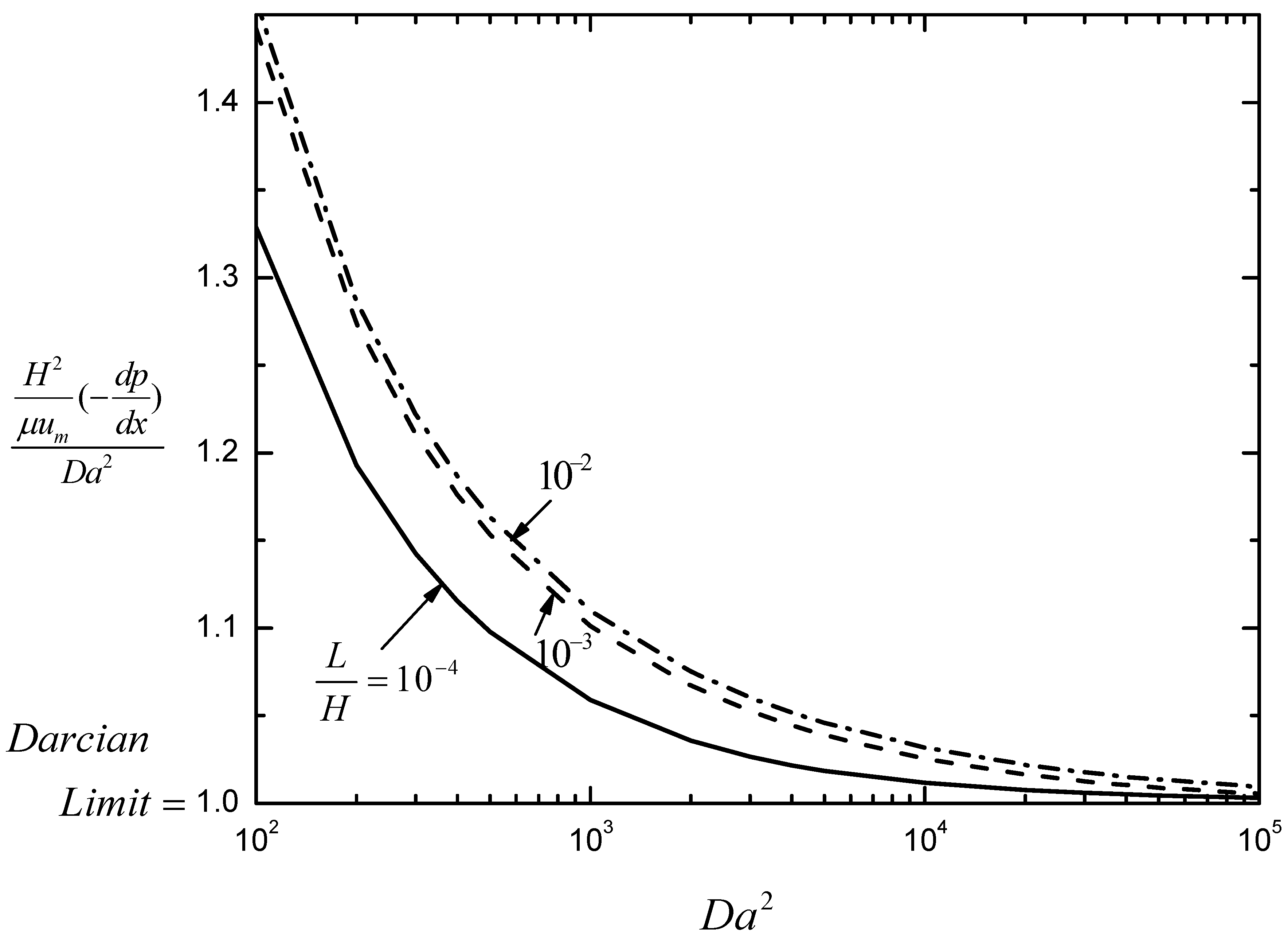
H. Figure 8 shows Eq.(10) as
is varied with
as third parameter for the case of
. For a case in which the wall layer thickness,
, is
of the channel half-depth,
, an increase of
in the mean velocity across the channel is predicted at
due to a higher flow velocity in the wall layer. Although a substantial reduction of the wall effect is observed as the magnitude of
is reduced from
to
, the wall effects remain important even at
for
.
Figure 7.
Schematic Diagram of Three Layer Model.
Figure 7.
Schematic Diagram of Three Layer Model.
Figure 8.
vs of the three layer model with .
Figure 8.
vs of the three layer model with .