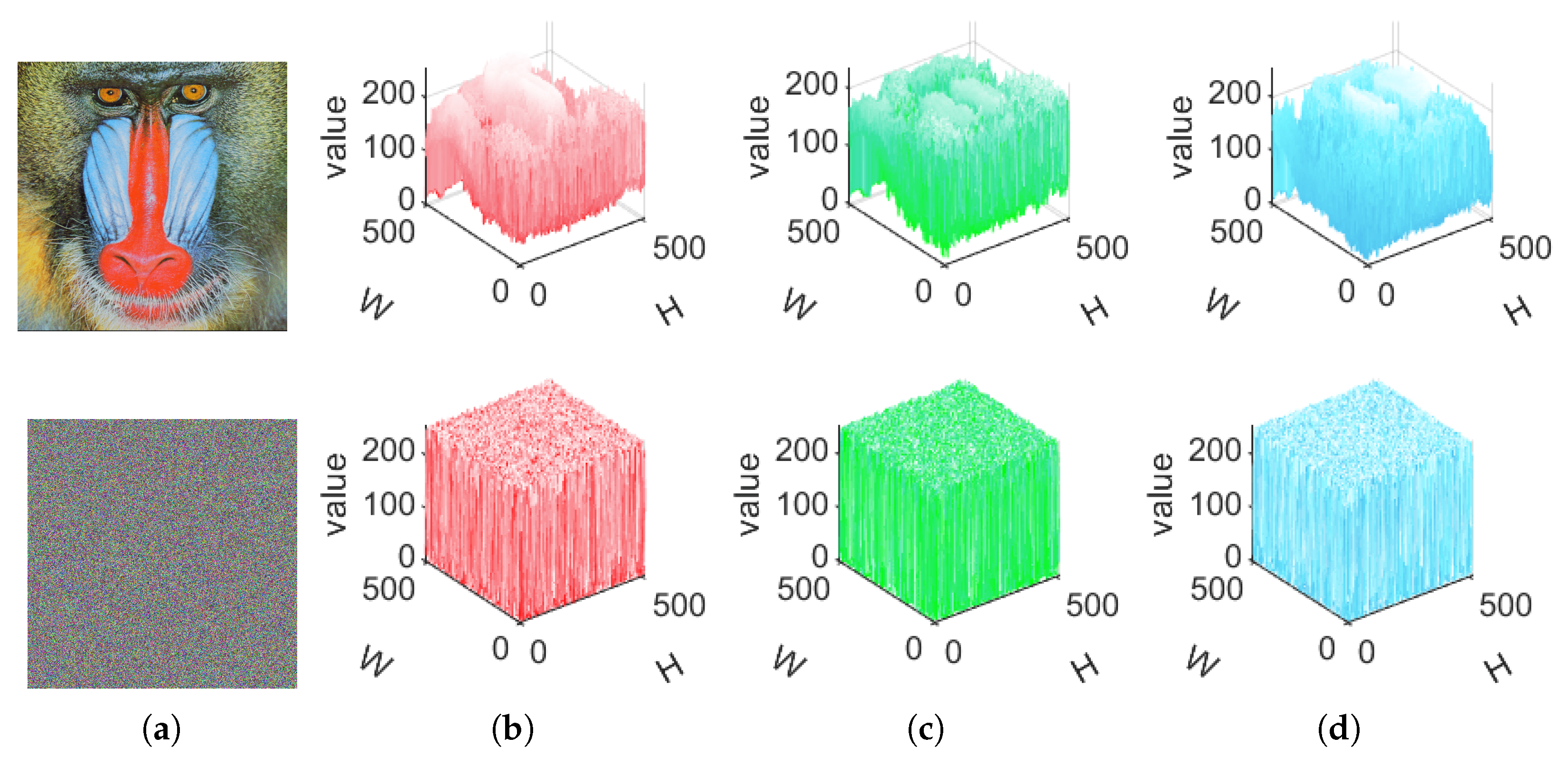
1. Introduction
As the Internet becomes increasingly popular, the transmission frequency of information on public network media has gradually become higher [
1,
2,
3]. Digital images are widely used as simple and intuitive carriers that carry a large amount of visual information [
4,
5,
6]. However, images are easily damaged and leaked when transmitted over the Internet, causing an incalculable loss and damage to users [
7,
8,
9,
10]. Therefore, the safeguarding of images has become the focus of attention, especially in areas such as personal privacy, business, and the military that require high confidentiality [
11,
12,
13,
14]. Images possess characteristics of high information content, substantial redundancy, and strong correlation [
15,
16,
17,
18]; this makes traditional text encryption methods like IDEA, DES, and AES less suitable for encrypting digital images [
19,
20,
21,
22]. In this context, chaos has garnered significant attention due to its characteristics of exhibiting behavior akin to randomness [
23,
24,
25,
26]. Chaotic systems exhibit remarkable sensitivity to starting conditions, leading to distinct trajectories for different initial states, ultimately generating unpredictable chaotic signals [
27,
28,
29,
30]. This property gives chaos a natural advantage in the field of cryptography; compared with the traditional text encryption method, it has a stronger scrambling effect on image encryption and can obtain a more excellent encryption effect. Therefore, it is considered to be a promising new method in digital image encryption.
In recent years, the international academic community has conducted in-depth research on the impact of chaotic systems and algorithms on the security of encryption systems. In 2022, Wang et al. [
31] suggested a bit-level and pixel-level image encryption scheme combining two chaotic systems. This scheme proves to have better security. In 2023, Wang et al. [
32] devised an innovative approach for encrypting images based on a two-dimensional sine-embedded coupling map that consist of bit-level cross-transformation and efficient diffusion processing. The designed algorithm is able to withstand common types of attacks. Besides the above-mentioned studies, the academic community has also explored the possibility of combining image encryption with biological coding techniques. Wu et al. [
33] proposed a DNA extension code with 3-bit binary streams for downlink data encryption in an orthogonal frequency division multiplexing passive optical network. The scheme increases security while having the ability to resist fiber nonlinearity and optical channel response. Jasra et al. [
34] suggested a new algorithm for encrypting images adopting elliptic curve cryptography, hyperchaotic systems, and dynamic DNA encoding. Results and analysis reveal that this method is computationally efficient and has strong robustness. Singh et al. [
35] presented a secure model encryption algorithm on images for Industrial Internet of Things incorporating DNA cryptography and chaos, demonstrating resilience against various attacks. In 2024, Wang et al. [
36] designed a novel chaotic two-dimensional hyperchaotic exponential adjusted Logistic and sine map, which combines a dynamic diffusion strategy and RNA operation to achieve high security of ciphertext images. The experimental results prove the feasibility of the proposed algorithm. In 2025, a novel Hénon nonlinear coupled mapping lattice for spatiotemporal chaos was proposed by Yang et al. [
37]. Image encryption is achieved by internal diffusion and RNA encoding operations. The experimental results show that the algorithm has high security.
Although existing chaotic encryption has made great progress, some algorithms cannot resist the chosen-plaintext attack, and the scrambling mechanism is not complex enough. Hence, we carried out this work from the perspective of security enhancement. In this article, the CIEA-RQ is proposed. Firstly, the color plaintext image is segmented into bit planes according to the information weights to obtain the high 4-bit and low 4-bit planes. Secondly, the hash function is employed to produce the key associated with the plaintext image as an input to the chaotic system to obtain chaotic sequences for block scrambling and RNA extended dynamic coding of the high 4-bit planes. Next, a lightweight XOR operation is performed on the low 4-bit planes by the chaotic sequence. Finally, the high 4-bit and low 4-bit planes are cross-iteratively diffused and synthesized to obtain a color ciphertext image. In block scrambling, the image is divided into multiple three-dimensional (3-D) submatrices of the same size and then encrypted. Compared with the two-dimensional (2-D) matrix, the dimension of image encryption is improved, the encryption correlation between layers is enhanced, separate encryption between bit planes is avoided, and the security is improved. Secondly, considering the information weight difference represented by each bit in the pixel value, the image is divided into high 4-bit planes and low 4-bit planes, and differential encryption strategies are adopted to achieve a better balance between security and efficiency. Compared with the common RNA coding rules in the existing literature, this paper significantly improves the diversity and randomness of pixel diffusion by extending the RNA bases and effectively improves the anti-attack ability of the system. The hierarchical encryption strategy, XOR operation, and coding operation proposed in this paper are easy to implement and are suitable for image protection in the Internet of Things. In addition, the algorithm has good modular characteristics, which can cut and optimize the encryption process according to the application requirements, so it has strong feasibility and applicability in actual deployment.
This paper’s primary contributions and innovations can be outlined as follows:
The algorithm introduces a new RNA extended coding mechanism with 384 coding rules, far exceeding the 8 of the traditional method, which greatly enhances the randomness and dynamic characteristics of the encryption and effectively enhances the algorithm’s resistance against various types of attacks.
The algorithm employs bit plane processing based on information weights to differentially encrypt the high 4-bit and low 4-bit planes, effectively balancing the security and efficiency performance of CIEA-RQ.
In this article, the hash function, RNA extended dynamic coding, high- and low-bit hierarchical encryption, and the cross-iterative diffusion mechanism are organically combined, and multi-level diffusion is used to enhance the resistance of the algorithm to various attacks.
The quantum Logistic map used in this paper not only has improved nonperiodicity and randomness but also has multiple initial values and control parameters, leading to an enlarged key space for the system.
The rest of this article is structured as follows.
Section 2 introduces the quantum Logistic map, RNA extended dynamic coding rules, and operation methods.
Section 3 presents the CIEA-RQ devised in this work.
Section 4 covers the simulation test as well as the analysis. The last section provides the summation of this article.
3. Proposed CIEA-RQ
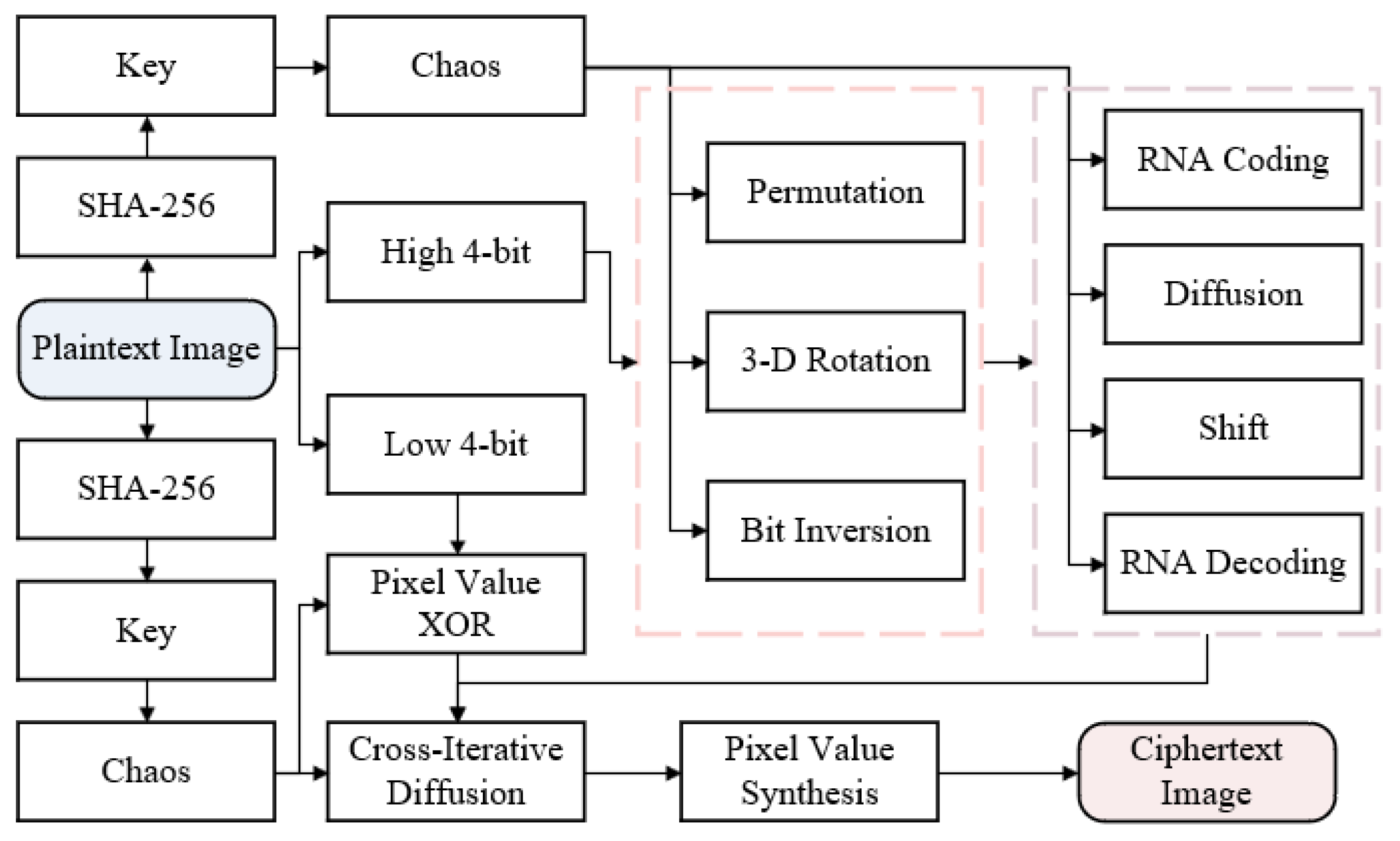
The three parts included in the CIEA-RQ are described in detail as follows. The first part is key generation. The key associated with the plaintext image is produced using SHA-256. The second part is the image encryption process. The precise encryption procedure consists of two main modules. The first module is the high 4-bit plane and low 4-bit plane encryption after pixel value segmentation, and the second module is the cross-iterative diffusion of high 4-bit and low 4-bit planes. The third part is the image decryption process, where the decryption order is the reverse of the encryption order, and each step in the decryption process is an encryption inverse operation.
Figure 1 depicts a flow diagram of the CIEA-RQ.
3.1. Key Generating
The pixel values of the plaintext image are applied as input to SHA-256, which outputs fixed 256 bits. The 256 bits are split into thirty-two 8-bit groups, each converted into a decimal number, resulting in 32 decimal numbers, each of which can be expressed as
, where
. The specific procedure is defined as follows:
where
,
,
,
,
,
are given initial values,
,
,
,
, and
are the keys of the quantum Logistic map, and ⊕ is the XOR operation.
3.2. Encryption Process
In the realm of image manipulation, given that each pixel point is meticulously divided into a depth of 8 bits, the high 4 bits tend to contribute more to the visual information, and therefore implementing more sophisticated encryption measures for these bits can effectively resist potential attacks. In comparison, the low 4 bits have a much smaller impact on the overall visual effect of the image than the high 4 bits. For the low 4 bits, the choice of lightweight encryption means a certain level of security can be maintained and avoids unnecessary overhead, thus realizing a clever balance between encryption efficiency and strength. Using a 3-D matrix P with a size of as an illustration, the specific procedure is outlined below.
3.2.1. Sequence Generation and Preprocessing
Using the keys
,
,
,
, and
as input parameters to the chaos equation, the pseudo-random sequences
,
,
,
,
,
,
, and
are generated, and then the pseudo-random sequences are transformed to obtain the final desired sequences
,
,
,
,
,
,
, and
, with the lengths of
,
,
,
,
,
,
, and
, respectively. The operation is shown as follows:
where
(·) denotes the modulo operation function and
(
x) returns the greatest integer less than or equal to x.
3.2.2. High 4-Bit Plane and Low 4-Bit Plane Encryption
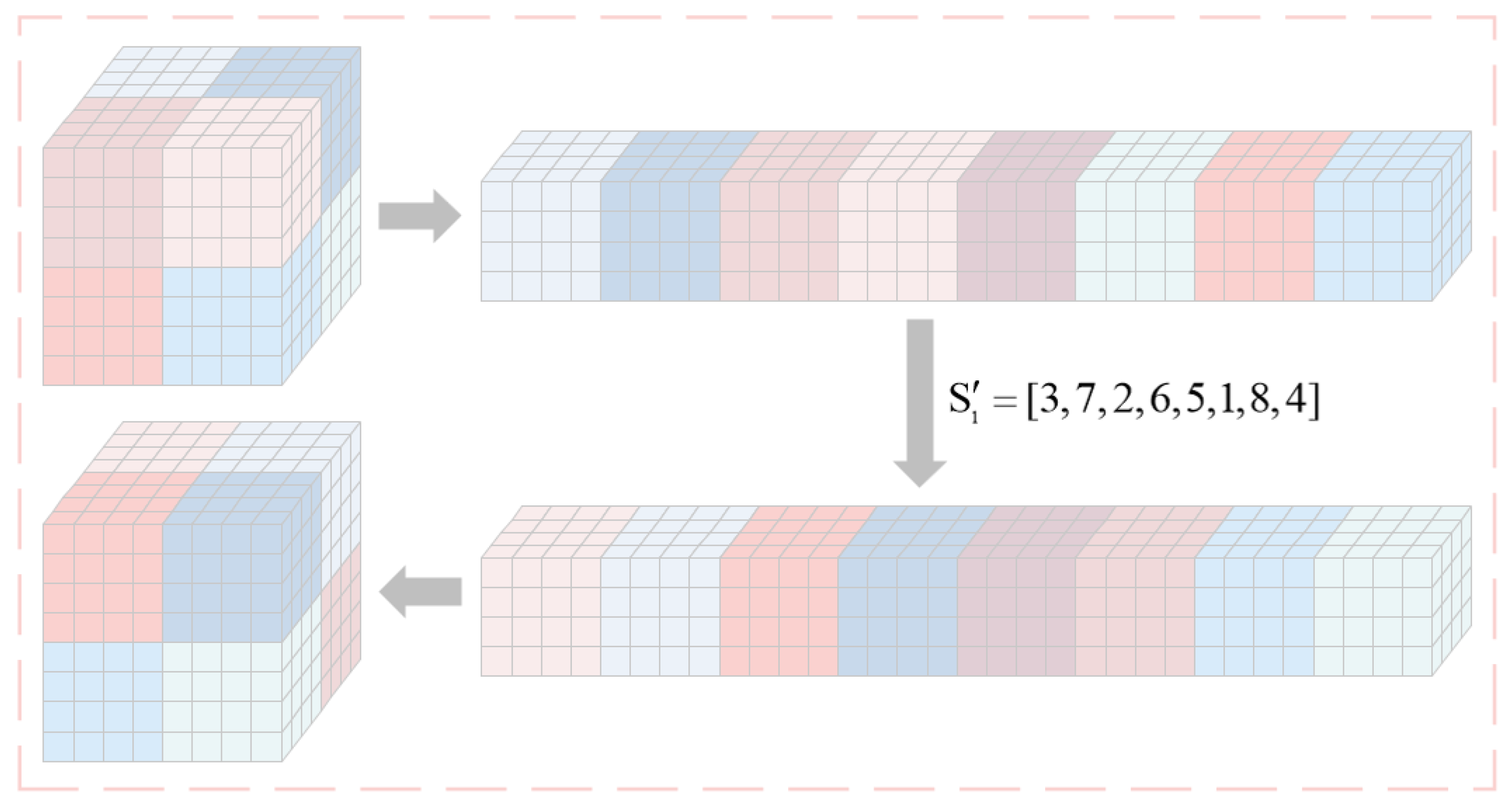
After extracting the high 4 bits of matrix P, decomposition is performed to form a 3-D matrix of .
The matrix
is divided into blocks, with each submatrix having a size of
. Then these submatrices are recombined sequentially into a row to obtain the submatrix sequence
,
.
is used to permute
; the operation is detailed as follows:
where
is the intermediate variable. Then the sequence of submatrices is sequentially recombine into the matrix
. Using a matrix of
as an example,
Figure 2 illustrates the flow diagram for the specific block permutation.
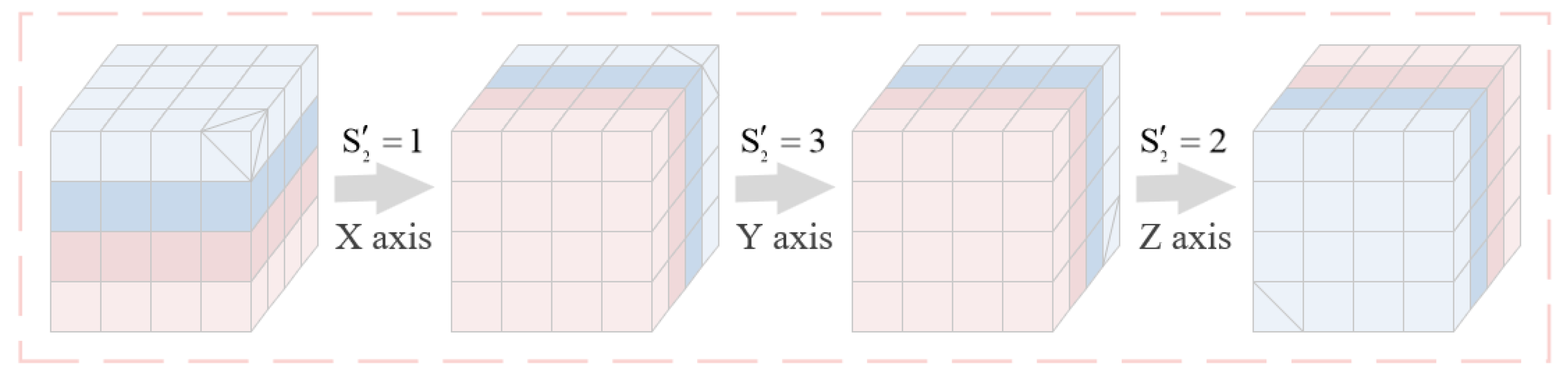
The submatrices after the block permutation are rotated, and the number of times each submatrix is rotated
counterclockwise around three axes is determined by sequence
to obtain the rotated matrix
. Using the rotation of a
submatrix as an example, the flow diagram of the block rotation is represented in
Figure 3. Finally the matrix
is inverted by the sequence
to obtain an inverted matrix
. The detailed inverse operation is shown below:
where
.
All the pixel values of the matrix
from bottom to top are combined into one octal number for every three binary numbers. The coding rules are chosen based on the first half of the sequence
, and then each octal number is encoded to obtain a matrix
with dimension
. The sequence
is recombined into a 2-D matrix of dimension
, which is encoded in the same way as the corresponding position of the first layer of the matrix
, and after encoding, the matrix
is obtained. Using the sequence
to select one of addition, subtraction, or XOR to perform the operation, the matrix
is iteratively diffused to obtain matrix
. The specific operation is shown as follows:
where
k denotes the number of layers,
,
, and
indicates addition, subtraction, or XOR operation, with the specific choices being controlled by sequence
.
For the matrix
, according to the coding rules corresponding to the sequence
, the next row is shifted to the right according to the last pixel value of the previous row, and the matrix
after the shift is obtained. The second half of the sequence
is selected for decoding. The decoded matrix is synthesized into a pixel value every 4 bits from bottom to top, and a 3-D matrix
of dimension
is obtained. The flow diagram of the RNA extended dynamic coding encryption is shown in
Figure 4. The specific shift operation is shown as follows:
where
k denotes the number of layers,
,
signifies the last pixel value of the row
,
denotes the last pixel value of the row
M, and
is the intermediate variable.
The low 4 bits of matrix P are extracted but not decomposed to form a 3-D matrix of dimension . The sequence is converted into a matrix of size , and then it performs the XOR operation with matrix to obtain matrix .
3.2.3. Pixel Value Cross-Iteration Diffusion
Matrices
and
are recombined into vectors. The sequence
is used to perform the add and modulo operation on vectors
and
, and finally the pixel values are synthesized to acquire the ciphertext image
C. Algorithm 1 gives the pseudo-code of pixel value cross-iterative diffusion.
| Algorithm 1: Pixel value cross-iterative diffusion. |
- Input:
Vectors and of length 3MN, sequence with length - Output:
Ciphertext image C - 1:
if
then - 2:
- 3:
else if i from 2 to then - 4:
- 5:
end if - 6:
if
then - 7:
- 8:
else if i from 2 to then - 9:
- 10:
end if - 11:
convert the vectors and into 3-D matrices and - 12:
|
3.3. Decryption Process
Performing the opposite operation on the encryption procedure yields the decrypted image. To decrypt the image, it is essential to securely transmit the key to the decryption end via a secure channel. In the image encryption stage, we first perform pixel value segmentation on the image, then encrypt the high 4-bit and the low 4-bit planes, respectively, and finally perform pixel values synthesis after cross-iterative diffusion. Therefore, in the decryption stage, we first perform pixel value segmentation. Secondly, the two segmented matrices are reversely iteratively diffused and then decrypted separately. Finally, the decrypted image is synthesized.