Abstract
The rapid development of Internet technology, while providing convenient services for users, has also aroused deep concern among the public about the issue of privacy leakage during image data transmission. To address this situation, this article proposes a color image encryption algorithm based on RNA extended dynamic coding and quantum chaos (CIEA-RQ). This algorithm significantly improves the ability of the system to withstand cryptographic attacks by introducing RNA extended dynamic encoding with 384 encoding rules. The employed quantum chaotic map improves the randomness of chaotic sequences and increases the key space. First, the algorithm decomposes the plaintext image into bit planes and obtains two parts, high 4-bit and low 4-bit planes, based on different weights of information. Then, the high 4-bit planes are partitioned into blocks and scrambled, and the scrambled planes are confused using RNA extended coding rules. Meanwhile, the low 4-bit planes employ a lightweight XOR operation to improve encryption efficiency. Finally, the algorithm performs cross-iterative diffusion on the processed high 4-bit and low 4-bit planes and then synthesizes a color ciphertext image. Experimental simulations and security assessments demonstrate the superior numerical statistical outcomes of the CIEA-RQ. According to the criteria of cryptanalysis, it can effectively resist known-plaintext attacks and chosen-plaintext attacks. Therefore, the CIEA-RQ presented in this article serves as an efficient digital image privacy safeguard technique, promising extensive applications in image secure transmission for the upcoming generation of networks.
1. Introduction
As the Internet becomes increasingly popular, the transmission frequency of information on public network media has gradually become higher [1,2,3]. Digital images are widely used as simple and intuitive carriers that carry a large amount of visual information [4,5,6]. However, images are easily damaged and leaked when transmitted over the Internet, causing an incalculable loss and damage to users [7,8,9,10]. Therefore, the safeguarding of images has become the focus of attention, especially in areas such as personal privacy, business, and the military that require high confidentiality [11,12,13,14]. Images possess characteristics of high information content, substantial redundancy, and strong correlation [15,16,17,18]; this makes traditional text encryption methods like IDEA, DES, and AES less suitable for encrypting digital images [19,20,21,22]. In this context, chaos has garnered significant attention due to its characteristics of exhibiting behavior akin to randomness [23,24,25,26]. Chaotic systems exhibit remarkable sensitivity to starting conditions, leading to distinct trajectories for different initial states, ultimately generating unpredictable chaotic signals [27,28,29,30]. This property gives chaos a natural advantage in the field of cryptography; compared with the traditional text encryption method, it has a stronger scrambling effect on image encryption and can obtain a more excellent encryption effect. Therefore, it is considered to be a promising new method in digital image encryption.
In recent years, the international academic community has conducted in-depth research on the impact of chaotic systems and algorithms on the security of encryption systems. In 2022, Wang et al. [31] suggested a bit-level and pixel-level image encryption scheme combining two chaotic systems. This scheme proves to have better security. In 2023, Wang et al. [32] devised an innovative approach for encrypting images based on a two-dimensional sine-embedded coupling map that consist of bit-level cross-transformation and efficient diffusion processing. The designed algorithm is able to withstand common types of attacks. Besides the above-mentioned studies, the academic community has also explored the possibility of combining image encryption with biological coding techniques. Wu et al. [33] proposed a DNA extension code with 3-bit binary streams for downlink data encryption in an orthogonal frequency division multiplexing passive optical network. The scheme increases security while having the ability to resist fiber nonlinearity and optical channel response. Jasra et al. [34] suggested a new algorithm for encrypting images adopting elliptic curve cryptography, hyperchaotic systems, and dynamic DNA encoding. Results and analysis reveal that this method is computationally efficient and has strong robustness. Singh et al. [35] presented a secure model encryption algorithm on images for Industrial Internet of Things incorporating DNA cryptography and chaos, demonstrating resilience against various attacks. In 2024, Wang et al. [36] designed a novel chaotic two-dimensional hyperchaotic exponential adjusted Logistic and sine map, which combines a dynamic diffusion strategy and RNA operation to achieve high security of ciphertext images. The experimental results prove the feasibility of the proposed algorithm. In 2025, a novel Hénon nonlinear coupled mapping lattice for spatiotemporal chaos was proposed by Yang et al. [37]. Image encryption is achieved by internal diffusion and RNA encoding operations. The experimental results show that the algorithm has high security.
Although existing chaotic encryption has made great progress, some algorithms cannot resist the chosen-plaintext attack, and the scrambling mechanism is not complex enough. Hence, we carried out this work from the perspective of security enhancement. In this article, the CIEA-RQ is proposed. Firstly, the color plaintext image is segmented into bit planes according to the information weights to obtain the high 4-bit and low 4-bit planes. Secondly, the hash function is employed to produce the key associated with the plaintext image as an input to the chaotic system to obtain chaotic sequences for block scrambling and RNA extended dynamic coding of the high 4-bit planes. Next, a lightweight XOR operation is performed on the low 4-bit planes by the chaotic sequence. Finally, the high 4-bit and low 4-bit planes are cross-iteratively diffused and synthesized to obtain a color ciphertext image. In block scrambling, the image is divided into multiple three-dimensional (3-D) submatrices of the same size and then encrypted. Compared with the two-dimensional (2-D) matrix, the dimension of image encryption is improved, the encryption correlation between layers is enhanced, separate encryption between bit planes is avoided, and the security is improved. Secondly, considering the information weight difference represented by each bit in the pixel value, the image is divided into high 4-bit planes and low 4-bit planes, and differential encryption strategies are adopted to achieve a better balance between security and efficiency. Compared with the common RNA coding rules in the existing literature, this paper significantly improves the diversity and randomness of pixel diffusion by extending the RNA bases and effectively improves the anti-attack ability of the system. The hierarchical encryption strategy, XOR operation, and coding operation proposed in this paper are easy to implement and are suitable for image protection in the Internet of Things. In addition, the algorithm has good modular characteristics, which can cut and optimize the encryption process according to the application requirements, so it has strong feasibility and applicability in actual deployment.
This paper’s primary contributions and innovations can be outlined as follows:
- The algorithm introduces a new RNA extended coding mechanism with 384 coding rules, far exceeding the 8 of the traditional method, which greatly enhances the randomness and dynamic characteristics of the encryption and effectively enhances the algorithm’s resistance against various types of attacks.
- The algorithm employs bit plane processing based on information weights to differentially encrypt the high 4-bit and low 4-bit planes, effectively balancing the security and efficiency performance of CIEA-RQ.
- In this article, the hash function, RNA extended dynamic coding, high- and low-bit hierarchical encryption, and the cross-iterative diffusion mechanism are organically combined, and multi-level diffusion is used to enhance the resistance of the algorithm to various attacks.
- The quantum Logistic map used in this paper not only has improved nonperiodicity and randomness but also has multiple initial values and control parameters, leading to an enlarged key space for the system.
The rest of this article is structured as follows. Section 2 introduces the quantum Logistic map, RNA extended dynamic coding rules, and operation methods. Section 3 presents the CIEA-RQ devised in this work. Section 4 covers the simulation test as well as the analysis. The last section provides the summation of this article.
2. Related Theory
2.1. Quantum Logistic Map
Chaotic systems are frequently employed in image processing owing to their randomness and remarkable sensitivity. One-dimensional chaotic systems have a simple structure and the generated orbits are easily predictable. The traditional Logistic chaotic map equation is articulated as follows:
where the control parameter , .
Goggin et al. [38] used the recoil rotor model to quantize the classical Logistic chaotic system and produce the corresponding quantum Logistic map. This chaotic map adds control parameters and includes a non-vanishing disturbance quantity at the end, which enhances the nonperiodicity and randomness of the system. It can be expressed as follows:
where , , and are the state values of the system, and are the complex conjugates of and , respectively, is a dissipative parameter, and r is an adjustable parameter. When the system parameters , , and the state values , , and , the system is in a chaotic state.
2.2. RNA Extended Dynamic Coding
RNA is a chain-like molecule that grows from ribonucleotides condensed by a phosphodiester bond. A ribonucleotide molecule consists of phosphate, ribose, and bases. In RNA, there are four types of bases, A, U, G, and C, with A-U and C-G as complementary base pairs. To enhance encryption randomness, four new bases, M, N, S, and W, are extended from the original bases, and these new bases follow specific pairing rules, i.e., M is paired with W and S is paired with N. Also, in binary, 0 and 1 are complementary and so are 000-111, 001-110, 010-101, and 011-100. Using base pairs to encode numbers, there are a total of 384 coding rules, as presented in Table 1, thus greatly improving the randomness of the matching. The operation between bases is realized by addition table, subtraction table or XOR table, as listed in Table 2, Table 3 and Table 4, respectively.

Table 1.
RNA extended coding rules.

Table 2.
RNA extended addition operation.

Table 3.
RNA extended subtraction operation.

Table 4.
RNA extended XOR operation.
3. Proposed CIEA-RQ
The three parts included in the CIEA-RQ are described in detail as follows. The first part is key generation. The key associated with the plaintext image is produced using SHA-256. The second part is the image encryption process. The precise encryption procedure consists of two main modules. The first module is the high 4-bit plane and low 4-bit plane encryption after pixel value segmentation, and the second module is the cross-iterative diffusion of high 4-bit and low 4-bit planes. The third part is the image decryption process, where the decryption order is the reverse of the encryption order, and each step in the decryption process is an encryption inverse operation. Figure 1 depicts a flow diagram of the CIEA-RQ.
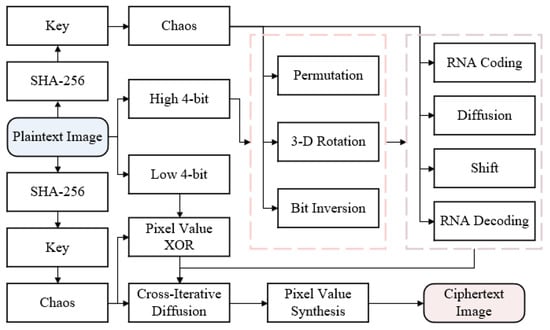
Figure 1.
Flow diagram of the CIEA-RQ.
3.1. Key Generating
The pixel values of the plaintext image are applied as input to SHA-256, which outputs fixed 256 bits. The 256 bits are split into thirty-two 8-bit groups, each converted into a decimal number, resulting in 32 decimal numbers, each of which can be expressed as , where . The specific procedure is defined as follows:
where , , , , , are given initial values, , , , , and are the keys of the quantum Logistic map, and ⊕ is the XOR operation.
3.2. Encryption Process
In the realm of image manipulation, given that each pixel point is meticulously divided into a depth of 8 bits, the high 4 bits tend to contribute more to the visual information, and therefore implementing more sophisticated encryption measures for these bits can effectively resist potential attacks. In comparison, the low 4 bits have a much smaller impact on the overall visual effect of the image than the high 4 bits. For the low 4 bits, the choice of lightweight encryption means a certain level of security can be maintained and avoids unnecessary overhead, thus realizing a clever balance between encryption efficiency and strength. Using a 3-D matrix P with a size of as an illustration, the specific procedure is outlined below.
3.2.1. Sequence Generation and Preprocessing
Using the keys , , , , and as input parameters to the chaos equation, the pseudo-random sequences , , , , , , , and are generated, and then the pseudo-random sequences are transformed to obtain the final desired sequences , , , , , , , and , with the lengths of , , , , , , , and , respectively. The operation is shown as follows:
where (·) denotes the modulo operation function and (x) returns the greatest integer less than or equal to x.
3.2.2. High 4-Bit Plane and Low 4-Bit Plane Encryption
- : Bit decomposition
After extracting the high 4 bits of matrix P, decomposition is performed to form a 3-D matrix of .
- : High 4-bit plane block scrambling
The matrix is divided into blocks, with each submatrix having a size of . Then these submatrices are recombined sequentially into a row to obtain the submatrix sequence , . is used to permute ; the operation is detailed as follows:
where is the intermediate variable. Then the sequence of submatrices is sequentially recombine into the matrix . Using a matrix of as an example, Figure 2 illustrates the flow diagram for the specific block permutation.
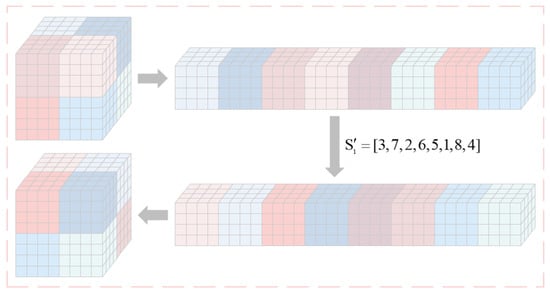
Figure 2.
Flow diagram of the proposed block permutation.
The submatrices after the block permutation are rotated, and the number of times each submatrix is rotated counterclockwise around three axes is determined by sequence to obtain the rotated matrix . Using the rotation of a submatrix as an example, the flow diagram of the block rotation is represented in Figure 3. Finally the matrix is inverted by the sequence to obtain an inverted matrix . The detailed inverse operation is shown below:
where .
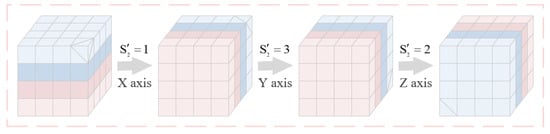
Figure 3.
Flow diagram of the proposed block rotation.
- : High 4-bit plane RNA extended dynamic coding diffusion
All the pixel values of the matrix from bottom to top are combined into one octal number for every three binary numbers. The coding rules are chosen based on the first half of the sequence , and then each octal number is encoded to obtain a matrix with dimension . The sequence is recombined into a 2-D matrix of dimension , which is encoded in the same way as the corresponding position of the first layer of the matrix , and after encoding, the matrix is obtained. Using the sequence to select one of addition, subtraction, or XOR to perform the operation, the matrix is iteratively diffused to obtain matrix . The specific operation is shown as follows:
where k denotes the number of layers, , , and indicates addition, subtraction, or XOR operation, with the specific choices being controlled by sequence .
- : High 4-bit plane RNA extended dynamic coding shift
For the matrix , according to the coding rules corresponding to the sequence , the next row is shifted to the right according to the last pixel value of the previous row, and the matrix after the shift is obtained. The second half of the sequence is selected for decoding. The decoded matrix is synthesized into a pixel value every 4 bits from bottom to top, and a 3-D matrix of dimension is obtained. The flow diagram of the RNA extended dynamic coding encryption is shown in Figure 4. The specific shift operation is shown as follows:
where k denotes the number of layers, , signifies the last pixel value of the row , denotes the last pixel value of the row M, and is the intermediate variable.
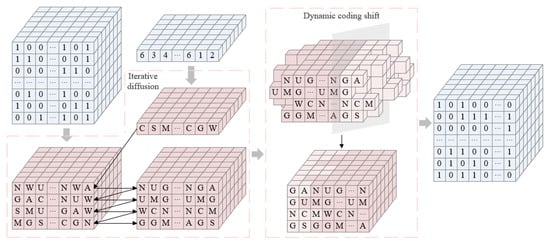
Figure 4.
Flow diagram of the RNA extended dynamic coding encryption.
- : Low 4-bit plane XOR operation
The low 4 bits of matrix P are extracted but not decomposed to form a 3-D matrix of dimension . The sequence is converted into a matrix of size , and then it performs the XOR operation with matrix to obtain matrix .
3.2.3. Pixel Value Cross-Iteration Diffusion
Matrices and are recombined into vectors. The sequence is used to perform the add and modulo operation on vectors and , and finally the pixel values are synthesized to acquire the ciphertext image C. Algorithm 1 gives the pseudo-code of pixel value cross-iterative diffusion.
| Algorithm 1: Pixel value cross-iterative diffusion. |
|
3.3. Decryption Process
Performing the opposite operation on the encryption procedure yields the decrypted image. To decrypt the image, it is essential to securely transmit the key to the decryption end via a secure channel. In the image encryption stage, we first perform pixel value segmentation on the image, then encrypt the high 4-bit and the low 4-bit planes, respectively, and finally perform pixel values synthesis after cross-iterative diffusion. Therefore, in the decryption stage, we first perform pixel value segmentation. Secondly, the two segmented matrices are reversely iteratively diffused and then decrypted separately. Finally, the decrypted image is synthesized.
4. Experimental Results and Analysis Discussion
We conducted experiments on a PC furnished with MATLAB R2022b software. The PC is powered by a 13th Gen Intel(R) Core(TM) i7-13650HX 2.60 GHz processor, with 16 GB of RAM and a 1TB hard disk. The operating system used is Windows 11. The experiment employed images from the USC-SIPI dataset (http://sipi.usc.edu/database/ (accessed on 15 June 2025)).
4.1. Encryption and Decryption Experiments
Figure 5 reveals the encryption and decryption results of the CIEA-RQ. It can be observed that the ciphertext image presents noise-like characteristics, which makes it difficult to identify any original content and effectively prevents attackers from obtaining useful information. After decryption with the correct key, the image can be completely restored without visual information loss. The experimental results verify the effectiveness of CIEA-RQ in image confidentiality and reversibility.
4.2. Histogram Analysis
The histogram portrays the occurrence frequency of individual pixel values within an image. A robust security scheme yields a ciphertext image histogram that is entirely different from the plaintext image histogram, and the ciphertext image should exhibit an near-uniform distribution of pixel values. In this experiment, we encrypt a color image of size and perform histogram experimental analysis. Figure 6 illustrates the simulation result. Notably, the ciphertext image’s histogram diverges from that of the plaintext image, displaying an almost uniform distribution of pixel values.

Figure 5.
Encryption and decryption results. (a) Plaintext image 4.1.03. (b) Ciphertext image of (a). (c) Decrypted image of (b). (d) Plaintext image 4.2.03. (e) Ciphertext image of (d). (f) Decrypted image of (e). (g) Plaintext image 2.2.01. (h) Ciphertext image of (g). (i) Decrypted image of (h).
4.3. Adjacent Pixel Correlation Analysis
To assess the degree of correlation, we randomly chose 3000 pairs of adjacent pixels from both the plaintext and ciphertext images for calculation. In the plaintext image, the differences between them are small and have a high correlation in horizontal, vertical, diagonal, and anti-diagonal directions. Nonetheless, superior algorithms can effectively disrupt this correlation, resulting in an insignificant correlation between adjacent pixels in the ciphertext image. The correlation coefficient between two adjacent pixel sequences X and Y can be formulated as follows:
where and denote the mathematical expectations of X and Y. In order to more clearly and intuitively display the extent of change in image correlation before and after encryption, we chose two forms to present the experimental results. Figure 7 displays the analysis of the correlation in different directions. Table 5 displays the correlation coefficients’ outcomes pertaining to the images before and after encryption, and Table 6 shows the results of CIEA-QR compared with other algorithms.

Table 5.
Adjacent pixel correlation test results.

Table 6.
Adjacent pixel correlation of image in different algorithms.
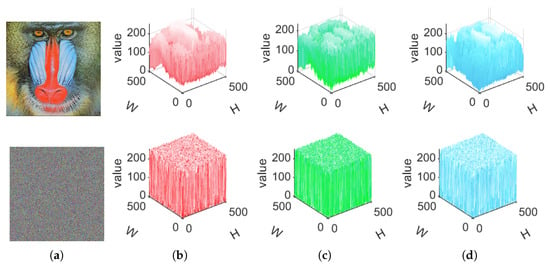
Figure 6.
Three-dimensional visualization of the image before and after encryption. (a) Plaintext image and ciphertext image. (b) Red channel. (c) Green channel. (d) Blue channel.
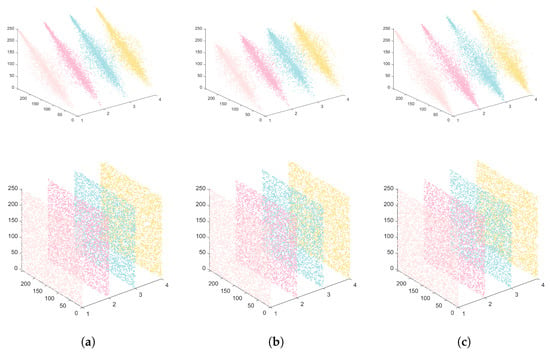
Figure 7.
Simulation results of adjacent pixels before and after image encryption. (a) Horizontal/vertical/diagonal/anti-diagonal for red channel of 4.2.03. (b) Horizontal/vertical/diagonal/anti-diagonal for green channel of 4.2.03. (c) Horizontal/vertical/diagonal/anti-diagonal for blue channel of 4.2.03.
4.4. Differential Attack Analysis
As a widely used cryptanalysis method, the effectiveness of differential attacks relies on the sensitivity of the algorithm to small input differences. To accurately evaluate the robustness of an image encryption scheme against differential attacks, the number of pixels change rate (NPCR) and the unified average changing intensity (UACI) are commonly applied as test metrics. Assuming that two ciphertext images, and , are the results of encrypting two plaintext images by just a one-bit difference, the NPCR and UACI between and are calculated as follows:
where Q represents the maximum value that a pixel in the image can reach, the total count of pixels is represented by H, and indicates the image size.
Wu et al. [42] have established a rigorous set of NPCR and UACI testing standards to comprehensively assess the performance of encryption. For an ideal encryption algorithm, NPCR should exceed a predetermined threshold, while the UACI needs to fall within a specific range. The calculation of the threshold for the NPCR test and the range for the UACI test can be summarized as follows:
where is the inverse cumulative density function of the standard normal distribution. With the significance level set at 0.05 in this article, the testing criteria for different image sizes are as follows: for images, is 99.5693% and the range is (33.2824%, 33.6447%); for images, is 99.5893% and the range is (33.3730%, 33.5541%); and for images, is 99.5994% and the range is (33.4183%, 33.5088%). The encryption results for images of different sizes are displayed in Table 7. The empirical outcomes suggest that the CIEA-RQ is resistant to differential attacks.

Table 7.
NPCR and UACI values.
4.5. Information Entropy Analysis
Information entropy is an important metric for evaluating the distribution of gray values in an image and gauging the randomness of image information. It is specifically described as follows:
where represents the frequency of information occurrence, and for an 8-bit grayscale image, F equals 8. The information entropy’s theoretical value stands at 8. When the outcome approaches 8, it signifies a great level of randomness in the image’s grayscale value distribution and reduces the likelihood of information leakage. In accordance with the experimental test outcomes as presented in Table 8, the algorithm shows higher randomness and lower information leakage probability, thus effectively resisting statistical analysis attacks.

Table 8.
Image information entropy.
4.6. Robustness Analysis
During the decryption process, some noise interference and data loss can affect the decryption effect. This section will introduce salt-and-pepper noise and cropping attacks to the ciphertext image, testing the scheme’s resistance to noise pollution and data loss during decryption and analyzing its overall robustness.
4.6.1. Salt-and-Pepper Noise Analysis
In the decryption process, salt-and-pepper noise with intensities of 0.005, 0.01, and 0.03 is introduced to the ciphertext image, followed by the decryption process. The outcomes are depicted in Figure 8. The test outcomes reveal that the information remains clear, demonstrating the algorithm’s effectiveness in resisting noise attacks and restoring ciphertext images.
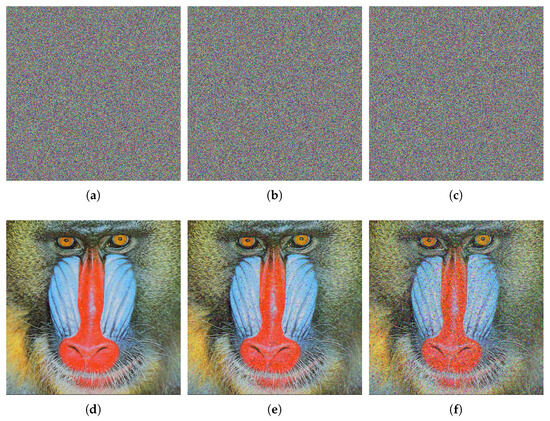
Figure 8.
Salt-and-pepper noise attack detection for ciphertext image of 4.2.03. (a) Salt-and-pepper noise (0.005). (b) Salt-and-pepper noise (0.01). (c) Salt and-pepper noise (0.03). (d) Decrypted image of (a). (e) Decrypted image of (b). (f) Decrypted image of (c).
4.6.2. Cropping Attack Analysis
During decryption, the ciphertext image undergoes varying levels of information loss, followed by the decryption operation. The outcomes are depicted in Figure 9. The experimental test demonstrates that the information remains clear, affirming the algorithm’s capability to effectively withstand cropping attacks and restore the ciphertext image.
4.7. Key Sensitivity Analysis
In this section, we explore encryption keys in detail and evaluate scheme performance. The security of a scheme is directly related to the property that minor adjustments to the key during encryption produces an entirely distinct result. This further emphasizes the complexity of evaluating the performance of security schemes, not only regarding the increase in encryption strength but also in terms of their sensitivity to input parameters. In the experiments, the original key and the scrambled key (original key+) are applied to encrypt a plaintext image. By calculating and comparing the NPCR and UACI between the ciphertext images obtained in the two cases, we were able to quantitatively assess the impact of minor variations in the key on the encryption results. Table 9 shows that the test data for the NPCR and UACI between the original ciphertext image and the scrambled ciphertext image meet the criteria, attesting to the robust key sensitivity of the CIEA-RQ; the test image is 4.2.03.

Table 9.
Key sensitivity analysis.
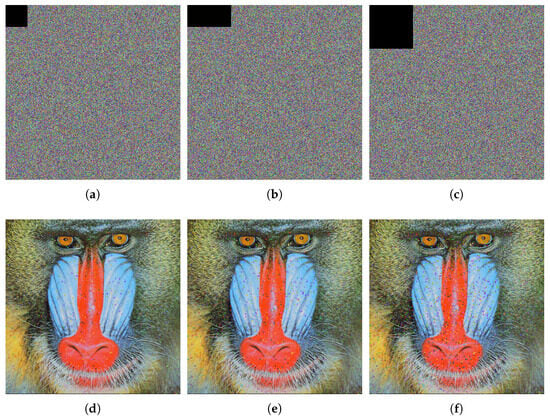
Figure 9.
Cropping attack test for ciphertext image of 4.2.03. (a) Cropping ciphertext image. (b) Cropping ciphertext image. (c) Cropping ciphertext image. (d) Decrypted image of (a). (e) Decrypted image of (b). (f) Decrypted image of (c).
4.8. Key Space
All the parameters applied to produce the key make up the key space. Whether the key space is large enough is one of the crucial factors in measuring the security of an encryption scheme. In the CIEA-RQ, we adopt a quantum Logistic map as the mechanism for key generation. Its key space can be represented as K = {, , , , }, where are keys with an accuracy of , and SHA-256 is the introduced hash function, which generates hash values of 256-bit length. The key space consisting of system parameters and the hash value is calculated to encompass approximately possible key combinations, with a key length of 489 bits. In consequence, the CIEA-RQ yields a considerable key space able to withstand exhaustive attacks. The comparison of the key space is presented in Table 10.

Table 10.
Key space analysis.
4.9. Efficiency Analysis
An effective encryption algorithm should not only ensure image security but also maintain high encryption efficiency to meet practical application demands. For the proposed CIEA-RQ, the average encryption time for three color images (4.1.03, 4.1.04, and 4.1.05) is 1.646906 s. Table 11 presents a comparison of encryption times between CIEA-RQ and other existing algorithms. As shown, CIEA-RQ requires less time, demonstrating superior encryption efficiency while maintaining strong security, making it more suitable for practical application scenarios.

Table 11.
Average encryption times (s) of different algorithms.
5. Conclusions
In the algorithm, to achieve a balance between encryption efficiency and strength, the color plaintext image is segmented into bit planes. Based on different weights of information, encryption with varying complexity is applied to the high 4-bit planes and the low 4-bit planes separately. Then, cross-iterative diffusion is performed. Finally, the processed planes are combined to synthesize the color ciphertext image. RNA extended dynamic coding is used to encrypt high 4-bit planes, which improves the efficiency of encryption as well as significantly enhances the ability of the CIEA-RQ to resist cryptographic attacks. Meanwhile, the cross-iterative diffusion between the high 4-bit planes and the low 4-bit planes further confuses the encrypted result. This greatly increases the difficulty of cracking for attackers. The simulation outcomes reveal that the method possesses excellent robustness and the key space can go against brute-force attacks. NPCR and UACI test results show that the CIEA-RQ is resistant to differential attacks. The potential of the algorithm in other areas such as video and audio will be further explored in future research. In addition, we will deepen the analysis of the CIEA-RQ’s effectiveness and embed the system into practical applications to more comprehensively evaluate its performance in real-world scenarios.
Author Contributions
X.Z. (Xiangyu Zhang) is mainly reponsible for the research design, code writing, and article writing. W.F. is mainly responsible for article revision. S.K. and Z.X. are mainly responsible for LaTeX typesetting and drawing. Y.L. and X.Z. (Xuexi Zhang) are mainly responsible for the literature search and format proofreading. H.W. is mainly responsible for supervision and leadership. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Guangdong Basic and Applied Basic Research Foundation under Grant 2023A1515011717, Special Projects for Key Fields of the Education Department of Guangdong Province under Grant 2024ZDZX1048, and Special Funds for the Cultivation of Guangdong College Students’ Scientific and Technological Innovation (“Climbing Program” Special Funds) under Grant pdjh2024a428.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used and analyzed during the current study available from the corresponding author on reasonable request. All data generated or analyzed during this study are included in this article.
Conflicts of Interest
The authors declare no competing interests.
References
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting newly designed fractional-order 3D Lorenz chaotic system and 2D discrete polynomial hyper-chaotic map for high-performance multi-image encryption. Fractal Fract. 2023, 7, 887. [Google Scholar]
- Luo, Y.; Liang, X.; Zhang, C.; Zeng, W.; Qiu, K. Redundancy-free key distribution using multiple phase offset for secure data center. J. Light. Technol. 2024, 42, 523–531. [Google Scholar]
- Lai, Q.; Zhang, H.; Kuate, P.D.K.; Xu, G.; Zhao, X.W. Analysis and implementation of no-equilibrium chaotic system with application in image encryption. Appl. Intell. 2022, 52, 11448–11471. [Google Scholar] [CrossRef]
- Wen, W.; Wei, K.; Zhang, Y.; Fang, Y.; Li, M. Colour light field image encryption based on DNA sequences and chaotic systems. Nonlinear Dyn. 2020, 99, 1587–1600. [Google Scholar]
- Lin, Y.; Xie, Z.; Chen, T.; Cheng, X.; Wen, H. Image privacy protection scheme based on high-quality reconstruction DCT compression and nonlinear dynamics. Expert Syst. Appl. 2024, 257, 124891. [Google Scholar] [CrossRef]
- Xue, R.; Ma, Y.; An, X.; Xiong, L.; Zhang, J. Design of a dissipative chaotic system based on Hamiltonian energy function and its application. Phys. Scr. 2025, 100, 025250. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Memiş, S.; Lai, Q.; Hu, G. An image encryption method based on multi-space confusion using hyperchaotic 2D Vincent map derived from optimization benchmark function. Nonlinear Dyn. 2023, 111, 20377–20405. [Google Scholar] [CrossRef]
- Zeng, W.; Zhang, C.; Liang, X.; Luo, Y.; Wang, X.; Qiu, K. Chaotic phase noise-like encryption based on geometric shaping for coherent data center interconnections. Opt. Express 2024, 32, 1595–1608. [Google Scholar] [CrossRef] [PubMed]
- Chai, X.; Wang, Y.; Chen, X.; Gan, Z.; Zhang, Y. TPE-GAN: Thumbnail preserving encryption based on GAN with key. IEEE Signal Process. Lett. 2022, 29, 972–976. [Google Scholar] [CrossRef]
- Li, C.; Shen, X.; Liu, S. Cryptanalyzing an image encryption algorithm underpinned by 2-D lag-complex logistic map. IEEE MultiMedia 2024, 31, 99–109. [Google Scholar] [CrossRef]
- Toktas, F.; Erkan, U.; Yetgin, Z. Cross-channel color image encryption through 2D hyperchaotic hybrid map of optimization test functions. Expert Syst. Appl. 2024, 249, 123583. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, X.; Zhang, J.; Qin, Z.; Zhang, J.; He, Y. Image encryption algorithm based on plane-level image filtering and discrete logarithmic transform. Mathematics 2022, 10, 2751. [Google Scholar] [CrossRef]
- Teng, L.; Wang, X.; Yang, F.; Xian, Y. Color image encryption based on cross 2D hyperchaotic map using combined cycle shift scrambling and selecting diffusion. Nonlinear Dyn. 2021, 105, 1859–1876. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, W.; Zhao, R.; Zhang, X.; Cao, X. F-TPE: Flexible thumbnail-preserving encryption based on multi-pixel sum-preserving encryption. IEEE Trans. Multimed. 2022, 25, 5877–5891. [Google Scholar]
- Hua, Z.; Liu, X.; Zheng, Y.; Yi, S.; Zhang, Y. Reversible data hiding over encrypted images via preprocessing-free matrix secret sharing. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 1799–1814. [Google Scholar]
- Chai, X.; Fu, J.; Gan, Z.; Lu, Y.; Zhang, Y.; Han, D. Exploiting semi-tensor product compressed sensing and hybrid cloud for secure medical image transmission. IEEE Internet Things J. 2022, 10, 7380–7392. [Google Scholar] [CrossRef]
- Lai, Q.; Hu, G.; Erkan, U.; Toktas, A. A novel pixel-split image encryption scheme based on 2D Salomon map. Expert Syst. Appl. 2023, 213, 118845. [Google Scholar]
- An, X.; Liu, S.; Xiong, L.; Zhang, J.; Li, X. Mixed gray-color images encryption algorithm based on a memristor chaotic system and 2D compression sensing. Expert Syst. Appl. 2024, 243, 122899. [Google Scholar]
- Liu, S.; Li, C.; Hu, Q. Cryptanalyzing two image encryption algorithms based on a first-order time-delay system. IEEE MultiMedia 2021, 29, 74–84. [Google Scholar]
- Chen, L.; Li, C.; Li, C. Security measurement of a medical communication scheme based on chaos and DNA coding. J. Vis. Commun. Image Represent. 2022, 83, 103424. [Google Scholar] [CrossRef]
- Alawida, M. A Novel Image Encryption Algorithm Based on Cyclic Chaotic Map in Industrial IoT Environments. IEEE Trans. Ind. Inform. 2024, 20, 10530–10541. [Google Scholar]
- Li, L. A novel chaotic map application in image encryption algorithm. Expert Syst. Appl. 2024, 252, 124316. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Lai, Q. 2D hyperchaotic system based on Schaffer function for image encryption. Expert Syst. Appl. 2023, 213, 119076. [Google Scholar]
- Li, C.; Wang, X.; Du, J.; Li, Z. Electrical activity and synchronization of HR-tabu neuron network coupled by Chua Corsage Memristor. Nonlinear Dyn. 2023, 111, 21333–21350. [Google Scholar] [CrossRef]
- Lu, Y.; Li, H.; Li, C. Electrical activity and synchronization of memristor synapse-coupled HR network based on energy method. Neurocomputing 2023, 544, 126246. [Google Scholar] [CrossRef]
- Bao, B.; Wang, Z.; Hua, Z.; Chen, M.; Bao, H. Regime transition and multi-scroll hyperchaos in a discrete neuron model. Nonlinear Dyn. 2023, 111, 13499–13512. [Google Scholar] [CrossRef]
- Toktas, A.; Erkan, U.; Ustun, D.; Lai, Q. Multiobjective Design of 2D Hyperchaotic System Using Leader Pareto Grey Wolf Optimizer. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 5237–5247. [Google Scholar]
- Li, H.; Li, C.; He, S. Locally active memristor with variable parameters and its oscillation circuit. Int. J. Bifurc. Chaos 2023, 33, 2350032. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, C.; Luo, Y.; Wang, X.; Qiu, K. Secure encryption and key management for OFDM-PON based on chaotic Hilbert motion. J. Light. Technol. 2022, 41, 1619–1625. [Google Scholar] [CrossRef]
- Andono, P.N.; Setiadi, D.R.I.M. Improved pixel and bit confusion-diffusion based on mixed chaos and hash operation for image encryption. IEEE Access 2022, 10, 115143–115156. [Google Scholar] [CrossRef]
- Wang, X.; Du, X. Pixel-level and bit-level image encryption method based on Logistic-Chebyshev dynamic coupled map lattices. Chaos Solitons Fractals 2022, 155, 111629. [Google Scholar]
- Wang, X.; Chen, X. Image encryption algorithm based on cross-scrambling and rapid-mode diffusion. Vis. Comput. 2023, 39, 5041–5068. [Google Scholar]
- Wu, T.; Zhang, C.; Huang, H.; Zhang, Z.; Wei, H.; Wen, H.; Qiu, K. Security improvement for OFDM-PON via DNA extension code and chaotic systems. IEEE Access 2020, 8, 75119–75126. [Google Scholar] [CrossRef]
- Jasra, B.; Moon, A.H. Color image encryption and authentication using dynamic DNA encoding and hyper chaotic system. Expert Syst. Appl. 2022, 206, 117861. [Google Scholar] [CrossRef]
- Singh, A.K.; Chatterjee, K.; Singh, A. An image security model based on chaos and DNA cryptography for IIoT images. IEEE Trans. Ind. Inform. 2022, 19, 1957–1964. [Google Scholar]
- Wang, M.; Fu, X.; Teng, L.; Yan, X.; Xia, Z.; Liu, P. A new 2D-HELS hyperchaotic map and its application on image encryption using RNA operation and dynamic confusion. Chaos Solitons Fractals 2024, 183, 114959. [Google Scholar]
- Yang, J.; Zhang, W.; Yu, H.; Zhu, Z. Spatiotemporal chaos in Hénon nonlinear coupling and its application in image encryption with RNA genetic encoding operations. Nonlinear Dyn. 2025, 113, 20285–20311. [Google Scholar] [CrossRef]
- Goggin, M.E.; Sundaram, B.; Milonni, P.W. Quantum logistic map. Phys. Rev. A 1990, 41, 5705. [Google Scholar] [CrossRef]
- Gao, X.; Sun, B.; Cao, Y.; Banerjee, S.; Mou, J. A color image encryption algorithm based on hyperchaotic map and DNA mutation. Chin. Phys. B 2023, 32, 030501. [Google Scholar] [CrossRef]
- Meng, F.; Gu, Z. A Color image-encryption algorithm using extended DNA coding and zig-zag transform based on a fractional-order laser system. Fractal Fract. 2023, 7, 795. [Google Scholar]
- Yan, S.; Jiang, D.; Cui, Y.; Zhang, H.; Li, L.; Jiang, J. A fractional-order hyperchaotic system that is period in integer-order case and its application in a novel high-quality color image encryption algorithm. Chaos Solitons Fractals 2024, 182, 114793. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. J. Sel. Areas Telecommun. (JSAT) 2011, 1, 31–38. [Google Scholar]
- Dong, W.; Li, Q.; Tang, Y. Image encryption-then-transmission combining random sub-block scrambling and loop DNA algorithm in an optical chaotic system. Chaos Solitons Fractals 2021, 153, 111539. [Google Scholar] [CrossRef]
- Wang, J.; Liu, L.; Xu, M.; Li, X. A novel content-selected image encryption algorithm based on the LS chaotic model. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 8245–8259. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Xu, C.; Yu, F. Brain-like initial-boosted hyperchaos and application in biomedical image encryption. IEEE Trans. Ind. Inform. 2022, 18, 8839–8850. [Google Scholar] [CrossRef]
- Wang, X.; Guan, N.; Zhao, H.; Wang, S.; Zhang, Y. A new image encryption scheme based on coupling map lattices with mixed multi-chaos. Sci. Rep. 2020, 10, 9784. [Google Scholar] [CrossRef] [PubMed]
- Ma, K.; Teng, L.; Wang, X.; Meng, J. Color image encryption scheme based on the combination of the fisher-yates scrambling algorithm and chaos theory. Multimed. Tools Appl. 2021, 80, 24737–24757. [Google Scholar] [CrossRef]
- Telem, A.N.K.; Tchapga, C.T.; Nkapkop, J.D.D.; Ndongmo, J.D.D.N.; Tsafack, N.; Boya, B.F.B.A. Hyperchaotic color image encryption scheme based on simultaneous color channel confusion-diffusion operations. Phys. Scr. 2024, 99, 075276. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Y.; Jahanshahi, H.; Wang, Z.; Mou, J. Color image encryption algorithm based on Double layer Josephus scramble and laser chaotic system. Optik 2023, 275, 170590. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).