Visualizing Three-Qubit Entanglement
Abstract
1. Introduction
2. Graphical Representation of Entanglement
- . This reflects that W can be written as a superposition of all three possible Bell pairs——so its entanglement is fully pair-wise-generated.
- . This reflects that for no pair-wise decomposition exists. In fact, , and , , so its tripartite entanglement is genuine.
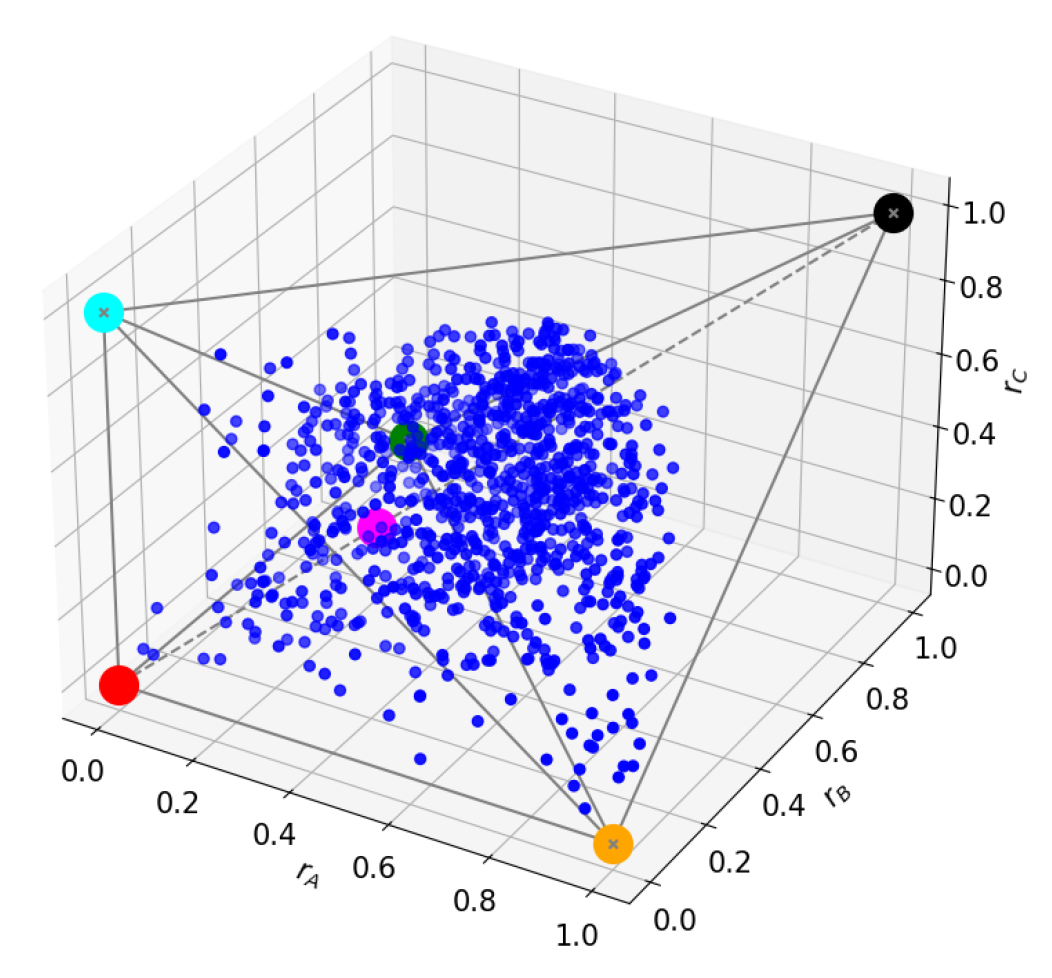
- Product state class/Type 1: This contains all three-qubit states with no entanglement, denoted as . It is the equivalence class of under LUs: . All states have and , so all states are mapped to in the polytope.
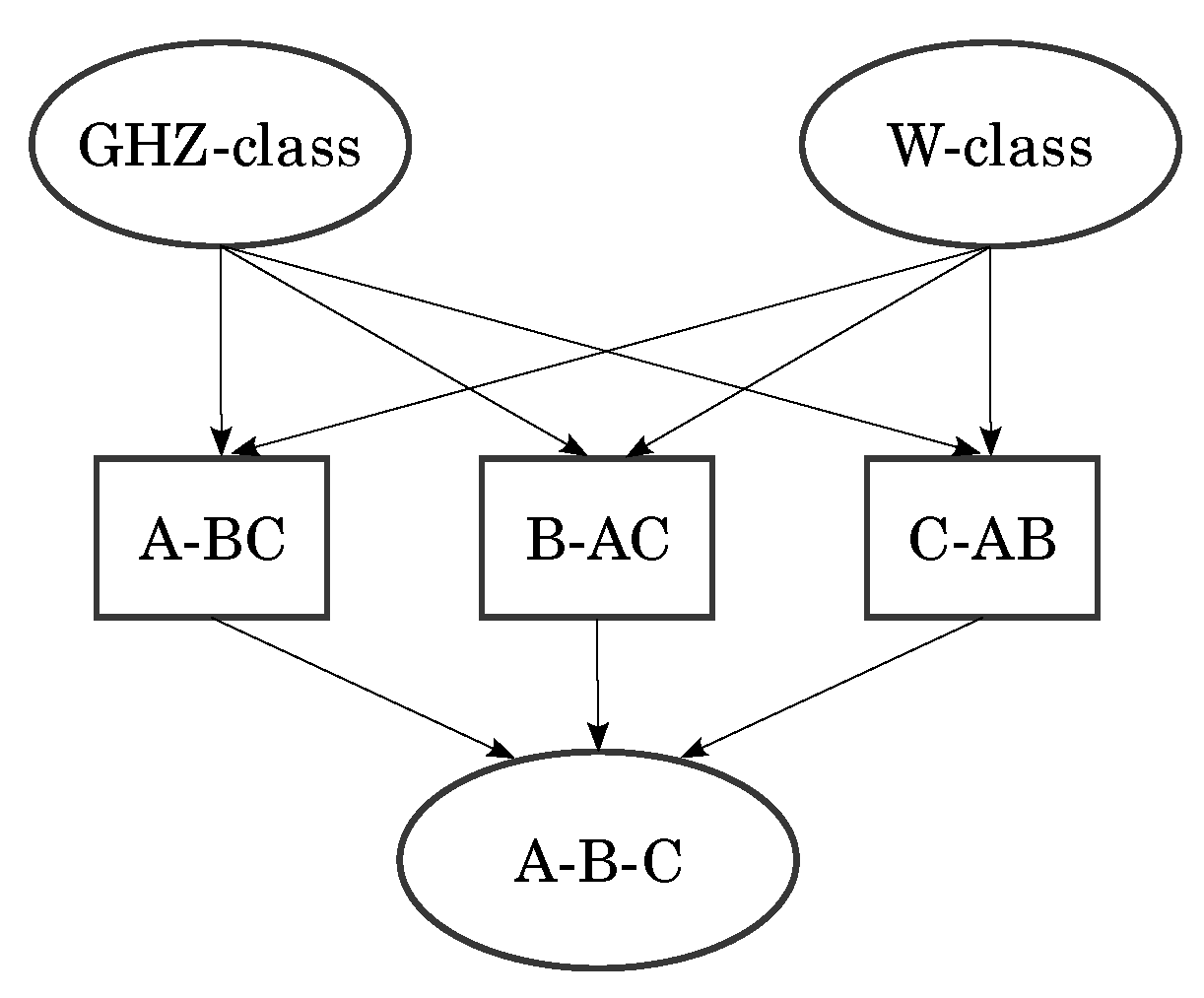
- Bipartite classes/Type 2a: States of the form ; that is, and . These states have for all l but one, which could be , or . States with correspond to class , to , and to . Each class covers one of the three edges of the upper tetrahedron connected to (see Figure 2b).
- W class: This includes all states with all three qubits entangled, without genuine tripartite entanglement. They can always be written in the following form:with and [13]. They can be of two types: Type 3a tri-Bell states and Type 4a. Type 3a states lie exclusively on the faces of the upper tetrahedron and have , corresponding to the family with in (7). The W state belongs to this type, with and , . Type 4a states have , corresponding to the family with in (7). They are located in the upper tetrahedron, and they accumulate near the point [25] (see Figure 2c).
- GHZ class: This contains states with genuine tripartite entanglement. There are five types:
- (a)
- Type 2b generalized GHZ states. They have , except for for . The standard GHZ state corresponds to the values . They lie on the central diagonal connecting and (see Figure 2d). Notice that for , they occupy the same point in the polytope as the W state.
- (b)
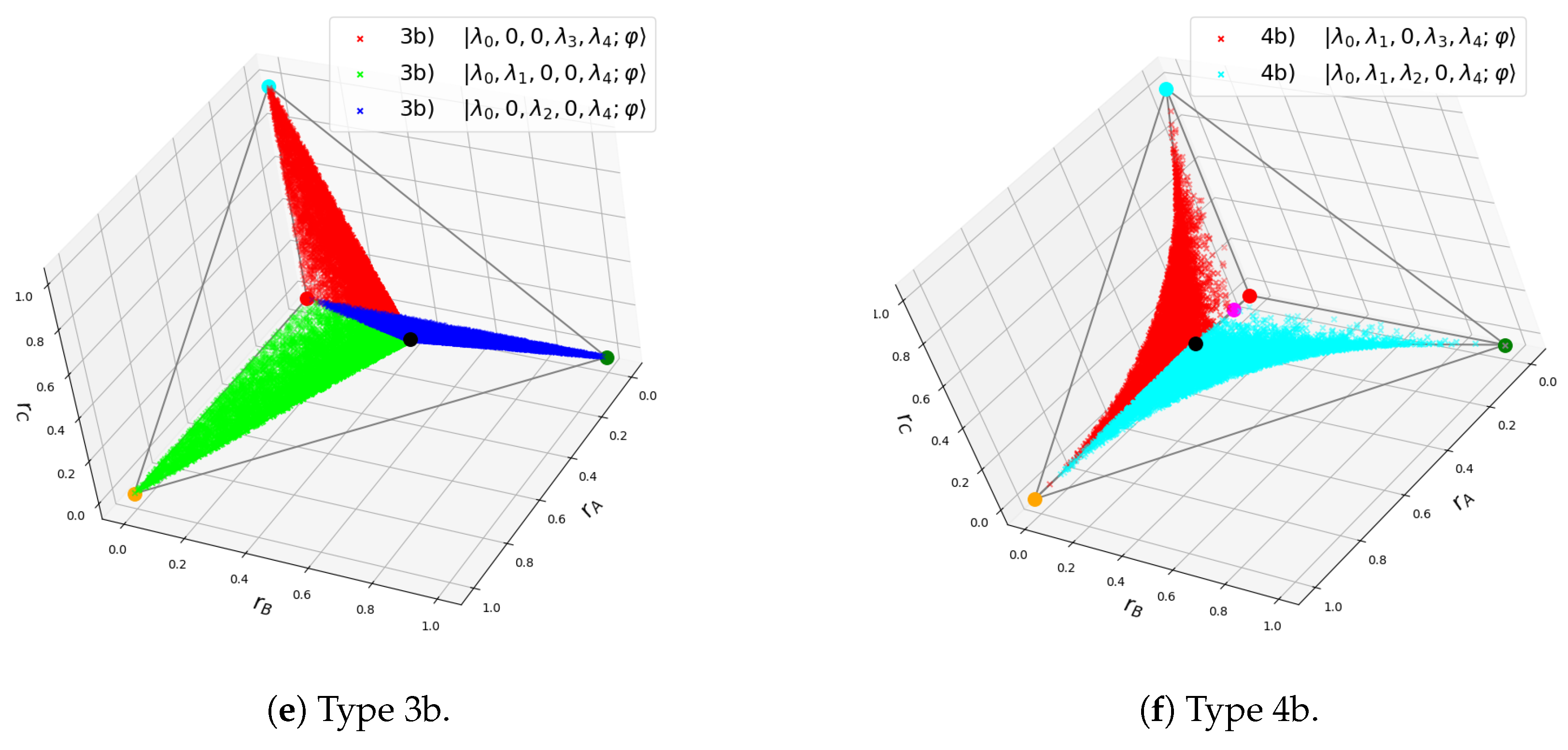
- Type 3b extended GHZ states: They have for with , so either , , or . Each one spans a different triangle connecting the main diagonal with any of the three vertices of the face (see Figure 2e).
- (c)
- Type 4b states have either or . They lie in the space between two of the three triangles defined by type 3b. If , they lie between the triangles of type 1-2 and 2-3, while if , then they lie between triangles of type 2-3 and 1-3. No states of type 4b lie between 1-3 and 2-3 (see Figure 2f).
- (d)
- Type 4c states have . These populate the polytope without any clear pattern.
- (e)
- Type 5 generic GHZ states: These have and , . They may lie anywhere in the polytope.
3. Geometry of the Tangle
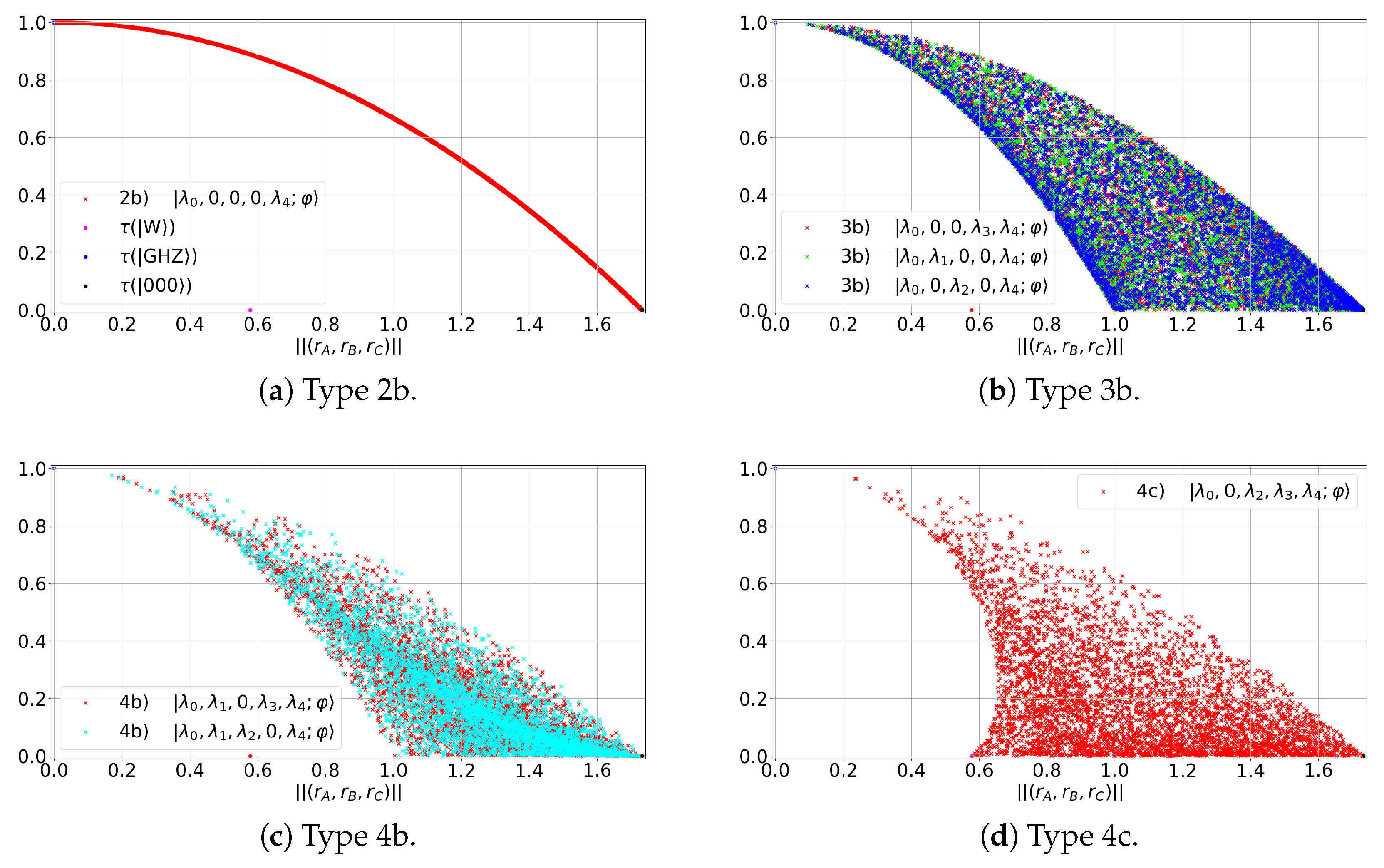
- Type 2a states occupy a curve (see Figure 3a), maximizing the value of for a given value of R.
- Type 3b and 4b states occupy a common area (see Figure 3b,c), bounded from above by and from below by .
- Type 4c and 5 states occupy a larger area than the previous cases (see Figure 3d), upper-bounded by and lower-bounded by a curve with two branches: and .
- States of types 3b, 4b and 4c deviate from the main diagonal (i.e., ) and have .
4. Study of the Tangle in Three-Qubit Spin Chains
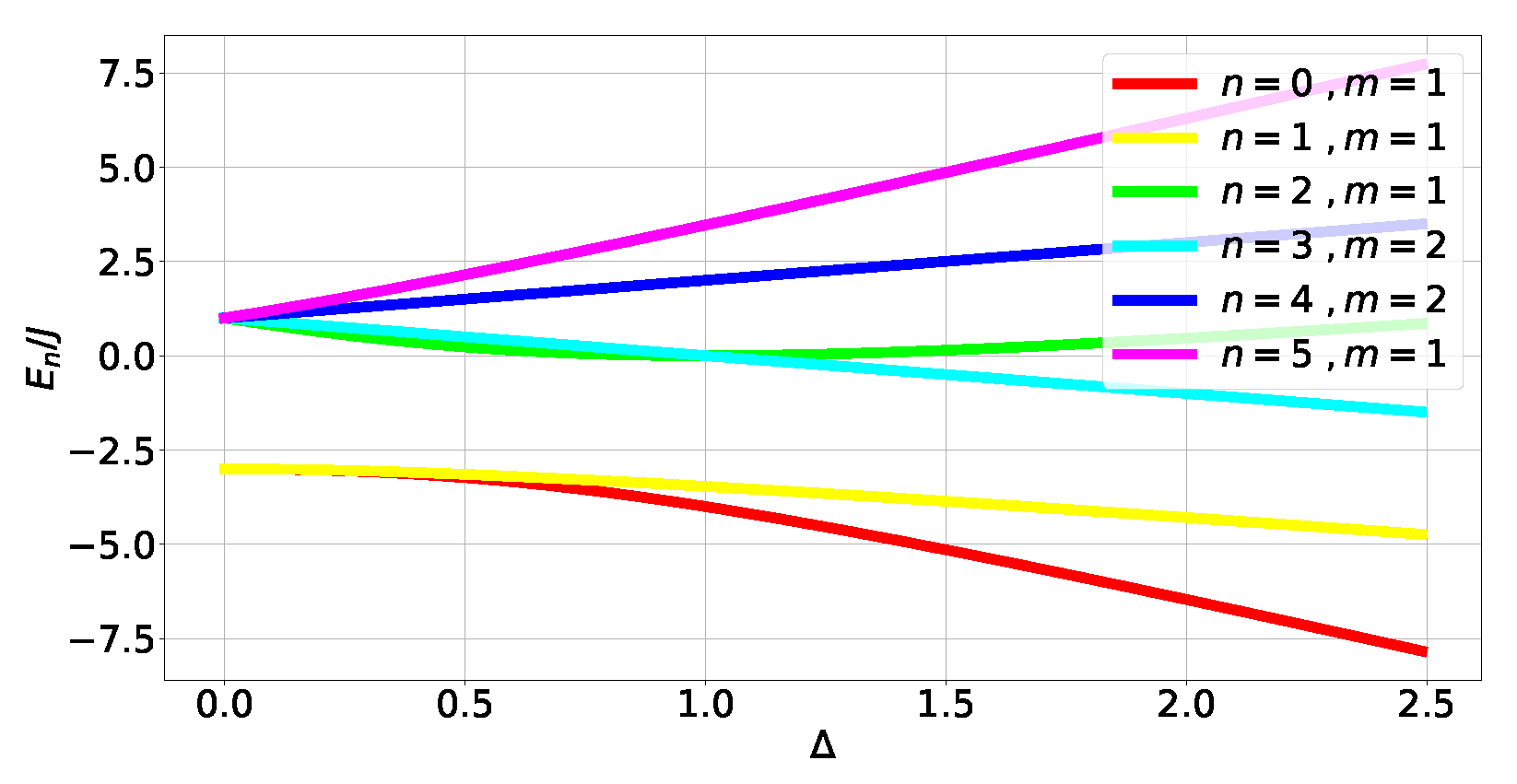
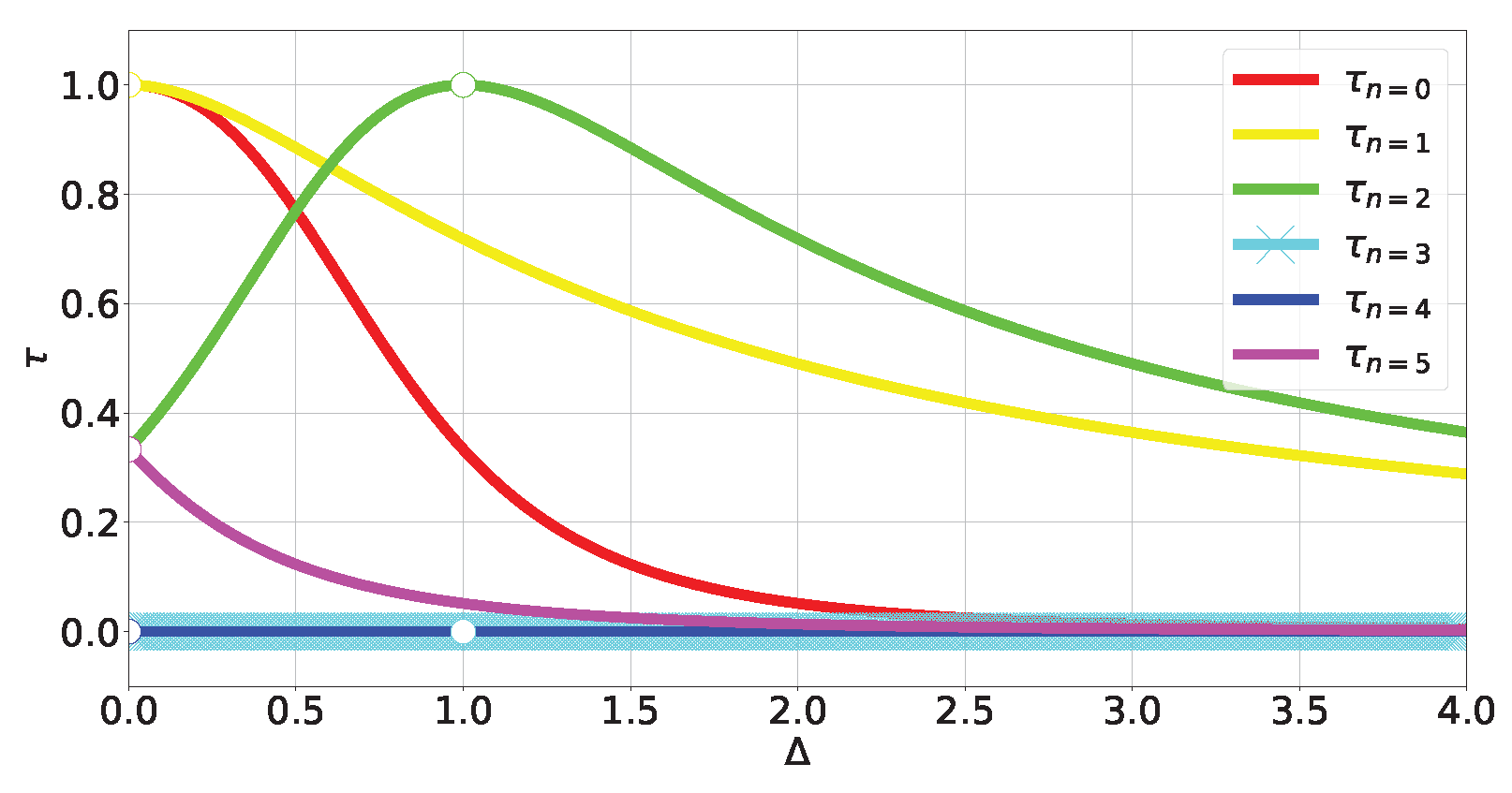
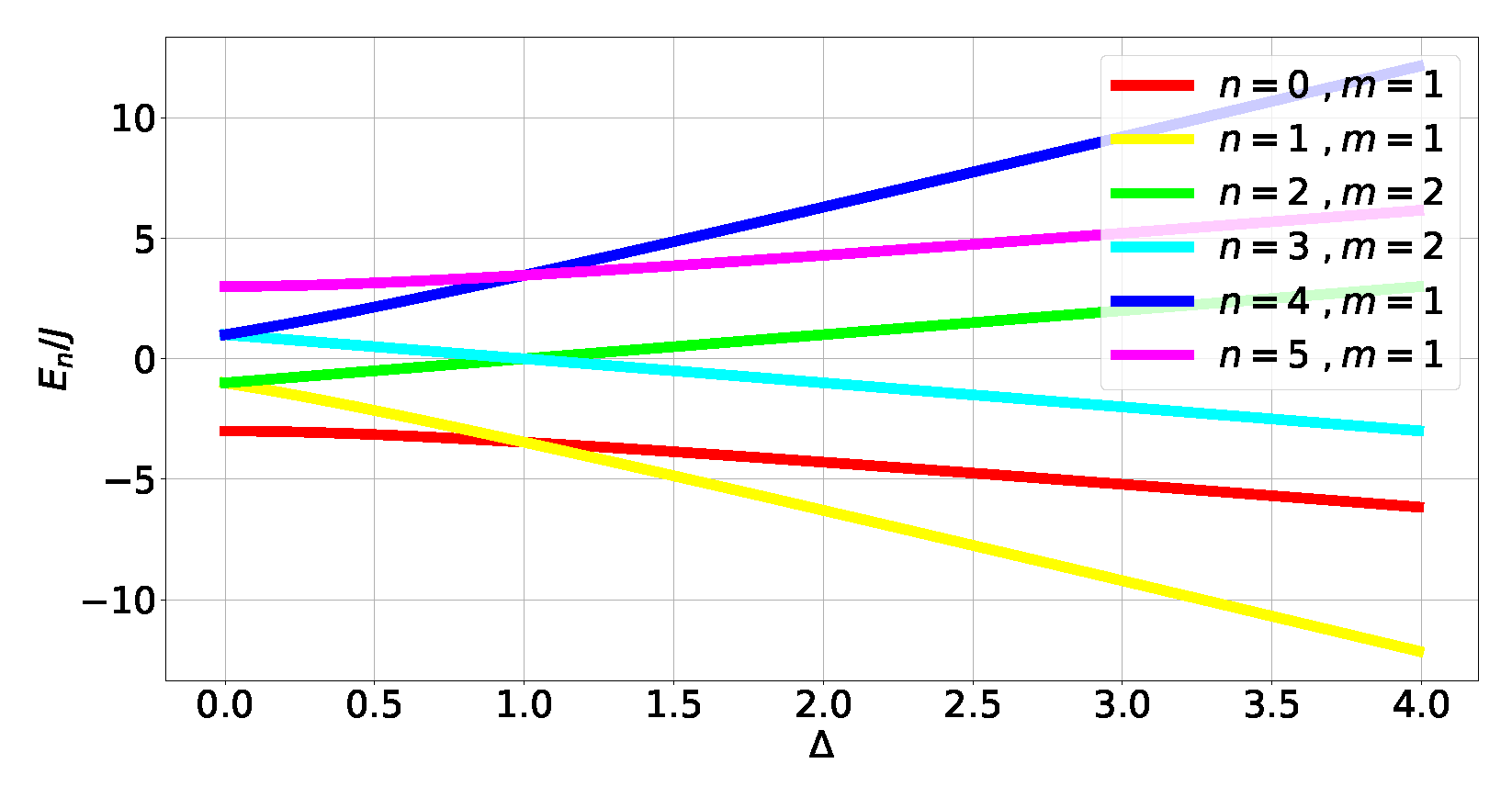
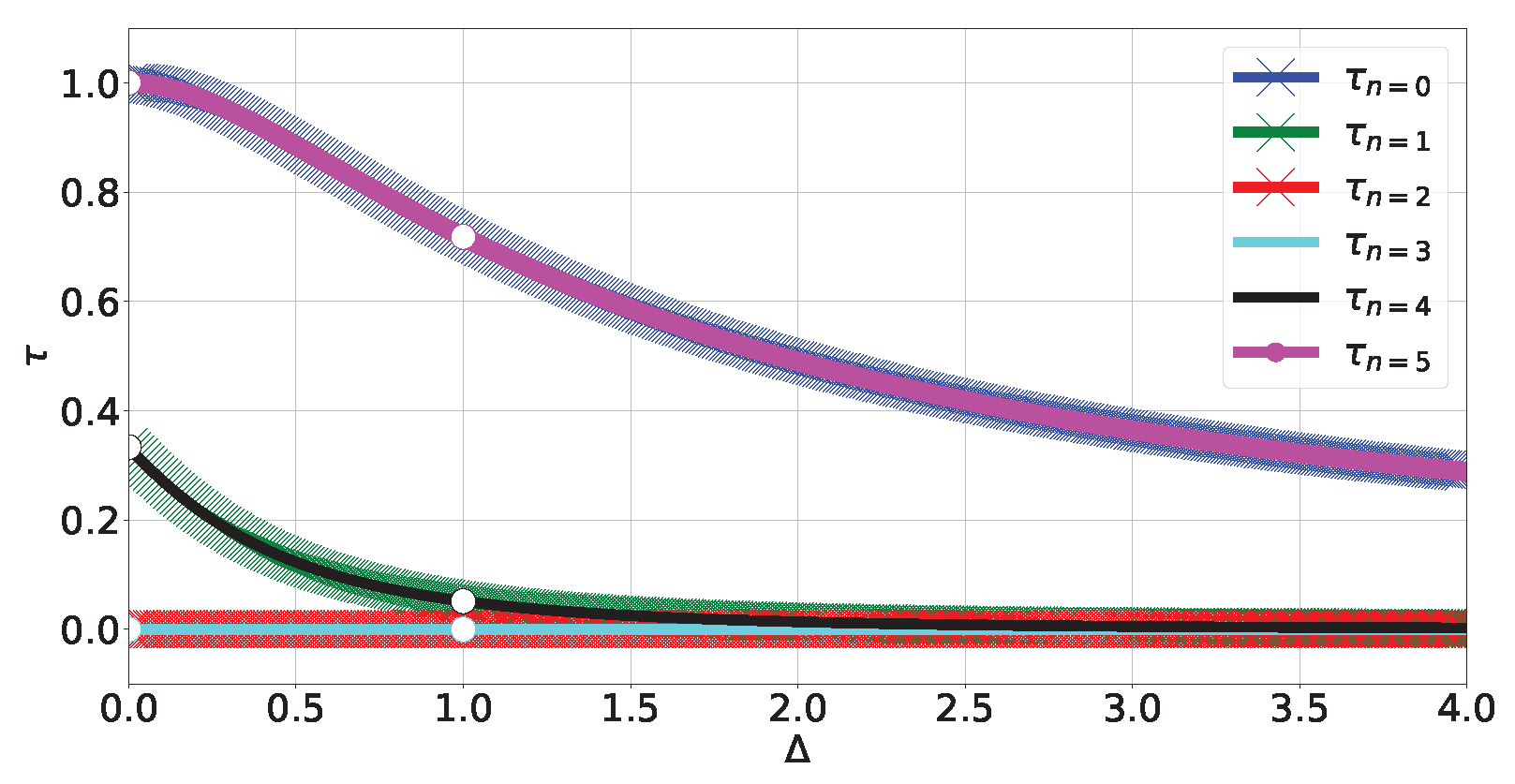
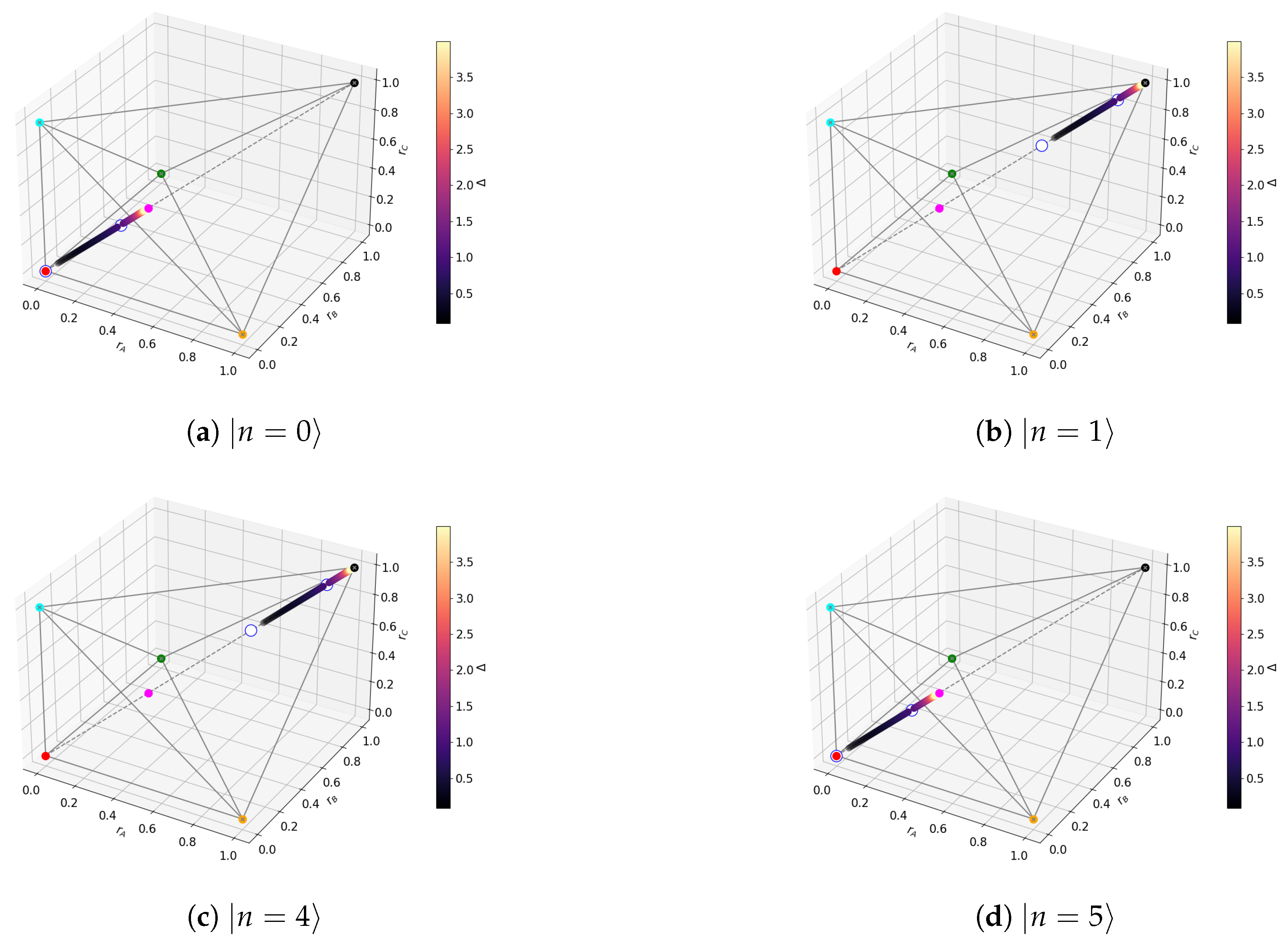
- Eigenstates with a robust tangle . This is because translation invariance causes all three Bloch-norms to be equal. This also explains why the instances of Bloch-norms that are not in the main diagonal correspond to degenerate subspaces: states there generally mix sectors with different momenta. Hence, the states with a robust tangle belong to the GHZ class type 5 subset spanned by simultaneous eigenstates of the translation and parity operators.
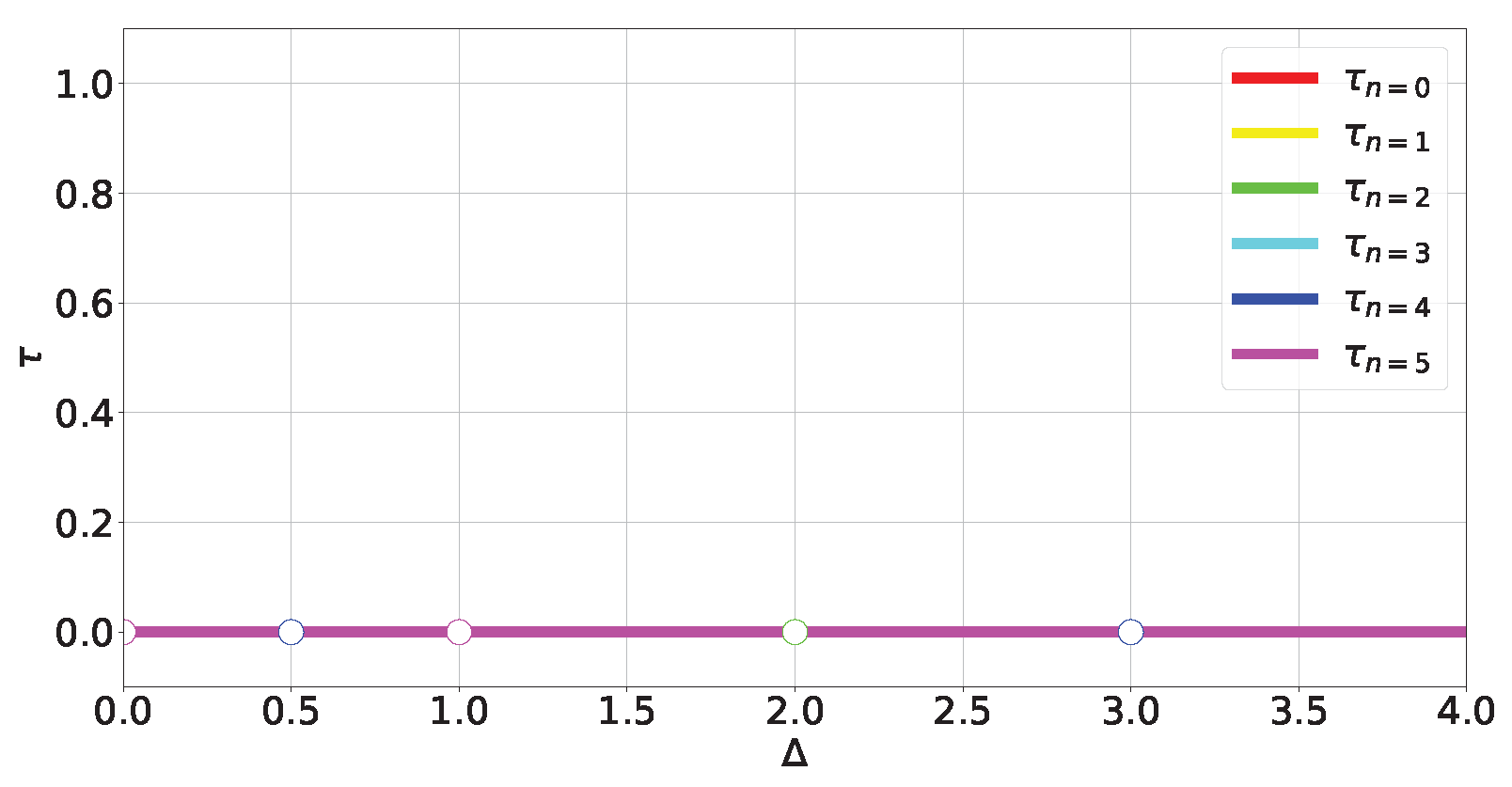
- Out-of-level-crossing degenerate levels in and have a null tangle. This is because, when projected onto those subspaces, the kinetic part of the Hamiltonian will commute with the potential term , causing the tangle to take the same constant value . Since for the resulting Hamiltonian cannot generate a tangle (since it is a collection of one-qubit operators), then necessarily .
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proofs of the Geometrical Properties of the Entanglement Types
| Vertices of the Face | |
|---|---|
Appendix B. (R, ) Surface Fibration by λ → Curves
Appendix C. Analytic Details of Three-Qubit Spin Chains
Appendix C.1. TFIM Analytics
Appendix C.1.1. TFIM Outside Level-Crossing Points
Appendix C.1.2. TFIM at Level-Crossing Points
Appendix C.2. XX Analytics
XX Outside Level-Crossing Points
Appendix C.3. XXX Analytics
XXX Outside Level-Crossing Points
Appendix C.4. XZX Analytics
XZX Outside Level-Crossing Points
References
- Horodecki, R.; Horodecki, P. Perfect correlations in the Einstein-Podolsky-Rosen experiment and Bell’s inequalities. Phys. Lett. A 1996, 210, 227–231. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Greenberger, D.M.; Horne, M.A.; Shimony, A.; Zeilinger, A. Bell’s theorem without inequalities. Am. J. Phys. 1990, 58, 1131–1143. [Google Scholar] [CrossRef]
- Schlienz, J.; Mahler, G. The maximal entangled three-particle state is unique. Phys. Lett. A 1996, 224, 39–44. [Google Scholar] [CrossRef]
- Linden, N.; Popescu, S.; Popescu, S. On Multi-Particle Entanglement. Fortschritte Phys. 1998, 46, 567–578. [Google Scholar] [CrossRef]
- Horodecki, M. Entanglement measures. Quantum Inf. Comput. 2001, 1, 3–26. [Google Scholar] [CrossRef]
- Bennett, C.H.; DiVincenzo, D.P.; Smolin, J.A.; Wootters, W.K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 1996, 54, 3824–3851. [Google Scholar] [CrossRef] [PubMed]
- Hill, S.A.; Wootters, W.K. Entanglement of a Pair of Quantum Bits. Phys. Rev. Lett. 1997, 78, 5022–5025. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar] [CrossRef]
- Coffman, V.; Kundu, J.; Wootters, W.K. Distributed entanglement. Phys. Rev. A 2000, 61, 052306. [Google Scholar] [CrossRef]
- Osborne, T.J.; Verstraete, F. General Monogamy Inequality for Bipartite Qubit Entanglement. Phys. Rev. Lett. 2006, 96, 220503. [Google Scholar] [CrossRef]
- Dür, W.; Vidal, G.; Cirac, J.I. Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 2000, 62, 062314. [Google Scholar] [CrossRef]
- Verstraete, F.; Dehaene, J.; De Moor, B.; Verschelde, H. Four qubits can be entangled in nine different ways. Phys. Rev. A 2002, 65, 052112. [Google Scholar] [CrossRef]
- Acín, A.; Andrianov, A.; Costa, L.; Jané, E.; Latorre, J.I.; Tarrach, R. Generalized Schmidt Decomposition and Classification of Three-Quantum-Bit States. Phys. Rev. Lett. 2000, 85, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Mosseri, R.; Dandoloff, R. Geometry of entangled states, Bloch spheres and Hopf fibrations. J. Phys. A Math. Gen. 2001, 34, 10243. [Google Scholar] [CrossRef]
- Mosseri, R. Two-Qubit and Three-Qubit Geometry and Hopf Fibrations. In Topology in Condensed Matter; Springer: Berlin/Heidelberg, Germany, 2006; pp. 187–203. [Google Scholar] [CrossRef]
- Sudbery, A. On local invariants of pure three-qubit states. J. Phys. A Math. Gen. 2001, 34, 643. [Google Scholar] [CrossRef]
- Cayley, A. On the theory of determinants. In Transactions of the Cambridge Philosophical Society; HardPress Publishing: Miami, FL, USA, 1843; pp. 1–16. [Google Scholar]
- Pérez-Salinas, A.; García-Martín, D.; Bravo-Prieto, C.; Latorre, J.I. Measuring the Tangle of Three-Qubit States. Entropy 2020, 22, 436. [Google Scholar] [CrossRef]
- Gelfand, I.; Kapranov, M.; Zelevinsky, A. Discriminants, Resultants, and Multidimensional Determinants; Birkhäuser Boston: Cambridge, MA, USA, 1994. [Google Scholar]
- Fano, U. Description of States in Quantum Mechanics by Density Matrix and Operator Techniques. Rev. Mod. Phys. 1957, 29, 74–93. [Google Scholar] [CrossRef]
- Walter, M.; Doran, B.; Gross, D.; Christandl, M. Entanglement Polytopes: Multiparticle Entanglement from Single-Particle Information. Science 2013, 340, 1205–1208. [Google Scholar] [CrossRef]
- Rajwade, A.R. Convex Polyhedra with Regularity Conditions and Hilbert’s Third Problem, 1st ed.; Texts and Readings in Mathematics, Hindustan Book Agency Gurgaon; Springer: Berlin/Heidelberg, Germany, 2001; p. 128. [Google Scholar] [CrossRef]
- Enríquez, M.; Delgado, F.; Życzkowski, K. Entanglement of Three-Qubit Random Pure States. Entropy 2018, 20, 745. [Google Scholar] [CrossRef] [PubMed]
- Luna-Hernández, S.; Enríquez, M.; Rosas-Ortiz, O. A geometric formulation to measure global and genuine entanglement in three-qubit systems. Sci. Rep. 2024, 14, 25684. [Google Scholar] [CrossRef]
- Vesperini, A.; Bel-Hadj-Aissa, G.; Capra, L.; Franzosi, R. Unveiling the geometric meaning of quantum entanglement: Discrete and continuous variable systems. Front. Phys. 2024, 19, 51204. [Google Scholar] [CrossRef]
- Cocchiarella, D.; Scali, S.; Ribisi, S.; Nardi, B.; Bel-Hadj-Aissa, G.; Franzosi, R. Entanglement distance for arbitrary M-qudit hybrid systems. Phys. Rev. A 2020, 101, 042129. [Google Scholar] [CrossRef]
- Haake, F. Level Repulsion. In Quantum Signatures of Chaos; Springer: Berlin/Heidelberg, Germany, 2001; pp. 37–45. [Google Scholar] [CrossRef]
- Rosenzweig, N.; Porter, C.E. “Repulsion of Energy Levels” in Complex Atomic Spectra. Phys. Rev. 1960, 120, 1698–1714. [Google Scholar] [CrossRef]
- Frank, W.; von Brentano, P. Classical analogy to quantum mechanical level repulsion. Am. J. Phys. 1994, 62, 706–709. [Google Scholar] [CrossRef]
- Novotny, L. Strong coupling, energy splitting, and level crossings: A classical perspective. Am. J. Phys. 2010, 78, 1199–1202. [Google Scholar] [CrossRef]
- Ma, T.; Serota, R.A. Level repulsion in integrable systems. Int. J. Mod. Phys. B 2012, 26, 1250095. [Google Scholar] [CrossRef]
- Briegel, H.J.; Raussendorf, R. Persistent Entanglement in Arrays of Interacting Particles. Phys. Rev. Lett. 2001, 86, 910–913. [Google Scholar] [CrossRef] [PubMed]
- Ghahi, M.G.; Akhtarshenas, S.J. Entangled graphs: A classification of four-qubit entanglement. Eur. Phys. J. D 2016, 70, 54. [Google Scholar] [CrossRef]
- Cervera-Lierta, A.; Gasull, A.; Latorre, J.I.; Sierra, G. Multipartite entanglement in spin chains and the hyperdeterminant. J. Phys. A Math. Theor. 2018, 51, 505301. [Google Scholar] [CrossRef]
- Acín, A.; Andrianov, A.; Jané, E.; Tarrach, R. Three-qubit pure-state canonical forms. J. Phys. A Math. Gen. 2001, 34, 6725. [Google Scholar] [CrossRef]
- Carteret, H.A.; Higuchi, A.; Sudbery, A. Multipartite generalization of the Schmidt decomposition. J. Math. Phys. 2000, 41, 7932–7939. [Google Scholar] [CrossRef]




| Class | ||||
|---|---|---|---|---|
| A-B-C | 0 | 0 | 0 | 0 |
| A-BC | 0 | >0 | >0 | 0 |
| B-AC | >0 | 0 | >0 | 0 |
| C-AB | >0 | >0 | 0 | 0 |
| W | >0 | >0 | >0 | 0 |
| GHZ | >0 | >0 | >0 | >0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benedito, A.; Sierra, G. Visualizing Three-Qubit Entanglement. Entropy 2025, 27, 800. https://doi.org/10.3390/e27080800
Benedito A, Sierra G. Visualizing Three-Qubit Entanglement. Entropy. 2025; 27(8):800. https://doi.org/10.3390/e27080800
Chicago/Turabian StyleBenedito, Alfred, and Germán Sierra. 2025. "Visualizing Three-Qubit Entanglement" Entropy 27, no. 8: 800. https://doi.org/10.3390/e27080800
APA StyleBenedito, A., & Sierra, G. (2025). Visualizing Three-Qubit Entanglement. Entropy, 27(8), 800. https://doi.org/10.3390/e27080800





