Energetic Variational Modeling of Active Nematics: Coupling the Toner–Tu Model with ATP Hydrolysis
Abstract
1. Introduction
2. Preliminaries
2.1. The Toner–Tu Model and Its Variants
2.2. Energetic Variational Approach for Chemo-Mechanical Systems
2.3. Energy Dissipation Analysis on a Simplified Toner–Tu Model
3. Toner–Tu Model with ATP Hydrolysis
3.1. Model Derivation
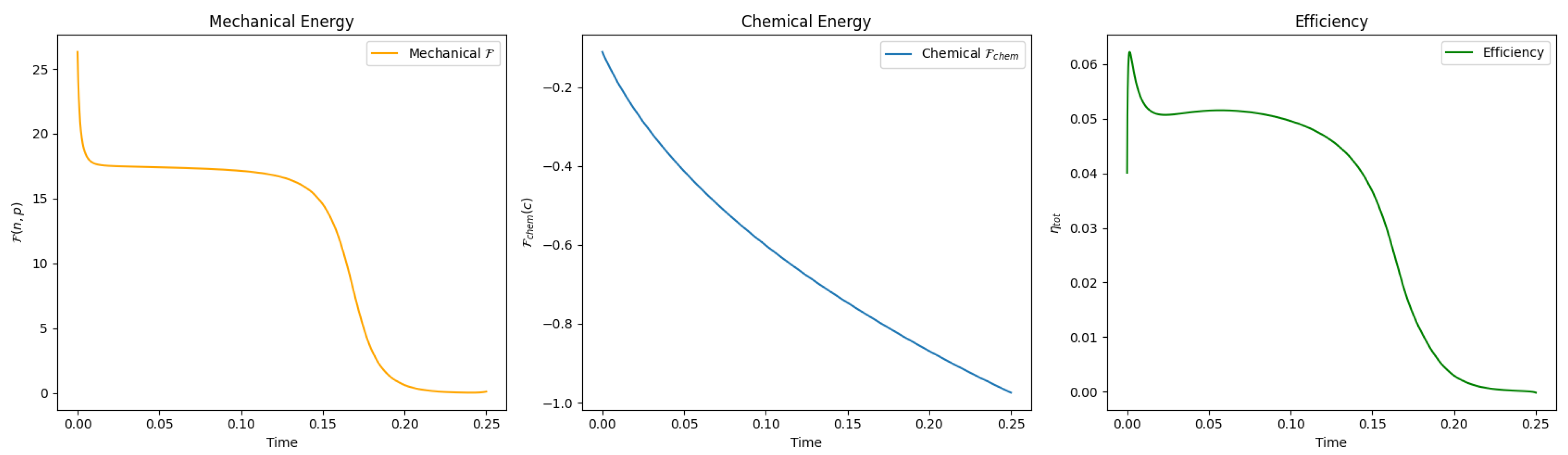
3.2. Energy Transduction and Efficiency
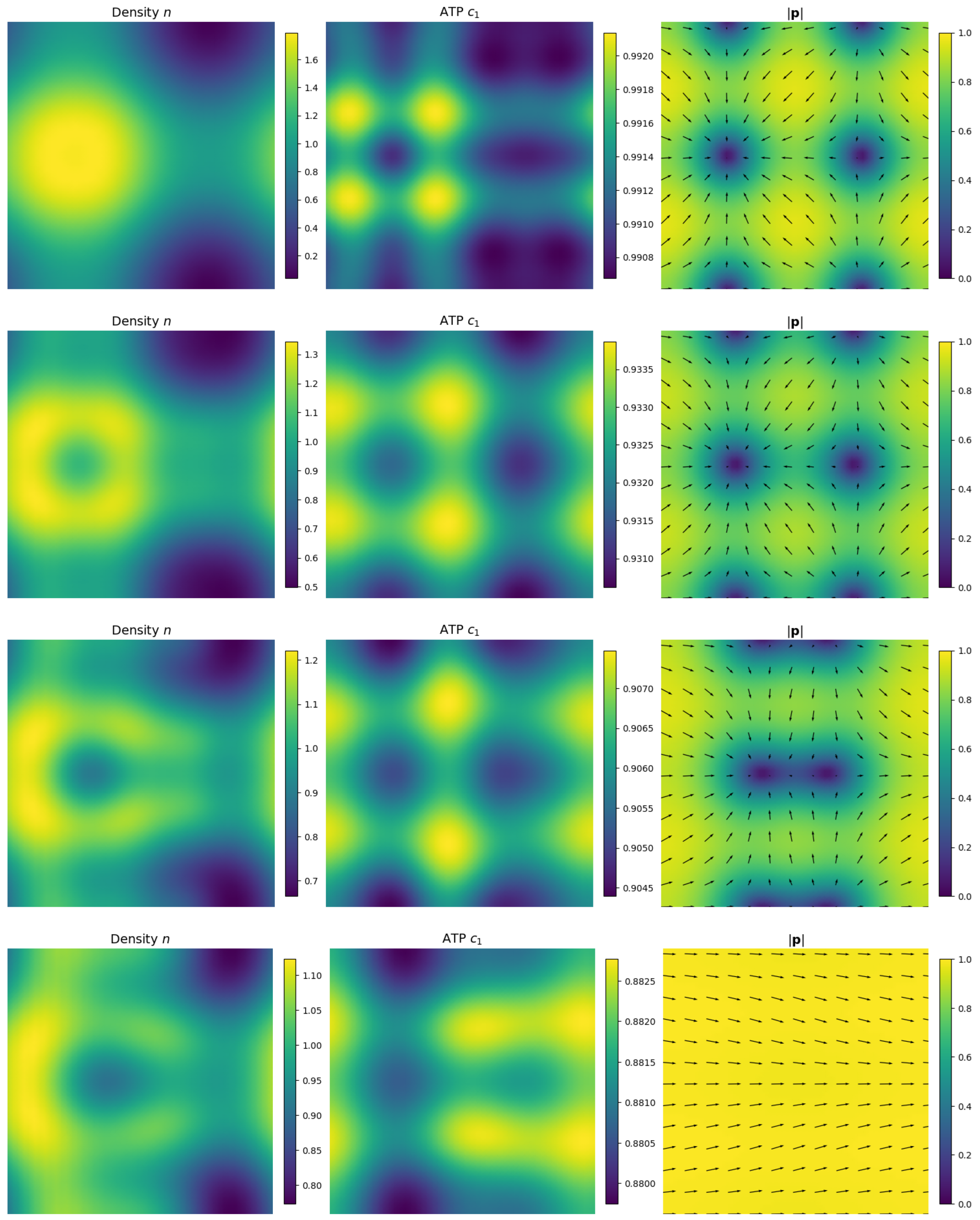
4. Numerics
5. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Das, M.; Schmidt, C.F.; Murrell, M. Introduction to active matter. Soft Matter 2020, 16, 7185–7190. [Google Scholar] [CrossRef]
- Doostmohammadi, A.; Ladoux, B. Physics of liquid crystals in cell biology. Trends Cell Biol. 2022, 32, 140–150. [Google Scholar] [CrossRef]
- Marchetti, M.C.; Joanny, J.F.; Ramaswamy, S.; Liverpool, T.B.; Prost, J.; Rao, M.; Simha, R.A. Hydrodynamics of soft active matter. Rev. Mod. Phys. 2013, 85, 1143. [Google Scholar] [CrossRef]
- Needleman, D.; Dogic, Z. Active matter at the interface between materials science and cell biology. Nat. Rev. Mater. 2017, 2, 1–14. [Google Scholar] [CrossRef]
- Aranson, I. Bacterial active matter. Rep. Prog. Phys. 2022, 85, 076601. [Google Scholar] [CrossRef] [PubMed]
- Saintillan, D.; Shelley, M.J. Instabilities, pattern formation, and mixing in active suspensions. Phys. Fluids 2008, 20, 123304. [Google Scholar] [CrossRef]
- Sanchez, T.; Chen, D.T.; DeCamp, S.J.; Heymann, M.; Dogic, Z. Spontaneous motion in hierarchically assembled active matter. Nature 2012, 491, 431–434. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, Y.; Kaiser, A.D.; Alber, M. Self-organization in bacterial swarming: Lessons from myxobacteria. Phys. Biol. 2011, 8, 055003. [Google Scholar] [CrossRef]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical applications of soft robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- Özkale, B.; Sakar, M.S.; Mooney, D.J. Active biomaterials for mechanobiology. Biomaterials 2021, 267, 120497. [Google Scholar] [CrossRef]
- Shah, A.; Malik, M.S.; Khan, G.S.; Nosheen, E.; Iftikhar, F.J.; Khan, F.A.; Shukla, S.S.; Akhter, M.S.; Kraatz, H.B.; Aminabhavi, T.M. Stimuli-responsive peptide-based biomaterials as drug delivery systems. Chem. Eng. J. 2018, 353, 559–583. [Google Scholar] [CrossRef]
- Alber, M.; Buganza Tepole, A.; Cannon, W.R.; De, S.; Dura-Bernal, S.; Garikipati, K.; Karniadakis, G.; Lytton, W.W.; Perdikaris, P.; Petzold, L.; et al. Integrating machine learning and multiscale modeling—Perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. NPJ Digit. Med. 2019, 2, 115. [Google Scholar] [CrossRef]
- Liu, A.P.; Appel, E.A.; Ashby, P.D.; Baker, B.M.; Franco, E.; Gu, L.; Haynes, K.; Joshi, N.S.; Kloxin, A.M.; Kouwer, P.H.; et al. The living interface between synthetic biology and biomaterial design. Nat. Mater. 2022, 21, 390–397. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Lervik, A. The energy conversion in active transport of ions. Proc. Natl. Acad. Sci. USA 2021, 118, e2116586118. [Google Scholar] [CrossRef]
- Blumenfeld, L. The physical aspects of energy transduction in biological systems. Q. Rev. Biophys. 1978, 11, 251–308. [Google Scholar] [CrossRef] [PubMed]
- O’Byrne, J.; Kafri, Y.; Tailleur, J.; van Wijland, F. Time irreversibility in active matter, from micro to macro. Nat. Rev. Phys. 2022, 4, 167–183. [Google Scholar] [CrossRef]
- Pearce, D.J.; Martínez-Prat, B.; Ignés-Mullol, J.; Sagués, F. Topological defects lead to energy transfer in active nematics. arXiv 2024, arXiv:2411.18214. [Google Scholar] [CrossRef]
- Wachtel, A.; Rao, R.; Esposito, M. Free-energy transduction in chemical reaction networks: From enzymes to metabolism. J. Chem. Phys. 2022, 157, 024109. [Google Scholar] [CrossRef]
- Yang, X.; Heinemann, M.; Howard, J.; Huber, G.; Iyer-Biswas, S.; Le Treut, G.; Lynch, M.; Montooth, K.L.; Needleman, D.J.; Pigolotti, S.; et al. Physical bioenergetics: Energy fluxes, budgets, and constraints in cells. Proc. Natl. Acad. Sci. USA 2021, 118, e2026786118. [Google Scholar] [CrossRef]
- Saintillan, D.; Shelley, M.J. Theory of active suspensions. In Complex Fluids in Biological Systems: Experiment, Theory, and Computation; Springer: Berlin/Heidelberg, Germany, 2014; pp. 319–355. [Google Scholar]
- Shaebani, M.R.; Wysocki, A.; Winkler, R.G.; Gompper, G.; Rieger, H. Computational models for active matter. Nat. Rev. Phys. 2020, 2, 181–199. [Google Scholar] [CrossRef]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Kjelstrup, S.; Bedeaux, D. Non-Equilibrium Thermodynamics of Heterogeneous Systems; World Scientific: Singapore, 2008. [Google Scholar]
- Liu, C. An introduction of elastic complex fluids: An energetic variational approach. In Multi-Scale Phenomena in Complex Fluids: Modeling, Analysis and Numerical Simulation; World Scientific: Singapore, 2009; pp. 286–337. [Google Scholar]
- Giga, M.H.; Kirshtein, A.; Liu, C. Variational modeling and complex fluids. In Handbook of Mathematical Analysis in Mechanics of Viscous Fluids; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–41. [Google Scholar]
- Wang, Y.; Liu, C. Some recent advances in energetic variational approaches. Entropy 2022, 24, 721. [Google Scholar] [CrossRef]
- Doi, M. Onsager’s variational principle in soft matter. J. Phys. Condens. Matter 2011, 23, 284118. [Google Scholar] [CrossRef]
- Wang, Q. Generalized onsager principle and it applications. In Frontiers and Progress of Current Soft Matter Research; Springer: Singapore, 2021; pp. 101–132. [Google Scholar]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620. [Google Scholar] [CrossRef]
- Öttinger, H.C.; Grmela, M. Dynamics and thermodynamics of complex fluids. II. Illustrations of a general formalism. Phys. Rev. E 1997, 56, 6633. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Liu, P.; Eisenberg, B. Field theory of reaction-diffusion: Law of mass action with an energetic variational approach. Phys. Rev. E 2020, 102, 062147. [Google Scholar] [CrossRef]
- Liu, C.; Sulzbach, J.E. The Brinkman-Fourier system with ideal gas equilibrium. Discret. Contin. Dyn. Syst. 2021, 42, 425–462. [Google Scholar] [CrossRef]
- Morrow, S.M.; Colomer, I.; Fletcher, S.P. A chemically fuelled self-replicator. Nat. Commun. 2019, 10, 1011. [Google Scholar] [CrossRef]
- Ge, H.; Qian, H. Dissipation, generalized free energy, and a self-consistent nonequilibrium thermodynamics of chemically driven open subsystems. Phys. Rev. E 2013, 87, 062125. [Google Scholar] [CrossRef]
- Ackermann, J.; Ben Amar, M. Onsager’s variational principle in proliferating biological tissues, in the presence of activity and anisotropy. Eur. Phys. J. Plus 2023, 138, 1103. [Google Scholar] [CrossRef]
- Klamser, J.U.; Kapfer, S.C.; Krauth, W. Thermodynamic phases in two-dimensional active matter. Nat. Commun. 2018, 9, 5045. [Google Scholar] [CrossRef]
- Mirza, W.; Torres-Sánchez, A.; Vilanova, G.; Arroyo, M. Variational formulation of active nematic fluids: Theory and simulation. New J. Phys. 2025, 27, 043025. [Google Scholar] [CrossRef]
- Gaspard, P. The non-equilibrium thermodynamics of active suspensions. arXiv 2025, arXiv:2505.21009. [Google Scholar] [CrossRef]
- Markovich, T.; Fodor, É.; Tjhung, E.; Cates, M.E. Thermodynamics of active field theories: Energetic cost of coupling to reservoirs. Phys. Rev. X 2021, 11, 021057. [Google Scholar] [CrossRef]
- Nardini, C.; Fodor, É.; Tjhung, E.; Van Wijland, F.; Tailleur, J.; Cates, M.E. Entropy production in field theories without time-reversal symmetry: Quantifying the non-equilibrium character of active matter. Phys. Rev. X 2017, 7, 021007. [Google Scholar] [CrossRef]
- Wang, H.; Qian, T.; Xu, X. Onsager’s variational principle in active soft matter. Soft Matter 2021, 17, 3634–3653. [Google Scholar] [CrossRef]
- Toner, J.; Tu, Y. Long-range order in a two-dimensional dynamical XY model: How birds fly together. Phys. Rev. Lett. 1995, 75, 4326. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 1995, 75, 1226. [Google Scholar] [CrossRef]
- Bolley, F.; Cañizo, J.A.; Carrillo, J.A. Mean-field limit for the stochastic Vicsek model. Appl. Math. Lett. 2012, 25, 339–343. [Google Scholar] [CrossRef]
- Ginelli, F. The physics of the Vicsek model. Eur. Phys. J. Spec. Top. 2016, 225, 2099–2117. [Google Scholar] [CrossRef]
- Gowrishankar, K.; Ghosh, S.; Saha, S.; Mayor, S.; Rao, M. Active remodeling of cortical actin regulates spatiotemporal organization of cell surface molecules. Cell 2012, 149, 1353–1367. [Google Scholar] [CrossRef]
- Choi, Y.P.; Kang, K.; Lee, W. Global existence and asymptotic stability for the Toner-Tu model of flocking. arXiv 2024, arXiv:2403.09114. [Google Scholar] [CrossRef]
- Lin, F.H.; Liu, C. Nonparabolic dissipative systems modeling the flow of liquid crystals. Commun. Pure Appl. Math. 1995, 48, 501–537. [Google Scholar] [CrossRef]
- Ericksen, J.L. Liquid crystals with variable degree of orientation. Arch. Ration. Mech. Anal. 1991, 113, 97–120. [Google Scholar] [CrossRef]
- Narayan, V.; Ramaswamy, S.; Menon, N. Long-lived giant number fluctuations in a swarming granular nematic. Science 2007, 317, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Ramaswamy, S.; Simha, R.A.; Toner, J. Active nematics on a substrate: Giantnumber fluctuations and long-time tails. Europhys. Lett. 2003, 62, 196. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals; Number 83; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Parmeggiani, A.; Jülicher, F.; Ajdari, A.; Prost, J. Energy transduction of isothermal ratchets: Generic aspects and specific examples close to and far from equilibrium. Phys. Rev. E 1999, 60, 2127. [Google Scholar] [CrossRef]
- Rayleigh, L. Some General Theorems Relating to Vibrations. Proc. Lond. Math. Soc. 1873, 4, 357–368. [Google Scholar]
- Onsager, L. Reciprocal relations in irreversible processes. I. Phys. Rev. 1931, 37, 405. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. II. Phys. Rev. 1931, 38, 2265. [Google Scholar] [CrossRef]
- Ericksen, J.L. Introduction to the Thermodynamics of Solids; Chapman and Hall: New York, NY, USA, 1992. [Google Scholar]
- Liu, C.; Wang, Y. A variational Lagrangian scheme for a phase-field model: A discrete energetic variational approach. SIAM J. Sci. Comput. 2020, 42, B1541–B1569. [Google Scholar] [CrossRef]
- Oster, G.F.; Perelson, A.S. Chemical reaction dynamics. Arch. Ration. Mech. Anal. 1974, 55, 230–274. [Google Scholar] [CrossRef]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- De Donder, T. Leçons de Thermodynamique et de Chimie Physique; Gauthier-Villars et cie: Paris, France, 1920. [Google Scholar]
- Beris, A.N.; Edwards, B.J. Thermodynamics of Flowing Systems: With Internal Microstructure; Number 36; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Liu, C.; Wang, C.; Wang, Y. A structure-preserving, operator splitting scheme for reaction-diffusion equations with detailed balance. J. Comput. Phys. 2021, 436, 110253. [Google Scholar] [CrossRef]
- Mielke, A. A gradient structure for reaction–diffusion systems and for energy-drift-diffusion systems. Nonlinearity 2011, 24, 1329. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y. Energetic Variational Modeling of Active Nematics: Coupling the Toner–Tu Model with ATP Hydrolysis. Entropy 2025, 27, 801. https://doi.org/10.3390/e27080801
Wang Y. Energetic Variational Modeling of Active Nematics: Coupling the Toner–Tu Model with ATP Hydrolysis. Entropy. 2025; 27(8):801. https://doi.org/10.3390/e27080801
Chicago/Turabian StyleWang, Yiwei. 2025. "Energetic Variational Modeling of Active Nematics: Coupling the Toner–Tu Model with ATP Hydrolysis" Entropy 27, no. 8: 801. https://doi.org/10.3390/e27080801
APA StyleWang, Y. (2025). Energetic Variational Modeling of Active Nematics: Coupling the Toner–Tu Model with ATP Hydrolysis. Entropy, 27(8), 801. https://doi.org/10.3390/e27080801







