Free-Fermion Models and Two-Dimensional Ising Models Under Zero Field and Imaginary Field i(π/2)kBT
Abstract
1. Introduction
2. Methods
2.1. Decorated Lattice Technique
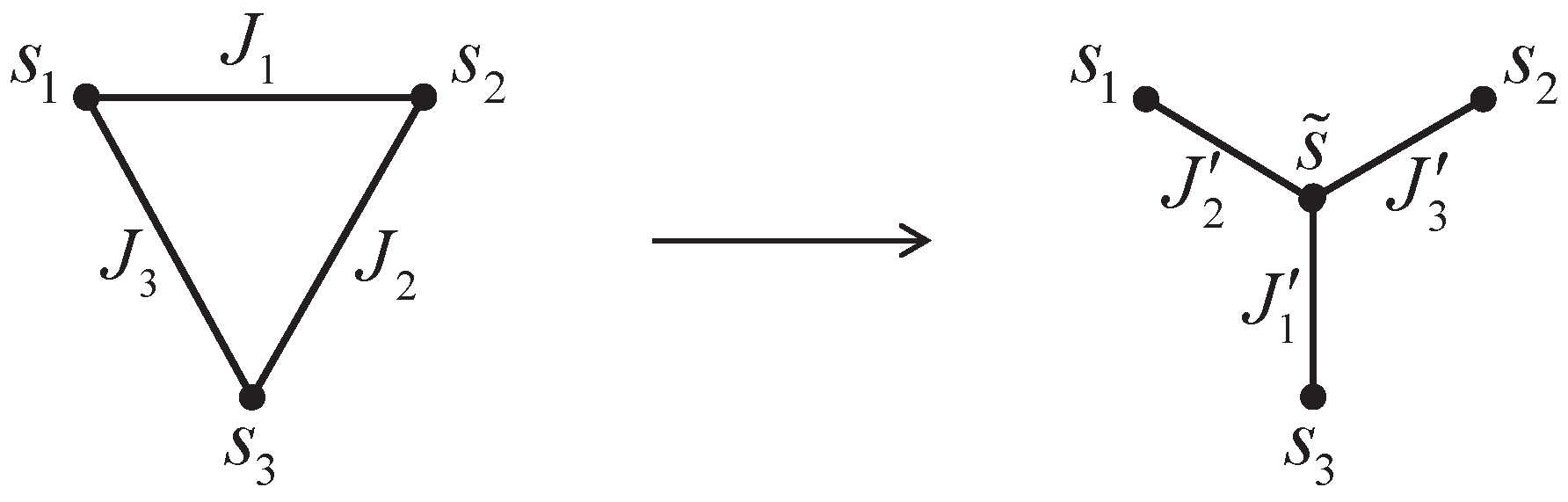
2.2. Star-Triangle Transformation
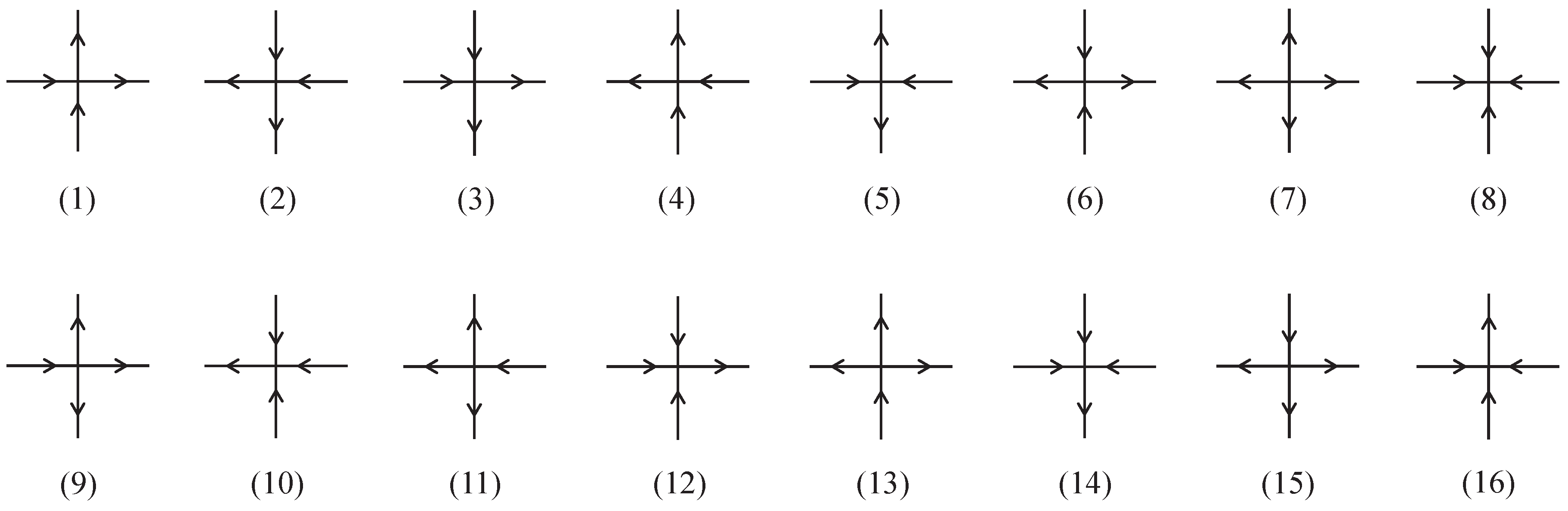
2.3. Weak-Graph Expansion
3. Results
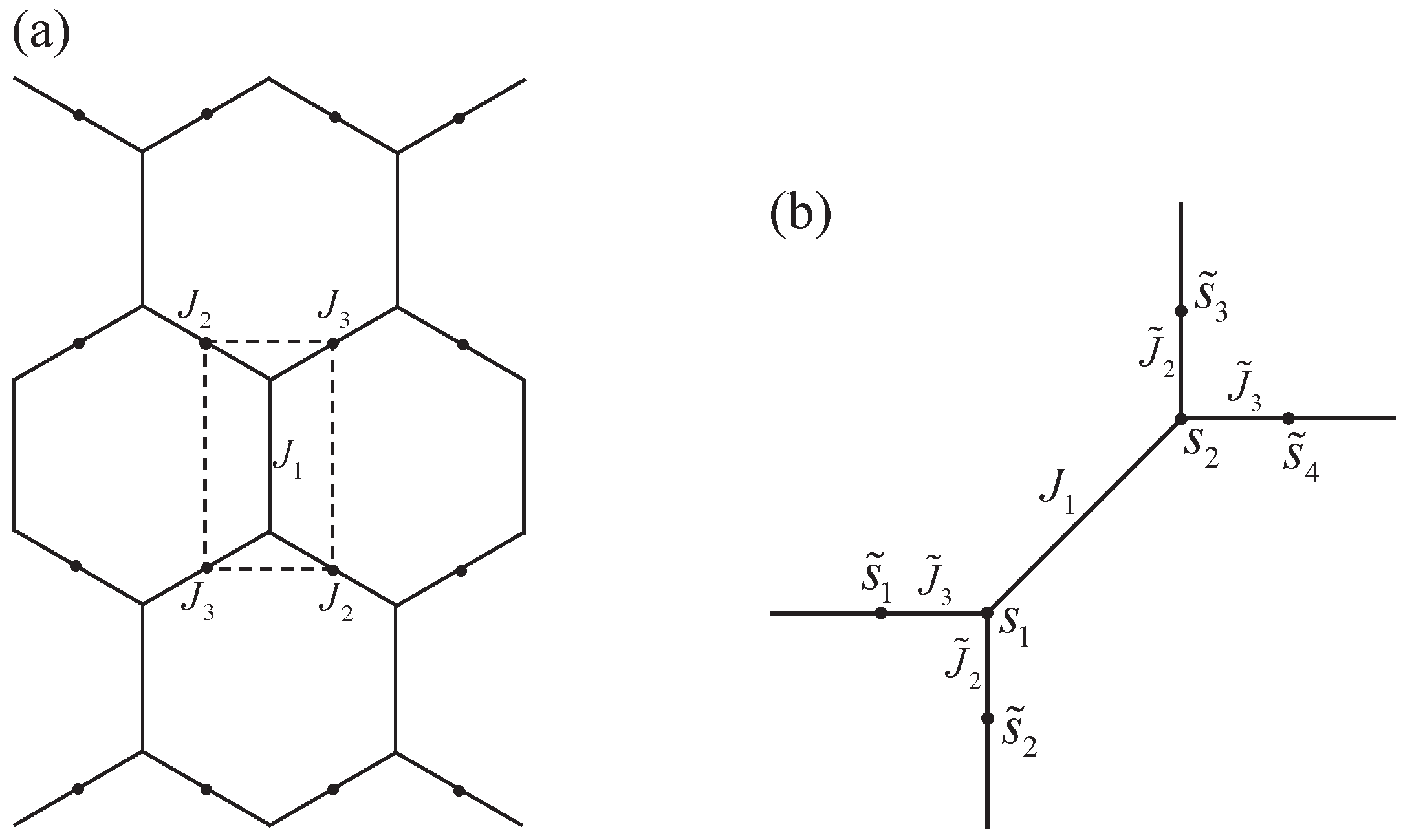
3.1. The Honeycomb Lattice
3.1.1. Zero-Field Case
3.1.2. Imaginary Field Case
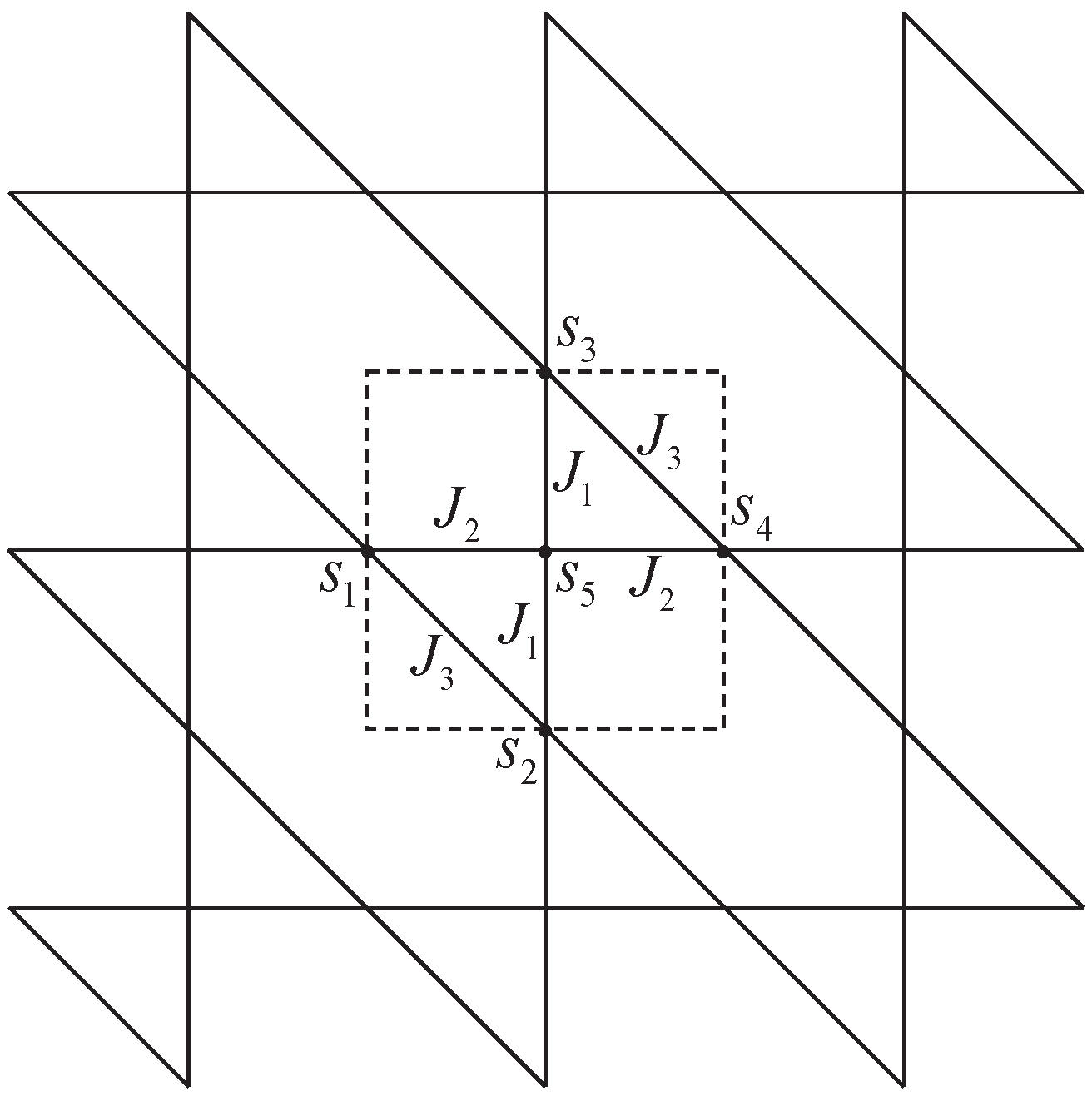
3.2. The Triangular Lattice
3.2.1. Zero-Field Case
3.2.2. Imaginary Field Case
3.3. The Kagomé Lattice
3.3.1. Zero-Field Case
3.3.2. Imaginary Field Case
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Niss, M. History of the Lenz-Ising Model 1920–1950: From Ferromagnetic to Cooperative Phenomena. Arch. Hist. Exact Sci. 2005, 59, 267–318. [Google Scholar] [CrossRef]
- Ising, E. Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 1925, 31, 253–258. [Google Scholar] [CrossRef]
- Kramers, H.A.; Wannier, G.H. Statistics of the Two-Dimensional Ferromagnet. Part I. Phys. Rev. 1941, 60, 252–262. [Google Scholar] [CrossRef]
- Kramers, H.A.; Wannier, G.H. Statistics of the Two-Dimensional Ferromagnet. Part II. Phys. Rev. 1941, 60, 263–276. [Google Scholar] [CrossRef]
- Onsager, L. Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition. Phys. Rev. 1944, 65, 117–149. [Google Scholar] [CrossRef]
- Kaufman, B. Crystal Statistics. II. Partition Function Evaluated by Spinor Analysis. Phys. Rev. 1949, 76, 1232–1243. [Google Scholar] [CrossRef]
- Nambu, Y. A Note on the Eigenvalue Problem in Crystal Statistics. Prog. Theor. Phys. 1950, 5, 1–13. [Google Scholar] [CrossRef]
- Kac, M.; Ward, J.C. A Combinatorial Solution of the Two-Dimensional Ising Model. Phys. Rev. 1952, 88, 1332–1337. [Google Scholar] [CrossRef]
- Schultz, T.D.; Mattis, D.C.; Lieb, E.H. Two-Dimensional Ising Model as a Soluble Problem of Many Fermions. Rev. Mod. Phys. 1964, 36, 856–871. [Google Scholar] [CrossRef]
- Hurst, C.A.; Green, H.S. New Solution of the Ising Problem for a Rectangular Lattice. J. Chem. Phys. 1960, 33, 1059–1062. [Google Scholar] [CrossRef]
- Hurst, C.A. New Approach to the Ising Problem. J. Math. Phys. 1966, 7, 305–310. [Google Scholar] [CrossRef]
- Gibberd, R.W.; Hurst, C.A. New Approach to the Ising ModeI. II. J. Math. Phys. 1967, 8, 1427–1435. [Google Scholar] [CrossRef]
- Fisher, M.E. On the Dimer Solution of Planar Ising Models. J. Math. Phys. 1966, 7, 1776–1781. [Google Scholar] [CrossRef]
- Samuel, S. The use of anticommuting variable integrals in statistical mechanics. I. The computation of partition functions. J. Math. Phys. 1980, 21, 2806–2814. [Google Scholar] [CrossRef]
- Newell, G.F.; Montroll, E.W. On the Theory of the Ising Model of Ferromagnetism. Rev. Mod. Phys. 1953, 25, 353–389. [Google Scholar] [CrossRef]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic Press: London, UK, 1982. [Google Scholar]
- Baxter, R.J. Solvable models in statistical mechanics, from Onsager onward. J. Stat. Phys. 1995, 78, 7–16. [Google Scholar] [CrossRef]
- Lieb, E.H. Some of the Early History of Exactly Soluble Models. Int. J. Mod. Phys. B 1997, 11, 3–10. [Google Scholar] [CrossRef]
- Baxter, R.J. Some comments on developments in exact solutions in statistical mechanics since 1944. J. Stat. Mech. 2010, 2010, P11037. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Statistical Theory of Equations of State and Phase Transitions. II. Lattice Gas and Ising Model. Phys. Rev. 1952, 87, 410–419. [Google Scholar] [CrossRef]
- Baxter, G. Weight Factors for the Two-Dimensional Ising Model. J. Math. Phys. 1965, 6, 1015–1021. [Google Scholar] [CrossRef]
- Baxter, G. Local Weights Which Determine Area, and the Ising Model. J. Math. Phys. 1967, 8, 399–405. [Google Scholar] [CrossRef]
- McCoy, B.M.; Wu, T.T. Theory of Toeplitz Determinants and the Spin Correlations of the Two-Dimensional Ising Model. II. Phys. Rev. 1967, 155, 438–452. [Google Scholar] [CrossRef]
- Marshall, T.W. The Ising model in a magnetic field of iπ/2. Mol. Phys. 1971, 21, 847–852. [Google Scholar] [CrossRef]
- Merlini, D. On the solution of the two-dimensional Ising model with an imaginary magnetic field βH=h=iπ/2. Lett. Nuovo Cimento 1974, 9, 100–104. [Google Scholar] [CrossRef]
- Gaaff, A. The 2-d Ising model in a magnetic field iπ/2 as a soluble case of the sixteen vertex model. Phys. Lett. A 1974, 49, 103–105. [Google Scholar] [CrossRef]
- Lin, K.Y.; Wu, F.Y. Ising Model in the Magnetic Field iπkT/2. Int. J. Mod. Phys. B 1988, 02, 471–481. [Google Scholar] [CrossRef]
- Husimi, K.; Syôzi, I. The Statistics of Honeycomb and Triangular Lattice. I. Prog. Theor. Phys. 1950, 5, 177–186. [Google Scholar] [CrossRef]
- Syôzi, I. The Statistics of Honeycomb and Triangular Lattice. II. Prog. Theor. Phys. 1950, 5, 341–351. [Google Scholar] [CrossRef]
- Houtappel, R.M.F. Order-disorder in hexagonal lattices. Physica 1950, 16, 425–455. [Google Scholar] [CrossRef]
- Temperley, H.N.V. Statistical mechanics of the two-dimensional assembly. Proc. R. Soc. Lond. A 1950, 202, 202–207. [Google Scholar] [CrossRef]
- Wannier, G.H. Antiferromagnetism. The Triangular Ising Net. Phys. Rev. 1950, 79, 357–364, Erratum in Phys. Rev. B 1973, 7, 5017. [Google Scholar] [CrossRef]
- Newell, G.F. Crystal Statistics of a Two-Dimensional Triangular Ising Lattice. Phys. Rev. 1950, 79, 876–882. [Google Scholar] [CrossRef]
- Potts, R.B. Combinatorial Solution of the Triangular Ising Lattice. Proc. Phys. Soc. A 1955, 68, 145. [Google Scholar] [CrossRef]
- Nourhani, A.; Crespi, V.H.; Lammert, P.E. Classical triangular lattice antiferromagnetic Ising model as a free-fermion/superconductor system. J. Phys. A Math. Theor. 2023, 56, 205001. [Google Scholar] [CrossRef]
- Syôzi, I. Statistics of Kagomé Lattice. Prog. Theor. Phys. 1951, 6, 306–308. [Google Scholar] [CrossRef]
- Kanô, K.; Naya, S. Antiferromagnetism. The Kagomé Ising Net. Prog. Theor. Phys. 1953, 10, 158–172. [Google Scholar] [CrossRef]
- Giacomini, H.J. Exact results for a checkerboard Ising model with crossing and four-spin interactions. J. Phys. A Math. Gen. 1985, 18, L1087–L1093. [Google Scholar] [CrossRef]
- Wu, F.Y. Two-dimensional Ising model with crossing and four-spin interactions and a magnetic field i(π/2)kT. J. Stat. Phys. 1986, 44, 455–463. [Google Scholar] [CrossRef]
- Fan, C.; Wu, F.Y. Ising Model with Second-Neighbor Interaction. I. Some Exact Results and an Approximate Solution. Phys. Rev. 1969, 179, 560–569. [Google Scholar] [CrossRef]
- Fan, C.; Wu, F.Y. General Lattice Model of Phase Transitions. Phys. Rev. B 1970, 2, 723–733. [Google Scholar] [CrossRef]
- Wu, F.Y.; Kunz, H. The Odd Eight-Vertex Model. J. Stat. Phys. 2004, 116, 67–78. [Google Scholar] [CrossRef]
- Baxter, R.J. Free-fermion, checkerboard and Z-invariant lattice models in statistical mechanics. Proc. R. Soc. Lond. A 1986, 404, 1–33. [Google Scholar] [CrossRef]
- Melotti, P. The Free-Fermion Eight-Vertex Model: Couplings, Bipartite Dimers and Z-Invariance. Commun. Math. Phys. 2021, 381, 33–82. [Google Scholar] [CrossRef]
- Slater, J.C. Theory of the Transition in KH2PO4. J. Chem. Phys. 1941, 9, 16–33. [Google Scholar] [CrossRef]
- Rys, F. Uber ein zweidimensionales klassisches Konfigurationsmodell. Helv. Phys. Acta 1963, 36, 537–559. [Google Scholar] [CrossRef]
- Lieb, E.H. Residual Entropy of Square Ice. Phys. Rev. 1967, 162, 162–172. [Google Scholar] [CrossRef]
- Lieb, E.H. Exact Solution of the Problem of the Entropy of Two-Dimensional Ice. Phys. Rev. Lett. 1967, 18, 692–694. [Google Scholar] [CrossRef]
- Wu, F.Y. Exactly Soluble Model of the Ferroelectric Phase Transition in Two Dimensions. Phys. Rev. Lett. 1967, 18, 605–607. [Google Scholar] [CrossRef]
- Lieb, E.H. Exact Solution of the F Model of An Antiferroelectric. Phys. Rev. Lett. 1967, 18, 1046–1048. [Google Scholar] [CrossRef]
- Lieb, E.H. Exact Solution of the Two-Dimensional Slater KDP Model of a Ferroelectric. Phys. Rev. Lett. 1967, 19, 108–110. [Google Scholar] [CrossRef]
- Sutherland, B. Exact Solution of a Two-Dimensional Model for Hydrogen-Bonded Crystals. Phys. Rev. Lett. 1967, 19, 103–104. [Google Scholar] [CrossRef]
- Yang, C.P. Exact Solution of a Model of Two-Dimensional Ferroelectrics in an Arbitrary External Electric Field. Phys. Rev. Lett. 1967, 19, 586–588. [Google Scholar] [CrossRef]
- Sutherland, B.; Yang, C.N.; Yang, C.P. Exact Solution of a Model of Two-Dimensional Ferroelectrics in an Arbitrary External Electric Field. Phys. Rev. Lett. 1967, 19, 588–591. [Google Scholar] [CrossRef]
- Wu, F.Y. Remarks on the Modified Potassium Dihydrogen Phosphate Model of a Ferroelectric. Phys. Rev. 1968, 168, 539–543. [Google Scholar] [CrossRef]
- Glasser, M.L. Evaluation of the Partition Functions for Some Two-Dimensional Ferroelectric Models. Phys. Rev. 1969, 184, 539–542. [Google Scholar] [CrossRef]
- Sutherland, B. Two-Dimensional Hydrogen Bonded Crystals without the Ice Rule. J. Math. Phys. 1970, 11, 3183–3186. [Google Scholar] [CrossRef]
- Baxter, R.J. Eight-Vertex Model in Lattice Statistics. Phys. Rev. Lett. 1971, 26, 832–833. [Google Scholar] [CrossRef]
- Baxter, R.J. Partition function of the Eight-Vertex lattice model. Ann. Phys. 1972, 70, 193–228. [Google Scholar] [CrossRef]
- Kadanoff, L.P.; Wegner, F.J. Some Critical Properties of the Eight-Vertex Model. Phys. Rev. B 1971, 4, 3989–3993. [Google Scholar] [CrossRef]
- Baxter, R. Eight-vertex model in lattice statistics and one-dimensional anisotropic heisenberg chain. I. Some fundamental eigenvectors. Ann. Phys. 1973, 76, 1–24. [Google Scholar] [CrossRef]
- Baxter, R. Eight-vertex model in lattice statistics and one-dimensional anisotropic heisenberg chain. II. Equivalence to a generalized ice-type lattice model. Ann. Phys. 1973, 76, 25–47. [Google Scholar] [CrossRef]
- Baxter, R. Eight-vertex model in lattice statistics and one-dimensional anisotropic heisenberg chain. III. Eigenvectors of the transfer matrix and hamiltonian. Ann. Phys. 1973, 76, 48–71. [Google Scholar] [CrossRef]
- Baxter, R.J. Solvable eight-vertex model on an arbitrary planar lattice. Philos. Trans. R. Soc. Lond. Ser. A 1978, 289, 315–346. [Google Scholar] [CrossRef]
- Baxter, R.J. The Six and Eight-Vertex Models Revisited. J. Stat. Phys. 2004, 116, 43–66. [Google Scholar] [CrossRef]
- Wu, F.Y. Critical Behavior of Two-Dimensional Hydrogen-Bonded Antiferroelectrics. Phys. Rev. Lett. 1969, 22, 1174–1176. [Google Scholar] [CrossRef]
- Wu, F.Y. Critical Behavior of Hydrogen-Bonded Ferroelectrics. Phys. Rev. Lett. 1970, 24, 1476–1478. [Google Scholar] [CrossRef]
- Wu, F.Y. Exact results on a general lattice statistical model. Solid State Commun. 1972, 10, 115–117. [Google Scholar] [CrossRef]
- Wu, F.Y. Phase Transition in a Sixteen-Vertex Lattice Model. Phys. Rev. B 1972, 6, 1810–1813. [Google Scholar] [CrossRef]
- Gaaff, A.; Hijmans, J. Symmetry relations in the sixteen-vertex model. Phys. A Stat. Mech. Its Appl. 1975, 80, 149–171. [Google Scholar] [CrossRef]
- Assis, M. The 16-vertex model and its even and odd 8-vertex subcases on the square lattice. J. Phys. A Math. Theor. 2017, 50, 395001. [Google Scholar] [CrossRef]
- Felderhof, B.U. Direct diagonalization of the transfer matrix of the zero-field free-fermion model. Physica 1973, 65, 421–451. [Google Scholar] [CrossRef]
- Felderhof, B.U. Diagonalization of the transfer matrix of the free-fermion model. II. Physica 1973, 66, 279–297. [Google Scholar] [CrossRef]
- Felderhof, B.U. Diagonalization of the transfer matrix of the free-fermion model. III. Physica 1973, 66, 509–526. [Google Scholar] [CrossRef]
- Bazhanov, V.V.; Stroganov, Y.G. Hidden symmetry of free Fermion model. Theor. Math. Phys. 1985, 62, 253–260. [Google Scholar] [CrossRef]
- Bazhanov, V.V.; Stroganov, Y.G. Hidden symmetry of free fermion model. II. Partition function. Theor. Math. Phys. 1985, 63, 519–527. [Google Scholar] [CrossRef]
- Bazhanov, V.V.; Stroganov, Y.G. Hidden symmetry of free fermion model. III. Inversion relations. Theor. Math. Phys. 1985, 63, 604–611. [Google Scholar] [CrossRef]
- Debauche, M.; Diep, H.T.; Azaria, P.; Giacomini, H. Exact phase diagram of a generalized Kagomé Ising lattice: Reentrance and disorder lines. Phys. Rev. B 1991, 44, 2369–2372. [Google Scholar] [CrossRef]
- Kooiman, A.; van Leeuwen, J.M.J. Free fermion approximation for the Ising model with further-neighbor interactions on a triangular lattice. J. Stat. Phys. 1992, 69, 247–275. [Google Scholar] [CrossRef]
- Morita, T.; Tanaka, K. Diagrammatical Techniques for Two-Dimensional Ising Models. III. Ising Model to Vertex Model. J. Phys. Soc. Jpn. 1993, 62, 873–879. [Google Scholar] [CrossRef]
- Krčmár, R.; Gendiar, A.; Šamaj, L. Ising ferromagnets and antiferromagnets in an imaginary magnetic field. Phys. Rev. E 2022, 105, 054112. [Google Scholar] [CrossRef]
- Fisher, M.E. Transformations of Ising Models. Phys. Rev. 1959, 113, 969–981. [Google Scholar] [CrossRef]
- Syôzi, I. Transformation of Ising Models. In Phase Transitions and Critical Phenomena. Volume 1: Exact Results; Academic Press: London, UK, 1972. [Google Scholar]
- Onsager, L. The Ising model in two dimensions. In Critical Phenomena in Alloys, Magnets and Superconductors; McGraw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Au-Yang, H.; Perk, J.H.H. Onsager’s Star-Triangle Equation: Master Key to Integrability. In Integrable Sys Quantum Field Theory; Academic Press: San Diego, CA, USA, 1989. [Google Scholar] [CrossRef]
- Nagle, J.F. Weak-Graph Method for Obtaining Formal Series Expansions for Lattice Statistical Problems. J. Math. Phys. 1968, 9, 1007–1019. [Google Scholar] [CrossRef]
- Wu, F.Y. Exact Solution of a Model of an Antiferroelectric Transition. Phys. Rev. 1969, 183, 604–607. [Google Scholar] [CrossRef]
- Nagle, J.F. Ferroelectric Models. In Phase Transitions and Critical Phenomena. Volume 3: Series Expansions for Lattice Models; Academic Press: London, UK, 1974. [Google Scholar]
- Giacomini, H.J. An exact result for the Kagome lattice Ising model with magnetic field. J. Phys. A Math. Gen. 1988, 21, L31. [Google Scholar] [CrossRef]
- Giacomini, H.J. An exact functional relation for the partition function of a 2D Ising model with magnetic field. J. Phys. A Math. Gen. 1988, 21, L599. [Google Scholar] [CrossRef]
- Lu, W.T.; Wu, F.Y. Soluble kagome Ising model in a magnetic field. Phys. Rev. E 2005, 71, 046120. [Google Scholar] [CrossRef]
- Wang, F.; Wu, F.Y. Exact solution of close-packed dimers on the kagomé lattice. Phys. Rev. E 2007, 75, 040105. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.-Z.; Wang, X.; Yang, X.-B. Free-Fermion Models and Two-Dimensional Ising Models Under Zero Field and Imaginary Field i(π/2)kBT. Entropy 2025, 27, 799. https://doi.org/10.3390/e27080799
Li D-Z, Wang X, Yang X-B. Free-Fermion Models and Two-Dimensional Ising Models Under Zero Field and Imaginary Field i(π/2)kBT. Entropy. 2025; 27(8):799. https://doi.org/10.3390/e27080799
Chicago/Turabian StyleLi, De-Zhang, Xin Wang, and Xiao-Bao Yang. 2025. "Free-Fermion Models and Two-Dimensional Ising Models Under Zero Field and Imaginary Field i(π/2)kBT" Entropy 27, no. 8: 799. https://doi.org/10.3390/e27080799
APA StyleLi, D.-Z., Wang, X., & Yang, X.-B. (2025). Free-Fermion Models and Two-Dimensional Ising Models Under Zero Field and Imaginary Field i(π/2)kBT. Entropy, 27(8), 799. https://doi.org/10.3390/e27080799





