Optimal Power Procurement for Green Cellular Wireless Networks Under Uncertainty and Chance Constraints
Abstract
1. Introduction
- We propose a novel time-continuous optimization framework for optimal power procurement for green wireless cellular networks, subject to SDE dynamics and chance constraints. Compared to the discrete-time formulation in previous studies [24,25,26], the proposed approach decouples the model development from the numerical approximation, enhancing the model fidelity (see Remark 3). This formulation also yields a continuous control curve over time, allowing its application for any time discretization scheme and eliminating the need for ad hoc interpolations [48].
- We calibrate the data-driven SDE model developed for instantaneous wind power in [30] using German wind power data from the year 2023. The calibrated SDE is a driving dynamic for the stochastic optimal control problem.
- We apply Lagrangian relaxation to the probabilistic QoS constraint, transforming the problem into a standard time-continuous stochastic optimization problem. Studies have explored numerical methods for time-continuous stochastic optimization with final-time chance constraints using Lagrangian relaxation [51,52,53] or reformulation as a stochastic target problem [54,55]. However, the proposed approach is novel in addressing a chance constraint that must be satisfied at every time point. Moreover, we implement this within the context of cellular wireless networks.
- We develop an iterative algorithm to optimize the dual function within a finite-dimensional function class numerically. Each iteration involves solving the HJB PDE to compute the dual function value and its noisy subgradient. The proposed approach extends the work in [48] on the time-continuous deterministic optimization of coupled hydrothermal power systems to the stochastic setting.
2. System Model
2.1. Base Station Model
2.2. Cellular Network Model
2.3. Renewable Power Model
2.4. Battery Model
2.5. Grid Power Model
2.6. Running Horizon Framework
2.7. Model Summary
3. Stochastic Optimal Control Formulation
3.1. HJB Equation Related to Problem 2
3.2. Finite-Dimensional Approximation of Problem 3
4. Numerical Approach
4.1. Numerically Solving the HJB PDE
4.2. Estimating Subgradient
4.3. Dual Problem Optimization
| Algorithm 1: Numerical dual optimization procedure |
Input: , , max-iter, , , , Output: Optimal controls , optimal Lagrange multiplier function Construct with using (35); Obtain using initialization Algorithm A3 with inputs ,, ; Construct with using (35); Obtain with the LMBM routine [65] with starting point , number of iterations and parameters specified in Table A3; Construct with using (35);  |
4.3.1. Lagrange Multiplier Refinement
4.3.2. Numerical Optimization
4.3.3. LMBM-Boosted Initialization
5. Numerical Experiments and Results
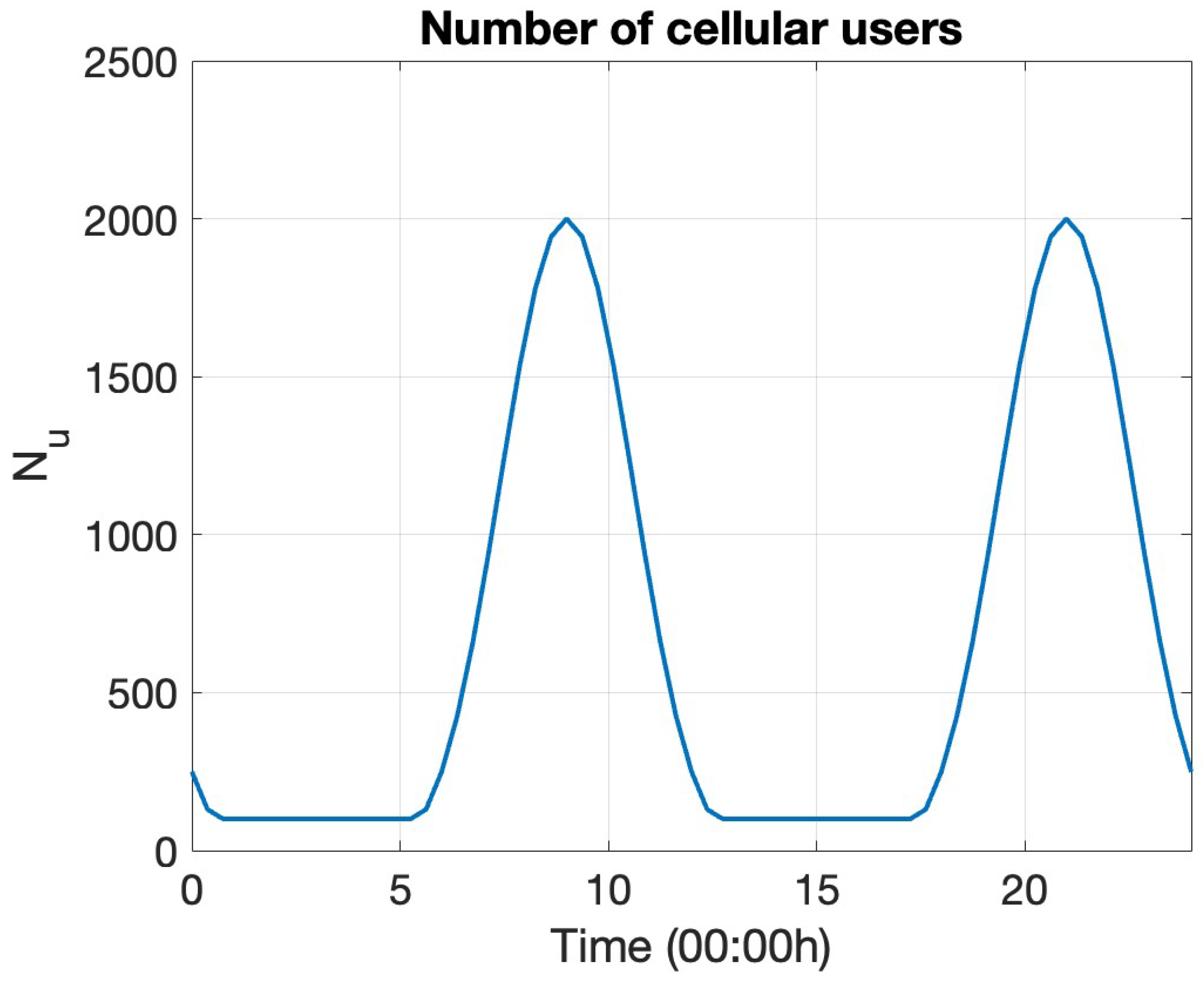
5.1. Description of Model Cellular Base Station System
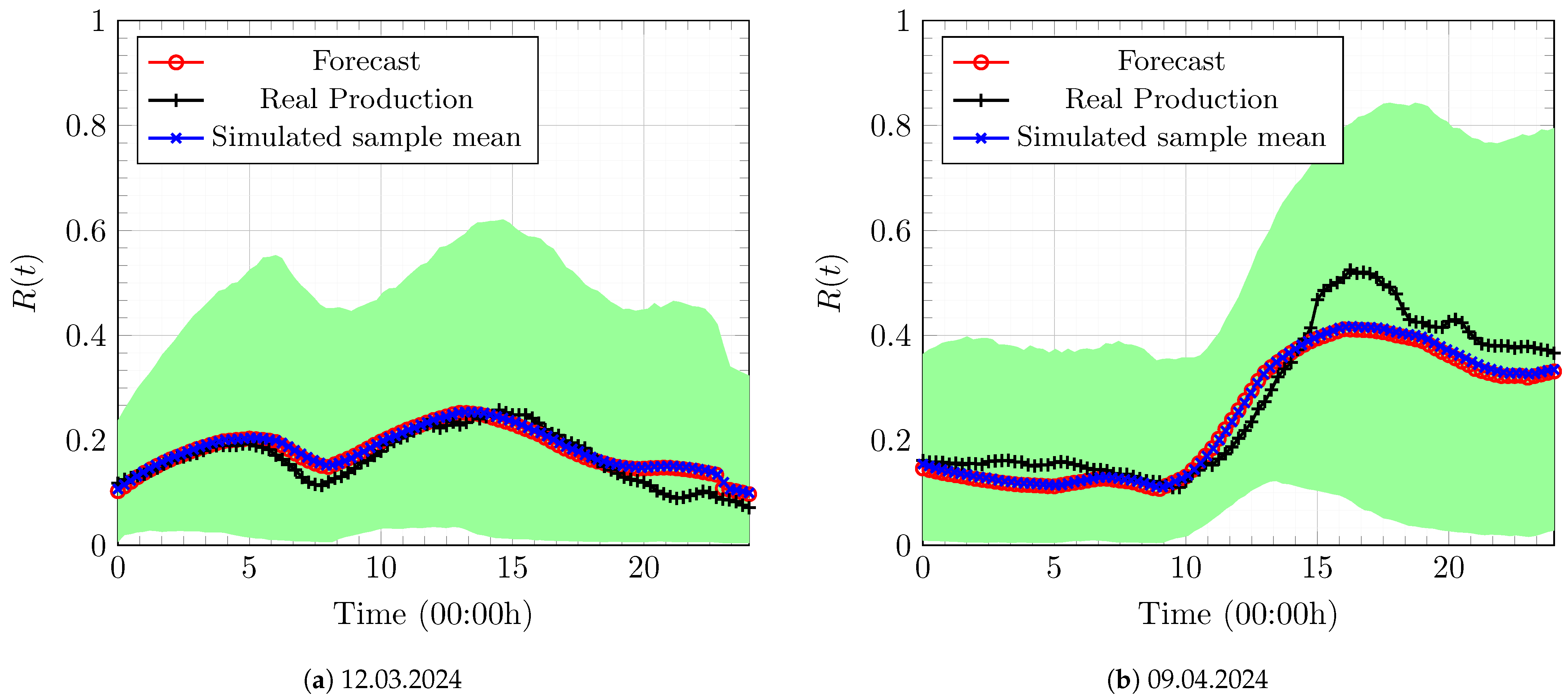
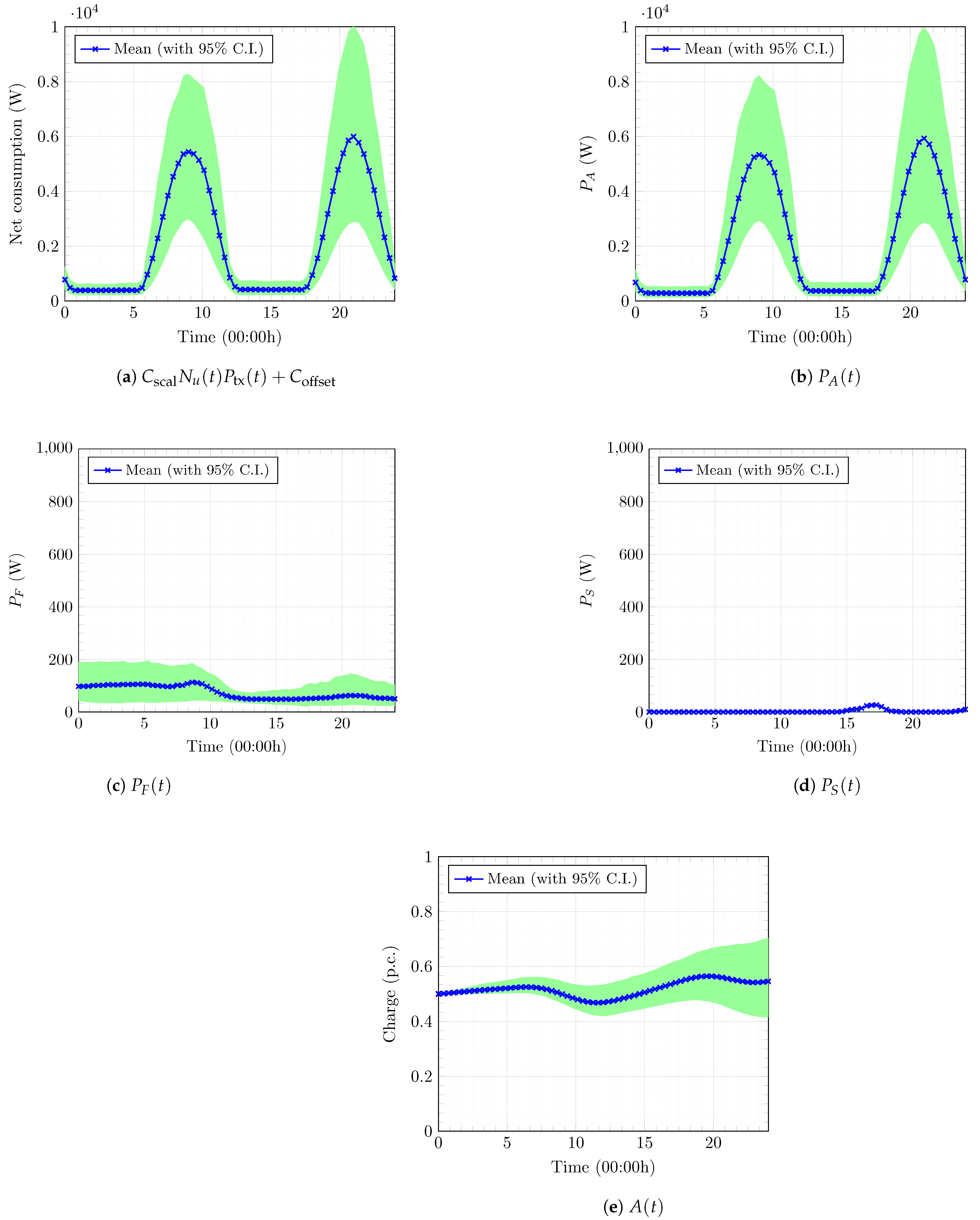
5.2. Numerical Results
5.2.1. Cost-to-Go Function of the Dual Problem
5.2.2. Obtaining Reference Costs for Comparison
5.2.3. Dual Optimization Results
5.2.4. Optimal Power-Procurement Policy
5.2.5. Sensitivity Analysis
- Scenario A: No incoming renewable power for a day ( for all ).
- Scenario B: The wireless fading channel is substantially low due to extreme weather ( is halved).
- Scenario C: High weight is assigned to minimizing operating expenditure ().
- Scenario D: The price users pay to connect to the network substantially reduces ( EUR/h per person).
- Scenario E: The probabilistic QoS constraint 2 must be satisfied with low confidence ().
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| a.s. | Almost surely |
| CFL | Courant–Friedrichs–Levy |
| dB | Decibel |
| HJB | Hamilton–Jacobi–Bellman |
| i.i.d. | Independent and identically distributed |
| LMBM | Limited memory bundle method |
| PDE | Partial differential equation |
| QoS | Quality of service |
| SDE | Stochastic differential equation |
| SNR | Signal-to-noise ratio |
| SSM | Stochastic subgradient method |
| ZB | Zettabyte |
Appendix A. Algorithms
Appendix A.1. Upwind Finite-Difference Numerical Solver for HJB PDE (33)
| Algorithm A1: HJB numerical solver |
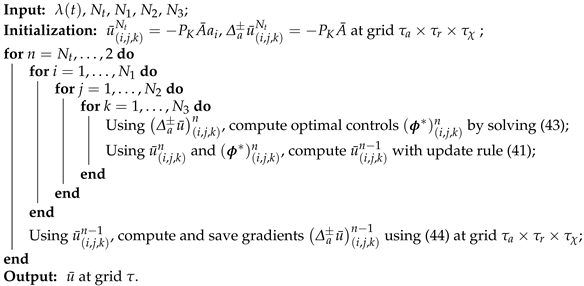 |
Appendix A.2. Euler–Maruyama Monte Carlo for Subgradient (47) Estimation
| Algorithm A2: Numerical subgradient estimation |
 |
Appendix A.3. Initialization Algorithm for ℓ = 1
| Algorithm A3: Initialization |
 |
Appendix A.4. Schematic Depictions of the Optimization Algorithms

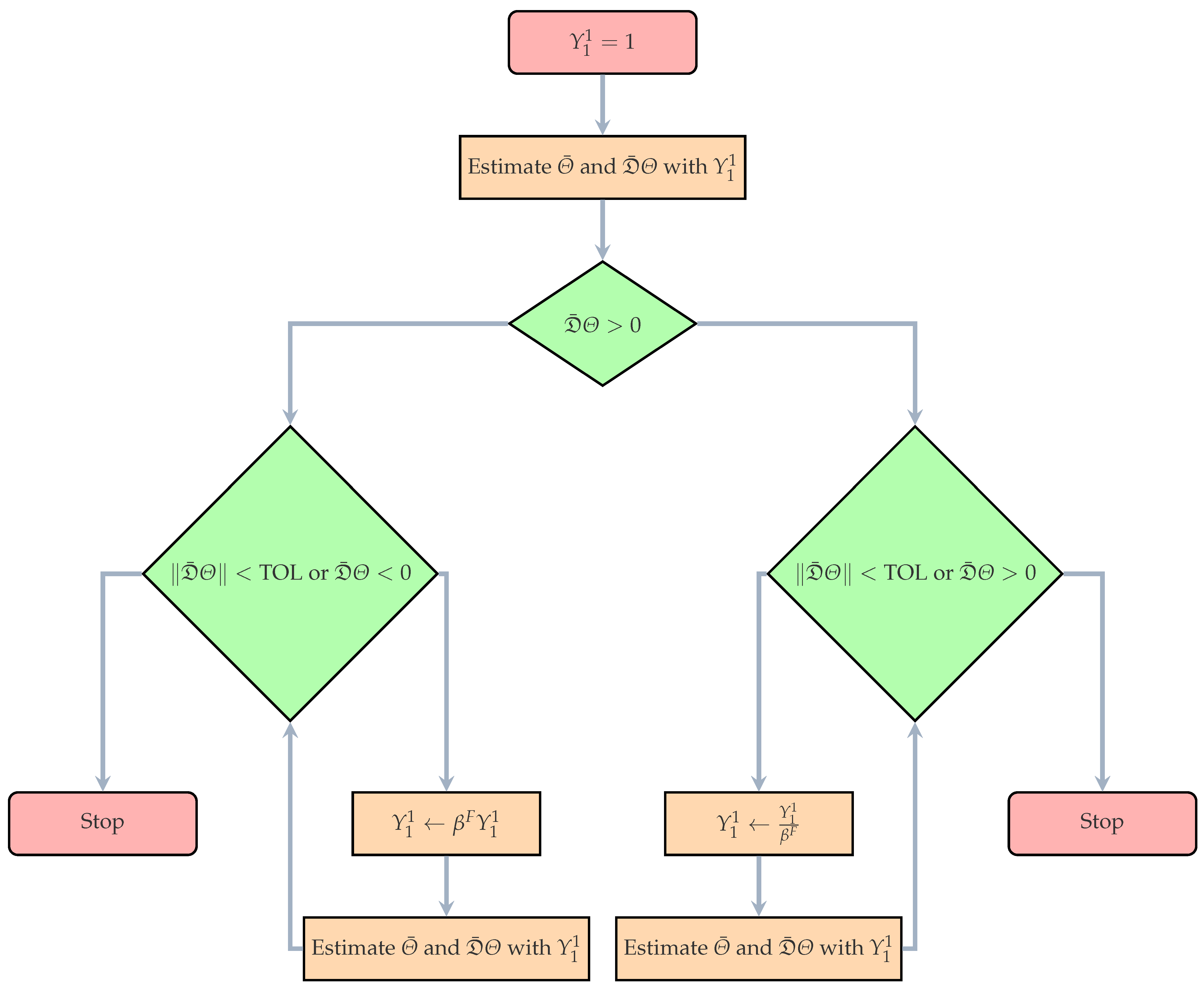
Appendix B. Details of Numerical Problem Described in Section 5
Appendix B.1. Model Parameters
| Parameter | Unit | Description | Value |
|---|---|---|---|
| Base station power-loss scaling factor | |||
| Watt (W) | Base station offset power | ||
| Watt (W) | Maximum base station transmission limit | ||
| Base station location | |||
| Path loss constant | 1 | ||
| Path loss exponent | 2 | ||
| Decibel (dB) | Signal-to-noise ratio threshold | 15 | |
| Watt (W) | Ambient transmission noise | ||
| Watt (W) | Maximum renewable power-production capacity | ||
| Watt-hour (Wh) | Maximum battery charge capacity | ||
| Watt (W) | Maximum battery charge capacity | ||
| Watt (W) | Maximum battery discharge capacity | ||
| EUR/Wh | Pollutant emission Coefficient 1 | ||
| EUR/h | Pollutant emission Coefficient 2 | ||
| EUR/Wh | Fictitious cost per unit battery charge | ||
| w | Pareto parameter |
Appendix B.2. Outage Proportion for Simple Cellular User Distributions
Appendix B.3. Analytical Solution of the Hamiltonian (34) for Simple Cellular User Distributions
Appendix B.4. Simulation Parameters in Section 5
| Parameter | Description | Value |
|---|---|---|
| Mobile user outage proportion threshold | ||
| Confidence level of violating the constraint in 2 | ||
| Normalized battery charge level at | ||
| Initial distribution of the wireless fading channel | ||
| Initial distribution of the normalized wind power | ||
| Discretization of (33) in the a domain | 10 | |
| Discretization of (33) in the r domain | 10 | |
| Discretization of (33) in the domain | 10 | |
| Discretization of (33) in the t domain | 800 | |
| Prescribed relative tolerance for Algorithm 1 | ||
| Prescribed relative tolerance for Algorithm A3 | 1 | |
| max-iter | Prescribed maximum iterations in Algorithm 1 | 50 |
| Initial number of SSM iterations with a constant step-size | 10 | |
| Prescribed number of LMBM [65] iterations | 50 | |
| Factor of increase/decrease in Algorithm A3 | 5 | |
| Number of sample paths in Algorithm A2 | ||
| Time discretization parameter in Algorithm A2 | 64 | |
| Time discretization parameter in Algorithm A2 |
| Parameter | Description | Value |
|---|---|---|
| RPAR(1) | Tolerance for changes in the function value | |
| RPAR(2) | Second tolerance for changes in the function value | (ignored) |
| RPAR(3) | Minimum acceptable function value | 0 |
| RPAR(4) | Tolerance for the first termination parameter | |
| RPAR(5) | Tolerance for the second termination parameter | |
| RPAR(6) | Distance measure parameter | |
| RPAR(7) | Line search parameter | |
| RPAR(8) | Maximum step size | 10 |
| IPAR(1) | Exponent for distance measure | 2 |
| IPAR(2) | Maximum iterations | 50 |
| IPAR(3) | Maximum function evaluations | 100 |
| IPAR(4) | Maximum iterations with changes of function values smaller than RPAR(1) | 5 |
| IPAR(5) | Printout specification | |
| IPAR(6) | Selection of method | 0 (LMBM) |
| IPAR(7) | Selection of scaling strategy | 0 |
Appendix B.5. Sensitivity Analysis Settings in Section 5
| Parameter | Distribution |
|---|---|
| w | |
References
- International Telecommunication Union. Measuring Digital Development: Facts and Figures 2024; Technical report; International Telecommunication Union Development Sector: Geneva, Switzerland, 2024. [Google Scholar]
- International Energy Agency. Tracking Clean Energy Progress 2023; Technical report; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Strielkowski, W.; Dvořák, M.; Rovnỳ, P.; Tarkhanova, E.; Baburina, N. 5G wireless networks in the future renewable energy systems. Front. Energy Res. 2021, 9, 714803. [Google Scholar]
- GSMA Intelligence. Going Green: Benchmarking the Energy Efficiency of Mobile Networks; Technical report; GSM Association: London, UK, 2023. [Google Scholar]
- Han, T.; Ansari, N. Powering mobile networks with green energy. IEEE Wirel. Commun. 2014, 21, 90–96. [Google Scholar]
- Saleem, A.; Zhang, X.; Xu, Y.; Albalawi, U.A.; Younes, O.S. A Critical Review on Channel Modeling: Implementations, Challenges and Applications. Electronics 2023, 12, 2014. [Google Scholar] [CrossRef]
- Klöppel, M.; Gabash, A.; Geletu, A.; Li, P. Chance constrained optimal power flow with non-Gaussian distributed uncertain wind power generation. In Proceedings of the 2013 12th International Conference on Environment and Electrical Engineering, Wroclaw, Poland, 5–8 May 2013; pp. 265–270. [Google Scholar] [CrossRef]
- Wu, H.; Shahidehpour, M.; Li, Z.; Tian, W. Chance-Constrained Day-Ahead Scheduling in Stochastic Power System Operation. IEEE Trans. Power Syst. 2014, 29, 1583–1591. [Google Scholar]
- Huang, Y.; Wang, L.; Guo, W.; Kang, Q.; Wu, Q. Chance constrained optimization in a home energy management system. IEEE Trans. Smart Grid 2018, 9, 252–260. [Google Scholar]
- Azgin, A.; Krunz, M. Scheduling in wireless cellular networks under probabilistic channel information. In Proceedings of the 12th International Conference on Computer Communications and Networks (IEEE Cat. No.03EX712), Dallas, TX, USA, 22 October 2003; pp. 89–94. [Google Scholar] [CrossRef]
- Farooq, M.J.; Ghazzai, H.; Kadri, A. A stochastic geometry-based demand response management framework for cellular networks powered by smart grid. In Proceedings of the 2016 IEEE Wireless Communications and Networking Conference, Doha, Qatar, 3–6 April 2016; pp. 1–6. [Google Scholar]
- Claßen, G. Optimisation Under Data Uncertainty in Wireless Communication Networks. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2015. [Google Scholar]
- Challita, U.; Dawy, Z.; Turkiyyah, G.; Naoum-Sawaya, J. A chance constrained approach for LTE cellular network planning under uncertainty. Comput. Commun. 2016, 73, 34–45. [Google Scholar]
- Ding, K.W.; Wang, M.H.; Huang, N.J. Distributionally robust chance constrained problem under interval distribution information. Optim. Lett. 2018, 12, 1315–1328. [Google Scholar]
- Chang, X.; Xu, Y.; Gu, W.; Sun, H.; Chow, M.Y.; Yi, Z. Accelerated Distributed Hybrid Stochastic/Robust Energy Management of Smart Grids. IEEE Trans. Ind. Inform. 2021, 17, 5335–5347. [Google Scholar]
- Zhou, A.; Yang, M.; Wu, T.; Yang, L. Distributionally Robust Energy Management for Islanded Microgrids With Variable Moment Information: An MISOCP Approach. IEEE Trans. Smart Grid 2023, 14, 3668–3680. [Google Scholar]
- Du, P.; Lei, H.; Ansari, I.S.; Du, J.; Chu, X. Distributionally robust optimization based chance-constrained energy management for hybrid energy powered cellular networks. Digit. Commun. Netw. 2023, 9, 797–808. [Google Scholar]
- An, D.; Yang, Q.; Yu, W.; Yang, X.; Fu, X.; Zhao, W. Sto2Auc: A Stochastic Optimal Bidding Strategy for Microgrids. IEEE Internet Things J. 2017, 4, 2260–2274. [Google Scholar]
- Bhattacharya, A.; Kharoufeh, J.P.; Zeng, B. Managing energy storage in microgrids: A multistage stochastic programming approach. IEEE Trans. Smart Grid 2018, 9, 483–496. [Google Scholar]
- Charnes, A.; Cooper, W.W.; Symonds, G.H. Cost Horizons and Certainty Equivalents: An Approach to Stochastic Programming of Heating Oil. Manag. Sci. 1958, 4, 235–263. [Google Scholar]
- Charnes, A.; Cooper, W.W. Chance-Constrained Programming. Manag. Sci. 1959, 6, 73–79. [Google Scholar]
- Nemirovski, A.; Shapiro, A. Convex Approximations of Chance Constrained Programs. SIAM J. Optim. 2006, 17, 969–996. [Google Scholar]
- Ma, S.; Sun, D. Chance Constrained Robust Beamforming in Cognitive Radio Networks. IEEE Commun. Lett. 2013, 17, 67–70. [Google Scholar]
- Liu, X.; Li, H.; Wang, H. Probability constrained robust multicast beamforming in cognitive radio network. In Proceedings of the 2013 8th International Conference on Communications and Networking in China (CHINACOM), Guilin, China, 14–16 August 2013; pp. 708–712. [Google Scholar]
- Ben Rached, N.; Ghazzai, H.; Kadri, A.; Alouini, M.S. Energy Management Optimization for Cellular Networks Under Renewable Energy Generation Uncertainty. IEEE Trans. Green Commun. Netw. 2017, 1, 158–166. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Z.; Xie, Y.; Chan, K.Y.; Yuan, Y.; Yang, Y. Power allocation in D2D enabled cellular network with probability constraints: A robust Stackelberg game approach. Ad Hoc Netw. 2022, 133, 102891. [Google Scholar]
- Møller, J.K.; Zugno, M.; Madsen, H. Probabilistic Forecasts of Wind Power Generation by Stochastic Differential Equation Models. J. Forecast. 2016, 35, 189–205. [Google Scholar]
- Elkantassi, S.; Kalligiannaki, E.; Tempone, R. Inference and Sensitivity in Stochastic Wind Power Forecast Models; ECCOMAS: Rhodes Island, Greece, 2017. [Google Scholar]
- Iversen, E.B.; Morales, J.M.; Møller, J.K.; Trombe, P.J.; Madsen, H. Leveraging stochastic differential equations for probabilistic forecasting of wind power using a dynamic power curve. Wind. Energy 2017, 20, 33–44. [Google Scholar]
- Caballero, R.; Kebaier, A.; Scavino, M.; Tempone, R. Quantifying uncertainty with a derivative tracking SDE model and application to wind power forecast data. Stat. Comput. 2021, 31, 64. [Google Scholar] [CrossRef]
- Iversen, E.B.; Morales, J.M.; Møller, J.K.; Madsen, H. Probabilistic forecasts of solar irradiance using stochastic differential equations. Environmetrics 2014, 25, 152–164. [Google Scholar]
- Iversen, E.B.; Juhl, R.; Møller, J.K.; Kleissl, J.; Madsen, H.; Morales, J.M. Spatio-temporal forecasting by coupled stochastic differential equations: Applications to solar power. arXiv 2017, arXiv:1706.04394. [Google Scholar]
- Badosa, J.; Gobet, E.; Grangereau, M.; Kim, D. Day-Ahead Probabilistic Forecast of Solar Irradiance: A Stochastic Differential Equation Approach. In Renewable Energy: Forecasting and Risk Management; Drobinski, P., Mougeot, M., Picard, D., Plougonven, R., Tankov, P., Eds.; Springer: Cham, Switzerland, 2018; pp. 73–93. [Google Scholar]
- Feng, T.; Field, T.R.; Haykin, S. Stochastic Differential Equation Theory Applied to Wireless Channels. IEEE Trans. Commun. 2007, 55, 1478–1483. [Google Scholar]
- Charalambous, C.; Bultitude, R.J.C.; Li, X.; Zhan, J. Modeling wireless fading channels via stochastic differential equations: Identification and estimation based on noisy measurements. IEEE Trans. Wirel. Commun. 2008, 7, 434–439. [Google Scholar]
- Mossberg, M.; Irshad, Y. A Stochastic Differential Equation for Wireless Channels Based on Jakes’ Model with Time-Varying Phases. In Proceedings of the 2009 IEEE 13th Digital Signal Processing Workshop and 5th IEEE Signal Processing Education Workshop, Marco Island, FL, USA, 4–7 January 2009; pp. 602–605. [Google Scholar] [CrossRef]
- Amar, E.B.; Rached, N.B.; Tempone, R.; Alouini, M.S. Stochastic differential equations for performance analysis of wireless communication systems. IEEE Trans. Wirel. Commun. 2025. [Google Scholar] [CrossRef]
- Bertsekas, D. Dynamic Programming and Optimal Control: Volume I; Athena Scientific, Massachusetts Institute of Techonology: Cambridge, MA, USA, 2012; Volume 4. [Google Scholar]
- Lemaréchal, C. Lagrangian Relaxation; Springer: Berlin/Heidelberg, Germany, 2001; pp. 112–156. [Google Scholar]
- Kushner, H.J. Numerical Methods for Stochastic Control Problems in Continuous Time. SIAM J. Control Optim. 1990, 28, 999–1048. [Google Scholar]
- Pham, H. Continuous-Time Stochastic Control and Optimization with Financial Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 61. [Google Scholar]
- Sun, B.; Guo, B.Z. Convergence of an Upwind Finite-Difference Scheme for Hamilton–Jacobi–Bellman Equation in Optimal Control. IEEE Trans. Autom. Control 2015, 60, 3012–3017. [Google Scholar]
- Lemarechal, C.; Oustry, F.; Zowe, J. Nonsmooth optimization. In Optimization and Operations Research—Volume II; Derigs, U., Ed.; Encyclopaedia of Life Support Systems: Paris, France, 1977. [Google Scholar]
- Mäkelä, M. Survey of Bundle Methods for Nonsmooth Optimization. Optim. Methods Softw. 2002, 17, 1–29. [Google Scholar]
- Karmitsa, N.; Bagirov, A.; Mäkelä, M.M. Comparing different nonsmooth minimization methods and software. Optim. Methods Softw. 2012, 27, 131–153. [Google Scholar]
- Boyd, S.; Xiao, L.; Mutapcic, A. Subgradient methods. In Lecture Notes of EE392o; Stanford University: Autumn, Quarter, 2003; Volume 2004. [Google Scholar]
- Boyd, S.; Mutapcic, A. Stochastic subgradient methods. In Lecture Notes for EE364b; Stanford University: Autumn, Quarter, 2008; Volume 97. [Google Scholar]
- Ben Hammouda, C.; Rezvanova, E.; von Schwerin, E.; Tempone, R. Lagrangian relaxation for continuous-time optimal control of coupled hydrothermal power systems including storage capacity and a cascade of hydropower systems with time delays. Optim. Control Appl. Methods 2024, 45, 2279–2311. [Google Scholar]
- Nakagami, M. The m-Distribution—A General Formula of Intensity Distribution of Rapid Fading. In Statistical Methods in Radio Wave Propagation; Hoffman, W., Ed.; Pergamon: Oxford, UK, 1960; pp. 3–36. [Google Scholar] [CrossRef]
- Forman, J.L.; Sørensen, M. The Pearson diffusions: A class of statistically tractable diffusion processes. Scand. J. Stat. 2008, 35, 438–465. [Google Scholar]
- Andrieu, L.; Cohen, G.; Vázquez-Abad, F.J. Gradient-based simulation optimization under probability constraints. Eur. J. Oper. Res. 2011, 212, 345–351. [Google Scholar]
- Pfeiffer, L. Sensitivity Analysis for Optimal Control Problems. Stochastic Optimal Control with a Probability Constraint. Theses, Ecole Polytechnique X. 2013. Available online: https://pastel.hal.science/pastel-00881119/ (accessed on 11 March 2025).
- Pfeiffer, L.; Tan, X.; Zhou, Y.L. Duality and Approximation of Stochastic Optimal Control Problems under Expectation Constraints. SIAM J. Control Optim. 2021, 59, 3231–3260. [Google Scholar]
- Bouchard, B.; Elie, R.; Imbert, C. Optimal Control under Stochastic Target Constraints. SIAM J. Control Optim. 2010, 48, 3501–3531. [Google Scholar]
- Bouchard, B.; Elie, R.; Touzi, N. Stochastic Target Problems with Controlled Loss. SIAM J. Control Optim. 2009, 48, 3123–3150. [Google Scholar]
- Haarala, M.; Miettinen, K.; Mäkelä, M.M. New limited memory bundle method for large-scale nonsmooth optimization. Optim. Methods Softw. 2004, 19, 673–692. [Google Scholar]
- Abdi, A.; Wills, K.; Barger, H.; Alouini, M.S.; Kaveh, M. Comparison of the level crossing rate and average fade duration of Rayleigh, Rice and Nakagami fading models with mobile channel data. In Proceedings of the Vehicular Technology Conference Fall 2000. IEEE VTS Fall VTC2000. 52nd Vehicular Technology Conference (Cat. No. 00CH37152), Boston, MA, USA, 24–28 September 2000; Volume 4, pp. 1850–1857. [Google Scholar] [CrossRef]
- Pearson, K.; Henrici, O.M.F.E. X. Contributions to the mathematical theory of evolution.—II. Skew variation in homogeneous material. Philos. Trans. R. Soc. Lond. (A) 1997, 186, 343–414. [Google Scholar]
- Brucker, J.; Bessler, W.G.; Gasper, R. Grey-box modelling of lithium-ion batteries using neural ordinary differential equations. Energy Informat. 2021, 4, 1–13. [Google Scholar]
- Tamilselvi, S.; Gunasundari, S.; Karuppiah, N.; Razak RK, A.; Madhusudan, S.; Nagarajan, V.M.; Sathish, T.; Shamim, M.Z.M.; Saleel, C.A.; Afzal, A. A Review on Battery Modelling Techniques. Sustainability 2021, 13, 10042. [Google Scholar] [CrossRef]
- Edge, J.S.; O’Kane, S.; Prosser, R.; Kirkaldy, N.D.; Patel, A.N.; Hales, A.; Ghosh, A.; Ai, W.; Chen, J.; Yang, J.; et al. Lithium ion battery degradation: What you need to know. Phys. Chem. Chem. Phys. 2021, 23, 8200–8221. [Google Scholar] [CrossRef] [PubMed]
- Farooq, M.J.; Ghazzai, H.; Kadri, A. Optimized energy procurement for cellular networks powered by smart grid based on stochastic geometry. In Proceedings of the 2015 IEEE Globecom Workshops (GC Wkshps), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Lefebvre, M. Applied Probability and Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Karmitsa, N. LMBM–FORTRAN subroutines for Large-Scale nonsmooth minimization: User’s manual’. TUCS Technol. Rep. 2007, 77, 856. [Google Scholar]
- Grimmer, B. Convergence Rates for Deterministic and Stochastic Subgradient Methods without Lipschitz Continuity. SIAM J. Optim. 2019, 29, 1350–1365. [Google Scholar]
- Marsan, M.A.; Meo, M. Energy efficient management of two cellular access networks. ACM SIGMETRICS Perform. Eval. Rev. 2010, 37, 69–73. [Google Scholar]
- Rached, N.B.; Ghazzai, H.; Kadri, A.; Alouini, M.S. A Time-Varied Probabilistic ON/OFF Switching Algorithm for Cellular Networks. IEEE Commun. Lett. 2018, 22, 634–637. [Google Scholar]
- Destatis, S.B. Official Population Statistics of Germany. 2025. Available online: https://www.destatis.de/EN/Home/_node.html (accessed on 19 January 2025).
- Statista. Number of 5G Base Stations in Germany. 2023. Available online: https://www.statista.com/statistics/1427492/number-of-5g-base-stations-in-eu-countries/ (accessed on 19 January 2025).
- Nguyen, S.; Akl, R. Approximating User Distributions in WCDMA Networks Using 2-D Gaussian. Citeseer. 2005. Available online: https://digital.library.unt.edu/ark:/67531/metadc30820/m2/1/high_res_d/Akl-2005-Approximating_User_Distributions_in_WCDMA.pdf (accessed on 11 March 2025).
- Germany, V. Vodafone Germany Tariffs. 2025. Available online: https://www.vodafone.de/privat/mobilfunk.html (accessed on 19 January 2025).
- 50Hertz. Wind Power Production Grid Feed-In Data. 2025. Available online: https://www.50hertz.com/en/Transparency/GridData/Productiongridfeed-in (accessed on 19 January 2025).
- SMARD. Market Data Download Center. 2025. Available online: https://www.smard.de/en/downloadcenter/download-market-data/ (accessed on 19 January 2025).



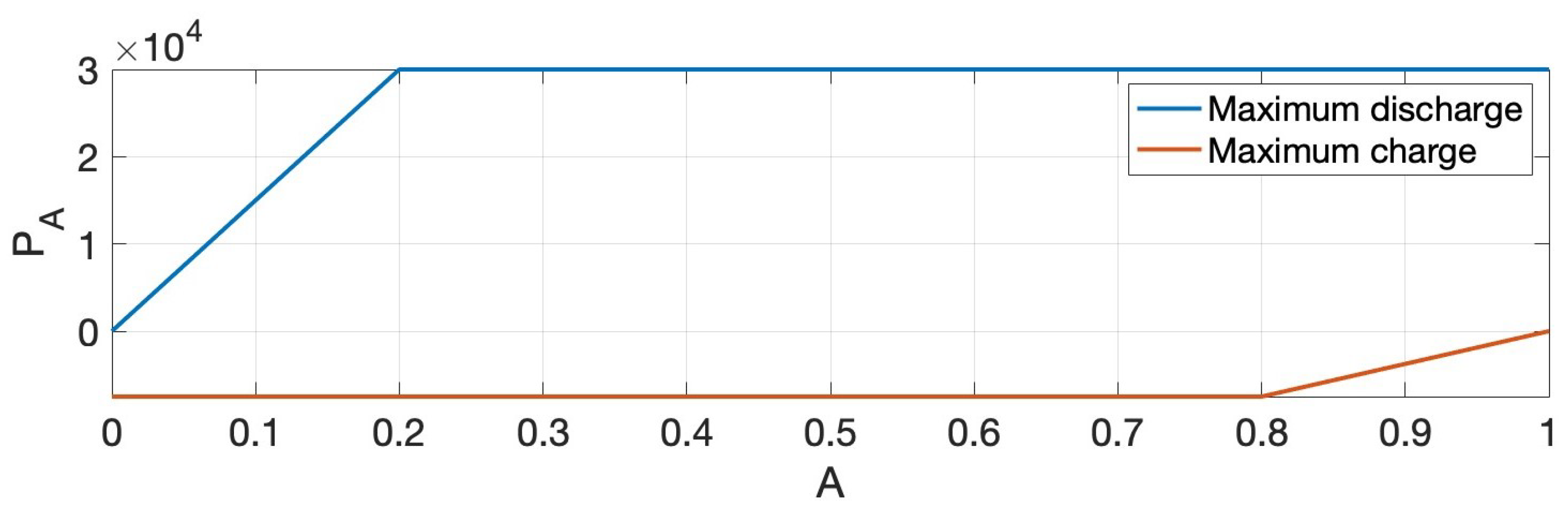
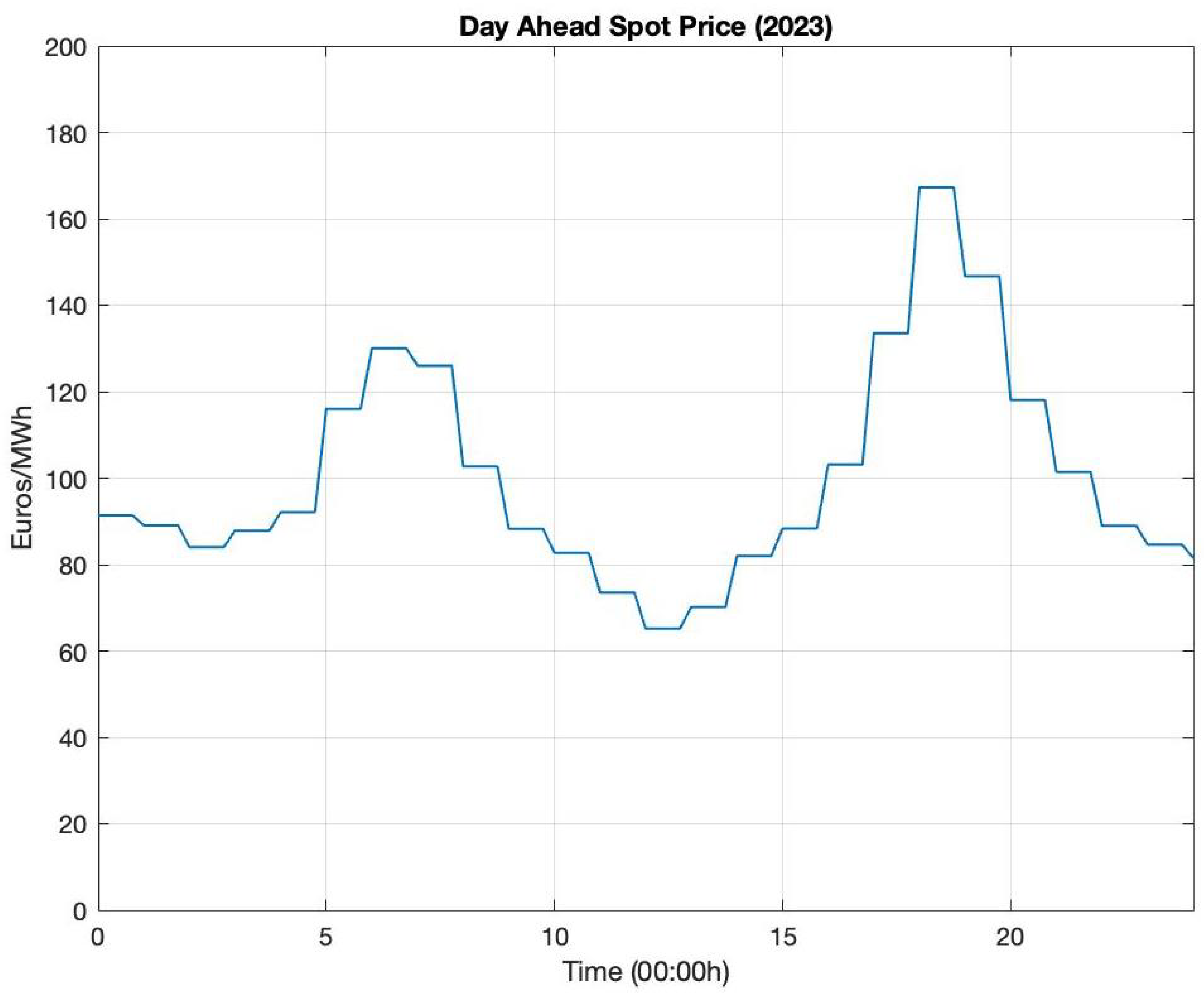



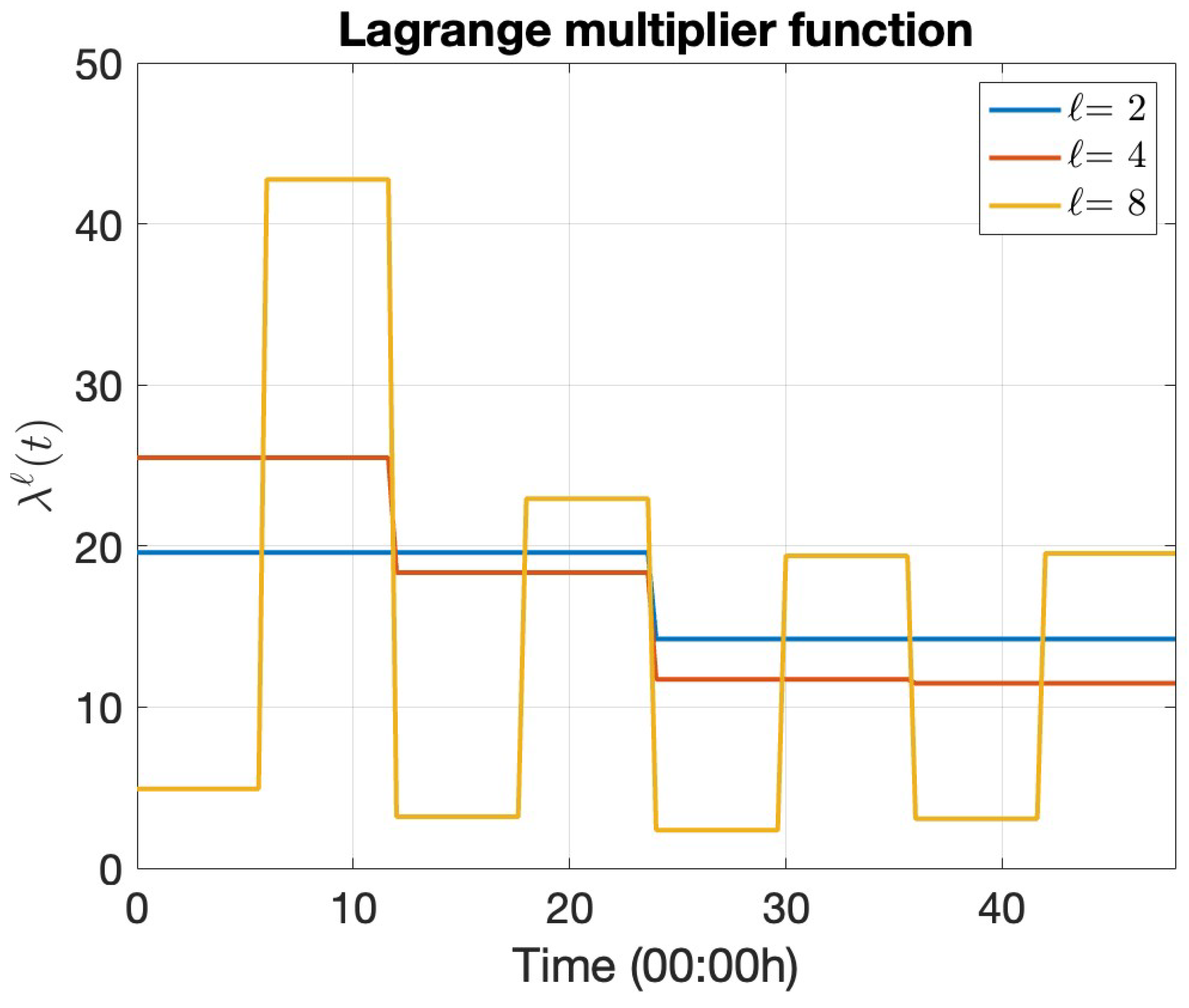


| Description | ℓ | Optimal Cost (EUR) |
|---|---|---|
| Problem 5 | ||
| Problem 6 | ||
| Initialization Algorithm A3 | 1 | |
| LMBM | 1 | |
| Dual optimization Algorithm 1 | 2 | |
| Dual optimization Algorithm 1 | 4 | |
| Dual optimization Algorithm 1 | 8 |
| Dual Algorithm 1 | Problem 6 | Problem 5 | |
|---|---|---|---|
| Scenario A | |||
| Scenario B | |||
| Scenario C | |||
| Scenario D | |||
| Scenario E |
| Expected Energy | Consumed | Battery | Bought | Sold |
|---|---|---|---|---|
| Base scenario | ||||
| Scenario A | ||||
| Scenario B | ||||
| Scenario C | ||||
| Scenario D | ||||
| Scenario E |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Rached, N.; Subbiah Pillai, S.M.; Tempone, R. Optimal Power Procurement for Green Cellular Wireless Networks Under Uncertainty and Chance Constraints. Entropy 2025, 27, 308. https://doi.org/10.3390/e27030308
Ben Rached N, Subbiah Pillai SM, Tempone R. Optimal Power Procurement for Green Cellular Wireless Networks Under Uncertainty and Chance Constraints. Entropy. 2025; 27(3):308. https://doi.org/10.3390/e27030308
Chicago/Turabian StyleBen Rached, Nadhir, Shyam Mohan Subbiah Pillai, and Raúl Tempone. 2025. "Optimal Power Procurement for Green Cellular Wireless Networks Under Uncertainty and Chance Constraints" Entropy 27, no. 3: 308. https://doi.org/10.3390/e27030308
APA StyleBen Rached, N., Subbiah Pillai, S. M., & Tempone, R. (2025). Optimal Power Procurement for Green Cellular Wireless Networks Under Uncertainty and Chance Constraints. Entropy, 27(3), 308. https://doi.org/10.3390/e27030308







