Research on Integrated Modularization of Supercritical Carbon Dioxide System for Aircraft Carrier Nuclear Power
Abstract
1. Introduction
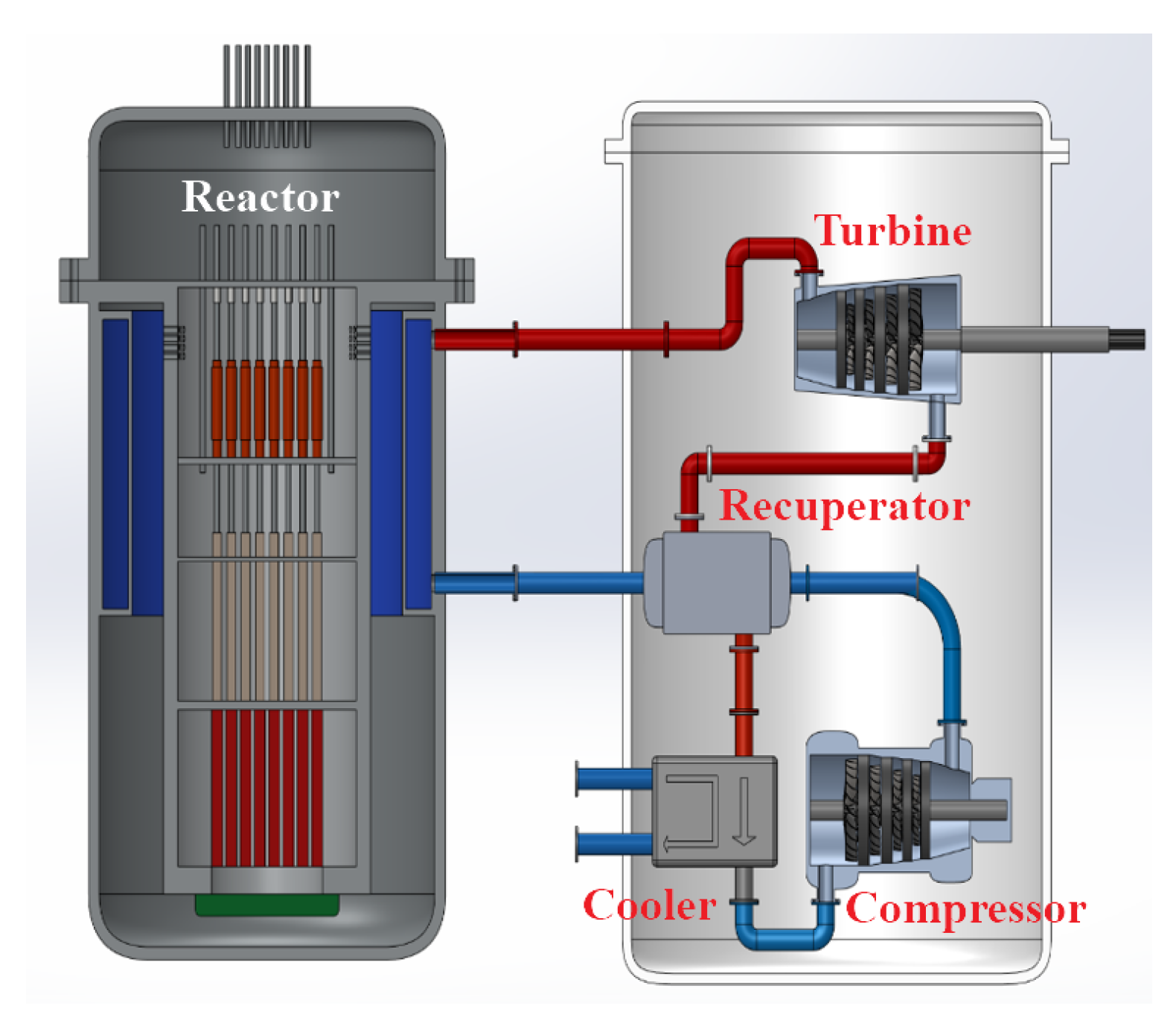
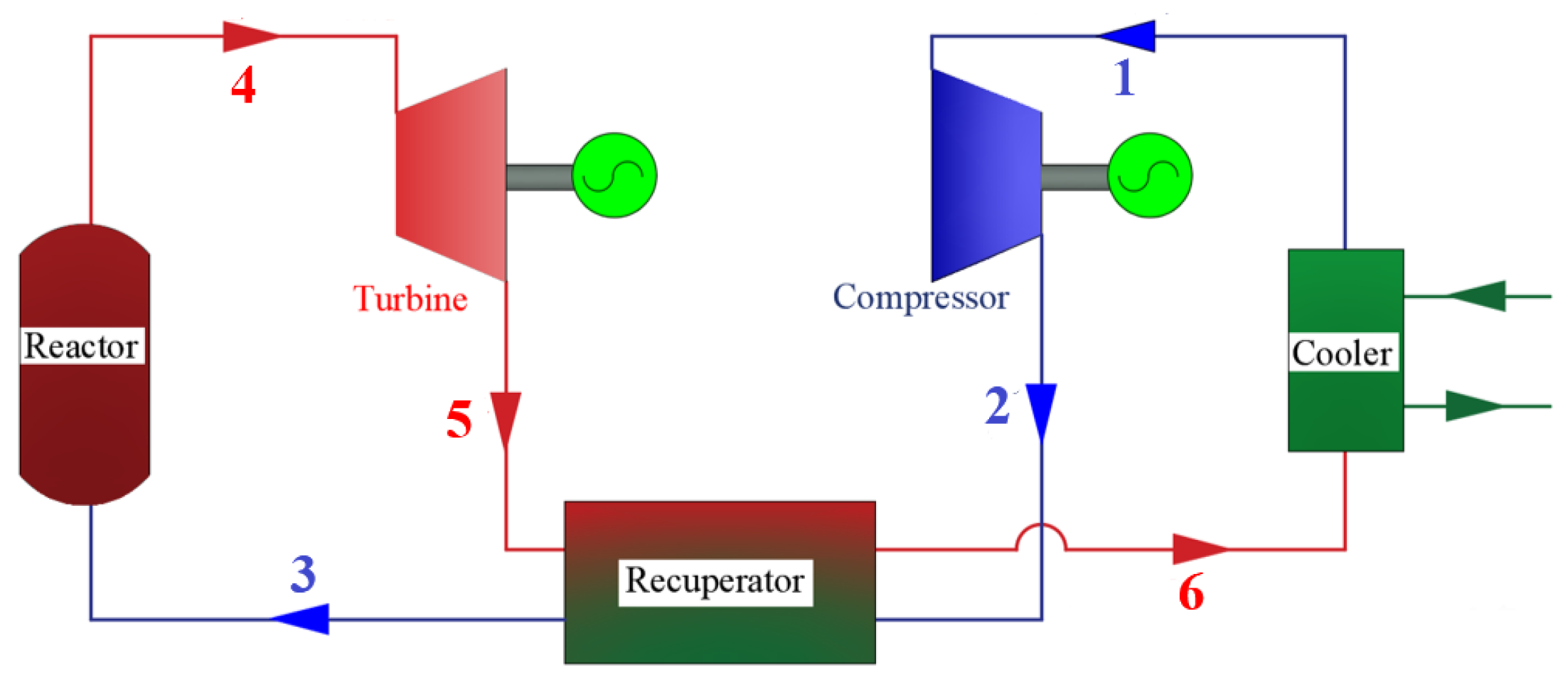
2. Cycle Description
- (1)
- The system maintains a stable operating state.
- (2)
- The pressure and temperature of the environmental conditions are 1.013 bar and 25 °C, respectively.
- (3)
- The variations in kinetic energy and potential energy can be negligible.
3. Mathematical Modeling
3.1. Thermodynamic Analysis Model
3.1.1. Heat Exchanger Model
- (1)
- Divide the printed circuit board heat exchanger into n units with equal heat exchange amounts, as depicted in Figure 4;
- (2)
- Compute the average temperature difference between carbon dioxide and water within each unit, , where i = 1, 2, …, n. The minimum heat-transfer temperature difference in the heat exchanger is 5 K.
3.1.2. Turbomachinery Model
3.2. Exergy Analysis Evaluation Model
3.3. Compactness Evaluation Model
3.4. Exergy–Economic Model
3.5. Model Validation
4. Results and Discussion
4.1. Mechanism Analysis of Compactness in Supercritical Carbon Dioxide Cycle
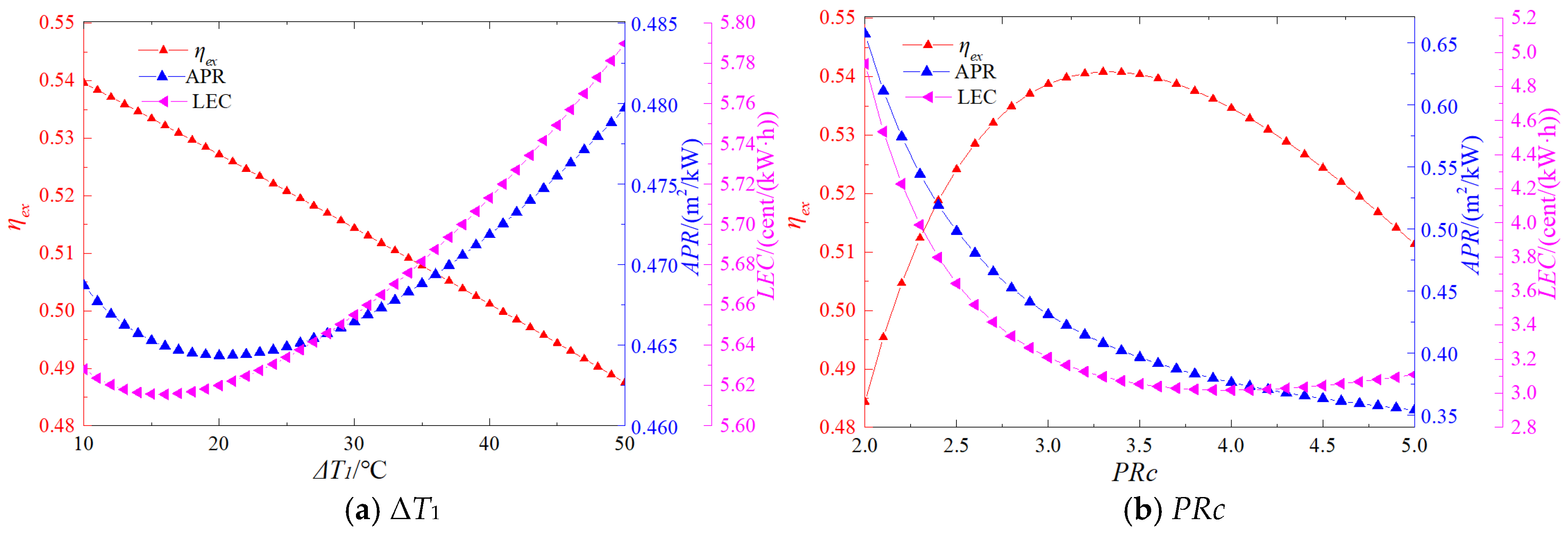
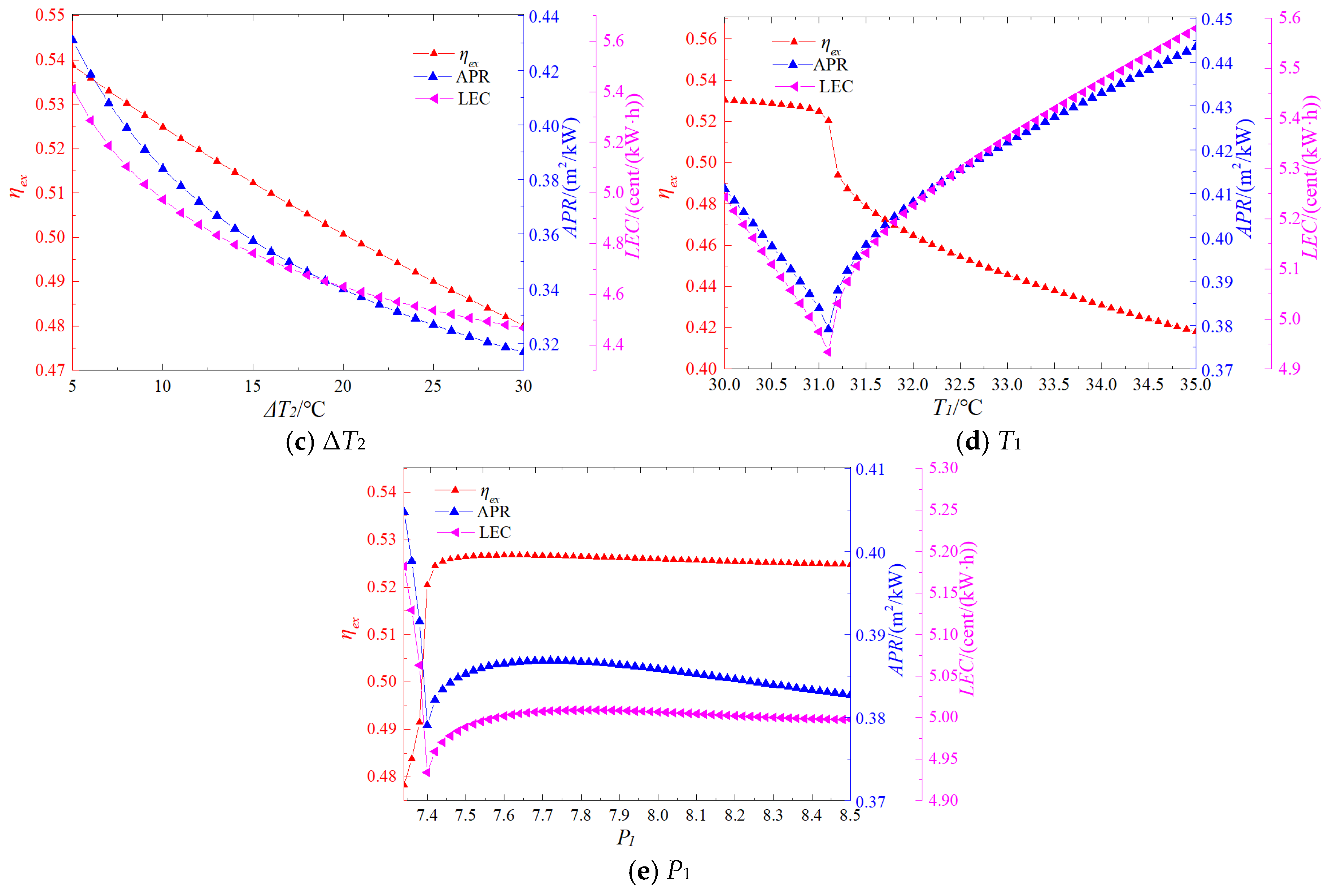
4.2. Parametric Studies
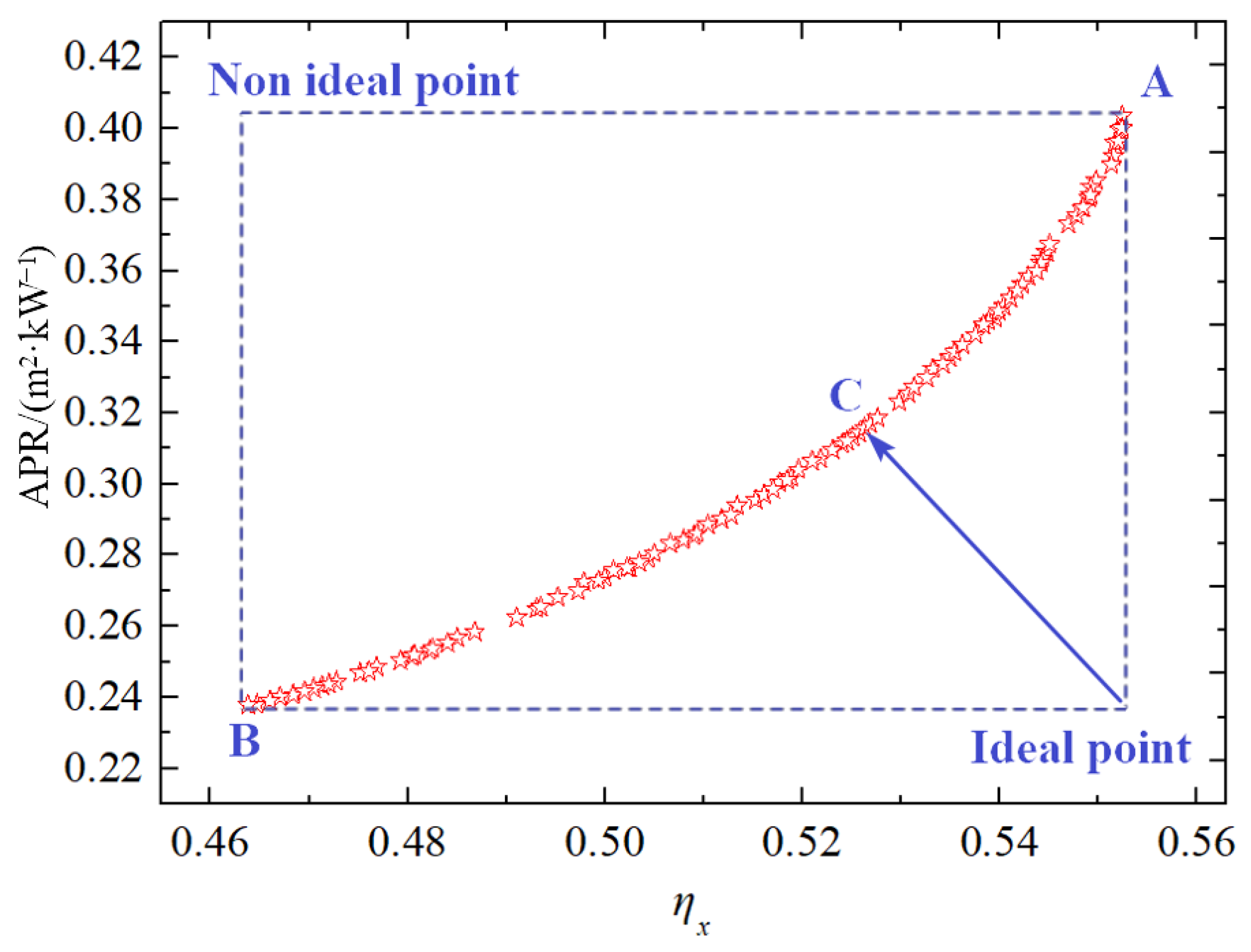
4.3. Multi-Objective Optimization Study
4.3.1. Dual-Objective Function Optimization
4.3.2. Three Objective Function Optimization
5. Summary and Conclusions
- (1)
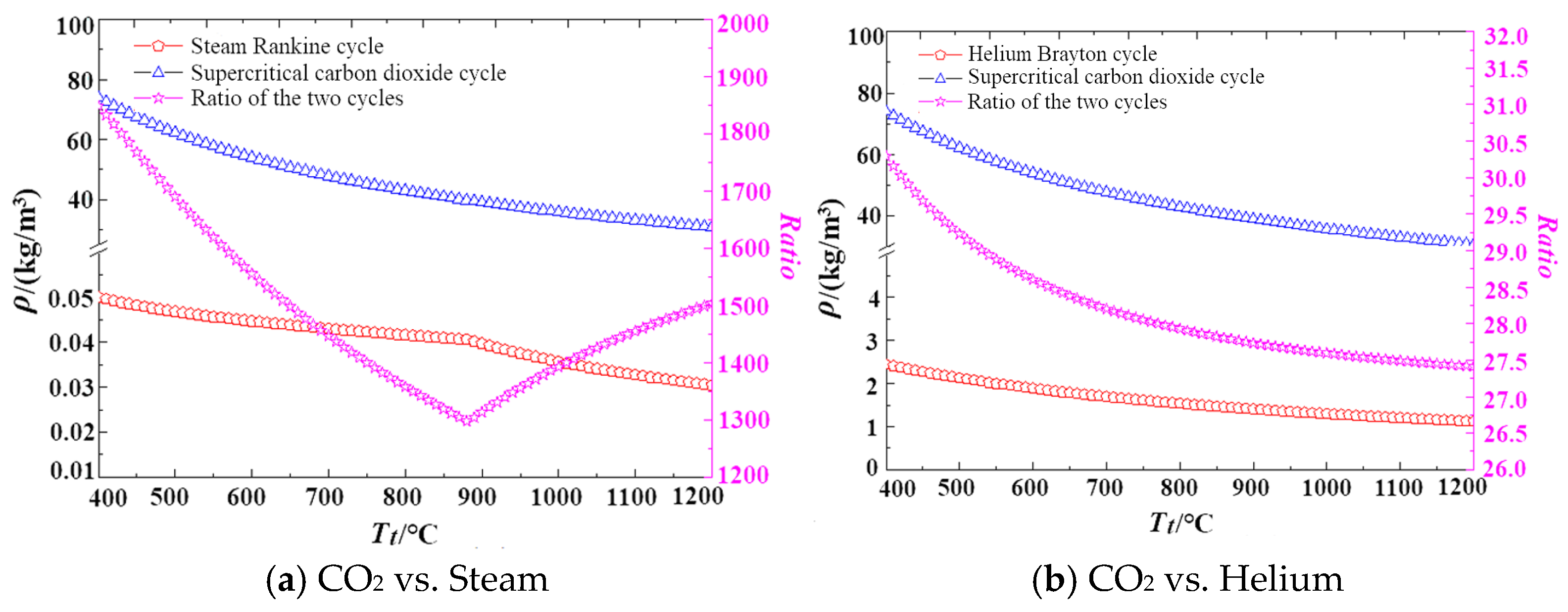
- The specific power volume flow rate of the steam Rankine cycle is over 100 times greater than that of the S-CO2 cycle, and that of the helium cycle is more than 10 times greater. The primary reason for the superior compactness of the S-CO2 cycle is its high density during the expansion process.
- (2)
- Optimal thermodynamic and economic performance is achieved when the compressor inlet conditions are near the critical point. This is due to the low power consumption required to compress carbon dioxide in this state.
- (3)
- The system was subjected to a dual-objective optimization with exergy efficiency and APR as the objective functions. The optimization outcomes demonstrated that the optimal exergy efficiency and APR were 52.8% and 0.312 m2 kw−1, respectively. The corresponding decision variables were as follows: ΔT1 was 27 °C, PRc was 2.7, ΔT2 was 12 °C, T1 was 31.5 °C, and P1 was 7.42 MPa.
- (4)
- The system was conducted with triple-objective optimization with exergy efficiency, APR, and LEC as the objective functions. The optimization results reveal that the optimal exergy efficiency, APR, and LEC are 51%, 0.272 m2 kW−1, and 4.5 cent/(kW·h), respectively. The corresponding decision variables are: ΔT1 is 24 °C, PRc is 2.8, ΔT2 is 14 °C, T1 is 31.6 °C, and P1 is 7.45 MPa. Therefore, the supercritical carbon dioxide power module exhibits high compactness and is feasible for application in the nuclear power of aircraft carriers.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rubel, R.C. The future of aircraft carriers. Nav. War Coll. Rev. 2011, 64, 12–27. [Google Scholar]
- Evans, M.L. USS Enterprise (CVN-65): The First Nuclear Powered Aircraft Carrier; McFarland: Jefferson, NC, USA, 2022. [Google Scholar]
- Upadhyaya, S. The aircraft carrier in the twenty-first century–fulcrum of the future fleet. Aust. J. Marit. Ocean. Aff. 2024, 1–16. [Google Scholar] [CrossRef]
- Zhu, S.; Zhang, K.; Deng, K. A review of waste heat recovery from the marine engine with highly efficient bottoming power cycles. Renew. Sustain. Energy Rev. 2020, 120, 109611. [Google Scholar] [CrossRef]
- Houtkoop, K.; Visser, K.; Sietsma, J.; de Vries, N. New potential for integration of nuclear power in marine propulsion systems. In Proceedings of the INEC, Delft, The Netherlands, 8–10 November 2022. [Google Scholar]
- Yu, A.; Su, W.; Lin, X.; Zhou, N. Recent trends of supercritical CO2 Brayton cycle: Bibliometric analysis and research review. Nucl. Eng. Technol. 2021, 53, 699–714. [Google Scholar] [CrossRef]
- Qu, J.; Feng, Y.; Zhu, Y.; Zhou, S.; Zhang, W. Design and thermodynamic analysis of a combined system including steam Rankine cycle, organic Rankine cycle, and power turbine for marine low-speed diesel engine waste heat recovery. Energy Convers. Manag. 2021, 245, 114580. [Google Scholar] [CrossRef]
- Kung, S.; Michael, C. Damage of Rankine Cycle Components in Concentrated Solar Power Plants. In Advances in Materials Technology for Power Plants; ASM International: Almere, The Netherlands, 2024; Volume 84871. [Google Scholar]
- Guo, T.; Chen, Y.; Shao, H.; Zhao, Q.; Liang, Z. Molecular dynamics, thermodynamics and experimental studies on the corrosion mechanism of T92 and TP347H steels in high-pressure CO2 and H2O at 600 °C. Appl. Surf. Sci. 2023, 621, 156879. [Google Scholar] [CrossRef]
- Li, M.-J.; Zhu, H.-H.; Guo, J.-Q.; Wang, K.; Tao, W.-Q. The development technology and applications of supercritical CO2 power cycle in nuclear energy, solar energy and other energy industries. Appl. Therm. Eng. 2017, 126, 255–275. [Google Scholar] [CrossRef]
- Ravi Kumar, K.; Krishna Chaitanya, N.V.V. Towards sustainable energy–exploring the supercritical carbon dioxide (S-CO2) Brayton cycle for various applications: A critical review. Int. J. Ambient Energy 2024, 45, 2378046. [Google Scholar] [CrossRef]
- Liao, G.; Liu, L.; E, J.; Zhang, F.; Chen, J.; Deng, Y.; Zhu, H. Effects of technical progress on performance and application of supercritical carbon dioxide power cycle: A review. Energy Convers. Manag. 2019, 199, 111986. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.-H. A newly proposed supercritical carbon dioxide Brayton cycle configuration to enhance energy sources integration capability. Energy 2022, 239, 121868. [Google Scholar] [CrossRef]
- Ming, Y.; Liu, K.; Zhao, F.; Fang, H.; Tan, S.; Tian, R. Dynamic modeling and validation of the 5 MW small modular supercritical CO2 Brayton-Cycle reactor system. Energy Convers. Manag. 2022, 253, 115184. [Google Scholar] [CrossRef]
- Wu, P.; Ma, Y.; Gao, C.; Liu, W.; Shan, J.; Huang, Y.; Wang, J.; Zhang, D.; Ran, X. A review of research and development of supercritical carbon dioxide Brayton cycle technology in nuclear engineering applications. Nucl. Eng. Des. 2020, 368, 110767. [Google Scholar] [CrossRef]
- Ma, T.; Li, M.-J.; Xu, J.-L.; Ni, J.-W.; Tao, W.-Q.; Wang, L. Study of dynamic response characteristics of S-CO2 cycle in coal-fired power plants based on real-time micro-grid load and a novel synergistic control method with variable working conditions. Energy Convers. Manag. 2022, 254, 115264. [Google Scholar] [CrossRef]
- Fang, L.; Li, Y.; Yang, X.; Yang, Z. Analyses of Thermal Performance of Solar Power Tower Station Based on a Supercritical CO2 Brayton Cycle. J. Energy Resour. Technol. 2020, 142, 031301. [Google Scholar] [CrossRef]
- Xu, L.; Wang, X.; Sun, E.; Li, M. Economic comparison between S-CO2 power cycle and water-steam Rankine cycle for coal-fired power generation system. Energy Convers. Manag. 2021, 238, 114150. [Google Scholar] [CrossRef]
- Kizilkan, O. Performance assessment of steam Rankine cycle and S-CO2 Brayton cycle for waste heat recovery in a cement plant: A comparative study for supercritical fluids. Int. J. Energy Res. 2020, 44, 12329–12343. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, N.; Yuan, T.; Yu, G. A multi-index evaluation method of supercritical CO2 Brayton cycle for nuclear power plants design. Int. J. Green Energy 2024, 21, 2042–2064. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Shao, Y.; Zhong, W. Research and development of supercritical carbon dioxide coal-fired power systems. J. Therm. Sci. 2020, 29, 546–575. [Google Scholar] [CrossRef]
- Li, Z.; Shi, M.; Shao, Y.; Zhong, W. Supercritical CO2 Cycles for Nuclear-Powered Marine Propulsion: Preliminary Conceptual Design and Off-Design Performance Assessment. J. Therm. Sci. 2024, 33, 328–347. [Google Scholar] [CrossRef]
- Lee, W.; Yoo, S.; Park, D.K.; Lee, K.-Y. Design considerations of the supercritical carbon dioxide Brayton cycle of small modular molten salt reactor for ship propulsion. Prog. Nucl. Energy 2023, 163, 104835. [Google Scholar] [CrossRef]
- Gumus, E. S-CO2 power cycle/reverse osmosis distillation system for water-electricity cogeneration in nuclear powered ships and submarines. Desalination 2024, 572, 117126. [Google Scholar] [CrossRef]
- Lehman, J.F.; Wills, S. Aircraft Carriers—Missions, Survivability, Size, Cost, Numbers. Nav. War Coll. Rev. 2021, 74, 15–36. [Google Scholar]
- Dostal, V. A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2004. [Google Scholar]
- Khonakdar, D.R.; Raveshi, M.R. Mixed convection on a vertical plate in supercritical fluids by selecting the best equation of state. J. Supercrit. Fluids 2016, 107, 549–559. [Google Scholar] [CrossRef]
- Teymourtash, A.R.; Khonakdar, D.R.; Raveshi, M.R. Natural convection on a vertical plate with variable heat flux in supercritical fluids. J. Supercrit. Fluids 2013, 74, 115–127. [Google Scholar] [CrossRef]
- Ahn, Y.; Bae, S.J.; Kim, M.; Cho, S.K.; Baik, S.; Lee, J.I.; Cha, J.E. Review of supercritical CO2 power cycle technology and current status of research and development. Nucl. Eng. Technol. 2015, 47, 647–661. [Google Scholar] [CrossRef]
- Moisseytsev, A.; Sienicki, J.J. Investigation of alternative layouts for the supercritical carbon dioxide Brayton cycle for a sodium—Cooled fast reactor. Nucl. Eng. Des. 2009, 239, 1362–1371. [Google Scholar] [CrossRef]
- Lee, S.-M.; Kim, K.-Y. Optimization of zigzag flow channels of a printed circuit heat exchanger for nuclear power plant application. J. Nucl. Sci. Technol. 2012, 49, 343–351. [Google Scholar] [CrossRef]
- Chen, M.; Sun, X.; Christensen, R.N.; Skavdahl, I.; Utgikar, V.; Sabharwall, P. Pressure drop and heat transfer characteristics of a high-temperature printed circuit heat exchanger. Appl. Therm. Eng. 2016, 108, 1409–1417. [Google Scholar] [CrossRef]
- Tafur-Escanta, P.; Valencia-Chapi, R.; Muñoz-Antón, J. Entropy analysis of new proposed Brayton cycle configurations for solar thermal power plants. Therm. Sci. Eng. Prog. 2025, 62, 103670. [Google Scholar] [CrossRef]
- Tafur-Escanta, P.; López-Paniagua, I.; Muñoz-Antón, J. Thermodynamics analysis of the supercritical CO2 binary mixtures for Brayton power cycles. Energy 2023, 270, 126838. [Google Scholar] [CrossRef]
- Tafur-Escanta, P.; Coco-Enríquez, L.; Valencia-Chapi, R.; Muñoz-Antón, J. Enhancing s-CO2 Brayton Power Cycle Efficiency in Cold Ambient Conditions Through Working Fluid Blends. Entropy 2025, 27, 744. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Wang, J.; Luo, F.; Lou, J.; Zhang, J. A nuclear-driven combined cooling and power system based on supercritical and transcritical CO2 cycles: Energy, exergy, and exergoeconomic analysis, multi-objective optimization and reactor startup analysis. Nucl. Eng. Des. 2025, 432, 113816. [Google Scholar] [CrossRef]
- Guccione, S.; Trevisan, S.; Guedez, R.; Laumert, B.; Maccarini, S.; Traverso, A. Techno-economic optimization of a hybrid PV-CSP plant with molten salt thermal energy storage and supercritical CO2 brayton power cycle. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Rotterdam, The Netherlands, 13–17 June 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022; Volume 86014. [Google Scholar]
- Xiong, Z.; Lv, J.; Xie, Z.; Xu, Y. Influence Factor of Naval Vessel’s Equipment under Optimized Sailing Strategy. Math. Probl. Eng. 2023, 2023, 5906332. [Google Scholar] [CrossRef]
- Adumene, S.; Islam, R.; Amin, T.; Nitonye, S.; Yazdi, M.; Johnson, K.T. Advances in nuclear power system design and fault-based condition monitoring towards safety of nuclear-powered ships. Ocean Eng. 2022, 251, 111156. [Google Scholar] [CrossRef]
- Hass, B.S. Strategies for the Success of Nuclear Powered Commercial Shipping; Connecticut Maritime Association: Stamford, CT, USA, 2014; pp. 2718–2724. [Google Scholar]
- Feng, F.; Li, T.; An, J.; Chen, H.; Wang, Y.; Xu, G.; Zhao, Q.; Liu, T. Performance assessment of a novel polygeneration system based on the integration of waste plasma gasification, tire pyrolysis, gas turbine, supercritical CO2 cycle and organic Rankine cycle. J. Therm. Sci. 2023, 32, 2196–2214. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, J.; Xia, J.; Guo, Y.; Zhao, P.; Dai, Y. Design and performance analysis of a supercritical CO2 radial inflow turbine. Appl. Therm. Eng. 2020, 167, 114757. [Google Scholar] [CrossRef]
- Lian, J.; Xu, D.; Chang, H.; Xu, Z.; Lu, X.; Wang, Q.; Ma, T. Thermal and mechanical performance of a hybrid printed circuit heat exchanger used for supercritical carbon dioxide Brayton cycle. Energy Convers. Manag. 2021, 245, 114573. [Google Scholar] [CrossRef]









| Parameters | Value |
|---|---|
| Rated thermal power of the reactor/MW | 385 |
| Fuel assembly type | CF3S17 × 17 square arrangement |
| Length of fuel active section/m | 2.15 |
| Quantity of fuel assemblies | 57 |
| Fuel reload period/year | 50 |
| Operating pressure of the reactor coolant system/MPa | 15 |
| Number of control rod driving mechanisms | 21 |
| The quantity of main cooling pumps | 4 |
| The inner diameter of the reactor pressure vessel/m | 3.36 |
| Components | Investment Cost |
|---|---|
| Reactor | |
| Turbine | |
| Compressor | |
| Heat exchangers |
| Operation and Performance Parameters | Reference | This Model | |
|---|---|---|---|
| Input parameters | MC inlet pressure/MPa | 8.5 | 8.5 |
| Pressure ratio | 2.9 | 2.9 | |
| Flow split ratio | 0.7 | 0.7 | |
| Thermal power/MWth | 60.97 | 60.97 | |
| Output parameters | Cycle Net power/MWe | 29.13 | 30.02 |
| Cycle efficiency/% | 47.78 | 47.93 | |
| Component | Turbine Verification [42] | Heat Exchanger Validation [43] | ||||
|---|---|---|---|---|---|---|
| Parameters | Reference | This Model | Parameters | Reference | This Model | |
| Input parameters | Turbine inlet temperature/K | 673.15 | 673.15 | Inlet temperature/°C | 76.2 | 76.2 |
| Turbine inlet temperature/MPa | 19.31 | 19.31 | Outlet temperature/°C | 34.4 | 34.4 | |
| Turbine exit pressure/MPa | 7.63 | 7.63 | Inlet pressure/MPa | 8.22 | 8.22 | |
| Mass flow rate/(kg/s) | 12.74 | 12.74 | Flow rate/(kg/s) | 18.06 | 18.06 | |
| Output parameters | Power output of turbine/MW | 1.16 | 1.20 | Heat transfer rate per unit volume/(MW/m3) | 16.54 | 17.12 |
| Turbine efficiency/% | 85.36 | 87.62 | Pressure drop/kPa | 4.20 | 4.05 | |
| Decision Variables | Lower Bound | Upper Bound |
|---|---|---|
| ΔT1/°C | 10 | 50 |
| PRc | 2 | 4.2 |
| ΔT2/°C | 5 | 30 |
| T1/°C | 31 | 35 |
| P1/MPa | 7.4 | 9 |
| Parameters | Unit | Value |
|---|---|---|
| Number of Stages | - | 2 × 6 |
| Rotational Speed | r/min | 3000 |
| Blade Height Range | mm | 68–107 |
| Root Diameter | mm | 650 |
| Configuration | - | Single—cylinder Double—flow |
| Efficiency | % | 85 |
| Shaft Power | MW | 128 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, S.; Chen, J.; Zhang, F.; Yang, Q. Research on Integrated Modularization of Supercritical Carbon Dioxide System for Aircraft Carrier Nuclear Power. Entropy 2025, 27, 1154. https://doi.org/10.3390/e27111154
Hou S, Chen J, Zhang F, Yang Q. Research on Integrated Modularization of Supercritical Carbon Dioxide System for Aircraft Carrier Nuclear Power. Entropy. 2025; 27(11):1154. https://doi.org/10.3390/e27111154
Chicago/Turabian StyleHou, Shengya, Junren Chen, Fengyuan Zhang, and Qiguo Yang. 2025. "Research on Integrated Modularization of Supercritical Carbon Dioxide System for Aircraft Carrier Nuclear Power" Entropy 27, no. 11: 1154. https://doi.org/10.3390/e27111154
APA StyleHou, S., Chen, J., Zhang, F., & Yang, Q. (2025). Research on Integrated Modularization of Supercritical Carbon Dioxide System for Aircraft Carrier Nuclear Power. Entropy, 27(11), 1154. https://doi.org/10.3390/e27111154






