Novel Entropy for Enhanced Thermal Imaging and Uncertainty Quantification
Abstract
1. Introduction
- A new entropy formulation that, more precisely, measures the informational content (uncertainty) of thermal images, outperforming traditional entropy metrics.
- Two sophisticated frameworks that incorporate this novel entropy measure with classic image enhancement techniques, adaptively optimizing parameters to elevate thermal image quality significantly.
- Extensive qualitative and quantitative evaluations of various image enhancement techniques across multiple thermal image datasets.
2. Background
2.1. Entropy and Contrast
2.2. Image Enhancement
3. Proposed Entropy-Based Image Quality Assessment
4. Results and Discussion
4.1. Datasets
- The Photovoltaic System Thermal Images (PSTI) dataset [29] consists of 277 thermographic aerial images captured using a Zenmuse XT IR camera with a wavelength range of 7 to 13 micrometers. These images were acquired using a DJI Matrice 100 quadcopter drone. In addition to the images themselves, this dataset provides environmental data including temperature, wind speed, and irradiance.
- The Thermal Image of Equipment (TIE) dataset [30] combines thermal images (IRT) for condition monitoring of both induction motors and transformers. This comprehensive dataset encompasses artificially generated internal faults specific to each equipment type, ensuring independence from external factors or initial setup component failures. The thermal images were acquired using a Dali-tech T4/T8 infrared thermal image camera at the Electrical Machines Laboratory workbench operating under an ambient temperature of 23 °C.
- The Wind Turbine Blade (WTB) Inspection thermal dataset [31] consists of 1000 uniformly processed thermal images, meticulously prepared for clarity and consistency. Each image is cropped, centered, and resized to a resolution of 320 × 320 pixels and classified as healthy or faulty, with 500 images in each category. Utilizing a FLIR C5 Compact Thermal Camera with Multi-Spectral Dynamic Imaging (MSX) technology enhances the thermal imaging process, integrating thermal data with standard RGB imagery to provide detailed and insightful images crucial for identifying and analyzing faults in wind turbine blades (WTBs).
- The Multi-Spectral Object Detection (MSOD) dataset [32] comprises multispectral images tailored for object detection in traffic scenarios. These images incorporate RGB, near-infrared, middle-infrared, and far-infrared spectra, providing comprehensive information for detection tasks. The dataset includes objects that may not be visually discernible in RGB images but can be detected in other spectra, such as far-infrared. This dataset is specifically generated for training a multispectral object detection system.
4.2. Evaluation of Existing Methods
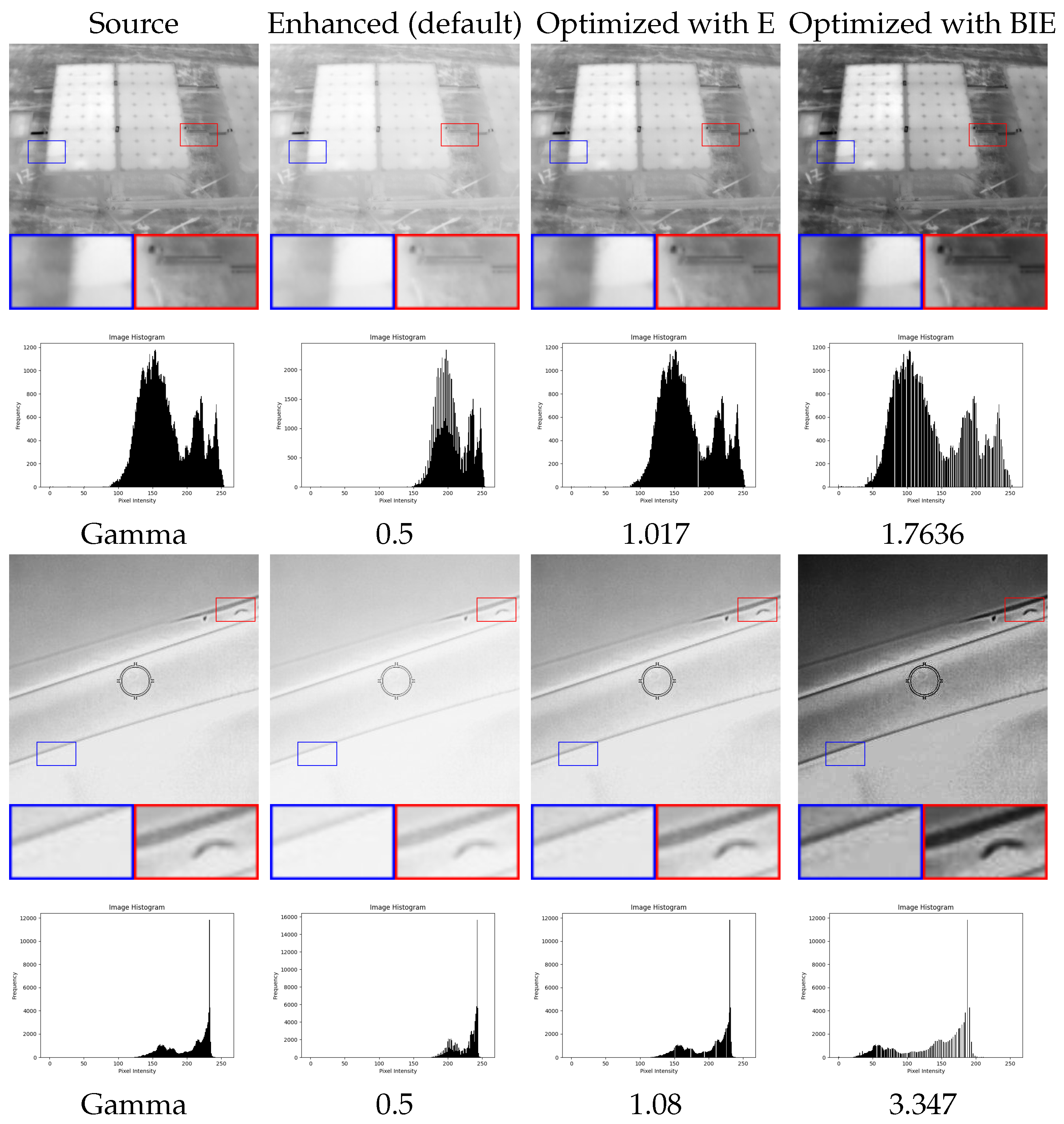
4.3. Optimized Thermal Image Enhancement Using Genetic Algorithms and BIE Metric
| Algorithm 1 Optimal thermal image enhancement using a genetic algorithm with a novel cost function. |
| Inputs: = source image Initialization: population = n, maximum number of iterations = N, Function objective() = Enhance() m = CalculateBIE() return m EndFunction Generate the initial number of n chromosomes Compute the fitness of each chromosome using the objective function while do Select a pair of chromosomes based on fitness Apply crossover on the selected pair Apply mutation operation Replace the old population with the newly generated one end while Return parameters with the best fitness Output: parameters |
| Algorithm 2 Optimal thermal image enhancement using a bat algorithm with a novel cost function. |
| Inputs: = source image Initialization: population = n, maximum number of iterations = N, , pulse rate = r, loudness = A Function objective() = Enhance() m = CalculateBIE() return m EndFunction while do Generate new solutions by adjusting the frequency Updating positions and velocities if rand > r then Select a random solution among the best solutions Generate a local solution around the selected solution end if Generate a new solution by flying randomly if rand < A and objective(new) < objective(best) then Accept the new solution Increase r and reduce A end if end while Return parameters with the best fitness Output: parameters |
4.4. Measure-Based Image Fusion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rai, M.; Maity, T.; Yadav, R. Thermal imaging system and its real time applications: A survey. J. Eng. Technol. 2017, 6, 290–303. [Google Scholar]
- Gallardo-Saavedra, S.; Franco-Mejia, E.; Hernández-Callejo, L.; Duque-Pérez, Ó.; Loaiza-Correa, H.; Alfaro-Mejia, E. Aerial thermographic inspection of photovoltaic plants: Analysis and selection of the equipment. In Proceedings of the ISES Solar World Congress, IEA SHC, Abu Dhabi, United Arab Emirates, 29 October–2 November 2017. [Google Scholar]
- Nguyen, T.X.B.; Rosser, K.; Chahl, J. A review of modern thermal imaging sensor technology and applications for autonomous aerial navigation. J. Imaging 2021, 7, 217. [Google Scholar] [CrossRef] [PubMed]
- Chrzanowski, K.; Matyszkiel, R.; Fischer, J.; Bareła, J. Uncertainty of temperature measurement with thermal cameras. Opt. Eng. 2001, 40, 1106–1114. [Google Scholar]
- Grigoryan, A.M.; Agaian, S.S. Quaternion and Octonion Color Image Processing with MATLAB; SPIE—The International Society for Optical Engineering: Bellingham, WA, USA, 2018. [Google Scholar]
- Wilson, A.; Gupta, K.A.; Koduru, B.H.; Kumar, A.; Jha, A.; Cenkeramaddi, L.R. Recent advances in thermal imaging and its applications using machine learning: A review. IEEE Sens. J. 2023, 23, 3395–3407. [Google Scholar] [CrossRef]
- Roslidar, R.; Rahman, A.; Muharar, R.; Syahputra, M.R.; Arnia, F.; Syukri, M.; Pradhan, B.; Munadi, K. A review on recent progress in thermal imaging and deep learning approaches for breast cancer detection. IEEE Access 2020, 8, 116176–116194. [Google Scholar] [CrossRef]
- Abreu de Souza, M.; Alka Cordeiro, D.C.; Oliveira, J.d.; Oliveira, M.F.A.d.; Bonafini, B.L. 3d multi-modality medical imaging: Combining anatomical and infrared thermal images for 3d reconstruction. Sensors 2023, 23, 1610. [Google Scholar] [CrossRef] [PubMed]
- Schuss, C.; Remes, K.; Leppänen, K.; Saarela, J.; Fabritius, T.; Eichberger, B.; Rahkonen, T. Detecting defects in photovoltaic panels with the help of synchronized thermography. IEEE Trans. Instrum. Meas. 2018, 67, 1178–1186. [Google Scholar] [CrossRef]
- Dall’O’, G.; Sarto, L.; Panza, A. Infrared screening of residential buildings for energy audit purposes: Results of a field test. Energies 2013, 6, 3859–3878. [Google Scholar] [CrossRef]
- Krišto, M. Review of Methods For the Surveillance and Access Control Using The Thermal Imaging System. Rev. Innov. Compet. A J. Econ. Soc. Res. 2016, 2, 71–91. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, Y.; Zhan, W.; Zhu, D. Improved Thermal Infrared Image Super-Resolution Reconstruction Method Base on Multimodal Sensor Fusion. Entropy 2023, 25, 914. [Google Scholar] [CrossRef]
- Panetta, K.; Gao, C.; Agaian, S. No reference color image contrast and quality measures. IEEE Trans. Consum. Electron. 2013, 59, 643–651. [Google Scholar] [CrossRef]
- Zhai, G.; Min, X. Perceptual image quality assessment: A survey. Sci. China Inf. Sci. 2020, 63, 1–52. [Google Scholar]
- Mello Román, J.C.; Vázquez Noguera, J.L.; Legal-Ayala, H.; Pinto-Roa, D.P.; Gomez-Guerrero, S.; García Torres, M. Entropy and contrast enhancement of infrared thermal images using the multiscale top-hat transform. Entropy 2019, 21, 244. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Bromiley, P.; Thacker, N.; Bouhova-Thacker, E. Shannon entropy, Renyi entropy, and information. Stat. Inf. Ser. 2004, 9, 2–8. [Google Scholar]
- Agaian, S.S.; Panetta, K.; Grigoryan, A.M. A new measure of image enhancement. In Proceedings of the IASTED International Conference on Signal Processing & Communication, Malaga, Spain, 19–22 September 2000; pp. 19–22. [Google Scholar]
- Agaian, S.S.; Silver, B.; Panetta, K.A. Transform coefficient histogram-based image enhancement algorithms using contrast entropy. IEEE Trans. Image Process. 2007, 16, 741–758. [Google Scholar] [CrossRef]
- Lu, L.; Zhou, Y.; Panetta, K.; Agaian, S. Comparative study of histogram equalization algorithms for image enhancement. Mob. Multimed. Image Process. Secur. Appl. 2010, 7708, 337–347. [Google Scholar]
- Grigoryan, A.M.; Agaian, S.S. Gradient based histogram equalization in grayscale image enhancement. In Proceedings of the Mobile Multimedia/Image Processing, Security, and Applications, Baltimore, MD, USA, 14–18 April 2019; Volume 10993, pp. 132–142. [Google Scholar]
- Huang, S.C.; Cheng, F.C.; Chiu, Y.S. Efficient contrast enhancement using adaptive gamma correction with weighting distribution. IEEE Trans. Image Process. 2012, 22, 1032–1041. [Google Scholar] [CrossRef]
- Rahman, S.; Rahman, M.M.; Abdullah-Al-Wadud, M.; Al-Quaderi, G.D.; Shoyaib, M. An adaptive gamma correction for image enhancement. EURASIP J. Image Video Process. 2016, 2016, 35. [Google Scholar] [CrossRef]
- Cao, G.; Huang, L.; Tian, H.; Huang, X.; Wang, Y.; Zhi, R. Contrast enhancement of brightness-distorted images by improved adaptive gamma correction. Comput. Electr. Eng. 2018, 66, 569–582. [Google Scholar] [CrossRef]
- Chen, S.D.; Ramli, A.R. Minimum mean brightness error bi-histogram equalization in contrast enhancement. IEEE Trans. Consum. Electron. 2003, 49, 1310–1319. [Google Scholar] [CrossRef]
- Wang, C.; Ye, Z. Brightness preserving histogram equalization with maximum entropy: A variational perspective. IEEE Trans. Consum. Electron. 2005, 51, 1326–1334. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Sui, X. Range limited bi-histogram equalization for image contrast enhancement. Optik 2013, 124, 425–431. [Google Scholar] [CrossRef]
- Agrawal, S.; Panda, R.; Mishro, P.K.; Abraham, A. A novel joint histogram equalization based image contrast enhancement. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 1172–1182. [Google Scholar] [CrossRef]
- Alfaro-Mejía, E.; Loaiza-Correa, H.; Franco-Mejía, E.; Restrepo-Girón, A.D.; Nope-Rodríguez, S.E. Dataset for recognition of snail trails and hot spot failures in monocrystalline Si solar panels. Data Brief 2019, 26, 104441. [Google Scholar] [CrossRef]
- Najafi, M.; Baleghi, Y.; Gholamian, S.A.; Mirimani, S.M. Fault diagnosis of electrical equipment through thermal imaging and interpretable machine learning applied on a newly-introduced dataset. In Proceedings of the 2020 6th Iranian Conference on Signal Processing and Intelligent Systems (ICSPIS), Mashhad, Iran, 23–24 December 2020; pp. 1–7. [Google Scholar]
- Memari, M.; Shekaramiz, M.; Masoum, M.A.; Seibi, A.C. Data Fusion and Ensemble Learning for Advanced Anomaly Detection Using Multi-Spectral RGB and Thermal Imaging of Small Wind Turbine Blades. Energies 2024, 17, 673. [Google Scholar] [CrossRef]
- Takumi, K.; Watanabe, K.; Ha, Q.; Tejero-De-Pablos, A.; Ushiku, Y.; Harada, T. Multispectral object detection for autonomous vehicles. In Proceedings of the on Thematic Workshops of ACM Multimedia, Mountain View, CA, USA, 23–27 October 2017; pp. 35–43. [Google Scholar]
- Ayunts, H.; Agaian, S. No-Reference Quality Metrics for Image Decolorization. IEEE Trans. Consum. Electron. 2023, 69, 1177–1185. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.S.; Hossein Gandomi, A. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Bulanon, D.; Burks, T.; Alchanatis, V. Image fusion of visible and thermal images for fruit detection. Biosyst. Eng. 2009, 103, 12–22. [Google Scholar] [CrossRef]
- Kishore, D.R.; Syeda, N.; Suneetha, D.; Kumari, C.S.; Ghantasala, G.P. Multi scale image fusion through Laplacian Pyramid and deep learning on thermal images. Ann. Rom. Soc. Cell Biol. 2021, 25, 3728–3734. [Google Scholar]








| Method | Description |
|---|---|
| GC | Gamma correction for image enhancement involves adjusting the brightness and contrast of an image by applying a power-law function to the pixel intensities. By manipulating the gamma parameter, typically greater than 1 to darken or less than 1 to brighten, gamma correction effectively enhances the image’s visual appearance, improving its overall quality and contrast. |
| AGCWD * [22] | Adaptive gamma correction with weighting distribution (AGCWD) leverages gamma correction and probability distribution of luminance pixels to enhance the contrast in images efficiently. AGCWD automatically adjusts histograms to improve dimmed images’ brightness and incorporates temporal information from video frames to reduce computational complexity while enhancing video quality. This method has an parameter. |
| AGCIE [23] | The enhancement works by classifying images based on their statistical information to understand their specific characteristics. Then, an adaptive gamma correction method is applied to adjust parameters tailored to each image class dynamically using the contrast threshold parameter. |
| IAGCWD [24] | Improved adaptive gamma correction enhances contrast in brightness-distorted images using negative images for bright images and gamma correction modulated by truncated cumulative distribution function (CDF) for dimmed ones. The brightness is calculated using the image mean and a threshold parameter. It also effectively addresses deficiencies of the previous adaptive gamma correction (AGC) methods. |
| HS | Histogram stretching is a simple image enhancement technique used to improve the contrast of an image by expanding the range of pixel intensities. It works by mapping the minimum and maximum intensity values in the original image to the desired minimum and maximum values, thereby stretching the histogram and enhancing the overall contrast. |
| HE | Histogram equalization is a technique used to enhance images’ contrast by redistributing pixel intensities. It transforms the image histogram to achieve a more uniform distribution of pixel values, thereby enhancing the overall visual appearance. |
| CLAHE | Contrast limited adaptive histogram equalization (CLAHE) is an extension of histogram equalization that limits amplification by constraining the contrast enhancement in localized regions. It divides the image into smaller tiles and individually applies histogram equalization to each tile, preventing overamplification of noise while improving contrast. This method has clip-limit and grid-size parameters. |
| MMBEBHE [25] | Minimum mean brightness error histogram equalization (MMBEBHE) is introduced as an extension of bihistogram equalization (BBHE), focusing on maximizing brightness preservation. Unlike BBHE, which partitions the input image’s histogram based on its mean before equalization, MMBEBHE employs a threshold level to minimize the absolute mean brightness error (AMBE) between input and output means. |
| BPHEME [26] | Brightness preserving histogram equalization with maximum entropy (BPHEME) is another extension of HE. Unlike HE, which focuses solely on maximizing entropy, BPHEME takes a variational approach to identify a target histogram that maximizes entropy while maintaining a fixed mean brightness. |
| RLBHE [27] | Range-limited bihistogram equalization (RLBHE) is an extension of BBHE. RLBHE begins by dividing the input histogram into two independent subhistograms using a threshold that minimizes intraclass variance, effectively separating objects from the background. Subsequently, RLBHE calculates the range of the equalized image to minimize the absolute mean brightness error between the original and equalized images. |
| JHE [28] | The joint histogram equalization (JHE) method enhances image contrast by incorporating neighborhood information through a two-dimensional joint histogram constructed from the original image and its average. Utilizing a two-dimensional cumulative distribution function, it achieves superior contrast enhancement without requiring a target uniform distribution, outperforming traditional histogram equalization techniques. Notably, JHE offers a block size parameter (set to 3 by default) to calculate box blur or average kernel for the joint histogram. |
| Image | E | EME * | AME * | BIE * | ||
|---|---|---|---|---|---|---|
| 7.202 | 4.868 | 39.89 | 9.892 | 0.289 | 0.114 | |
| 7.202 | 4.868 | 39.89 | 18.12 | 0.345 | 0.045 | |
| 7.202 | 4.868 | 39.89 | 28.63 | 0.315 | 0.027 |
| Dataset/Method | PSTI | TIE | WTB | MSOD (NIR) | MSOD (MIR) | MSOD (FIR) |
|---|---|---|---|---|---|---|
| CG | 0.131225 | 0.114127 | 0.174474 | 0.107295 | 0.070008 | 0.113759 |
| AGCWD 1 | 0.121893 | 0.056851 | 0.161423 | 0.091712 | 0.048232 | 0.085563 |
| AGCIE 1 | 0.132142 | 0.307129 | 0.173178 | 0.134844 | 0.215065 | 0.215004 |
| IAGCWD 2 | 0.136830 | 0.167381 | 0.197043 | 0.128173 | 0.141313 | 0.155291 |
| HS | 0.122064 | 0.144739 | 0.163316 | 0.075483 | 0.042351 | 0.078151 |
| HE | 0.140560 | 0.296211 | 0.258534 | 0.173492 | 0.256054 | 0.225867 |
| CLAHE | 0.041823 | 0.083092 | 0.050132 | 0.050319 | 0.062201 | 0.037420 |
| MMBEBHE 1 | 0.116236 | 0.138361 | 0.194525 | 0.102352 | 0.061688 | 0.107872 |
| BPHEME 1 | 0.105918 | 0.077046 | 0.199875 | 0.111392 | 0.109252 | 0.122866 |
| RLBHE 1 | 0.130715 | 0.127087 | 0.211147 | 0.114962 | 0.123220 | 0.127129 |
| JHE 3 | 0.141045 | 0.276221 | 0.232145 | 0.159640 | 0.222642 | 0.183019 |
| GC | 7.107045 | 4.167276 | 6.911269 | 6.197074 | 5.156433 | 5.961607 |
| AGCWD | 7.055865 | 4.024257 | 6.911652 | 6.159424 | 4.915914 | 5.912801 |
| AGCIE | 7.116036 | 4.077704 | 6.837698 | 6.145100 | 5.141924 | 5.917889 |
| IAGCWD | 7.415705 | 4.140406 | 6.917079 | 6.153405 | 5.137077 | 5.932568 |
| HS | 7.056457 | 4.183180 | 6.924741 | 6.213012 | 5.164501 | 5.977861 |
| HE | 7.976455 | 4.088996 | 6.798583 | 5.988436 | 5.078228 | 5.843730 |
| CLAHE | 7.931252 | 6.585075 | 7.753867 | 7.264123 | 7.715504 | 7.928340 |
| MMBEBHE | 7.718064 | 4.120297 | 6.766051 | 6.067690 | 5.079954 | 5.822866 |
| BPHEME | 7.870770 | 4.096193 | 6.793633 | 6.027675 | 5.112614 | 5.834179 |
| RLBHE | 7.656321 | 4.069276 | 6.791951 | 5.989375 | 5.062980 | 5.814365 |
| JHE | 7.987631 | 4.829197 | 7.668669 | 6.855445 | 6.045323 | 7.701134 |
| GC | 0.277226 | 0.165962 | 0.206059 | 0.257479 | 0.167880 | 0.249846 |
| AGCWD | 0.268677 | 0.193579 | 0.201233 | 0.265715 | 0.194074 | 0.271587 |
| AGCIE | 0.278811 | 0.204682 | 0.197064 | 0.264849 | 0.252005 | 0.254256 |
| IAGCWD | 0.282340 | 0.223702 | 0.231461 | 0.270470 | 0.232619 | 0.260823 |
| HS | 0.268791 | 0.194817 | 0.205581 | 0.267110 | 0.250820 | 0.288561 |
| HE | 0.224824 | 0.200093 | 0.260688 | 0.240598 | 0.245118 | 0.262848 |
| CLAHE | 0.181485 | 0.259575 | 0.228548 | 0.218206 | 0.262472 | 0.156850 |
| MMBEBHE | 0.267313 | 0.185009 | 0.240230 | 0.237901 | 0.239084 | 0.262351 |
| BPHEME | 0.229850 | 0.236151 | 0.247598 | 0.246017 | 0.261423 | 0.257686 |
| RLBHE | 0.299803 | 0.182122 | 0.252002 | 0.265422 | 0.255065 | 0.261913 |
| JHE | 0.224310 | 0.199160 | 0.258897 | 0.240835 | 0.243770 | 0.264548 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayunts, H.; Grigoryan, A.; Agaian, S. Novel Entropy for Enhanced Thermal Imaging and Uncertainty Quantification. Entropy 2024, 26, 374. https://doi.org/10.3390/e26050374
Ayunts H, Grigoryan A, Agaian S. Novel Entropy for Enhanced Thermal Imaging and Uncertainty Quantification. Entropy. 2024; 26(5):374. https://doi.org/10.3390/e26050374
Chicago/Turabian StyleAyunts, Hrach, Artyom Grigoryan, and Sos Agaian. 2024. "Novel Entropy for Enhanced Thermal Imaging and Uncertainty Quantification" Entropy 26, no. 5: 374. https://doi.org/10.3390/e26050374
APA StyleAyunts, H., Grigoryan, A., & Agaian, S. (2024). Novel Entropy for Enhanced Thermal Imaging and Uncertainty Quantification. Entropy, 26(5), 374. https://doi.org/10.3390/e26050374








