Identifying Ordinal Similarities at Different Temporal Scales
Abstract
1. Introduction
2. Permutation Jensen–Shannon Distance
3. An Illustrative Numerical Example
4. Practical Application: Semiconductor Lasers Subject to Optical Feedback
4.1. Theoretical Model
4.2. Description of Experimental Setup
4.3. Numerical Results
4.4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PJSD | Permutation Jensen–Shannon distance |
| JSD | Jensen–Shannon divergence |
| BP | Bandt and Pompe |
| OPD | Ordinal probability distribution |
| MG | Mackey–Glass |
| LK | Lang–Kobayashi |
| RO | Relaxation oscillation |
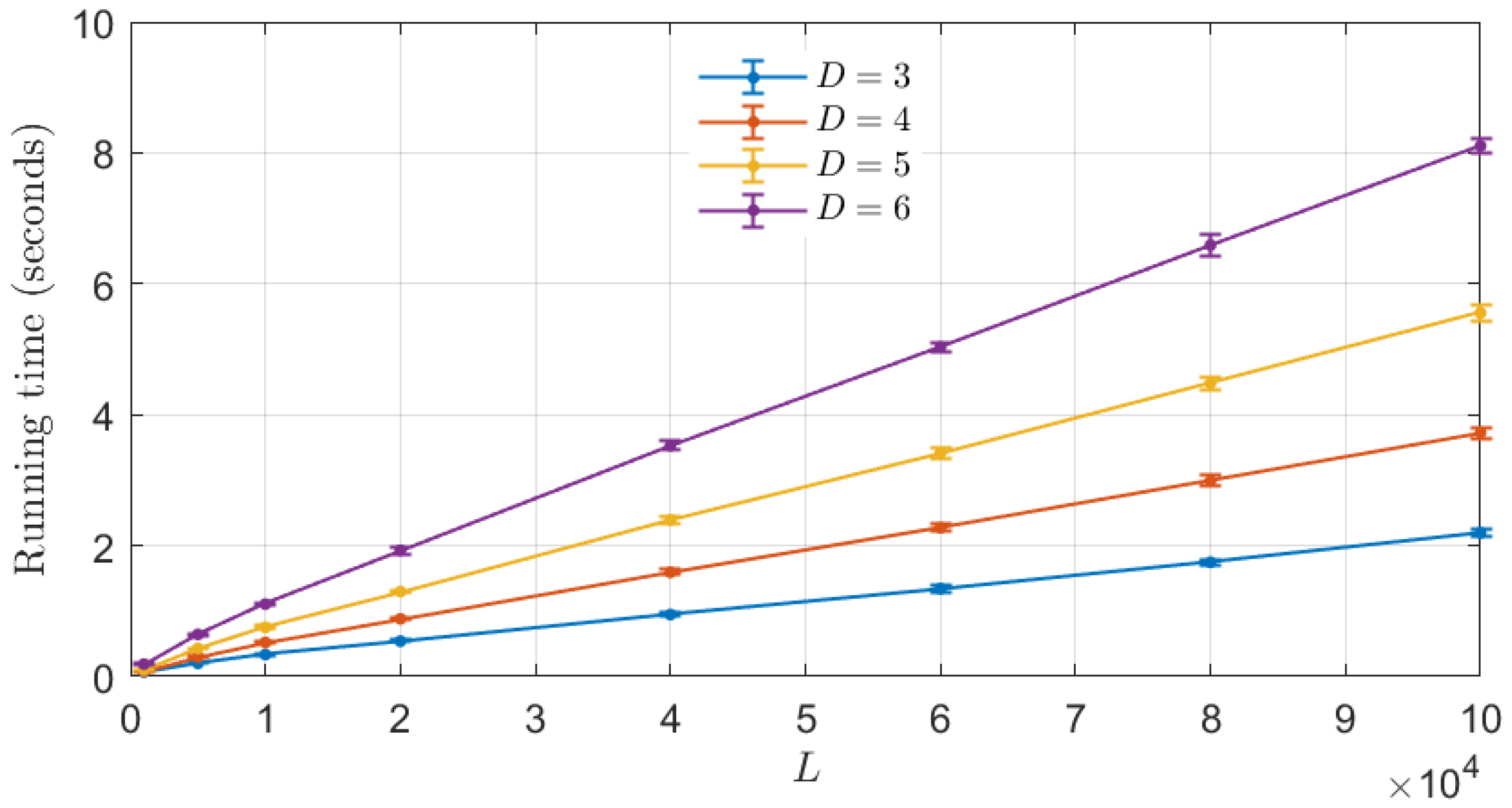
Appendix A. Computational Time
References
- Serrà, J.; Arcos, J.L. An empirical evaluation of similarity measures for time series classification. Knowl.-Based Syst. 2014, 67, 305–314. [Google Scholar] [CrossRef]
- Górecki, T.; Łuczak, M.; Piasecki, P. An exhaustive comparison of distance measures in the classification of time series with 1NN method. J. Comput. Sci. 2024, 76, 102235. [Google Scholar] [CrossRef]
- Jiang, Y.; Qi, Y.; Wang, W.K.; Bent, B.; Avram, R.; Olgin, J.; Dunn, J. EventDTW: An improved dynamic time warping algorithm for aligning biomedical signals of nonuniform sampling frequencies. Sensors 2020, 20, 2700. [Google Scholar] [CrossRef]
- Li, W.; He, R.; Liang, B.; Yang, F.; Han, S. Similarity measure of time series with different sampling frequencies based on context density consistency and dynamic time warping. IEEE Signal Process. Lett. 2023, 30, 1417–1421. [Google Scholar] [CrossRef]
- Zhang, B.; An, B. Clustering time series based on dependence structure. PLoS ONE 2018, 13, e0206753. [Google Scholar] [CrossRef]
- Doan, T.; Phan, T.; Nguyen, P.; Than, K.; Visani, M.; Takasu, A. Partial ordered Wasserstein distance for sequential data. Neurocomputing 2024, 595, 127908. [Google Scholar] [CrossRef]
- Zunino, L.; Olivares, F.; Ribeiro, H.V.; Rosso, O.A. Permutation Jensen-Shannon distance: A versatile and fast symbolic tool for complex time-series analysis. Phys. Rev. E 2022, 105, 045310. [Google Scholar] [CrossRef]
- Zunino, L. Revisiting the characterization of resting brain dynamics with the permutation Jensen–Shannon distance. Entropy 2024, 26, 432. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Parlitz, U.; Suetani, H.; Luther, S. Identification of equivalent dynamics using ordinal pattern distributions. Eur. Phys. J. Spec. Top. 2013, 222, 553–568. [Google Scholar] [CrossRef]
- Cánovas, J.S.; Guillamón, A.; Ruiz-Abellón, M.C. Using permutations for hierarchical clustering of time series. Entropy 2019, 21, 306. [Google Scholar] [CrossRef]
- Endres, D.; Schindelin, J. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef]
- Grosse, I.; Bernaola-Galván, P.; Carpena, P.; Román-Roldán, R.; Oliver, J.; Stanley, H.E. Analysis of symbolic sequences using the Jensen-Shannon divergence. Phys. Rev. E 2002, 65, 041905. [Google Scholar] [CrossRef] [PubMed]
- Daw, C.S.; Finney, C.E.A.; Tracy, E.R. A review of symbolic analysis of experimental data. Rev. Sci. Instrum. 2003, 74, 915–930. [Google Scholar] [CrossRef]
- Amigó, J.M.; Keller, K.; Unakafova, V.A. Ordinal symbolic analysis and its application to biomedical recordings. Phil. Trans. R. Soc. A 2015, 373, 20140091. [Google Scholar] [CrossRef]
- Amigó, J.M.; Keller, K.; Kurths, J. Recent progress in symbolic dynamics and permutation complexity—Ten years of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 241–247. [Google Scholar] [CrossRef]
- Zanin, M.; Olivares, F. Ordinal patterns-based methodologies for distinguishing chaos from noise in discrete time series. Commun. Phys. 2021, 4, 190. [Google Scholar] [CrossRef]
- Leyva, I.; Martínez, J.H.; Masoller, C.; Rosso, O.A.; Zanin, M. 20 years of ordinal patterns: Perspectives and challenges. Europhys. Lett. 2022, 138, 31001. [Google Scholar] [CrossRef]
- Amigó, J.M.; Rosso, O.A. Ordinal methods: Concepts, applications, new developments, and challenges—In memory of Karsten Keller (1961–2022). Chaos 2023, 33, 080401. [Google Scholar] [CrossRef]
- Kottlarz, I.; Parlitz, U. Ordinal pattern-based complexity analysis of high-dimensional chaotic time series. Chaos 2023, 33, 053105. [Google Scholar] [CrossRef]
- Olivares, F.; Zunino, L. Multiscale dynamics under the lens of permutation entropy. Phys. A Stat. Mech. Its Appl. 2020, 559, 125081. [Google Scholar] [CrossRef]
- Zunino, L.; Soriano, M.C.; Rosso, O.A. Distinguishing chaotic and stochastic dynamics from time series by using a multiscale symbolic approach. Phys. Rev. E 2012, 86, 046210. [Google Scholar] [CrossRef]
- Parlitz, U.; Berg, S.; Luther, S.; Schirdewan, A.; Kurths, J.; Wessel, N. Classifying cardiac biosignals using ordinal pattern statistics and symbolic dynamics. Comput. Biol. Med. 2012, 42, 319–327. [Google Scholar] [CrossRef]
- Bandt, C. Small order patterns in big time series: A practical guide. Entropy 2019, 21, 613. [Google Scholar] [CrossRef]
- Soriano, M.C.; Zunino, L.; Rosso, O.A.; Fischer, I.; Mirasso, C.R. Time scales of a chaotic semiconductor laser with optical feedback under the lens of a permutation information analysis. IEEE J. Quantum Electron. 2011, 47, 252–261. [Google Scholar] [CrossRef]
- Soriano, M.C.; Zunino, L. Time-delay identification using multiscale ordinal quantifiers. Entropy 2021, 23, 969. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.A.; Martin, M.T.; Plastino, A.; Fuentes, M.A. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102. [Google Scholar] [CrossRef]
- Zhao, X.; Shang, P.; Huang, J. Permutation complexity and dependence measures of time series. Europhys. Lett. 2013, 102, 40005. [Google Scholar] [CrossRef]
- Olivares, F.; Plastino, A.; Rosso, O.A. Contrasting chaos with noise via local versus global information quantifiers. Phys. Lett. A 2012, 376, 1577–1583. [Google Scholar] [CrossRef]
- Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control systems. Science 1977, 197, 287–289. [Google Scholar] [CrossRef] [PubMed]
- Farmer, J.D. Chaotic attractors of an infinite-dimensional dynamical system. Phys. D Nonlinear Phenom. 1982, 4, 366–393. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Phys. D Nonlinear Phenom. 1983, 9, 189–208. [Google Scholar] [CrossRef]
- van Tartwijk, G.H.M.; Lenstra, D. Semiconductor lasers with optical injection and feedback. Quantum Semiclassical Opt. J. Eur. Opt. Soc. Part B 1995, 7, 87. [Google Scholar] [CrossRef]
- Ohtsubo, J. Semiconductor Lasers: Stability, Instability and Chaos; Springer: Berlin/Heidelberg, Germany, 2017; Volume 111. [Google Scholar]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Ahlers, V.; Parlitz, U.; Lauterborn, W. Hyperchaotic dynamics and synchronization of external-cavity semiconductor lasers. Phys. Rev. E 1998, 58, 7208–7213. [Google Scholar] [CrossRef]
- Porte, X.; Soriano, M.C.; Fischer, I. Similarity properties in the dynamics of delayed-feedback semiconductor lasers. Phys. Rev. A 2014, 89, 023822. [Google Scholar] [CrossRef]
- Vicente, R.; Mirasso, C.R.; Fischer, I. Simultaneous bidirectional message transmission in a chaos-based communication scheme. Opt. Lett. 2007, 32, 403–405. [Google Scholar] [CrossRef]
- Uchida, A. Optical Communication with Chaotic Lasers: Applications of Nonlinear Dynamics and Synchronization; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Porte, X.; Soriano, M.C.; Brunner, D.; Fischer, I. Bidirectional private key exchange using delay-coupled semiconductor lasers. Opt. Lett. 2016, 41, 2871–2874. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zunino, L.; Porte, X.; Soriano, M.C. Identifying Ordinal Similarities at Different Temporal Scales. Entropy 2024, 26, 1016. https://doi.org/10.3390/e26121016
Zunino L, Porte X, Soriano MC. Identifying Ordinal Similarities at Different Temporal Scales. Entropy. 2024; 26(12):1016. https://doi.org/10.3390/e26121016
Chicago/Turabian StyleZunino, Luciano, Xavier Porte, and Miguel C. Soriano. 2024. "Identifying Ordinal Similarities at Different Temporal Scales" Entropy 26, no. 12: 1016. https://doi.org/10.3390/e26121016
APA StyleZunino, L., Porte, X., & Soriano, M. C. (2024). Identifying Ordinal Similarities at Different Temporal Scales. Entropy, 26(12), 1016. https://doi.org/10.3390/e26121016







