Control Power in Continuous Variable Controlled Quantum Teleportation
Abstract
1. Introduction
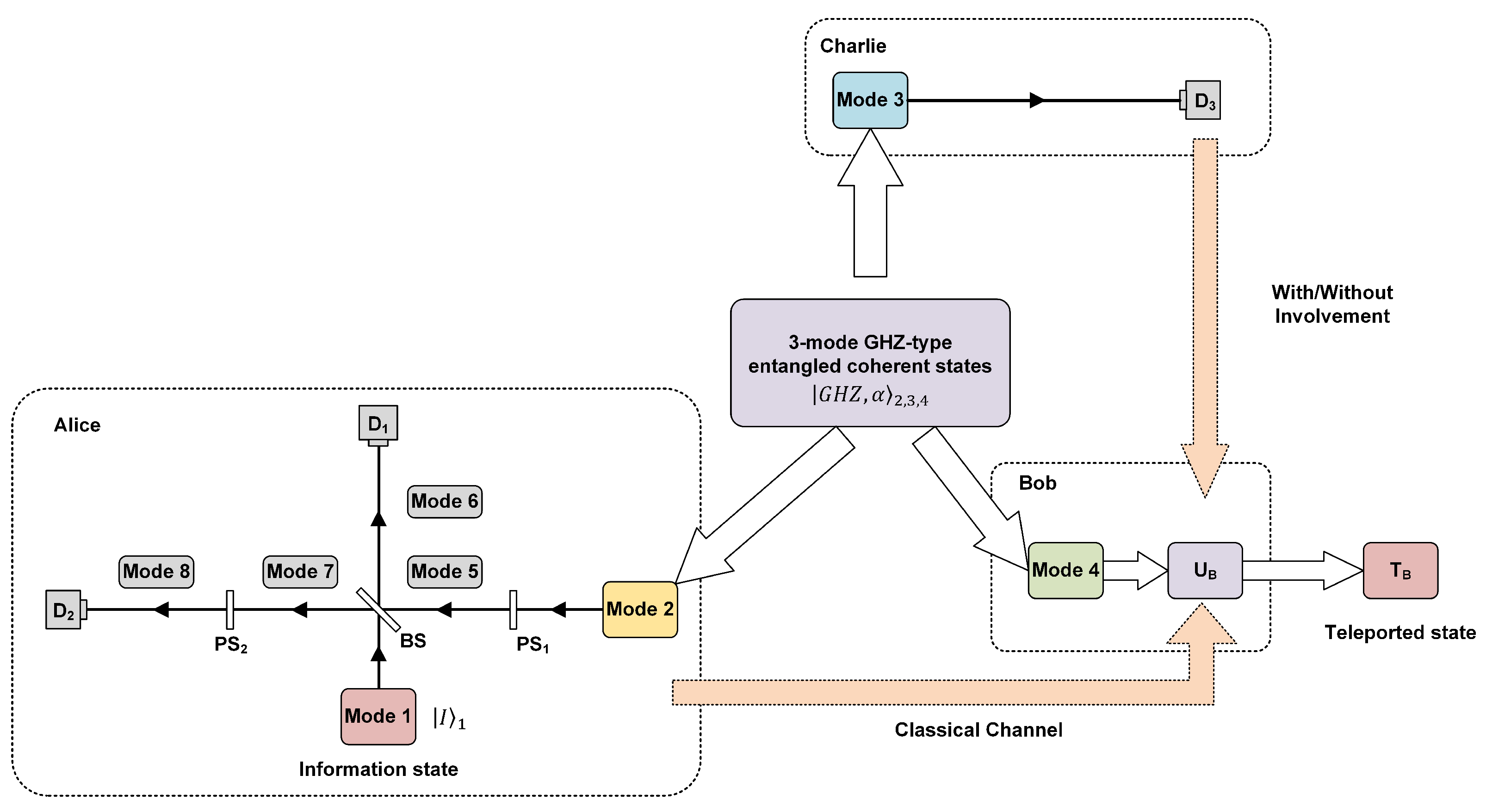
2. Continuous Variable Quantum Controlled Teleportation via GHZ-Type Entangled Coherent State Channels
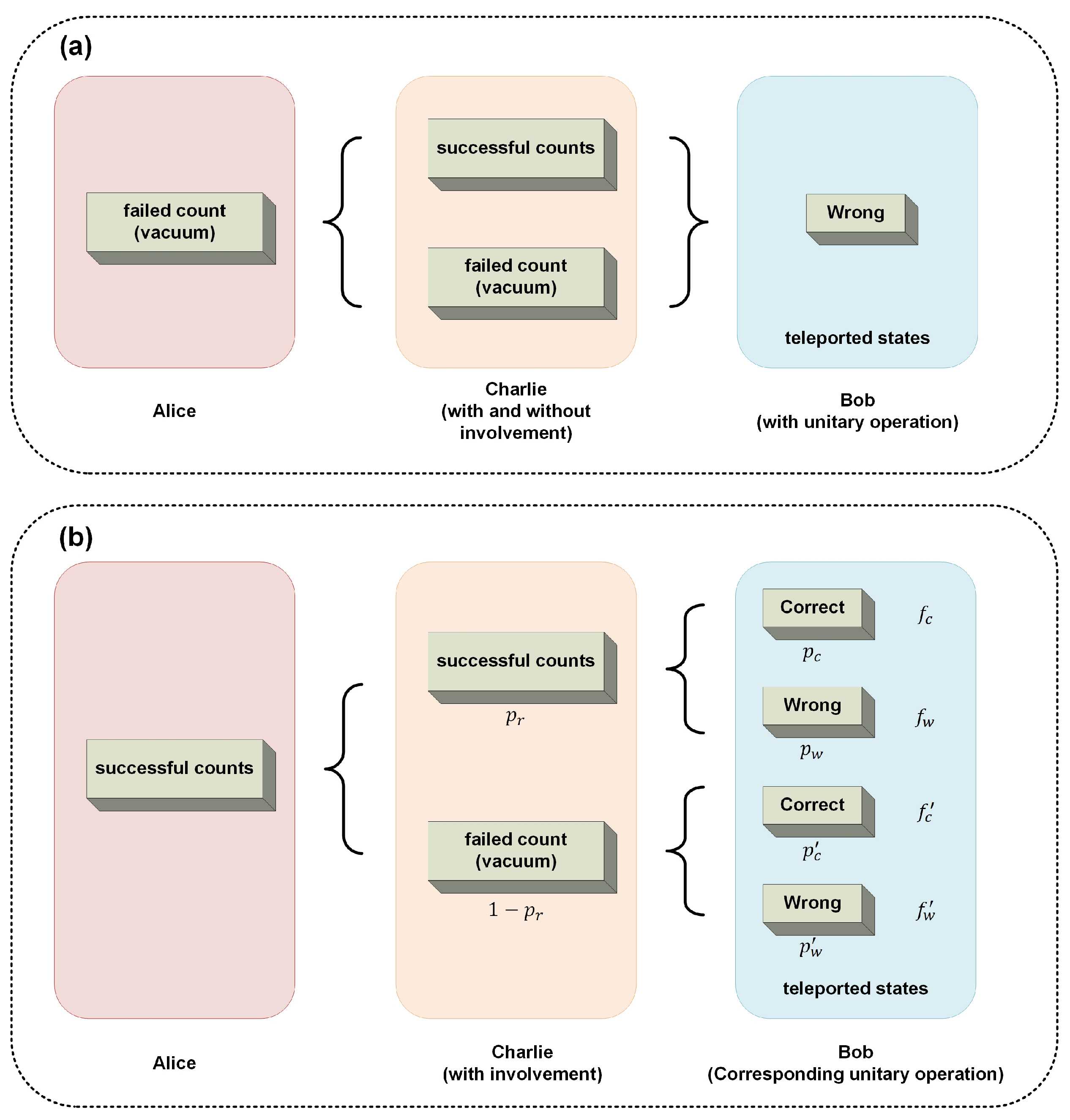
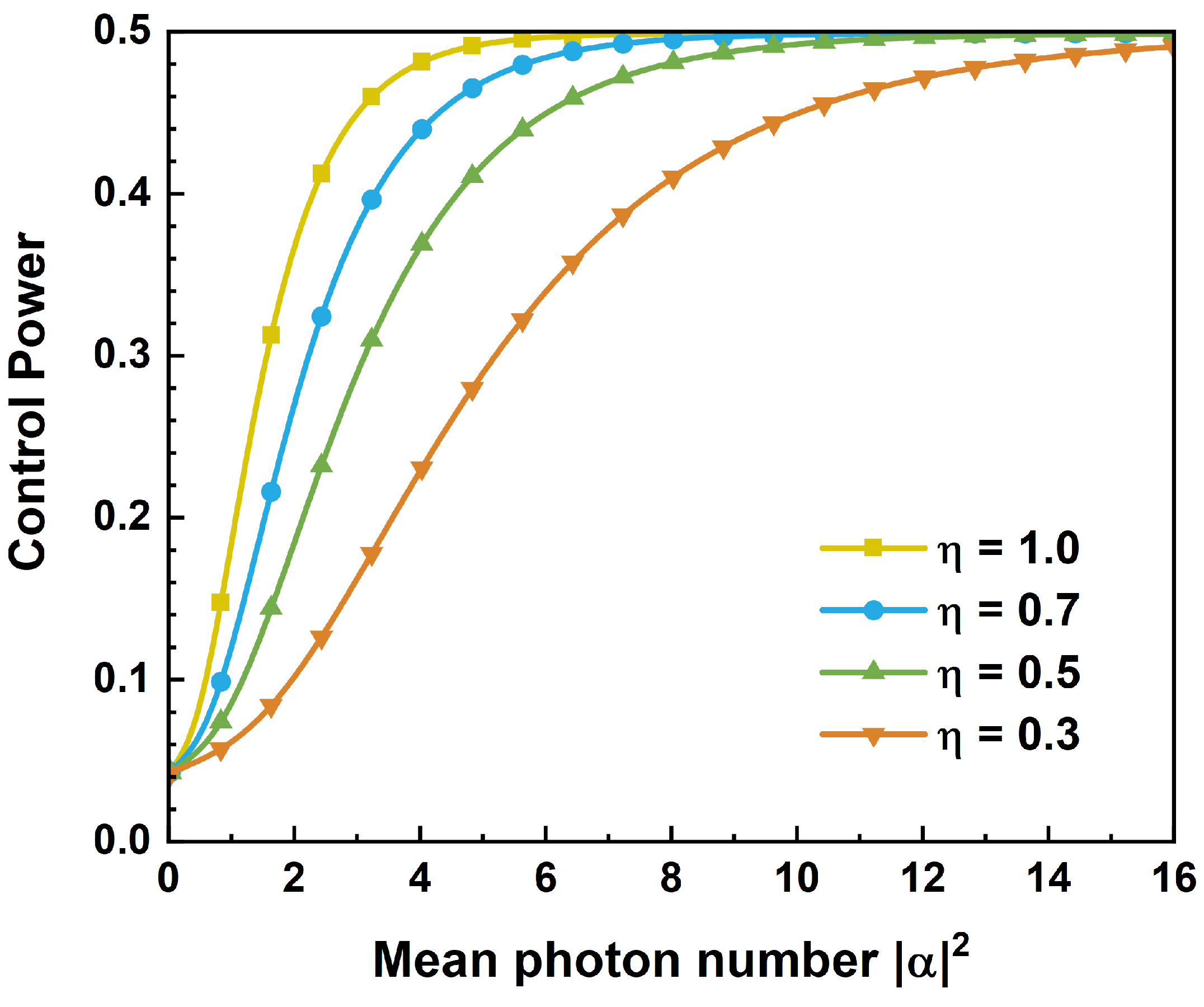
3. Control Power of the Supervisor in Continuous Variable Controlled Quantum Teleportation
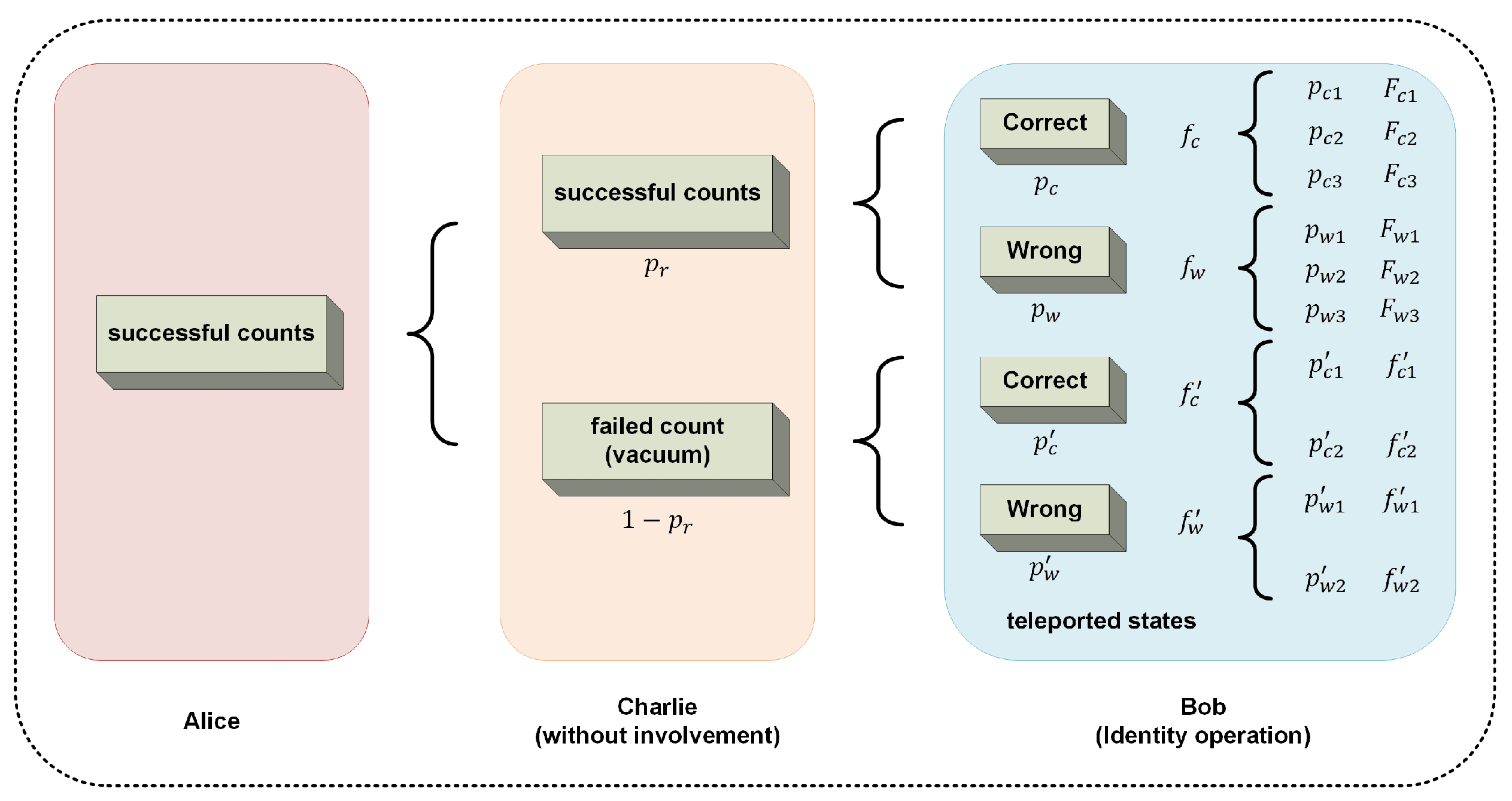
4. Analysis of Robustness
5. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Diverse Possible Results of PC Measurement
| m | Alice’s PC Results | Charlie’s PC Result | Probability | Unitary Operation | Bob’s State | Teleported State | Fidelity | |
|---|---|---|---|---|---|---|---|---|
| (6) | (8) | (3) | (4) | |||||
| 1 | 0 | 0 | 0 | |||||
| 2 | 0 | 0 | NZE | |||||
| 3 | 0 | 0 | ODD | I | ||||
| 4 | NZE | 0 | 0 | |||||
| 5 | NZE | 0 | NZE | |||||
| 6 | NZE | 0 | ODD | I | 1 | |||
| 7 | 0 | NZE | 0 | |||||
| 8 | 0 | NZE | NZE | |||||
| 9 | 0 | NZE | ODD | 1 | ||||
| 10 | ODD | 0 | 0 | I | 1 | |||
| 11 | ODD | 0 | NZE | I | 1 | |||
| 12 | ODD | 0 | ODD | |||||
| 13 | 0 | ODD | 0 | 1 | ||||
| 14 | 0 | ODD | NZE | 1 | ||||
| 15 | 0 | ODD | ODD | |||||
References
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.M.; Guo, Y.; Liu, B.H.; Li, C.F.; Guo, G.C. Progress in quantum teleportation. Nat. Rev. Phys. 2023, 5, 339–353. [Google Scholar] [CrossRef]
- Lv, M.Y.; Hu, X.M.; Gong, N.F.; Wang, T.J.; Guo, Y.; Liu, B.H.; Huang, Y.F.; Li, C.F.; Guo, G.C. Demonstration of controlled high-dimensional quantum teleportation. Sci. China Phys. Mech. Astron. 2024, 67, 230311. [Google Scholar] [CrossRef]
- Pan, J.-W. Quantum information technology: Current status and prospects. Acta Phys. Sin. 2024, 73, 010301. [Google Scholar] [CrossRef]
- Lou, Y.; Lv, Y.; Wang, J.; Liu, S.; Jing, J. Orbital angular momentum multiplexed deterministic all-optical quantum erasure-correcting code. Phys. Rev. Lett. 2024, 132, 040601. [Google Scholar] [CrossRef]
- Vaidman, L. Teleportation of quantum states. Phys. Rev. A 1994, 49, 1473. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513. [Google Scholar] [CrossRef]
- Wang, X.B.; Hiroshima, T.; Tomita, A.; Hayashi, M. Quantum information with Gaussian states. Phys. Rep. 2007, 448, 1–111. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Liu, S.; Lv, Y.; Wang, X.; Wang, J.; Lou, Y.; Jing, J. Deterministic all-optical quantum teleportation of four degrees of freedom. Phys. Rev. Lett. 2024, 132, 100801. [Google Scholar] [CrossRef]
- Deng, X.; Xiang, Y.; Tian, C.; Adesso, G.; He, Q.; Gong, Q.; Su, X.; Xie, C.; Peng, K. Demonstration of monogamy relations for Einstein-Podolsky-Rosen steering in Gaussian cluster states. Phys. Rev. Lett. 2017, 118, 230501. [Google Scholar] [CrossRef] [PubMed]
- Cavaillès, A.; Le Jeannic, H.; Raskop, J.; Guccione, G.; Markham, D.; Diamanti, E.; Shaw, M.D.; Verma, V.B.; Nam, S.W.; Laurat, J. Demonstration of Einstein-Podolsky-Rosen steering using hybrid continuous-and discrete-variable entanglement of light. Phys. Rev. Lett. 2018, 121, 170403. [Google Scholar] [CrossRef] [PubMed]
- Andersen, U.L.; Neergaard-Nielsen, J.S.; Van Loock, P.; Furusawa, A. Hybrid discrete-and continuous-variable quantum information. Nat. Phys. 2015, 11, 713–719. [Google Scholar] [CrossRef]
- Wen, J.; Novikova, I.; Qian, C.; Zhang, C.; Du, S. Hybrid entanglement between optical discrete polarizations and continuous quadrature variables. Photonics 2021, 8, 552. [Google Scholar] [CrossRef]
- Djordjevic, I.B. Hybrid CV-DV quantum communications and quantum networks. IEEE Access 2022, 10, 23284–23292. [Google Scholar] [CrossRef]
- Bose, S.; Jeong, H. Quantum teleportation of hybrid qubits and single-photon qubits using Gaussian resources. Phys. Rev. A 2022, 105, 032434. [Google Scholar] [CrossRef]
- Xu, J.; Liu, T. Implementing a cross-Kerr interaction between microwave and optical cavities and its application in generating a hybrid continuous-variable–discrete-variable entangled state. Phys. Rev. A 2024, 109, 033705. [Google Scholar] [CrossRef]
- Singh, P.; Chakrabarty, I. Controlled state reconstruction and quantum secret sharing. Phys. Rev. A 2024, 109, 032406. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, Q.; Wang, X.; Lou, Y.; Liu, S.; Jing, J. Deterministic all-optical quantum state sharing. Adv. Photonics 2023, 5, 026006. [Google Scholar] [CrossRef]
- Karlsson, A.; Bourennane, M. Quantum teleportation using three-particle entanglement. Phys. Rev. A 1998, 58, 4394. [Google Scholar] [CrossRef]
- Deng, F.G.; Li, C.Y.; Li, Y.S.; Zhou, H.Y.; Wang, Y. Symmetric multiparty-controlled teleportation of an arbitrary two-particle entanglement. Phys. Rev. A 2005, 72, 022338. [Google Scholar] [CrossRef]
- Wang, T.J.; Yang, G.Q.; Wang, C. Control power of high-dimensional controlled teleportation. Phys. Rev. A 2020, 101, 012323. [Google Scholar] [CrossRef]
- Gangopadhyay, S.; Wang, T.; Mashatan, A.; Ghose, S. Controlled quantum teleportation in the presence of an adversary. Phys. Rev. A 2022, 106, 052433. [Google Scholar] [CrossRef]
- Moreno, M.; Brito, S.; Nery, R.V.; Chaves, R. Device-independent secret sharing and a stronger form of Bell nonlocality. Phys. Rev. A 2020, 101, 052339. [Google Scholar] [CrossRef]
- Mao, Y.L.; Li, Z.D.; Yu, S.; Fan, J. Test of genuine multipartite nonlocality. Phys. Rev. Lett. 2022, 129, 150401. [Google Scholar] [CrossRef]
- Bancal, J.D.; Barrett, J.; Gisin, N.; Pironio, S. Definitions of multipartite nonlocality. Phys. Rev. A 2013, 88, 014102. [Google Scholar] [CrossRef]
- Yonezawa, H.; Aoki, T.; Furusawa, A. Demonstration of a quantum teleportation network for continuous variables. Nature 2004, 431, 430–433. [Google Scholar] [CrossRef]
- Barasiński, A.; Černoch, A.; Lemr, K. Demonstration of controlled quantum teleportation for discrete variables on linear optical devices. Phys. Rev. Lett. 2019, 122, 170501. [Google Scholar] [CrossRef]
- Gong, N.F.; Wang, T.J.; Ghose, S. Control power of a high-dimensional controlled nonlocal quantum computation. Phys. Rev. A 2021, 103, 052601. [Google Scholar] [CrossRef]
- Barasiński, A.; Svozilík, J. Controlled teleportation of qubit states: Relation between teleportation faithfulness, controller’s authority, and tripartite entanglement. Phys. Rev. A 2019, 99, 012306. [Google Scholar] [CrossRef]
- Jeong, K.; Kim, J.; Lee, S. Minimal control power of the controlled teleportation. Phys. Rev. A 2016, 93, 032328. [Google Scholar] [CrossRef]
- van Enk, S.J.; Hirota, O. Entangled coherent states: Teleportation and decoherence. Phys. Rev. A 2001, 64, 022313. [Google Scholar] [CrossRef]
- Wang, X. Quantum teleportation of entangled coherent states. Phys. Rev. A 2001, 64, 022302. [Google Scholar] [CrossRef]
- An, N.B. Teleportation of coherent-state superpositions within a network. Phys. Rev. A 2003, 68, 022321. [Google Scholar] [CrossRef]
- Prakash, H.; Chandra, N.; Prakash, R.; Shivani. Improving the teleportation of entangled coherent states. Phys. Rev. A 2007, 75, 044305. [Google Scholar] [CrossRef]
- Liu, J.C.; Li, Y.H.; Nie, Y.Y. Controlled teleportation of an ECS by using a four-mode CTECS. Int. J. Theor. Phys. 2011, 50, 1852–1857. [Google Scholar] [CrossRef]
- Prakash, R.; Pandey, R.K.; Prakash, H. Controlled entanglement diversion using GHZ type entangled coherent state. Int. J. Theor. Phys. 2019, 58, 1227–1236. [Google Scholar] [CrossRef]
- Pandey, R.K.; Yadav, P.S.; Prakash, R.; Prakash, H. Controlled bidirectional quantum teleportation of superposed coherent state using five-mode cluster-type entangled coherent state as a resource. Int. J. Theor. Phys. 2022, 61, 104. [Google Scholar] [CrossRef]
- Li, B.H.; Xie, Y.M.; Li, Z.; Weng, C.X.; Li, C.L.; Yin, H.L.; Chen, Z.B. Long-distance twin-field quantum key distribution with entangled sources. Opt. Lett. 2021, 46, 5529–5532. [Google Scholar] [CrossRef]
- Yin, H.L.; Chen, Z.B. Coherent-state-based twin-field quantum key distribution. Sci. Rep. 2019, 9, 14918. [Google Scholar]
- Pandey, R.K.; Prakash, R.; Prakash, H. Controlled quantum teleportation of superposed coherent state using GHZ entangled coherent state. Int. J. Theor. Phys. 2019, 58, 3342–3351. [Google Scholar] [CrossRef]
- Dodonov, V.; Malkin, I.; Man’Ko, V. Even and odd coherent states and excitations of a singular oscillator. Physica 1974, 72, 597–615. [Google Scholar] [CrossRef]
- Lund, A.P.; Ralph, T.C.; Haselgrove, H.L. Fault-tolerant linear optical quantum computing with small-amplitude coherent states. Phys. Rev. Lett. 2008, 100, 030503. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.; An, N.B. Greenberger-Horne-Zeilinger–type and W-type entangled coherent states: Generation and Bell-type inequality tests without photon counting. Phys. Rev. A 2006, 74, 022104. [Google Scholar] [CrossRef]
- Deng, X.; Tian, C.; Su, X.; Xie, C. Avoiding disentanglement of multipartite entangled optical beams with a correlated noisy channel. Sci. Rep. 2017, 7, 44475. [Google Scholar] [CrossRef]
- Van Enk, S. Decoherence of multidimensional entangled coherent states. Phys. Rev. A 2005, 72, 022308. [Google Scholar] [CrossRef]
- Prakash, H.; Chandra, N.; Prakash, R.; Shivani. Effect of decoherence on fidelity in teleportation using entangled coherent states. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 1613. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Cai, D.; Gong, N.; Li, Y.; Qian, L.; Zhang, R.; Huang, Z.; Wang, T. Control Power in Continuous Variable Controlled Quantum Teleportation. Entropy 2024, 26, 1017. https://doi.org/10.3390/e26121017
Tian Y, Cai D, Gong N, Li Y, Qian L, Zhang R, Huang Z, Wang T. Control Power in Continuous Variable Controlled Quantum Teleportation. Entropy. 2024; 26(12):1017. https://doi.org/10.3390/e26121017
Chicago/Turabian StyleTian, Yuehan, Dunbo Cai, Nengfei Gong, Yining Li, Ling Qian, Runqing Zhang, Zhiguo Huang, and Tiejun Wang. 2024. "Control Power in Continuous Variable Controlled Quantum Teleportation" Entropy 26, no. 12: 1017. https://doi.org/10.3390/e26121017
APA StyleTian, Y., Cai, D., Gong, N., Li, Y., Qian, L., Zhang, R., Huang, Z., & Wang, T. (2024). Control Power in Continuous Variable Controlled Quantum Teleportation. Entropy, 26(12), 1017. https://doi.org/10.3390/e26121017





