Quantum-Like Approaches Unveil the Intrinsic Limits of Predictability in Compartmental Models
Abstract
1. Introduction
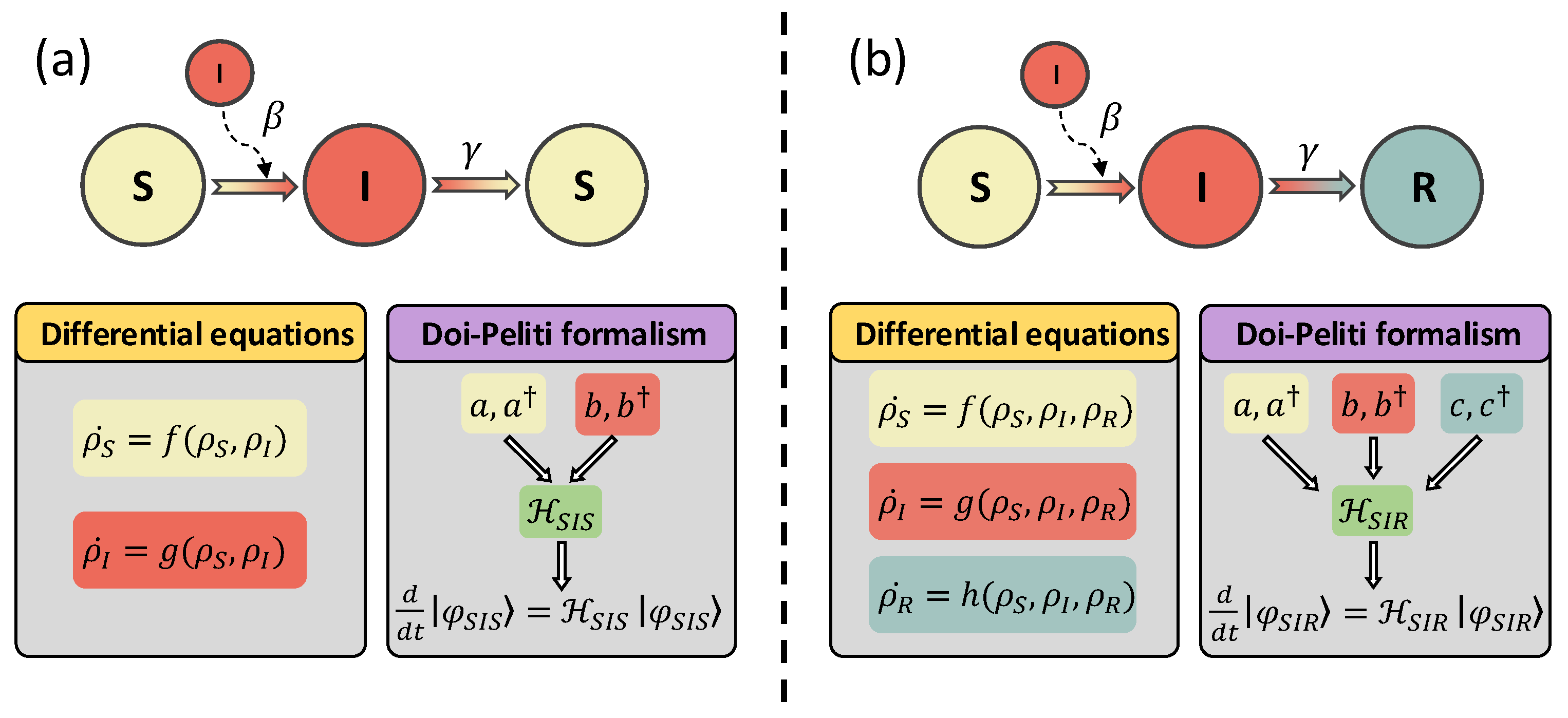
2. Doi–Peliti Approach to Compartmental Models
2.1. Deterministic Equations for the SIS and SIR Models
2.2. The Doi–Peliti Master Equation
2.3. The Doi–Peliti Approach to the SIS Model
2.4. The Doi–Peliti Approach to the SIR Model
3. Results
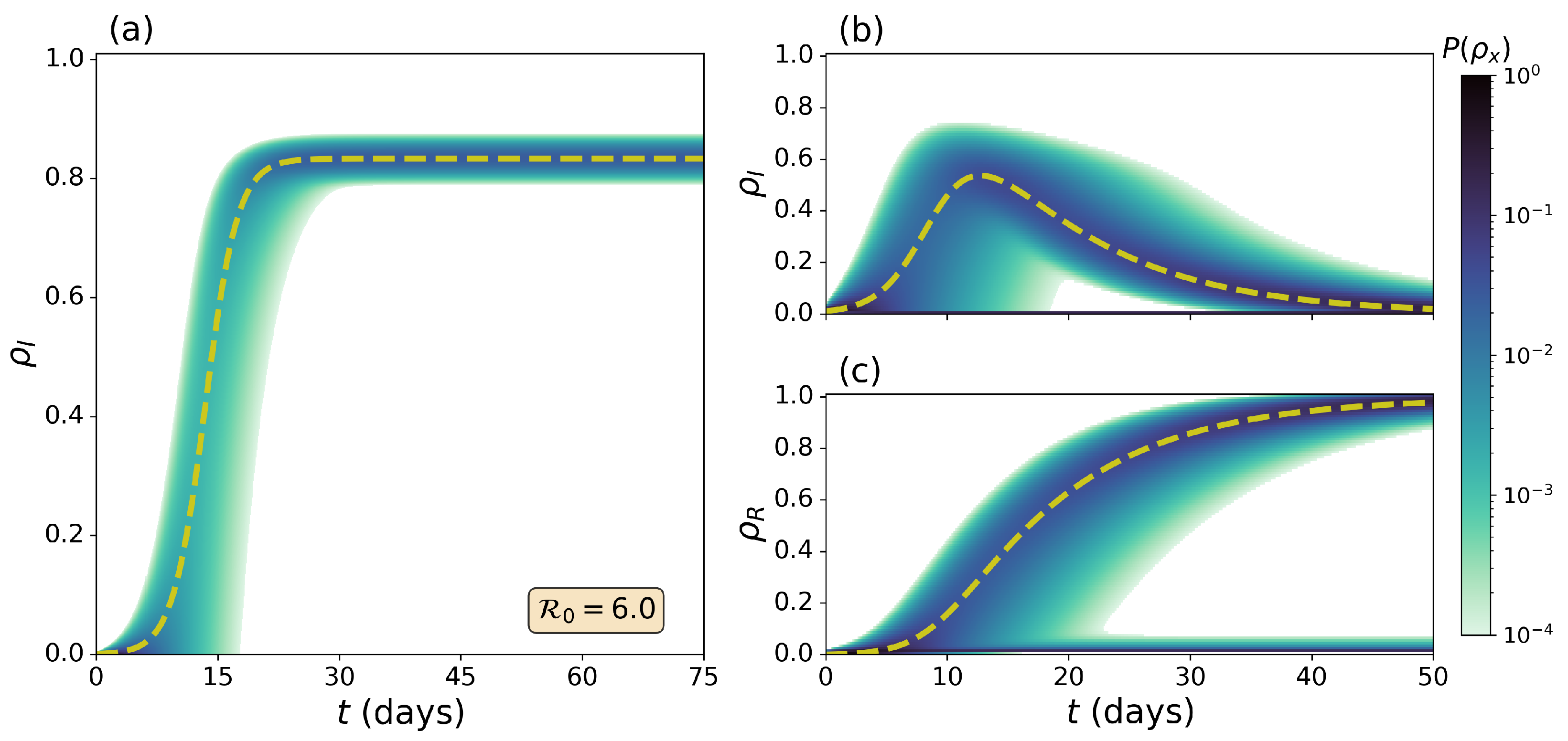
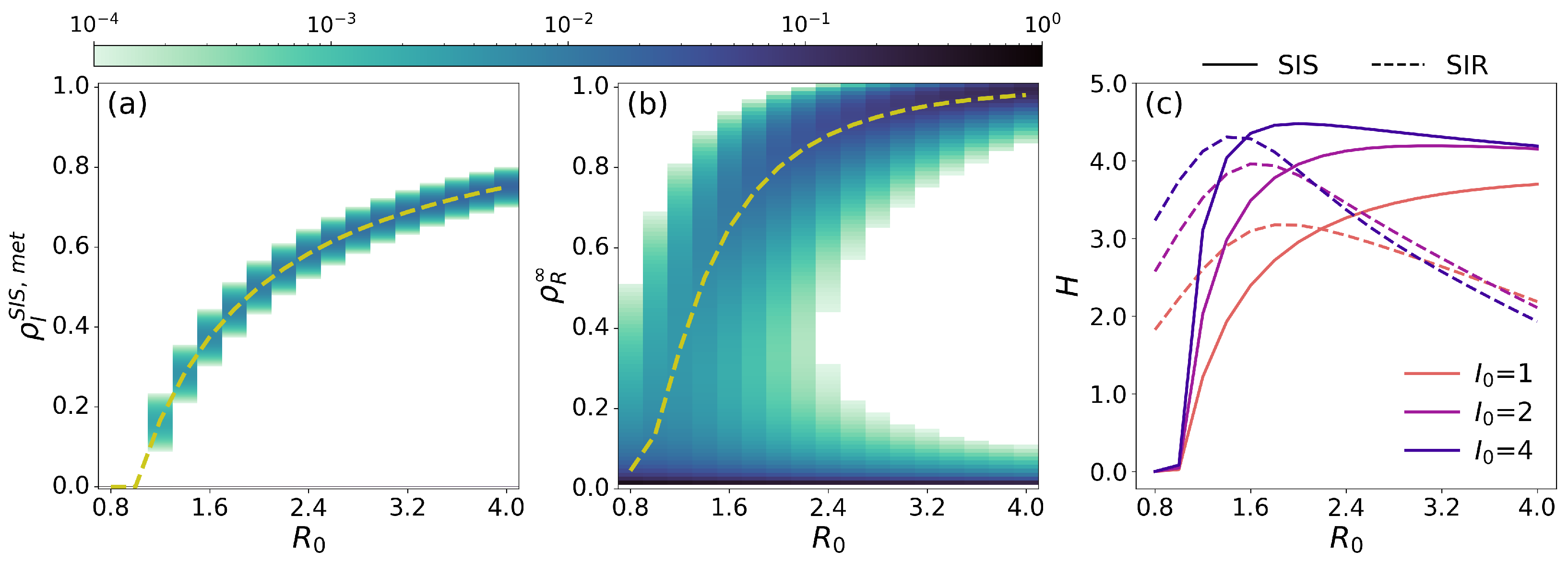
3.1. Dynamics of the Doi–Peliti Master Equation
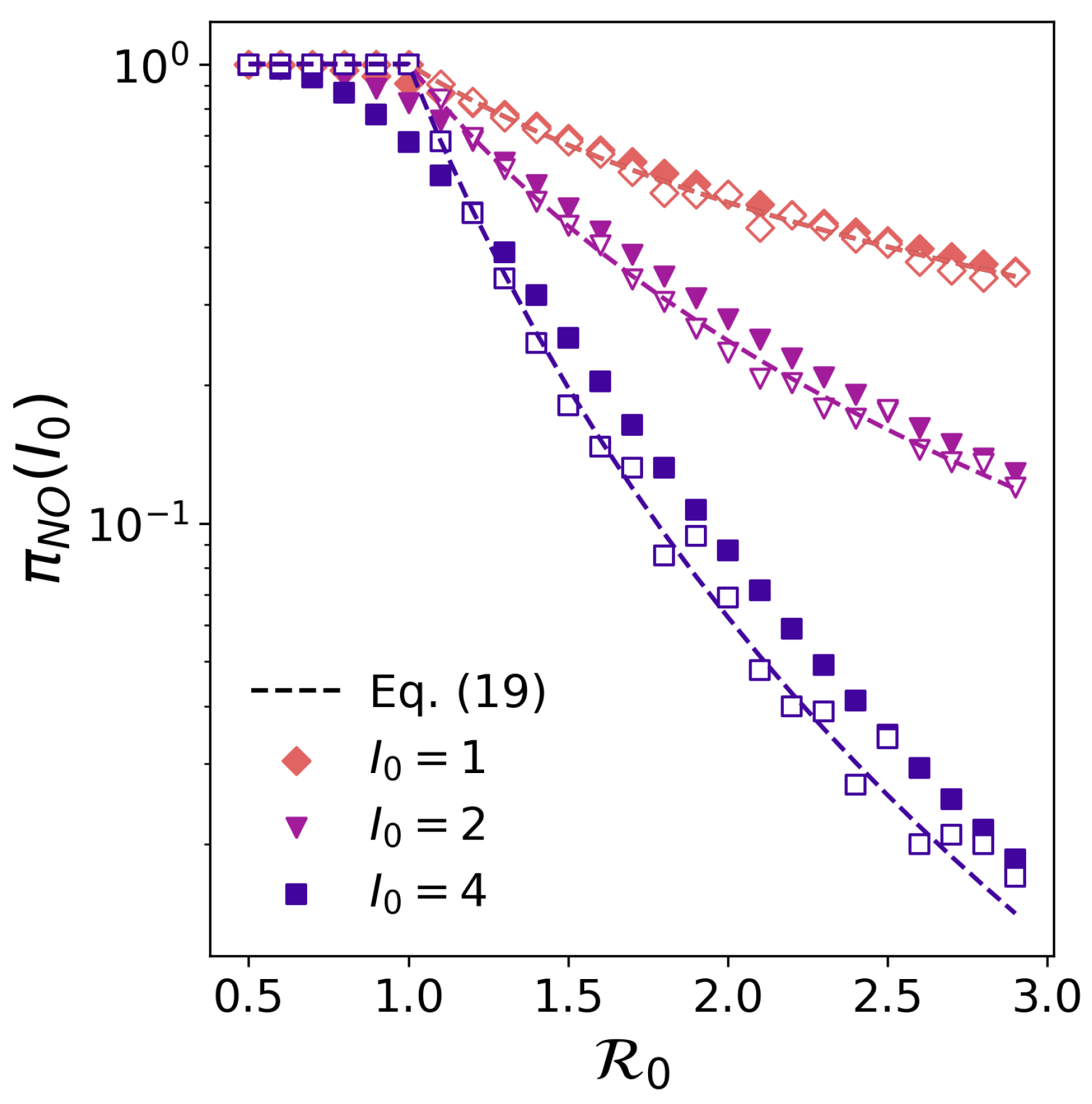
3.2. The Probability of No-Outbreak in the Doi–Peliti Formalism
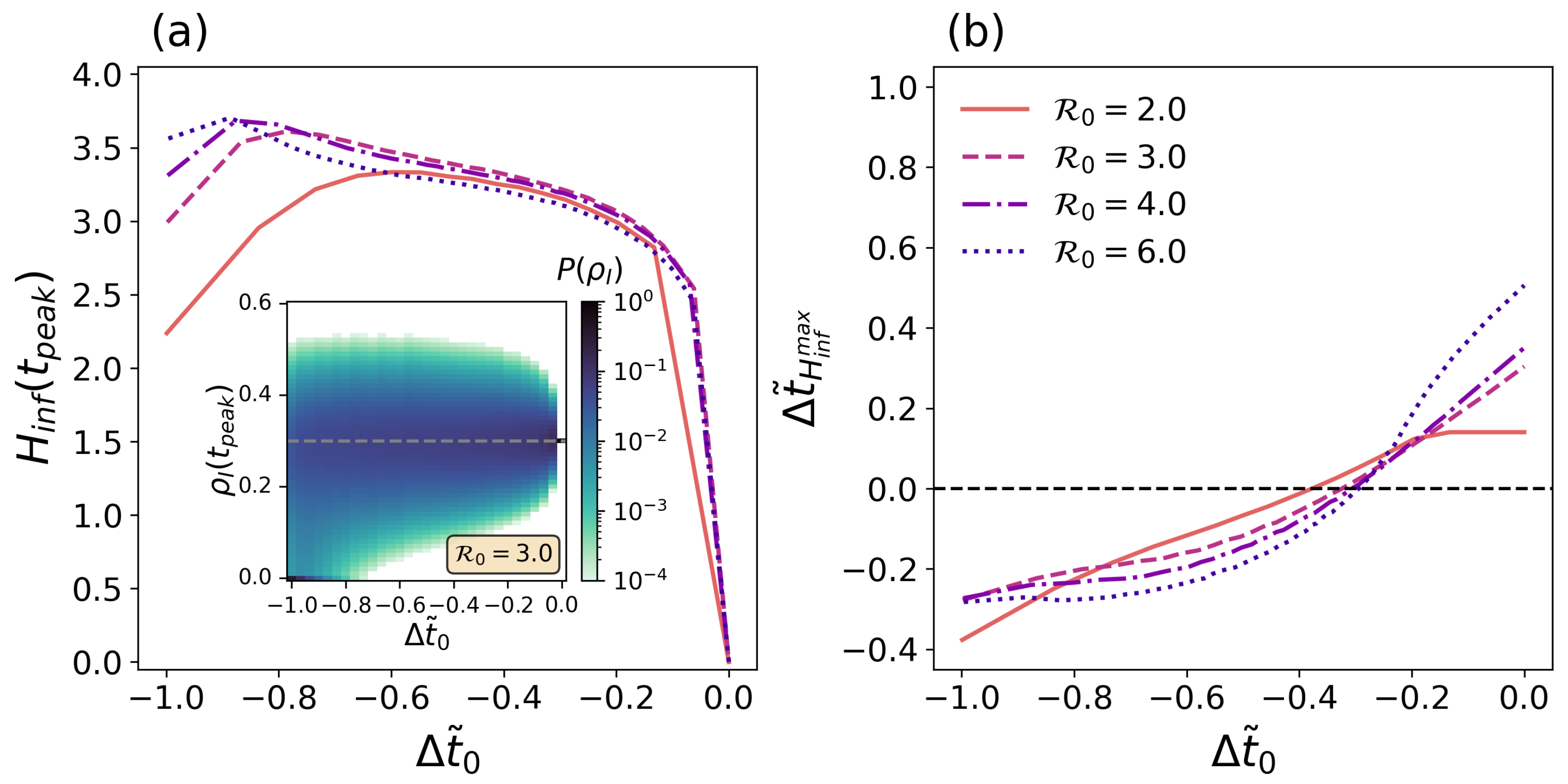
3.3. The Predictability Problem of the SIR Model
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morris, D.H.; Rossine, F.W.; Plotkin, J.B.; Levin, S.A. Optimal, near-optimal, and robust epidemic control. Commun. Phys. 2021, 4, 78. [Google Scholar] [CrossRef]
- Castioni, P.; Gòmez, S.; Granell, C.; Arenas, A. Rebound in epidemic control: How misaligned vaccination timing amplifies infection peaks. arXiv 2024, arXiv:2405.17189. [Google Scholar]
- Kermack, W.; Mckendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.; Metz, J. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef]
- Desai, A.N.; Kraemer, M.U.; Bhatia, S.; Cori, A.; Nouvellet, P.; Herringer, M.; Cohn, E.L.; Carrion, M.; Brownstein, J.S.; Madoff, L.C.; et al. Real-time epidemic forecasting: Challenges and opportunities. Health Secur. 2019, 17, 268–275. [Google Scholar] [CrossRef]
- Moran, K.R.; Fairchild, G.; Generous, N.; Hickmann, K.; Osthus, D.; Priedhorsky, R.; Hyman, J.; Valle, S.Y.D. Epidemic Forecasting is Messier Than Weather Forecasting: The Role of Human Behavior and Internet Data Streams in Epidemic Forecast. J. Infect. Dis. 2016, 214, S404–S408. [Google Scholar] [CrossRef]
- Krapivsky, P.; Redner, S. Epidemic forecast follies. npj Complex. 2024, 1, 7. [Google Scholar] [CrossRef]
- Penn, M.J.; Laydon, D.J.; Penn, J.; Whittaker, C.; Morgenstern, C.; Ratmann, O.; Mishra, S.; Pakkanen, M.S.; Donnelly, C.A.; Bhatt, S. Intrinsic randomness in epidemic modelling beyond statistical uncertainty. Commun. Phys. 2023, 6, 146. [Google Scholar] [CrossRef]
- Colizza, V.; Barrat, A.; Barthélemy, M.; Vespignani, A. Predictability and epidemic pathways in global outbreaks of infectious diseases: The SARS case study. BMC Med. 2007, 5, 34. [Google Scholar] [CrossRef]
- Datilo, P.M.; Ismail, Z.; Dare, J. A review of epidemic forecasting using artificial neural networks. Epidemiol. Health Syst. J. 2019, 6, 132–143. [Google Scholar]
- Scarpino, S.V.; Petri, G. On the predictability of infectious disease outbreaks. Nat. Commun. 2019, 10, 898. [Google Scholar] [CrossRef] [PubMed]
- Bavel, J.J.V.; Baicker, K.; Boggio, P.S.; Capraro, V.; Cichocka, A.; Cikara, M.; Crockett, M.J.; Crum, A.J.; Douglas, K.M.; Druckman, J.N.; et al. Using social and behavioural science to support COVID-19 pandemic response. Nat. Hum. Behav. 2020, 4, 460–471. [Google Scholar] [CrossRef] [PubMed]
- Markov, P.V.; Ghafari, M.; Beer, M.; Lythgoe, K.; Simmonds, P.; Stilianakis, N.I.; Katzourakis, A. The evolution of SARS-CoV-2. Nat. Rev. Microbiol. 2023, 21, 361–379. [Google Scholar] [CrossRef] [PubMed]
- Shea, K.; Borchering, R.K.; Probert, W.J.; Howerton, E.; Bogich, T.L.; Li, S.L.; van Panhuis, W.G.; Viboud, C.; Aguás, R.; Belov, A.A.; et al. Multiple models for outbreak decision support in the face of uncertainty. Proc. Natl. Acad. Sci. USA 2023, 120, e2207537120. [Google Scholar] [CrossRef]
- Sherratt, K.; Gruson, H.; Johnson, H.; Niehus, R.; Prasse, B.; Sandmann, F.; Deuschel, J.; Wolffram, D.; Abbott, S.; Ullrich, A.; et al. Predictive performance of multi-model ensemble forecasts of COVID-19 across European nations. eLife 2023, 12, e81916. [Google Scholar] [CrossRef]
- Gallo, L.; Frasca, M.; Latora, V.; Russo, G. Lack of practical identifiability may hamper reliable predictions in COVID-19 epidemic models. Sci. Adv. 2022, 8, 5234. [Google Scholar] [CrossRef]
- Gutenkunst, R.N.; Waterfall, J.J.; Casey, F.P.; Brown, K.S.; Myers, C.R.; Sethna, J.P. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 2007, 3, e189. [Google Scholar] [CrossRef]
- Melikechi, O.; Young, A.L.; Tang, T.; Bowman, T.; Dunson, D.; Johndrow, J. Limits of epidemic prediction using SIR models. J. Math. Biol. 2022, 85. [Google Scholar] [CrossRef]
- Case, B.K.; Young, J.G.; Hébert-Dufresne, L. Accurately summarizing an outbreak using epidemiological models takes time. R. Soc. Open Sci. 2023, 10, 230634. [Google Scholar] [CrossRef]
- Castro, M.; Ares, S.; Cuesta, J.A.; Manrubia, S. The turning point and end of an expanding epidemic cannot be precisely forecast. Proc. Natl. Acad. Sci. USA 2020, 117, 26190–26196. [Google Scholar] [CrossRef]
- Greenwood, P.E.; Gordillo, L.F. Stochastic Epidemic Modeling. In Mathematical and Statistical Estimation Approaches in Epidemiology; Springer: Dordrecht, The Netherlands, 2009; pp. 31–52. [Google Scholar] [CrossRef]
- Allen, L.J. A primer on stochastic epidemic models: Formulation, numerical simulation, and analysis. Infect. Dis. Model. 2017, 2, 128–142. [Google Scholar] [CrossRef] [PubMed]
- Champredon, D.; Li, M.; Bolker, B.M.; Dushoff, J. Two approaches to forecast Ebola synthetic epidemics. Epidemics 2018, 22, 36–42. [Google Scholar] [CrossRef] [PubMed]
- Artalejo, J.R.; Economou, A.; Lopez-Herrero, M.J. Stochastic epidemic models revisited: Analysis of some continuous performance measures. J. Biol. Dyn. 2012, 6, 189–211. [Google Scholar] [CrossRef] [PubMed]
- Artalejo, J.; Economou, A.; Lopez-Herrero, M. The stochastic SEIR model before extinction: Computational approaches. Appl. Math. Comput. 2015, 265, 1026–1043. [Google Scholar] [CrossRef]
- Papageorgiou, V.E.; Tsaklidis, G. A stochastic SIRD model with imperfect immunity for the evaluation of epidemics. Appl. Math. Model. 2023, 124, 768–790. [Google Scholar] [CrossRef]
- Papageorgiou, V.E. Novel stochastic descriptors of a Markovian SIRD model for the assessment of the severity behind epidemic outbreaks. J. Frankl. Inst. 2024, 361, 107022. [Google Scholar] [CrossRef]
- Papageorgiou, V.E.; Tsaklidis, G. An improved epidemiological-unscented Kalman filter (hybrid SEIHCRDV-UKF) model for the prediction of COVID-19. Application on real-time data. Chaos Solitons Fractals 2023, 166, 112914. [Google Scholar] [CrossRef]
- Sebbagh, A.; Kechida, S. EKF-SIRD model algorithm for predicting the coronavirus (COVID-19) spreading dynamics. Sci. Rep. 2022, 12, 13415. [Google Scholar] [CrossRef]
- Nakamura, G.M.; Martinez, A.S. Hamiltonian dynamics of the SIS epidemic model with stochastic fluctuations. Sci. Rep. 2019, 9, 15841. [Google Scholar] [CrossRef]
- Merbis, W.; Domenico, M.D. Emergent information dynamics in many-body interconnected systems. Phys. Rev. E 2023, 108, 014312. [Google Scholar] [CrossRef]
- Merbis, W.; de Domenico, M. Complex information dynamics of epidemic spreading in low-dimensional networks. arXiv 2023, arXiv:2305.05429. [Google Scholar]
- Visco, G.V.; Artime, O.; Nauta, J.; Scagliarini, T.; Domenico, M.D. Effective one-dimension reduction of multi-compartment complex systems dynamics. arXiv 2024, arXiv:2404.11366. [Google Scholar]
- Doi, M. Second quantization representation for classical many-particle system. J. Phys. A Math. Gen. 1976, 9, 1465. [Google Scholar] [CrossRef]
- Peliti, L. Path integral approach to birth-death processes on a lattice. J. Phys. 1985, 46, 1469–1483. [Google Scholar] [CrossRef]
- Dodd, P.J.; Ferguson, N.M. A many-body field theory approach to stochastic models in population biology. PLoS ONE 2009, 4, e6855. [Google Scholar] [CrossRef][Green Version]
- Dirac, P.A.M. The Principles of Quantum Mechanics; Clarendon Press: Oxford, UK, 1930. [Google Scholar]
- Whittle, P. The outcome of a stochastic epidemic—A note on Bailey’s paper. Biometrika 1955, 42, 116–122. [Google Scholar] [CrossRef]
- House, T.; Ross, J.V.; Sirl, D. How big is an outbreak likely to be? Methods for epidemic final-size calculation. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20120436. [Google Scholar] [CrossRef]
- Arenas, A.; Gómez-Gardeñes, J.; Granell, C.; Soriano-Paños, D. Epidemic spreading: Tailored models for COVID-19. Europhys. News 2020, 51, 38–40. [Google Scholar] [CrossRef]
- Tolles, J.; Luong, T. Modeling epidemics with compartmental models. JAMA 2020, 323, 2515–2516. [Google Scholar] [CrossRef]
- Myasnikova, E.; Spirov, A. Relative sensitivity analysis of the predictive properties of sloppy models. J. Bioinform. Comput. Biol. 2018, 16, 1840008. [Google Scholar] [CrossRef]
- Rosenkrantz, D.J.; Vullikanti, A.; Ravi, S.; Stearns, R.E.; Levin, S.; Poor, H.V.; Marathe, M.V. Fundamental limitations on efficiently forecasting certain epidemic measures in network models. Proc. Natl. Acad. Sci. USA 2022, 119, e2109228119. [Google Scholar] [CrossRef] [PubMed]
- Sudhakar, T.; Bhansali, A.; Walkington, J.; Puelz, D. The disutility of compartmental model forecasts during the COVID-19 pandemic. Front. Epidemiol. 2024, 4, 1389617. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E. COVID-19 and SARS-CoV-2. Modeling the present, looking at the future. Phys. Rep. 2020, 869, 1–51. [Google Scholar] [CrossRef] [PubMed]
- Cota, W.; Ferreira, S.C.; Ódor, G. Griffiths effects of the susceptible-infected-susceptible epidemic model on random power-law networks. Phys. Rev. E 2016, 93, 032322. [Google Scholar] [CrossRef]
- Cota, W.; Ódor, G.; Ferreira, S.C. Griffiths phases in infinite-dimensional, non-hierarchical modular networks. Sci. Rep. 2018, 8, 9144. [Google Scholar] [CrossRef]
- Balcan, D.; Vespignani, A. Invasion threshold in structured populations with recurrent mobility patterns. J. Theor. Biol. 2012, 293, 87–100. [Google Scholar] [CrossRef][Green Version]
- Colizza, V.; Vespignani, A. Invasion threshold in heterogeneous metapopulation networks. Phys. Rev. Lett. 2007, 99, 148701. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rojas-Venegas, J.A.; Gallarta-Sáenz, P.; Hurtado, R.G.; Gómez-Gardeñes, J.; Soriano-Paños, D. Quantum-Like Approaches Unveil the Intrinsic Limits of Predictability in Compartmental Models. Entropy 2024, 26, 888. https://doi.org/10.3390/e26100888
Rojas-Venegas JA, Gallarta-Sáenz P, Hurtado RG, Gómez-Gardeñes J, Soriano-Paños D. Quantum-Like Approaches Unveil the Intrinsic Limits of Predictability in Compartmental Models. Entropy. 2024; 26(10):888. https://doi.org/10.3390/e26100888
Chicago/Turabian StyleRojas-Venegas, José Alejandro, Pablo Gallarta-Sáenz, Rafael G. Hurtado, Jesús Gómez-Gardeñes, and David Soriano-Paños. 2024. "Quantum-Like Approaches Unveil the Intrinsic Limits of Predictability in Compartmental Models" Entropy 26, no. 10: 888. https://doi.org/10.3390/e26100888
APA StyleRojas-Venegas, J. A., Gallarta-Sáenz, P., Hurtado, R. G., Gómez-Gardeñes, J., & Soriano-Paños, D. (2024). Quantum-Like Approaches Unveil the Intrinsic Limits of Predictability in Compartmental Models. Entropy, 26(10), 888. https://doi.org/10.3390/e26100888





